1 Introduction

Optimization is defined as the selection of the best feasible solution from a set of available alternatives based on solution objectives and some constraints (Deb 2001). Optimization problems are categorized into two types based on the number of objectives: single objective and multi-objective optimization. Single objective optimization is concerned with solving a single objective function and with finding the best solution. This type of optimization provides a decision making tool that gives insights into the nature of the problem, although it cannot handle multiple objectives. The second type is multi-objective optimization, which is concerned with solving multiple conflicting objectives simultaneously (Ehrgott 2005), (Miettinen 1999). Many real-world problems are considered as multi-objective problems because of their nature where two or more conflicting objectives need to be simultaneously optimized (Fogel 1999; Goldberg 1989; Ahn 2006; Sivanandam and Deepa 2008; Rechenberg 1965; Knowles and Corne 1999). In economics, most of the problems involve a process of optimizing multiple conflicting objectives (e.g. consumer’s demands for various goods). In finance, the well-known portfolio problem provides a challenge to minimize the risk and maximize the return simultaneously. In the medical field, micro data classifications especially for cancer datasets need to reduce the number of misclassifications in both testing and learning datasets and extract the appropriate features that have many conflicts (Hamdi-Cherif and Kara-Mohammed 2011). Other applications like electronic chip design formulates the design tradeoffs such as processing time, power consumption and architecture cost as multi-objective problem (Erbas et al. 2006).

Most of the evolutionary algorithms are used for single objective problems (SOPs). When dealing with such problems, one criterion is used to compare all the solutions because there is only one objective. Mathematically, the solutions of a single objective problem are composed of a set of ordered solutions. The selection of the best solution for this type of optimization is given as the minimum or maximum solution, which is related to the nature of the problem. Existing optimization techniques use an evolutionary process that consists of several steps: reproduction, mutation, recombination and selection to guide the search towards optimal solutions. If a problem has multiple objectives that are not conflicting with each other then they can be unified into a single objective and hence form a single objective problem (Michalewicz 1994). Otherwise, if the objectives are conflicting then the problem is called a multi-objective problem (MOP).

Multi-Objective Evolutionary Algorithms (MOEAs) were introduced in 1985 which involve decision making criteria with evolutionary algorithms to find solutions called pareto-optimal solutions for multiple conflicting objectives (Schaffer 1985). Such problems pose a challenge for researchers in providing efficient algorithms that are capable of helping decision makers. The main goal when solving such type of problems is to avoid the problem of premature convergence and stagnation scenario to produce good pareto optimal solutions. Pointing at the developed techniques, we can refer to: Pareto Archived Evolutionary Strategy (PAES) (Knowles and Corne 2000), Strength Pareto Evolutionary Algorithm (SPEA) (Zitzler et al. 2001) and Non-dominated Sorting Genetic Algorithm (NSGA) (Deb et al. 2002).

DE has been successfully extended to solve multi-objective optimization problems. In Babu et al. (2003), a differential evolution with penalty function and a weighing factor method is used to find pareto-optimum sets for an engineering application of a cantilever design problem. In Iorio and Li (2004), a DE approach has been proposed based on correlated self-adapting mutation step sizes to solve rotated multi-objective problems. In Kukkonen and Lampinen (2004), a generalized DE technique that uses a crowdedness mechanism for maintaining good non-dominated solutions is proposed for constrained multi-objective problems. A new paradigm of self-adaptive differential evolution for multi-objective optimization has been introduced in Huang et al. (2009). Furthermore, the hybrid DE approaches have been introduced in, which other evolutionary algorithms or kinds of local search have been merged with DE. In Santana-Quintero et al. (2010) the DEMORS technique, which is a hybrid multi-objective optimization algorithm using differential evolution and a local search based on a rough set theory, has been introduced to solve constrained problems. Another hybridization that combines a self-adaptive DE with a local search method based on sequential quadratic programming can be found in Zamuda et al. (2009).

In this paper, we introduce a differential evolution algorithm with an improved mutation strategy and summation of normalized objectives method. The proposed algorithm uses the differential evolution algorithm, because it is a simple and powerful technique to solve diverse type of problems with stochastic direct search and because of its simplicity. The proposed algorithm is the first to use one of the greedy strategies of differential evolution algorithm in multi-objective optimization. The conflicting objectives state a challenge to choose one of the objectives in a reasonable time. A modified mutation strategy has been proposed, which is able to benefit from all the best knowledge of the best objective-wise solutions. The best objective-wise solution is the solution, which has the best value for one of the objectives. The new mutation strategy, namely “DE/rand-to-nbest”, uses the best normalized individual in terms of all the objectives to guide the search in each optimization step. An external archive is used to store the non-dominated solutions in each generation. The summation of normalized objective value has been used for non-domination sorting to select the well-distributed solutions. This method aims at developing a new sorting method capable of solving the issues that other algorithms have such as computational overhead. The results prove the effectiveness of selecting non-dominated solutions that approximate the true pareto front. The following sections delineate the proposed technique in detail and analyze its structure. Section 2 introduces a review of various multi-objective differential evolution algorithms. Section 3 gives some preliminaries for multi-objective optimization and differential evolution algorithm. Section 4 presents the proposed algorithm in detail. Section 5 presents experimental results. Section 6 draws conclusions of this work.

2 Related work

Differential evolution was proposed by Storn and Price (1997) as a metaheuristic evolutionary algorithm that was designed to solve optimization problems over continuous spaces. Different types of mutation and crossover strategies were proposed for DE (Price et al. 2005; Brest et al. 2006; Das et al. 2009). The individuals are represented as chromosomes and each decision parameter is encoded by a real value. The initial population space is generated and then evaluated based on an objective function. After that, the selection process, which usually uses three random parents to generate a new child takes place. The difference vector between two parents is computed and added to the third one. For single objective optimization, if the value of the objective function using the newly obtained solution is better than its parent, the child replaces its parent. While in the context of multi-objective optimization, the domination concepts are used to compare both individuals. DE is considered as an effective global optimizer and a robust technique for producing the optimal for many optimization problems and real world applications (Joshi and Sanderson 1999; Zhang et al. 2008).

The classical DE performance is highly dependent on the choice of the mutation strategy and the associated control parameter values for the scaling factor (F), crossover rate (CR) and population size (NP). Any inappropriate use of those control parameters or mutation strategy may lead to premature convergence (Zhang et al. 2009; Gamperle et al. 2002). The early work introduced by Storn and Price (1997) suggested a reasonable value of NP should be between 5D and 10D where D is the problem dimensions and 0.5, 0.1 were the initial values of F and CR, respectively. Recent works suggested different values for NP, F and CR based on results from experimental studies (Swagatam et al. 2016). These values are fine-tuned according to the tested benchmark problems to help avoiding premature convergence. From such studies, Swagatam et al. concluded that if the population reaches a stagnation state, either F or NP can be increased or the value of CR can be decreased.

Many multi-objective differential evolution algorithms have been successfully introduced to solve multi-objective problems. In Abbass (2002) a self-adaptive pareto DE (SPDA) algorithm has been introduced. In each iteration, a new population space is generated using basic mutation and crossover operations except that a self-adaptive normal distribution is used. In Babu et al. (2003), a new differential evolution technique for MOPs was proposed that uses a penalty function method, and a weighting factor method to find the Pareto optimum set for an engineering application of cantilever design problem. In Iorio and Li (2004), a new DE approach has been proposed based on correlated self-adapting mutation step sizes to solve rotated multi-objective problems. Another approach based on pareto evaluation is applied to optimize the cycle time and cost objectives for an enterprise planning problem (Xue 2003). In Madavan (2002), the elitism, ranking and non-dominated sorting incorporated in NSGA-II Deb et al. (2002) have also been used in differential evolution method. Kukkonen and Lampinen (2004) proposed a generalized DE technique that used a crowdedness mechanism for maintaining the good non-dominated solutions for constrained multi-objective problems. Many other approaches can be found in Mezura-Montes et al. (2008) and Parsopoulos et al. (2004). A new paradigm of self-adaptive differential evolution for multi-objective optimization has been introduced (Huang et al. 2007). The SaDE algorithm (Brest et al. 2006) was extended to MOSaDE by introducing the domination concept when comparing trial and target vectors. A modified version of the aforementioned technique has been introduced in which their proposed DE technique learns its suitable strategy and associated parameters for each objective separately (Huang et al. 2009).

Hybrid DE approaches have been introduced in which other evolutionary algorithms or local searches were merged with DE. In Santana-Quintero et al. (2010) the DEMORS technique, as a multi-objective optimization algorithm that hybridizes differential evolution and local search based on a rough set theory has been introduced for solving constrained multi-objective optimization problems. In their approach there are two main steps, the first step is to use a multi-objective DE technique to generate an initial solution of the pareto front. The second one is a local search technique of a rough set theory to find out more solutions and guide the search towards better solutions. Another hybridization that combines a self-adaptive DE with a local search method based on sequential quadratic programming can be found in Zamuda et al. (2009). An enhanced version of DE algorithm has been merged with simulated annealing algorithm (Chen et al. 2014). In this algorithm, a new acceptance function based on a probability computation is used to utilize simulated annealing for better guiding the search towards better regions. Another technique that aims at reducing the complexity of multi-objective differential evolution by computing the domination ranks and crowding distance is presented in Drozdik (2014). A memetic search that used probabilistic solution principles in the differential evolution algorithm is introduced in Kumar et al. (2014). An advanced teaching–learning technique has been merged with a modified differential evolution algorithm for solving the reactive power dispatch problem as can be found in Ghasemi et al. (2014). The fuzzy clustering problem has been solved using a multi-objective differential evolution algorithm (Das 2014).

The summation of normalized objective value (SNOV) method was used in this context by the multi-objective evolutionary algorithms. In Patel et al. (2011), an improved selection scheme using the SNOV method is used with genetic algorithm. In this algorithm, the SNOV method is used as an improved ranking scheme to select the parents for mutation in genetic algorithm. The summation of normalized objective value is also used in the differential evolution algorithm. In Qu and Suganthan (2010), the authors replace the non-domination sorting by the use of SNOV and a diversified selection. The solutions are sorted according to a normalized rank that represents the summation of all the individual objectives ranks.

Recently, a modified differential evolution algorithm for multi-objective reactive power (VAR) is introduced (Singh and Srivastava 2014). The aim of this work is to formulate VAR as a multi-objective problem and to use a modified differential evolution algorithm to address the problem of minimizing the real power losses and voltage deviation, simultaneously. The algorithm used a time varying chaotic mutation and crossover to avoid time and effort in tuning DE parameters. A modified differential evolution algorithm for multi-objective optimization is also introduced (Ali et al. 2012). This algorithm uses the concept of random localization in mutation and also a new selection mechanism for generating pareto optimal front. A multi-objective differential evolution algorithm is also proposed in feature selection of classification tasks (Xue et al. 2014). The aim of this work is to minimize the classification error and the number of features at the same time. A differential evolution algorithm for solving multi-label feature selection is also introduced in Zhang et al. (2015). The differential evolution algorithm is also used to solve tunable multi-objective engineering problems (Adeyemo and Olofintoye 2014). In this algorithm, the multi-objective differential evolution and pareto selection methods are used to introduce a new selection scheme. An enhanced differential evolution algorithm is hybridized with simulated annealing for solving multi-objective optimization problems (Chen et al. 2014). Another application that uses a two-phase differential evolution algorithm for solving time–cost trade-offs in resource constrained construction projects is also introduced in Cheng and Tran (2014). More recently, a modified differential evolution algorithm that uses a new diversity maintenance strategy is introduced (Chen et al. 2015). In this algorithm, a new cluster degree measure is used to determine a better spread of non-dominated solutions. An enhanced version of differential evolution algorithm that uses an archive-base mutation is also proposed to provide new direction information toward true pareto front by utilizing useful inferior solutions (Fan and Yan 2015).

3 Scientific background

3.1 Basic concepts of multi-objective optimization

Multi-objective optimization problems consist of several incommensurable and conflicting objectives that need to be optimized simultaneously. They are usually expressed as follows:

$$\begin{aligned} & {\text{Min}}/{\text{Max}}\quad f(x): = \left\{ {f_{1} (x),\,f_{2} (x), \ldots ,\;f_{k} (x)} \right\}, \\ & {\text{Subject}}\,{\text{to}}:\quad g_{a} (x) \le 0\quad a = 1,2, \ldots ,n \\ & \quad \quad \quad \quad \quad \,h_{b} (x) = \;0\;\;\;b = 1,2, \ldots ,p \\ \end{aligned}$$
(1)

where \(x = (x_{1} ,x_{2} , \ldots ,x_{n} )^{T}\) is the decision variables vector such that \(f_{i} :\Re^{n} \to \Re\), \(i = 1, \ldots ,m\) is the objective function, \(k\) is the number of objective functions, \(g_{a} ,h_{b} :\Re^{n} \to \Re ,\;a = 1, \ldots ,n,\;b = 1, \ldots ,p\) are the constraint functions of the problem.

The domination concept is used to relate the association between the two solutions \(x,y\) according to the following definitions:

Definition 1

We say \(x\) dominates \(y\) (denoted by \(x \prec_{1 \ldots k} y\)) if both conditions below are met:

  1. 1.

    \(x\) is not worse than \(y\) in all objectives \(i = 1, \ldots ,k\) and

  2. 2.

    \(x\) is strictly better than \(y\) in at least one objective.

$$x \prec_{1 \ldots k} y\,\,iff\,\left\{ {\;f_{i} (x) \le f_{i} (y),\,\,\,\forall i \in 1, \ldots ,k\;\; \wedge \;\exists j \in 1, \ldots ,k\,\, \Rightarrow \,\,\,f_{j} (x) < f_{j} (y)} \right.\left. {} \right\}$$
(2)

Definition 2

The solution \(\bar{x}\) is said to be a non-dominated or Pareto-optimal solution if it is not possible to find another \(\hat{x} \in \chi\) such that \(\hat{x} \prec x\) where \(\chi\) is the set of non-dominated solutions.

Definition 3

The set of pareto-optimal solutions is called Pareto Front \(\rho F^{*}\) which is defined by:

$$\rho F^{*} = \left\{ {f_{1} (x) \cdots f_{m} (x) \in \Re^{m} |x \in \rho^{*} } \right\}$$
(3)

where \(\rho^{*}\) is the pareto optimal set which corresponds to decision variable vectors for the pareto-optimal solutions that can be expressed as:

$$\rho^{*} = \left\{ {x \in \chi |x\,is\;Pareto - optimal} \right\}$$
(4)

3.2 Classical differential evolution

The differential evolution algorithm is one of the most promising population-based evolutionary algorithms because of its simplicity with powerful stochastic direct search technique. The algorithm consists of several steps as shown in the following sub-sections.

3.2.1 Initialization step

The standard DE consists of a population of NP individuals. Each individual is represented as a vector of D-dimensional parameters as follows:

$$X_{i,G} = \left\{ {x_{i,G}^{1} , \ldots ,x_{i,G}^{D} } \right\},\quad i = 1, \ldots ,NP$$
(5)

where G is the generation number and NP is the number of individuals in the population space. The DE algorithm aims at evolving the population space towards the global optima distributing random individuals within the search space and preserving the lower and upper bounds of parameters for the problem being solved represented by \(X_{\hbox{min} } = \left\{ {x_{\hbox{min} }^{1} , \ldots ,x_{\hbox{min} }^{D} } \right\}\) and \(X_{\hbox{max} } = \left\{ {x_{\hbox{max} }^{1} , \ldots ,x_{\hbox{max} }^{D} } \right\}\), receptively. Hence, the initialization of the population space at generation G = 0 is formulated in the following equation:

$$x_{i,0}^{j} = x_{\hbox{min} }^{j} + rand(0,1) \cdot (x_{\hbox{max} }^{j} - x_{\hbox{min} }^{j} )\quad j = 1,2, \ldots ,D$$
(6)

where j is the index of parameter value in the \(i^{th}\) individual at generation G = 0, and \(rand(0,1)\) is a uniformly distributed random generator in the range [0,1].

3.2.2 Mutation operation

Five mutation strategies were suggested for the original DE (Price et al. 2005) as described below:

$$\begin{aligned} &DE/rand/1:\;v_{i}^{{}} (t)\, = \,x_{{r_{1} }}^{{}} (t) + F \cdot \left( {x_{{r_{2} }}^{{}} (t) - x_{{r_{3} }}^{{}} (t)} \right) \hfill \\& DE/best/1:\;v_{i}^{{}} (t)\, = \,x_{best}^{{}} (t) + F \cdot \left( {x_{{r_{1} }}^{{}} (t) - x_{{r_{2} }}^{{}} (t)} \right) \hfill \\& DE/current{\text{-}}to{\text{-}}best/1:\;v_{i}^{{}} (t)\, = \,x_{i}^{{}} (t) + F \cdot \left( {x_{best}^{{}} (t) - x_{i}^{{}} (t) + x_{{r_{1} }}^{{}} (t) - x_{{r_{2} }}^{{}} (t)} \right) \hfill \\ & DE/best/2:\;v_{i}^{{}} (t)\, = \,x_{best}^{{}} (t) + F \cdot \left( {x_{{r_{1} }}^{{}} (t) - x_{{r_{2} }}^{{}} (t) + x_{{r_{3} }}^{{}} (t) - x_{{r_{4} }}^{{}} (t)} \right) \hfill \\ & DE/rand/2:\;v_{i}^{{}} (t)\, = \,x_{{r_{1} }}^{{}} (t) + F \cdot \left( {x_{{r_{2} }}^{{}} (t) - x_{{r_{3} }}^{{}} (t) + x_{{r_{4} }}^{{}} (t) - x_{{r_{5} }}^{{}} (t)} \right) \hfill \\ \end{aligned}$$
(7)

The \(V_{i,G} = \{ v_{i,G}^{1} ,v_{i,G}^{2} , \ldots ,v_{i,G}^{D} \}\) is the mutant vector, which is generated for each individual \(X_{i,G}\) in the population space.\(r_{1}^{i} ,r_{2}^{i} ,r_{3}^{i} ,r_{4}^{i} ,r_{5}^{i}\) are random integer numbers. These numbers represent the indices of chosen individuals within the range [1, NP]. These numbers and the super index i should be mutually exclusive integers. F is the mutation control parameter (scaling factor) and assumes positive values for controlling the scaling ratio of the difference vector. The best individual vector of lowest fitness value in the current population space at generation G is denoted as \(X_{best,G} .\)

After the initialization step, the mutation phase starts in which each individual \(X_{i,G}\) in the population space is mutated according to one of the abovementioned strategies to generate a mutant vector \(V_{i,G}\). The scaling factor F controls the speed and convergence of the search space in which the lower values exploit the search towards the local optima and the larger values explore the search towards the global optimum solution.

3.2.3 Crossover operation

After mutant vectors have been generated, the crossover phase is applied to generate new offspring or trial vector \(U_{i,G} = \{ u_{i,G}^{1} ,u_{i,G}^{2} , \ldots ,u_{i,G}^{D} \}\). The original DE has defined a binomial crossover as follows (Storn and Price 1997):

$$u_{i,G}^{j} = \left\{ \begin{array} {ll}v_{i,G}^{j} ,&\quad if\,(with\;probability\;of\;CR)\;or\,(j = j_{rand} ) \hfill \\ x_{i,G}^{j} ,&\quad otherwise \hfill \\ \end{array} \right\}\; j = 1,2, \ldots ,D$$
(8)

CR is the crossover rate, which is a user-defined value within the range [0,1] to control the percentage of parameter values of mutant vectors that should be copied to form a new child solution.\(j_{rand}\) is a random index of a position in the mutant vector within the range 1…D.

3.2.4 Selection operation

To ensure that the new trial vectors are within upper and lower bounds, DE must check parameter values of its trial vectors and when they exceed the search range, their values will be reinitialized. After that, the fitness values of trial vectors are calculated by computing the objective function of the problem being solved. Then, a selection criterion is performed as in Eq. 9 to fill in the population space with new individuals for the next generation by comparing fitness values of target and trial vectors.

$$\begin{aligned} X_{i,G + 1} = \left\{ \begin{array}{ll} U_{i,G} , &\quad if\,f(U_{i,G} ) \le f(X_{i,G} ) \hfill \\ X_{i,G} ,& \quad otherwise \hfill \\ \end{array} \right\} \hfill \\ \hfill \\ \end{aligned}$$
(9)

The above DE steps including mutation, crossover and selection will be repeated until a termination criterion is met, which is usually after finishing a specified number of generations. When dealing with multi-objective optimization, the domination concepts are needed to compare the trial and target vectors as shown in the following sub-section.

4 Proposed algorithm

A new multi-objective differential evolution is explained in this section. The proposed algorithm introduces a new mutation “DE/rand-to-nbest” and uses the summation of normalized objective value (SNOV) method for selecting the best individual and non-dominated solutions. The following subsections explain the MOnDE algorithm in detail.

4.1 DE/rand-to-nbest

The most widely used strategy in differential evolution is DE/rand/1 that is said to be the most successful mutation strategy (Price et al. 2005). However, greedy strategies such as DE/best/k and DE/current-to-best provide some advantages by benefiting from the information of the best solution in the search process (Gamperle et al. 2002). In this paper, we introduce an improved greedy mutation suitable for multi-objective optimization namely DE/rand-to-nbest. The key difference between this new mutation and the original DE/rand-to-best is in the way of selecting the best individual. In single optimization, the selection of the best individual during the search is carried out according to the lowest fitness value. However, in multi-objective optimization the conflicting objectives pose a challenge for selecting the best individual. Using the crowding distance to determine the best individual in terms of all objectives at each generation is very time-consuming and imposes a high risk on the diversity of solutions, especially when the number of objectives is more than two (Kukkonen and Deb 2006). The DE/rand-to-nbest is proposed to overcome the problem of choosing the best individual in multi-objective optimization based on the summation of normalized objective value (SNOV) method. The SNOV assigns one normalized value for an individual to represent all the different objectives as being from different ranges and without normalization, the obtained distribution might distort. It starts by finding the minimum and maximum value of each objective from the current DE solutions. Then new normalized objective values are assigned to the individuals after adding all the computed values to form one value for each individual. Finally, the individual with the lowest normalized value is returned and is used as the best individual to guide the evolution process by benefiting from the information of all the objective values.

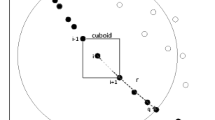
The mutant vector in “DE/rand-to-nbest’’ is generated as shown in Fig. 1. The selection of the best individual is chosen based on SNOV. This process is called in each time the mutant vector is generated. Using this approach, we guarantee that the best M objectives will be used in each generation to guide the search using the best solutions from all objectives. To ensure that the new trial vector \(v_{i}\) is within bounds, lines 3–6 check the values and when they exceed boundaries, their values are reinitialized.

Fig. 1
figure 1

DE/rand-to-nbest mutation based on summation of normalized objective value (SNOV)

Full size image

4.2 MOnDE algorithm

The mutation strategy and its control parameters are the dominant settings that reflect the DE performance. The literature studies suggested many ways to enhance the performance of the DE algorithm. The MOnDE algorithm aims at finding the most suitable way of incorporating all the different objectives of the problem being solved. The algorithm suggests a new mutation strategy to overcome the trade-off due to conflicting objectives and chooses the best solution that can guide the search toward pareto optimal solutions. Using the best solution in terms of one objective guides the search in only one direction for only one objective. This leads to an increase in the search speed for one objective without having any enhancement for others. To find a balanced way that aims at enhancing the search for all the objectives, the DE/rand-to-nbest is proposed. In each generation, this new mutation strategy is called after selecting the best normalized solution. This selection is done by computing the normalized rank for each objective of each solution in the population space then summing all these ranks to have one rank. After that, the solutions are sorted to find the best solution that has the lowest value.

It is known that choosing the non-dominated solutions is the key step for every MOO optimization algorithm, and is considered a time-consuming step. After testing the ability of normalization in selecting the best solution in each generation, a new method based on normalization is also used to select the best non-dominated solutions. After the termination criterion is met and the external archive is filled with the non-dominated solutions in each generation, this method is called. It starts by finding a normalization rank for each solution in the external archive by summing all the normalized values for each objective. Then all the solutions are sorted and the best non-dominated solutions with least values are selected. The number of selected solutions is determined by a pre-defined value and the used summation process keeps the archive domination-free.

The pseudo-code of MOnDE algorithm is presented in Fig. 2. It starts by initializing a population of random individuals and evaluates the initial values of objectives for the problem being solved. In each generation, the Summation of Normalized Objective Value (SNOV) method is called and takes the current population as an input to select the best normalized individual. The SNOV assigns one normalized value for each individual to represent all the objectives. This is because the different objectives might be in very different value ranges. Without normalization, the obtained distribution might be distorted. After that the “DE/rand-to-nbest” is used to generate the mutant vector for each individual using the best normalized individual that benefits from its fast convergence by incorporating information from the best solution for all the objectives in the evolutionary search. After evaluating the trial vector, it is compared with the corresponding target vector. If the new trial vector dominates the target vector, replacement occurs and the trial vector enters the external archive if it dominates some individuals in the archive or if it is non-dominated with all the archive solutions. The aforementioned steps are repeated until the maximum number of function evaluations is reached. Finally, the size of the external archive is adjusted to choose the best non-dominated solutions with the allowable size. To enhance the time complexity and quality of solutions that are considered some of the major shortcomings of other heuristics, which is crucial in the MOO area, we used the normalization sorting in which the solutions are sorted according to their normalized values that the SNOV method computed. Normalization sorting aims at discarding the worst individuals from being selected as the best individual to guide the evolutionary search and also use the best information from all the objectives to keep the search as diverse as possible.

Fig. 2
figure 2

Pseudo-code of MOnDE algorithm

Full size image

5 Experimental results

5.1 Experimental setup

To test the performance of the proposed algorithm, the CEC 2009 benchmark suite for multi-objective optimization (Zhang et al. 2009a, b) is used. This benchmark suite consists of 13 unconstrained multi-objective instances including 7 functions of two-objectives, 3 functions of 3 objectives and 3 functions of five objectives (Zhang et al. 2009a, b). The algorithm was coded using Java 1.7, and was run on a PC with 2.4 GHz Core processor and 8 GB RAM on windows 7. The experiments are performed with a maximum number of 300,000 function evaluations (FEs) and the sizes of the external archive are 100, 150 and 800 for problems with 2, 3 and 5 objectives, respectively. After extensive experiments and tuning the parameters, the control parameters of the proposed algorithm have been chosen. A sensitivity analysis for F, CR and NP is presented in Table 1. Four values are used to test each parameter. The best settings Based on experimentations for scaling factor (F) is 0.5, crossover rate (CR) is 0.01 and the size of population space (NP) is 200 for all the problems instances. 30 independent runs have been executed for each test problem using the proposed algorithm.

Table 1 Average IGD value for a sensitivity analysis for F, CR and NP for MOnDE
Full size table

5.2 Performance measure

In multi-objective optimization, a performance metric is needed to compare the performance of different algorithms from two points of view: (1) diversity and (2) convergence approximation set of obtained pareto-optimal solutions. The inverted generalized distance (IGD) (Zhang et al. 2009a, b) performance metric is used as shown in Eq. (10).

$$IGD(A,P^*) = \frac{{\sum\limits_{v \in P^*} {d(v,A)} }}{|P^*|}$$
(10)

where \(d(v,A)\) is the minimum Euclidean distance between true pareto front \(P^*\) and a set of solutions obtained by an algorithm \(A.\) Smaller IGD values are better for measuring the diversity and convergence of the algorithm.

5.3 Simulations results

The numerical results of the proposed algorithm MOnDE are presented in Table 2. The statistical measure of the IGD performance metric including best, worst, mean and standard deviation over 30 independent runs for all the test functions, are shown in Table 2. Note that most of these results have small values for the mean measure on all the functions F 1 –F 13 except for F 12 , however the mean value for this function, which equals to 8.03E+00, shows a superior result compared to other MOEAs as the following sub-sections show. Referring to this table, one can find that at 30D, the obtained mean values are of order 10−4 in 3 problems (F1, F2 and F4), 10−3 in 7 other problems (F3, F6–F11), 10−2 in 2 problems (F5 and F13) and greater than zero in one problem (F12). Referring to the best and worst values of each problem over 30 independent runs as shown in Table 2, the results reveal the stability of MOnsDE algorithm when generating the optimal pareto front solutions. Moreover, the algorithm was able to converge to the true pareto front very smoothly.

Table 2 The IGD value statistical results of the final approximation set obtained for each test problem for MOnDE algorithm at 30D
Full size table

The results in Table 2 reveal that MOnDE appears to provide high quality results when optimizing multi-objective problems that consist of 2–5 difficult conflicting objectives at the same time. Results assert the fact that the proposed method effectively solves the multi-objective benchmark problems that reflect complicated real-life problems. The IGD performance metric affirms that MOnDE was capable of finding a set of non-dominated solutions that approximate the true pareto front. The smaller mean values of IGD show high diversity and convergence of MOnDE algorithm that provide very competitive results to the best known results from other powerful MOEAs as the following sub-sections demonstrate.

5.4 Algorithm running time

The average running time for each multi-objective problem in the benchmark set for 30 independent runs per function is presented in Table 3. It is apparent from the table that the running time of the problems raises slightly as the number of objectives increases. The average running time for the problems of 2 objectives (F 1–F 7) does not have a big difference from those problems with 3 objectives (F 8–F 10). The average elapsed time for solving (F 1–F 7) is ranged between (0.06 and 0.086) min and (0.074 and 0.098) min for (F 8–F 10). The last three functions appear to require more time ranged from (0.15 to 4.41) min since they consist of 5 objectives that need to be optimized at the same time. However functions F 11 and F 12 are slightly different compared to other problems with 2 or 3 objectives but F 13 took an average of 4 min because of its complexity and difficult nature with new extended rotated features that reflect the real world applications (Huband et al. 2006).

Table 3 Average CPU time for each test problem over 30 independent runs for MOnDE algorithm
Full size table

5.4.1 Comparison with other MODE algorithms

In this section, the performance of MOnDE algorithm is compared with other algorithms from the literature. Comparisons with other MOEAs algorithms are presented. The chosen MODE algorithms are summarized as follows:

  1. 1.

    GDE3 (Kukkonen and Lampinen 2009): The third version of the generalized differential evolution. The authors proposed a new concept called constraint domination to compare solutions for constrained problems. The authors didn’t use an external archive for holding non-dominated solutions. Instead, they used a population space of size equals to the size of the approximation set. They also used a pruning technique in each generation if the size of the population space exceeds the allowable size since they added the target and trial individuals if they are non-dominated by each other. The F and CR were set to 0.5 and 0.0 respectively.

  2. 2.

    OWSaDE (Huang et al. 2009): An objective-wise self-adaptive differential evolution algorithm in which suitable mutation strategies and control parameters were learned for each objective. The authors used DE/rand/1 and DE/rand/2 with binomial crossover. The scaling factor F is generated using a normal distribution of a mean ranging from [1.0, 0.05] and a standard deviation of 0.1. The crossover rate CR is also generated using normal distribution of a mean changed dynamically based on the success during previous generations and a standard deviation of 0.1. The population size is set to 50 and for non-domination sorting they used harmonic average distance.

  3. 3.

    DECMOSA-SQP (Zamuda et al. 2009): A hybrid approach that combines Differential Evolution with Self-adaptation and sequential quadratic programming as local search. The authors assigned F and CR for each individual in the population and adapted their values in each generation using a Gaussian distribution between 0 and 1. The size of the population is set to the same size of the approximation set.

  4. 4.

    MO-ABC/DE (Rubio-Largo et al. 2012): A multi-objective artificial bee colony with differential evolution for unconstrained multi-objective optimization. In this hybrid approach, the collective intelligence of bee swarms and differential evolution properties are combined together to develop a new enhanced algorithm that is capable of solving multi-objective problems.

A comparison between MOnDE algorithm and the aforementioned MODE algorithms is presented in Table 4. The table shows the mean values of IGD performance metric over 30 independent runs. This comparison tests the validity and performance between our proposed algorithm and other variations of multi-objective differential evolution algorithms which follow in three categories. Generalized differential evolution with constant values for F and CR (GDE3), self-adaptive differential evolution (OWMOSaDE, DECMOSA-SQP and MOnDE) and hybrid differential evolution with local search (DECMOSA-SQP, MO-ABC/DE and MOnDE). The results show that MOnDE outperforms the three categories on all the benchmark functions. This affirms the effectiveness of using Cauchy and Normal distributions to adapt the F and CR values compared to the self-adaptive style used in OWMOSaDE and DECMOSA-SQP algorithms. Another perspective of comparison is the use of hybrid approaches. Our proposed technique outperforms other hybrid approaches that uses sequential quadratic programming in DECMOSA-SQP algorithm and artificial bee colony in MO-ABC/DE. The MOnDE algorithm showed its capability when optimizing problems of five objectives as shown in the last three functions compared with other MODE algorithms. Those functions are considered the most difficult problems in multi-objective benchmark problems in general because of their complex nature with 5 conflicting objectives that resemble sample complicated real-life applications. Hence it represents a good measure for studying the performance of any MOEA algorithm. It is clear that the proposed algorithm (MOnDE) was better than all other MODE algorithms in those functions with a big difference especially for F 12 which is a round E+02.

Table 4 Average IGD value for a comparison between MODE algorithms and MOnDE
Full size table
Table 5 Average IGD value for a comparison between MOEAs algorithms
Full size table

5.4.2 Comparison with other MOEAs algorithms

Other recent multi-objective evolutionary algorithms are also used for comparisons and they are briefly described as follows:

  1. 1.

    NSGAIILS (Sindhya et al. 2009): The last version of non-sorting GA, which is hybridized with an achievement scalarizing function (ASF) as a local search to approximate pareto front points only.

  2. 2.

    MOEA/D (Zhang et al. 2009a, b): Multi-Objective Evolutionary Algorithm based on decomposition. They converted the multi-objective problem to a number of single optimization problems using Tchebycheff approach.

  3. 3.

    MTS (Tseng and Chen 2009): Multiple trajectory search for the multi-objective optimization. The technique consists of three local search methods with different size of neighborhood regions to generate foreground and background solutions.

  4. 4.

    ClusteringMOEA (Wang et al. 2009): Clustering multi-objective evolutionary algorithm based on orthogonal and uniform design.

  5. 5.

    LiuLiAlgorithm (Liu and Li 2009): Multi-objective evolutionary algorithm based on determined weight and sub-regional search.

  6. 6.

    DMOEADD (Liu et al. 2009): Multi-objective evolutionary algorithm based on domain decomposition to divide the decision variable domain into different sub-domains.

  7. 7.

    MOPC (Waldock and Corne 2010): Multi-objective probability collectives. This algorithm uses the probability collectives to evaluate multi-objective optimization.

  8. 8.

    MOPC/D (Morgan et al. 2013) A new probability collectives algorithm for multi-objective optimization. This algorithm is an enhanced version of MOPC which uses decomposition strategies.

  9. 9.

    AMGA (Tiwari et al. 2009): A hybrid archive-based micro genetic algorithm with gradient-based optimizer.

  10. 10.

    OMOEAII (Gao et al. 2009): Multi-objective evolutionary algorithm based on orthogonal lower-dimensional crossover and linear breeding operator.

  11. 11.

    SNOVMOGA (Patel et al. 2011): An improved ranking scheme for selection of parents in multi-objective genetic algorithm.

The new algorithm (MOnDE) is compared with these MOEAs as the best performing algorithms from the literature on the used benchmarks. It is worth noticing that all the compared algorithms including MODE algorithms used the same general control parameters which are: number of function evaluations as 300,000, the size of external archive is set to 100, 150 and 800 for 2, 3 and 5 objectives-problems, respectively. And the same true pareto front have been used for computing IGD values.

The mean values for IGD are presented in Tables 4 and 5. As shown in the results, there is a clear difference between MOnDE and all the other algorithms. The MOnDE obtained the best results for all the functions except for F 5. MOnDE got the second best for this function with a difference equals to 0.0151 compared to MTS algorithm, which obtained the first rank when tested using this function. Tables 4 and 5 shows a significant difference in F11, F12, and F13. Those problems are considered the most difficult problems as pointed earlier. Referring to those results, one can simply notice that the proposed algorithm outperformed all MODE and the other MOEAs algorithms that reported the best results in the literature on these benchmarks.

The results in Table 5 that the proposed algorithm is able to generate good solutions near to the true pareto front solutions in most of the functions. The final approximation set for F3, F4, and F5 is small, as a result when a solution is considered as a non-dominated solution, a large number of weak solutions have been removed from the optimal true pareto set. The MOnDE algorithm was able to generate limited number of non-dominated solutions and this reflects the IGD value for those functions. That explains that our proposed algorithm is ranked the second in F5 after the MTS algorithm. F6 follows the same behavior except that F6 consists of two continuous regions as F5.

An extensive statistical analysis was added for the purpose of evaluating the statistical significance of observed performance differences. For an input of n algorithms, this analysis employs a statistical test procedure to rank the performance of each compared algorithm. The test highlights whether there are statistical significant differences in the performance ranking of at least one pair of these compared algorithms. For this purpose, the Friedman test which is a non-parametric multiple comparison test is used to test the differences between the 15 compared algorithms (including MOnDE). Table 6 presents the average rankings using the Friedman test. The last two rows in Table 6 show the test-statistic for this test and the corresponding measured p value, respectively. These p values suggest that there are significant differences among the compared algorithms at the 0.05 significance level. Friedman test assigns the lowest rank to the best performing algorithm. As it can be seen in this table, the lowest rank score was obtained by MOnDE (rank = 1.6000) with a clear difference compared to MTS as the second-best performing algorithm (rank = 5.5000). Furthermore, a post hoc analysis is used to inspect which algorithm exhibits significant variation relative to the MOnDE as a base algorithm. Table 7 demonstrates the results of the post hoc Holm, Holland, Rom and Finner tests. Referring to the p value for each post hoc test with a p value ≤0.05, there is a statistical significant difference between the proposed work and all the other contestant algorithms.

Table 6 Average ranking of competitor algorithms, achieved by the Friedman test
Full size table
Table 7 A comparison of adjusted p values (control method: MOnDE)
Full size table

5.5 Comparison on the second benchmark test suits

For the sake of having a thorough comparison with the recent algorithms, we selected the algorithm named: multi-objective differential evolution based on the summation of normalized objectives and improved selection method namely SNOV_IS (Kukkonen and Deb 2006). This algorithm replaces the non-domination sorting with the use of SNOV method and diversified selection methods. They used fixed values for F and CR parameters and they set to 0.5 and 0.1, respectively. Since they didn’t mention what the mutation strategy they used and because they used different benchmark problems, we were forced to run the algorithms on their functions in order to get a fair comparison. The used problems are the CEC2007 benchmark (Zhang et al. 2007). Another important performance measure which was used is the R indicator that can be expressed as follows:

$$I_{R2} = \frac{{\sum\nolimits_{\lambda \in \wedge } {u^{*} (\lambda ,A) - u^{*} (\lambda ,R)} }}{| \wedge |}$$
(11)

where R is a reference set, u* is the maximum value reached by the utility function u with weight vector λ on an approximation set A. We choose the augmented Tchebycheff function as the utility function. Table 8 shows the comparison for average R value for 30 independent runs. The proposed algorithm shows a superior performance in comparison to all the algorithms that competed in the CEC2007 benchmark problems but we did not add all their results from their tables and instead compared our work to the results from SNOV_IS algorithm which obtained the first rank in that completion. One can notice that the proposed algorithm shows good performance comparing to SNOV_IS algorithm for all the functions and this proves the power of using the normalization in MOnDE algorithm.

Table 8 Average R value for a comparison between MOnDE and SNOV_IS algorithms over 30 independent runs
Full size table

6 Conclusion

In this study, we introduce an improved mutation strategy for Differential Evolution (DE) that is based on the summation of normalized objective values (SNOV) method for solving multi-objective optimization problems. “DE/rand-to-nbest” is used to help getting out of premature convergence and finding new feasible optimal solutions by choosing the best normalized individual for all the objectives at the same time to guide the evolution process. The conflicting objectives might have different value ranges and using un-normalized solution might distort the DE distribution. For non-domination sorting, we used SNOV method to fill in the external archive with the best non-dominated solutions and to overcome the time complexity that other methods have. Normalization is capable of discarding the bad solutions which cannot locate the optimal front. The CEC 2009 benchmark suite for multi-objective optimization was used to test the performance of our approach. The IGD metric is used to assess the results. Experimental results indicate that, the proposed algorithm is better and more powerful than other well-known state-of-the-art MOEAs algorithms.