Intelligent fault diagnosis of rolling element bearings using sparse wavelet energy based on overcomplete DWT and basis pursuit

Abstract

This paper explores sparse time-frequency distribution (TFD) using overcomplete discrete wavelet transform (DWT) and sparse representation techniques. This distribution is discovered for characterizing the periodic transient information embedded in rolling element bearings and extracting effective features that can discriminate different fault conditions. Based on the sparse TFD, a new sparse wavelet energy (SWE) feature is obtained by three main steps: first, an overcomplete discrete DWT is employed to decompose the fault signal and construct a redundant dictionary; second, the redundant dictionary is optimized by basis pursuit to obtain the sparsest TFD; finally, SWE is calculated from the new TFD to produce a feature vector for each signal. SWE features that combine the merits of overcomplete DWT and sparse representation techniques can precisely reveal fault-induced information, thereby exhibiting valuable properties for automatic fault identification by intelligent classifiers. The effectiveness and advantages of the proposed features are confirmed by simulation and the practical fault pattern recognition of rolling bearings.

Introduction

Rapid development in modern industry has generated more complex machines. Condition monitoring and fault diagnosis for modern mechanical equipment is increasingly important to prevent economic loss and numerous researches have been conducted in this field (Zhang et al. 2013; Wells et al. 2013; Yu et al. 2014). Defects in rolling element bearings are major factors in machinery failure and have elicited considerable attention. Bearing fault diagnosis is conducted by data acquisition, feature extraction and intelligent classification. Data acquisition and intelligent classification are relatively easy to implement. Typical method to collect data from a mechanical system is using accelerometers attached to the machines, and several widely used algorithms have been employed to create the intelligent classifier, such as the $k$-nearest neighbor (Gharavian et al. 2013), fisher discriminant analysis (Jiang et al. 2013), artificial neural network (Wang and Cui 2013; He et al. 2013; Mortada et al. 2014), and the support vector machine (SVM) (Konar and Chattopadhyay 2011). However, feature extraction remains challenging because fault-induced transient impulses existing in vibration signals are usually contaminated by noise.

Researchers have proposed numerous methods to extract features in different situation, for example, Boskoski and Juricic extracted Renyi entropy values from wavelet packet coefficients of vibration signals to detect mechanical faults in rotational drives (Bokoski and Juricic 2012), Li used adaptive filter and robust statistical features to detect faults in wind turbine transmission system (Li and Frogley 2013). These studies found that features can be extracted in three domains including time domain, frequency domain, and time frequency domain. Time domain features are extracted based on time series analysis, such as the statistical features (variance, kurtosis) and the autoregressive model (Li et al. 2012). Frequency domain features are achieved from spectrum analysis, such as subband energy (Zhao et al. 2005). Features in the time or frequency domains focus only on specific signal content that cannot comprehensively consider fault-related information because defect-induced impulses are non-stationary with time-varying frequencies. Contrarily, time-frequency features can present a synthetic consideration for mechanical fault detection by characterizing varying frequency information at different times. Commonly used time-frequency analysis methods include short-time Fourier transform (Klein et al. 2001), Wigner–Ville distribution (Baydar and Ball 2001), wavelet transform (WT) (Wang et al. 2011) and empirical mode decomposition (Peng et al. 2005; Rai and Mohanty 2007). Among these techniques, WT is outstanding in rotary machine diagnosis because its multi-resolution merit is suitable for analyzing signals with transient impulses. Continuous wavelet transform (CWT) and discrete wavelet transform (DWT) are two categories of WT, each with its own merits as well as deficiencies.

CWT can calculate wavelet coefficients on any scale to reveal signal features completely (Lin and Zuo 2003). However, the high computation cost hinders fast diagnosis. DWT (Mori et al. 1996) can improve decomposition efficiency, but limitations exist in two aspects: (1) lack in shift-invariance causes waveform distortion and (2) fixed frequency domain sampling manner leads to low resolution and severe frequency aliasing. Wavelet packet transform (WPT) (Zhang et al. 2013; Pandya et al. 2014), as an extension of DWT, can decompose signals with higher frequency resolution by analyzing them in both low and high frequency bands. However, it inherits the other problems of DWT. These drawbacks sometimes prevent DWT or WPT from effectively capturing the fault information of rolling bearings.

Recently, overcomplete techniques have become a well recognized tool in signal processing (Kovacevic and Chebira 2007), and numerous overcomplete WT have been designed and utilized for application (Chui and He 2000; Selesnick 2011). Comparing with traditional DWT and WPT, overcomplete DWT have significant advantages. First, overcomplete DWT can achieve higher frequency resolution. Second, overcomplete DWT can be approximately shift-invariant. Third, the redundant basis can help solve the frequency aliasing problems. Besides, with a certain set of basis functions, overcomplete DWT can focus on specific physical properties of the signal. In the current study, Selsnick‘s tunable Q-factor wavelet transform (TQWT) (Selesnick 2011), as a kind of overcomplete DWT, will be empolyed because it can reflect the oscillatory behavior of the signal except for the mentioned advantages.

In order to find a better representation for signal, sparsity-based method is proposed and has received several notable achievements in the field of machinery fault diagnosis (Liu et al. 2002; Yang et al. 2005; Feng and Chu 2007). Its basic principle is to construct a signal as a linear combination of transform basis (atoms) from an overcomplete dictionary (Grbovic et al. 2012). Two well-known methods are utilized to obtain a sparse representation of the signal, which are respectively matching pursuit (Mallat and Zhang 1993) and basis pursuit (Chen et al. 2001). Matching pursuit is suitable for orthogonal dictionary and has fast computational speed, whereas basis pursuit is characterized by super-resolution and better sparsity. The advantages of basis pursuit indicates it has the capacity to extract more informative intrinsic features accurately from vibration signals without frequency aliasing. The process can be conducted by the following two steps: redundant dictionary design and sparse coefficients solving. Redundant dictionary can be designed by K-SVD algorithm (Rusu and Dumitrescu 2012), shift-invariant sparse coding algorithm (Plumbley et al. 2006), or redundant signal transform basis like wavelet packet basis (Yang et al. 2005). Sparse coefficients can be calculated by greedy pursuit algorithms (Bahmani et al. 2013), $l_p$ norm regularization algorithms (Marjanovic and Solo 2012) and iterative shrinkage algorithms (Beygi et al. 2012).

Considering the merits of overcomplete DWT and sparse representation technique, this paper proposes a pioneering sparse wavelet energy (SWE) feature for diagnosing rolling element bearings. SWE features are achieved from a sparse representation of wavelet-based time-frequency distribution obtained by basis pursuit. The redundant dictionary for basis pursuit is designed by TQWT, which can reveal the oscillatory properties of the signal. Then, the dictionary is optimized to achieve the sparse wavelet-based distribution by the split variable augmented Lagrangian shrinkage algorithm (SALSA) (Selesnick 2011), which can efficiently handle various problems. After optimization, SWE features can be obtained from sparse wavelet-based distribution. Its physical meaning is easy to interpret and has the property of sparsity and high resolution. Moreover, SWE feature is suitable for exploring the intrinsic characteristics of bearing fault signals due to its sensitivity to impulses, which greatly benefits machinery diagnosis. The advantages of SWE features are confirmed in both simulation and experiment by comparing with several traditional features.

The remainder of this paper is organized as follows. “Sparsity-related theory” section introduces the basic theory of sparse representation method. “Overcomplete DWT” section presents the design of redundant dictionary by overcomplete DWT. “Automactic fault diagnosis based on SWE” section describes the realization of intelligent diagnosis based on SWE features. “Simulation” section illustrates the procedure and preliminary validation of the proposed method using simulated bearing data. “Engineering validation” section further confirms the advantages of SWE features by experiment. Conclusions are drawn in “Conclusion” section.

Sparsity-related theory

Basis pursuit

Consider signal $\mathbf{x }$ with $p$ points, which can be viewed as a vector in ${\mathbb {R}}^p$. A redundant dictionary $\mathbf{A } = \{\mathbf{a }^1, \mathbf{a }^2, \dots , \mathbf{a }^n\}$ consists of $n$ vectors $\mathbf{a }^j \in {\mathbb {R}}^p$, that span the entire space ${\mathbb {R}}^p$ with $n > p$. Signal $\mathbf{x }$ can be represented as the superposition of basis functions:

$$\begin{aligned} \mathbf{x } = \mathbf{A }\mathbf{s } = \sum _{j=1}^{n}{\mathbf{a }^{j}s^{j}}, \end{aligned}$$

(1)

where $\mathbf{s } = [s^1, s^2, \dots , s^n]^T$ are the coefficients for basis functions. Among all possible coefficient sets, the sparsest can be achieved by the minimization of $l_0$ norm (Donoho and Huo 2001), which is defined as the number of nonzero elements. This process can be expressed as Eq. (2).

$$\begin{aligned} \mathop {\text {argmin}}_{\mathbf{s }}\Vert \mathbf{s }\Vert _0,\quad s.t.\quad \mathbf{x } = \mathbf{As }. \end{aligned}$$

(2)

Unfortunately, Eq. (2) is a non-convex optimization problem which is difficult to deal with. Therefore, in practice, the sparse solution to Eq. (1) is usually obtained by solving the optimization problem in Eq. (3),

$$\begin{aligned} \mathop {\text {argmin}}_{\mathbf{s }}\Vert \mathbf{s }\Vert _1,\quad s.t.\quad \mathbf{x } = \mathbf{As }, \end{aligned}$$

(3)

where $\Vert \mathbf{s }\Vert _1$ is the $l_1$ norm of $\mathbf{s }$ as defined in Eq. (4).

$$\begin{aligned} \Vert \mathbf{s }\Vert _1 := \sum _{n=0}^{N-1}|s(n)|. \end{aligned}$$

(4)

Equation (3) is known as the basis pursuit (BP) problem (Chen et al. 2001) that can provide the sparsest solution for the $l_0$ problem for most large scale redundant systems (Donoho 2006).

Signal $\mathbf{x }$ usually contains noise in practice. Thus, solving Eq. (3) exactly is unreasonable. Generally, we can find an approximate solution by changing the optimization function to Eq. (5), which is called the basis pursuit denoising (BPD) problem (Gunn et al. 2002),

$$\begin{aligned} \mathop {\text {argmin}}_{\mathbf{s }}\Vert \mathbf{x } - \mathbf{As }\Vert _2^2 + \lambda \Vert \mathbf{s }\Vert _1, \end{aligned}$$

(5)

where $\Vert \mathbf{x }\Vert _2^2:=\sum _{n=0}^{N-1}|x(n)|^2$, and the Lagrange multiplier $\lambda$ is a function of $\mathbf{x }$.

Algorithm to solve the BP and BPD problems

Several effective approaches have been developed for solving the BP and BPD problems, such as primal-dual log barrier interior point method (Chen et al. 1998) and iterative shrinkage/thresholding algorithm (ISTA) (Michailovich 2011). Recently, a novel SALSA method is proposed by Afonso (Afonso et al. 2010). SALSA will be used in the present study because of its flexibility in handling various problems and its fast convergence in practice. SALSA will change the unconstrained optimization formulation in Eq. (5) to a constrained problem [Eq. (6)] based on a variable splitting technique,

$$\begin{aligned} \mathop {\text {argmin}}_{\mathbf{s }, \mathbf{u }}\Vert \mathbf{x } - \mathbf{Au }\Vert _2^2 + \lambda \Vert \mathbf{u }\Vert _1,\quad s.t.\quad \mathbf{s } - \mathbf{u } = 0. \end{aligned}$$

(6)

where $\mathbf{u }$ is the created new variable. This problem can be solved by an augmented Lagrangian method (ALM) (Mateos et al. 2010), more specifically, the alternating direction method of multipliers (ADMM) (Mateos et al. 2010) by the following update equations:

$$\begin{aligned} \mathbf{u }^{(k+1)}&= \mathop {\text {argmin}}_{\mathbf{u }}\lambda \Vert \mathbf{u }\Vert _1 + \frac{\mu }{2}\Vert \mathbf{u }-\mathbf{s }^{(k)} -\mathbf{d }^{(k)}\Vert _2^2,\nonumber \\ \mathbf{s }^{(k+1)}&= \mathop {\text {argmin}}_{\mathbf{s }}\frac{1}{2}\Vert \mathbf{x } -\mathbf{As }\Vert _2^2 + \frac{\mu }{2}\Vert \mathbf{u }^{(k+1)}-\mathbf{s } -\mathbf{d }^{(k)}\Vert _2^2,\nonumber \\ \mathbf{d }^{(k+1)}&= \mathbf{d }^{(k)} - \left( \mathbf{u }^{(k)} - \mathbf{s }^{(k)}\right) , \end{aligned}$$

(7)

where $k$ is the iteration index and $\mu$ is a user specified penalty parameter.

According to the previously mentioned theory, we need to find a set of basis to construct an underdetermined system that can be optimized by SALSA to achieve a sparse signal representation. In the current study, overcomplete DWT will be used to construct the undetermined system because it can highlight impulses representing fault information of rolling bearings.

Overcomplete DWT

DWT

The WT of signal $x(n)\,(n = 1, 2, \ldots N)$ is shown in Eq. (8),

$$\begin{aligned} W(a, b) = \langle x(n), \psi _{a, b}(n)\rangle = \sum _{n=1}^{N}x(n)\frac{1}{\sqrt{a}}\psi ^*\left( \frac{n - b}{a}\right) , \end{aligned}$$

(8)

where the asterisk represents complex conjugate, $\psi$ is the mother wavelet function, $a$ and $b$ denote the scale factor and translational factor, respectively. In practice, DWT is usually employed to implement the transform in Eq. (8) for the benefit of computational convenience and easy invertibility. By making $a = 2^j, b = k2^j$, DWT can be realized as

$$\begin{aligned} dwt(j, k) = \frac{1}{\sqrt{2^j}}\sum _{n=1}^{N} x(n)\psi ^*\left( \frac{n-k2^j}{2^j}\right) dt. \end{aligned}$$

(9)

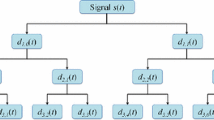
Practically, DWT can be implemented by Mallat’s iterated algorithm (Rajpoot et al. 2008), which recursively convolves the low-pass channel series with low pass filter $h(n)$ and band pass filter $g(n)$ and subsequently downsamples the filtered series in each channel by a factor of 2. The process of a three-level DWT can be illustrated by Fig. 1a, and the frequency partition manner is described in Fig. 1b. DWT has been proven a powerful tool for time-frequency signal analysis. However, the frequency aliasing problem and its poor frequency resolution limits its application in mechanical fault diagnosis because it cannot effectively identify periodic impulses.

Fig. 1

Demonstration of the DWT process: a the decomposition procedure and b the corresponding frequency partition manner

Realization of overcomplete DWT

Overcomplete DWT is also implemented by an iterated two-channel filterbank. In the current paper, Selsnick‘s TQWT (Selesnick 2011) is employed to conduct overcomplete DWT, which is conceptually simple and can be implemented efficiently.

Unlike DWT, the filters, on which TQWT is based are specified directly in the frequency domain. Transform is implemented by iteratively applying the two-channel filter banks on its low-pass channel, followed by the low-pass scaling and high-pass scaling operations. For low-pass scaling with parameter $\alpha$, the output signal has a sampling rate of $\alpha f_s$, where $f_s$ is the sampling rate of the input signal. Similarly, for high-pass scaling with parameter $\beta$, the output signal has a sampling rate of $\beta f_s$. The scaling parameters satisfy $0 < \alpha < 1$, and $0 < \beta \le 1$ to ensure that the WT will not be overly redundant. Meanwhile, to achieve a oversampled results, we also require $\alpha + \beta > 1$. Generally, the parameters are set based on Eq. (10),

$$\begin{aligned} \beta = \frac{2}{Q+1}, \quad \alpha = 1 - \frac{\beta }{r}, \end{aligned}$$

(10)

where $Q$ is the quality factor and $r$ is the redundant factor. The physical interpretation and selection principle of $Q$ and $r$ can be found in (Selesnick 2011). The low-pass filter and high-pass filter are defined as Eqs. (11) and (12),

$$\begin{aligned} H(\omega )&= {\left\{ \begin{array}{ll} 1, &{} |\omega | \le (1 - \beta )\pi \\ \theta \left( \frac{\omega + (\beta -1)\pi }{\alpha + \beta - 1}\right) , &{} (1 - \beta )\pi < |\omega | < \alpha \pi \\ 0, &{} \alpha \pi \le |\omega | \le \pi \end{array}\right. } \end{aligned}$$

(11)

$$\begin{aligned} G(\omega )&= {\left\{ \begin{array}{ll} 0, &{} |\omega | \le (1 - \beta )\pi \\ \theta \left( \frac{\alpha \pi - \omega }{\alpha + \beta - 1}\right) , &{} (1 - \beta )\pi < |\omega | < \alpha \pi \\ 1, &{} \alpha \pi \le |\omega | \le \pi \end{array}\right. } \end{aligned}$$

(12)

where $\theta (\omega ) = \frac{1}{2}(1 + \text {cos}(\omega ))\sqrt{2 - \text {cos}(\omega )}, |\omega | \le \pi$. The mathematical expression of the low-pass scaling and high-pass scaling can be found in Eq. (13).

$$\begin{aligned} \text {LPS}(\alpha ): Y(\omega )&= X(\alpha \omega ), \quad |\omega | \le \pi , \nonumber \\ \text {HPS}(\beta ): Y(\omega )&= X\left( \beta \omega + \frac{\omega }{|\omega |}(1 - \beta )\omega \right) , \nonumber \\ 0&< |\omega | \le \pi . \end{aligned}$$

(13)

The TQWT decomposition process is completely illustrated in Fig. 2a, whereas the corresponding inverse transform is shown in Fig. 2b. With the achieved overcomplete DWT results, it will be possible for us to get more accurate sparse decomposition results by the optimization algorithm.

Fig. 2

Demostration of the TQWT process: a the decomposition procedure and b the inverse TQWT process

Automatic fault diagnosis based on SWE

TQWT decomposition level determination for bearing diagnosis

For certain TQWT decomposition parameters, corresponding wavelets represent different frequency subbands and the decomposition result should cover the informative frequencies of the signal. Accordingly, we synthesize the fault-related frequency band and the frequency response of wavelets for TQWT for an effective diagnosis. The informative frequency band can be easily localized in the 2-D time-frequency distribution.

Supposing a signal with period transient impulses has a CWT-based TFD shown in Fig. 3a, the normalized fault-related frequency lies in [0.15, 0.35] as the dash line indicates. The frequency responses of the wavelets for TQWT are shown in Fig. 3b. For fully cover the interested part highlight in Fig. 3b, we should define the lower boundary $J_{\text {low}} \le 2$ and the upper boundary $J_{\text {up}} \ge 7$. Generally, the range can be set a little larger than necessary. With the decomposition boundary determined, $J_{\text {up}} - J_{\text {low}} +2$ subbands are obtaned according to Fig. 2a. In practical fault diagnosis containing multiple fault classes, the boundary should be determined by the union of different cases, which will be further discussed in the engineering section (“Engineering validation” section).

Fig. 3

Determination of the decomposing level: a CWT result of a signal and b frequency responses of wavelets in TQWT

SWE features

A set of oversampled DWT coeffients $\mathbf{s }$ is obtained by applying TQWT to a signal $\mathbf{x }$ as shown in Eq. (14).

$$\begin{aligned} \mathbf{s } = \text {TQWT}(\mathbf{x }). \end{aligned}$$

(14)

To achieve an ideal set of coefficients, which is the sparsest, we need to solve the optimization problem expressed in Eq. (15),

$$\begin{aligned} \mathop {\text {argmin}}_{\mathbf{s }}\Vert \mathbf{x } - \text {ITQWT}(\mathbf{s })\Vert _2^2 + \lambda \Vert \mathbf{s }\Vert _1, \end{aligned}$$

(15)

where ITQWT stands for the inverse transform of TQWT. The above equation is the BPD problem described in “Basis pursuit” section, and can be efficiently solved by SALSA. The sparsest result has the most concentrated energy best reflecting the period impulses of the machinery signal. The proportion of subband average energy can be regarded as a significant feature for machinery fault diagnosis, which is the proposed SWE feature. Suppose signal $\mathbf{X }$ has $m$ subbands $\{\mathbf{w }^{(1)}, \mathbf{w }^{(2)}, \dots , \mathbf{w }^{(m)}\}$. The SWE feature of the $i$th subband with $l(i)$ points can be calculated as shown in Eq. (16).

$$\begin{aligned} \text {SWE}(i) = \frac{E_i}{E_{\text {total}}} = \frac{\left( \sum _{j=1}^{l(i)}w^{(i)}(j)^2 \right) /l(i)}{\sum _{i=1}^{m} \left( \left( \sum _{j=1}^{l(i)}w^{(i)}(j)^2\right) /l(i)\right) }.\quad \end{aligned}$$

(16)

Automatic fault diagnosis

The diagnosis process includes the training part which infers a feature space for fault types and the testing part which evaluates the accuracy of the training model. The detailed steps to conduct intelligent fault diagnosis based on SWE features can be summarized as follows:

• Step 1: The dataset is randomly divided into the training and testing sets.

• Step 2: TQWT is applied to obtain the oversampled DWT subbands of each sample.

• Step 3: SALSA is employed to achieve the sparse representation of the oversampled DWT subbands.

• Step 4: The proportion of subband energy is calculated as the SWE features for fault diagnosis.

• Step 5: A classifier is trained by the SWE features of the training samples.

• Step 6: The misclassification rate of testing samples is checked to evaluate the performance of the classifier. If the classification accuracy rate is satisfactory, then the classifier can be finally used to conduct intelligent fault diagnosis.

Simulation

Vibration model construction

To illustrate the procedure and the preliminary validation of the proposed SWE features, a simulated bearing fault signal is contructed. The periodical impulses representing fault information can be described in Eq. (17),

$$\begin{aligned} I(t)&= \sum _{k=1}^{t}A\text {exp}\left\{ \frac{-\xi }{\sqrt{1-\xi ^2}}\left[ 2\pi f_0(t-kT)\right] \right\} \nonumber \\&\text {sin}\left[ 2\pi f_0(t-kT)\right] , \end{aligned}$$

(17)

where $A = 4$ is the initial magnitude of the simulated vibration signal, $f_0 = 2000\,\hbox {Hz}$ is the central frequency of the resonance band, $\xi = 0.04$ represents the damping ratio and $T = 0.02\,\hbox {s}$ denotes the repetition period. The vibration signal of the rolling bearing generally includes periodic impulses, harmonic components, and noise. Therefore, the vibration model is constructed as shown in Eq. (18), where $n(t)$ denotes white noise.

$$\begin{aligned} h(t) = I(t) + B\text {sin}(2\pi f_1 t) + C\text {cos}(2\pi f_2 t) + Dn(t). \end{aligned}$$

(18)

In this case, $B=0.2$, $C=0.15$, $D=0.4$, $f_1=500$, and $f_2=900\,\text {Hz}$. The waveform of the simulated signal is presented in Fig. 4.

Fig. 4

Waveform of the simulated signal

SWE features of the simulated signal

The CWT-based TFD of the simulated signal is demonstrated in Fig. 3a. With the analysis in “SWE features” section, the decomposition boundaries of TQWT are set to be $J_{\text {low}}=1$ and $J_{\text {up}} = 8$ based on the wavelet frequency responses in Fig. 3b $(Q=4, r=3)$. Period impulses are detected in four subbands (subband 4–7) as shown in Fig. 5a because of the aliasing of different subbands. This result can be improved through sparse-related techniques. By applying SALSA, a sparse representation of overcomplete DWT coefficients can be obtained and the result is shown in Fig. 6. Obviously, distribution in Fig. 6a is much clearer, with period impulses concentrated in subbands 5 and 6. The sparsity can reduce frequency aliasing and ensure intrinsic energy flow from low to high level with little noise, which can be considered as the intrinsic structure embedded in the signal. It can be inferred that different health states of the bearing signal possess different energy flows, which motivates its application in machinery fault diagnosis. Therefore, we use the average energy proportion of each subband as a signature representing the fault information calculated by Eq. (16). The result is illustrated in Fig. 6b.

Fig. 5

Illustration of the overcomplete DWT: a the distribution of coefficients in each subband and b the corresponding subband energy distribution

Fig. 6

Illustration of the sparsity-based wavelet transform: a the distribution of coefficients in each subband and b the corresponding SWE features

Comparison with other methods

The same simulated signal is analyzed by DWT and WPT for comparison, which are widely used in fault diagnosis. According to “SWE features of the simulated signal” section, energy flow is captured from TFD. An 8-level DWT decomposition result and its corresponding subband energy is shown in Fig. 7. Figure 7a with five periodic impulses indicates the effectiveness of DWT decomposition, and energy flow in Fig. 7b reflects the energy distribution in different subbands. However, the distribution in Fig. 7a has a few confusing fuzzy lines and the impulse information can be found in subband six except the energy-concentrated subbands (7 and 8), which is caused by the frequency aliasing of DWT. Contrarily, the SWE-based method proposed in this paper can compensate for the drawback and achieve accurate energy flow. Moreover, the little energy in subbands 1–4 in Fig. 7b indicates the low frequency resolution of DWT, which may lead to the missing of signal information.

Fig. 7

Illustration of the DWT: a the distribution of coefficients in each subband and b the corresponding subband energy features

WPT is conducted in three levels for the simulated signal with $2^3 = 8$ subbands obtained. The transform coefficients and corresponding subband energy are presented in Fig. 8a. WPT performs a complete decomposition in each level to achieve both low-frequency and high-frequency components, thereby obtaining a higher frequency resolution than DWT. The WPT coefficients in Fig. 8a demonstrate obvious periodic impulses embedded in the signal in subbands 4–6. However, the distribution is not as clear as Fig. 6a and frequency aliasing still exists, leading to a more dispersed energy along the frequency axis as shown in Fig. 8b.

Fig. 8

Illustration of the WPT: a the distribution of coefficients in each subband and b the corresponding subband energy features

The comparison verifies that the proposed processing method based on overcomplete DWT and SALSA guarantees high resolution in frequency and accurate reflection of fault information. These merits are beneficial to characterize a more representative intrinsic energy pattern of the fault signal than traditional WT techniques, thereby rendering the new SWE features recognizable for mechanical fault identification.

Engineering validation

Instruction of the dataset

The proposed SWE feature is evaluated on a rolling bearing dataset from the Case Western Reserve University Bearing Data Center. The experimental apparatus presented in Fig. 9 consists of the following main parts: a 2 hp motor on the left, a torque transducer and a dynamometer in the middle and a load motor on the right. The testing groove ball bearing supports the motor shaft at the drive end, on which single-point faults are seeded. Vibration data are collected by accelerometers attached to the housing with magnetic bases at the 12 o‘clock position at the drive end. The sampling frequency is set at 12 kHz. The dataset includes four health conditions of the rolling bearing: healthy; rolling element defect; inner-race defect and outer-race defect. Each fault condition has defects with three different sizes: 0.007, 0.014 and 0.021 inches. Detailed parameters are listed in Table 1. Typically, sample signals and their corresponding Fourier spectrum under 10 different states are illustrated in Fig. 10.

Fig. 9

Experimental setup for acquiring vibration signals of the rolling element bearings

Fig. 10

Demonstration of the bearing signals: a the original waveform and b the corresponding Fourier spectrum

Table 1 Parameters of the rolling bearings

TQWT decomposition level determination for bearing signals

In this rolling bearing case, $Q$ is set to 4 and $r$ is set to 4 to obtain the preliminary wavelet in advance referring to (Selesnick 2011). The same bearing fault locations usually share similar fault-related frequency bands in TFD. Thus, we select three typical defective signals in different locations to determine the effective energy band. The obtained CWT results and frequency responses of wavelets used in TQWT are shown in Fig. 11. The fault-related band is [0.15, 0.35] for rolling-element defect; [0.1, 0.37] for inner-raceway defect and [0.1, 0.3] for outer-raceway defect. The final frequency band determined by the union of three conditions is [0.1, 0.37]. According to Fig. 11d, the decomposition boundary should be determined as $J_{\text {low}} \le 2$ and $J_{\text {up}} \ge 14$. A larger decomposition level is needed to ensure the whole fault information is embodied. Therefore, $J_{\text {low}}$ is set to 1 and $J_{\text {up}}$ is set to 15.

Fig. 11

Determination of the decomposing level: a CWT result of the rolling-element fault case, b CWT result of the inner-raceway fault case, c CWT result of the outer-raceway fault case and d frequency response of the wavelets in TQWT

SWE feature extraction

After a redundant dictionary is constructed by TQWT, SALSA is utilized to achieve a sparse set of coefficients. The SWE features calculated by Eq. (16) for samples under 10 conditions are shown in Fig. 12a. It can be learned that energy is mainly concentrated in 1 or 2 subbands, each of which presents unique energy distribution that is beneficial for classifiers to identify the condition of the bearing signals. To illustrate the classification capability of the SWE feature intuitively, principle component analysis (PCA) (Humberstone et al. 2012; Shao et al. 2014) is applied to the features as a dimension reduction method. The target dimension is set to 3 to generate a visualization clustering result as shown in Fig. 12b. The SWE features in low-dimension show reasonable distribution for original high-dimensional features. Samples in the same class are gathered to a cluster and separated from the others with a significant distance. The remarkable clustering result is strong proof that the SWE feature is effective in fault identification of the rolling bearings.

Fig. 12

Illustration of the SWE features of the bearings: a the distribution of the SWE features in 10 cases and b the intuitive clustering result

To highlight the advantages of the SWE features, the DWT and WPT subband energy features are extracted as a comparison. In this case, 15-level DWT is employed and the DWT features extracted from the samples of 10 cases are presented in Fig. 13a. It can be seen that energy concentrated in subbands 2 and 3 express similarities among many conditions, indicating that DWT-based energy flow cannot effectively identify bearing faults. The frequency aliasing and low frequency resolution render DWT ignore some unique signal information as discussed in “Simulation” section. Such a result can also explain the weakness of DWT-based features in bearing fault diagnosis. More intuitive proof can be achieved by PCA clustering result presented in Fig. 13b. DWT-based PCA clustering results are completely indiscernible. The only fault type we can identify is the healthy one, which is consistent with the result in Fig. 13a. Thus, DWT subband features cannot express intrinsic fault information in this rolling bearing diagnosis.

Fig. 13

Illustration of the DWT subband energy features of the bearings: a the distribution of the DWT-based features in 10 cases and b the intuitive clustering result

WPT has higher resolution than DWT, therefore, WPT subband energy feature has arguably more elaborate information than DWT. The level of WPT is set to 4 to obtain $2^4 = 16$ subbands. WPT subband energy of samples from 10 different conditions are shown in Fig. 14a. WPT subband energy features perform better than the DWT subband energy features with most conditions presenting distinguishable characteristics. However, similarities remain in WPT-based features, such as S2, S3, S4 and S8. These features cannot be inferred to rival SWE features for the following reasons: (1) WPT-based features are not as concentrated as the SWE features for frequency aliasing and (2) the extracted WPT-based features cannot reveal fault impulse information as clearly as SWE features according to “Simulation” section. Similar with SWE and DWT-based features, the WPT features are illustrated intuitively by PCA in Fig. 14b. WPT demonstrates better clustering than DWT, however, significant overlapping is found between S2 and S5, as well as S3 and S8. The overlapping is detrimental for effective and accurate fault pattern recognition. Moreover, it puts forward higher requests to the classifier.

Fig. 14

Illustration of the WPT subband energy features of the bearings: a the distribution of the WPT-based features in 10 cases and b the intuitive clustering result

The advantages of SWE features can be preliminarily seen by the comparison with DWT and WPT subband energy features in both feature distribution and PCA-based clustering. To further confirm the effectiveness and practical value of SWE features, two commonly used intelligent classifiers were employed to achieve the final diagnosis result, as provided in “Intelligent fault diagnosis based on SWE features” section.

Intelligent fault diagnosis based on SWE features

The last step of intelligent fault pattern recognition is conducted by intelligent classifiers. In the current study, two commonly used intelligent classifiers are employed: nearest neighbor classifier (Gharavian et al. 2013) and SVM (Konar and Chattopadhyay 2011). The nearest neighbor classifier is based on the intuitive concept that data instances of the same class should be closer in the feature space. It is conducted by calculating the distance of a new sample to all samples in the training data, and class is determined by the sample nearest to the new one. The SVM classifier is developed from the optimal separating plane under linearly separable condition. It determines the optimal separating hyperplane that minimizes the generalization error by maximizing the margin between the separating hyperplane and the nearest sample points, thereby realizing the classification. The nearest neighbor classifier is simple and intuitive while the SVM classifier generally has higher accuracy. Moreover, to confirm the merits of SWE features, the subband energy features obtained by DWT and WPT are also used for the same classifiers as a comparison.

The simple nearest neighbor classifier is first employed for the 10-class problem. The classification recognition rate $\eta$ and standard deviation $\sigma$ are calculated by Eqs. (19) and (20),

$$\begin{aligned} \eta&= 1 - \sum _{i=1}^{M}P(\omega _i)\frac{k_i}{N_i}, \end{aligned}$$

(19)

$$\begin{aligned} \sigma&= \sum _{i=1}^{M}P^2(\omega _i)\frac{P_i(1-P_i)}{N_i}, \end{aligned}$$

(20)

where $M$ is the class number, $P(\omega _i)$ is the occurrence probability of class $\omega _i$ with $N_i$ samples, $k_i$ is the misclassified number in $\omega _i$, $P_i = k_i/N_i$. A higher $\eta$ means a better classification and a smaller $\sigma$ indicates a more convincing result. It can be inferred from Eq. (20) that the recognition rate estimated by Eq. (19) is asymptotically consistent only as $N_i \rightarrow \infty$. In this case, the training set has 50 samples and the testing set has 20 samples according to Table 1. In order to get more convincing evaluation, we conduct a cross validation by randomly selecting training and testing samples for 50 times. Diagnosis results of three feature extraction techniques based on the nearest neighbor classier over 50 runs are listed in Table 2. The standard deviation is around $10^{-4}$ for all the three features, which indicates the estimation result is acceptable. In comparison, the DWT subband energy feature has the lowest recognition rate, where nearly 1/4 testing samples are misclassified. This poor performance is consistent with feature distribution in Fig. 13a and sample clustering in Fig. 13b. The WPT subband energy feature with higher frequency resolution has a more satisfactory recognition rate, which proves that WPT-based feature is more effective than DWT-based feature. This better classification ability can be inferred from the feature demonstration in Fig. 14. SWE feature has the highest recognition rate because it is the sparse optimal result of a high resolution overcomplete DWT. Stated differently, SWE can reflect more elaborate content of the signal and reveal the intrinsic fault-related information.

Table 2 Classification results of the bearing data by the nearest neighbor classifier

Classification is then conducted by SVM classifier. As listed in Table 3, the recognition rate is higher than the nearest neighbor classifier for the testing samples and the standard deviation is smaller, which indicates a better performance of the SVM classifier.

Table 3 Classification results of the bearing data by the SVM classifier

In this case, the WPT-based feature remains more effective than the DWT-based one, and the SWE feature steadily exhibits the highest mean recognition rate. All of these results powerfully prove that SWE has significant advantages over DWT and WPT-based features for bearing fault classification.

Discussions

• 1. The main contribution of this paper is proposing a new SWE feature based on overcomplete DWT and sparsity theory. Overcomplete DWT brings high frequency resolution to time-frequency decomposition and the sparsity-related technique can effectively eliminate the frequency aliasing to obtain a concentrated energy distribution. Therefore, SWE feature can accurately reveal fault-related information, thereby approaching the intrinsic pattern of fault bearing signals. The above studies have comprehensively shown the benefits of the SWE feature in clustering and classification.

• 2. PCA is used to generate a visualization clustering result for intuitively interpreting the advantages of SWE features. Final diagnosis process by classifiers is performed on original SWE features rather than dimension-reduced features because PCA as a linear dimension reduction method will sacrifice non-linear information, which may be important to pattern recognition.

• 3. Two intelligent classifiers were employed in this study: nearest neighbor classifier and SVM classifier. Nearest neighbor classifier is almost the simplest method to emphasize the benefits of the SWE features, and SVM classifier is more advanced and illustrates the practical application. Some parameters need to be determined in practice for SVM, such as kernel function, kernel argument and penalty parameter (Gharavian et al. 2013). In this study, radial basis function kernel with kernel argument set to 1 is employed and the penalty parameter is set to 2500. The parameters are chosen roughly by experiment because the main point of this paper is highlighting the advantages of SWE features. More theoretical and elaborate parameters determination methods can be found in (Hsu and Lin 2002; Lorena and de Carvalho 2008).

• 4. Fault feature extraction by basis pursuit can also be conducted using wavelet packet dictionary according to (Yang et al. 2005) with experiments exhibiting the effectiveness. However, unlike the overcomplete DWT dictionary employed in this paper, the wavelet packet dictionary has little redundant information in frequency domain, thus limiting the sparse optimization (Chen et al. 2001). Take the simulated signal in Eq. (18) for further discussion, the basis pursuit result using wavelet packet dictionary is shown in Fig. 15. Comparing Figs. 5a and 15a, we can find that both of them indicate obvious period concentration around impulses along the time axis, but the result using wavelet packet dictionary (Fig. 15b) is severely dispersed along frequency axis in contrary to the result using overcomplete DWT dictionary (Fig. 5b). Stated differently, basis pursuit using wavelet packet dictionary cannot solve the frequency aliasing problem. Therefore, the proposed SWE feature with redundant information in both time and frequency domains perform better than basis pursuit using wavelet packet dictionary.

Fig. 15

Illustration of basis pursuit result using wavelet packet dictionary: a the distribution of coefficients in each subband and b the corresponding subband energy features

Conclusion

In this study, a new energy-related feature, called SWE is proposed based on overcomplete DWT and basis pursuit. SWE feature is the sparse optimization result of the wavelet redundant dictionary, and reveals signal impulse information, which means it can be a meaningful characteristic for fault pattern recognition of rolling bearings. Compared with traditional DWT and WPT subband energy features, SWE has the advantages of high resolution, concentrated energy and clear physical significance. With the parameters set properly, the SWE feature is evaluated to have remarkable clustering result, outperforming the DWT-based feature and the WPT-based feature. The practical application of SWE features in distinguishing bearing fault signals under 10 health conditions further confirms its merits, with the highest recognition rate in both the nearest neighbor classification and the SVM classification. All evidence indicates that the SWE feature has valuable potential and significant practicability in rolling bearing fault diagnosis.