Fault feature extraction of rolling element bearings based on wavelet packet transform and sparse representation theory

Abstract

Extracting reliable features from vibration signals is a key problem in machinery fault recognition. This study proposes a novel sparse wavelet reconstruction residual (SWRR) feature for rolling element bearing diagnosis based on wavelet packet transform (WPT) and sparse representation theory. WPT has obtained huge success in machine fault diagnosis, which demonstrates its potential for extracting discriminative features. Sparse representation is an increasingly popular algorithm in signal processing and can find concise, high-level representations of signals that well matches the structure of analyzed data by using a learned dictionary. If sparse coding is conducted with a discriminative dictionary for different type signals, the pattern laying in each class will drive the generation of a unique residual. Inspired by this, sparse representation is introduced to help the feature extraction from WPT-based results in a novel manner: (1) learn a dictionary for each fault-related WPT subband; (2) solve the coefficients of each subband for different classes using the learned dictionaries and (3) calculate the reconstruction residual to form the SWRR feature. The effectiveness and advantages of the SWRR feature are confirmed by the practical fault pattern recognition of two bearing cases.

Introduction

Condition monitoring and fault diagnosis for modern mechanical equipment are increasingly important to prevent severe economic losses and casualties (Wells et al. 2013; Mortada et al. 2014; Yu et al. 2014). Rolling element bearings as major components in rotating machinery cover a broad range of mechanical equipments from heavy machinery (e.g., aircraft engines, train and wind turbines) to light machinery (e.g., cooling fans and lathe machines). Therefore, bearing fault diagnosis has elicited considerable attention and is still a hot topic today. Many fault diagnostic approaches have been published in literature (Zarei and Poshtan 2007; Li et al. 2008, 2012). In the current study, diagnosis is executed by following the roadmap of data acquisition, feature extraction and intelligent classification. The acquired raw signals cannot be directly employed in diagnostic decision because of its high dimensionality and noise interference. Thus, feature extraction from raw signals is necessary.

Fig. 1

Procedure of SWRR feature extraction method

Previous studies (Baillie and Mathew 1996; Zhao et al. 2005; Wang et al. 2011) showed that features can be extracted in the time, frequency and time–frequency domains. Features of the time or frequency domains only focus on specific signal content that cannot comprehensively consider fault-related information because defect-induced impulses are non-stationary with time–varying frequencies. Contrarily, time–frequency features can present a synthetic consideration for mechanical fault detection by characterizing varying frequency information at different times. Commonly used time–frequency analysis methods include short-time Fourier transform (Klein et al. 2001), Wigner–Ville distribution (Baydar and Ball 2001), wavelet transform (Wang et al. 2011; Dong et al. 2013), and empirical mode decomposition (Yang et al. 2014). Among these techniques, wavelet transform is outstanding in bearing fault diagnosis because its multi-resolution merit is suitable for analyzing signals with transient impulses (Yan et al. 2014).

As one of the most widely used wavelet transform methods, wavelet packet transform (WPT) is well-known for its orthogonal, complete, and local properties (Coifman and Wickerhauser 1992). Features extracted from the wavelet coefficients of WPT are popular for characterizing machine faults. For example, Zarei and Poshtan (2007) utilized sub-frequency band energy as fault index to detect bearing faults, Bokoski and Juricic (2012) extracted Renyi entropy values to detect faults in rotational drives, Li et al. (2008) employed Kurtosis values of WPT coefficients for damage detection and classification. Such features are simple and calculated in a certain manner to reflect specific signal characteristics such as the impulses or energy distribution. These researches have demonstrated the effectiveness of WPT for mechanical fault diagnosis, and the choice of optimal discriminative features is the key to achieve good classification.

Recently, sparse representation theory is proposed and has received several notable achievements in the field of machinery fault diagnosis (Liu et al. 2002; Feng and Chu 2007). Its basic principle is to represent a signal by a linear combination of a few transform basis (atoms) from a dictionary. The process can be conducted by the following two steps: dictionary design and sparse coefficient solving. The dictionary can be achieved by predefined transform basis, such as sinusoidal functions, wavelets, curvelets, or compound overcomplete dictionaries (Lewicki and Sejnowski 2000). It can also be learned from data by algorithms such as the method of optimal directions (MOD) (Engan et al. 1999), k-singular value decomposition (K-SVD) (Aharon et al. 2006) and shift-invariant sparse coding (Plumbley et al. 2006; Blumensath and Davies 2007). Once the dictionary is determined, the corresponding sparse coefficients can be calculated by any of the following methods, including greedy pursuit algorithms (Bahmani et al. 2013), $l_p$ norm regularization algorithms (Marjanovic and Solo 2012) and iterative shrinkage algorithms (Beygi et al. 2012).

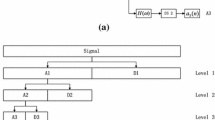
According to sparse representation theory, dictionary learning aims to organize the characteristic patterns in the learning signals by atoms, which have great adaptability to the class they are learned from. However, for different classes, the atoms naturally cannot be activated to approximate input signals as well as the training class because of differences in data structure, thereby inducing different reconstruction residuals. Inspired by this idea, sparse representation is introduced for feature extraction on the basis of the residual data generated from WPT subbands, which is the sparse wavelet reconstruction residual (SWRR) feature. A scheme is drawn up to implement the feature extraction in Fig. 1, and brief description of the procedure is summarized as follows: (1) decompose the signal by WPT and select the fault-related subbands; (2) learn a dictionary $\mathbf{A}_i$ for each fault-related subband by training samples; (3) represent each fault-related subband in a sparse way based on the learned dictionary and (4) calculate the reconstruction residual of each fault-related subband and arrange them in a vector, which is the final SWRR feature. During this process, the dictionary is learned atom-by-atom by K-SVD, thus making it efficient to well match the data structure (Aharon et al. 2006). Sparse coefficient solving is implemented by orthogonal matching pursuit (OMP), which is an efficient greedy pursuit algorithm (Mallat 1989).

The remainder of this study is organized as follows. “WPT” section describes the theoretical background on WPT. “Sparse representation theory” section presents the basic theory of sparse representation, where both dictionary learning and coefficient solving algorithms are discussed. “Fault feature extraction based on WPT and sparse representation” section introduces the SWRR feature extraction method and its application in fault diagnosis. “Engineering validation” section illustrates the advantages of SWRR features by two experiments on rolling element bearings. Conclusions are drawn in “Conclusion” section.

WPT

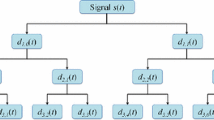
WPT is an excellent signal decomposition tool widely used in signal processing. Practically, WPT can be implemented by means of a pair of low-pass and high-pass filters, denoted as h(k) and g(k), respectively. These filters are constructed from the selected wavelet function $\psi (t)$ and its corresponding scaling function $\phi (t)$ (Mallat 1989), as described in Eq. (1),

$$\begin{aligned} \phi (t)= & {} \sqrt{2}\sum _{k}h(k)\phi (2t-k) \nonumber \\ \psi (t)= & {} \sqrt{2}\sum _{k}g(k)\phi (2t-k) \end{aligned}$$

(1)

where $\sum _{k}h(k) = \sqrt{2}$ and $\sum _k g(k) = 0$. Using the wavelet filters, the signal is decomposed into a set of wavelet packet nodes with the form of a binary tree (Coifman and Wickerhauser 1992), as expressed in Eq. (2),

$$\begin{aligned} d_{j+1,2n}= & {} \sum _{m}h(m-2k)d_{j,n} \nonumber \\ d_{j+1,2n+1}= & {} \sum _{m}g(m-2k)d_{j,n} \end{aligned}$$

(2)

where j indicates the decomposition level, n represents the node in level j, and m is the number of wavelet coefficients. As illustrated in Fig. 2, a 3-level WPT generates a total of eight subbands, and each subband covers one eighth of the frequency information successively.

Fig. 2

Illustration of WPT

Sparse representation theory

Sparse representation of signal

Sparse theory allows us to represent a signal as the linear combination of atoms in a dictionary. Consider signal $\mathbf{y}$ with p points, which can be viewed as a vector in $\mathbb {R}^p$. A redundant dictionary $\mathbf{A} = \{\mathbf{a}^1, \mathbf{a}^2, \ldots , \mathbf{a}^n\}$ consists of n atoms $\mathbf{a}^j \in \mathbb {R}^p$, that span the entire space with $n > p$. Signal $\mathbf{y}$ can be represented as the superposition of basis functions:

$$\begin{aligned} \mathbf{y} = \mathbf{Ax} = \sum _{j=1}^{n}\mathbf{a}^{j}x^{j} \end{aligned}$$

(3)

where $\mathbf{x} = [x^1, x^2, \ldots , x^n]^T$ are the coefficients for basis functions. Among all possible coefficient sets, the sparsest can be achieved by optimizing Eq. (4),

$$\begin{aligned} \text {arg}~\mathop {\text {min}}_{\mathbf{x}}\Vert \mathbf{x}\Vert _0,\quad s.t.\quad \mathbf{y} = \mathbf{Ax} \end{aligned}$$

(4)

where $\Vert \cdot \Vert _0$ denotes the $l_0$ norm, which is defined as the number of nonzero elements (Donoho and Huo 2001). As seen from Eq. (4), to find the optimal sparse representation of a signal, two problems need to be solved: (1) the designing of dictionary A and (2) the coefficients solving of Eq. (4). These two problems will be discussed in the following two subsections.

Coefficients solving

Exact determination of the sparse representation of a signal using a generic dictionary is proved to be NP-hard (Davis et al. 1997), thus, approximate solutions are usually sought. Any standard technique (Chen et al. 1998) can be used but a greedy pursuit algorithm such as OMP (Mallat 1989; Polo et al. 2009) is often employed due to its efficiency (Tropp 2004). Details about the OMP algorithm are stated as follows Polo et al. (2009):

• Step 1: Initialize the residual $\mathbf{r}_0 = \mathbf{y}$ and initialize the set of selected variables $X(\mathbf{c}_0) = \emptyset$. Set the iteration counter $i = 1$.

• Step 2: Find the variable $\mathbf{X}_{t_i}$ by optimizing

  $$\begin{aligned} \mathop {\text {max}}_{t}|\mathbf{X}_t^T\mathbf{r}_{i-1}| \end{aligned}$$

  (5)

  and add the variable $\mathbf{X}_{t_i}$ to the set of selected variables. Update $\mathbf{c}_i = \mathbf{c}_{i-1} \cup t_i$.

• Step 3: Let $\mathbf{P}_i = X(\mathbf{c}_i)(X(\mathbf{c}_i)^TX(\mathbf{c}_i))^{-1}X(\mathbf{c}_i)^T$ denote the projection onto the linear space spanned by the elements of $X(\mathbf{c}_i)$. Update $\mathbf{r}_i = (\mathbf{I}-\mathbf{P}_i)\mathbf{y}$

• Step 4: If the stopping condition is achieved, stop the algorithm. Otherwise, set $i = i+1$ and return to Step 2.

Two commonly used stoping rules are expressed as Eqs. (6) and (7),

$$\begin{aligned} \Vert \mathbf{r}^k\Vert _2< & {} \varepsilon _0 \end{aligned}$$

(6)

$$\begin{aligned} \Vert \mathbf{x}\Vert _0< & {} k_0 \end{aligned}$$

(7)

where $\varepsilon _0$ and $k_0$ are set according to noise level. $\Vert \cdot \Vert _2$ means the $l_2$ norm defined as

$$\begin{aligned} \Vert \mathbf{x}\Vert _2^2 = \sqrt{\sum _ix_i^2} \end{aligned}$$

(8)

In this study, we will use the stopping rule in Eq. (7) because residuals are more intuitive to evaluate the performance of the sparse representation.

Dictionary learning

Learning a dictionary directly from data rather than using a predetermined dictionary (such as sinusoidal functions or wavelet) usually leads to better representation and hence can provide improved results in practice (Rubinstein et al. 2010). Designing dictionaries based on training is a much recent approach to find a proper dictionary which is strongly motivated by recent advances in the sparse representation theory (Engan et al. 1999; Aharon et al. 2006; Rubinstein et al. 2010).

In dictionary learning, given a set of samples $\mathbf{Y} = [\mathbf{y}_1, \mathbf{y}_2, \ldots , \mathbf{y}_M]$, the objective is to find a dictionary $\mathbf{A}$ that provides the best representation for each sample in this set. Mathematically, it can be described by Eq. (9),

$$\begin{aligned}&\mathop {\text {min}}_{\mathbf{A}, \mathbf{X}}\Vert \mathbf{Y} - \mathbf{AX}\Vert _F^2 = \mathop {\text {min}}_{\mathbf{A}, \{\mathbf{x}_i\}_{i=1}^{M}}\sum _{i=1}^{m}\Vert \mathbf{y}_i - \mathbf{A}\mathbf{x}_i\Vert _2^2 \nonumber \\&\quad \text {subject to} \quad \Vert \mathbf{x}_i\Vert _0 \le k_0, 1 \le i \le M. \end{aligned}$$

(9)

where $\mathbf{X} = [\mathbf{x}_1, \mathbf{x}_2, \ldots , \mathbf{x}_M]$ is the sparse coefficient. $\Vert \cdot \Vert _F^2$ represents the Frobenius norm defined in Eq. (10).

$$\begin{aligned} \Vert \mathbf{X}\Vert _F^2 = \sqrt{\sum _{ij}\mathbf{X}_{ij}^2} \end{aligned}$$

(10)

Commonly used algorithms to find such dictionary are the MOD (Engan et al. 1999) and K-SVD (Aharon et al. 2006) algorithms. Both MOD and K-SVD are iterative methods and they alternate between sparse-coding and dictionary update steps. MOD updates all the atoms simultaneously by solving a quadratic problem and usually suffers from the high complexity of the matrix inversion. Contrarily, K-SVD updates the dictionary atom-by-atom, thereby achieving more efficient solution. Therefore, K-SVD is adopted in the current study and details about this method are presented as follows Bruckstein et al. (2009).

• Step 1: Set the iteration counter $k = 0$, the column index $j_0 = 1$ and initialize $\mathbf{A}_{(0)} \in \mathbb {R}^{n\times m}$ either by using random entries or using m randomly chosen examples.

• Step 2: Increment k by 1 and use OMP to approximate the solution of Eq. (11) to obtain sparse representation $\mathbf{x}_i$ for $1 \le i \le M$, which forms matrix $\mathbf{X}_{(k)}$.

  $$\begin{aligned} \hat{\mathbf{x}}_i = \text {arg}\mathop {\text {min}}_\mathbf{x}\Vert \mathbf{y}_i - \mathbf{A}_{(k-1)}\mathbf{x}\Vert _2^2, \quad \text {subject to} \Vert \mathbf{x}\Vert _0 \le k_0 \end{aligned}$$

  (11)

• Step 3: Define the group of examples that use the atom $\mathbf{a}_{j_0}$ as Eq. (12).

  $$\begin{aligned} {\varOmega }_{j_0} = \{i|1 \le i \le M, \mathbf{X}_{(k)}[j_0, i] \ne 0\} \end{aligned}$$

  (12)

• Step 4: Compute the residual matrix using Eq. (13), where $\mathbf{x}^j$ are the jth rows in the matrix $\mathbf{X}_{(k)}$.

  $$\begin{aligned} \mathbf{E}_{j_0} = \mathbf{Y} - \sum _{j \ne j_0}\mathbf{a}_j\mathbf{x}_j^T \end{aligned}$$

  (13)

• Step 5: Restrict $\mathbf{E}_{j_0}$ by choosing only the columns corresponding to ${\varOmega }_{j_0}$, and obtain $\mathbf{E}_{j_0}^{R}$.

• Step 6: Apply SVD decomposition $\mathbf{E}_{j_0}^R = \mathbf{U}\varvec{{\varDelta }}\mathbf{V}^T$. Update the dictionary atom $\mathbf{a}_{j_0} = \mathbf{u}_1$ ($\mathbf{u}_1$ is the first column in $\mathbf{U}$) and the representations by $\mathbf{x}_R^{j_0} = \varvec{{\varDelta }}[1, 1]\cdot \mathbf{v}_1$ ($\mathbf{v}_1$ is the first column in $\mathbf{V}$).

• Step 7: Repeat Step 3 to Step 6 for $j_0 = 1, 2, \ldots , m$ to update the columns of the dictionary and obtain $\mathbf{A}_{(k)}$.

• Step 8: If $\Vert \mathbf{Y} - \mathbf{A}_{(k)}\mathbf{X}_{(k)}\Vert _F^2$ is smaller than a preselected threshold or the iteration count reach the predefined value, stop the algorithm. Otherwise, apply another iteration from Step 2 to Step 7.

Fault feature extraction based on WPT and sparse representation

WPT is able to identify defect-induced transient components embedded within the bearing vibration data (Gao and Yan 2006), and features extracted from wavelet coefficients of WPT have also been widely used for characterizing machine faults (Zarei and Poshtan 2007; Bokoski and Juricic 2012). These features are simple and always lead to fast algorithms, but fall short in well matching the structures in the analyzed data (Lewicki and Sejnowski 2000). Sparse representation as an information-oriented signal processing technique benefitting from dictionary learning can capture the data structure of the learning signals and hide it in atoms. The approximation of the input signal depends on the activation of the atoms. Considering WPT is effective to reflect the unique fault-induced patten for each fault type, if we approximate different classes by a specific dictionary, the final reconstruction residuals will be distinguishable due to its different intrinsic data structure. Driven by this idea, a feature extraction method for fault diagnosis is proposed in this section, which is composed of three main parts, namely, WPT band selection, dictionary learning and SWRR feature extraction.

Fig. 3

Illustration of the energy distribution of a WPT spectrum

WPT frequency band selection

As described in “WPT” section, WPT decomposes a signal into several subbands and each subband covers parts of the frequency information successively. Generally, fault impulses will be concentrated in some specific frequency bands that display local energy concentration as well as fault features. Frequency bands outside the region carry insignificant information that will decrease computational efficiency. Therefore, we are only concerned with those informative subbands for feature learning. The fault-related frequency band can be selected by the distribution of average energy for each subband. Suppose a signal has m subbands $\{\mathbf{w}^{(1)}, \mathbf{w}^{(2)}, \ldots , \mathbf{w}^{(m)}\}$, the average energy of the ith subband with l(i) points can be calculated as shown in Eq. (14).

$$\begin{aligned} \text {AE}(i) = \frac{E_i}{E_{\text {total}}} = \frac{\left( \sum _{j=1}^{l(i)}w^{(i)}(j)^2\right) /l(i)}{\sum _{i=1}^{m}\left( \left( \sum _{j=1}^{l(i)}w^{(i)}(j)^2\right) /l(i)\right) } \end{aligned}$$

(14)

Considering the case shown in Fig. 3, energy in subbands 7–10 is much larger than the others, which means these subbands contain the major vibration information of the signal. Therefore, these frequency bands should be selected for further analysis. In practice, the WPT band should cover the frequency information of all fault types, thus, the final result is determined by the union of the frequency bands representing different faults.

Feature extraction

Benefiting from dictionary learning, sparse coding will find concise, high-level representations of input signals (Aharon et al. 2006). Generally, each fault class has its corresponding sparse representation. A dictionary that well matches the structure of data can lead to better sparse representation with high sparsity and small residual. If we reconstruct the signal by using a specific dictionary with certain sparsity, the residual will be different for different fault signals. This result stems from the data structure of the analyzed signals expressing dissimilarity in different degrees, thus activating the atoms of dictionary to different extents. Given dictionary $\mathbf{A}$, a sparse representation of signal $\mathbf{y}$ can be achieved by solving Eq. (4). By denoting the reconstruction signal $\hat{\mathbf{y}} = \mathbf{A}\mathbf{x}$, the residuals are defined as Eq. (15).

$$\begin{aligned} r = \sqrt{\frac{\sum _{i = 1}^n(y(i) - \hat{y}(i))^2}{n}} \end{aligned}$$

(15)

The dictionary should be designed properly to realize classification. For bearing fault diagnosis, all fault signals can be considered the superposition of the fault-related part and healthy part in some degree. The data structure for healthy signals with few impulses is more discriminative among others. Therefore, learning a dictionary from the healthy signal for further diagnosis is reasonable. In the current study, considering the merits of WPT in bearing diagnosis, the dictionary will be trained by the selected WPT coefficients of the healthy signal. The general frame for SWRR feature extraction is illustrated in Fig. 1. Suppose p fault-related frequency bands are selected for each sample by “WPT frequency band selection” section, the detailed process can be summarized as follows:

• Step 1: Performing K-SVD on each of the selected WPT subbands from healthy samples to obtain corresponding p dictionaries $\mathbf{A}_i\,(i = 1, 2, \ldots , p)$.

• Step 2: Use $\mathbf{A}_i$ to calculate the sparse representation of each sample. The coefficients are solved by OMP.

• Step 3: Calculate the reconstruction residuals $r_i\,(i = 1, 2,$ $\ldots , p)$ to obtain the SWRR feature vector $[r_1, r_2,$ $\ldots , r_p]$.

The practicability and advantages of SWRR features will be confirmed by the experiments described in “Engineering validation” section.

Engineering validation

Bearing case I

Data instruction

The SWRR feature is first evaluated by the test data of rolling element bearings from the Case Western Reserve Lab (CWRU). This data set has been analyzed by a number of other researchers (Lei et al. 2008; He 2013) and considered as a benchmark. The experimental apparatus is presented in Fig. 4. It consists of the following main parts: a 2 hp motor on the left, a torque transducer and a dynamometer in the middle and a load motor on the right. The testing groove ball bearing supports the motor shaft at the drive end. Vibration data are collected by accelerometers attached to the housing with magnetic bases. Sampling frequency is set at 12 kHz. Single point faults are introduced to the test bearings using electro-discharge machining with fault diameters of 0.007, 0.014, 0.021 and 0.028 in. In this study, bearings with 0.007 fault diameter were used to evaluate the proposed method. Four different bearing states, namely, healthy, rolling-element defect, inner-race defect and outer-race defect were simulated in the test under four different loads (0, 1, 2 and 3 hp). The motor speeds varied under different loads. Typical waveforms of the samples from the four cases are illustrated in Fig. 5.

Fig. 4

Experimental setup for acquiring vibration signals of bearing case I

Fig. 5

Typical waveforms of signals in bearing case I

In this case, 50 samples, each containing 1024 points, are first collected from the healthy signal under one load condition. These 200 samples are used for dictionary learning, which are denoted as $S_0$. Thereafter, 50 samples, each containing 1024 points, are collected for one fault type under one load condition (samples from healthy signal are different from those used for dictionary learning), thus, totally 800 ($50 \times 4_\text {loads} \times 4_\text {classes}$) samples are collected, with 200 samples in each health condition. 100 samples are randomly selected from each state to construct the training dataset and the remaining 100 samples are used for testing, thereby achieving a 400-sample training set ($S_1$) and a 400-sample testing set ($S_2$). The ratio of training and testing sample number is 1:1 to effectively evaluate the classification model as well as highlight the advantage of the proposed feature (He 2013).

WPT subband selection for bearing case I

In this case, a 4-level WPT is performed on the signal. Results for defective signals are shown in Fig. 6a, c, which display the WPT spectrums as well as the corresponding energy distributions. The healthy signal is demonstrated in Fig. 6d. The energy-concentrated subbands are 7–10 for signals with defects in the rolling element, 7–11 for signals with defects in the inner and outer raceways. According to the theory in “WPT frequency band selection” section, subbands 7–11 are selected for distinguishing different fault types, which cover most of the interested vibration information.

Fig. 6

WPT spectrums and the corresponding energy distribution of different health conditions in bearing case I: a rolling-elements defect; b inner-raceway defect; c outer-raceway defect and d healthy

Dictionary learning for bearing case I

The dictionary is learned from the selected WPT subbands of $S_0$ by solving Eq. (9). In this case, five subbands (subbands 7–11) are selected, indicating five dictionaries should be trained, respectively. For a certain subband, considering a signal has a length of 1024, each subband of the 4-level WPT should has a length of $1024/2^4 = 64$, thus achieving a $64 \times 200$ training set $\mathbf{Y}_i$ (each column in $\mathbf{Y}_i$ indicates a subband of a sample). $\mathbf{A}_i$ measuring $n \times m$ generally satisfies $m>n$, n is set to be 64 and m is set to 120 accordingly. Sparsity level T could be set as $T \le n/10$, and is set at 12 in this case. K-SVD can be stopped by monitoring the reconstruction residue or the iteration number as presented in Step 8 of the algorithm (“Dictionary learning” section). In this study, we choose to control the iteration number because it is simple and intuitive. The iteration number is set at 80, which is enough for convergence, and the reconstruction residuals for the 5 subbands based on the corresponding dictionaries are presented in Fig. 7. The reconstruction residuals converge to a small value for all the 5 subbands, thus indicating that the learned dictionaries can successfully capture the characteristics of the training set. Atoms in this dictionary are most likely to be actived to approximate the learned class of data. In our research, we use the dictionary learned from healthy signal because of its discriminability of different health conditions. The fault-induced impulses of different classes activate the atoms in the dictionary in different degrees, thus leading to the difference of reconstruction residuals for each subband, which can be regarded as a reflection of fault information.

Fig. 7

Reconstruction residuals during the K-SVD process for bearing case I

Fig. 8

SWRR features for different subbands in bearing case I

Fig. 9

WPE features for different subbands in bearing case I

Fig. 10

Kurtosis features for different subbands in bearing case I

SWRR feature extraction for bearing case I

As discussed in “Feature extraction” section, SWRR feature can be calculated based on the learned dictionaries and WPT. Training set $S_1$ is first analyzed. The SWRRs for the selected WPT subbands of each sample are shown in Fig. 8. The SWRR features for healthy signals are distributed near zero, which can be viewed as a standard value. For defective signals, the SWRR features are clustered at a certain value that deviated from the standard value to different extents. This deviation is caused by the differences between healthy and defective signals, and the differences among defective signals are due to the different fault-induced data structure. The SWRR feature for the outer-race defect show relatively poor clustering performance, but the between-class distances are far enough to separate this class from the others. The combination of all SWRR features expresses the accumulated pattern dissimilarity in each fault-related subband, and the fault pattern recognition performance will be further discussed in “Classification evaluation” section.

To highlight the advantages of SWRR feature, two commonly used WPT-based features, namely, wavelet packet energy (WPE) (Ocak et al. 2007; Zarei and Poshtan 2007) and Kurtosis (Li et al. 2008), are calculated for comparison. These two features for the selected subbands are shown in Figs. 9 and 10. Both WPE and Kurtosis features exhibit overlaps in many subbands and show rather worse clustering performance than the SWRR feature. These two features are not as clear and regular as SWRR because they only focus on a specific characteristic, such as energy or impulse, whereas SWRR can comprehensively analyze the WPT results and capture the major structure of the data. A more precise evaluation of SWRR features can be found in the classification result in “Classification evaluation” section.

Table 1 Classification accuracy for different features of bearing case I

Classification evaluation

To investigate the effectiveness of SWRR features for fault diagnosis, the nearest neighbor classifier as one of the simplest and the most intuitive classifiers is employed (Gharavian et al. 2013). Nearest neighbor classifier is based on the intuitive concept that data instances of the same class should be closer in the feature space. It is conducted by calculating the distance of a new sample to all samples in the training data, and class is determined by the sample nearest to the new one.

As described in “Data instruction” section, samples are randomly selected to construct the training and testing dataset, which contains 400 samples, respectively. Cai et al. (2007) and Zheng et al. (2011) conducted the random selection for 20 times to evaluate algorithms for face recognition. In the current study, we randomly split the samples for 50 times to obtain a more convincing evaluation as did in Li et al. (2011). The best and mean classification accuracies of each type of feature based on the nearest neighbor classifier during the 50 runs are summarized in Table 1. It can be seen from Table 1 that the SWRR feature performs better than the other two features obviously. The best recognition rates of the nearest neighbor classifier achieved 100 percent by using SWRR features as the input vector. The mean classification rates were also steadily higher with 99.47 %, while the mean performances of WPE and Kurtosis are 98.17 and 95.65 %, respectively. The experiment results show that the proposed SWRR feature can reliably recognize different fault types of bearings. Moreover, SWRR feature exhibits great advantages in recognition accuracy over WPE and Kurtosis features, which makes it much more appealing for bearing fault diagnosis.

Bearing case II

Data instruction

To further confirm the reliability of the SWRR feature in bearing fault diagnosis, another experiment on rolling element bearings was conducted. Figure 11 illustrates the experimental setup.

Fig. 11

Experimental setup for acquiring vibration signals of bearing case II

Defect groove was separately set across the outer raceway, inner raceway and rolling element as presented in Fig. 12. The vibration signals including four working conditions (healthy, rolling-element defect, inner-raceway defect, outer-raceway defect) were acquired by accelerometers mounted on the outer case of the testing bearings with the sampling frequency of 10 kHz under four different rotation speeds (900, 1200, 1350, 1450 rpm). Typical waveforms of the four health conditions are illustrated in Fig. 13, A 200-sample dictionary learning set $S_0$, a 400-sample training set $S_1$ and a 400-sample testing set $S_2$, each containing 1024 points, are constructed using the same method as bearing case I.

Fig. 12

Defectives in bearing case II: a rolling-element defect; b inner-raceway defect and c outer-raceway defect

Fig. 13

Typical waveforms of signals in bearing case II

WPT subband selection for bearing case II

In this case, a three-level WPT is applied to the analyzed signal. The WPT spectrums and the corresponding energy distributions of defective bearing signals as well as the healthy signals are shown in Fig. 14. The energy-concentrated subbands are 3 to 5 for signals with defect in rolling element, 3 to 8 for signals with defect in inner and outer raceways. Therefore, subbands 3 to 8 are selected by the union of the three conditions for distinguishing different fault types.

Fig. 14

WPT spectrums and the corresponding energy distribution of different fault types in bearing case II: a rolling-elements defect; b inner-raceway defect; c outer-raceway defect and d healthy

Dictionary learning for bearing case II

A dictionary is learned from selected WPT subbands of $S_0$ by solving Eq. (9). In this case, six dictionaries that correspond to six selected subbands should be learned, respectively. Each subband of the 3-level WPT should has a length of $1024/2^3 = 128$, thus achieving a $128 \times 200$ training set $\mathbf{Y}_i$. The size of $\mathbf{A}_i$ is set at $128 \times 160$ and the sparsity level T is set at 15. During the 80 iterations of K-SVD, the reconstruction residuals for the six subbands based on the corresponding dictionaries are presented in Fig. 15. The reconstruction residuals consistently converge to a small value for all the 6 subbands, thus indicating the effectiveness of the learned dictionaries.

Fig. 15

Reconstruction residuals during the K-SVD process for bearing case II

Fig. 16

SWRR features for different subbands in bearing case II

Fig. 17

WPE features for different subbands in bearing case II

SWRR feature extraction for bearing case II

The SWRR features of training samples $S_1$ is presented in Fig. 16. The figure indicates that the clustering performance is good. Features in the same class are concentrated in a specific value that can separate them for the other classes, which shows the effectiveness of SWRR.

As a comparison, WPE and Kurtosis features for the selected subbands are shown in Figs. 17 and 18. However, these two features vary in a relative large range for samples in the same class, and show indistinct boundaries among different fault types, thus causing difficulty to precise fault pattern recognition. Accordingly, we can preliminarily infer that the SWRR features with more regular distributions will perform better than WPE and Kurtosis features. This result again confirms that SWRR features can precisely capture the major structure of the data.

Fig. 18

Kurtosis features for different subbands in bearing case II

Classification evaluation

The nearest neighbor classifier is still employed in this case to investigate the effectiveness of SWRR features for fault diagnosis. Similar to bearing case I, we conducted random sample selection for 50 times to obtain a convincing evaluation. The best and mean classification accuracies of each type of feature based on the nearest neighbor classifier over the 50 runs are summarized in Table 2. Comparing the three features, the SWRR feature is still more effective than WPE and Kurtosis. The best recognition rates of SWRR reaches the highest 100 %. The mean classification rates were also steadily higher with 99.27 %, which is much better than WPE and Kurtosis features with 97.95 and 94.90 %, respectively. The experiment results again exhibits the effectiveness and advantages of SWRR features for bearing fault classification.

Discussions

The main contribution of this study is the proposal of a new SWRR feature based on WPT and sparse representation theory. WPT is used to detect transient impulses of the signal, whereas sparse representation theory is employed to learn a dictionary from healthy signals and reflect fault types by reconstruction residuals (SWRR). This idea is mainly inspired by dictionary learning. Research has proven that exactly solving the unique dictionary is impractical but a stable dictionary is feasible (Aharon et al. 2006). Hence, learning a dictionary with a small enough objective function value can make atoms in dictionary with strong representativeness. The atom‘s role is weakened when the data structure of input signal is different, which leads to different reconstruction residuals. Therefore, combining learning residuals from WPT subbands as the feature is reasonable. Experiments have comprehensively shown the effectiveness and benefits of SWRR features in fault type classification.

Table 2 Classification accuracy for different features of bearing case II

In this study, the dictionaries are learned from healthy signals and the number of dictionaries is determined by the fault-related WPT subbands alone regardless of the situation number. Generally, fault-related information will concentrate in a small range in the time–frequency space. Therefore, the number of dictionaries won‘t be larger than 8 in most of the cases, thus proving the practicality of SWRR. Besides, a larger sample dimension p indicates more atoms in dictionary A (atom number $n>p$ as shown in Eq. (3)), which calls for more samples for training. WPT subband has a much smaller dimension than the original data as shown in “Engineering validation” section, which reduces the dictionary dimension as well as the need for sample number.

Our experiments were performed by using desktop computer with a dual-core AMD Athlon 7750 2.70 GHz CPU and 6 GB memory. For the dictionary learning process of each subband, time was less than 4 s for running 80 iterations for bearing case I (200 samples, each with 64 data points) and less than 8 s for bearing case II (200 samples, each with 128 data points). The following SWRR feature extraction part took about 0.2 s for both cases. Therefore, with a learned dictionary, the feature extraction part is fast that can fit the conventional offline and online diagnosis.

In this study, only the intuitive nearest neighbor classifier is applied for classification to highlight the benefits of SWRR features. In practical diagnosis, more advanced intelligent classifiers, such as neural network (Zhang et al. 2013; Wang and Cui 2013; Bilski 2014) and support vector machine (Cui and Wang 2011) can be used for better classification performance, particularly for complex fault diagnosis.

Conclusion

This study proposes a SWRR feature extraction scheme for rolling element bearing diagnosis based on WPT and sparse representation theory. In this scheme, WPT can explore fault-induced impulses embedded in the signals, and fault characteristics can be reflected by sparse representation theory in a novel way. Compared with traditional WPE and Kurtosis features that only focus on a specific aspect of the signal, SWRR has significant advantage by comprehensively exploring data structure. In the diagnosis experiments with two rolling bearing cases, SWRR feature is evaluated to have clear and regular feature distribution, outperforming WPE and Kurtosis features. Furthermore, the practical application of SWRR in distinguishing different bearing faults by the nearest neighbor classifier further confirms its merits with the highest recognition rate. All evidence indicates that the SWRR feature has valuable practicality and significant advantages in rolling bearing fault diagnosis.