A reinforcement learning based approach for a multiple-load carrier scheduling problem

Abstract

This paper studies the problem of scheduling a multiple-load carrier which is used to deliver parts to line-side buffers of a general assembly (GA) line. In order to maximize the reward of the GA line, both the throughput of the GA line and the material handling distance are considered as scheduling criteria. After formulating the scheduling problem as a reinforcement learning (RL) problem by defining state features, actions and the reward function, we develop a Q($\lambda$) RL algorithm based scheduling approach. To improve performance, forecasted information such as quantities of parts required in a look-ahead horizon is used when we define state features and actions in formulation. Other than applying traditional material handling request generating policy, we use a look-ahead based request generating policy with which material handling requests are generated based not only on current buffer information but also on future part requirement information. Moreover, by utilizing a heuristic dispatching algorithm, the approach is able to handle future requests as well as existing ones. To evaluate the performance of the approach, we conduct simulation experiments to compare the proposed approach with other approaches. Numerical results demonstrate that the policies obtained by the RL approach outperform other approaches.

Introduction

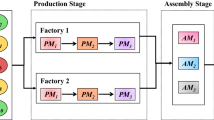
A general assembly (GA) line is a system where parts are assembled into products. As an example, the GA line shown in Fig. 1 consists of a series of six assembly workstations. Before the GA line, there are incoming semi-products from upstream manufacturing processes. A semi-product will be first loaded to Workstation 1 of the GA line and then to Workstation 2 and go on. At each workstation, operators pick up certain types of parts from line-side buffers at the station and assemble them into the semi-product. The semi-product is then transferred to the next workstation or to the warehouse when it becomes a final-product after the assembly operation in Workstation 6 is finished. Because capacities of line-side buffers are limited, a dolly train is used by the material handling system (MHS) of the GA line to deliver parts from a stocking area to the line-side buffers. The dolly train is a multiple-load carrier that can carry multiple containers of parts at a time. To maximize the profit of the GA line, the MHS has to replenish parts in time to make sure that there are enough parts for assembly. Otherwise the throughput of the GA line cannot be maximized. Furthermore, because material handling cost plays an important part of manufacturing cost (Joe et al. 2012), the MHS has to minimize material handling cost. Therefore, an efficient material handling scheduling approach is very important for the GA line. In this paper, we study the problem of scheduling the dolly train in a real-time fashion. Because we aim at optimizing the profit of the GA line, both the throughput of the GA line and the material handling distance are considered.

Fig. 1

A general assembly line

However, the material handling scheduling problem considered here is very difficult. Firstly, according to our previous study (Chen et al. 2011), it’s very difficult to optimize both criteria at the same time even if it’s not impossible. Higher throughput usually means longer material handling distance while shorter distance often indicates lower throughput. Secondly, due to the fluctuation and variation of market requirement and production plans, the consumption rates of parts are not constant from a short-term perspective. Therefore we should find a policy that is able to schedule according to the real-time status of the GA line. Thirdly, information necessary for scheduling of the entire scheduling period is not available before scheduling in practice. Actually, at each decision epoch, the scheduling system can only access to information within a short period of time. Hence, we need to make decisions based on local information despite that we focus on long-term performance. As a result, it’s important but difficult to evaluate the performance of a decision from a long-term perspective. Furthermore, scheduling multiple-load carriers is considered to be far more complicated than scheduling unit-load carriers (Berman et al. 2009).

The importance and the difficulties of material handling scheduling problems have attracted a lot of attentions. In the literature, different scheduling approaches have been developed. For example, Ozden (1988) use a simple pick-all-send-nearest rule for a carrier scheduling problem. There are also other researches study simple scheduling approaches which consider only a few attributes of system status (e.g., Occena and Yokota 1993; Nayyar and Khator 1993). Sinriech and Kotlarski (2002) categorize multiple-load carrier scheduling rules into three categories, namely idle carrier dispatching rules, load pick-up rules and load drop-off rules.

To further improve the performance of MHSs, more complex methods have been proposed (e.g. Potvin et al. 1992; Chen et al. 2010; Dang et al. 2013). Such approaches include fuzzy logic based methods (Kim and Hwang 2001), genetic algorithm based methods (Orides et al. 2006), particle swarm optimization based methods (Belmecheri et al. 2013), neural network based methods (Min and Yih 2003; Wang and Chen 2012), hybrid meta-heuristic methods (Vahdani et al. 2012), etc. Vis (2006), Le-Anh and De Koster (2006) and Sarin et al. (2010) provide comprehensive reviews on material handling scheduling problems.

Recently, because of RL methods’ ability in finding optimal/near-optimal policies in dynamic environments, RL algorithms have been applied to production scheduling problems (e.g., Wang and Usher 2005; Gabel and Riedmiller 2011; Zhang et al. 2012). Li et al. (2002) apply an RL algorithm based on Markov games to determine an agent’s best response to others’ response in an automated-guided vehicle dispatching problem. Jeon et al. (2011) consider the problem of determining shortest-time routes for vehicles in port terminals. They use Q-learning methods to estimate waiting times of vehicles during travelling. However, previous studies have not thoroughly explored the application of RL algorithms to material handling scheduling problems, especially to the multiple-load carrier scheduling problem considered in this paper.

Furthermore, most of the studies in the literature focus on manufacturing systems where MHSs are used to transfer materials between workstations. In these type of manufacturing systems, a material handling request is generated whenever a workstation completes a load (see Ho et al. 2012 for an example). It’s quite obvious to do so because after a workstation completes a load, the load should be delivered to another workstation for processing. On the other hand, for the GA line we study here, when to generate material handling requests is a question need to be answered first by scheduling approaches. In automotive industry, the reorder-point (ROP) policy is usually applied in practice. With the ROP policy, a request for the $i$th type of part, $P_i$, will be generated when the inventory level of $P_i$’s buffer is no more than its reorder point, i.e., ${ buf}_i \le { RP}_i$. However, using the ROP policy in a dynamic environment could cause problems sometimes. For instance, if ${ buf}_i = 0$ but $P_i$ is not required in the near future, requesting for $P_i$ is not necessary and could lead to extra cost (such as holding cost).

Although it’s impossible to obtain information of the entire scheduling period before scheduling in practice, information in a look-ahead horizon is usually available even in a stochastic environment. To improve performance of MHSs in such dynamic and stochastic manufacturing environments, it’s necessary to develop look-ahead methods that consider forecasted information (Le-Anh et al. 2010). De Koster et al. (2004) show that using look-ahead information leads to significant improvement in the performance for a unit-load carrier scheduling problem. On the other hand, Grunow et al. (2004) develop an algorithm which considers orders initiated in a look-ahead time window for a multiple-load AGV dispatching problem. However, because these studies pay no attention to the problem of generating material handling requests, we need to further investigate how to incorporate look-ahead information in material handling request generating policies.

Moreover, in most studies, MHSs are only allowed to handle existing requests. This is because every request corresponds to a load completed by a workstation in those studies. And it’s impossible to move a load that is not yet output from a workstation. However, there is no such restriction for the case we study here. The dolly train is allowed to replenish $P_i$ even though there is no request for $P_i$ yet. Actually, it’s beneficial to do so sometimes. For instance, consider two types of parts, $P_1$ and $P_2$, whose buffer locations are close to each other. Assume that there is a request for $P_1$ but no request for $P_2$ at time $t_0$. Also assume that ${ buf}_2$ is very close to ${ RP}_2$, which means a request for $P_2$ will soon be generated shortly after $t_0$. Then it’s better to replenish $P_1$ together with $P_2$. Otherwise the dolly train has to start a new trip for $P_2$ after $P_1$ is replenished. Hence, it’s necessary to develop an approach to consider both existing requests and future requests.

To address the issues above, we first propose a new method to generate material handling requests based on forecasted information in a look-ahead horizon. We also propose a heuristic dispatching algorithm that is able to consider future requests as well as existing requests. Using the new request generating policy and the heuristic algorithm, we formulate the material handling scheduling problem as a reinforcement learning (RL) problem by defining state features, actions and reward function. Finally, we apply a Q($\lambda$) algorithm to find the optimal policy of the material handling scheduling problem.

The remainder of the paper is organized as follows. The next section describes the scheduling problem investigated in this paper and formulates it as an RL problem. After problem formulation, the RL based scheduling approach is proposed. Next, simulation experiments are conducted to evaluate the performance of the proposed approach. The last section draws conclusions and highlights areas for further research.

Problem formulation

Notations

The following notations will be used throughout this paper:

$N_w$ :

the number of workstations in the GA line;

$N_p$ :

the number of part types will be assembled into semi-products; also the number line-side buffers;

$N_A$ :

the number of product models;

$N_c$ :

the capacity of a dolly train, i.e., the maximum number of containers a dolly train can handle at the same time;

${ CT}$ :

the cycle time of the GA line;

$P_i$ :

the $i$th type of parts;

${ SPQ}_i$ :

standard pack quantity of $P_i$, i.e., the quantity of $P_i$ that will be loaded to one container in the stocking area; also the capacity of $P_i$’s line-side buffer;

${ buf}_i$ :

the inventory level of $P_i$’s line-side buffer;

${ ULL}_i$ :

the threshold that determines whether extra unloading time is needed to unload $P_i$

$t_{ load}$ :

loading time per container;

$t_{{ unload}}$ :

unloading time per container;

$t_{ extra}$ :

extra unloading time per container

$d_i$ :

the distance between the stocking area and $P_i$’s line-side buffer;

$T$ :

the length of the entire scheduling period;

$M$ :

the throughput of the GA line in $T$;

$w_M$ :

the coefficient of $M$;

$D$ :

the material handling distance in $T$;

$w_D$ :

the coefficient of $D$;

$v$ :

the velocity of a dolly train;

$l_i$ :

the maximum number of assembly orders that $P_i$’s line-side buffer can support without replenishment;

$W(i)$ :

the workstation that $P_i$ is assembled into semi-products;

$I({W,t})$ :

the no. of the semi-product that is the first to enter workstation $W$ after time $t$;

$B(j)$ :

the model of the $j$th semi-product;

$H({B,i})$ :

the quantity of $P_i$ required by a semi-product whose model is $B$;

$J(t)$ :

the no. of the latest semi-product arrived in the look-ahead period $[{t,t+L}]$;

$u_i$ :

the quantity of $P_i$ required by a semi-product on average;

${ RP}_i$ :

$P_i$’s reorder point defined in the ROP policy;

${ RP}_i^{L}$ :

$P_i$’s reorder point defined in the look-ahead based reorder point policy;

$n_{req}$ :

the number of material handling requests generated;

$t_{{ next}}$ :

the time left for the GA line to proceed to the next assembly cycle; $X=\left\{ {x_1 ,x_2,\ldots , x_n} \right\}$ is a drop-off sequence; $x_k \left( {k=1,2,\ldots , n} \right)$ is the type of parts in the $k$th container to deliver;

$n$ :

the number of loads to handle in a drop-off sequence;

$t_{{ total}}$ :

the amount of time to execute a drop-off sequence;

$t_{{ stop}}$ :

the amount of time that the GA line is not working during the execution of a drop-off sequence;

$t_a$ :

$t_a =t_{{ total}} -t_{{ stop}}$ is the actual working time of the GA line during the execution of a drop-off sequence;

${ SMD}_i$ :

the standard material handling distance to deliver a unit quantity of $P_i$;

${ ARQ}_i$ :

the actual replenished quantity of $P_i$;

$d_{{ eff}} (X)$ :

the effective material handling distance during the execution of $X$;

$d_{{ total}} (X)$ :

the total material handling distance to execute $X$;

$d_{ saved} (X)$ :

the total saved distance to execute $X$;

${ ASR}$ :

the average standard reward to assemble a unit product;

$\rho$ :

the standard reward rate;

${ SR}(X)$ :

the standard reward received during the execution of $X$;

${ ER}(X)$ :

the expected reward received during the execution of $X$;

$\tilde{r}(X)$ :

the expected reward rate during the execution of $X$;

$\mathbf{s}, \mathbf{{s}'}$ :

state vectors

$t_{{ wait}}$ :

the maximum amount of time that the dolly train should wait in the stocking area until the next decision epoch;

$N_a$ :

the number of actions;

$\phi _g (\mathbf{s})$ :

the $g$th Gaussian radial basis function (RBF);

$G$ :

the number of RBFs;

$\theta _g^a$ :

the weights of $\phi _g (\mathbf{s})$;

$\mathbf{C}_g$ :

the center of $\phi _g (\mathbf{s})$;

$\sigma _g$ :

the width of $\phi _g (\mathbf{s})$;

${\varvec{\Theta }}^{a}$ :

${\varvec{\Theta }}^{a}=( {\theta _1^a,\theta _2^a, \ldots , \theta _G^a} )^{T}$ is the vector of weights;

${\varvec{\Phi }}$ :

${\varvec{\Phi }}=({\phi _1 (\mathbf{s} ),\phi _2 (\mathbf{s} ),\ldots ,\phi _G (\mathbf{s} )})^{T}$ is the vector of RBFs;

$\mathbf{Y}(a)$ :

$\mathbf{Y}(a)=({y_1^a, y_2^a, \ldots , y_G^a })^{T}$ is a vector of the eligibility traces for action $a$;

Problem description

The multiple-load carrier scheduling problem considered in this paper can be described as follows. The GA line is a serial line consisting of $N_w$ workstations. The workstations are synchronized because of the usage of a synchronized conveyor transferring semi-products between workstations. Therefore, the cycle time ${ CT}$ is equal to the longest cycle time of the workstations; and the entire GA line will stop working whenever a workstation stops. During assembly, parts will be assembled into semi-products in these workstations. The GA line employs a dolly train whose capacity is $N_c$ to replenish parts. To schedule the dolly train, the MHS usually needs to (1) generate material handling requests based on a request generating policy (e.g., the ROP policy); (2) decide whether the dolly train should deliver parts or wait in the stocking area when it is idle; (3) select parts to deliver if “deliver” decision has been made; and (4) determine the drop-off sequence for the parts selected. Therefore, the multiple-load carrier scheduling problem involves four sub-problems. For clarity and simplicity, the following assumptions are made:

• (1) If the dolly train is idle, it must stay in the stocking area unless there are one or more material handling requests;

• (2) If the GA line is stopped because there is no enough parts for assembly, the dolly train is not allowed to be idle in the stocking area;

• (3) If the dolly train is busy, it must finish tasks currently assigned to it before it can be dispatched to handle new tasks;

• (4) Drop-off sequence of parts cannot be changed once it’s determined;

• (5) The dolly train’s velocity $v$ is constant;

• (6) The types of parts in different containers carried by the dolly train at the same time must be different;

• (7) Different types of parts cannot be mixed in the same container;

• (8) Breakdown and maintenance of the dolly train are not considered;

• (9) If the GA line is not stop and ${ buf}_i >{ ULL}_i$, it is not allowed to unload $P_i$;

• (10) It takes $t_{{ unload}}$ time units to unload $P_i$ if ${ buf}_i \le { ULL}_i$. Otherwise it takes $t_{{ unload}} +t_{ extra}$ time units, because more efforts are required in such cases;

• (11) ${ buf}_i$ is equal to ${ SPQ}_i$ right after $P_i$ is replenished;

• (12) The distance between the unloading point of $P_i$ and that of $P_j$ is given by $| {d_i -d_j }|$;

• (13) The first workstation (Workstation 1) will never starve;

• (14) The last workstation (Workstation $N_w$) will never be blocked;

• (15) The semi-products arrive to the GA line are numbered sequentially starting from 1; and

• (16) The information of semi-products that will arrive to the GA line in the next $L$ time units is assumed to be available.

The objective of the problem is to maximize $f_T$, the total reward of a given scheduling period $T$, i.e.,

$$\begin{aligned} f_T =w_M M-w_D D. \end{aligned}$$

(1)

Look-ahead based request generating policy

In this section, we first discuss the problem of generating material handling requests because it is the basis to make other decisions.

As described in Introduction, the MHS will monitor the inventory levels when the ROP policy is used. It will generate a request for $P_i$ if the following condition is met and there is no request for $P_i$ yet.

$$\begin{aligned} { buf}_i \le { RP}_i, \quad \forall i\in \left\{ {1,2,\ldots ,N_p } \right\} . \end{aligned}$$

(2)

When assembly orders arrive in a way that models of products distribute evenly over time, larger ${ buf}_i$ means longer remaining life of $P_i$’s buffer, i.e., $P_i$’s buffer can support more assembly cycles without replenishment. However, this is usually not the case in a dynamic environment where consumption rates of parts fluctuate frequently from a short-term perspective. Therefore, it’s possible to improve the performance of the scheduling system by using a better request generating policy in such an environment.

Since ${ buf}_i$ is not a good indicator of the remaining life of $P_i$’s buffer in a dynamic environment, we directly monitor the remaining lives of buffers instead of the inventory levels, i.e., the inequities (2) become

$$\begin{aligned} l_i \le { RP}_i^L , \quad \forall i\in \left\{ {1,2,\ldots ,N_p} \right\} . \end{aligned}$$

(3)

Then the request generating policy used in this paper can be described as: generate a request for $P_i$ if condition (3) is satisfied and there is no request for $P_i$ yet.

Unlike the inventory level, however, the remaining life of a buffer cannot be directly observed. In order to determine $l_i$ for each $P_i$, the following algorithm (Algorithm 1) is used.

Because the information of semi-products that arrive in the near future is required to calculate $l_i$ s in Algorithm 1, the request generating policy used in this paper is a look-ahead request generating policy (LRGP).

In order to analyze the computational complexity of Algorithm 1, let $n_{ orders} =J(t)-I({N_w ,t})$ be the number of semi-products currently in the GA line plus the number of semi-products that will arrive in the following $L$ time units. Then it takes $O({n_{ orders}})$ efforts in the Step 2. And since we have $N_p$ types of parts, it takes $O({n_{ orders} N_p })$ efforts to compute all the $l_i$ s.

A heuristic dispatching algorithm

After a “deliver” decision has been made by the MHS, dispatching approaches are used to select parts to deliver and determine their drop-off sequence. When requests correspond to outputs from workstations, it’s impossible to handle requests not yet generated because the corresponding loads don’t exist. Therefore, dispatching approaches used for such environments consider only existing requests. However, this is not the case for the problem we study in this paper. The MHS is allowed to replenish parts even though there are no requests for them. And as discussed in the Introduction, it could be beneficial to do so.

Because material handling requests are generated based on remaining lives of buffers, those types of parts that are requested should be given higher priorities than others that are not. Otherwise the GA line might stop working because the parts requested replenishment might become out of stock. Assume that there exists a load pick-up rule $R_{ PICK}$ and a load drop-off rule $R_{ DROP}$ to select requests and determine an initial drop-off sequence. Then the dispatching problem can be simplified as selecting types of parts that are not yet requested and then inserting them to the initial drop-off sequence.

To implement the above idea, we first define the expected reward rate $\tilde{r}$ for a drop-off sequence.

Let $X=\left\{ {x_1 ,x_2 ,\ldots ,x_n } \right\}$ be a drop-off sequence. And “executing” $X$ means delivering all the loads in $X$. Let ${ SMD}_i$, which is given by Eq. (4), be the standard material handling distance to deliver a unit quantity of $P_i$; and ${ ARQ}_i$, which is given by Eq. (5), be the actual replenished quantity of $P_i$. Then $d_{{ eff}}( X )$ is defined by Eq. (6).

$$\begin{aligned} { SMD}_i&= {2d_i }/{{ SPQ}_i }\end{aligned}$$

(4)

$$\begin{aligned} { ARQ}_i&= { SPQ}_i -{ buf}_i\end{aligned}$$

(5)

$$\begin{aligned} d_{{ eff}} \left( X \right)&= \sum _{k=1}^n {{ SMD}_{x_k } { ARQ}_{x_k } }\nonumber \\&= \sum _{k=1}^n {\frac{2d_{x_k } }{{ SPQ}_{x_k } }\left( {{ SPQ}_{x_k } -{ buf}_{x_k } } \right) } \end{aligned}$$

(6)

It is easy to see that the $d_{{ eff}} (X)$ equals to the total standard material handling distance to deliver the same amount of parts as $X$ does. Then $d_{ saved} (X)$ is defined by Eq. (7).

$$\begin{aligned} d_{ saved} \left( X \right) =d_{{ eff}} \left( X \right) -d_{{ total}} \left( X \right) . \end{aligned}$$

(7)

For two different sequences $X$ and ${X}'$ whose loads are the same, i.e., $\forall x_k \in X\Leftrightarrow x_k \in {X}'$, $X$ is considered to be more efficient than ${X}'$ in terms of material handling distance if $d_{ saved} (X)>d_{ saved} ( {{X}'})$, because the distance required to replenish the same amount of parts is relatively shorter by executing $X$ instead of ${X}'$.

According to Eqs. (1) and (4), the average standard reward to assemble a unit product is ${ ASR}=w_M -w_D \sum _{i=1}^{N_p } {u_i { SMD}_i }$. Therefore we have $\rho ={{ ASR}}/{{ CT}}$. And the standard reward received during the execution of $X$ is given by

$$\begin{aligned} { SR}\left( X \right) =\rho t_{{ total}} . \end{aligned}$$

(8)

Then the expected reward ${ ER}(X)$ is defined as

$$\begin{aligned} { ER}\left( X \right)&= { SR}\left( X \right) -\rho t_{{ stop}} +w_D d_{ saved} \left( X \right) \nonumber \\&= \rho t_a +w_D d_{ saved} \left( X \right) , \end{aligned}$$

(9)

Finally, the expected reward rate $\tilde{r}(X)$ is given by

$$\begin{aligned} \tilde{r}\left( X \right) ={{ ER}\left( X \right) }/{t_{{ total}} }. \end{aligned}$$

(10)

A drop-off sequence $X$ can be considered to be more efficient with a greater $\tilde{r}(X)$ because the GA line receives more reward per unit time in such case. Based on this idea, we propose the following heuristic algorithm (Algorithm 2) to pick up loads and determine their drop-off sequence.

With the above algorithm, the dolly train will always pick up as many requests as possible. If its capacity is not exceeded, it will also select other types of part not yet selected when the expected reward rate can be improved to do so (i.e., a greater $\tilde{r}(X)$ is achieved).

Note that $R_{ PICK}$ and $R_{ DROP}$ are not specified in Algorithm 2. This allows us to specify suitable rules in different situations. After all, there is no such rule that is globally optimal (Montazeri and Wassenhove 1990). By specifying different load pick-up rules and load drop-off rules in the above algorithm, we can also define different actions for the RL problem. Because the shortest-slack-time-first-picked (SSFP) rule and the shortest-distance-first-picked (SDFP) rule outperform other load pick-up rules and the shortest-distance-first-delivered (SDFD) rule outperforms other load drop-off rules according to Chen et al. (2011), we will use the SSFP rule and the SDFP rule as load pick-up rules and the SDFD rule as the load drop-off rule to define the actions.

The worst-case computational complexity of Algorithm 2 is analyzed as follows. Because that the exact load pick-up and load drop-off rules are specified later, we focus on analyzing Step 4, the process to generate new drop-off sequences. In the inner loop of Step 4.b, we have $n+1\le N_c$ because the capacity of the dolly train is $N_c$. Therefore it takes $O({N_c N_p })$ efforts in Step 4.b. After Step 4.b, $X$ either remains the same or is replaced by a new candidate sequence ${X}'$ which satisfies $|{{X}'} |=|{X^*}|+1$. The outer loop of Step 4 will stop in the former case and will continue if $|X|<N_c$ in the latter one. Hence, it takes $O({N_c})$ efforts in the outer loop of Step 4. Therefore the worst-case computational complexity of Step 4 is $O({N_c^2 N_p } )$.

Reinforcement learning formulation

In order to apply RL algorithms to scheduling problems, we need to formulate the scheduling problems as RL problems. There are three major steps in the formulation, including defining state features, constructing actions and defining the reward function (Zhang et al. 2011).

State features

The objective of an RL algorithm is to find an optimal policy that is able to choose optimal actions for any given state. Theoretically, anything that is variable and related to the GA system (either the GA line itself or the MHS), such as status of workstations, status of the dolly train, information of semi-products that are being assembled currently, incoming assembly orders, etc., can be considered as states. However, for a complex manufacturing system, it’s impossible to take all kinds of such information into consideration and it would make the RL problem way too complex. Therefore, we need to carefully define state features concisely such that the state space is compressed and it’s easier for learning. More importantly, they should be able to represent the major characteristics of the GA system that impact the scheduling of MHS considerably. In this paper, we define the state features as follows:

State feature 1 ($s_1$). Let $s_1$ indicate if the GA line is stopped and define

$$\begin{aligned} s_1 =\left\{ {{\begin{array}{l@{\quad }l} 0&{} {\hbox {if the GA line is working}} \\ 1&{} {\hbox {if the GA line is stopped }} \\ \end{array} }} \right. . \end{aligned}$$

(11)

State feature 2 ($s_2$). Let $t_{{ next}}$ denote the time left for the GA line to proceed to the next assembly cycle and define

$$\begin{aligned} s_2 =t_{{ next}} /{ CT}. \end{aligned}$$

(12)

State feature 3 ($s_{3,i}, i\in \left\{ {1,2,\ldots , N_p } \right\} ).~s_{3,i}$ is defined as

$$\begin{aligned} s_{3,i} ={{ buf}_i }/{{ SPQ}_i }. \end{aligned}$$

(13)

State feature 4 ($s_{4,i} , i\in \{ {1,2,\ldots ,N_p } \})$. Let $l_i^{{ MAX}}$ be the maximum possible value of $l_i$ which is given by

$$\begin{aligned} l_i ^{{ MAX}}=\left\lceil {\frac{L}{{ CT}}+W\left( i \right) -1+\frac{\left( {{ SPQ}_i +1} \right) }{u_i }} \right\rceil . \end{aligned}$$

(14)

Then $s_{4,i}$ is defined as

$$\begin{aligned} s_{3,i} ={l_i }/{l_i ^{{ MAX}}}. \end{aligned}$$

(15)

With the definition of the state features, the system state at time $t$ can be represented as

$$\begin{aligned} \mathbf{s}_t&= \left( s_1 ,s_2 ,s_{3,i} \left( {i=1,2,\ldots ,N_p } \right) ,\right. \nonumber \\&\quad \left. s_{4,i} \left( {i=1,2,\ldots ,N_p } \right) \right) . \end{aligned}$$

(16)

Note that actions are taken only at decision epochs. We call time $t$ a decision epoch if one of the following conditions is met:

• (1) The dolly train becomes idle;

• (2) The GA line is stopped because a certain type of part becomes out of stock; and

• (3) A new material handling request is generated.

The states at decision epochs are also called decision states.

Actions

The actions of an RL problem are decisions made at decision epochs. There are a lot of decisions can be made at decision epochs for the multiple-load carrier scheduling problem we study here, such as waiting in the stocking area, dispatching the dolly train to deliver $P_1$, dispatching the dolly train to deliver $P_2$ and $P_3$ with a drop-off sequence $X=\left\{ {2,3} \right\}$, dispatching the dolly train to deliver $P_3$ and $P_4$ with a drop-off sequence $X=\left\{ {4,3} \right\}$ and so on. It would be inefficient for learning if we define each possible decision as an action. Because the dolly train is either idle in the stocking area or dispatched to replenish parts, we define actions as follows:

Action 1 ($a_1$). Wait in the stocking area until one of the following conditions is met:

• (1) The dolly train has been idle for more than $t_{{ wait}}$ time units since the last Action 1 is taken; and

• (2) The system state transits to a new decision state.

Action 2 ($a_2$). Use Algorithm 2 to pick up loads and to determine the drop-off sequence with the SSFP rule as $R_{ PICK}$ and the SDFD as $R_{ DROP}$, deliver the loads then come back to the stocking area.

Action 3 ($a_3$). Use Algorithm 2 to pick up loads and to determine the drop-off sequence with the SDFP rule as $R_{ PICK}$ and the SDFD as $R_{ DROP}$, deliver the loads then come back to the stocking area.

After defining the actions, the action space can be represented as $\mathbf{A} = \left\{ {a_1 ,a_2 ,a_3 } \right\}$. And the number of actions is $N_a = \left| \mathbf{A} \right|$.

Reward function

Because the objective of the RL problem is to maximize the accumulated reward such that the reward of the GA line can be maximized, the definition of the reward function should be also related to both throughput and the material handling distance.

Consider the case of the state of the system at decision epoch $t, \mathbf{s}$, transiting to a new state, $\mathbf{s}^{\prime }$, at the next decision epoch $t^{\prime }$ after action $a_t \in \mathbf{A}$ is performed at $t$. Based on Eq. (9), the reward received in the period of $[{t,t^{\prime }}]$ is defined as

$$\begin{aligned} r\left( {\mathbf{s},a_t ,\mathbf{s}^{\prime }} \right) =\rho \left( {t^{\prime }-t-t_{{ stop}} } \right) +w_D d_{ saved} . \end{aligned}$$

(17)

The reinforcement learning based scheduling approach

In the previous section, we formulate the multiple-load carrier scheduling problem as an RL problem. To apply RL in scheduling, we need to solve the RL problem first. Because the time spent in state transition is part of the reward function, algorithms developed for problems in MDP context cannot be applied to the RL problem directly. In order to solve the RL problem, the discount factor $\gamma$ is replaced by $e^{-\beta ( {t^{\prime }-t})}$ and the reward received in the period of $[{t,t^{\prime }}]$ becomes

$$\begin{aligned} r\left( {\mathbf{s},a_t ,\mathbf{s}^{\prime }} \right) =\int _t^{t^{\prime }} {e^{-\beta \left( {\tau -t} \right) }\xi \left( \tau \right) } d\tau , \end{aligned}$$

(18)

where $\xi (\tau )(\tau \in ({t,t^{\prime }}])$ is the reward rate function within $[ {t,t^{\prime }}]$ which is given by

$$\begin{aligned} \xi \left( \tau \right) ={\left[ {\rho \left( {t^{\prime }-t-t_{{ stop}} } \right) +w_D d_{ saved} } \right] }/{\left( {t^{\prime }-t} \right) }. \end{aligned}$$

(19)

Also note that all the state features are continuous except for $s_1$. Thus the state space is infinite, which makes the use of tabular form RL algorithms impossible. In such cases, function approximators, such as linear approximator, neural networks approximator and kernelized approximator, etc. are usually used to approximate value functions. In this paper, we use a linear function with a gradient-descent method to approximate value function for each action $a$. Each approximator is a linear combination of a set of radial basis functions (RBFs), i.e.,

$$\begin{aligned} Q\left( {\mathbf{s},a} \right) =\sum _{g=1}^G {\theta _g^a \phi _g \left( \mathbf{s} \right) } , \end{aligned}$$

(20)

where $\phi _g (\mathbf{s})(g\in \left\{ {1,2,\ldots ,G} \right\} )$ are Gaussian RBFs given by Eq. (21).

$$\begin{aligned} \phi _g \left( \mathbf{s} \right) =e^{-{\left\| {\mathbf{s}-\mathbf{C}_g } \right\| ^{2}}/{2\sigma _g^2 }} \end{aligned}$$

(21)

According to Eqs. (20) and (21), we need to determine $G$, $\mathbf{C}_g$, $\sigma _g$ and $\theta _g^a$ in order to approximate the Q-value function. In this paper, we set $G$ to 20 by convenience and apply Hard K-Means (Duda and Hart 1973) based heuristic method to determine $\mathbf{C}_g$ and $\sigma _g$. And then we use a gradient-descent method to update $\theta _g^a$ during learning. To solve the multiple-load carrier scheduling problem, a Q($\lambda$) RL algorithm with function approximation is proposed as Algorithm 3.

In the following we analyze the worst-case computational complexity of Algorithm 3. In Step 1, it takes $O({N_a G})$ efforts to initialize weights and eligibility traces. According to the computational complexity of Algorithm 1, it takes $O( {n_{ orders} N_p })$ efforts in Step 3 because we need to compute $l_i\hbox {s}$ to determine the system state $\mathbf{s}$. It takes $O({N_p N_a G} )$ efforts to choose an action in Step 4. Similar to Step 3, Step 5 requires $O({n_{ orders} N_p })$ efforts to determine the next system state $\mathbf{{s}'}$. In Step 6, it takes $O({N_p N_a G} )$ efforts to update $\mathbf{Y}(a)$ and ${\varvec{\Theta }}^{a}$ and $O({n_{ orders} N_p })$ efforts to calculate $r( {\mathbf{s}_t ,a_t ,\mathbf{s}_{t^{\prime }} })$. Hence the worst-case computational complexity of an iteration of Algorithm 3 is $O({N_p({n_{ orders} +N_a G})})$.

Note that Algorithm 3 is executed before real-time scheduling. Once Algorithm 3 is terminated, ${\varvec{\Theta }}^{a}$ determined in Algorithm 3 can be used in multiple-load carrier scheduling. Let the system state be $\mathbf{s}$ at an arbitrary decision epoch during scheduling. Then the scheduling system will take action $a^{*}( \mathbf{s})=\mathop {\arg \max }\nolimits _{a\in \mathbf{A}(\mathbf{s})} Q({\mathbf{s},a})$ at the decision epoch. If $a^{*}(\mathbf{s})=a_1$, the dolly train will wait until the next decision epoch. And if $a^{*}(\mathbf{s})=a_2$, the dolly train will use Algorithm 2 with the SSFP rule as $R_{ PICK}$ and the SDFD as $R_{ DROP}$ to determine a drop-off sequence $X$. And then the dolly train will replenish parts according to $X$. Similarly, if $a^{*}(\mathbf{s})=a_3$, the dolly train will also replenish parts. However, SDFP will be used as $R_{ PICK}$ in such cases.

Performance evaluation

To evaluate the performance of the proposed approach, we conduct simulation experiments to compare the approach with other scheduling approaches based on a numerical example.

Experimental conditions

The GA line used for simulation experiments consists of six workstations. Operators will assemble 14 part types into three types of product models, M1, M2 and M3. The product mix of the three product models is $({0.3,0.3,0.4})$ which means among all the products to be assembled, 30 % are M1, 30 % are M2 and 40 % are M3. The cycle time of the GA line is 72 s. The capacity of the dolly train is three. The velocity of the dolly is 3.05 m/s. For loading and unloading operations, $t_{ load} =36.6\,\hbox {s}$, $t_{{ unload}} =43.2\,\hbox {s}$, and $t_{ extra} =60\,\hbox {s}$. The look-ahead horizon is 1,080 seconds, i.e., $L=1{,}080\,\hbox {s}$. The coefficients of throughput and material handling distance, $w_M$ and $w_D$, are 5,000 and 4.92, respectively. Table 1 gives the layout information of the GA line. Table 2 presents the bill of material (BOM) and the SPQs. The threshold for unloading is given by Eq. (22).

$$\begin{aligned} { ULL}_i ={{ SPQ}_i }/{10}, \quad i=1,2,\ldots ,N_p \end{aligned}$$

(22)

The scheduling approaches selected to compare with the RL approach include the minimum batch size (MBS-z, Neuts 1967) rule (including MBS-1, MBS-2 and MBS-3) based approaches, the next arrival control heuristic (NACH, Fowler et al. 1992) based approaches and the minimum cost rate (MCR, Weng and Leachman 1993) based approaches. These approaches use MBS-z rules, NACH algorithm or MCR algorithm to decide when to dispatch the dolly train to handle material handling requests. All of them use the SDFP rule to pick up loads and the SDFD rule to drop off loads. These approaches can use either ROP or LRGP to generate material handling requests. The reorder points of ROP and LRGP are given by Eqs. (23) and (24) respectively.

$$\begin{aligned} { RP}_i&= \left\lceil \left( {\frac{1}{v}\left( {d_i +2\times \max \nolimits _j d_j } \right) +\sigma } \right) \!\times \, \frac{u_i }{{ CT}} \right\rceil ,\quad i=1,2,\ldots ,N_p ,\end{aligned}$$

(23)

$$\begin{aligned} { RP}_i^L&= \left\lceil \left( {\frac{1}{v}\left( {d_i +2\times \max \nolimits _j d_j } \right) +\sigma ^{L}} \right) \!\times \, \frac{u_i }{{ CT}} \right\rceil , \quad i=1,2,\ldots ,N_p, \end{aligned}$$

(24)

In Eqs. (23) and (24), $\sigma$ and $\sigma ^{L}$ are parameters to change reorder point settings.

Table 1 The layout of the GA line

Table 2 Bill of material and the SPQs

For the RL approach, we set $\mu =0.001$ and $\beta = 0.00005$ using a heuristic method presented in Zhang et al. (2011). Because the cycle time is 72 s, $t_{{ wait}}$ should not be $>$72. Otherwise the scheduling system is not able to react to changes of the GA line in time. And it is too frequent to make decisions with a too small $t_{{ wait}}$. Hence, we set $t_{{ wait}} =20\,\hbox {s}$ after we search a suitable setting for $t_{{ wait}}$ within the interval $[{10,72}]$ through pilot simulation experiments.

Simulation results

Although Q-learning methods are proved to converge (Peng and Williams 1996), there is no convergence result for Q-learning methods with function approximators. Therefore, before we evaluate the performance of the proposed RL approach, we first study its convergence.

Let ${ PD}_k$ be the mean value of the square of the difference of all the ${\varvec{\Theta }}^{a}$s between the $({k+1})$th iteration and the $k$th iteration, defined as Eq. (25) where $\phi _{g,k}^a$ denotes the value of $\phi _g^a$ in the $k$th iteration. Figure 2 presents how ${ PD}_k$ varies with the number of iterations. As Fig. 2 indicates, ${ PD}_k$ decreases sharply before 50,000 iterations. And then it decreases much more slowly after 100,000 iterations. Therefore Fig. 2 shows that the weights of RBFs become stable gradually and they converge asymptotically.

$$\begin{aligned} { PD}_k =\sum _{g=1}^G {\sum _{a\in \mathbf{A}} {{\left( {\phi _{g,k+1}^a -\phi _{g,k}^a } \right) ^{2}}/{N_a G}} } \end{aligned}$$

(25)

Fig. 2

Variation of ${ PD}_k$ with respect to the number of iterations

In order to evaluate the performance of the proposed RL approach, we conduct simulation experiments to compare throughput, material handling distance and the reward of different approaches. The simulation experiments consist of 50 tests, each of which lasts for 300 h. And for each test, the warm-up period is 10 h. In the experiments, both parameters for ${ RP}_i$ and ${ RP}_i^L$, $\sigma$ and $\sigma ^{L}$, are set to 480. Note that Algorithm 3 is executed to solve the RL problem before real-time scheduling in the RL approach. The simulation results are shown in Table 3.

Table 3 Results of the case example

As shown in Table 3, there is no such approach that yields shortest distance and largest throughput at the same time, which agrees with Chen et al. (2011)’s observation. Among all the approaches, MBS-3(ROP), i.e. the MBS-3 approach using the ROP policy, is the best in terms of material handling distance while MBS-1(LRGP) is the worst. Their gap is 38.5 %. This result indicates that if we want to minimize the material handling distance, we should dispatch the dolly train to handle more requests at a time.

On the other hand, the proposed RL approach is the best approach in terms of throughput. Compared to the worst approach, MBS-3(LRGP), the RL approach improves the throughput by 23.1 %. The RL approach is also the best approach that yields maximum reward. It’s 24.1 % better than MBS-3(LRGP) which is the worst approach in terms of reward. The smallest gap between the RL approach and other approaches is 4.6 %.

Because the cycle time is 72 s, the maximum number of products the GA line can possibly assemble in 300 h is $M^{*}={300\times 3{,}600}/72=14{,}750$. Assuming that there is a hypothetical approach whose throughput is 14,750 and its distance is the same as the MBS-3(ROP) approach’s, then its reward would be $6.93\times 10^{7}$. Compared to the hypothetical approach’s performance, the RL approach’s performance is only 4.8 % worse, which further indicates the effectiveness of the RL approach.

Considering that reorder point settings can affect the performance of scheduling, by changing $\sigma$ and $\sigma ^{L}$, we also conduct simulation experiments with different reorder point settings. In these experiments, all the parameters except for $\sigma$ and $\sigma ^{L}$ are the same as the previous ones.

As shown in Table 4, the reorder point settings indeed affect the performance of different approaches. For example, the performance of MCR(LRGP) can be improved 5.7 % by changing the $\sigma ^{L}$ from 60 to 540. However, the RL approach is still the best approach even with different reorder point settings. On average, the RL approach is 4.9 % better than the second best approach.

Table 4 Results of experiments with different reorder point settings

Because prices of products and the cost per unit material handling distance might change over time due to the fluctuation of the dynamic environment, it’s very important to make sure that the proposed approach can perform well in such environments. Therefore, we conduct experiments with four different $w_M$ values, 2,000, 3,000, 4,000 and 6,000. In all the experiments we use the same $w_D = 4.92$. And other parameters also remain the same.

Table 5 indicates that, the rewards of different approaches varies significantly because of the changes of $w_M$. Nevertheless, the proposed RL approach still outperforms other approaches in terms of reward for different settings of $w_M$ s.

Table 5 Results of experiments with different $w_M$

Note that offline RL is conducted before each setting of $w_M$ when the RL approach is applied. In order to show that the RL approach can learn a good solution to adapt the environment, we compare throughput and ${ ADUP}$, the average distance per unit product, for different $w_M$ s. According to Eq. (26), a larger ${ ADUP}$ means more cost for a unit product assembled. And smaller ${ ADUP}$ indicates that less cost is required to assemble a unit product.

$$\begin{aligned} { ADUP}=D/M \end{aligned}$$

(26)

Since $w_M$ is the coefficient of throughput, when it increases, the importance of throughput also increases according to Eq. (1). And the importance of distance decreases relatively. In such cases, the GA line should focus more on throughput even though it has to pay more cost in material handling. As indicated by Fig. 3, both throughput and ${ ADUP}$ increase at the same time when $w_M$ increases. It means that through RL, the RL approach adjusts its policy to achieve higher throughput with the price of higher unit cost when $w_M$ increases.

Fig. 3

Average distance per unit product and throughput under different settings of $w_M$

We can also compare the RL approach with the hypothetical approach for different $w_M$ s. The rewards of the hypothetical approach for the four different $w_M$ values are $2.51\times 10^{7}, 3.98\times 10^{7}, 5.46\times 10^{7}$ and $8.41\times 10^{7}$. Thus the gaps between the RL approach and the hypothetical approach are 8.0, 6.0, 5.5 and 4.7 %, respectively.

From the above simulation results, we can see that the proposed RL approach outperforms other approaches in terms of reward in all of the experiments. More importantly, Fig. 3 indicates that the RL approach can change its policy to adapt the environment through RL. By doing this, the RL approach performs well in all of the experiments. As indicated by the results of comparing the RL approach and the hypothetical approach, the performance of the RL approach is close to that of the hypothetical approach. Because it’s almost impossible to find a realistic approach that can perform as well as the hypothetical approach does, the RL approach is suitable for the multiple-load carrier scheduling problem studied in this paper.

Conclusion

In this paper we investigate the problem of scheduling a dolly train, a multiple-load carrier in a GA line. The objective of the scheduling problem is to maximize the reward of the GA line. Thus we consider two scheduling criteria, the throughput of the GA line and the material handling distance. Based on look-ahead information, we propose a look-ahead based material handling request generating policy. We also develop a heuristic dispatching algorithm to pick up loads and to determine the order of delivery. After modeling the scheduling problem as a RL problem with continuous time and space, we propose a Q($\lambda$) RL algorithm to solve the RL problem. In the RL algorithm, a linear function with a gradient-descent method is used to approximate Q-value functions.

To evaluate the performance of the proposed approach, we compare the performance of the proposed RL approach with that of other approaches. The results show that the proposed approach outperforms other approaches with respect to the reward of the GA line. Therefore, the proposed approach is an appropriate real-time multiple-load carrier scheduling approach in a dynamic manufacturing environment.

In this paper, we use a look-ahead based request generating policy other than the traditional ROP policy. However, because the scheduling system can always dispatch the dolly train to deliver parts regardless of the status of line-side buffers, it’s not necessary to have a request generating policy in the GA line theoretically. As a matter of fact, a scheduling system without a request generating policy is identical to a scheduling system in which reorder points are set to some sufficiently large number. Therefore, it’s very interesting to develop approaches without request generating policies. Furthermore, only three types of actions are defined in our RL formulation despite that there are a lot of possible actions can be defined. It’s very important to discuss this issue in the future in order to improve the performance of the scheduling approach.