1 Introduction

The energetic applications of Industry 4.0 have attracted the attention of researchers in various fields. Recently, booming global demand and the rapid development of advanced communication technologies, such as 5G and the Internet of Things, have driven the development of the distributed manufacturing system (DMS) and accelerated the pace of production globalization. The application of DMS can effectively manage complex production decisions for the supply chain system to reduce production costs, shorten response times, increase production flexibility, improve product quality, and reduce management risk (Renna 2012). Production planning must integrate the production schedules of each member of the supply chain to enhance the performance of the DMS (Rossit et al. 2019). The distributed scheduling problem (DSP) is a vital issue in the globalization of production scheduling, which can help facilitate autonomous manufacturing and take a step towards Industry 4.0. Therefore, DSP has received increasing attention from researchers and practitioners (Lin and Ying 2013; Ying and Lin 2017; Cheng et al. 2019; Pourhejazy et al. 2021) and is becoming one of the most critical developments in the field of production scheduling.

DSP was first proposed by Jia et al. (2002), who presented a web-based scheduling system for a distributed manufacturing environment. Since then, DSP has been one of the prime examples of growing recognition, motivated by the fact that advanced communication systems can be used to make efficient production decisions in various DMSs (Ying et al. 2022). Many pioneering works on various DSPs have been proposed and become widely used in the automotive, consumer electronics, and other globalized manufacturing industries; for example, Chan et al. (2005, 2006) presented genetic algorithms for DSPs in five multi-factory models and a flexible manufacturing system environment; Naderi and Ruiz (2010) proposed the distributed permutation flowshop scheduling problem (DPFSP) and proposed six mixed integer linear programming (MILP) models, two simple factory assignment rules, and 14 algorithms to minimize the makespan among factories. The research boundaries of DSP were extended to distributed jobshop scheduling problems by Jia et al. (2007), De Giovanni and Pezzella (2010), and Naderi and Azab (2014), and to the distributed parallel-machine scheduling problem by Behnamian (2014). Based on the seminal study by Naderi and Ruiz (2010), some extensions of the basic DPFSP setting have been proposed for other modern industrial manufacturing systems. Among these pioneering research works, the distributed assembly permutation flowshop scheduling problem with flexible assembly (DAPFSP-FA, Zhang et al. 2018) is one of the most significant problems.

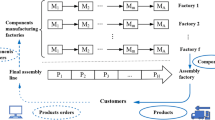
Sequence-dependent setup times are the essential production factors considered in many practical DMSs. Moreover, unrelated parallel machines have more general settings than the uniform parallel machines used in the assembly stage of DAPFSP-FA. However, to the best of our knowledge, there has been no research on the DAPFSP-FA with unrelated assembly machines and sequence-dependent setup times, which is a significant production setting in a variety of industries. These facts inspired our research to extend DAPFSP-FA to include unrelated assembly machines and sequence-dependent setup times for a more general and practical globalized production scheduling mode. As shown in Fig. 1, the DMS of DAPFSP-FASDST has the two stages of production and assembly. The first stage (production) consists of a distributed production system with \(g\) homogeneous factories/shops capable of handling all jobs/components, and each factory/shop is a permutation flowshop equipped with \(m\) machines disposed of in series. The second stage (flexible assembly) is equipped with \(q\) unrelated parallel machines that are functionally equivalent but have different processing speeds for different products. In line with a predefined assembly plan,\(n\) components/jobs are assembled into \(t\) products, where each component/job belongs to only one product. Each component/job \(j\)\((j \in \{ 1, \, 2, \, ..., \, n\} )\) must be assigned and produced in one of the factories, and the processing time of component/job \(j\)\((j \in \{ 1, \, 2, \, ..., \, n\} )\) on the production machine \(PM_{i}\) \((i \in \{ 1, \, 2, \, ..., \, m\} )\) is \(P_{j,i}\). The processing sequence of the components/jobs assigned to the same factory/shop remains unchanged on each machine. A product can be assembled when all of its jobs/components have been completed in the production stage. Each product \(p\) \((p = 1, \, 2, \, ..., \, t)\) requires a single assembly operation on any one of the assembly machines, denoted as \(AM_{s}\)\((s = 1, \, 2, \, ..., \, q)\), with corresponding assembly time \(AP_{ \, p, \, s}\), depending on the assembly machine to which it is assigned. The speeds of the assembly machines are not in constant proportion to each other. Before processing each component/job, a job sequence-dependent setup time,\(S_{j^{\prime}, \, j, \, i}\) \((j^{\prime} = 0, \, 1, \, ..., \, n;\) \(j = 1, \, 2, \, ..., \, n; \, j^{\prime} \ne j; \, i = 1, \, 2, \, ..., \, m),\) is incurred when job \(j\) is processed immediately after job \(j^{\prime}\) on production machine \(i\). Similarly, the machines at the assembly stage have product sequence-dependent setup times, denoted as \(AS_{p^{\prime}, \, p, \, s}\) \((p^{\prime} = 0, \, 1, \, ..., \, t; \, p = 1, \, 2, \, ..., \, t; \, p^{\prime} \ne p{; }s = 1, \, 2, \, ..., \, q),\) if product \(p\) is assembled on assembly machine \(s\) immediately after product \(p^{\prime}\). The objective is to generate the corresponding production sequence of jobs/components in each factory/shop and the corresponding assembly sequence in each assembly machine, in order to minimize the makespan.

Fig. 1
figure 1

Schematic diagram of DAPFSP-FASDST

Full size image

Using the three-field notation proposed by Framinan et al. (2019), the addressed DAPFSP-FASDST is signified as \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max } ,\) where \(DF_{m} \to R_{m}\) denotes that the DMS has two stages. The first stage, i.e., the production stage, consists of distributed flowshops, and the second stage, i.e., the flexible assembly stage, is equipped with unrelated parallel machines; \(prmu\) designates that the shop type of each component production factory/shop in the production stage is a permutation flowshop; \(ST_{sd}\) represents that sequence-dependent setup times are considered in both the production and assembly stages; and \(C_{\max }\) indicates that the objective of the schedule is to minimize the makespan. Without the production stage, the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem is reduced to the solution of the unrelated parallel machine scheduling problem with sequence-dependent setup times, which is an NP-hard problem in the strong sense (Ying et al. 2012). Therefore, we can easily conclude that the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem is also an NP-hard problem in the strong sense.

In addition, the following basic assumptions and limitations are asserted for the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem addressed in this study:

  • Once a component/product is assigned to a factory/machine, the planner cannot interrupt the processing/assembly operation of a component/product or transfer it to other factories/machines.

  • Each component/product can only be processed on one production/assembly machine at a time, and each production/assembly machine can handle only one component/product at a time. Once the process has begun on a production/assembly machine, it cannot be interrupted until it is completed.

  • The ready times of all components/jobs are assumed to be zero; i.e., the components/jobs are available at the beginning of the planning horizon.

  • The component/product orders are independent of each other; therefore, the sequence of the component/product does not affect the production/assembly time.

  • The production/assembly machine is available throughout the planning horizon, and there are no maintenance issues, failures, or other issues throughout the planning horizon.

  • The number of factories/machines, the number of components/products, the production/assembly times, and the job/product sequence-dependent setup times are given by deterministic nonnegative integers.

  • Excluding the trivial cases, the number of components/jobs is larger than the number of production/assembly machines.

Given the originality of the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem, a MILP model and a novel IG-based metaheuristic, called the reinforcement learning iterated greedy (RLIG) algorithm, are presented in this study to minimize the makespan. The main novelty and contributions of this study are to fill the research gap on the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem and offer a practical method for the promotion of real-world applications in a variety of industries.

2 Literature review

The DPFSP has been extended to various production settings, such as DMSs with heterogeneous factories (Li et al. 2020a, 2020b; Meng and Pan 2021), group scheduling (Pan et al. 2022), hybrid flowshops (Ying and Lin 2018; Li et al. 2020c; Lei and Wang 2020), and integrated assembly-production flowshops (Lin 2018; Wu et al. 2018, 2019; Lei et al. 2021). In addition, DPFSPs have been integrated with a number of practical features that facilitate their application in the real world; blocking conditions (Zhang et al. 2018; Li et al. 2019; Zhao et al. 2020), limited buffer constraints (Zhang and Xing 2019), no-wait (Lin and Ying 2016; Komaki and Malakooti 2017; Li et al. 2020a), no-idle (Ying et al. 2017; Cheng et al. 2019; Zhao et al. 2021), customer order-priority (Meng et al. 2019), time window constraints (Jing et al. 2020), machine-breakdowns (Wang et al. 2016), and preventive maintenance (Mao et al. 2021) are notable examples.

This section reviews the most important literature regarding the two well-known branches of the DPFSP, i.e., the distributed assembly permutation flowshop scheduling problem (DAPFSP, Hatami et al. 2013) and the distributed assembly permutation flowshop scheduling problem with flexible assembly (DAPFSP-FA, Zhang et al. 2018). Regarding the first branch of DPFSPs, Hatami et al. (2013) first added an assembly stage to DPFSP to form DAPFSP, which has the two stages of production and assembly. In the first stage (production), all jobs/components are assigned to a distributed permutation flowshop manufacturing system, and upon completing all the jobs/components of a particular product, product assembly is conducted in the second stage (assembly) using an assembly machine. This setting usually occurs when different manufacturers supply the components and an assembly center in the parent company processes the final products. Hatami et al. (2013) proposed three construction heuristics and a variable neighborhood descent (VND) metaheuristic to minimize the makespan of DAPFSPs. The following year, Hatami et al. (2014) extended the DAPFSP problem to include sequence-dependent setup time constraints and presented two constructive heuristics for solving the distributed assembly permutation flowshop scheduling problem with sequence-dependent setup times. After that, Hatami et al. (2015) proposed two construction heuristic algorithms and an iterated greedy (IG)-based algorithm to solve this problem, and their computational results revealed that the IG-based algorithm performed better than the VND algorithm. To further improve the solution quality of the algorithms presented by Hatami et al. (2013), Li et al. (2015) presented a genetic algorithm (GA), Lin and Zhang (2016) presented a hybrid biogeography-based optimization (HBBO) algorithm, and Wang and Wang (2016) proposed an estimation of the distribution algorithm-based memetic algorithm (EDAMA) to solve DAPFSPs. Their experimental results showed that GA is superior to the three construction heuristic algorithms of Hatami et al. (2013), and HBBO and EDAMA outperform VND. Following these studies, Lin et al. (2017) presented a backtracking search hyper-heuristic (BS-HH) algorithm, and their results showed that BS-HH provides better solution quality and a shorter computation time than VND, HBBO, and EDAMA. Then, Pan et al. (2019) presented two VND metaheuristics and an IG-based approach for minimizing the makespan of DAPFSPs, and the experimental results of 810 benchmark test problems confirmed that their approaches significantly outperform VND, GA, HBBO, EDAMA, BS-HH, and other existing algorithms. Huang et al. (2021) considered the DAPFSP problem with the criterion of total flow time and proposed an IG-based algorithm (gIGA) to solve it, and their computational results showed that gIGA is superior to the seven algorithms available in the literature. These breakthrough studies on DAPFSPs could effectively and efficiently coordinate the production components and final assembly scheduling to optimize the global supply chain system. More recently, Pourhejazy et al. (2022) extended the limited literature on DAPFSPs to the distributed two-stage production-assembly scheduling problems, proposed a meta-Lamarckian-based iterated greedy algorithm and compared it with the current-best-performing algorithm in the literature. The computational results revealed that this approach is a strong benchmark algorithm for solving this problem. Although this setting is widely used in globalized production, very little attention has been paid to this branch of the problem.

Regarding the second branch of DPFSPs, Zhang et al. (2018) first introduced DAPFSP-FA, which extends the assembly stage of DAPFSP from a single machine to multiple machines. In the first stage (production), all jobs/components are first assigned to a distributed permutation flowshop manufacturing system. As existing globalization production systems usually require greater flexibility during the assembly stage to accommodate the paradigms of concurrent and mass production, the product assembly work is carried out directly after the production stage with a uniform parallel machine in the second stage (assembly). DAPFSP-FAs are widely used in many industries, especially globalized manufacturing companies, such as automotive and consumer electronics, which have many outsourced components. Zhang et al. (2018) proposed two metaheuristics, the hybrid variable neighborhood search (HVNS) and hybrid particle swarm optimization (HPSO), for minimizing the makespan on the DAPFSP with flexible assembly and sequence-independent setup times, and the extensive numerical results revealed that the performance of HPSO is superior to that of HVNS. Subsequently, Zhang et al. (2020) further investigated this new generation of scheduling problems and proposed a MILP model and a memetic algorithm to solve the same problem more effectively than HPSO. More recently, Yang and Xu (2021) proposed the distributed assembly permutation flowshop scheduling problem with flexible assembly and batch delivery to coordinate the supply chain scheduling of production and transportation, and presented four heuristics algorithms, one VND algorithm, and two IG-based approaches (IG_desP and IG_desJ) to minimize the total cost of delivery and tardiness. The computational results revealed that IG_desJ provides higher quality solutions among the approaches. Pourhejazy et al. (2021) developed another IG-based algorithm, named iterated greedy with a product destruction mechanism (IGPD), to solve the DAPFSP with flexible assembly and sequence-independent setup times, and the computational results showed that IGPD significantly outperforms the HPSO and HVNS methods. More recently, Ying et al. (2022) extended DAPFSP to consider flexible assembly and sequence-independent setup times in a supply chain-like setting and proposed a MILP model, a constructive heuristic, and customized metaheuristic algorithms to solve this problem. The computational results showed that the proposed algorithms outperformed the best performing algorithms and yielded the best-known solutions in almost all benchmark instances. As only a handful of articles have been published, and all of them were submitted in the last five years, further studies are needed to support the development of this new branch of DPFSPs.

3 Methodology

3.1 MILP model

In this sub-section, a novel MILP model for solving small-size \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problems was formulated. For this purpose, the various indices, parameters, and decision variables are defined, as follows.

3.1.1 Indices

\(j^{\prime},j\): Job, \(j \in \left\{ {1, \, 2, \, ..., \, n} \right\}\) and \(j^{\prime} \in \left\{ {0, \, 1, \, ..., \, n} \right\}\), where 0 represents the dummy job.

\(i\): Machine, \(i \in \left\{ {1, \, 2, \, ..., \, m} \right\}\) at the production stage.

\(f\): Factory/Shop, \(f \in \left\{ {1, \, 2, \, ..., \, g} \right\}\) at the production stage.

\(p,p^{\prime}\): Product, \(p,p^{\prime} \in \left\{ {0, \, 1, \, 2, \, ..., \, t} \right\}\), where 0 represents the dummy product.

\(s\): Machine, \(s \in \left\{ {1, \, 2, \, ..., \, q} \right\}\) at the assembly stage.

3.1.2 Parameters

\(n\): Number of jobs to be processed.

\(m\): Number of available production machines.

\(g\): Number of production factories.

\(t\): Number of products.

\(q\): Number of available assembly machines (\(q \le t\)).

\(P_{j,i}\): Processing time of job \(j\) on the production machine \(i\).

\(S_{j^{\prime}, \, j, \, i}\): Setup time of job \(j\) on the production machine \(i\) when it is processed after job \(j^{\prime}\).

\(AP_{ \, p, \, s}\): Assembly time of product \(p\) on the assembly machine \(s\).

\(AS_{p^{\prime}, \, p, \, s}\): Setup time of product \(p\) on the assembly machine \(s\) when it is processed after product \(p^{\prime}\).

\(G_{p}\): The jobs associated with product \(p\).

\({\text{M}}\): A sufficiently large constant.

3.1.3 Decision variables

\(C_{k, \, i, \, f}\): Completion time of the job in position k on machine \(i\) at factory/shop f.

\(X_{j, \, k, \, f}\): Binary variable that takes value 1 if job j occupies position k in factory/shop f, and 0 otherwise.

\(Y_{p^{\prime}, \, p, \, s}\): Binary variable; \(= 1\) if product \(p\) is assembled after product \(p^{\prime}\) on assembly machine \(s\); \(= 0\), otherwise.

\({\text{Z}}_{p, \, s}\): Binary variable; \(= 1\) if product \(p\) is dispatched to assembly machine \(s\); \(= 0\), otherwise.

\(AR_{ \, p, \, s}\): Starting time of assembling the product \(p\) on the assembly machine \(s\).

\(AC_{p, \, s}\): Completion time of assembling product \(p\) on the assembly machine \(s\).

This study proposed a position-based MILP model for the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem, as follows.

Minimize \(C_{max}\)

subject to

$$\sum\limits_{k = 1}^{n} {\sum\limits_{f = 1}^{g} {X_{j, \, k, \, f} } } = 1,\;j = 0, \, 1, \, ..., \, n$$
(1)
$$\sum\limits_{j = 1}^{n} {X_{j, \, k, \, f} } \le 1,\;k = 1, \, 2, \, ..., \, n; \, f = 1, \, 2, \, ..., \, g$$
(2)
$$C_{1, \, 1, \, f} = \sum\limits_{j = 1}^{n} {X_{j, \, 1, \, f} \cdot (p_{j, \, 1} + S_{0, \, j, \, 1} } ), \, f = 1, \, 2, \, ..., \, g$$
(3)
$$C_{k,i,f} \ge C_{k,i - 1,f} + \sum\limits_{j = 1}^{n} {X_{j,k,f} } \cdot P_{j,i} + (\sum\limits_{j = 1}^{n} {X_{j,k,f} } - 1) \cdot {\text{M}},\;k = 1, \, 2, \, ..., \, n; \, i = 2, \, 3, \, ..., \, m; \, f = 1, \, 2, \, ..., \, g$$
(4)
$$C_{k,i,f} \ge C_{k - 1,i,f} + P_{j,i} + S_{j^{\prime},j, \, i} + (X_{j,k,f} + X_{j^{\prime},k - 1,f} - 2) \cdot {\text{M}},\;k = 1,2, \, ..., \, n; \, i = 1, \, 2, \, ..., \, m; \, f = 1, \, 2, \, ..., \, g;\;j^{\prime} = 0, \, 1, \, ..., \, n;,j = 1, \, 2, \, ..., \, n; \, j \ne j^{\prime}$$
(5)
$$\sum\limits_{j = 1}^{n} {X_{j,k - 1,f} } \ge \sum\limits_{j = 1}^{n} {X_{j,k,f} ,} \, k = 1,2, \, ..., \, n; \, f = 1, \, 2, \, ..., \, g$$
(6)
$$\sum\limits_{\begin{subarray}{l} p^{\prime} = 0 \\ p^{\prime} \ne p \end{subarray} }^{t} {Y_{p^{\prime},p,s} - } \sum\limits_{\begin{subarray}{l} p^{\prime} = 0 \\ p^{\prime} \ne p \end{subarray} }^{t} {Y_{p,p^{\prime},s} = 0;\;p = 1,2, \cdots ,n;s = 1,2, \cdots ,q,}$$
(7)
$$\sum\limits_{s = 1}^{q} {\sum\limits_{p^{\prime} = 0, \, p^{\prime} \ne p}^{t} {Y_{p^{\prime},p, \, s} } } = 1 \, ; \, p = 1, \, ..., \, t$$
(8)
$$\sum\limits_{s = 1}^{q} {\sum\limits_{p = 1, \, p^{\prime} \ne p}^{t} {Y_{p^{\prime},p, \, s} } } \le 1 \, ; \, p^{\prime} = 1, \, 2, \, ..., \, t$$
(9)
$$\sum\limits_{p = 1}^{t} {Y_{0,p, \, s} } = 1,\;s = 1, \, 2, \, ..., \, q$$
(10)
$$Y_{ \, p^{\prime}, \, p, \, s} + Y_{p,p^{\prime}, \, s} \le 1 \, , \, p^{\prime} = 1, \, 2, \, ..., \, t - 1; \, p > p^{\prime}; \, s = 1, \, 2, \, ..., \, q$$
(11)
$$Z_{p,s} - \sum\limits_{p^{\prime}}^{t} {Y_{p^{\prime},p,s} = 0;p = 1, \cdots t;s = 1, \cdots q;}$$
(12)
$$AR_{ \, p, \, s} \ge C_{k,m, \, f} + (X_{j,k,f} + {\text{Z}}_{p, \, s} - 2) \cdot {\text{M, }}p = 1, \, ..., \, t; \, s = 1, \, 2, \, ..., \, q; \, j \in G_{p} ; \, k = 1, \, 2, \, ..., \, n; \, ; \, f = 1, \, 2, \, ..., \, g$$
(13)
$$AC_{p, \, s} \ge AR_{{ \, p,{\text{ s}}}} + AP_{ \, p, \, s} + ({\text{Z}}_{p, \, s} - 1) \cdot {\text{M}}, \, s = 1, \, 2, \, ..., \, q; \, p = 0, \, 1, \, ..., \, t$$
(14)
$$AC_{p, \, s} \ge AC_{p^{\prime}, \, s} + AS_{ \, p^{\prime},p, \, s} + AP_{ \, p, \, s} + \left( {Y_{ \, p^{\prime}, \, p, \, s} - 1} \right) \cdot {\text{M }},s = 1, \, 2, \, ..., \, q; \, p, \, p^{\prime} = 0, \, 1, \, ..., \, t; \, p \ne p^{\prime}$$
(15)
$$C_{max} \ge AC_{p, \, s} , \, p = 0, \, 1, \, ..., \, t; \, s = 1, \, 2, \, ..., \, q$$
(16)
$$C_{k,i,f} \ge 0 \, ; \, k = 1, \, 2, \, ..., \, n; \, i = 1, \, 2, \, ..., \, m; \, f = 1, \, 2, \, ..., \, g$$
(17)
$$C_{0,i,f} = 0 \, ; \, i = 1, \, 2, \, ..., \, m; \, f = 1, \, 2, \, ..., \, g$$
(18)
$$X_{j,k,f} \in \left\{ {0,1} \right\}, \, j = 0, \, 1, \, ..., \, n; \, i = 1, \, 2, \, ..., \, m; \, f = 1, \, 2, \, ..., \, g$$
(19)
$$X_{0,0,f} = 1, \, f = 1, \, 2, \, ..., \, g$$
(20)
$$Y_{ \, l, \, k, \, s} \in {{ \{ 0, 1\} }}l, \, k = 0, \, 1, \, ..., \, t; \, l \ne k; \, s = 1, \, 2, \, ..., \, q$$
(21)
$${\text{Z}}_{p, \, s} \in {{ \{ 0, 1\} , }}p = 0, \, 1, \, ..., \, t; \, s = 0, \, 1, \, ..., \, q;$$
(22)
$$C_{j, \, i} \ge 0 \, ; \, j = 0, \, 1, \, ..., \, n; \, i = 1, \, 2, \, ..., \, m$$
(23)
$$AR_{{ \, k,{\text{ s}}}} \ge 0 \, ; \, k = 0, \, 1, \, ..., \, t; \, s = 1, \, 2, \, ..., \, q$$
(24)
$$AC_{k, \, s} \ge 0 \, ; \, k = 0, \, 1, \, ..., \, t; \, s = 1, \, 2, \, ..., \, q$$
(25)

Constraint sets 1 and 2 restrict that a component/job can be assigned to only one position in a factory/shop, and a position in each factory/shop can be assigned one component/job at most. Constraint set 3 computes the completion times of the first component/job to be processed on the first machine in each factory/shop. Constraint sets 4 and 5 set the inequality relationships between the completion times of the components/jobs on successive machines and priorities, respectively. Constraint set 6 ensures that the positions of the assigned components/jobs in each factory/shop are consecutive. Constraint set 7 guarantees that the products are assembled on each machine sequentially. Constraint sets 8 to 11 specify that a product can have only one predecessor and at most one successor. Constraint set 12 establishes a link between the two binary decision variables of \(Y_{p^{\prime}, \, p, \, s}\) and \({\text{Z}}_{p, \, s}\). Constraint set 13 defines the start times of the products at the assembly machines. Constraint set 14 defines the inequality relations between the completion times and start times of the products at the assembly machines. Constraint set 15 defines the inequality relation between the completion time of a product and its predecessor. Constraint set 16 calculates the maximum completion time of the products, i.e., the makespan. Finally, constraint sets 17 to 25 define the range for each decision variable. This MILP model has a large number of binary variables, which makes it superior in terms of both model size and computational complexity.

3.2 Proposed metaheuristic

In recent decades, various optimization algorithms have been developed to solve complex problems (Vanchinathan and Valluvan 2018; Vanchinathan and Selvaganesan 2021; Vanchinathan et al. 2021; Khalifa et al. 2021). IG-based algorithms (Pourhejazy et al. 2021, 2022) have gained recognition among researchers due to their effectiveness and efficiency in solving various DAPFSPs. Considering that the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem is NP-hard in the strong sense, this work proposed a novel IG-based metaheuristic called RLIG to solve this complex supply-chain-integrated scheduling problem.

The flowchart of the RLIG is shown in Fig. 2. First, a set of initial solutions \({{\varvec{\Pi}}} = \{ \Pi^{1} , \, \Pi^{2} , \, ..., \, \Pi^{{N_{\max } }} \}\) are generated using a specific constructive heuristic. Second, let \(\Pi_{best}\) be the best solution among \(\{ \Pi^{1} , \, \Pi^{2} , \, ..., \, \Pi^{{N_{\max } }} \}\) and \(C_{{{\text{max}}}} (\Pi_{best} )\) is the objective function value of the best solution \(\Pi_{best}\). For each iteration, a solution \(\Pi^{N}\) is chosen from \(\{ \Pi^{1} , \, \Pi^{2} , \, ..., \, \Pi^{{N_{\max } }} \}\) by applying the \(\varepsilon { - }\)greedy strategy and setting it as the incumbent solution, \(\Pi_{incumbent}^{{}}\). Then, apply the destruction and reconstruction operator to generate a new solution \(\Pi_{new}\). Furthermore, the acceptance criteria are used to assess whether \(\Pi^{N}\) and \(\Pi_{best}\) are replaced by \(\Pi_{new}\). The Boltzmann function, \(Exp( - 100*\Delta E),\) is used to determine whether or not \(\Pi^{N}\) is replaced by an inferior new solution, which may contribute to the search procedure escaping from the local optimum. A random number, \(r \in (0,1)\), is produced for this process. If \(r < Exp( - 100*\Delta E)\), \(\Pi^{N}\) is replaced by \(\Pi_{new^{\prime}}\); otherwise, \(\Pi_{new^{\prime}}\) must be discarded. At the end of each iteration, the fitness values of solutions \(\{ \Pi^{1} , \, \Pi^{2} , \, ..., \, \Pi^{{N_{\max } }} \}\) are updated. If the computational time exceeds the maximum allowable computation time, the RLIG procedure is terminated. Following the termination of the RLIG procedure, the (near) global optimal schedule can be derived using the \(\Pi_{best}\). The RLIG algorithm is explained in more detail in the following subsections.

Fig. 2
figure 2

Flowchart of the RLIG algorithm

Full size image

3.2.1 Solution representation

In this study, solution \(\Pi\) is represented by a single vector \((S_{{\text{Stage 1}}} |S_{{\text{Stage 2}}} )\), where \(S_{{\text{Stage 1}}}\) and \(S_{{\text{Stage 2}}}\) are the sequence of jobs/components of the production stage and the sequence of products of the assembly stage, respectively. \(S_{{\text{Stage 1}}}\) consists of a permutation of \(n\) jobs/components divided into \(g\) divisions by \(g - 1\) “0”, where the \(f^{th}\) \((f = 1, \, 2, \, ..., \, g)\) division represents the processing sequence of jobs/components in the \(f^{th}\) factory. Similarly, \(S_{{\text{Stage 2}}}\) consists of a permutation of \(t\) products divided into \(q\) divisions by \(q - 1\) “0”, where the \(s^{th}\)\((s = 1, \, 2, \, ..., \, q)\) division represents the processing sequence of the products on the \(s^{th}\) assembly machine.

For example, solution \(\Pi = (S_{{\text{Stage 1}}} |S_{{\text{Stage 2}}} ) =\)(2, 3, 5, 0, 1, 4, 6 | 1, 2, 0, 3) can be decoded, as follows. In the production stage, six jobs/components are assigned to two factories. The process sequences of jobs/components for factories 1 and 2 are 2–3–5 and 1–4–6, respectively. Then, these components are assigned and assembled into three products in the assembly stage using two assembly machines. The assembly sequences of the products for assembly machines 1 and 2 are 1–2 and 3, respectively.

3.2.2 Main steps of RLIG

The main steps of RLIG are, as follows:

3.2.2.1 Step 1: generate an initial solution set

Step 1.1: Sort \(t\) products in non-ascending order of the total processing times of their jobs/components on all production machines,\(\sum\nolimits_{{j \in G_{p} }} {\sum\nolimits_{i = 1}^{m} {P_{j,i} } }\), and insert them into the initial list of products,\(L_{P} : = {{\{ }}P_{[1]} , \, ..., \, P_{[t]} \} ,\) where \(P_{[p]}\) denotes the product in the position \(p\) \({(}p = 1, \, 2, \, ..., \, t).\) Then, sort the corresponding jobs/components of each product in \(L_{P}\) in non-ascending order of their total processing times on all production machines,\(\sum\nolimits_{i = 1}^{m} {P_{j,i} } ,\) and insert them into the initial list of jobs/components, \(L_{C} : = {{\{ }}\pi_{[1]} , \, ...., \, \pi_{[n]} \} ,\) where \(\pi_{[j]}\) denotes the job in the position \(j\)\({(}j = 1, \, 2, \, ..., \, n).\)

Step 1.2: Initialize the partial sequence of the production stage, \(S_{{\text{Stage 1}}} : = {{\{ }}\pi_{[1]} \} ,\) and remove the corresponding job/component from \(L_{C}\).

Step 1.3: Sequence the first job/component in \(L_{C}\) with the minimum makespan in the respective position in the current partial job/component sequence, \(S_{{\text{Stage 1}}}\), and remove this job/component from \(L_{C}\). Repeat this procedure until all jobs/components in \(L_{C}\) are sequenced and a complete schedule of jobs/components, \(S_{{\text{Stage 1}}}\), is yielded.

Step 1.4: Initialize the partial sequence of the assembly stage, \(S_{{\text{Stage 2}}} : = {{\{ }}P_{[1]} \} ,\) and remove the corresponding product from \(L_{P}\).

Step 1.5: Sequence the first product in \(L_{P}\) with the minimum makespan in the respective position in the current partial product sequence, \(S_{{\text{Stage 2}}}\), and remove this product from \(L_{P}\). Repeat this procedure until all products in \(L_{P}\) are sequenced and a complete schedule of products, \(S_{{\text{Stage 2}}}\), is yielded.

Step 1.6: Let \(\Pi_{{}}^{N} : = (S_{{\text{Stage 1}}} |S_{{\text{Stage 2}}} )\),\(\forall N = 1, \, ..., \, N_{\max }\), and \(\Pi_{best}^{{}} : =\)\((S_{{\text{Stage 1}}} |S_{{\text{Stage 2}}} )\).

3.2.2.2 Step 2: \(\varepsilon { - }\)greedy destruction phase

Step 2.1: Apply the \(\varepsilon { - }\)greedy strategy to select solution \(\Pi^{N}\) from the current solution set,\(\{ \Pi^{1} , \, \Pi^{2} , \, ..., \, \Pi^{{N_{\max } }} \} ,\) and set it as the incumbent solution, \(\Pi_{incumbent}\). When applying the \(\varepsilon { - }\)greedy strategy, there is a probability of \(1 - \varepsilon\) \({(0} < \varepsilon < 1)\) selecting \(\Pi_{best}^{{}}\) and a probability of \(\varepsilon\) selecting a solution from other \(N_{\max } - 1\) solutions using the roulette wheel selection technique.

Step 2.2: Select a product from the assembly machine with the maximum makespan among all assembly machines and randomly select \(\beta - 1 \, (\beta \le t)\) products from other assembly machines. Remove the jobs/components of the selected products from \(\Pi_{incumbent}\) to \(\Pi_{d}\) in their selecting order, and set the residual partial solution of \(\Pi_{incumbent}\) after removing the jobs/components of the selected products as \(\Pi_{p}\). To avoid removing too many jobs/components, each job/component of the removed products has a 50% probability of being removed.

3.2.2.3 Step 3: reconstruction phase

Reinsert the jobs/components in \(\Pi_{d}\) into \(\Pi_{p}\) one by one until a new complete solution, \(\Pi_{new}\), is reconstructed. When inserting a job/component in \(\Pi_{d}\) into \(\Pi_{p}\), evaluate and select the best one among all possible positions.

3.2.2.4 Step 4: acceptance criteria

Use the following criteria to assess whether or not \(\Pi^{N}\) and \(\Pi_{best}\) are replaced by \(\Pi_{new}\):

IF \(C_{\max } (\Pi_{new} ) \le C_{\max } (\Pi^{N} )\), set \(\Pi^{N} : = \Pi_{new}\).

ELSE_IF generate \(\Pi_{new^{\prime}}\) by swapping/inserting the components/products of \(\Pi_{new}\).

IF \(C_{\max } (\Pi_{new^{\prime}} ) \le C_{\max } (\Pi^{N} )\), set \(\Pi^{N} : = \Pi_{new^{\prime}}\)

ELSE_IF \(C_{\max } (\Pi_{new^{\prime}} ) > C_{\max } (\Pi^{N} )\), generate r ~ U (0,1);

IF \(r < Exp( - 100 \cdot \Delta E),\), set \(\Pi^{N} : = \Pi_{new^{\prime}}\).

Otherwise, reject \(\Pi_{new^{\prime}}\).

IF \(C_{\max } (\Pi^{N} ) \le C_{\max } (\Pi_{best} )\), set \(\Pi_{best} : = \Pi^{N}\).

Here, \(C_{\max } ( \bullet )\) is the makespan of a specific solution \(( \bullet )\); \(r \in [0,1]\) denotes a random number that is randomly generated from the uniform distribution U(0,1); and \(\Delta E = [C_{\max } (\Pi_{new^{\prime}} ) - C_{\max } (\Pi_{incumbent} )]/[C_{\max } (\Pi_{incumbent} )]\).

3.2.2.5 Step 5: update the fitness function values

Apply the following formula to update the fitness function value of \(\Pi^{N}\):

$$fit_{iter}^{N} = \frac{{n^{N} - 1}}{{n^{N} }} \cdot fit_{iter - 1}^{N} + \frac{1}{{n^{N} }} \cdot [C_{\max } (\Pi_{incumbent} ) - C_{\max } (\Pi_{new} )]$$

where \(fit_{iter}^{N}\) denotes the fitness function value of \(\Pi^{N}\) used in the next iteration of the roulette wheel selection procedure, and \(n^{N}\) means the cumulative selected times of \(\Pi^{N}\) in the solution procedure.

3.2.2.6 Step 6: stop criterion

Repeat Steps 2 to 5 until the maximum allowable computation time, \(T_{\max }\), is reached. In this study, \(T_{\max } = \tau \cdot (g + m + q) \cdot (n + t)/1000\) (CPU time in seconds), in which \(\tau\) is a parameter that controls the maximum allowed computation time.

The proposed RLIG algorithm benefits from both the multi-seed hill-climbing strategy and the \(\varepsilon { - }\)greedy selection strategy. The multi-seed hill-climbing strategy can effectively improve the diversification of traditional hill-climbing, which is one of the simplest and oldest local search technologies (Ying and Lin 2020, 2022). As the use of multi-seed can prevent the search from being trapped in the local optima, this mechanism usually leads to relatively high-quality results (Lin et al. 2011, 2013; Lin and Ying 2013; 2015). To implement the multi-seed hill-climbing strategy, in Step 1, \(N_{\max }\) initial solutions were generated using the famous NEH constructive heuristic (Nawaz et al. 1983) to increase diversification and escape local optimums. Steps 2 and 3 are tailored \(\varepsilon { - }\)greedy destruction and reconstruction mechanisms that are repeatedly used to improve the incumbent and best solutions found so far. The RLIG algorithm removed the selected products and 50% of the associated jobs/components from the incumbent solution using the \(\varepsilon { - }\)greedy selection strategy in the deconstruction mechanism. The \(\varepsilon { - }\)greedy selection strategy is one of the most popular exploration methods used in reinforcement learning (Maqbool et al. 2012). This mechanism can be used as a perturbation mechanism to better balance the dilemma between exploration and exploitation in solving many combination optimization problems (Guo et al. 2020), as it allows more effective searching during the iterative process through reinforcement learning, thus, escaping the local optimum. Although the greedy algorithm has a strong exploitation capability, it neglects ‘inferior’ incumbent solutions, which can be significantly improved in the future; therefore, the main point of the \(\varepsilon { - }\)greedy selection strategy is to adjust the utilization rate of the greedy or random algorithm by the probability \(\varepsilon\) (\(\varepsilon < 1\)). After that, the reconstruction mechanism was applied to insert the removed jobs/components back into the remaining partial solution one by one, in order to generate a new complete solution. In Step 4, the acceptance criteria were applied to judge whether \(\Pi^{N}\) and \(\Pi_{best}\) are updated by \(\Pi_{new}\) or the neighborhood solution \(\Pi_{new^{\prime}}\) as generated by swap or insertion operations. In Step 5, the fitness function value of \(\Pi^{N}\), which is used in the next iteration of the roulette wheel selection procedure, was updated according to the formula modified from the \(\varepsilon { - }\)greedy algorithm. To ensure a fair comparison with different compared algorithms, the iterative solution procedure was repeated until the termination condition, i.e., the maximum allowed computation time, is reached.

4 Numerical analysis

The following section presents the experimental results to demonstrate the performance of RLIG and the MILP model in solving the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem. All compared algorithms were programmed using Visual C +  + (2019) and executed on a PC with the following specifications: an Intel® Xeon® E3-1245 3.7 GHz V6 processor with 64 GB of RAM, and a Windows 10 operating system. The numerical analysis began with a description of the dataset, performance measurement, and calibration parameters of the algorithm, followed by the solution of the MILP formulation using Gurobi version 9.0, and concluded with a discussion of the performance of RLIG in the context of solving test problems of different sizes.

4.1 Test problem set

The numerical experiments in this study were performed using the benchmark instances created by Zhang et al. (2018). The dataset contained tiny-, small- and large-sized test instances. The tiny-size test instances were generated based on \(n = 10\) jobs, \(f = \{ 2, \, 3\}\) factories, \(m = \{ 2, \, 3\}\) machines, \(t = \{ 4, \, 5\}\) products, and \(q = \{ 2, \, 3, \, 4\}\) assembly machines, and one test instance was generated for each of the \({1} \times {2}^{{3}} \times {3} = 24\) combinations, thus, 24 tiny-size test instances were used in this study. The small-size test instances were generated based on \(n = \{ 20, \, 24, \, 30\}\) jobs, \(f = \{ 2, \, 3\}\) factories, \(m = \{ 2, \, 3\}\) machines, \(t = \{ 6, \, 8\}\) products, and \(q = \{ 2, \, 3, \, 4\}\) assembly machines, and ten test instances were generated for each of the \({3} \times {2}^{{3}} \times {3} = 72\) combinations; therefore, \(72 \times 10 = 720\) small-size test instances were used in this study. The large-size test instances were generated based on \(n = \{ 100, \, 200\}\) jobs, \(f = \{ 6, \, 8\}\) factories, \(m = \{ 5, \, 10\}\) machines, \(t = \{ 30, \, 40\}\) products, and \(q = \{ 6, \, 8\}\) assembly machines, and ten test instances were generated for each of the \({2}^{5} \,=\,32\) combinations; hence, \(32 \times 10 = 320\) large-size test instances, as created by Zhang et al. (2018), were used in this study. To evaluate the performance of the compared algorithms on larger test instances, we generated \(32 \times 10 = 320\) very large-size test instances based on \(n = \{ 500, \, 1000\}\) jobs,\(f = \{ 10,20\}\) factories,\(m = \{ 12, \, 16\}\) machines,\(t = \{ 30, \, 40\}\) products, and \(q = \{ 60,80\}\) assembly machines, and ten test instances were generated for each of the \({2}^{5} \,=\,32\) combinations, therefore, a total of 640 large-size test instances were used in this study. Following the approach of Zhang et al. (2018), six small-size and six large-size test instances were generated to calibrate the parameters of RLIG, and the processing times of the jobs/components, the assembly times of the products, and the sequence-dependent setup times were all randomly generated from uniform distribution U[1, 99] and U[1, 20], respectively.

4.2 Parameter calibration

As with many metaheuristics, the setting of the parameter values affected the performance of the RLIG algorithm. In this study, four levels for each of the \(N_{\max }\),\(\beta\),\(\varepsilon\), and \(\tau\) parameters were considered for the calibration of the RLIG algorithm, where \(N_{\max }\) is the number of solutions in the solution set; \(\varepsilon\) is the selection probability used in the \(\varepsilon { - }\)greedy selection strategy; \(\beta\) is the number of products to be removed in the destruction phase; and \(\tau\) is a parameter controlling the maximum allowable computation time. A summary of the calibration configurations can be found in Table 1. The calibration experiments were performed with 12 test instances considering 44 possible scenarios of parameter values. In order to efficiently obtain the best setting for each parameter, type B of the Taguchi L16 orthogonal experimental design was employed, including 16 combinations of parameter settings that underwent 20 runs for each random test instance, resulting in a total of \(20 \times 16 \,=\,320\) runs. To evaluate the performance of different scenarios of parameter values, we used the average relative percentage deviation (ARPD) of the obtained makespan value, which was calculated using the following equation, as the desired performance measure:

$$ARPD = \left( {\sum\limits_{r = 1}^{12} {\frac{{C_{\max }^{ave} {(}\pi {)} - C_{\max }^{best} {(}\pi {)}}}{{C_{\max }^{best} {(}\pi {)}}} \times 100} } \right)/12$$
(26)
Table 1 Orthogonal array and the obtained ARPDs
Full size table

where \(C_{\max }^{ave} {(}\pi {)}\) denotes the average makespan value for a particular parameter combination obtained by the algorithm in one run for a particular instance, and \(C_{\max }^{best} {(}\pi {)}\) represents the best makespan value obtained by the algorithm when considering all 16 parameter combinations and 20 runs for the same test instance.

A comparison of the ARPDs obtained using different levels of each parameter is presented in Table 2. According to the range of the ARPDs,\(\beta\) was the most significant parameter among the four parameters. Under a fixed maximal allowed computation time, the larger the value of \(\beta\), the more products and their associated jobs/components would be selected and removed from the incumbent solution, resulting in more time spent in the subsequent reconstruction phase. In other words, it would require more computation time to perform one iteration of the algorithm, resulting in fewer total iterations. Consequently, if the maximum computation time was fixed, a larger \(\beta\) value would result in fewer candidate solutions being evaluated and the best solution not being found. Among the four parameters, the allowed maximum computation time,\(\tau\), was the second significant parameter. When the value of \(\tau\) was increased, better solutions could be obtained with more computation time. Compared with \(\beta\) and \(\tau\), parameters \(N_{\max }\) and \(\varepsilon\) had no significant impacts on the performance of RLIG. According to the parameter calibration experimental results, the parameter values of \(N_{\max }\),\(\beta\),\(\varepsilon\), and \(\tau\) were set to 6, 2, 0.4, and 60, respectively. In related studies (Pan et al 2019; Zhang et al. 2020; Huang et al. 2021), the maximal computational time is set to \(\tau \cdot m \cdot n/1000\) seconds, in which \(\tau\) is a parameter that controls the maximum allowed computation time, and n and m is the number of jobs and number of machines, respectively. In this study, m and n are expanded to \((n + t)\) and \((g + m + q)\). Based on these estimates, the maximum allowable computation time of the RLIG algorithm in the following experiments was set to \(T_{\max } = 60 \cdot (g + m + q) \cdot (n + t)/1000\)(CPU time in seconds) to achieve an equilibrium between solution quality and computing time.

Table 2 ARPDs obtained by different levels of each parameter
Full size table

4.3 Numerical results

To evaluate the performance of the compared algorithms from a broader perspective, the average relative percentage deviation (ARPD) was used to measure solutions obtained by different algorithms. The formula for calculating ARPD is, as follows:

$$ARPD = \sum\limits_{i = 1}^{n} {\frac{{C_{\max }^{{}} {(}\pi {)} - C_{\max }^{best} {(}\pi {)}}}{{C_{\max }^{best} {(}\pi {)}}}/n \times 100}$$
(27)

where \(C_{{{\text{max}}}} (\pi )\) is the makespan value obtained by a single run of the algorithm for a given test instance, and \(C_{\max }^{best} {(}\pi {)}\) denotes the best makespan value obtained by all compared algorithms performing five runs for that test instance. An algorithm with smaller ARPDs would indicate that it could produce higher quality solutions than the compared algorithms. Finally, the paired t-test was performed to determine whether the differences between the computational results of RLIG and IG were statistically significant.

To the best of our knowledge, in existing literature, IG-based algorithms are by far the best meta-heuristics for solving DAPFSP-FA problems. Therefore, this study used the IG (i.e., the RLIG algorithm without the reinforcement learning mechanism) as the benchmark algorithms to evaluate the performance of RLIG. In order to compare the performance of RLIG with that of IG (i.e., the RLIG algorithm without the reinforcement learning mechanism) and the MILP model for solving the 24 tiny-size instances, the makespan value of the best solution (\(C_{\max }\)), the average makespan value (Ave.\(C_{\max }\)), and the average computation time (T(s)) for five runs of each instance was summarized, as shown in Table 3. The MILP model was solved using Gurobi version 9.0, which is one of the strongest and widely used solvers with a maximum computation time of 7200 s. As can be seen in Table 3, RLIG and IG achieved the same best solutions for each tiny-size instance. The solution quality of IG was as good as that of RLIG, except that the average makespan value of test instance T14, as obtained with IG, was slightly worse than that of RLIG. As shown in Table 3, both IG and RLIG yielded the same optimal solutions for the 19 test instances that could be optimally solved within 7200 s using the MILP model. Regarding the remaining five test instances that could not be optimally solved within 7200 s using the MILP model, the best solutions, as obtained using both IG and RLIG, were superior to the feasible solutions obtained using the MILP model. Since the computation times required by the RLIG and IG algorithms were significantly shorter than those of the MILP model, we could conclude that these algorithms were more appropriate for solving tiny-size problems.

Table 3 Computational results of tiny-scale instances (best in bold)
Full size table

In order to compare the performance of RLIG with that of IG for solving the small- and large-size test instances, the average makespan value of the best solution (\(C_{\max }\)), the average makespan value of five runs (Ave.\(C_{\max }\)), and the average computation time (T(s)) for five runs of each subset test instance with different configurations are summarized in Table 4. In order to evaluate the performance of RLIG and IG from a broader perspective, the best ARPD values and total average ARPD values of their obtained makespan values with different configurations of the small- and large-size test instances are summarized in Table 5. As shown in Tables 4 and 5, RLIG was superior to IG for all examined workloads and production scales, except for the subset of test instances \(n =20\) and \(q =2\). The larger the production scale and workload, the greater the differences between RLIG and IG performance.

Table 4 Results analysis for small- and large-size test instances (best in bold)
Full size table
Table 5 ARPDs for small- and large-size test instances (best in bold)
Full size table

The overall computational results were visually compared with various configurations, as shown in Fig. 3. As depicted in Fig. 3, the RLIG algorithm performed better with different production scales, such as the number of machines, factories, products, and assembly machines. When testing different workloads and production scales, IG performed slightly better than RLIG for \(n =20\) and \(q =2\) test instances; however, as the workload and production scales were increased, the visual analysis of the computational results clearly revealed that RLIG was superior to IG.

Fig. 3
figure 3

Visual analysis of the computational results

Full size image

In order to verify whether the differences between the computational results of RLIG and IG were statistically significant, paired t-testing was performed, as shown in Table 6. The t-values in Table 6 confirmed at the confidence interval of 0.05 that RLIG was significantly better than IG, indicating that the multi-seed hill-climbing strategy and \(\varepsilon { - }\)greedy selection strategy could improve the performance of IG and help RLIG find the best solution for the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem.

Table 6 Statistical test of significance for the benchmark results for RPD
Full size table

5 Discussion

This study presented a MILP model and a highly effective and efficient RLIG algorithm to solve the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem. The analytical results, as based on extensive benchmark instances, show that the proposed RLIG algorithm is better than the MILP model in solving tiny-size problems. In addition, it significantly outperformed the IG algorithm in solving small and large test instances.

The advantage of the proposed RLIG algorithm is that it applies a multi-seed hill-climbing strategy, which is a framework to achieve diversification for preventing the search from being trapped in a local optimum, to generate the initial solution set founded on the NEH constructive heuristic. Furthermore, this study embedded an \(\varepsilon { - }\)greedy selection strategy in the destruction phase of RLIG, which is used in reinforcement learning to formalize the notion of decision making under uncertainty. The \(\varepsilon { - }\)greedy selection strategy can combine the random algorithm and the IG-based algorithm to handle the exploration and exploitation dilemma through reinforcement learning during the iterative process. While traditional IG-based algorithms have strong exploitation ability, they easily get stuck in the local optimum. The \(\varepsilon { - }\)greedy selection strategy is a perturbation mechanism that uses knowledge reinforcement, as learned from historical search results, to adjust the exploration and exploitation of the RLIG algorithm and help the algorithm escape the local optimum. Without the multi-seed hill-climbing strategy and the \(\varepsilon { - }\)greedy selection strategy, the IG-based algorithm may be localized in a small region of the solution space, and thus, be trapped in a local optimum, which eliminates the possibility of finding an optimal solution.

The drawback of the proposed RLIG algorithm is that the multi-seed hill-climbing strategy and the \(\varepsilon { - }\)greedy selection strategy may not work very well for small test instances, e.g., the subset test instances of \(n \,=\,20\) and \(q =2\). The possible reasons are that the diversification, as resulted from the multi-seed hill-climbing strategy, and the perturbation, as resulted from the \(\varepsilon { - }\)greedy selection strategy, are not able to exploit and explore the existing solutions to find the best solution for small test instances. The major limitation of the proposed RLIG algorithm is the computation time required for very large problems, e.g., \(n \,=\,500\) and 1000, which needs to be improved to make it more suitable for solving real-time scheduling problems. An additional limitation of this research is that the operational parameters were assumed to be deterministic.

6 Conclusions and future research directions

Globalization and the rapid development of communication technology have accelerated the development of DMSs, and scheduling literature has evolved significantly with the integration of production and assembly operations in DMSs. This study addressed the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem, which has wide application in globalized production but has never been explored. Given the novelty of the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem, we first contribute to the literature by developing a MILP model for the problem to fill the research gap of the scheduling theory. Considering that the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem is NP-hard in the strong sense, an effective and efficient RLIG algorithm was also presented to solve this problem. The RLIG algorithm uses a multi-seed hill-climbing strategy and an \(\varepsilon { - }\)greedy selection strategy that could exploit and explore the existing solutions to find the best solutions for the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem. Extensive numerical analysis with 1360 test instances shows that RLIG can achieve high quality solutions under different production scales and workloads, which makes it a viable approach for use in various industries with supply-chain-integrated scheduling requirements and a strong benchmark algorithm for optimizing the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem.

Future research can be extended in several directions. First, as this study is the first theoretical advance made on the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem, further studies are desirable, and in particular, the development of sophisticated exact, approximation, and heuristic algorithms to solve this problem. Second, the DAPFSP-FASDST problem with other performance criteria, e.g. the total weighted completion time, the total weighted tardiness, and the number of tardy jobs, deserves further study. Third, the DAPFSP-FASDST problem with process-related constraints, such as blocking, no-wait, and no-idle, in the distributed flowshops of the production stage is worthy of further investigation. Fourth, a corresponding stochastic model of the \(DF_{m} \to R_{m} |prmu,ST_{sd} |C_{\max }\) problem is needed to bridge the gap between theoretical progress and industrial practice with non-deterministic operational parameters. Fifth, further investigation is essential to solve multi-objective DAPFSP-FASDST. Finally, the related problems of production and assembly stages with additional or heterogeneous shop types, e.g., non-permutation flowshops, jobshops, and openshops, deserve further discussion.