1 Introduction

As one of the most critical clean energy resources, hydropower has been developed on a large scale to meet the power demands of the economy in China. Long-term generation scheduling (LGS) is important for improving the development efficiency of hydropower after building many cascade hydropower systems (CHSs) (Lior 2010; Zhang et al. 2014). In the last two decades, numerous studies have been conducted with an emphasis on maximum annual hydropower generation, which is important in a CHS (Wang et al. 2015; Yoo 2009; Liao et al. 2017). However, these conventional scheduling results tend to release less water to raise the water levels and hydraulic heads of CHS during dry season (Niu et al. 2018), which may damage the downstream river ecosystem. Hence, multi-objective long-term generation scheduling (MLGS) has been developed to schedule CHS with considering ecological flow demands (Zhang et al. 2013), which is classified as a multi-objective optimization problem (MOP) due to the addition of the ecological objective. MLGS aims to increase the annual hydropower generation of a CHS while meeting its ecological flow demands of the downstream river ecosystem as much as possible (Zhang et al. 2019). Meanwhile, when solving a MLGS problem, many complex constraints must be taken into account. These complex constraints and the conflicting objectives of annual hydropower generation and ecological flow demands make MLGS problems difficult to solve (Al-Aqeeli et al. 2016; Feng et al. 2018; Li et al. 2015b). Therefore, this paper focuses on the MLGS problem of a CHS in which maximum annual hydropower generation and minimum annual ecological underflow and overflow water volume are considered simultaneously when satisfying a set of complex constraints.

Solving the MLGS problem aims to provide a set of optimal solutions as diverse and convergent as possible to represent its true Pareto front instead of one optimal solution (Hakimi-Asiabar et al. 2010). Various optimization methods have been applied by a number of researchers, and these methods can be roughly classified into two categories: single-objective and multi-objective methods. In the first group, MLGS is transformed into a single-objective optimization problem (SOP), which is easier to solve by single-objective methods (Feng et al. 2017). This kind of transfer approach, including the constraint method (Bai et al. 2015), weighting method (Kamodkar and Regulwar 2014) and ideal point method (Zhou et al. 2015), is simple but not effective and efficient. This kind of approach may diminish the solution space and not provide enough useful information on the Pareto optimal front (PF) with one run. Therefore, an increasing number of studies have investigated the performance of the methods in the second group, which are mainly multi-objective evolutionary algorithms (MOEAs). Compared with single-objective optimization methods that provide one optimal solution, MOEAs can optimize the competing objectives simultaneously and then provide a set of Pareto optimal solutions (PSs) with a single run. Many MOEAs, such as non-dominated sorting genetic algorithm II (NSGA-II) (Zhou et al. 2018), multi-objective particle swarm optimization (MOPSO) (Liao et al. 2017; Niu et al. 2018; Feng et al. 2017), multi-objective differential evolution (MODE) (Zhang et al. 2013; Schardong et al. 2012), multi-objective cultural algorithm (MOCA) (Zhang et al. 2012), multi-objective shuffled frog leaping algorithm (MOSFLA) (Li et al. 2010), multi-objective immune algorithm (MOIA) (Luo et al. 2015), multi-objective evolutionary algorithm based on decomposition (MOEA/D) (Zhang et al. 2016) and multi-objective gravitational search algorithm (MOGSA) (Li et al. 2015a), have been widely proposed to solve MLGS problems with great success. However, work is still needed to overcome the decrease in population diversity and the imbalance between global exploration and local exploitation during the evolutionary process, which will result in prematurely converging to the local Pareto front and require much time to converge to the global Pareto front (Feng et al. 2017; Zheng et al. 2016). In other words, it is essential to develop new efficient MOEAs to precisely solve MLGS problems.

Particle swarm optimization (PSO) was first proposed by Eberhart and Kennedy (1995). As a bioinspired technique, PSO draws inspiration from the social behaviors of bird flocking or fish schooling, and it has become one of the most efficient optimization techniques. Therefore, MOPSO has been heavily researched and applied to many MOPs and has shown very good results (Liao et al. 2017; Niu et al. 2018; Feng et al. 2017; Reddy and Kumar 2007). When extending PSO to solve MOPs, dominance-based and decomposition-based approaches are two widely used ways to determine the utility of each particle. Dominance-based MOPSOs, such as MOPSO (Coello and Lechuga 2002) and TV-MOPSO (Tripathi et al. 2007), perform well in convergence but need additional techniques to overcome the loss of population diversity (Fonseca and Fleming 1993; Laumanns et al. 2002), and decomposition-based MOPSOs, such as MOPSO/D (Peng and Zhang 2008) and dMOPSO (Martínez and Coello 2011), have a lower computation complexity but might fail to obtain uniformly distributed PSs (Li et al. 2015c). Meanwhile, hybrid approaches that combine dominance and decomposition have been reported by Al Moubayed et al. (2014) and can use the advantages of each method to develop a better MOPSO. At the same time, to design an efficient MOPSO for MOPs, various novel techniques can be adopted to improve its performance. For instance, a time varying flight parameter mechanism was proposed to update the inertia weight and acceleration coefficients in Tripathi et al. (2007). The results show that the MOPSO with these adaptive flight parameters can balance the diversity and convergence of non-dominated solutions efficiently. Reddy and Kumar (2007) developed a hybrid algorithm by incorporating an efficient elitist-mutation operator into MOPSO (EM-MOPSO) to solve the problem of premature convergence to the local (PF). Feng et al. (2017) presented a MOPSO to solve cascaded hydropower system operation problem. In this MOPSO, logistic map is used to increase the diversity of the initial population. In Han et al. (2017), the population spacing information was proposed to obtain the distribution of particles. An adaptive flight parameter mechanism using this information was implemented to develop a MOPSO with suitable global exploration and local exploitation abilities which have been demonstrated in the results. However, all those MOPSOs are developed by incorporating one or several of the above-mentioned improvements in PSO independently, which may restrict them to achieve a better possible performance. Few studies have investigated the performance of a MOPSO which is developed by combining various improvements together. Whether such an algorithm can obtain better solutions for the MLGS problem should be validated in practice.

Motivated by the above analysis, this paper develops a novel adaptive MOPSO based on decomposition and dominance (D2AMOPSO) using multiple methods: chaotic initialization, normal cloud mutation (Wu et al. 2008), dominance-based external archive update, decomposition-based personal best and global best selection and adaptive flight parameter adjustment mechanism. In D2AMOPSO, the personal best and global best are selected based on an improved Tchebycheff approach where the geometric properties of sub-problem objective functions (Ma et al. 2018) and the impacts of different measurement units and value ranges of objective functions are considered. By using the concept of Pareto dominance, the non-dominated solutions are collected in an external archive where crowding distance (Sierra and Coello 2005) and elitist learning strategy (ELS) (Zhan et al. 2009) are performed to emphasize its diversity. The inertia weight and acceleration coefficients are adaptively controlled by an adjustment mechanism based on the Pareto entropy (Hu and Yen 2015). Moreover, a normal cloud mutation operator is adopted to keep the population diversity and escape local minima for D2AMOPSO. Finally, with the initial population obtained by chaotic initialization, the proposed D2AMOPSO algorithm is applied to address the MLGS problems of the Three Gorges Cascade hydropower system (TGC) in three typical years, where the repair strategy and individual constraints and group constraints (ICGC) technique (Li et al. 2015a) are used to handle their constraints.

The rest of this paper is organized as follows: In Section 2, the formulation of a MLGS problem is presented. In Section 3, an overview of PSO is given. In Section 4, the implementation of the proposed method for MLGS is described in detail. In Section 5, a case study is developed. In Section 6, the conclusion is given, followed by the acknowledgment.

2 Problem Formulation

2.1 Nomenclature

f1, f2

Annual hydropower generation and ecological underflow and overflow water volume objectives of a CHS during the whole scheduling period.

t

Index of the scheduling period.

Δt

Length of scheduling period t.

T

Total number of scheduling periods.

n

Index of the reservoir.

N

Total number of reservoirs.

K n

Power output coefficient of reservoir n.

H n, t

Hydraulic head of reservoir n at period t.

\( {Z}_{n,t}^{down} \)

Average tail water level of reservoir n at period t.

P n, t

Power output of reservoir n at period t.

\( {P}_{n,t}^{\mathrm{min}} \), \( {P}_{n,t}^{\mathrm{max}} \)

Lower and upper output bounds of reservoir n at period t.

Vn, t, Vn, t + 1

Initial and final storage volumes of reservoirn at period t.

\( {Q}_{n,t}^I \), \( {Q}_{n,t}^O \)

Inflow and outflow of reservoir n at period t.

\( {Q}_{n,t}^P \), \( {Q}_{n,t}^S \)

Power discharge rate and spillage rate of reservoir n at period t.

\( {Q}_{n,t}^{O,\min } \), \( {Q}_{n,t}^{O,\max } \)

Minimum and maximum water outflow rates of reservoir n at period t.

\( {\underline{Q}}_{n,t}^{eco} \), \( {\overline{Q}}_{n,t}^{eco} \)

Lower and upper ecological flow demands of reservoir n at period t.

Zn, t, Zn, t + 1

Initial and final water levels of reservoir n at period t.

\( {Z}_{n,t}^{\mathrm{max}} \), \( {Z}_{n,t}^{\mathrm{min}} \)

Upper and lower initial water level limits of reservoir n at period t.

Zn, 1, Zn, T + 1

Initial and terminal water levels of reservoir n.

\( {Z}_n^{begin} \),\( {Z}_n^{end} \)

Initial and terminal water level limits of reservoir n.

vn(⋅)

Storage-capacity curve of reservoir n.

zn(⋅)

Function between the tail water level and outflow of reservoir n.

qn(⋅)

Function between the water level and maximum outflow of reservoir n.

2.2 Objective Functions

In this paper, the maximum annual hydropower generation objective aims to utilize the availability of water resources while the minimum annual ecological underflow and overflow water volume is used as the ecological objective function to protect the downstream river ecosystem health when operating a CHS (Zhang et al. 2013). These objective functions can be written as follows:

$$ {f}_1=\max \sum \limits_{t=1}^T\sum \limits_{n=1}^N{K}_n{Q}_{n,t}^P{H}_{n,t}\varDelta t=\max \sum \limits_{t=1}^T\sum \limits_{n=1}^N{P}_{n,t}\varDelta t $$
(1)
$$ {f}_2=\min \sum \limits_{t=1}^T\sum \limits_{n=1}^N\left[\max \left(0,{Q}_{n,t}^O-{\overline{Q}}_{n,t}^{eco}\right)+\max \Big(0,{\underline{Q}}_{n,t}^{eco}-{Q}_{n,t}^O\Big)\right]\varDelta t $$
(2)

2.3 Constraints

The following are various equality and inequality constraints that should be satisfied while solving the MLGS problem.

  1. (1)

    Reservoir water balance equation:

$$ {V}_{n,t+1}={V}_{n,t}+\left({Q}_{n,t}^I-{Q}_{n,t}^O\right)\varDelta t\kern1.5em t=1,2,\dots, T,\kern1.5em n=1,2,\dots, N $$
(3)

(2) Reservoir storage conversion:

$$ {V}_{n,t}={v}_n\left({Z}_{n,t}\right)\kern1.5em t=1,2,\dots, T+1,\kern1.5em n=1,2,\dots, N $$
(4)

(3) Reservoir water head:

$$ {Z}_{n,t}^{down}={z}_n\left({Q}_{n,t}^O\right)\kern1.5em t=1,2,\dots, T,\kern1.5em n=1,2,\dots, N $$
(5)
$$ {H}_{n,t}={v}_n^{-1}\left[\left({V}_{n,t}+{V}_{n,t+1}\right)/2\right]-{Z}_{n,t}^{down}\kern1.5em t=1,2,\dots, T,\kern1.5em n=1,2,\dots, N $$
(6)

(5) Reservoir water level constraints:

$$ {Z}_{n,t}^{\mathrm{min}}\le {Z}_{n,t}\le {Z}_{n,t}^{\mathrm{max}}\kern1.5em t=1,2,\dots, T+1,\kern1.5em n=1,2,\dots, N $$
(7)
$$ {Z}_{n,1}={Z}_n^{begin}\kern1.5em n=1,2,\dots, N $$
(8)
$$ {Z}_{n,T+1}={Z}_n^{end}\kern1.5em n=1,2,\dots, N $$
(9)

(6) Reservoir power output constraints:

$$ {P}_{n,t}={K}_n{Q}_{n,t}^P{H}_{n,t}\kern1.5em t=1,2,\dots, T,\kern1.5em n=1,2,\dots, N $$
(10)
$$ {P}_{n,t}^{\mathrm{min}}\le {P}_{n,t}\le {P}_{n,t}^{\mathrm{max}}\kern1.5em t=1,2,\dots, T,\kern1.5em n=1,2,\dots, N $$
(11)

(7) Reservoir outflow constraints:

$$ {Q}_{n,t}^O={Q}_{n,t}^P+{Q}_{n,t}^S\kern1.5em t=1,2,\dots, T,\kern1.5em n=1,2,\dots, N $$
(12)
$$ {Q}_{n,t}^{O,\min}\le {Q}_{n,t}^O\le {Q}_{n,t}^{O,\max}\kern1.5em t=1,2,\dots, T,\kern1.5em n=1,2,\dots, N $$
(13)
$$ {Q}_{n,t}^{O,\max }={q}_n\left\{{v}_n^{-1}\left[\left({V}_{n,t}+{V}_{n,t+1}\right)/2\right]\right\}\kern1.5em t=1,2,\dots, T,\kern1.5em n=1,2,\dots, N $$
(14)

3 Particle Swarm Optimization

PSO is a stochastic population-based optimization algorithm where each solution within the decision space represents a particle position in the search web (Eberhart and Kennedy 1995). Two vectors are associated with each particle, namely, position and velocity. Updating each particle’s position and velocity with the information of its personal best and global best is the significant characteristic of PSO, which makes PSO have a better global search. In PSO, each particle of the swarm updates its position vector and velocity vector according to the following formulas:

$$ {v}_{i,d}^{k+1}={w}^k{v}_{i,d}^k+{c}_1^k{r}_1\left({pbest}_{i,d}^k-{x}_{i,d}^k\right)+{c}_2^k{r}_2\left({gbest}_{i,d}^k-{x}_{i,d}^k\right) $$
(15)
$$ {x}_{i,d}^{k+1}={x}_{i,d}^k+{v}_{i,d}^{k+1} $$
(16)

where d = 1, 2, …, D and D is the dimension of the decision space; i = 1, 2, …, NS, and NS is the size of the swarm; \( {x}_i^{k+1}=\left[{x}_{i,1}^{k+1},{x}_{i,2}^{k+1},\dots, {x}_{i,D}^{k+1}\right] \) and \( {x}_i^k=\left[{x}_{i,1}^k,{x}_{i,2}^k,\dots, {x}_{i,D}^k\right] \) are the position vectors of particle i at iterations k + 1 and k, respectively; \( {v}_i^{k+1}=\left[{v}_{i,1}^{k+1},{v}_{i,2}^{k+1},\dots, {v}_{i,D}^{k+1}\right] \) and \( {v}_i^k=\left[{v}_{i,1}^k,{v}_{i,2}^k,\dots, {v}_{i,D}^k\right] \) are the velocity vectors of particle i at iterations k + 1 and k, respectively;\( {pbest}_i^k=\left[{pbest}_{i,1}^k,{pbest}_{i,2}^k,\dots, {pbest}_{i,D}^k\right] \) and \( {gbest}_i^k=\left[{gbest}_{i,1}^k,{gbest}_{i,2}^k,\dots, {gbest}_{i,D}^k\right] \) are the personal best and global best, respectively, of particle i at iteration k; r1 and r2 are two random numbers in range [0, 1]; wk is the inertia weight at iteration k; and \( {c}_1^k \) and \( {c}_2^k \) are two acceleration coefficients at iteration k.

4 Implementation of the D2AMOPSO Algorithm for MLGS

4.1 Constraint Handling Method

There are two kinds of constraints that should be taken into account in a MLGS problem: equality and inequality constraints. Equality constraints are forced to be satisfied when calculating the objective function values of solutions. Because water levels are used as decision variables in this paper, the following repair strategy can be used to effectively handle the reservoir water level constraints when some decision variables are outside the lower and upper water level limits.

$$ {x}_{i,d}^k=\left\{\begin{array}{l}{x}_d^{\mathrm{max}}\kern1.5em \mathrm{if}\kern0.5em {x}_d^{\mathrm{max}}<{x}_{i,d}^k\\ {}{x}_{i,d}^k\kern2em \mathrm{if}\kern0.5em {x}_d^{\mathrm{min}}<{x}_{i,d}^k\le {x}_d^{\mathrm{max}}\\ {}{x}_d^{\mathrm{min}}\kern1.5em \mathrm{if}\kern0.5em {x}_{i,d}^k\le {x}_d^{\mathrm{min}}\end{array}\right.\kern1.5em i=1,2,\dots, {N}_S,\kern0.5em d=1,2,\dots, D $$
(17)

where \( {x}_{i,d}^k \) is the dth variable of solution i; \( {x}_d^{\mathrm{min}} \) and \( {x}_d^{\mathrm{max}} \) are the lower and upper bounds of the dth variable.

For the reservoir power output and outflow constraints, the ICGC technique (Li et al. 2015a) is adopted. In this paper, the ICGC technique is coupled with dynamic maximum outflow capacity where the maximum outflow capacity is not a predetermined value but changes with water level during each scheduling period. This method is more practical and effective in diminishing the search space and alleviating the influence of infeasible search space on the quality of solutions. Assume that reservoir n runs on minimum and maximum outflow capacities respectively for each scheduling period from the first interval to the t ‐ 1th interval; then, by using a positive sequence, calculate the positive maximum and minimum storage limits according to Eq. (18) with \( {V}_{n,1}^{pos,\max } \)=\( {V}_{n,1}^{pos,\min } \)=\( {v}_n\left({Z}_n^{begin}\right) \). Meanwhile, by using a negative sequence with the same assumption for each scheduling period from the tth interval to the last interval, the negative maximum and minimum storage limits are determined by Eq. (18) with \( {V}_{n,T+1}^{neg,\max } \)=\( {V}_{n,T+1}^{neg,\min } \)=\( {v}_n\left({Z}_n^{end}\right) \).

$$ \left\{\begin{array}{l}{V}_{n,t}^{pos,\max }={V}_{n,1}^{pos,\max }+\sum \limits_{i=1}^{t-1}\left\{\left({Q}_{n,i}^I-{Q}_{n,i}^{O,\min}\right)\varDelta t\right\}\\ {}{V}_{n,t}^{pos,\min }={V}_{n,1}^{pos,\min }+\sum \limits_{i=1}^{t-1}\left\{\left({Q}_{n,i}^I-{Q}_{n,i}^{O,\max}\right)\varDelta t\right\}\\ {}{V}_{n,t}^{neg,\max }={V}_{n,T+1}^{neg,\max }-\sum \limits_{i=t}^T\left\{\left({Q}_{n,i}^I-{Q}_{n,i}^{O,\min}\right)\varDelta t\right\}\\ {}{V}_{n,t}^{neg,\min }={V}_{n,T+1}^{neg,\min }-\sum \limits_{i=t}^T\left\{\left({Q}_{n,i}^I-{Q}_{n,i}^{O,\max}\right)\varDelta t\right\}\end{array}\right.\kern1.5em t=2,3,\dots, T $$
(18)

Next, the feasible space can be obtained by combining these positive and negative boundaries with the reservoir water level constraints according to the following formula.

$$ \left\{\begin{array}{l}{\overset{\frown }{Z}}_{n,t}^{\mathrm{max}}=\min \left\{{v}_n^{-1}\left({V}_{n,t}^{pos,\max}\right),{v}_n^{-1}\left({V}_{n,t}^{neg,\max}\right),{Z}_{n,t}^{\mathrm{max}}\right\}\\ {}{\overset{\frown }{Z}}_{n,t}^{\mathrm{min}}\kern0.4em =\max \left\{{v}_n^{-1}\left({V}_{n,t}^{pos,\min}\right),{v}_n^{-1}\left({V}_{n,t}^{neg,\min}\right),{Z}_{n,t}^{\mathrm{min}}\right\}\end{array}\right. $$
(19)

Note that the repair strategy and ICGC technique will work together for each solution with the amended reservoir water level limits by Eq. (19). For each scheduling period, if the reservoir outflow violates its upper or lower bounds, then it is repaired to the nearest boundary. Finally, the reservoir water balance equation and reservoir storage conversion are used to obtain the repaired final water level. Similarly, the reservoir power output constraints can also be addressed by the above procedure.

4.2 Initial Population Generation

Compared with a randomized search, the coarse-grained global search by chaotic ergodicity has the best potential to improve the quality and diversity of the initial population (Han et al. 2017). An improved logistic map (He et al. 2013) is used to produce the chaotic sequence, which can be formulated by the following formula:

$$ {u}_{i+1}=1-r\cdot {\left({u}_i\right)}^2,\kern1.5em 0<r\le 2,\kern1.5em {u}_i\in \left(-1,1\right),\kern1.5em i=1,2,\dots $$
(20)

where r is a control parameter. As in He et al. (2013), r is equal to 2 in this paper. After producing the chaotic sequences, the following formula is used to map chaotic variables to variable space of optimization.

$$ {x}_{i,d}^1={x}_d^{\mathrm{min}}+\left({x}_d^{\mathrm{max}}-{x}_d^{\mathrm{min}}\right)\cdot \left({u}_{i,d}+1\right)/2,\kern1.5em d=1,2,\dots, D $$
(21)

Thus, a set of solutions with the following solution structure can be obtained:

$$ {X}^k=\left[\begin{array}{l}\kern0.2em {Z}_{1,1}^k\kern2.5em {Z}_{1,2}^k\kern1.8em \cdots \kern1.7em {Z}_{1,D}^k\\ {}\kern0.2em {Z}_{2,1}^k\kern2.3em {Z}_{2,2}^k\kern1.7em \cdots \kern1.6em {Z}_{2,D}^k\\ {}\kern1.2em \vdots \kern4.7em \vdots \kern3.2em \cdots \kern2.5em \vdots \kern1.5em \\ {}{Z}_{N_S,1}^k\kern1.7em {Z}_{N_S,2}^k\kern1.2em \cdots \kern1.2em {Z}_{N_S,D}^k\end{array}\right] $$
(22)

4.3 Improved Tchebycheff Approach

An improved Tchebycheff approach with an l2-norm constraint on direction vectors is used to decompose the MLGS problem. In this method, the sub-problems have more uniform update region, the sub-problem objective functions have more favorable geometric property (which is in terms of Euclidean distance) and the impacts of different measurement units and variation ranges is eliminated by standardization (Ma et al. 2018). The improved Tchebycheff approach is as follows:

$$ \left\{\begin{array}{l}\min \mathrm{imize}\kern1.5em {g}^{2-\mathrm{ITch}}\left(F\left({x}_i^k\right)|{\lambda}_i,{z}^{\ast}\right)=\underset{1\le j\le {N}_O}{\max}\left\{\frac{1}{\lambda_{i,j}}\cdot \frac{f_j\left({x}_i^k\right)-{z}_j^{\ast }}{z_j^{worst}-{z}_j^{best}+\varepsilon}\right\}\\ {}\mathrm{subject}\kern0.5em \mathrm{to}\kern1.5em {x}_i^k\in \Omega \end{array}\right.\kern1.5em i=1,2,\dots, {N}_S $$
(23)

where λi=\( \left({\lambda}_{i,1},{\lambda}_{i,2},\dots, {\lambda}_{i,{N}_O}\right) \) with ‖λi‖2=1 and \( {\lambda}_{i,1},{\lambda}_{i,2},\dots, {\lambda}_{i,{N}_O} \)>0 is a direction vector; NO is the number of objectives; ε=0.00001 is a small positive number; and \( {z}_j^{best} \) and \( {z}_j^{worst} \) are the best and worst values of the jth objective function, respectively. In the MLGS problem, \( {z}_j^{best} \) and \( {z}_j^{worst} \) are the maximum and minimum values, respectively, when the jth objective function is the maximum annual hydropower generation, whereas \( {z}_j^{best} \) and \( {z}_j^{worst} \) are the minimum and maximum values, respectively, when the jth objective function is the minimum annual ecological underflow and overflow water volume. z∗=\( \left({z}_1^{\ast },{z}_2^{\ast },\dots, {z}_{N_O}^{\ast}\right) \) is the reference point with \( {z}_j^{\ast } \)=\( {z}_j^{best} \) for each j = 1, 2, …, NO.

Meanwhile, the following equation is adopted to generate a uniform distribution of NS direction vectors which satisfy the l2-norm constraint for the MLGS problem.

$$ \left\{\begin{array}{l}{\lambda}_i=\left[\cos \left({\theta}_i\right),\sin \left({\theta}_i\right)\right]\\ {}{\theta}_i=\frac{\pi }{2}\cdot \frac{i-1}{N_S-1}\end{array}\right.\kern1.5em i=1,2,\dots, {N}_S $$
(24)

4.4 Improved PSO Operator

4.4.1 Global Best and Personal Best Update

The personal best of a particle represents its previous best position. In the initialization, because there is no previous movement, the personal best of each particle is initialized as its initial position, i.e., \( {pbest}_i^1 \)=\( {x}_i^1 \) for i = 1, 2, …, NS. At each cycle, if the position of the offspring particle is better than its previous personal best, then the personal best is replaced with the position of the offspring particle; otherwise, the personal best remains unchanged.

Similar to many other variants of MOPSO, the way in which the global best of each particle is selected from an external archive that saves the PSs found so far by all particles is used in the D2AMOPSO algorithm. According to the improved Tchebycheff approach, the solution that minimizes each sub-problem is selected as its global best. Denote the external archive as A. In the initialization, all the non-dominated particles are collected into A. During evolution, the newly generated particle will be added to A if no particle in A can dominate it. Meanwhile, the dominated particles will be removed from A. Notably, the external archive repair mechanism based on crowding distance is used to determine which particles should be removed when the size of A is more than its prefixed maximal size. In addition, the ELS is developed as a perturbation method here to help A search the potentially better space. Its pseudocode can be found in Zhan et al. (2009).

4.4.2 Adaptive Flight Parameter Mechanism

Adaptive wk, \( {c}_1^k \) and \( {c}_2^k \) adjustment is a flexible mechanism to balance exploration and exploitation in PSO. According to Hu and Yen (2015), the time-varying Pareto entropy detected in Parallel Cell Coordinate System (PCCS) is used to reflect the evolutionary status, and the following steps are used to adjust wk, \( {c}_1^k \) and \( {c}_2^k \).

Step 1: For each l = 1, 2, …, L, the objective vector of the lth PS \( {a}_l^k \) in A is mapped into the PCCS according to Eq. (25).

$$ {I}_{l,m}=\left[L\frac{f_m\left({a}_l^k\right)-{f}_m^{\mathrm{min}}}{f_m^{\mathrm{max}}-{f}_m^{\mathrm{min}}}\right] $$
(25)

where L is the current number of solutions in A. [⋅] is a ceiling function. \( {f}_m^{\mathrm{min}} \)=\( \underset{1\le l\le L}{\min }{f}_m\left({a}_l^k\right) \) and \( {f}_m^{\mathrm{max}} \)=\( \underset{1\le l\le L}{\max }{f}_m\left({a}_l^k\right) \). Il, m is an integer index number transformed from the mth objective of \( {a}_l^k \). Specifically, if \( {f}_m\left({a}_l^k\right) \)=\( {f}_m^{\mathrm{min}} \), then Il, m is set to one.

Step 2: Entropy and ΔEntropy of A in the PCCS are calculated according to Eq. (26) at generation k.

$$ \left\{\begin{array}{l}\varDelta Entropy(k)= Entropy(k)- Entropy\left(k-1\right)\\ {} Entropy(k)=-\sum \limits_{l=1}^L\sum \limits_{m=1}^{N_O}\frac{Cell_{l,m}(k)}{L\cdot {N}_O}\log \frac{Cell_{l,m}(k)}{L\cdot {N}_O}\end{array}\right. $$
(26)

where Celll, m(k) is the number of solutions for which the mth objective is mapped to the cell located at the lth row and mth column in PCCS.

Step 3: The maximal probable variation in entropy is calculated according to Eq. (27).

$$ \delta =-2{N}_O\frac{1}{L\cdot {N}_O}\log \frac{1}{L\cdot {N}_O} $$
(27)

Step 4: The flight parameters wk, \( {c}_1^k \) and \( {c}_2^k \) are calculated according to Eqs. (28), (29) and (30), respectively.

$$ {w}^k=\left\{\begin{array}{l}{w}^{k-1}\kern20.5em \mathrm{if}\kern0.5em \varDelta Entropy(k)=0\\ {}{w}^{k-1}+2{Step}_w\left(1+\left|\varDelta Entropy(k)\right|\right)\kern1.5em \mathrm{if}\kern0.5em 0<\left|\varDelta Entropy(k)\right|<\delta \\ {}{w}^{k-1}-{Step}_w\left|\varDelta Entropy(k)\right|\kern5.6em \mathrm{if}\kern0.5em \left|\varDelta Entropy(k)\right|\ge \delta \end{array}\right. $$
(28)
$$ {c}_1^k=\left\{\begin{array}{l}{c}_1^{k-1}\kern20.6em \mathrm{if}\kern0.5em \varDelta Entropy(k)=0\\ {}{c}_1^{k-1}\kern0.5em +2{Step}_{c_1}\left(1+\left|\varDelta Entropy(k)\right|\right)\kern1.7em \mathrm{if}\kern0.5em 0<\left|\varDelta Entropy(k)\right|<\delta \\ {}{c}_1^{k-1}\kern0.5em -{Step}_{c_1}\left|\varDelta Entropy(k)\right|\kern5.8em \mathrm{if}\kern0.5em \left|\varDelta Entropy(k)\right|\ge \delta \end{array}\right. $$
(29)
$$ {c}_2^k=\left\{\begin{array}{l}{c}_2^{k-1}\kern20.8em \mathrm{if}\kern0.5em \varDelta Entropy(k)=0\\ {}{c}_2^{k-1}-2{Step}_{c_2}\left(1+\left|\varDelta Entropy(k)\right|\right)\kern1.7em \mathrm{if}\kern0.5em 0<\left|\varDelta Entropy(k)\right|<\delta \\ {}{c}_2^{k-1}+{Step}_{c_2}\left|\varDelta Entropy(k)\right|\kern5.8em \mathrm{if}\kern0.5em \left|\varDelta Entropy(k)\right|\ge \delta \end{array}\right. $$
(30)

where Stepw=(wmax − wmin)/(K − 1), \( {Step}_{c_1} \)=\( \left({c}_1^{\mathrm{max}}-{c}_1^{\mathrm{min}}\right)/\left(K-1\right) \), and \( {Step}_{c_2} \)=\( \left({c}_2^{\mathrm{max}}-{c}_2^{\mathrm{min}}\right)/\left(K-1\right) \). K is the maximum iteration. According to Ratnaweera et al. (2004), wmax and wmin are set to 0.9 and 0.4, respectively, whereas \( {c}_1^{\mathrm{max}} \)=\( {c}_2^{\mathrm{max}} \) and \( {c}_1^{\mathrm{min}} \)=\( {c}_2^{\mathrm{min}} \) are set to 2.5 and 0.5, respectively. The initial values of wk, \( {c}_1^k \) and \( {c}_2^k \) are set to 0.9, 1.5 and 1.5, respectively.

4.5 Normal Cloud Mutation Operator

Because of its properties of randomness and stable tendency, a normal cloud mutation operator is integrated into D2AMOPSO to maintain the diversity of solutions (Raquel and Naval 2005). The eigenvector (Ex, En, He) of cloud model for a randomly selected solution \( {x}_i^{k+1} \) is formulated as follows:

$$ \left\{\begin{array}{l} Ex={x}_{i,d}^{k+1}\\ {} En=\left|{x}_d^{\mathrm{max}}-{x}_d^{\mathrm{min}}\right|/20\sqrt{k+1}\\ {} He= En/10\end{array}\right. $$
(31)

where Ex, En and He are the expectation value, entropy and hyper-entropy, respectively, and d is the randomly selected dimension. The variable \( {x}_{i,d}^{k+1} \) will mutate as follows:

$$ {\overset{\frown }{x}}_{i,d}^{k+1}=\left\{\begin{array}{l}\mathrm{CloudDrp}(1)\kern1em \mathrm{if}\kern0.3em \mathrm{CloudDrp}(2)>\mathit{\operatorname{rand}}\left(0,1\right)\\ {}{x}_{i,d}^{k+1}\kern5.199997em \mathrm{else}\kern0.1em \end{array}\right. $$
(32)

where \( {\overset{\frown }{x}}_{i,d}^{k+1} \) is the mutated value and rand(0, 1) is a random number between (0,1).(CloudDrp(1), CloudDrp(2)) is a cloud drop which can be formulated as follows:

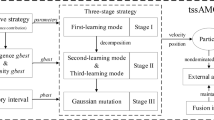
$$ \left\{\begin{array}{l}\mathrm{CloudDrp}(1)= normrnd\left( Ex,{En}^{\ast },1,1\right)\\ {}\mathrm{CloudDrp}(2)=\exp \left[-{\left(\mathrm{CloudDrp}(1)- Ex\right)}^2/2{\left({En}^{\ast}\right)}^2\right]\\ {}{En}^{\ast }= normrnd\left( En, He,1,1\right)\end{array}\right. $$
(33)

4.6 Outline of D2AMOPSO for MLGS

In this section, the detailed procedure of D2AMOPSO for solving MLGS problem is presented in Fig. 1.

Fig. 1
figure 1

The flowchart of the D2AMOPSO algorithm for the MLGS problem

Full size image

5 Case Study

5.1 Case Study Description

A case study is conducted to investigate the feasibility and effectiveness of D2AMOPSO for solving the MLGS problems of the TGC. This hydropower system is located at the end of the upper reaches of the Yangtze River in China, which consists of the Three Gorges hydropower project (TGP) and Gezhouba hydropower project (GP). As the largest hydropower station in the world, the TGP plays a vitally important role in the exploitation and utilization of the Yangtze River with multiple benefits, including flood control, power generation, navigation improvement, ecological protection, etc. The GP sits 38 km downstream from the TGP and has the functions of power generation, improving the navigation channel, etc. In our study, some basic constraints are set as follows. The lower and upper water level bounds of the TGP in the flood season (i.e., from June to September) are set to 144.9 m and 146.5 m, respectively. Meanwhile, the TGP’s water level cannot exceed the normal water level of 175 m during the non-flood season, and fall below 155 m before the end of April. The initial and terminal water levels of the TGP are both set to 175 m. The TGP and GP are installed with capacities of 22,500 and 2715 MW and guaranteed power outputs of 4990 and 1040 MW, respectively. The minimum outflow is 5000 m3/s for both the TGP and GP. These constraints can guarantee that the TGC is operated to maintain the economy and environment on the premise of satisfying the basic requirements of flood control and navigation. Since the main function of GP is hydropower generation, the GP is assumed to operate at 65 m during the whole scheduling period. The other parameters are set the same as in Zhang et al. (2014).

To clarify the superiority of the proposed method, the optimal results of D2AMOPSO, dMOPSO (Martínez and Coello 2011), MOEA/D (Zhang and Li 2007) and MOPSO (Coello and Lechuga 2002) and NSGA-III (Deb and Jain 2014) for the MLGS problems of the TGC are investigated within three typical years: wet (30%), normal (50%) and dry (70%) years. The inflows of the TGC in these three typical years are given in Fig. 2 where the whole scheduling period is divided into 12 time intervals with one month for each interval. For each typical year, the annual ecological underflow and overflow water volume is calculated by comparing the outflow of the TGC with maximum and minimum ecological flow demands at the Yichang (YC) hydrological station, which is located 44 km downstream from the TGP. The details of these ecological flow demands are also shown in Fig. 2.

Fig. 2
figure 2

Inflows and ecological flow demands for three typical years

Full size image

5.2 Parameter Settings

All the algorithms are implemented in MATLAB version 2018b and executed on a PC with a 1.9 GHz CPU and 8 GB RAM for all typical years. A few parameters must be set in this section because most of the parameters have been controlled adaptively in the sections above. Based on previous experience and numerous numerical experiments, the population size and maximum iteration are set to 100 and 1000, respectively, for all implementations to obtain fair results. The external archive size is set to 100 for both D2AMOPSO and MOPSO while the neighborhood size is set to 20 for MOEA/D. Note that the dMOPSO algorithm used here adopts the Tchebycheff approach to decompose the MOPs instead of the penalty boundary intersection (PBI) method used in Martínez and Coello (2011). The settings for other parameters of dMOPSO, MOEA/D, MOPSO and NSGA-III are the same as their corresponding references. Meanwhile, each method is run in 20 simulations independently to obtain the final PFs.

5.3 Result and Discussion

In our study, the constraint handling method in Section 4.1 and the population initialization strategy in Section 4.2 are used for all the algorithms. Figure 3 presents the final PFs obtained by different algorithms in wet, normal and dry years. Obviously, all the algorithms provide a set of PSs for each typical year. Meanwhile, in these PFs, the annual hydropower generation increases while the annual ecological underflow and overflow water volume increases. This result means that hydropower generation and ecological protection have a clear competitive relationship because increasing annual hydropower generation will inevitably increase annual ecological underflow and overflow water volume. A visual comparison with other PFs shows that the PF obtained by D2AMOPSO has better convergence and diversity performance and a broader range of choices than those obtained by other algorithms in each typical year.

Fig. 3
figure 3

PFs obtained by different algorithms in a wet, b normal and c dry years

Full size image

Spacing (SP) (Schott 1995) and hypervolume (HV) (Zitzler et al. 2000) metrics are adopted to further demonstrate the advantage of D2AMOPSO. Usually, a smaller SP value and a greater HV value represent that the algorithm has a better performance in diversity and convergence, respectively. The maximum (Max), mean (Mean), minimum (Min) and standard deviation (Std) values of SP and HV are shown in Table 1 where the bold values refer to the best minimum SP, maximum HV and minimum standard deviation among those test algorithms in each typical year. In Table 1, D2AMOPSO can obtain the second smallest SP for wet and normal years and the smallest SP for dry year, which means that D2AMOPSO is superior to dMOPSO, MOEA/D and MOPSO but slightly inferior to NSGA-III in terms of SP. Meanwhile, according to the HV values, D2AMOPSO is considered superior to other test algorithms for all typical years. The SP and HV convergence curves of different algorithms are shown in Fig. 4 where the first rows show the whole convergence trajectory and the second rows focus on the detailed convergence processes in iteration 1 to 200. It is clear that D2AMOPSO is the first to converge to a relatively good level and flatten out at this level for all typical years. The average execution times are also listed in Table 1. After 20 independent runs, the average execution times of D2AMOPSO are 215.1 s, 227.4 s and 221.3 s in wet, normal and dry years, respectively. The computational efficiency of D2AMOPSO is better than that of the other test algorithms in the normal year and slightly worse than that of MOPSO in the wet year and MOEA/D in the dry year. From what has been discussed above, the superiority of D2AMOPSO for solving the MLGS problems of the TGC in three typical years within a reasonable computational time has been verified.

Table 1 SP and HV metric values and average execution times of different algorithms in three typical years
Full size table
Fig. 4
figure 4

SP (left column) and HV (right column) convergence curves of different algorithms in three typical years during iteration 1 to 1000 (first rows) and 1 to 200 (second rows)

Full size image

Figure 3 shows that the available decision spaces are decreasing for both annual hydropower generation and ecological underflow and overflow water volume with the reduction in inflow. To investigate the effectiveness of the constraint handling method and population initialization strategy, we select three typical schemes (black marks in Fig. 3) from the final PF obtained by D2AMOPSO in each typical year. The water level, power output and outflow of the selected schemes are shown in Fig. 5 where the water level of GP is not presented because it is a fixed value. Note that Schemes 1, 50 and 100 are featured with the maximum annual hydropower generation, minimum annual ecological underflow and overflow water volume and compromise schemes, respectively. Figure 5 shows that the water level, output and outflow of the TGC in the selected schemes for three typical years are limited to their preset feasible regions during the whole scheduling period, illustrating that the constraint handling method and population initialization strategy used in this paper works well. Furthermore, taking the wet year as an example, the water level trajectories of the TGP in the selected schemes are similar during the flood season because its water level is fixed to the flood-limited water level. During the flood season, the outflow and total power output of the TGC in each selected scheme change with its inflow and may be restrained by its maximum outflow and power output capacities. An obvious difference between both the TGP water level and outflow of the selected schemes exists in the non-flood season. Meanwhile, the differences in water level and outflow also lead to the total power output deviation of the selected schemes in the same period. During the non-flood season, Schemes 1 and 100 have the highest and lowest TGP water level, respectively. The outflow of Scheme 1 best fits the ecological flow demands while the outflow of Scheme 100 shows the most telling difference. In terms of Scheme 50, its water level, power output and outflow are a compromise of those of Schemes 1 and 100 with similar change processes. Meanwhile, similar results can be obtained by analyzing the normal and dry years.

Fig. 5
figure 5

The detailed information of the selected schemes for wet (first row), normal (second row) and dry (third row) years

Full size image

6 Conclusions

MLGS is a complicated MOP that simultaneously considers annual hydropower generation and ecological underflow and overflow water volume while satisfying various equality and inequality constraints. In this paper, D2AMOPSO was proposed to solve the MLGS problem effectively. The significant characteristics of D2AMOPSO are as follows. A decomposition-based selection mechanism based on an improved Tchebycheff approach is adopted to update the personal best and global best for each particle. The non-dominated solutions found so far are stored in an external archive where crowding distance and ELS are performed to improve its diversity. A mechanism based on Pareto entropy is introduced for the inertia weight and acceleration coefficients adjustment to balance the global exploration and local exploitation abilities. A normal cloud mutation operator is integrated to overcome the loss of population diversity and escape the local minima. Finally, the D2AMOPSO algorithm was applied to the MLGS problems of the TGC in three typical years with the proposed constraint handling method and population initialization strategy. The results show that compared with dMOPSO, MOEA/D, MOPSO and NSGA-III, D2AMOPSO has a significant advantage in obtaining more annual hydropower generation and less annual ecological underflow and overflow water volume schemes within a reasonable computational time. These schemes are closer to the true Pareto front and more evenly distributed. This paper provides a novel effective alternative to solving the MLGS problem for CHS but pays a little attention to the modeling of real ecological problems, such as the impacts of the operation of the TGC on China sturgeon in the Yangtze River. Further work should use D2AMOPSO to solve the MLGS problem with considering the impacts of reservoir operation on more detailed ecological problems.