1 Introduction

As technology advances at an accelerating pace, the scaling down of device dimensions with other device properties has resulted in major challenges including the reduction of power dissipation and leakage currents. In this regard, the nanoscale regime is one field that has opened up for further research. Since metal–oxide–semiconductor field-effect transistors (MOSFETs) have formed the backbone of integrated circuits for more than half a century but their size reduction has now reached a limit, it has become essential to propose new device structures for use in integrated circuits with properties including low power consumption, optimized area for circuit implementation, and high speeds to enable circuits to operate at higher frequencies [1, 2]. Tunnel FETs have been widely investigated in this regard owing to their extraordinary capabilities such as steeper subthreshold slope (SS) and low threshold voltage (VT) combined with a high ION/IOFF current ratio for use in ultralow-power applications [3,4,5].

Despite the above-mentioned benefits, TFETs also suffer from their own set of problems, including the weak ION current and the occurrence of ambipolarity, which induces a rise in the IOFF current due to leakage that cannot be completely eliminated [6,7,8]. The lower ION current is due to the poor efficiency of band-to-band tunneling (B2BT) which occurs due to various factors such as the wider and indirect nature of the bandgap and the high effective carrier mass [9, 10]. Despite these limitations, extended studies have been carried out to increase the value of ION of silicon TFETs, which involves the use of heterojunctions with narrower-bandgap materials such as Ge, InAs, and SiGe as well as high-k dielectric oxide materials [11]. Also, arranging the source, channel, and drain in the vertical direction can enhance the scalability of simulated devices. Various aspects of such vertical TFETs have been extensively studied using TCAD simulations [12, 13]. However, to provide further insight into the operation of these devices and to carry out effective simulations of circuits using them, compact analytical modeling is still required. Compared with MOSFET models, the channel of tunneling devices should be modeled considering both the electrostatics and carrier transport process [14,15,16].

Earlier studies on single-metal-gate TFET modeling in literature suffer from various drawbacks [17,18,19], for example, the use of series expansions to describe the surface potential of the channel, which is comparatively complicated and computationally inefficient [20,21,22]. In the cited article, detailed TCAD simulations demonstrate that, as one moves from along the channel from the source to drain, the surface potential tends to fluctuate within the drain depletion region until reaching the drain potential. This finding leads to the conclusion that the drain depletion region cannot be ignored when computing such models. Therefore, a basic analytical model for the double-gate vertical t-shaped TFET is needed, taking into account the source and drain depletion regions as well as the B2BT at both junctions.

Such a 2-D analytical model for the surface potential of the double-gate vertical t-shaped TFET is discussed herein using a pseudo-2-D Poisson’s equation to the source and drain depletion regions with an accurate device channel length using an iterative approach. The model is developed by integrating the band-two-band generation rate at the source–channel and channel–drain depletion regions [9, 23]. The drive current model uses the Kane model for the tunneling process, under the assumption that the electric field is uniform at both the source–channel and channel–drain junctions. In the following section, the analytical model is validated by comparing its results with TCAD simulation results.

2 The development of the surface potential model

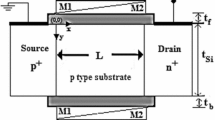
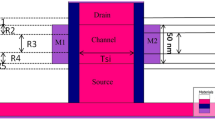
Figure 1 shows a schematic diagram of the double-gate vertical t-shaped TFET device considered herein, with the following assumptions: p++ source doping (Ns) = 5 × 1020 cm−3, n+ channel doping (Nch) = 1 × 1015 cm−3, and n++ drain doping (Nd) = 1 × 1018 cm−3, with HfO2 as the gate oxide with thickness tox = 2 nm. The channel length (Lc) of the device is 60 nm, and the metal gate work function (ϕm) is taken as 4.15 eV. The length of the source and drain regions is kept at 30 nm each. To maintain a low IOFF current, the drain-to-source doping ratio is kept low. The electron affinity (χSi) and bandgap (Eg) of silicon are taken at the default values of 4.17 eV and 1.1 eV, respectively, from the TCAD Synopsis manual [24, 25]. For convenience, the source–channel and drain-channel junctions are supposed to be abrupt. The source voltage (Vs) of the device is kept grounded and considered as the reference voltage. The gate voltage (Vg) is variable, while the drain voltage (Vd) operates as the input voltage and is fixed at 0.8 V. As shown in Fig. 1, the entire unit is separated into regions. R1 and R4 are the source and drain depletion region, respectively, whereas the channel section is considered to be Rch, where the inversion charge layer forms, being split into three separate regions R2, R3 or Rch, and R4, respectively, corresponding to the tunneling gate. L1, L2, L3, and L4 are the lengths of the depletion region formed in the source–channel and channel–drain junctions. The length L2 is comparatively greater than L1 in the source–channel junction, and vice versa in the drain–channel junction. This occurs due to the inverse proportionality between the depletion length and doping concentration. The concentration at the source and the drain is higher at the source and the drain region as discussed. The device parameters used in modeling and simulation are presented in Table 1.

Fig. 1
figure 1

A schematic diagram of the n-channel DG V t-TFET, separated into five regions (R1, R2, R3, R4 and R5), with interfaces at L0, L1, L2, L3, Lg, and L4 and corresponding surface potentials \(zs_{1} \left( x \right), zs_{2} \left( x \right), zs_{3} \left( x \right), zs_{4} \left( x \right)\), and \(zs_{5} \left( x \right)\), respectively

Full size image
Table 1 The parameter values used in the device simulations
Full size table

The energy band diagram for the proposed device is shown in Fig. 2, clearly demonstrating the distinction between the ON and OFF states of the silicon-material n-type DG V t-shaped TFET device, where Ec and Ev are the conduction and valence band of the device. The 2-D Poisson equation is solved in all these regions using appropriate boundary conditions to determine the 2-D potential and thereby the electrical field. Using a parabolic approximation for the potential, an iterative approach is applied to measure the depletion lengths associated with regions R1 and R4.

Fig. 2
figure 2

The energy band diagram of the double-gate silicon vertical t-shaped tunnel FET as a function of Vgs = 0 V and 0.6 V for the ON and OFF state at Vds = 0.5 V

Full size image

2.1 The model for the surface potential

The entire DG vertical t-shaped TFET device is divided into five regions as shown in Fig. 1. Regions R1 and R2 are defined due to the depletion area formed at the source–channel interface, while region R3 is a lightly doped intrinsic channel. Similarly, regions R4 and R5 are the depletion region at the channel–drain interface.

To model the surface potential of the device, the simple 2D Poisson equation is applied and solved using boundary conditions appropriate for the device [26, 27]. The generation rate of carriers corresponding to the band-to-band tunneling (B2BT) process depends on the electrical field in the tunneling junction. The electrostatics of the device is not greatly affected by mobile charges [24] when the device makes the transition from the OFF- to ON-state. Therefore, the 2-D Poisson equation can be written as

$$\frac{{\partial^{2} \varphi_{i} \left( {x,y} \right)}}{{\partial x^{2} }} + \frac{{\partial^{2} \varphi_{i} \left( {x,y} \right)}}{{\partial y^{2} }} = \frac{{qN_{\text{R}} }}{{\varepsilon_{\text{Si}} }},$$
(1)

where \(\varphi_{i} \left( {x,y} \right)\) represents the electrostatic potential in region R1 and R2 (source–channel interface) and region R4 and R5 (drain–channel interface), q is the Coulomb charge, εSi is the permittivity of silicon, and Nr is the area assumed to be doped. For DG devices, the parabolic potential approximation using a second-order polynomial is expressed as

$$\varphi_{i} \left( {x,y} \right) = a_{0} \left( x \right) + a_{1} \left( x \right)y + a_{2} \left( x \right)y^{2},$$
(2)

where \(a_{0} \left( x \right), a_{1} \left( x \right)y\), and \(a_{2} \left( x \right)y^{2}\) are the coefficients of the function x to be found from the boundary conditions in the y-direction. The basic boundary conditions are obtained by applying the continuity of the potential and electric field displacement vector in regions R1 and R2 (front side) and regions R4 and R5 (back side) of the body–oxide interfaces [28] as follows:

(1) The first boundary condition arises from the fact that the potential at the semiconductor–oxide interface is equal to the surface potential \(\varphi_{i} \left( x \right)\), which provides the following equations:

$$\varphi_{i} \left( {x,0} \right) = \varphi_{i} \left( {x,t_{\text{Si}} } \right) = \varphi_{i} \left( x \right).$$
(3)

(2) The second boundary is obtained from the definition of the electrical field displacement vector, which is constant across the semiconductor–oxide interface, giving the relationship

$$\frac{{\partial \varphi_{i} \left( {x,y} \right)}}{\partial y} = - \frac{{\varepsilon_{\text{ox}} }}{{\varepsilon_{\text{Si}} t_{\text{ox}} }}\left( {V_{{{\text{g}}1}} - \varphi_{i} \left( {x,0} \right)} \right).$$
(4)

This equation is evaluated at y = 0, where cox is the capacitance of the gate oxide per unit area (which must be equal to εox/t), εSi is the permittivity of silicon, εox is the permittivity of the oxide material, and the effective oxide thickness is t = tox for regions R2 and R3, whereas for regions R1 and R4, t = tox/2 is used to take account of the effect of fringing fields on the surface potential caused by the gate. Vg1 is the potential difference between the gate–source voltage and the flat-band voltage, given as:

$$V_{\text{g1}} = V_{\text{gs}} - V_{\text{fb}}.$$
(5)
$$\frac{{\partial \varphi_{i} \left( {x,y} \right)}}{\partial y} = \frac{{\varepsilon_{\text{ox}} }}{{\varepsilon_{\text{Si}} t_{\text{ox}} }}\left( {V_{\text{g1}} - \varphi_{i} \left( {x,t_{\text{Si}} } \right)} \right).$$
(5.1)

This condition is evaluated at y = tSi (back-side surface potential), where tSi is the thickness of the device silicon body.

$$\frac{{\partial \varphi_{i} \left( {x,y} \right)}}{\partial y} = \frac{{\varepsilon_{\text{ox}} }}{{\varepsilon_{\text{Si}} t_{\text{ox}} }}\left( {V_{\text{g1}} - \varphi_{i} \left( x \right)} \right).$$
(6)

(3) The third boundary conditions results from the fact that, at y = tSi/2, the electric field must be zero.

The mentioned constants are then derived using these boundary conditions, resulting in the following values after solving Eqs. (2)–(6):

$$a_{0} \left( x \right) = \varphi_{i} \left( x \right),$$
(7)
$$a_{1} \left( x \right) = - \frac{{c_{\text{ox}} }}{{\varepsilon_{\text{Si}} }}\left( {V_{\text{g1}} - \varphi_{i} \left( x \right)} \right),$$
(8)
$$a_{2} \left( x \right) = \frac{{c_{\text{ox}} }}{{2\varepsilon_{\text{Si}} t_{\text{Si}} }}\left( {V_{\text{g1}} - \varphi_{i} \left( x \right)} \right).$$
(9)

Application of these constants in the original equation yields second-order differential equations for the surface potential, an equation that also takes into account the fringing capacitance (Cf), which can be further subdivided into inner (Cinf) and outer fringing capacitances (Coutf) due to the fringing effect at the interface [29]. The resulting relationship can be expressed as

$$\frac{{{\text{d}}^{2} zs_{1} \left( x \right)}}{{{\text{d}}x^{2} }} - \frac{{zs_{1} \left( x \right)}}{{\omega_{1}^{2} }} = - \frac{{\left( {V_{\text{g1}} - \frac{{qN_{\text{a}} t_{\text{Si}} }}{{2C_{\text{f}} }}} \right)}}{{\omega_{1}^{2} }},$$
(10)
$$\omega_{1} = \sqrt {\frac{{t_{\text{Si}} \varepsilon_{\text{Si}} }}{{2C_{\text{f}} }}},$$
(11)

where

$$C_{\text{f}} = C_{ \inf } + C_{\text{outf}} - \frac{{\varepsilon_{\text{ox}} }}{{t_{\text{ox}} }}.$$
(12)

Additionally, in region R3, the inner fringing capacitance is a function of the surface potential. Meanwhile, the capacitance of the outer fringing depends on the thickness tox of the gate oxide. \(zs_{1} \left( y \right)\) is the surface potential in region R1, whereas for region R2, it is \(zs_{2} \left( y \right)\). This is done to avoid confusion in the software work and the typical protocol that is applied. These expressions are given as follows:

$$C_{\inf } = C_{\inf ,\hbox{max} } \exp \left| {\frac{{V_{\text{g2}} - \frac{{\phi_{\text{dg}} }}{2}}}{{\frac{{3\phi_{\text{dg}} }}{2}}}} \right|^{2},$$
(13)

and

$$C_{\inf ,\hbox{max} } = \frac{{2\varepsilon_{\text{Si}} }}{{\pi \left( {t_{\text{Si}} /2} \right)}}\ln \left( {1 + \frac{{t_{\text{Si}} }}{{2t_{\text{ox}} }}} \right),$$
(14)
$$C_{\text{outf}} = \frac{{2\varepsilon_{\text{ox}} }}{{\pi t_{\text{ox}} }}\ln \left( {1 + \frac{{h_{\text{g}} }}{{t_{\text{ox}} }}} \right),$$
(15)

where hg is the height of the gate stack resulting from conformal mapping.

To obtain the particular solution of the equation, the boundary conditions at the tunneling junctions must be applied, thus yielding the depletion width L1 and L2 in region R1 and R2, respectively, and likewise for regions R4 and R5, thus finally giving the lengths L3 and L4. Two boundary conditions are used to solve the equation for region R1 and R2:

$$zs_{1} \left( { - L_{1} } \right) = - \phi_{\text{f}},$$
(16)
$$\frac{{\partial zs_{1} \left( x \right)}}{\partial x} \approx 0.$$
(17)

This condition is evaluated at x = −L1 and gives the solution for the surface potential in region R1 in terms of the depletion width L1. The surface potential relation is

$$zs_{1} \left( x \right) = - \frac{{qN_{\text{seff}} \left( {x + L_{1} } \right)^{2} }}{{2\varepsilon_{\text{Si}} }} - \phi_{\text{f}},$$
(18)

where

$$N_{\text{seff}} = \frac{{2\varepsilon_{\text{Si}} }}{q}\left( {\frac{{qN_{\text{a}} }}{{2\varepsilon_{\text{Si}} }} - \frac{{C_{\text{ox}} V_{\text{g1}} }}{{\varepsilon_{\text{Si}} t_{\text{Si}} }}} \right)$$
(19)

and

$$\phi_{\text{f}} = V_{\text{th}} \ln \left( {\frac{{N_{\text{a}} }}{{N_{\text{i}} }}} \right).$$
(20)

Similarly, the following expression for the surface potential in region R2 can be derived using the same method:

$$zs_{2} \left( x \right) = V_{\text{g2}} - \left( {V_{\text{g2}} - \phi_{\text{dg}} } \right)\cosh \left( {\frac{{\left( {x - L_{2} } \right)}}{{\omega_{2} }}} \right),$$
(21)

where

$$\omega_{2} = \sqrt {\frac{{t_{\text{Si}} \varepsilon_{\text{Si}} }}{{2C_{\text{ox}} }}}.$$
(22)

Since the potential and electrical field are constant at the source–channel junction [24], the above-mentioned surface potential expressions for regions R1 and R2 can be equated with the surface potential at x = 0 to determine the two unknowns L1 and L2:

$$zs_{1} \left( x \right) = zs_{2} \left( x \right) \equiv \varphi \left( 0 \right),$$
(23)

and

$$\frac{{\partial zs_{1} \left( x \right)}}{\partial x} = \frac{{\partial zs_{2} \left( x \right)}}{\partial x}.$$
(24)

To determine the unknown, this expression is evaluated at x = 0, with φ(0) given as

$$\varphi \left( 0 \right) = - \left( {\left( {V_{\text{gs}} - V_{\text{fb1}} - \phi_{\text{dg}} } \right)^{2} + 2\left( {V_{\text{gs}} - V_{\text{fb1}} } \right)\phi + \phi^{2} } \right)^{0.5} + \left( {V_{\text{gs}} - V_{\text{fb1}} + \phi } \right),$$
(25)

where

$$\phi = \frac{{qN_{\text{seff}} \omega_{2}^{2} }}{{\varepsilon_{\text{Si}} }},$$
(26)

which gives

$$L_{1} = \sqrt {\frac{{2\varepsilon_{\text{Si}} \left( {\varphi \left( 0 \right) - \phi_{f} } \right)}}{{qN_{\text{seff}} }}}$$
(27)

and

$$L_{2} = \omega \cosh^{ - 1} \left( {\frac{{V_{\text{gs}} - V_{\text{fb1}} - \varphi \left( 0 \right)}}{{V_{\text{gs}} - V_{\text{fb1}} - \phi_{\text{dg}} }}} \right).$$
(28)

The surface potential in the channel region is also modeled, resulting in a continuous function X that depends on both biases and also describes the assumed dual modulation effect, i.e., the transition from the gate- to drain-controlled regime. The X function can be expressed as

$$X = \frac{1}{2}\left[ {V_{\text{ds}} + \varphi + \varphi_{\text{chd}} - \sqrt {\left( { - V_{\text{ds}} - \varphi + \varphi_{\text{chd}} } \right)^{2} + \alpha^{2} } } \right],$$
(29)
$$\varphi_{\text{chd}} = \frac{1}{2}\left( {\sqrt {V_{\text{gs}} - V_{\text{fb}} + \frac{{\gamma_{1}^{2} }}{4}} - \frac{{\gamma_{1} }}{2}} \right)^{2},$$
(30)

and

$$\varphi = V_{\text{th}} \ln \left( {\frac{{N_{\text{a}} N_{\text{i}} }}{{n_{\text{i}}^{2} }}} \right).$$
(31)

Also,

$$\gamma_{1} = \frac{{\sqrt {2\varepsilon_{\text{Si}} qN_{\text{Si}} } }}{{C_{\text{ox}} }}.$$
(32)

For each iteration, we take α as a small factor equal to 0.04 [22]. Ultimately, this yields an expression for the surface potential in the channel (region R3) denoted by φchc and expressed as

$$\varphi_{\text{chc}} = X + V_{\text{th}} \ln \left( {\frac{1}{{V_{\text{th}} }}\left( {V_{\text{th}} + \frac{\sqrt X }{{\sqrt X + \gamma_{1} }} \left( {V_{\text{gs}} - V_{\text{fb}} - X} \right) + \frac{1}{2}\left( {\frac{X}{{\left( {\sqrt X + \gamma_{1} } \right)^{2} }} - \frac{{\gamma_{1} \left( {X - 2} \right)}}{{2\left( {\sqrt X + \gamma_{1} } \right)^{3} }}} \right)\left( {V_{\text{gs}} - V_{\text{fb}} - X} \right)^{2} } \right)} \right).$$
(33)

The calculations for determining the surface potential at the drain–channel interface in regions R4 and R5 are identical to those used for the source–channel interface, i.e., for regions R1 and R2, but with the changes associated with the voltages, thus influencing the potential and the length of the device, based on which the surface potential is obtained as

$$zs_{4} \left( x \right) = V_{\text{g2}} - \left( {V_{\text{g2}} - \phi_{\text{dg}} } \right)\cosh \left( {\frac{{\left( {x - L_{\text{g}} + L_{3} } \right)}}{{\omega_{2} }}} \right),$$
(34)
$$zs_{5} \left( x \right) = - \frac{{qN_{\text{deff}} \left( {x - L_{1} - L_{4} } \right)^{2} }}{{2\varepsilon_{\text{Si}} }} - \phi_{\text{f1}},$$
(35)

where

$$\phi_{\text{f1}} = V_{\text{th}} \ln \left( {\frac{{N_{\text{d}} }}{{N_{\text{i}} }}} \right)$$
(36)

and

$$N_{\text{deff}} = \frac{{2\varepsilon_{\text{Si}} }}{q}\left( {\frac{{qN_{\text{d}} }}{{2\varepsilon_{\text{Si}} }} - \frac{{C_{\text{ox}} V_{\text{g2}} }}{{\varepsilon_{\text{Si}} t_{\text{Si}} }}} \right).$$
(37)

Equations (4) and (5) are evaluated at x = Lg and are equated at the same boundary conditions as in the case of regions R1 and R2 but changing the length in the equation. The depletion lengths L3 and L4 are thus extracted next, and according to the light doping of the channel relative to the drain, the depletion width L3 is greater than L4.

The results obtained from Eqs. (18), (21), (33), (34), and (35) are now compared with those obtained from the TCAD simulations conducted using the Sentaurus simulation tool to verify their consistency for regions R1, R2, R3, R4, and R5. Figure 3 shows the results obtained for the surface potential using the TCAD simulations in comparison with those of the proposed model, revealing a good match between the two sets of observations. The potential depends linearly on the gate bias but will saturate for the drain bias, from which it can be concluded that the DG V t-TFET has a high output resistance and can thus be used in low-power circuits or applications [4, 14].

Fig. 3
figure 3

A comparison of the results obtained from the TCAD simulations and the model derived herein for the surface potential versus the distance along the channel of the device at Vgs = 0.6 V and Vds = 0.5 V

Full size image

2.2 The gate regulation of the surface potential in the channel

Figure 4 shows the surface potential of the channel (φchc) when the gate bias is varied from 0.55 to 0.8 V but keeping the drain bias constant at 0.5 V. Inspection of this figure reveals that, for low gate voltage, the surface potential increases linearly with Vgs. However, for high gate voltage, the surface potential saturates at the potential \(\varphi_{\text{ch,sat}}^{{\prime }}\) and becomes independent of the gate bias voltage. This occurs because the inversion charge mode, which is similar to the strong inversion mode of a MOSFET, screens the surface potential from additional bending in the bias regime.

Fig. 4
figure 4

A comparison of the results obtained from the TCAD simulations versus the model derived herein for the variation of the surface potential in the channel when changing the gate terminal voltage for Vds = 0.5 V

Full size image

The estimation of band bending with reference to the DG V t-TFET is quite different. First, an extremely low magnitude of the inversion charge density Ninv, which is equivalent to the doping concentration of the channel Nch, corresponds to effective screening of the gate modulation due to the light channel doping of the device, occurring when the surface potential reaches 2φfp, where φfp is defined as the potential difference between the intrinsic Fermi potential Efi and the hole Fermi potential Efp, characterized as \(\ln \left( {N_{\text{ch}} /n_{\text{i}} } \right)kT/q\). The surface potential will continue to increase even after \(\varphi_{\text{chc}} = 2\varphi fp\), unless and until there is sufficient inversion charge to screen the gate modulation effectively. Therefore, in this case, the screening parameter for the gate modulation changes from \(\varphi_{\text{ch,sat}}^{\prime } = - 2\varphi fp\) for a MOSFET to \(\varphi_{\text{ch,sat}}^{{\prime }} = \phi\) for the DG V t-TFET, where ϕ is the potential required to obtain an adequate inversion charge to screen the gate modulation.

$$\phi = \left( {\frac{KT}{q}} \right)\ln \left( {\frac{{N_{\text{ch }} N_{\text{inv}} }}{{n_{\text{i}}^{2} }}} \right) ,$$
(38)

where ni is the intrinsic carrier concentration of silicon, Nch is the doping concentration of the channel, and Ninv is the density of inversion charges actually required to screen the gate modulation.

Using the simple 2-D Poisson equation, the potential in regions R1 and R2 can be calculated. This equation is then solved using the homogeneous differential equation approach with two boundary conditions that must be balanced in the source–channel region with L1 and L2 as the solutions for the depletion lengths. It is important to estimate the surface potential accurately, as it generates the formula to determine the drain current of the device. The model presented herein therefore includes the effect of both biasing voltages on the drain and gate terminals, which is referred to as the dual modulation effect. The inversion charges in the gate-controlled region are considered to be negligible, as the equation thus modeled for the surface potential in this region can be expressed as

$$\varphi_{\text{ch,sat}}^{{^{{\prime }} }} = \left[ {\sqrt {V_{\text{gs}} - V_{\text{fb}} + \frac{{\gamma^{2} }}{4}} - \frac{\gamma }{2}} \right]^{2}.,$$
(39)

In comparison with the simulations, the model obtained using these equations yields excellent results.

2.3 The drain regulation of the surface potential in the channel

The saturation of the surface potential also depends on the drain bias, thus the transition of the device from the gate- to drain-controlled region is given by the equation below, where γ is the body factor defined as

\(\sqrt {2E_{\text{Si}} qN_{\text{ch}} /C_{\text{ox}} }\) and Vfb is the flat-band voltage:

$$V_{\text{tr}} = V_{\text{fb}} + V_{\text{ds}} + \phi + \gamma \sqrt {V_{\text{ds}} + \phi }.$$
(40)

When Vtr crosses this voltage level, the channel is biased towards the drain-controlled regime. Figure 5 shows the variation of the surface potential with the drain bias, revealing that the surface potential is linearly related to the drain bias voltage Vds in the range from 0.45 to 0.7 V while keeping the gate bias constant at 0.8 V. Moreover, as the voltage Vds increases and as soon as Vds and Vgs fulfill the transition condition, the device is again biased in the gate-controlled region, where the effect of the gate voltage is more prominent and thus the surface potential is no longer under the influence of the drain voltage.

Fig. 5
figure 5

A comparison of the results obtained from the TCAD simulations versus the model derived herein for the variation in the channel surface potential with the drain terminal voltage for Vgs = 0.8 V

Full size image

Thus, the surface potential of the device saturates with the device current and the tunnel width output. The drain saturation voltage during this transition from drain to gate control can be expressed as

$$V_{\text{dss}} = \left[ {\sqrt {V_{\text{gs}} - V_{\text{fb}} + \frac{{\gamma^{2} }}{4}} - \frac{\gamma }{2}} \right]^{2} - \phi.$$
(41)

From the discussion above, it can be concluded that the surface potential of the device is regulated alternatively by the gate terminal voltage (Vgs) and drain terminal voltage (Vds) in the gate- and drain-controlled regime, respectively. The transition from one region to the other must thus be treated carefully; this regulation of the surface potential by the two terminal voltages is called the dual modulation effect in DG V t-TFET devices.

The approximations used to obtain these results lead to a large error when applying this surface potential model to develop the drain current model. Inversion charges cannot screen the gate modulation perfectly at the transition point, thus the device’s potential increases slightly, as shown by the slight slope in the result obtained.

2.4 The validation of the model results

Additional results are obtained by varying some other parameters such as the device material, different dielectric constants, as well as the work function of the gate metal. Such modifications lie within the field of gate or material engineering to improve the ON current of the device. First of all, the influence of the dielectric constant on the potential of the device is considered, assuming that all the other parameters of the device are kept constant. From the expressions above, it can be concluded that the the surface potential of the device is exponentially related to the dielectric constant [9]. The results obtained are plotted in Fig. 6. There are a few advantages of using a high-k dielectric constant, and HfO2 is used as the dielectric material in this work because it decreases the corresponding oxide thickness without reducing its physical thickness, although it can be reduced to a certain extent to avoid direct tunneling of charge carriers through the gate.

Fig. 6
figure 6

A comparison of the results obtained from the TCAD simulations versus the model derived herein for the variation of the surface potential of the channel due to the variation in the dielectric constant for Vgs = 0.8 V

Full size image

Increasing the work function of the gate metal will make it more of a p-type material, so increasing this work function for the n-type DG vertical t-shaped TFET device will degrade its performance, as this will decrease the surface potential of the device [28]. Increasing the work function above 4.1 eV will make it p-type, thus there will be more hole carriers, which will impede the tunneling of electrons from the source; likewise, if the work function is decreased below 4.1 eV, the number of carriers that allow current to flow in the device will increase, as will the surface potential. The results obtained using the model derived herein and the TCAD simulations are assembled and presented for comparison in Fig. 7.

Fig. 7
figure 7

A comparison of the results obtained from the TCAD simulations versus the model derived herein for the variation in the channel surface potential due to the variation in the work function for Vgs = 0.8 V

Full size image

As the bandgap of validated silicon technologies is somewhat higher, the TFET made from silicon exhibits a low tunneling current. Therefore, to improve the ON current of the device, the use of compound semiconductors is investigated with the main objective of reducing the bandgap and thereby increasing the current, while at the same time recalling that the OFF current of the device should not rise above a limit which increases the leakage current [6,7,8]. Compound semiconductors can be a combination of two elements, e.g., GaAs and InAs here, being known as binary compound semiconductors. The corresponding results are plotted for comparison with other semiconductors along with the simulated results. The results obtained for the ternary compound semiconductor InGaAs are also presented. The other main reason for using compound semiconductors is that their carriers exhibit direct tunneling while silicon has an indirect tunneling mechanism. As the bandgap is reduced, the current increases, as well as the surface potential of the device [14, 17]. The effective bandgap is reduced to allow a greater number of carriers to tunnel and thereby conduct the current. InAs has the lowest bandgap (0.35 eV) among all the compound semiconductors used in this comparative study, thus the plot of the surface potential of the DG V t-TFET shows a maximum saturated value for InAs but the lowest for silicon material. Figure 8 shows the resulting comparison among the considered materials.

Fig. 8
figure 8

A comparison of the results obtained from the TCAD simulations versus the model derived herein for the variation in the channel surface potential due to the variation in the material used at Vgs = 0.6 V and Vds = 0.5 V

Full size image

3 The model for the drain current

The current Ids mechanism in the DG V-tTFET is based on band-to-band tunneling of electrons from the valence band of the source to the conduction band of the channel region. The tunneling generation rate (GB2BT) can be determined using the Kane model [30]. The cumulative drain current is determined by integration of the band-two-band generation rate per unit volume of the device. Therefore,

$$I_{\text{ds}} = q{\iint }G_{\text{B2BT}} {\text{d}}x{\text{d}}y.$$
(42)

Kane’s model is used to calculate the tunneling generation rate (GB2BT) as

$$G_{\text{B2BT}} = A\frac{{\left| E \right|^{2.5} }}{{\sqrt {E_{\text{g}} } }}\exp \left[ { - B\frac{{E_{g}^{{3/2}} }}{{\left| E \right|}}} \right],$$
(43)

where Eg is the energy bandgap of silicon.

In this expression, |E| is the magnitude of the electric field, being defined as \(\left| E \right| = \sqrt {E_{x}^{2} + E_{y}^{2} }\), while A and B are model parameters, taking the values 4 × 1014 cm−3 s−1 and 1.9 × 107 V/cm, respectively [23]. The distribution of the electric field along the channel length can be obtained by differentiating the surface potential. The vertical electric field Ex and lateral electric field Ey are then given by

$$E_{x} \left( {x,y} \right) = - \frac{{\partial \varphi_{i} \left( {x,y} \right)}}{\partial x},$$
(44)
$$E_{y} \left( {x,y} \right) = - \frac{{\partial \varphi_{i} \left( {x,y} \right)}}{\partial y}.$$
(45)

Figure 9 shows the logIds−Vgs characteristics given by the model using Eq. (42) at Vds = 0.5 V. The subthreshold slope (SS) of the device is reported to be 32.15 mV/decade as derived via the constant-current method. This figure also shows a comparison of the simulated and analytical results, revealing that the drain current results obtained using the derived model are in good agreement with the simulations in the subthreshold region.

Fig. 9
figure 9

A comparison of the transfer curves of drain current log(Ids) versus gate voltage (Vgs) for the DG V t-TFET obtained from the simulations and the analytical model at Vds = 0.5 V for a channel length of 60 nm

Full size image

4 Conclusions

A 2-D analytical model for the surface potential and drain current of a DG vertical t-shaped TFET is developed. The model shows excellent agreement with the results of TCAD simulations for the variation of the surface potential with the gate and drain biases. The equations for the model are derived and the smallest depletion length obtained at Vgs = 0.6 V and Vds = 0.5 V. The depletion lengths L1 and L2 for region R1 and R2 are obtained as 5.25 nm and 27 nm, while the depletion lengths L3 and L4 are calculated as 26 nm and 4.59 nm for region R4 and R5, respectively. These results can also be explained theoretically as the doping profile of the channel is lighter than that of the source or drain, hence its depletion width is greater. Finally, an expression for the surface potential of the channel (region R3) that accurately captures its variation with the drain and gate biases is obtained. The tunneling widths derived from this surface potential model are further extended using the Kane model to derive the tunneling current, assuming an average constant electric field along the tunneling path. The resulting model is accurate in both the subthreshold and ON-state (strong inversion) operating regions.