1 Introduction

Combination of mechanical and electrical parts in micro scales causes new challenges in both mechanical and electrical concepts. The mechanical behaviour of each component in micro and nano-scales is different from normal dimensions due to various factors that affect the normal operation of the entire device. Micro machined pressure sensors have been developed because of their small size, high performance, high reliability and low cost. Different kinds of pressure sensor are piezoresistive, piezoelectric, capacitive sensors which have been widely used in various fields. Pressure sensors are required in applications including bio-medical systems, environmental monitoring and industrial process control. Today many companies fabricate self bulk-micro machined pressure sensors for different applications listed above. The measurement range of these sensors is very high with excellent reliability (Lin and Yun 1998). Therefore, the design and fabrication of this kind of systems become more complicated which leads to more considerations in advance. It also highlights the role of analytical approaches and simulation results to achieve the best design. Based on the conducive requirement of the design different cases for circular diaphragm based pressure sensor can be proposed. Traditionally a lot of analysis and paper has been presented on clamped edge condition of the diaphragm but freely supported edge has not been explored.

This paper presents a new case study for circular diaphragm pressure sensor. The freely supported edge condition is undertaken and analytically explored and simulated. Design optimization for piezoresistive sensing resistors including position, orientation and length is addressed.

2 Operation principle

When a uniform pressure is applied to a silicon micro diaphragm, deflection occurs and the internal strain of the diaphragm changes. Silicon is a piezoresistive material (Smith 1954) such that its resistance changes when the internal strain varies. If the pressure sensing resistors are placed on top of the thin diaphragm, pressure can be measured by monitoring the resistance changes. In this paper along with the detailed analysis of stress, strain and deflection, Wheatstone bridge type circuitry has been used to give voltage outputs for pressure measurement. Two sensing resistors are placed inside the diaphragm and the other two reference resistors are placed outside the diaphragm.

2.1 Small deflection theory

In order to determine the optimal design of the sensing resistors including position, orientation and length, conventional theories of solid mechanics have been investigated. Since the desired response is linear, small deflection theory is used. Diaphragm under consideration is of circular shape. It is discussed and analyzed.

2.2 Circular plates under small deflection

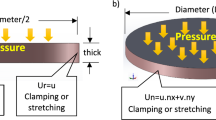
We use a thin circular plate to model the circular diaphragm as shown in Fig. 1 where w is the deflection perpendicular to the plate; E is Young’s Modulus; ν is Poisson’s ratio; t is the thickness of the plate.

Fig. 1
figure 1

Small deflection of circular plate showing applied moments and forces per unit length

Full size image

To be noted, polar coordinates are used to define the parameters as listed below: strain in the radial direction (Timoshenko and Woinowsky-Kreiger 1959)

$$\varepsilon_{r} = z\frac{d\theta }{dr}$$

Strain in tangential direction

$$\varepsilon_{t} = z\frac{\theta }{r}$$

Corresponding radial stress

$$\sigma_{r} = \frac{Ez}{{(1 - \nu^{2} )}}\left[ {\frac{d\theta }{dr} + \nu \frac{\theta }{r}} \right]$$

Corresponding tangential stress

$$\sigma_{t} = \frac{Ez}{{(1 - \nu^{2} )}}\left[ {\nu \frac{d\theta }{dr} + \frac{\theta }{r}} \right]$$

Bending moment per unit length in radial direction

$$M_{r} = D\left[ {\frac{d\theta }{dr} + \nu \frac{\theta }{r}} \right]$$

Bending moment per unit length in tangential direction

$$M_{t} = D\left[ {\nu \frac{d\theta }{dr} + \frac{\theta }{r}} \right]$$

where

$$D = \frac{{Et^{3} }}{{12(1 - \nu^{2} )}}$$

Considering the equilibrium conditions of the element of circular plate as shown in Fig. 1, we can get four governing Eqs. (1)–(4), by summing the forces, summing the moments and consider the relationship between radial and tangential strain (Ross 1999; Jindal and Raghuwanshi 2013).

In summary, we have a set of governing equations as following:

$$M_{r} + r\frac{{dM_{r} }}{dr} - M_{t} + Fr = 0$$
(1)
$$\frac{d}{dr}\left[ {\frac{1}{r}\frac{d}{dr}\left( {r\frac{dw}{dr}} \right)} \right] = - \frac{qr}{2D}$$
(2)
$$\theta = \frac{dw}{dr} = - \frac{{qr^{3} }}{16D} + C_{1} \frac{r}{2} + \frac{{C_{2} }}{r}$$
(3)
$$w = - \frac{{qr^{4} }}{64D} + \frac{{C_{1} r^{2} }}{4} + C_{2} \log_{e} r + C_{3}$$
(4)

where r is radial coordinate in the cylindrical coordinate system \(C_{1} ,C_{2} ,C_{3}\) are the constants to be determined by the boundary condition of the diaphragm.

2.3 Analytical solution for uniformly loaded circular plate with edges freely clamped

Now we have a set of equation governing the bending and deflection behaviour of circular plate. Our task is to solve \(C_{1} ,C_{2}\) and \(C_{3}\) to get an explicit expression for w(r) and related stress and strain (Eaton et al. 1999; Hao-jiang et al. 2005; Khakpour et al. 2010).

First, we have slope (θ) is not infinite at the centre of the plate, \(C_{2}\) = 0.

Taking the origin at the centre of the deflected plate, w = 0 when r = 0. Therefore, from Eq. (4), \(C_{3}\) = 0. Condition to solve for the constant \(C_{1}\) is required.

Here we make use of the fact that the bending moment is always zero at any free support,

\(M_{{_{r} }} = 0\) i.e at r = R

$$D\left[ {\frac{d\theta }{dr} + \nu \frac{\theta }{r}} \right] = 0$$
(5)

Substituting Eq. (3) with r = R and \(C_{2}\) = 0, we get

$$- \frac{{3qR^{2} }}{16D} + \frac{{C_{1} }}{2} = - \nu \left[ { - \frac{{qR^{2} }}{16D} + \frac{{C_{1} }}{2}} \right]$$
$$C_{1} = \frac{{qR^{2} }}{8D}\left[ {\frac{{\left( {3 + \nu } \right)}}{{\left( {1 + \nu } \right)}}} \right]$$
(6)

The maximum deflection is at the centre and again equal to the deflection of the supports relative to the centre.

Substituting for the constants with r = R in Eq. (4)

$$w_{\hbox{max} } = - \frac{{qR^{4} }}{64D} + \frac{{qR^{2} }}{8D}\frac{(3 + \nu )}{{\left( {1 + \nu } \right)}}\frac{{R^{2} }}{4} = \frac{{qR^{4} }}{64D}\left[ {\frac{(5 + \nu )}{{\left( {1 + \nu } \right)}}} \right]$$

i.e. substituting for D,

$$w_{\hbox{max} } = \frac{{3qR^{4} }}{{16Et^{3} }}(5 + \nu )\left( {1 - \nu } \right)$$
(7)

Substituting dθ/dr and θ/r from Eq. (3) to general eqn. of stress above we get

$$\sigma_{r} = \frac{Ez}{{(1 - \nu^{2} )}}\left[ { - \frac{{qr^{2} }}{16D}(3 + \nu ) + \frac{{qR^{2} }}{16D}(3 + \nu )} \right]$$

To get the maximum stress at the centre where r = 0 i.e. at z = t/2 we have

$$\sigma_{{r_{\hbox{max} } }} = \frac{E}{{(1 - \nu^{2} )}}\left[ {\frac{t}{2}\frac{{qR^{2} }}{16D}(3 + \nu )}\right] = \frac{{3qR^{2} }}{{8t^{2} }}(3 + \nu ) $$
(8)

Similarly

$$\sigma_{{t_{\hbox{max} } }} = \frac{{3qR^{2} }}{{8t^{2} }}(3 + \nu )$$
(9)

For micro diaphragm with freely supported edge, the radial and circumferential strain can be derived from (4) as:

$$\varepsilon_{r} = - \frac{{3qr^{2} t}}{32D} + \frac{{qR^{2} t}}{32D}\left( {\frac{3 + \nu }{1 + \nu }} \right)$$
(10)
$$\varepsilon_{t} = - \frac{{qr^{2} t}}{32D} + \frac{{qR^{2} t}}{32D}\left( {\frac{3 + \nu }{1 + \nu }} \right)$$
(11)

3 Sensitivity of piezoresistivity

Piezoresistivity of silicon can be analyzed in two directions: parallel and perpendicular to the direction of the electrical current. Fpar and Fper are the gauge factors, respectively. They are represented with respect to the piezoresistive constant \(\varPi\) as (Lin et al. 1999):

$$F_{par} = \frac{{E\left( {\prod_{l} + \nu \prod_{t} } \right)}}{{(1 - \nu^{2} )}}$$
(12)
$$F_{per} = \frac{{E\left( {\prod_{t} + \nu \prod_{l} } \right)}}{{(1 - \nu^{2} )}}$$
(13)

And the change in resistance is written as:

$$\frac{\varDelta R}{R} = F_{par} \varepsilon_{r} + F_{per} \varepsilon_{t}$$
(14)

Which can further be written as:

$$\frac{\varDelta R}{R} = \left( {F_{par} + \frac{1}{1 - \nu }} \right)\varepsilon_{r} + \left( {F_{per} + \frac{1 - 2\nu }{1 - \nu }} \right)\varepsilon_{t}$$
(15)

The sensitivity of the circular diaphragm can be calculated according to the above analytical equation.

4 Optimization of resistor length

After the sensitivity distribution for the piezoresistive resistor is calculated the optimal positions for sensing resistors are obtained. The next step is to determine the geometry of the resistors including length and shape for optimal sensitivity. In order to maximize the piezoresistive effects, line shapes resistors are designed for strain changes parallel to the direction of the input current. These line shape resistors are placed at the edges of the circular diaphragm to gain maximum sensitivity. Since misalignments are unavoidable during the fabrication processes, the sensing resistors are designed to have an non-effective portion of 2 μm outside the diaphragm. Only the effective parts of the sensor that are inside the diaphragm will be active during pressure measurement.

4.1 Configuration of the piezoresistive pressure sensor

Figure 2a, b illustrates the overall circuit design and configuration for the pressure sensor that is considered in this analysis, and the wheatstone bridge circuit used to drive and sense the response of pressure sensor, respectively. A quarter sensors bridge, rather than half or full, is all that is needed to demonstrate the effect of strain on the sensor. Here \(R_{1}\) is the piezoresistor that is patterned on the membrane, across which a pressure differential is applied. Also \(R_{2}\) is the variable resistor that is used to null the voltage output \(V_{out} = V_{A} - V_{B}\), as shown in Fig. 2b, when the pressure is not applied across the membrane. Also \(R_{3}\) is fixed resistance to balance the bridge, and \(R_{4}\) is the reference resistor that is identical in dimension and nominal resistance to \(R_{1}\). The wheatstone bridge is used since this configuration has maximum sensitivity of the output voltage, \(V_{out}\), over the varied resistance (Bae et al. 2004).

Fig. 2
figure 2

a The physical configuration of the pressure sensor and circuit on a membrane suspended on a Si substrate. Rsensor is a piezoresistor that changes resistance with the strain of the membrane, across which a pressure differential is applied. b The wheatstone quarter bridge circuit used to sense the change in resistance of Rsensor

Full size image

4.2 Sensor output analysis (when a voltage is applied)

When no pressure is applied, the output can be expressed for the quarter bridge circuit shown in Fig. 2 as

$$V_{out} = \frac{{R_{1} R_{3} - R_{2} R_{4} }}{{\left( {R_{1} + R_{2} } \right)\left( {R_{3} + R_{4} } \right)}}V_{in}$$
(16)

If all the resistances are the same as R at the initial stage and the pressure is applied, Vout can be expressed as:

$$\frac{\varDelta R}{{2\left( {2R + \varDelta R} \right)}}V_{in}$$
(17)

where ΔR is the varied resistance of R.

Hence the output voltage can be written by as

$$V_{out} = \frac{{\varDelta R_{eff} }}{{2\left\{ {2\left( {R_{non} + R_{eff} } \right) + \varDelta R_{eff} } \right\}}}V_{in}$$

or

$$V_{out} = \frac{{\left( {R + \varDelta R} \right)R - R^{2} }}{{\left( {2R + \varDelta R} \right)2R}}V_{in}$$
(18)

where \(\varDelta R_{eff}\) is the variation of the effective resistance. From Eq. (16), it can be seen that it is important to maximize \(\varDelta R_{eff}\) in order to maximize the output voltage and \(R_{non}\) is the magnitude of non-effective resistance. \(R_{eff}\) is the value of the effective resistance. It can be derived as:

$$\frac{{\varDelta R_{eff} }}{{R_{eff} }} = \frac{1}{l}\int\limits_{L}^{L - l} {\frac{\varDelta R}{R}} dx$$
(19)

where \(l\) is the length of the effective resistor, is the characteristic length of the diaphragm (radius for a circular shape diaphragm).

5 Results and discussion

Stress distribution is obtained from previous derived Eqs. (8) and (9). It is apparent from Fig. 3 that at centre the stress is maximum and decreases towards edge. It also shows that at the centre both the radial and tangential stress have the same value as discussed theoretically.

Fig. 3
figure 3

Radial and tangential stress distributions in circular plates with freely supported edges

Full size image

Figure 4 shows the strain distributions of a circular diaphragm (100 μm in diameter, 2 μm in thickness) which is under a uniform pressure of 100 psi. It can be concluded that the radial strain at the center of the diaphragm has a higher value than other positions.

Fig. 4
figure 4

Radial and tangential strain distributions for freely supported edges

Full size image

Figure 5 shows the displacement of the circular diaphragm under uniform load of 100 psi. The displacement is maximum at the centre, decreases towards the edges and minimum at the supported positions.

Fig. 5
figure 5

Displacement of the freely supported circular diaphragm under uniform load

Full size image

The optimal length of the effective resistor is calculated by using Eqs. (18) and (19). Figure 6 shows the simulation result for the circular diaphragm with above mentioned dimensions. It is observed that the diaphragm has an optimal output when the effective resistor length is about 14 μm. It decreases whether we increase or decrease the length.

Fig. 6
figure 6

Optimization analysis of effective resistor length on a circular diaphragm

Full size image

6 Conclusion

In this paper we have provided all the analytical steps for the calculation of the freely supported case. The results have been matched with the existing literature. Design and modelling of pressure sensor have been successfully established and exactly matched with the result of solidworks software. The orientation, length and position of the sensing resistors have been fully analyzed. Several specific conclusions can be drawn for the sensors geometries discussed in this paper. For circular shape diaphragms, the most sensitive portions are to be found at the center of the diaphragm. The sensing resistors must be placed in the radial directions and the optimal length is 14 μm. These optimal designs have been analyzed based on the conventional solid mechanics theories of shell and plates. We have done the numerical analysis and the analytical solutions has been derived. These analytical solutions provide important design guidelines when the dimensions, shapes and orientations of the diaphragm or the sensing resistors are changed. Moreover the literature has also been supported with simulation result of solidworks.