1 Introduction

During the past decade, capacitive pressure sensor has been successfully fabricated on silicon wafers by help of silicon micromachining techniques. This on chip electronics has many advantages such as reduced parasitic capacitance, improved reliability, reduced device size, low cost and its ability to integrate (Lee and Choi 2015). They have lower noise levels with high stability and reliability when compared with the pressure sensors based on piezoresistive and piezoelectric effect. Touch mode capacitive pressure sensor (TMCPS) is an improvement in this category of sensors. They are enjoying a growing interest in recent years due to their numerous advantages over the classical non-touch sensors (Daigle et al. 2007).

Due to the recent advances in micro scale fabrication technology these sensors are now being fabricated for a pressure range of ultra-low to extremely high (Saleh et al 2006).

These sensors have been extensively used in the field of medical science, automobile industry, avionics, industrial and commercial application (Gupta et al. 2003).

Vehicle tire pressure monitoring is one of the major applications of this type of sensor (Lee et al. 2013). The concept of inductive coupling is used for energy and information transfer using capacitive sensors. This is particularly useful for wireless application where space is an issue, such as biomedical implants. Blood pressure sensor is the most popular device used in medical applications.

At present traditional metal diaphragm of the capacitive pressure sensor has been replaced by silicon and polymer materials. As a result of this the material and overall processing cost has been reduced. The sensor is now more compact, lightweight, highly reliable and has an affinity to get easily integrated (Eswaran and Malarvizhi 2013).

There are basically three modes of operation for a capacitive pressure sensor as defined in the literature till date. They are normal mode of operation, single touch mode and double touch mode. In normal mode operation the diaphragm and the substrate are kept at a distance apart (Ko and Wang 1999; Meng and Ko 1999). A device is said to be TMCPS when a capacitive pressure sensor is designed to operate in such a pressure range where diaphragm touches the bottom of substrate (along with an insulator). The first finding in this category was single sided touch mode capacitive pressure sensor (STMCPS). Here the capacitance developed is larger than that in normal mode of operation of capacitive pressure sensor. STMCPS has properties such as no turn on temperature drift, robust structure, higher sensitivity and its ability to withstand large overload. It is very suitable for industrial application due to the fact that it can withstand large over distortion. This is achievable because in this case the diaphragm of the MEMS device touches the bottom substrate and has one or two order of higher magnitude sensitivity than normal mode, when operating in near-linear range (Timoshenko and Kreiger 1959; Timoshenko 1959). Due to this contact mode the device has an extended dynamic range and anti-interference ability which is not possible in normal mode sensors. The basic theory, underlying expressions and simulation results for STMCPS can be studied in detail in reference (Jindal et al. 2015; Jindal and Raghuwanshi 2015).

Coming to the latest upgradation of single sided TMCPS a DTMCPS is what is dealt with in this study. DTMCPS has even better sensitivity than single sided ones. They are more reliable because even if one side of the diaphragm fails to work the other side still works for the same operation range. The design of sensor under consideration is achievable without increasing fabrication cost significantly. The volume of the sensor also remains almost the same as of single sided ones. These are some of the achievements of the double sided ones over its counterpart but what really counts is the capacitance and then the evaluation of sensitivity (Lv et al. 2008; Gaopan et al. 2001).

The paper is organized as follows: the basic structure is described in Sect. 2. In Sect. 3 capacitance for DTMCPS is completely derived. Section 4 deals with result and discussion of the MATLAB plots. Moreover a comparative study is done between DTMCPS and Single sided-TMCPS for the performance parameters and the interpretations are made.

2 Basic structure of DTMCPS

A capacitive pressure curve is used to describe the behaviour of micro-machined capacitive pressure sensor. It is divided into three zones: normal, transition and touch mode. Touch mode is again divided into two regions: linear and saturation. Normal mode is referred to the region before the top plate touches the bottom of the cavity as shown in Fig. 1a. A similar structure of normal TMCPS is double notch TMCPS. Here an additional notch is fabricated at the bottom electrode as shown in Fig. 1b.

Fig. 1
figure 1

Basic structure of double-notch touch mode capacitive pressure sensor. Where h is thickness of diaphragm, r is radius of first notch, r n is radius of second notch, g is gap between diaphragm and first notch, g n is gap between first and second notch, and t m is thickness of isolation layer. a Initial state. b Touch state

Full size image

3 Theoretical formulation for evaluation of capacitance for DTMCPS

In general, under applied load pressure, the capacitance can be given by Eq. (1). This equation is calculated using Gauss numerical integration method.

$$C = \int\limits_{0}^{{r_{n} }} {\frac{{2\pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} r_{1} dr_{1} }}{{\varepsilon_{a} t + \varepsilon_{i} (g_{n} + g - w(r_{1} ))}} + \int\limits_{{r_{n} }}^{r} {\frac{{2\pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} r_{2} dr_{2} }}{{\varepsilon_{a} t + \varepsilon_{i} (g - w(r_{2} ))}}} }$$
(1)

where \(\varepsilon_{0}\) is permittivity in vacuum; \(\varepsilon_{a}\) and \(\varepsilon_{i}\) are dielectric constant of air and isolation layer material, respectively; t is the thickness of the insulation layer. r1 is the gaussian point in the range 0 to rn and r2 is the gaussian point in the range rn to R. w(r1) and w(r2) are the deflection of the gauss points on regions 0 to rn and rn to r respectively.

The deflection (w) due to the applied pressure (P) at a distance (r) from the center is given by:

$$w(r) = \frac{{P(R^{2} - r^{2} )^{2} }}{64D} = w_{0} \left[ {1 - \left( {\frac{r}{R}} \right)^{2} } \right]^{2}$$
(2)

where P is the differential pressure; D is the flexural rigidity, D = Eh 3/[12(1 − v 2)]; E is the Young’s modulus and v is the Poisson’s ratio.

Substituting Eq. (2) in Eq. (1) for r = r1 and r2 separately we get:

$$C = \int\limits_{0}^{{r_{n} }} {\frac{{2\pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} r_{1} dr_{1} }}{{\varepsilon_{a} t + \varepsilon_{i} \left( {g_{n} + g - \frac{{w_{0} (R^{2}\, -\, r_{1}^{2} )^{2} }}{{R^{4} }}} \right)}} + \int\limits_{{r_{n} }}^{R} {\frac{{2\pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} r_{2} dr_{2} }}{{\varepsilon_{a} t + \varepsilon_{i} \left( {g - \frac{{w_{0} (R^{2} \,- \,r_{2}^{2} )^{2} }}{{R^{4} }}} \right)}}} }$$
(3)

Now considering first half of Eq. (3) and solving it in parts:

$$C_{1} = 2\pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} \int\limits_{0}^{{r_{n} }} {\frac{{r_{1} dr_{1} }}{{\varepsilon_{a} t + \varepsilon_{i} g_{n} + \varepsilon_{i} g - \frac{{\varepsilon_{i} w_{0} (R^{2} - r_{1}^{2} )^{2} }}{{R^{4} }}}}}$$
(4)
$$C_{1} = 2\pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} \int\limits_{0}^{{r_{n} }} {\frac{{r_{1} dr_{1} }}{{\left( {\varepsilon_{i} g_{n} + \varepsilon_{i} g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\left( {\varepsilon_{i} g_{n} + \varepsilon_{i} g} \right)}}} \right) - \frac{{\varepsilon_{i} w_{0} (R^{2} - r_{1}^{2} )^{2} }}{{R^{4} }}}}}$$
(5)

Rearranging Eq. (5) in convenient form we get:

$$C_{1} = \frac{{2\pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} }}{{\left( {\varepsilon_{i} g_{n} + \varepsilon_{i} g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\left( {\varepsilon_{i} g_{n} + \varepsilon_{i} g} \right)}}} \right)}}\int\limits_{0}^{{r_{n} }} {\frac{{r_{1} dr_{1} }}{{1 - \frac{{\varepsilon_{i} w_{0} (R^{2} - r_{1}^{2} )^{2} }}{{R^{4} \left( {\varepsilon_{i} g_{n} + \varepsilon_{i} g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\left( {\varepsilon_{i} g_{n} + \varepsilon_{i} g} \right)}}} \right)}}}}}$$
(6)
$$C_{1} = \frac{{2\pi \varepsilon_{0} \varepsilon_{a} }}{{\left( {g_{n} + g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\int\limits_{0}^{{r_{n} }} {\frac{{r_{1} dr_{1} }}{{1 - \frac{{w_{0} (R^{2} - r_{1}^{2} )^{2} }}{{R^{4} \left( {g_{n} + g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}}}}$$
(7)

Let \(R^{2} - r_{1}^{2} = z_{1}\)

$$- 2r_{1} dr_{1} = dz_{1}$$
$$r_{1} dr_{1} = - \frac{{dz_{1} }}{2}$$

Since \(r_{1} = 0\) to \(r_{n}\)

$$z_{1} = R^{2} \,{\text{to}}\,r^{2} - r_{n}^{2}$$

Substituting the above in Eq. (7) we get:

$$C_{1} = \frac{{2\pi \varepsilon_{0} \varepsilon_{a} }}{{\left( {g_{n} + g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\left( {\frac{1}{2}} \right)\int\limits_{{R^{2} - r_{n}^{2} }}^{{R^{2} }} {\frac{{dz_{1} }}{{1 - \frac{{w_{0} z_{1}^{2} }}{{R^{4} \left( {g_{n} + g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}}}}$$
(8)

By rearranging Eq. (8) in known standard form we get:

$$C_{1} = \frac{{\pi \varepsilon_{0} \varepsilon_{a} }}{{\left( {g_{n} + g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\int\limits_{{R^{2} - r_{n}^{2} }}^{{R^{2} }} {\left\{ {\frac{{dz_{1} }}{{1 - \left( {\left( {\frac{{w_{0} }}{{\left( {g_{n} + g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}} \right)^{{\frac{1}{2}}} \frac{{z_{1} }}{{R^{2} }}} \right)^{2} }}} \right\}}$$
(9)
$$C_{1} = \frac{{\pi \varepsilon_{0} \varepsilon_{a} }}{{\left( {g_{n} + g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}} \cdot \frac{1}{{\left( {\frac{{w_{0} }}{{\left( {g_{n} + g} \right)}}} \right)^{{\frac{1}{2}}} \cdot \frac{1}{{\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\frac{1}{{R^{2} }}}}\tanh^{ - 1} \left[ {\left( {\frac{{w_{0} }}{{\left( {g_{n} + g} \right)}}} \right)^{{\frac{1}{2}}} \cdot \frac{1}{{\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\frac{{z_{1} }}{{R^{2} }}} \right]_{{R^{2} - r_{n}^{2} }}^{{R^{2} }}$$
(10)

By substituting the limits of integration in Eq. (10) and solving it we get:

$$C_{1} = \frac{{\pi \varepsilon_{0} \varepsilon_{a} r^{2} }}{{\left( {g_{n} + g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}} \cdot \frac{1}{{\left( {\frac{{w_{0} }}{{\left( {g_{n} + g} \right)}}} \right)^{{\frac{1}{2}}} .\frac{1}{{\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}}}\tanh^{ - 1} \left[ {\left( {\left( {\frac{{w_{0} }}{{\left( {g_{n} + g} \right)}}} \right)^{{\frac{1}{2}}} \cdot \frac{1}{{\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}} \right) - \left( {\left( {\frac{{w_{0} }}{{\left( {g_{n} + g} \right)}}} \right)^{{\frac{1}{2}}} \cdot \frac{1}{{\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\left( {1 - \frac{{r_{n}^{2} }}{{R^{2} }}} \right)} \right)} \right]$$
(11)
$$C_{1} = \frac{{\pi \varepsilon_{0} \varepsilon_{a} R^{2} }}{{\left( {g_{n} + g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\tanh^{ - 1} \left\{ {\left( {\frac{{w_{0} }}{{\left( {g_{n} + g} \right)}}} \right)^{{\frac{1}{2}}} \cdot \frac{1}{{\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\left( {\frac{{r_{n}^{2} }}{{R^{2} }}} \right)} \right\} \cdot \frac{1}{{\left( {\frac{{w_{0} }}{{\left( {g_{n} + g} \right)}}} \right)^{{\frac{1}{2}}} \cdot \frac{1}{{\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}}}$$
(12)

Finally we get first part of integration as:

$$C_{1} = \frac{{\pi \varepsilon_{0} \varepsilon_{a} R^{2} }}{{\left( {g_{n} + g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\tanh^{ - 1} \left[ {\frac{{\left( {\frac{{w_{0} }}{{\left( {g_{n} + g} \right)}}} \right)^{{\frac{1}{2}}} \frac{1}{{\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\left( {\frac{{r_{n}^{2} }}{{R^{2} }}} \right)}}{{\frac{{w_{0} }}{{\left( {g_{n} + g} \right)}}^{{\frac{1}{2}}} \cdot \frac{1}{{\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}}}} \right]$$
(13)

Now solving second half of Eq. (3) i.e.

$$C_{2} = \int\limits_{{r_{n} }}^{R} {\frac{{2\pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} r_{2} dr_{2} }}{{\varepsilon_{a} t + \varepsilon_{i} \left( {g - \frac{{w_{0} (R^{2} - r_{2}^{2} )^{2} }}{{R^{4} }}} \right)}}}$$
(14)
$$C_{2} = 2\pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} \int\limits_{{r_{n} }}^{R} {\frac{{r_{2} dr_{2} }}{{\varepsilon_{a} t + \varepsilon_{i} g - \frac{{\varepsilon_{i} w_{0} (R^{2} - r_{2}^{2} )^{2} }}{{R^{4} }}}}}$$
(15)
$$C_{2} = 2\pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} \int\limits_{{r_{n} }}^{R} {\frac{{r_{2} dr_{2} }}{{\varepsilon_{i} g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right) - \frac{{\varepsilon_{i} w_{0} (R^{2} - r_{2}^{2} )^{2} }}{{R^{4} }}}}}$$
(16)

By rearranging Eq. (16) in convenient form we get:

$$C_{2} = 2\pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} \int\limits_{{r_{n} }}^{R} {\frac{{r_{2} dr_{2} }}{{\varepsilon_{i} g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)\left\{ {1 - \frac{{\varepsilon_{i} w_{0} (R^{2} - r_{2}^{2} )^{2} }}{{R^{4} \varepsilon_{i} g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}} \right\}}}}$$
(17)

Let \(R^{2} - r_{2}^{2} = z_{2}\)

$$- 2r_{2} dr_{2} = dz_{2}$$
$$r_{2} dr_{2} = - \frac{{dz_{2} }}{2}$$

As \(r_{2} = r_{n}\) to R

$$z_{2} = R^{2} - r_{n}^{2} \quad {\text{to}}\quad 0$$

Substituting the above values in Eq. (17) we get:

$$C_{2} =\frac{{ 2\pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} }}{{\varepsilon_{i} g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}\left( { - \frac{1}{2}} \right)\int\limits_{{R^{2} - r_{n} }}^{0} {\frac{{dz_{2} }}{{1 - \frac{{\varepsilon_{i} w_{0} z_{2}^{2} }}{{R^{4} \varepsilon_{i} g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}}}}$$
(18)
$$C_{2}= \frac{{ \pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} }}{{\varepsilon_{i} g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}\int\limits_{0}^{{R^{2} - r_{n} }} {\frac{{dz_{2} }}{{1 - \left( {\left( {\frac{{w_{0} }}{{g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}} \right)^{{\frac{1}{2}}} \frac{{z_{2} }}{{R^{2} }}} \right)^{2} }}}$$
(19)

Clearly the above Eq. (19) is the standard form of integration which directly reduces to:

$$C_{2} = \frac{{\pi \varepsilon_{0} \varepsilon_{a} \varepsilon_{i} }}{{\varepsilon_{i} g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}\frac{1}{{\left( {\frac{{w_{0} }}{{g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}} \right)^{{\frac{1}{2}}} \frac{1}{{R^{2} }}}}\tanh^{ - 1} \left[ {\left( {\frac{{w_{0} }}{{g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}} \right)^{{\frac{1}{2}}} \frac{{R^{2} - r_{n}^{2} }}{{R^{2} }}} \right]$$
(20)

Finally we get second part of integration as:

$$C_{2} = \frac{{\pi \varepsilon_{0} \varepsilon_{a} }}{{g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}\frac{{R^{2} }}{{\left( {\frac{{w_{0} }}{{g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}} \right)^{{\frac{1}{2}}} }}\tanh^{ - 1} \left[ {\left( {\frac{{w_{0} }}{{g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}} \right)^{{\frac{1}{2}}} \left( {1 - \frac{{r_{n}^{2} }}{{R^{2} }}} \right)} \right]$$
(21)

Substituting the above obtained values of C1 and C2 in Eq. (3) we get:

$$C = C_{1} + C_{2}$$
$$\begin{aligned} C & = \frac{{\pi \varepsilon_{0} \varepsilon_{a} R^{2} }}{{\left( {g_{n} + g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\tanh^{ - 1} \left[ {\frac{{\left( {\frac{{w_{0} }}{{\left( {g_{n} + g} \right)}}} \right)^{{\frac{1}{2}}} \cdot \frac{1}{{\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\left( {\frac{{r_{n}^{2} }}{{R^{2} }}} \right)}}{{\left( {\frac{{w_{0} }}{{\left( {g_{n} + g} \right)}}} \right)^{{\frac{1}{2}}} \cdot \frac{1}{{\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}}}} \right] \\ & \quad + \frac{{\pi \varepsilon_{0} \varepsilon_{a} }}{{g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}\frac{{R^{2} }}{{\left( {\frac{{w_{0} }}{{g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}} \right)^{{\frac{1}{2}}} }}\tanh^{ - 1} \left[ {\left( {\frac{{w_{0} }}{{g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}} \right)^{{\frac{1}{2}}} \left( {1 - \frac{{r_{n}^{2} }}{{R^{2} }}} \right)} \right] \\ \end{aligned}$$
(22)
$$C = \pi \varepsilon_{0} \varepsilon_{a} R^{2} \left\{ {\frac{1}{{g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}\frac{{\tanh^{ - 1} \left[ {\left( {\frac{{w_{0} }}{{g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}} \right)^{{\frac{1}{2}}} \left( {1 - \frac{{r_{n}^{2} }}{{R^{2} }}} \right)} \right]}}{{\left( {\frac{{w_{0} }}{{g\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} g}}} \right)}}} \right)^{{\frac{1}{2}}} }} + \frac{1}{{\left( {g_{n} + g} \right)\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\tanh^{ - 1} \left[ {\frac{{\left( {\frac{{w_{0} }}{{\left( {g_{n} + g} \right)}}} \right)^{{\frac{1}{2}}} \cdot \frac{1}{{\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}\left( {\frac{{r_{n}^{2} }}{{R^{2} }}} \right)}}{{\left( {\frac{{w_{0} }}{{\left( {g_{n} + g} \right)}}} \right)^{{\frac{1}{2}}} \cdot \frac{1}{{\left( {1 + \frac{{\varepsilon_{a} t}}{{\varepsilon_{i} \left( {g_{n} + g} \right)}}} \right)}}}}} \right]} \right\}$$
(23)

4 Result and discussion

As mentioned in Sect. 1, a comparative study between STMCPS and DTMCPS is elaborated in this paper work. This comparative study is mathematically formulated and is verified and plotted using MATLAB in this section. This section also deals with the discussion regarding the plots obtained via simulations.

For better understanding of the results it is worth mentioning that the major specifications for the sensor is the linear range of operation and the sensitivity. These are determined by material properties and structural parameters used such as Young’s Modulus, poisson’s ratio, gap depth, radius of the diaphragm, thickness of the insulator etc. and more specifically radius of second notch and its gap depth for DTMCPS.

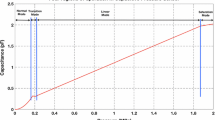
Figure 2 in this section indicates the variation of DTMCPS capacitance within the applied pressure range in normal/non-touch mode. The pressure range defined for the normal mode operation of this design is 0–0.2 MPa.

Fig. 2
figure 2

Capacitance variation of DTMCPS w.r.t pressure in normal mode having h = 5 μm, r = 180 µm, g = 2 µm, gn = 1 µm, rn = 50 µm

Full size image

While switching from normal mode to touch mode a new mode called transition mode exists in between. This switch is highly non-linear as the sensing diaphragm just starts to touch the bottom electrode. The transition mode creates noise and hence is discarded. It is non-linear and hence of no concern. The pressure range for the transition region is 0.2–0.28 MPa.

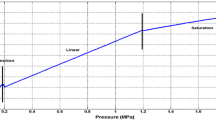
Figure 3 indicates the variation of DTMCPS capacitance within the applied pressure range in touch mode. It is noted from Fig. 1b of Sect. 2 that in this touch mode design—double touch of diaphragm on substrate takes place, which increases the capacitance range in touch mode of the proposed design. Hence Fig. 3 is plotted in MATLAB with the help of Eqs. (1) and (23) for capacitance variation of DTMCPS in touch mode having pressure range of 0.28–2 MPa.

Fig. 3
figure 3

Capacitance variation of DTMCPS w.r.t pressure in touch mode having h = 5 µm, r = 180 µm, g = 2 µm, gn = 1 µm, rn = 50 µm

Full size image

It clearly depicts that the total touch mode region can be seen as two different sub regions (i) linear (ii) saturation. The linear region is the heart of the design for touch mode operation. The capacitance variation for the linear region of touch mode is linear so it can be easily calibrated in terms of pressure with negligible error. At saturation region a very less variation of capacitance takes place and ultimately capacitance reaches to a peak value of 2.7 pF.

Figure 4 Shows the comparative plots for STMCPS with DTMCPS for different parameters in normal mode pressure range. It can be interpreted that in normal mode capacitance variation is more or less equal for same parameters. This means that the notch has almost negligible effect on the capacitance variation in normal mode. The results obtained and the interpretation has been marked in Table 1.

Fig. 4
figure 4

Comparative plot between DTMCPS of proposed dimensions and singe TMCPS of different dimensions stated below for capacitance variation w.r.t pressure in normal mode

Full size image
Table 1 Comparative table for STMCPS and DTMCPS in normal mode operation
Full size table

In this paper work is basically carried out for touch mode. With the help of equations calculated in Sect. 3 for DTMCPS, a Capacitance curve is simulated in MATLAB as shown in Fig. 5. Plot also shows single TMCPS capacitance curve in touch mode for pressure range of 0.28–2 MPa.

Fig. 5
figure 5

Comparative plot between DTMCPS of proposed dimensions and single TMCPS of different dimensions as stated above for capacitance variation w.r.t pressure in touch mode

Full size image

A point worthy of note in the proposed model of Fig. 1b is that here two touch point pressure points are present-additional due to presence of notch. As sensitivity is inversely proportional to touch point pressure hence for the proposed design of DTMCPS the first touch point results in higher sensitivity whereas the second touch point (when diaphragm touches the notch) results in high linear range in touch mode region of the proposed model.

Clearly from Fig. 5 a wide capacitance range in touch mode region of DTMCPS is achieved in comparison to Single TMCPS for similar dimensions. Hence a higher sensitivity is achievable due to double touch points for the reasons stated above. The results obtained and the interpretation has been marked in Table 2.

Table 2 Comparative table for STMCPS and DTMCPS in touch mode operation
Full size table

5 Conclusion

Due to addition of a notch to the existing TMCPS structure—DTMCPS is designed. For the proposed design we have seen that the linearity and sensitivity of the device significantly improves and hence we can interpret that due to these enhanced features the device will have good stability, large overload ability and low power consumption. All depends on the choice of how appropriately we choose the dimensions of the additional notch because second touch point pressure plays the key role in enhancing the sensitivity of the device.

Since only a notch is added to the existing design so it will not increase the fabrication cost significantly and hence the device promises to be of good utility in industrial mass production.