Continuous semianalytical modeling of vertical surrounding-gate tunnel FET: analog/RF performance evaluation

Abstract

A continuous and accurate model based on the two-dimensional (2D) potential solution of a tunnel field-effect transistor (TFET) with undoped vertical surrounding-gate (VSG) structure is proposed. Both ambipolarity and dual modulation effects are included to obtain a more accurate analytical model, whose validity is demonstrated by comparison with two-dimensional numerical simulations using ATLAS-2D. The continuity of the proposed model enables extraction of analog/radiofrequency (RF) parameters and device figures of merit. Moreover, the effect of introducing a high-$\kappa$ layer on the gate oxide in improving the behavior of the VSG-TFET is explored for use in high-performance analog/RF applications. The proposed continuous analytical model can be easily implemented in commercial simulators to study and investigate VSG-TFET-based nanoelectronic circuits.

1 Introduction

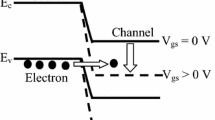
As complementary metal–oxide–semiconductor (CMOS) downscaling approaches its physical limits due to the emergence of major degradation mechanisms, new transistor structures using multiple gates, novel materials, and doping engineering have been successfully employed to extend performance [1,2,3,4]. However, to follow the technology roadmap, and the growing requirements for low operating and leakage powers, as well as reliability against short-channel effects (SCEs) and process fluctuations, use of nonconventional devices based on different physical phenomena that overcome classical limitations is highly desired, especially tunneling field-effect transistors (TFETs). The TFET is considered to be an emerging logic device, representing a potential alternative for use in future high-performance and low-power processor chips [5]. Experiments have confirmed the viability of the complementary TFET architecture [6], including fabrication of a fully functional low-power Si gate-all-around (GAA) nanowire tunnel field-effect transistor (NWTFET) inverter with suppressed ambipolarity and large noise margin. Enhanced electrostatic control of the gate-all-around structure compared with planar TFETs has also been demonstrated [7]. The ambipolar behavior of a TFET depends on the drain doping concentration. Generally, such devices are characterized by low leakage current, steep subthreshold slope, efficient transconductance, and high intrinsic gain. Experiments and studies have shown the potential of tunneling transistors for use in low-power amplifiers, logic devices, and analog/RF and sensing applications [6,7,8,9]. At circuit level, various new mixed CMOS–TFET designs with different reliability issues have been presented [8, 10]. The main difficulty with such mixed designs is how to align the operating voltage of both devices and keep it as low as possible, thus lowering power consumption. Even if TFETs have better immunity against SCEs than conventional metal–oxide–semiconductor field-effect transistors (MOSFETs), this feature is drastically degraded beyond 30 nm, where drain-induced barrier thinning (DIBT) exponentially increases [11, 12]. Moreover, the analog/RF performance and linearity are also affected by SCEs [13]. Therefore, new practical design solutions such as high-$\kappa$ dielectric materials, drain underlap, source/drain doping, gate material engineering, heterojunctions, and III–V materials have been proposed to overcome these physical limitations [11,12,13,14]. On the other hand, compact and continuous models that can be applied in both sub- and superthreshold operating domains are useful for understanding both types of device and for circuit simulation. Tunneling phenomena in semiconductor materials are well understood and can be efficiently modeled in Zener diodes and p–i–n junction or tunneling transistors, for which several approaches have been proposed to investigate the quantum and tunnel transport mechanisms in semiconductor devices [15,16,17,18,19,20]. All these models are directly dependent on the potential profile as a basis to calculate the current, by means of energy bands for nonlocal models or electric field for local ones. In TFETs, the tunneling effect occurs at both channel junctions, viz. source/channel and drain/channel, if ambipolarity is considered. In this case, development of an accurate potential profile model is complex due to the additional processes that have to be taken into account, such as depletion, the fringing effect on source–drain extensions (SDEs), and the impact of the high lateral field near the junctions [21,22,23,24,25,26]. In addition, the assumption of a constant electric field used in local tunneling models overestimates the current and produces a nonzero current at equilibrium, although this can be resolved by introducing a Fermi occupancy factor difference between the source and drain [26]. The complex barrier shape in TFET devices indicates that a nonlocal approach based on the Wentzel–Kramers–Brillouin (WKB) approximation and Landauer formula is more appropriate [18, 27, 28]. Nevertheless, the exact barrier profile cannot be used when elaborating such analytical models, so an arbitrary shape is adopted. The assumption of the simplest triangular barrier is equivalent to the Kane approach (i.e., constant electric field) and thus results in the same overestimation [9, 27]. On the other hand, the exponential shape is more accurate, but unfortunately the resulting expression for the tunneling probability cannot be integrated analytically, requiring use of numerical integration methods [28].

Recently, several analytical models were developed to investigate TFET devices [24,25,26,27,28,29,30]. However, in these models, the simplified Kane’s generation rate is used to replace the total electric field by an average one based on the tunneling distance or tunneling window. This approach does not evaluate the generation rate over the entire tunneling barrier and thus fails to reproduce the characteristic response profile. Besides, these models produce complex expressions, making their mathematical differentiation intractable. The derivatives of such formulas are primarily used for extraction of various parameters and figures of merit (FOMs) for assessment of device performance. Furthermore, most of these elaborated models do not take into account drain modulation. In this context, new analytical and continuous models that capture the physics of tunneling transport accurately and efficiently and are suitable for implementation in commercial simulators are required to study and design TFET-based nanoelectronic circuits.

In this work, an undoped vertical surrounding-gate TFET device with high-$\kappa$ dielectric stack is considered. A continuous semianalytical model is developed by mathematical integration over the channel length of the complete Kane generation rate expression for direct local tunneling. This integral has the merit of preserving the spatial distribution of the generation rate, yielding an accurate response. Both ambipolarity and dual modulation effects are investigated. The electric field expression is derived from an accurate solution of Poisson’s equation using Bessel–Fourier series. The analog/RF parameters and various FOMs of the device are deduced from the proposed drain-current model. Moreover, the role of such gate dielectric material engineering in improving the analog/RF performance is investigated. The analytical results are validated against numerical simulations, revealing good agreement for a wide range of design parameters [31].

The remainder of this manuscript is organized as follows: Section 2 is devoted to a description of the various steps for the derivation of the drain-current model. The main simulation results are provided in Sect. 3, where both analog/RF parameters and linearity criteria are treated. We complete this work in Sect. 4 with a summary and some guidelines for future work.

2 Current model derivation

The device considered is a vertical surrounding-gate structure as presented in Fig. 1. The source/drain extensions are symmetric and heavily doped to around $10^{20}\,\hbox {cm}^{-3}$. The introduction of this high dopant concentration is motivated by attenuation of the depletion effect [32] and attaining a high built-in potential, which in turn will lead to significant tunneling generation. With the channel length of 100 nm, short-channel effects are considerably reduced and the assumption of an intrinsic body is well justified, where only mobile charges define the electrostatic distribution [12]. However, both charge types have to be taken into account to obtain a high transfer characteristic over both positive and negative gate supply values. The dielectric gate stack is composed of silicon oxide with thickness of 2 nm and a high-$\kappa$ dielectric material with thickness of 1 nm to reduce gate current leakage. Two-dimensional numerical simulations were performed to validate the current model based on Boltzmann statistics and drift–diffusion transport. In addition, we adopted the Kane direct tunneling model to support the tunneling generation phenomenon.

Fig. 1

Cross-sectional view of vertical surrounding-gate TFET structure ($L=100\,\hbox {nm}$, $N_{\mathrm{AS}}=N_{\mathrm{DD}}=10^{20}\,\hbox {cm}^{-3}$, $t_\mathrm{ox1}=2\,\hbox {nm}$, $t_\mathrm{ox1}=1\,\hbox {nm}$)

The first step in the derivation of the model is to extract the potential profile over the channel by solving the 2D Poisson’s equation, which can be expressed in cylindrical coordinates as

$$\begin{aligned}&\frac{\partial ^{2}\psi }{\partial r^{2}}+\frac{1}{r}\cdot \frac{\partial \psi }{\partial r}+\frac{\partial ^{2}\psi }{\partial z^{2}}=-\frac{q}{\varepsilon _\mathrm{Si} }\rho \end{aligned}$$

(1a)

$$\begin{aligned}&\rho =\left\{ {\begin{array}{l} -n_\mathrm{i} \mathrm {e}^{\left( {\frac{\psi -V_{\mathrm{q}n} }{V_\mathrm{t} }} \right) }\hbox { for }V_\mathrm{gs} \ge 0 \\ n_\mathrm{i} \mathrm {e}^{\left( {\frac{-\psi +V_{\mathrm{q}p} }{V_\mathrm{t} }} \right) }\hbox { for } V_\mathrm{gs} <0 \\ \end{array}} \right. , \end{aligned}$$

(1b)

where $\psi$ represents the 2D electrostatic potential, $\varepsilon _\mathrm{Si}$ is the silicon dielectric constant, q is the electron charge, $n_\mathrm{i}$ is the intrinsic carrier concentration, $V_\mathrm{t}$ is the thermal voltage, and $\rho$ is the channel mobile charge concentration.

Depending on the polarity of the gate supply, current transport by only the majority carriers in the channel are considered. Indeed, such neglect of the minority carriers has no consequence even near charge equilibrium, where the center channel potential varies linearly. The quasi-Fermi level $V_\mathrm{q}$ included in the boundary conditions is assumed to be constant over the radius and varies from 0 at the source side to $V_\mathrm{ds}$ at the drain side [33]. At the channel center, the quasi-Fermi levels associated with both carrier types ($V_{\mathrm{q}n}$, $V_{\mathrm{q}p }$) equal, respectively, $V_\mathrm{ds}$ and 0. To solve Poisson’s equation, it must be projected onto two components [33], i.e., a one-dimensional (1D) Poisson equation where the potential $V_\mathrm{c}(r)$ represents the solution of Gauss’s law in a disk of finite charge density, while the potential U(z, r) in the 2D Laplace equation represents the solution of Gauss’s law in a finite cylinder of null charge density. The sum of these two terms gives the total potential distribution in the channel and is expressed with boundary conditions as

$$\begin{aligned}&\frac{\partial ^{2}V_\mathrm{c} }{\partial r^{2}}+\frac{1}{r}\cdot \frac{\partial V_\mathrm{c} }{\partial r}=-\frac{q}{\varepsilon _\mathrm{Si} }\rho \end{aligned}$$

(2a)

$$\begin{aligned}&\left\{ {\begin{array}{l} \frac{\partial V_\mathrm{c} \left( r \right) }{\partial r}\left| {\begin{array}{l} \\ r=a \\ \end{array}} \right. =\frac{C_\mathrm{ox} }{\varepsilon _\mathrm{Si} }\left[ {V_\mathrm{g}^*-V_\mathrm{c} \left( a \right) } \right] \\ \frac{\partial V_\mathrm{c} \left( r \right) }{\partial r}\left| {\begin{array}{l} \\ r=0 \\ \end{array}} \right. =0 \\ \end{array}} \right. \nonumber \\&\quad \hbox { with } \quad V_\mathrm{g}^*=V_\mathrm{gs} -V_\mathrm{fb} \end{aligned}$$

(2b)

$$\begin{aligned}&\frac{\partial ^{2}U}{\partial r^{2}}+\frac{1}{r}\cdot \frac{\partial U}{\partial r}+\frac{\partial ^{2}U}{\partial z^{2}}=0 \end{aligned}$$

(3a)

$$\begin{aligned}&\left\{ {\begin{array}{l} \frac{\partial U\left( {z,r} \right) }{\partial r}\left| {\begin{array}{l} \\ r=a \\ \end{array}} \right. =\frac{C_\mathrm{ox} }{\varepsilon _\mathrm{Si} }\left[ {-U\left( {z,a} \right) } \right] \\ \frac{\partial U\left( {z,r} \right) }{\partial r}\left| {\begin{array}{l} \\ r=0 \\ \end{array}} \right. =0 \\ \end{array}} \right. \end{aligned}$$

(3b)

$$\begin{aligned}&\left\{ {\begin{array}{l} U\left( {0,r} \right) =V_\mathrm{biS} -V_\mathrm{c} =-Vt\ln \left( {\frac{N_{\mathrm{AS}} }{n_\mathrm{i} }} \right) -V_\mathrm{c} \\ U\left( {L,r} \right) =V_\mathrm{biD} +V_\mathrm{ds} -V_\mathrm{c} =Vt\ln \left( {\frac{N_\mathrm{DD}}{n_\mathrm{i} }} \right) +V_\mathrm{ds} -V_\mathrm{c} \\ \end{array}} \right. \end{aligned}$$

(3c)

$$\begin{aligned}&C_\mathrm{ox} =\frac{\varepsilon _\mathrm{ox} }{a\ln (1+{t_\mathrm{oxeff} }/a)}\hbox { with }t_\mathrm{oxeff} \nonumber \\&\quad =t_\mathrm{ox1} +t_\mathrm{ox2} {\varepsilon _\mathrm{ox1} }/{\varepsilon _\mathrm{ox2} }\hbox { and }a={t_\mathrm{Si} }/2, \end{aligned}$$

(3d)

where $V_\mathrm{fb}$ represents the flat-band voltage, $C_\mathrm{ox}$ is the oxide capacitance, $\varepsilon _\mathrm{ox}$ is the silicon oxide dielectric constant, and $t_\mathrm{oxeff}$ is the effective oxide stack thickness (EOT) depending on the thicknesses of the two (oxide and high-$\kappa$) layers and their dielectric constants. Note that, near the channel center, the 2D potential component is neglected so that only the 1D component is involved in the charge concentration expression. Following the Chambré method [34] for solving the Poisson–Boltzmann equation and using the boundary conditions (2b), the channel center potential depending upon the gate polarity is given by

$$\begin{aligned} V_\mathrm{c}= & {} V_\mathrm{ds} +V_\mathrm{t} \log \left( {\frac{8\beta }{\delta (\beta -r^{2})^{2}}} \right) \hbox { for }V_\mathrm{gs} \ge 0 \end{aligned}$$

(4a)

$$\begin{aligned} V_\mathrm{c}= & {} V_\mathrm{t} \log \left( {\frac{\delta (\beta -r^{2})^{2}}{8\beta }} \right) \hbox { for }V_\mathrm{gs} <0, \end{aligned}$$

(4b)

where $\delta ={qn_\mathrm{i} }/{\varepsilon _\mathrm{Si} V_\mathrm{t} }$ and the constant $\beta$ is obtained by substituting (4) into (2b), resulting in the formulas

$$\begin{aligned}&\frac{C_\mathrm{ox} }{\varepsilon _\mathrm{Si} }\left( {V_\mathrm{g}^*-V_\mathrm{ds} -V_\mathrm{t} \ln \left( {\frac{8\beta }{\delta \left( {\beta -a^{2}} \right) ^{2}}} \right) } \right) \nonumber \\&\quad =\frac{4aV_\mathrm{t} }{\left( {\beta -a^{2}} \right) }\hbox { for }V_\mathrm{gs} \ge 0 \end{aligned}$$

(5a)

$$\begin{aligned}&\frac{C_\mathrm{ox} }{\varepsilon _\mathrm{Si} }\left( {V_\mathrm{g}^*-V_\mathrm{t} \ln \left( {\frac{\delta \left( {\beta -a^{2}} \right) ^{2}}{8\beta }} \right) } \right) \nonumber \\&\quad =\frac{4aV_\mathrm{t} }{\left( {a^{2}-\beta } \right) }\hbox { for }V_\mathrm{gs} <0. \end{aligned}$$

(5b)

Using the boundary conditions in (3b) and (3c), the solution of the 2D Laplace equation can be expressed based on Bessel–Fourier series as [35]

$$\begin{aligned} U(z,r)=\sum _{n=1}^\infty {\frac{J_0 (\lambda _n r)}{\sinh (\lambda _n L)}} \left[ {A_n \sinh (\lambda _n (L-z))+B_n \sinh (\lambda _n z)} \right] \nonumber \\ \end{aligned}$$

(6)

where $\lambda _{n}$ is the nth root of the Robin condition ${\lambda _n }/C={J_0 (\lambda _n a)}/{J_1 (\lambda _n a)}$ and $C={C_\mathrm{ox} }/{\varepsilon _\mathrm{Si} }$ [36]. The Bessel coefficients $A_{n}$ and $B_{n}$ are given by [35]

$$\begin{aligned} A_n= & {} \frac{2J_1 (\lambda _{n} a)}{\lambda _{n} aJ_{0}^{2} (\lambda _{n}a)(1+{C^{2}}/{\lambda _{n}^{2} })}\left( {V_\mathrm{biS} -V_\mathrm{C} } \right) \end{aligned}$$

(7a)

$$\begin{aligned} B_n= & {} \frac{2J_1 (\lambda _{n} a)}{\lambda _{n} aJ_0^2 (\lambda _{n} a)(1+{C^{2} }/{\lambda _{n}^{2} })}\left( {V_\mathrm{biD} +V_\mathrm{ds} -V_\mathrm{C} } \right) . \end{aligned}$$

(7b)

The expression for the total electric field is then deduced by differentiating the potential expression over the length and radius dimensions. However, the channel potential (4) is neglected in the transversal field component to simplify the subsequent analytical integration. The total electric field expression is divided into two components, corresponding to the source and drain sides, as indicated in (8), to calculate the tunneling current separately for each junction so that the ambipolarity behavior can be obtained.

$$\begin{aligned} \left\{ {\begin{array}{l} E_\mathrm{S} =\left[ {\sum _{n=1}^\infty {\frac{\lambda _n^2 A_n^2 \left( {J_0^2 (\lambda _n r)+J_1^2 (\lambda _n r)} \right) }{4\sinh (\lambda _n L)}} \exp \left( {2\lambda _n (L-z)} \right) } \right] ^{1/2} \\ E_\mathrm{D} =\left[ {\sum _{n=1}^\infty {\frac{\lambda _n^2 B_n^2 \left( {J_0^2 (\lambda _n r)+J_1^2 (\lambda _n r)} \right) }{4\sinh (\lambda _n L)}} \exp \left( {2\lambda _n z} \right) } \right] ^{1/2} \\ \end{array}} \right. . \end{aligned}$$

(8)

At this stage, even if the channel potential at the center is accurately modeled, a substantial part of the electrostatic potential at the junctions may be lost due to the numerous assumptions and simplifications applied. The first assumption used to explicitly solve Poisson’s equation neglects the 2D potential part in the charge concentration term, which is valid only near the channel center [33,34,35,36,37]. Secondly, simulations show that the quasi-Fermi levels included in the boundary conditions (3c) differ from their ideal values, as shown in Fig. 2. In addition, the channel potential $V_\mathrm{c}$ is assumed to be constant over the radius in the expressions for the integrals used to obtain the Bessel coefficients (7).

Fig. 2

Surface potential and quasi-Fermi level for $T_\mathrm{Si}=10$ nm, EOT $=$ 3 nm, $V_\mathrm{gs}=0.5$ V, and $V_\mathrm{ds}=0.5$ V

As mentioned above, the effect of depletion and fringing on the source/drain extensions impacts on the potential of the junctions. These effects depend directly on the voltage supply to both the drain and gate terminals. Note that many studies have included such depletion and fringing field effects when modeling various types of structure [21, 22, 29, 38]. Nevertheless, the remarkable lack of accuracy depicted by the outcomes of the cited works makes addition of fitting parameters inevitable to adjust the boundary potential. Although in our case the depletion effect is neglected due to the high SDE doping, numerical simulations show an important linear variation in the boundary potentials at the silicon interface, which attenuates in depth direction. As use of additional parameters seems necessary, it is preferable to avoid such effects when modeling and rather include fitting parameters and functions directly at the level of the final obtained expressions to simplify their extraction. Consequently, a correction potential $V_\mathrm{p}$ is added to the boundary potentials (3c). Guided by the numerical fitting, we observe that this potential depends only on geometrical parameters.

Since analytical integration of the tunneling generation rate over the radius can be difficult under some situations, only the surface total electric field in (8) is considered. Moreover, the process of integrating a long or infinite series is an intractable task, justifying the simplification of expressions (8) by focusing on the first order, given by

$$\begin{aligned} E_\mathrm{S} =A\exp \left( {-\lambda z} \right) \end{aligned}$$

(9a)

with

$$\begin{aligned}&A=\frac{-\lambda \left( {1+J_1^2 (\lambda a)/J_0^2 (\lambda a)} \right) ^{\frac{1}{2}}\exp (\lambda L)}{2\sinh (\lambda L)}\left( V_\mathrm{p}\right. \nonumber \\&\qquad \,\,\,\left. +\,V_\mathrm{biS} -V_\mathrm{c} \exp \left( {V_\mathrm{cn} \left( {1-\frac{V_\mathrm{c} }{V_\mathrm{g}^*}} \right) } \right) \right) \nonumber \\&E_\mathrm{D} =B\exp \left( {\lambda z} \right) \end{aligned}$$

(9b)

with

$$\begin{aligned} B= & {} \frac{\lambda \left( {1+J_1^2 (\lambda a)/J_0^2 (\lambda a)} \right) ^{\frac{1}{2}}}{2\sinh (\lambda L)}\hbox {abs}\left( -V_\mathrm{p} \right. \nonumber \\&\left. +\,V_\mathrm{biD} +V_\mathrm{ds} -V_\mathrm{c} \exp \left( {V_\mathrm{cp} \left( {1-\frac{V_\mathrm{c} }{V_\mathrm{g}^*}} \right) } \right) \right) . \end{aligned}$$

The exponential term describes the dual modulation effect. In the gate modulation regime, one has $V_\mathrm{c} =V_\mathrm{g}^*$, so the exponential term equals one; otherwise the channel-to-gate potential ratio determines the amount of drain modulation on tunneling generation, corrected using the coefficients $V_\mathrm{cn}$ and $V_\mathrm{cp}$, whose values vary around one and are dependent on geometrical parameters and the drain supply for $V_\mathrm{cn}$.

These simplified expressions for the electric field are analogous to the exponential surface potential distribution used in pseudo-2D potential models [18, 21, 24], as well as the root of the Robin condition, whose inverse is equivalent to the characteristic length. This parameter defines the barrier bending profile, or more specifically the electric field amplitude. Near the junctions, the effect of the high lateral field cannot be neglected, which means that the classical MOSFET interface boundary condition (3b) used to extract the Robin condition roots is no longer valid. In [30], the first-order electric field expression is multiplied by a fitting coefficient to compensate for the truncation of the Fourier series to first order. Moreover, the dependence of the characteristic length on the gate bias was demonstrated and modeled in [23]. To achieve satisfactory accuracy for the potential distribution and reduce the series expression for the total electric field to first order, a dimensionally dependent fitting function is used in the Robin condition as ${C_\mathrm{p} C}/\lambda ={J_1 (\lambda a)}/{J_0 (\lambda a)}$, with $C_\mathrm{p }$ defined by

$$\begin{aligned} C_\mathrm{p}= & {} \frac{(\alpha _1 t_\mathrm{Si} +\beta _1 )}{((\alpha _1 t_\mathrm{Si} +\beta _1 )^{2}+(\varepsilon _\mathrm{ox2} +\pi )^{2})}\nonumber \\&+\,\mu \mathrm {e}^{(-\mu (\alpha _2 t_\mathrm{Si} +\beta _2 ))}+\nu \mathrm {e}^{(\rho (\alpha _2 t_\mathrm{Si} +\beta _2 ))}, \end{aligned}$$

(10)

where all the parameters can be fit numerically. The Kane tunneling generation rate used in this work is given by $G_\mathrm{T} =A_\mathrm{k} E^{G_\mathrm{k}}\exp \left( {{-B_\mathrm{k} }/E} \right)$, where $A_\mathrm{k}= 3.3679 \times 10^{21}$, $B_\mathrm{k} = 2.5253 \times 10^{7}$ for silicon material, and $G_\mathrm{k} = 2$, since only the direct tunneling process is considered. By replacing the total electric field E by expressions (9a) and (9b), the generation rate for each channel side becomes

$$\begin{aligned} G_\mathrm{TS} =A_\mathrm{k} (A^{2}\exp (-2\lambda z))\exp \left( {\frac{-B_\mathrm{k} \exp (\lambda z)}{A}} \right) , \end{aligned}$$

(11a)

$$\begin{aligned} G_\mathrm{TD} =A_\mathrm{k} (B^{2}\exp (2\lambda z))\exp \left( {\frac{-B_\mathrm{k} \exp (-\lambda z)}{B}} \right) . \end{aligned}$$

(11b)

Fig. 3

Tunneling generation rate distribution for $T_\mathrm{Si}=10$ nm, EOT $=$ 3 nm, $V_\mathrm{ds}=0.5$ V, and $V_\mathrm{gs}=0.5$ V

Fig. 4

Tunneling current versus gate bias for a different oxide thicknesses ($T_\mathrm{Si}=10$ nm and $V_\mathrm{ds}=0.5$ V) and b different channel diameters (EOT $=$ 3nm and $V_\mathrm{ds}=0.5$ V)

Fig. 5

Tunneling current versus a gate bias for different drain biases ($T_\mathrm{Si}=10$ nm and EOT $=$ 3 nm), and b drain bias for different high-$\kappa$ values ($T_\mathrm{Si}=12$ nm and $V_\mathrm{gs}=1$ V)

Figure 3 shows good agreement of the modeled tunneling generation rate with the simulated responses. As expected, the rate is maximum at the junctions, where the major tunneling process occurs, but drops drastically when receding from the channel boundaries. Hence, one can obtain the total tunneling current by summing the integrals of the generation rate equations over the channel length and radius at the junction locations, as illustrated below:

$$\begin{aligned} I_\mathrm{T} =I_\mathrm{TS} +I_\mathrm{TD} =q2\pi \int \limits _0^L {\int \limits _0^a {r\left( {G_\mathrm{TS} +G_\mathrm{TD} } \right) } } \mathrm{d}r\mathrm{d}z \end{aligned}$$

(12)

$$\begin{aligned}&I_\mathrm{TS} =-q\pi a^{2}A_\mathrm{k} \left( {\frac{B_\mathrm{k}^2 Ei\left( {\frac{-B_\mathrm{k} }{A}} \right) +A\exp \left( {\frac{-B_\mathrm{k} }{A}} \right) \left( {B_\mathrm{k} -A} \right) }{2D\lambda }} \right) \end{aligned}$$

(13a)

$$\begin{aligned}&I_\mathrm{TD} =-q\pi a^{2}A_\mathrm{k} \left( {\frac{\left( {B_\mathrm{k}^2 Ei\left( {\frac{-B_\mathrm{k} \mathrm {e}^{-\lambda L}}{B}} \right) +B\exp \left( {\frac{-B_\mathrm{k} \mathrm {e}^{-\lambda L}}{B}+2\lambda L} \right) \left( {B_\mathrm{k} \mathrm {e}^{-\lambda L}-B} \right) } \right) }{2D\lambda }} \right) \end{aligned}$$

(13b)

$$\begin{aligned}&\hbox { with }D=\left( {\frac{\lambda }{(\eta (t_\mathrm{Si} )t_\mathrm{oxeff} +\sigma (t_\mathrm{Si} ))}} \right) ^{\tau }\left( {1+\frac{\Delta _\mathrm{r} }{\left( {1+\left( {\frac{V_\mathrm{g} -V_\mathrm{gm} }{\iota }} \right) ^{2}} \right) ^{2}}} \right) \end{aligned}$$

(13c)

with D a fitting function that evaluates the depth of the tunneling process when only the surface electric field is involved. The second term is a correction function that permits the relative error against numerical simulations to be reduced to around 0.1 % during gate modulation, where $V_\mathrm{gm}$ is the gate voltage and $\Delta _\mathrm{r}$ is the relative error corresponding to the minimum current.

The next figures validate the current model for different configurations and voltage supplies. As can be deduced from the model, reducing the oxide layer thickness will increase the oxide capacitance, electric field, and tunneling current in turn, as illustrated in Figs. 4a and 5b. In an analogous manner, reduction of the channel radius leads to an increase in the tunneling current.

Fig. 6

a Multiple derivates of the current with respect to the applied gate voltage ($T_\mathrm{Si}=14$ nm, EOT $=$ 3 nm, and $V_\mathrm{ds}=1$ V); the inset illustrates the simulated third derivative with more accuracy. b First derivative of the current with respect to applied drain voltage ($T_\mathrm{Si}=12$ nm and $V_\mathrm{gs}=1$ V)

The ambipolarity behavior is well described, as well as the dual modulation effect. The tunneling current on the drain side increases relative to the drain bias and shifts the minimum current forward with gate voltage. Furthermore, it is clearly shown that, during gate modulation, the tunneling process on the source side is totally independent of the drain bias. The dual modulation effect is also described in Fig. 5b, where for low drain bias, the tunneling on the source side is controlled by the drain modulation. The channel potential varies linearly with the drain bias until the drain boundary potential exceeds the channel potential. Then, the regime switches to gate modulation, where the constant gate bias fixes the tunneling near the source side and raises its value at the drain side.

The next step is differentiation of the expression for the current with respect to the gate and drain supplies, with the aim of extracting different analog/RF parameters. Note that only the source tunneling current is considered.

$$\begin{aligned} \frac{\partial I_\mathrm{TS} }{\partial V_\mathrm{gs} }=q\pi a^{2}A_\mathrm{k} \left( {\frac{A\mathrm {e}^{\left( {\frac{-B_\mathrm{k} }{A}} \right) }}{D\lambda }\frac{\partial A}{\partial V_\mathrm{gs} }} \right) \end{aligned}$$

(14)

with

$$\begin{aligned} \frac{\partial A}{\partial V_\mathrm{gs} }= & {} -\lambda \left( {1+J_{1}^{2} (\lambda a)/J_0^2 (\lambda a)} \right) ^{\frac{1}{2}}\left( \frac{V_\mathrm{cn} V_\mathrm{c} \left( {V_\mathrm{g}^*\frac{\partial V_\mathrm{c} }{\partial V_\mathrm{gs} }-V_\mathrm{c} } \right) }{V_\mathrm{g}^{*2}}\right. \nonumber \\&\left. \quad -\,\frac{\partial V_\mathrm{c} }{\partial V_\mathrm{gs} } \right) \exp \left( {V_\mathrm{cn} \left( {1-\frac{V_\mathrm{c} }{V_\mathrm{g}^*}} \right) } \right) \end{aligned}$$

and

$$\begin{aligned} \frac{\partial V_\mathrm{c} }{\partial V_\mathrm{gs} }=\left( {1+\frac{4a\beta }{C\left( {\beta ^{2}-a^{4}} \right) }} \right) ^{-1}. \end{aligned}$$

The last equation is obtained by differentiation of expression (4a) then replacing the derivative of $\beta$ by

$$\begin{aligned} \frac{\partial \beta }{\partial V_\mathrm{gs} }=\left( {\frac{-\beta \left( {\beta -a^{2}} \right) }{V_\mathrm{t} \left( {\beta +a^{2}} \right) }} \right) \frac{\partial V_\mathrm{c} }{\partial V_\mathrm{gs} }. \end{aligned}$$

Following the same methodology, the derivative with respect to the drain supply is given by

$$\begin{aligned} \frac{\partial I_\mathrm{TS} }{\partial V_\mathrm{ds} }=q\pi a^{2}A_\mathrm{k} \left( {\frac{A\mathrm {e}^{\left( {\frac{-B_\mathrm{k} }{A}} \right) }}{D\lambda }\frac{\partial A}{\partial V_\mathrm{ds} }} \right) , \end{aligned}$$

(15)

where

$$\begin{aligned} \frac{\partial A}{\partial V_\mathrm{ds} }=\lambda \left( {1+J_1^2 (\lambda a)/J_0^2 (\lambda a)} \right) ^{\frac{1}{2}}\left( {V_\mathrm{c} \frac{\partial V_\mathrm{ce} }{\partial V_\mathrm{ds} }+V_\mathrm{ce} \frac{\partial V_\mathrm{c} }{\partial V_\mathrm{ds} }} \right) \end{aligned}$$

and

$$\begin{aligned} \frac{\partial V_\mathrm{c} }{\partial V_\mathrm{ds} }=\left( {1+\frac{C\left( {\beta ^{2}-a^{4}} \right) }{4a\beta }} \right) ^{-1}\hbox { and }\frac{\partial \beta }{\partial V_\mathrm{ds} }=\left( {\frac{\left( {\beta -a^{2}} \right) ^{2}}{4aV_\mathrm{t} }} \right) \frac{\partial V_\mathrm{c} }{\partial V_\mathrm{ds} }. \end{aligned}$$

Here, the fitting function $V_\mathrm{ce}$ replaces the exponential term since the drain-bias-dependent parameter $V_\mathrm{cn}$ is difficult to model and by doing so the derivative expression is simplified. The numerical fitting provides the formula $V_\mathrm{ce} =4\left( {V_\mathrm{c} +c_1 } \right) ^{-1/4}+c_2 V_\mathrm{ds} +c_3$.

Fig. 7

a $\text {SS}_\mathrm{min }$ (solid) and $I_\mathrm{on}/I_\mathrm{off }$ (dashed) as functions of channel diameter for different drain biases (EOT $=$ 3 nm and $L=100$ nm). b $\text {SS}_\mathrm{min}$ (solid) and $I_\mathrm{on}$/$I_\mathrm{off}$ (dashed) as functions of channel length for different high-$\kappa$ dielectric constant ($T_\mathrm{Si}=12$ nm and $V_\mathrm{ds}=0.5$ V)

The transition from gate to drain modulation of the tunneling barrier is reflected in the third derivative in Fig. 6a. This transition occurs smoothly over an interval of gate bias. The start point corresponds to the maximum of the third derivative, while the end point is revealed by a kink effect. On the basis of the expressions elaborated above, any degree of differentiation can be obtained with good agreement in comparison with its numerical counterpart, especially during the gate modulation, as depicted in Fig. 6. Nevertheless, the exponential term accounting for the drain modulation must be accurately modeled. One of the important parameters obtained from the expression for the derivative of the current to assess TFET performance is the subthreshold slope (SS), expressed as

$$\begin{aligned} \text {SS}=\frac{\partial V_\mathrm{gs} }{\partial \log _{10} (I_\mathrm{T} )}=\log (10)\frac{\left( {I_\mathrm{TS} +I_\mathrm{TD} } \right) }{\partial I_\mathrm{TS} /\partial V_\mathrm{gs} +\partial I_\mathrm{TD} /\partial V_\mathrm{gs} }\nonumber \\ \end{aligned}$$

(16)

with

$$\begin{aligned} \frac{\partial I_\mathrm{TD} }{\partial V_\mathrm{gs} }=q\pi a^{2}A_\mathrm{k} \left( {\frac{B\mathrm {e}^{\left( {2\lambda L-\frac{B_\mathrm{k} \exp (-\lambda L)}{B}} \right) }}{D\lambda }\frac{\partial B}{\partial V_\mathrm{gs} }} \right) , \end{aligned}$$

where

$$\begin{aligned} \frac{\partial B}{\partial V_\mathrm{gs} }=-\frac{\lambda \left( {1+J_1^2 (\lambda a)/J_0^2 (\lambda a)} \right) ^{\frac{1}{2}}}{2\sinh (\lambda L)}. \end{aligned}$$

Note that the derivative of the term B is limited to the gate modulation regime, where the exponential term equals one. The next figures illustrate the variation of the minimum subthreshold slope and $I_\mathrm{on}/I_\mathrm{off}$ current ratio for different dimensions and drain supplies ($I_\mathrm{on}$ at $V_\mathrm{gs}=1$ V and $I_\mathrm{off}=I_\mathrm{Tmin}$). As mentioned above, reduction of the channel diameter or oxide thickness enhances the on-current. Unfortunately, the off-current is increased as well, by an amount that exceeds the magnitude of the on-current increase. Consequently, the $I_\mathrm{on}/I_\mathrm{off }$ current ratio as well as $\text {SS}_\mathrm{min}$ degrade for reduced channel diameter and oxide thickness (Fig. 7a, b). Furthermore, these degradations are accentuated with drain bias increase. Such major alterations can be attributed to the wide bandgap of silicon and the enhanced ambipolar current. In practice, many solutions are available to improve TFET performance. In this regard, the validity of the developed model for any material may be useful to explore the impact of material engineering. Nevertheless, as our model is based on a local tunneling approach, it is not suitable for heterostructure TFETs, for which a nonlocal model should be applied [18, 28].

Fig. 8

a Transconductance as function of channel diameter. b Intrinsic gain and output conductance as functions of high-$\kappa$ dielectric constant for $T_\mathrm{Si}=12$ nm, $V_\mathrm{ds}=1$ V, and $V_\mathrm{gs}=1$ V

To obtain a more reliable modeling framework, the model must be adapted to describe SCEs. Indeed, the model is derived based on the assumption that $\sinh (\lambda L) \approx \hbox { exp}(\lambda L)/2$, which is correct only for long channel lengths. Furthermore, drain-induced barrier thinning will modify the electrostatic distribution, resulting in higher lateral electric field, indicating the need to include the effect of the length on the root of the Robin condition $\lambda$ [11]. To avoid additional modeling complexity, the impact of length variation is added to the parameters D and $V_\mathrm{p}$ by means of a fitting coefficient expressed as $1+\alpha ^{{\prime }}\hbox { exp}(\beta ^{{\prime }}L)$. This solution gives good agreement of the model with numerical results, as illustrated in Fig. 7b.

As reported in literature [11, 12], the TFET exhibits good immunity against SCEs, while this feature is drastically degraded beyond 30 nm, where the subthreshold slope as well as $I_\mathrm{on}/I_\mathrm{off }$ ratio are degraded in an exponential manner, as depicted in Fig. 7b. Note that the direct and trap-assisted tunneling from source to drain that become possible for lengths approaching 20 nm are not taken into account but may further degrade device performance [9]. However, the high-$\kappa$ layer attenuates the SCEs, with $\text {SS}_\mathrm{min}$ varying around 4 % for a layer with dielectric constant of 80 compared with 9 % for a device without a high-dielectric layer.

Fig. 9

a Cutoff frequency as function of channel diameter ($V_\mathrm{ds}=\hbox { 1\,V and }V_\mathrm{gs}=1\,V$). b Transconductance generation factor as function of channel diameter ($V_\mathrm{ds}=1$ V and $G_\mathrm{m}=0.4\,\mu \hbox {S}$)

3 Results and discussion

This section is composed of two parts. The first subsection is dedicated to the presentation of the analog/RF measures, while the second part is reserved for analysis of different linearity criteria.

3.1 Analog/RF parameters

Investigation of the scaling capability, device performance, and linearity in the high-frequency regime is mandatory for circuit design purposes. The TFET paradigm has been considered as a competitive alternative to MOSFET devices for use in analog/RF applications. Device performance can be assessed by compact modeling of the analog/RF parameters jointly with FOM analysis [13, 39]. The next figures depict various analog/RF criteria for different geometrical parameters in gate modulation mode ($V_\mathrm{gs}=V_\mathrm{ds}$=1 V). The transconductance, defined as $\partial I_\mathrm{ds} /\partial V_\mathrm{gs}$, is shown in Fig. 8a as a function of channel diameter for different high-$\kappa$ values. Similarly to the case of the current, reducing the channel or the effective oxide thickness increases the transconductance. However, attenuation of the high-$\kappa$ layer effect is observed for a value of 10 nm. Likewise, the output conductance, defined as $\partial I_\mathrm{ds} /\partial V_\mathrm{ds}$, shows an increasing tendency with respect to the high-$\kappa$ dielectric value (Fig. 8b). Note that, even if the transconductance of the TFET is relatively low with respect to MOSFETs, the output conductance is as much lower, leading to an acceptable intrinsic gain expressed as $A_\mathrm{v} =G_\mathrm{m} /G_\mathrm{d}$. However, the impact of the high-$\kappa$ layer is more pronounced on $G_\mathrm{d}$ than $G_\mathrm{m}$, resulting in degradation of the gain, as highlighted in Fig. 8b.

As a consequence of the transconductance enhancement, the unity-gain cutoff frequency is improved in the same way, as shown in Fig. 9a. It is expressed as $f_\mathrm{t} \approx {G_\mathrm{m} }/{(2\pi C_\mathrm{gg} )}$, where $C_\mathrm{gg} =C_\mathrm{gs} +C_\mathrm{gd}$ represents the total gate capacitance extracted numerically.

The transconductance generation factor, expressed by $\mathrm{TGF}={G_\mathrm{m} }/{I_\mathrm{d} }$, is another important criterion for analog/RF applications, playing a vital role in the field of RF circuit design [40]. It can be interpreted as the efficiency of a device to convert current (or implicitly power) into transconductance and therefore gain and frequency [41]. To evaluate the effect of the gate stack and radius on the TGF, it is shown at constant transconductance in Fig. 9b. It seems that the TGF drops with reduction of the channel thickness. However, this degradation is largely compensated by the reduction of the effective oxide thickness.

Fig. 10

a Second-order voltage intercept point and b third-order voltage intercept point as function of channel diameter ($V_\mathrm{ds}=1$ V and$V_\mathrm{gs}=1$ V)

Fig. 11

a Third-order input power intermodulation intercept point as function of channel diameter ($V_\mathrm{ds}=1$ V and $V_\mathrm{gs}=1$ V). b 1-dB compression point as function of high-$\kappa$ dielectric constant ($V_\mathrm{ds}=1$ V, $V_\mathrm{gs}=$ 1.8 V)

3.2 Linearity analysis

As for MOSFETs, nonlinearity is an inherent TFET characteristic. In analog/RF applications such as low-noise amplifiers (LNAs) or filters, linearity in the operating range must be obtained to preserve circuit performance. Due to high second- and third-order transconductance derivatives, gain compression, distortion, and intermodulation become important, leading to signal corruption and loss of output power [42]. In a nonlinear system, the output can be expressed in a Taylor series expansion as a function of the alternating-current (AC) gate voltage as [43]

$$\begin{aligned} I_\mathrm{ds} =I_0 +\sum _{i=1} {\frac{g_{\mathrm{m}i} }{i!}v_\mathrm{gs}^i }, \end{aligned}$$

(17)

where $I_{0}$ is the direct-current (DC) component and $g_{\mathrm{m}i} =\frac{\partial ^{i}I_\mathrm{ds} }{\partial v_\mathrm{gs}^i }$ is the ith derivative of the drain current. Based on the previous expression, the linearity FOMs can be extracted as follows [44]:

$$\begin{aligned} \text {VIP}_2= & {} \frac{4g_\mathrm{m1} }{g_\mathrm{m2} }, \end{aligned}$$

(18a)

$$\begin{aligned} \text {VIP}_3= & {} \sqrt{\frac{24g_\mathrm{m1} }{g_\mathrm{m3} }}, \end{aligned}$$

(18b)

$$\begin{aligned} \text {IIP}_3= & {} \frac{4g_\mathrm{m1} }{R_\mathrm{s} g_\mathrm{m3} }. \end{aligned}$$

(18c)

The second and third voltage intercept points, denoted by VIP$_{2}$ and $\hbox {VIP}_{3}$, respectively, represent the voltage at which the second and third harmonics reach the fundamental tone and determine the amount of signal distortion [44]. Therefore, higher values of these FOMs indicate a wider linear operating range. Ideally, in a system with odd symmetry, harmonics of even order vanish, while in a real circuit, symmetry corruption yields a finite number of even-order harmonics [42]. As illustrated in Fig. 10, reducing the channel width and effective oxide thickness widens the linear operating range. For an input comprising two tones, additional nonharmonic components are generated from the frequency difference, a phenomenon called intermodulation (IM). In analogy with $\hbox {VIP}_{3}$, the third-order intermodulation intercept point $\hbox {IIP}_{3}$ represents the input at which the amplitude of the generated third-order IM components equals that of the fundamentals [42, 45]. In the case of a differential LNA, the extrapolated voltage input ($\sqrt{{8g_\mathrm{m1} }/{g_\mathrm{m3} }})$ is squared and divided by twice the ideal input resistance $R_\mathrm{s}$ of $50\,\Omega$ to yield $\hbox {IIP}_{3}$ in terms of power [46]. As for the previous FOMs, $\hbox {IIP}_{3}$ (Fig. 11a) exhibits the same improvement trend.

Even if the increase of the signal amplitude worsens the distortion, the second and third harmonics can be filtered, which is not the case for the total amplitude of the fundamental, for which the increase of the negative second term yields signal compression [45, 46]. This term is generated by the third harmonic and is generally neglected for very small signals. Its effect for higher amplitudes can be extrapolated by means of the 1-dB compression point, defined as the input at which the fundamental amplitude drops by 1 dB, expressed as $0.38\sqrt{\left| {{6g_\mathrm{m1} }/{g_\mathrm{m3} }} \right| }$ for one-tone input and $0.22\sqrt{\left| {{6g_\mathrm{m1} }/{g_\mathrm{m3} }} \right| }$ for input of two tones with the same amplitude [42, 45]. Note that $g_\mathrm{m3}$ becomes negative above the threshold voltage and during drain modulation. As observed in Fig. 6a, the results computed for the modeled current derivatives show an important error for high $V_\mathrm{gs}$. Thus, a more accurate expression for the exponential term describing the drain modulation as $\exp \left( {V_\mathrm{cn} \left( {1-\left( {\frac{V_\mathrm{c} }{V_\mathrm{g}^*}} \right) ^{{V}'_\mathrm{cn} }} \right) } \right)$ is used. Figure 11b shows the 1-dB compression point input power extracted for both one and two tones, respectively, in the case of a single-ended LNA and a differential LNA for $50\,\Omega$ input resistance at 1.8 V DC gate bias. It is shown that, by reducing either the channel diameter or effective oxide thickness, the 1-dB compression point can be lowered, thereby reducing the dynamic operating range.

4 Conclusions

A continuous, accurate tunneling current model based on a cylindrical harmonics solution of the 2D potential was developed for a vertical surrounding-gate structure. The model describes the ambipolar tunneling and dual modulation effects remarkably well. The continuity and high transfer characteristic permit evaluation of device scaling capability, analog/RF performance, and linearity. The results show that decreasing either the channel diameter or effective oxide thickness improves the current and the majority of device FOMs. Moreover, the role of introducing a high-$\kappa$ layer on the gate oxide in improving the behavior of the VSG-TFET is investigated for use in high-performance analog/RF applications, revealing strong effects on the power consumption and dynamic operating range. Thus, the dimensions and operating supply range should be carefully chosen depending upon the device application. Overall, the results demonstrate a comfortable upper limit of the dynamic operating range with high gain and acceptable cutoff frequency, making such TFET structures promising candidates for use in low-power analog/RF applications.