A nonlocal approach for semianalytical modeling of a heterojunction vertical surrounding-gate tunnel FET

Abstract

A semianalytical model based on a nonlocal approach is proposed for an undoped tunnel field-effect transistor (TFET) with a vertical surrounding-gate structure. The heterostructure band alignment is computed by applying the affinity rule on suitable potential expressions obtained from the two-dimensional (2-D) electrostatic solution for all device regions. The fringing field, doping-induced degeneracy, ambipolarity, and dual modulation effects are included with the aim of obtaining a large domain of validity. The core model is completed with expressions for the capacitance of the terminals and validated against numerical simulations obtained using ATLAS-2D software. An investigation of the types of band alignment and the impact of doping on the device performance is also conducted. The developed models could be implemented into commercial simulators to investigate circuits based on such multigate field-effect transistors (FETs).

1 Introduction

Over the past decade, III–V materials and heterostructures have gained attention to boost the performance of TFETs. The advantage of such heterostructures has been demonstrated in many experimental and simulation studies [1,2,3,4]. Variation of the material composition, especially when using ternary compounds, offering great flexibility in terms of physical properties such as the bandgap, effective masses of carrier, and type of band alignment, yields tremendous possibilities to enhance device performance, targeting either high performance or low power specifications. Indeed, the on-current and subthreshold slope have been experimentally obtained for different III–V heterostructure TFETs [5]. The impact of source doping on the subthreshold slope has been highlighted in the past, suggesting the existence of an optimal doping level that offers the best compromise between the off- and on-state characteristics [6]. Therefore, heterostructure TFETs require more attention and deeper investigation of the device physics and performance for effective performance enhancement. For this purpose, it is necessary to develop accurate models that facilitate this task.

Modeling heterostructure TFETs implies the use of a nonlocal tunneling model, as the assumption of a constant electric field is no longer applicable to the heterojunction. It is worth mentioning that some local models based on Kane’s generation rate and the effective bandgap have been developed recently [7,8,9]. However, besides being applicable only to staggered-gap configurations, such oversimplified approaches cannot provide a correct evaluation of the current in the complex-shaped heterojunction tunneling barrier, especially at band discontinuities, where Kane’s formulation is not applicable. Rather, a reliable evaluation of the tunneling current should be based on a self-consistent solution of the Poisson equation to reproduce the electrostatic distribution accurately. This requirement is also justified by the fact that the analytical description of the impact of the fringing electric field on the source and drain, which is important due to its effect on the tunneling junction extensions, remains a very difficult challenge. Furthermore, the deformation of the electrostatic distribution and the nonequilibrium state induced by the high tunneling current injection and the resulting charge dipole creation become cumbersome. In addition, the inclusion of the Schrödinger equation in the simulation scheme permits a precise evaluation of the tunneling and quantum transport. Therefore, the study of heterostructure TFETs using either commercial simulators, or tools developed based on the nonequilibrium Green’s function (NEGF) formalism as in Ref. [3], is certainly a more reliable albeit highly time-consuming solution. Moreover, the use of such tools for simulation of large circuits or for optimization purposes is further complicated and may require the use of lookup tables [10].

On the other hand, the feasibility of analytical modeling of heterostructure TFETs has been studied [4, 11, 12]. The basis of this approach consists in the evaluation of the tunneling probability for each material separately, followed by a summation to give the total probability. Although this approach may not be physically correct, it nonetheless provides an acceptable quantitative description of the evolution of the tunneling probability [4, 12]. Furthermore, the assumption of an exponential barrier, which applies to long channels, simplifies the integral of the imaginary wavevector and provides analytical expressions for the tunneling probability [11, 12]. Nevertheless, previous studies only covered the evaluation of the tunneling probability or limit the current computation to the source junction. Moreover, the depletion approximation applied to the source potential is unreliable.

In this paper, a semianalytical model for a heterostructure vertical surrounding-gate (VSG) TFET is presented. This model is valid for a wide range of device dimensions, materials, and supplies. The drain modulation is also described, as well as the ambipolar current that is essential for a reliable assessment of the device performance. The electrostatic distribution is solved using the exponential approximation, which is consistent with the solution based on cylindrical harmonics developed in a previous work [13]. A good estimation of the boundary potentials of the junctions is performed using both Fermi–Dirac and Boltzmann statistics. Furthermore, a conformal transformation is used to obtain the potential profile of the extension. The heterostructure band alignment is calculated using the affinity rule. By applying the nonlocal tunneling model and the Wentzel–Kramers–Brillouin (WKB) approximation, the proposed model provides encouraging findings in both quantitative and qualitative terms. The model is calibrated and validated against two-dimensional (2-D) numerical simulations [14,15,16]. An analysis of the impact of the device material choice and doping on the device characteristics is also performed. Moreover, expressions for the capacitances of the terminals are also derived.

The rest of this manuscript is organized as follows: Section 2 highlights various stages of the derivation of the electrostatic model associated with the proposed design. Section 3 is dedicated to a succinct description of the bandgap alignment. Then, Sect. 4 presents the development of the expression of the tunneling current in addition to the impact of some material properties. The core model is completed by including the formulas for the capacitances of the terminals in Sect. 5. The work ends with some concluding remarks in Sect. 6.

2 The derivation of the electrostatic model

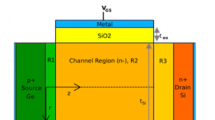
In this study, a vertical surrounding-gate structure is considered, as illustrated in Fig. 1. During the development of the model, we focus on obtaining validity for a wide range of dimensions and material parameters. A major effort is dedicated to the influence of the materials definitions while keeping the following parameters constant: t_ox = 3 nm, ε_ox = 3.9, T_c = 10 nm, L = 100 nm, L_s = 30 nm, L_d = 70 nm, t_g = 1 nm, and Φ_m = 5.1 eV. The basic geometrical parameters are limited to these well-specified values to avoid short-channel effects (SCEs), direct source-to-drain tunneling, and quantum confinement. The source doping varies between 10¹⁹ and 10²⁰ cm⁻³, while the drain doping is fixed at 10¹⁹ cm⁻³ to ensure the formation of ohmic contacts and avoid further current limitation.

Fig. 1

A cross-sectional view of the vertical surrounding-gate heterojunction TFET structure

Because the presented tunneling model is based on a nonlocal approach, it is essential to develop an accurate potential profile for the whole structure. Based on the mathematical development elaborated in Ref. [13], the electrostatic solution in the channel includes two components: the solution to the one-dimensional (1-D) Poisson equation, denoted by V_c(r), and the 2-D component, which is simplified from the cylindrical harmonic solution to an exponential-based expression, valid for long channels. The final channel potential can be written as

$$ \begin{aligned} \psi (r,z) & = V_{\text{c}} (r) + \left( {V_{\text{ps}} (r) - V_{\text{c}} (r)} \right)\exp \left( { - \lambda_{\text{c}} z} \right) \\ & \quad + \,\left( {V_{\text{pd}} (r) - V_{\text{c}} (r)} \right)\exp \left( {\lambda_{\text{c}} z} \right)/\left( {2\sinh (\lambda_{\text{c}} L)} \right) \\ \end{aligned} $$

(1)

with $\lambda_{\text{c}} = {{(3} \mathord{\left/ {\vphantom {{(3} \pi }} \right. \kern-0pt} \pi })^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}} \lambda \exp \left( {1 - V_{\text{c}} /V_{\text{gc}}^{*} } \right),$ where λ represents the inverse of the classical scaling length obtained from the pseudo-2-D solution of the Poisson equation and is defined as $\lambda = \sqrt {{{2C} \mathord{\left/ {\vphantom {{2C} a}} \right. \kern-0pt} a}}$ with the channel radius $a = {{T_{\text{c}} } \mathord{\left/ {\vphantom {{T_{\text{c}} } 2}} \right. \kern-0pt} 2}$, $C = {{C_{\text{ox}} } \mathord{\left/ {\vphantom {{C_{\text{ox}} } {\varepsilon_{\text{c}} }}} \right. \kern-0pt} {\varepsilon_{\text{c}} }}$, and C_ox and ε_c being the oxide capacitance and the channel material permittivity, respectively [17, 18]. The prefactor is found from simulations and permits compensation for the impact of the lateral electric fields near the junctions [19]. Also, the exponential term accounts for the drain modulation effect, as introduced in Ref. [13]. The terms V_ps and V_pd are the source and drain junction potentials, respectively, being controlled by the depletion effect induced by both the channel and the gate potentials. For their extraction, the following drain/source Poisson equation is considered:

$$ \begin{aligned} & \frac{{\partial^{2} \psi_{\rm s,d} (r,z)}}{{\partial z^{2} }} + \frac{1}{r}\frac{{\partial \psi_{\rm s,d} (r,z)}}{\partial r} \\ & \quad + \,\frac{{\partial^{2} \psi_{\rm s,d} (r,z)}}{{\partial r^{2} }} = - \frac{q}{{\varepsilon_{\rm s,d} }}\rho_{\rm s,d} (r,z). \\ \end{aligned} $$

(2)

Assuming a parabolic potential profile in the radial direction, the perpendicular electric field at r = 0 tends toward zero, thus the Poisson equation can be set as

$$ \frac{{\partial^{2} \psi_{\text{s}} (0,z)}}{{\partial z^{2} }} = \frac{q}{{\varepsilon_{\text{S}} }}\left( {N_{\text{AS}} - N_{\text{vs}} F_{1/2} \left( {\frac{{ - \psi_{\text{s}} (0,z) - E_{\text{is}} - E_{\text{fp}} }}{{V_{\text{t}} }}} \right)} \right), $$

(3.1)

with $E_{\text{is}} = \frac{{E_{\text{gs}} }}{2} + \frac{{V_{\text{t}} }}{2}\log \left( {\frac{{N_{\text{vs}} }}{{N_{\text{cs}} }}} \right),$

$$ \frac{{\partial^{2} \psi_{\text{s}} (0,z)}}{{\partial z^{2} }} = \frac{q}{{\varepsilon_{\text{S}} }}\left( {N_{\text{AS}} - n_{\text{is}} \exp \left( {\frac{{ - \psi_{\text{s}} (0,z) + V_{\text{fp}} }}{{V_{\text{t}} }}} \right)} \right), $$

(3.2)

where ψ_s, ε_s, N_AS, N_vs, N_cs, n_is, E_gs, E_is, E_fp, and V_fp are the source potential, permittivity, doping, hole and electron density of states, intrinsic carrier concentration, bandgap, intrinsic Fermi level, and hole quasi-Fermi level and its corresponding potential, respectively. Here, Fermi–Dirac statistics are considered with the aim of obtaining a more realistic description of the behavior at the heavily doped tunneling junctions. If Boltzmann statistics are preferred, expression (3.2) is used. F_1/2 represents the complete Fermi–Dirac integral of order 1/2. Note also that the energies are expressed in volts for simplification. In an analogous manner, the drain-side Poisson equation takes the form

$$ \frac{{\partial^{2} \psi_{\text{d}} (0,z)}}{{\partial z^{2} }} = \frac{q}{{\varepsilon_{\text{d}} }}\left( { - N_{\text{DD}} + N_{\text{cd}} F_{1/2} \left( {\frac{{\psi_{\text{d}} (0,z) + E_{\text{id}} - E_{\text{gd}} + E_{\text{fn}} }}{{V_{\text{t}} }}} \right)} \right), $$

(4.1)

with $E_{\text{id}} = \frac{{E_{\text{gd}} }}{2} + \frac{{V_{\text{t}} }}{2}\log \left( {\frac{{N_{\text{vd}} }}{{N_{\text{cd}} }}} \right),$

$$ \frac{{\partial^{2} \psi_{\text{d}} (0,z)}}{{\partial z^{2} }} = \frac{q}{{\varepsilon_{\text{d}} }}\left( { - N_{\text{DD}} + n_{\text{id}} \exp \left( {\frac{{\psi_{\text{d}} (0,z) - V_{\text{fn}} }}{{V_{\text{t}} }}} \right)} \right), $$

(4.2)

where the parameters are defined in a similar way to the source side. Assuming a zero lateral electric field at the source and drain contacts, the junction potentials at the body center can be obtained using the method proposed in Ref. [20], i.e., by multiplying both sides of the preceding expressions by ${{\partial \psi } \mathord{\left/ {\vphantom {{\partial \psi } {\partial z}}} \right. \kern-0pt} {\partial z}}$ and integrating once with respect to the potential, yielding

$$ \begin{aligned} \frac{{E_{{\parallel {\text{ps}}}} (0)}}{\sqrt 2 } & = \text{sgn} \left( {V_{\text{ps}} (0) - V_{\text{bis}} } \right) \\ & \quad \sqrt {\frac{q}{{\varepsilon_{\text{S}} }}\left| {\begin{array}{*{20}l} {N_{\text{AS}} \left( {V_{\text{ps}} (0) - V_{\text{bis}} } \right)} \hfill \\ { - V_{\text{t}} N_{\text{vs}} \left( {F_{3/2} \left( {\frac{{ - V_{\text{ps}} (0) - E_{\text{is}} - E_{\text{fp}} }}{{V_{\text{t}} }}} \right) - F_{3/2} \left( {\frac{{ - V_{\text{bis}} - E_{\text{is}} - E_{\text{fp}} }}{{V_{\text{t}} }}} \right)} \right)} \hfill \\ \end{array} } \right.} \\ \end{aligned} $$

(5)

Similarly to the source side, the drain Poisson equation leads to

$$ \begin{aligned} \frac{{E_{{\parallel {\text{pd}}}} (0)}}{\sqrt 2 } & = \text{sgn} \left( {V_{\text{bid}} - V_{\text{pd}} (0)} \right) \\ & \quad \sqrt {\frac{q}{{\varepsilon_{\text{d}} }}\left| {\begin{array}{*{20}l} { - N_{\text{DD}} \left( {V_{\text{bid}} - V_{\text{pd}} (0)} \right)} \hfill \\ { + V_{\text{t}} N_{\text{cd}} \left( {F_{3/2} \left( {\frac{{V_{\text{bid}} + E_{\text{id}} - E_{\text{gd}} + E_{\text{fn}} }}{{V_{\text{t}} }}} \right) - F_{3/2} \left( {\frac{{V_{\text{pd}} (0) + E_{\text{id}} - E_{\text{gd}} + E_{\text{fn}} }}{{V_{\text{t}} }}} \right)} \right)} \hfill \\ \end{array} } \right.} \\ \end{aligned} $$

(6)

The continuity of the electric field at the junctions implies that $E_{{\parallel {\text{ps}}}} (0) = \lambda_{\text{c}} \left( {V_{\text{ps}} (0) - V_{\text{c}} (0)} \right)$ and $E_{{\parallel {\text{pd}}}} (0) = - \lambda_{\text{c}} \left( {V_{\text{pd}} (0) - V_{\text{c}} (0)} \right)$. Finally, the boundary potential solutions have to be computed numerically. By following the same approach, the equivalent equations based on the Boltzmann statistics can be expressed as

$$ \begin{aligned} \frac{{E_{{\parallel {\text{ps}}}} (0)}}{\sqrt 2 } & = \text{sgn} \left( {V_{\text{ps}} (0) - V_{\text{bis}} } \right) \\ & \quad \sqrt {\frac{q}{{\varepsilon_{\text{S}} }}\left| {N_{\text{AS}} \left( {V_{\text{ps}} (0) - V_{\text{bis}} } \right) - V_{\text{t}} n_{\text{is}} \left( {\exp \left( {\frac{{ - V_{\text{ps}} (0) + V_{\text{fp}} }}{{V_{\text{t}} }}} \right) - \exp \left( {\frac{{ - V_{\text{bis}} + V_{\text{fp}} }}{{V_{\text{t}} }}} \right)} \right)} \right|}, \\ \end{aligned} $$

(7)

$$ \begin{aligned} \frac{{E_{{\parallel {\text{pd}}}} (0)}}{\sqrt 2 } & = \text{sgn} \left( {V_{\text{bid}} - V_{\text{pd}} (0)} \right) \\ & \quad \sqrt {\frac{q}{{\varepsilon_{\text{d}} }}\left| { - N_{\text{DD}} \left( {V_{\text{bid}} - V_{\text{pd}} (0)} \right) + V_{\text{t}} n_{\text{id}} \left( {\exp \left( {\frac{{V_{\text{bid}} - V_{\text{fn}} }}{{V_{\text{t}} }}} \right) - \exp \left( {\frac{{V_{\text{pd}} (0) - V_{\text{fn}} }}{{V_{\text{t}} }}} \right)} \right)} \right|}, \\ \end{aligned} $$

(8)

where V_bis and V_bid are the source and drain potentials at the contacts, composed of the built-in potentials and the quasi-Fermi levels. These potentials can be obtained by solving the following expressions:

$$ N_{\text{vs}} F_{1/2} \left( {\frac{{ - V_{\text{bis}} - E_{\text{is}} - E_{\text{fp}} }}{{V_{\text{t}} }}} \right) = N_{\text{AS}}, $$

(9)

$$ N_{\text{cd}} F_{1/2} \left( {\frac{{V_{\text{bid}} + E_{\text{id}} - E_{\text{gd}} + E_{\text{fn}} }}{{V_{\text{t}} }}} \right) = N_{\text{DD}}. $$

(10)

For Boltzmann statistics, the previous definitions simplify to

$$ V_{\text{bis}} = - V_{\text{t}} \log \left( {{{N_{\text{AS}} } \mathord{\left/ {\vphantom {{N_{\text{AS}} } {n_{\text{is}} }}} \right. \kern-0pt} {n_{\text{is}} }}} \right) + V_{\text{fp}}, $$

(11)

$$ V_{\text{bid}} = V_{\text{t}} \log \left( {{{N_{\text{DD}} } \mathord{\left/ {\vphantom {{N_{\text{DD}} } {n_{\text{id}} }}} \right. \kern-0pt} {n_{\text{id}} }}} \right) + V_{\text{fn}}. $$

(12)

The next step is to extract the junction potentials at the surface. This can be achieved by following the preceding procedure, but in the radial direction this time. Therefore, the Poisson equation of the two junctions for both types of statistics gives

$$ \begin{aligned} E_{{ \bot {\text{ps}}}} (a) & = \text{sgn} \left( {V_{\text{ps}} (a) - V_{\text{ps}} (0)} \right) \\ & \quad \sqrt {\frac{q}{{\varepsilon_{\text{S}} }}\left| {\begin{array}{*{20}l} {N_{\text{AS}} \left( {V_{\text{ps}} (a) - V_{\text{ps}} (0)} \right)} \hfill \\ { - V_{\text{t}} N_{\text{vs}} \left( {F_{3/2} \left( {\frac{{ - V_{\text{ps}} (a) - E_{\text{is}} - E_{\text{fp}} }}{{V_{\text{t}} }}} \right) - F_{3/2} \left( {\frac{{ - V_{\text{ps}} (0) - E_{\text{is}} - E_{\text{fp}} }}{{V_{\text{t}} }}} \right)} \right)} \hfill \\ \end{array} } \right.} \\ \end{aligned} $$

(13)

$$ \begin{aligned} E_{{ \bot {\text{pd}}}} (a) & = \text{sgn} \left( {V_{\text{pd}} (a) - V_{\text{pd}} (0)} \right) \\ & \quad \sqrt {\frac{q}{{\varepsilon_{\text{d}} }}\left| {\begin{array}{*{20}l} { - N_{\text{DD}} \left( {V_{\text{pd}} (a) - V_{\text{pd}} (0)} \right)} \hfill \\ { + V_{\text{t}} N_{\text{cd}} \left( {F_{3/2} \left( {\frac{{V_{\text{pd}} (a) + E_{\text{id}} - E_{\text{gd}} + E_{\text{fn}} }}{{V_{\text{t}} }}} \right) - F_{3/2} \left( {\frac{{V_{\text{pd}} (0) + E_{\text{id}} - E_{\text{gd}} + E_{\text{fn}} }}{{V_{\text{t}} }}} \right)} \right)} \hfill \\ \end{array} } \right.} \\ \end{aligned} $$

(14)

$$ \begin{aligned} E_{{ \bot {\text{ps}}}} (a) & = \text{sgn} \left( {V_{\text{ps}} (a) - V_{\text{ps}} (0)} \right) \\ & \quad \sqrt {\frac{q}{{\varepsilon_{\text{S}} }}\left| \begin{array}{l} N_{\text{AS}} \left( {V_{\text{ps}} (a) - V_{\text{ps}} (0)} \right) \hfill \\ - V_{\text{t}} n_{\text{is}} \left( {\exp \left( {\frac{{ - V_{\text{ps}} (a) + V_{\text{fp}} }}{{V_{\text{t}} }}} \right) - \exp \left( {\frac{{ - V_{\text{ps}} (0) + V_{\text{fp}} }}{{V_{\text{t}} }}} \right)} \right) \hfill \\ \end{array} \right|} \\ \end{aligned} $$

(15)

$$ \begin{aligned} E_{{ \bot {\text{pd}}}} (a) & = \text{sgn} \left( {V_{\text{pd}} (a) - V_{\text{pd}} (0)} \right) \\ & \quad \sqrt {\frac{q}{{\varepsilon_{\text{d}} }}\left| \begin{array}{l} - N_{\text{DD}} \left( {V_{\text{pd}} (a) - V_{\text{pd}} (0)} \right) \hfill \\ + V_{\text{t}} n_{\text{id}} \left( {\exp \left( {\frac{{V_{\text{pd}} (a) - V_{\text{fn}} }}{{V_{\text{t}} }}} \right) - \exp \left( {\frac{{V_{\text{pd}} (0) - V_{\text{fn}} }}{{V_{\text{t}} }}} \right)} \right) \hfill \\ \end{array} \right|} \\ \end{aligned} $$

(16)

Here, the perpendicular electric field satisfies the continuity conditions at the channel–oxide and junction interfaces, i.e., $\left. {\frac{{\partial \psi_{\text{c}} }}{\partial r}} \right|_{r = a} = \frac{{C_{\text{ox}} }}{{\varepsilon_{\text{c}} }}\left( {V_{\text{g}}^{*} - \psi (a,z)} \right)$ and $\left. {\frac{{\partial \psi_{\rm s,d} }}{\partial r}} \right|_{\begin{subarray}{l} r = a \\ z = 0,L \end{subarray} } = \left. {\frac{{\partial \psi_{c} }}{\partial r}} \right|_{\begin{subarray}{l} r = a \\ z = 0,L \end{subarray} }$ which gives $E_{{ \bot {\text{ps}},{\text{d}}}} (a) = \frac{{C_{\text{ox}} }}{{\varepsilon_{\text{c}} }}\left( {V_{\text{g}}^{*} - V_{{{\text{ps}},{\text{d}}}} (a)} \right)$. The term $V_{\text{g}}^{*}$ is the effective gate voltage, defined as $V_{\text{g}}^{*} = V_{\text{g}}^{{}} - V_{\text{fb}}$, where $V_{\text{fbc}}^{{}} = \varPhi_{\text{m}} - \chi_{\text{c}} - E_{\text{gc}} + E_{\text{ic}}$ denotes the flat-band voltage, with Φ_m and χ_c representing the gate work function and channel electron affinity, respectively. The next step is to model the electrostatic profile of the extensions, or at least its surface potential. The potential of the extensions can be evaluated using a pseudo-2-D solution of the Poisson equation such as [17]

$$ \psi_{\rm s,d} (r,z) = C_{0} (z) + C_{1} (z)(r - a) + C_{2} (z)(r - a)^{2}, $$

(17)

which transforms the Poisson equation with the right boundary conditions $\left. {\frac{{\partial \psi_{\rm s,d} }}{\partial r}} \right|_{r = a} = \frac{{C_{\text{ox}} (z)}}{{\varepsilon_{\rm s,d} }}\left( {V_{{{\text{g}}(s,d)}}^{*} - \psi_{\rm s,d} (a,z)} \right)$ to

$$ \begin{aligned} & \frac{{\partial^{2} \psi_{\rm s,d} (a,z)}}{{\partial z^{2} }} + \frac{{2C_{\text{ox}} (z)\left( {V_{{{\text{g}}\left( {\rm s,d} \right)}}^{*} - \psi_{\rm s,d} (z,a)} \right)}}{{a\varepsilon_{\rm s,d} }} \\ & = - \frac{q}{{\varepsilon_{\rm s,d} }}\rho_{\rm s,d} (a,z). \\ \end{aligned} $$

(18)

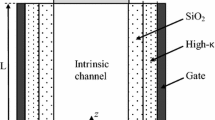
The main difficulty in solving this equation is the consideration of the gate electrode fringing fields, which yields a variable oxide capacitance. This problem was previously treated in a simple manner in Ref. [17], where a coefficient of π/2 was introduced into the classical capacitance expression. A more developed analysis was carried out in Ref. [21] to produce an analytical expression for the surface potential using a conformal mapping technique. Performing a similar approach to that used in Refs. [22, 23], a conformal transformation of the electric field lines into the oxide region is introduced here, as illustrated in Fig. 2. Using the appropriate transformation function w = sin(z), the coordinates can be mapped as follows:

$$ (r - a)\overrightarrow {R} + Nz\overrightarrow {Z} = t_{\text{ox}} \sin \left( {u\overrightarrow {U} + v\overrightarrow {V} } \right), $$

(19)

with $N_{\rm s,d} = \frac{{ - t_{\text{ox}} }}{{L_{\rm s,d} }}\sinh \left( {\cosh^{ - 1} \left( {\frac{{t_{\text{ox}} + t_{\text{g}} }}{{t_{\text{ox}} }}} \right)} \right).$

Fig. 2

An illustration of the fringing electric field lines in the original coordinates (left) and the transformed representation (right)

The expression for the original coordinate axes as a function of the transformed ones gives $z = \frac{{t_{\text{ox}} }}{{N_{\rm s,d} }}\sinh \left( v \right)$ for r = a and $r - a = t_{\text{ox}} \sin \left( u \right)$ for z = 0. Accordingly, the transformation of the extension lengths and oxide thickness yields $d_{\rm s,d} = \sinh^{ - 1} \left( {\frac{{ - N_{\rm s,d} L_{\rm s,d} }}{{t_{\text{ox}} }}} \right)$ and $e = \frac{(1 + 2n)\pi }{2}$.

Applying these transformed dimensions, the oxide capacitance in the new coordinate system takes the form

$$ \begin{aligned} C_{{{\text{ox}}\,s,d}} = \frac{{\varepsilon_{\rm s,d} }}{{a_{\rm s,d}^{\prime } \log \left( {1 + \frac{e}{{a_{\rm s,d}^{\prime } }}} \right)}} \hfill \\ {\text{where}}\quad a_{\rm s,d}^{\prime } = \sinh^{ - 1} \left( {\frac{{aN_{\rm s,d} }}{{t_{\text{ox}} }}} \right). \hfill \\ \end{aligned} $$

(20)

A correct conformal representation has some implications. The first one is that Laplace’s equation takes the same form as in the original coordinates. By extension, this implication is also valid for the Poisson’s equation with the introduction of a scale factor to give physical lengths to the transformed variables u and v, as these are dimensionless [23]. The second implication of the conformal representation is that $\frac{\partial v}{\partial z} = \frac{\partial u}{\partial r}$. Knowing from the axis transformation that $\partial z = \frac{{N_{\rm s,d} }}{{t_{\text{ox}} }}\cosh (v)\partial v$, the scale factor is then $\frac{{N_{\rm s,d} }}{{t_{\text{ox}} }}\cosh (v)$. Consequently, the Poisson equation in the new coordinates can be rewritten as

$$ \begin{aligned} & \left( {\frac{{N_{\rm s,d} }}{{t_{\text{ox}} \cosh \left( v \right)}}} \right)^{2} \left( {\frac{{\partial^{2} \psi_{\rm s,d} (u,v)}}{{\partial v^{2} }} + \frac{1}{u}\frac{{\partial \psi_{\rm s,d} (u,v)}}{\partial u}} \right. \\ & \quad \left. { + \,\frac{{\partial^{2} \psi_{\rm s,d} (u,v)}}{{\partial u^{2} }}} \right) = - \frac{q}{{\varepsilon_{\rm s,d} }}\rho_{\rm s,d} (u,v). \\ \end{aligned} $$

(21)

Considering the solution in the vicinity of the junction interfaces, where cosh(v) tends toward 1, and neglecting the majority carriers, the Poisson equation can be simplified to

$$ \begin{aligned} & \frac{{\partial^{2} \psi_{\rm s,d} (0,v)}}{{\partial v^{2} }} + \frac{{2C_{{{\text{ox}}\,s,d}} \left( {V_{{g\left( {\rm s,d} \right)}}^{*} - \psi_{\rm s,d} (0,v)} \right)}}{{a_{\rm s,d}^{\prime } \varepsilon_{\rm s,d} }} \\ & \approx \pm \left( {\frac{{t_{\text{ox}} }}{{N_{\rm s,d} }}} \right)^{2} \frac{q}{{\varepsilon_{\rm s,d} }}N_{{{\text{AS}},{\text{DD}}}}. \\ \end{aligned} $$

(22)

The oxide capacitance being now constant, the pseudo-2-D solution with the boundary conditions is expressed as

$$ \psi_{\rm s,d} (0,v) = V_{{{\text{bis}},\text{d}}} + (V_{{{\text{ps}},\text{d}}} (a) - V_{{{\text{bis}},\text{d}}} )\exp (v/\lambda_{\rm s,d}^{*} ). $$

(23)

Replacing v by its equivalent in the original coordinates, the surface potential takes the final form

$$ \psi_{\text{s}} (a,z) = V_{\text{bis}} + (V_{\text{ps}} (a) - V_{\text{bis}} )\exp \left( {\frac{{\sinh^{ - 1} \left( {{{zN_{\text{s}} } \mathord{\left/ {\vphantom {{zN_{\text{s}} } {t_{\text{ox}} }}} \right. \kern-0pt} {t_{\text{ox}} }}} \right)}}{{\lambda_{\text{s}}^{*} }}} \right), $$

(24)

$$ \psi_{\text{d}} (a,z) = V_{\text{bid}} + (V_{\text{pd}} (a) - V_{\text{bid}} )\exp \left( {\frac{{\sinh^{ - 1} \left( {{{\left( {z - L} \right)N_{\text{d}} } \mathord{\left/ {\vphantom {{\left( {z - L} \right)N_{\text{d}} } {t_{\text{ox}} }}} \right. \kern-0pt} {t_{\text{ox}} }}} \right)}}{{\lambda_{\text{d}}^{*} }}} \right). $$

(25)

Note that these expressions differ to some extent from what the solution of Eq. (22) should give and is obtained by identification. Also, the gate voltage is not explicitly expressed. This information is therefore included in the scaling length. As for λ_c, simulations highlight that the scaling lengths of the extensions show a strong dependence on the gate voltage; Denoted by $\lambda_{\rm s,d}^{*}$, this can be obtained from the expression

$$ \frac{{V_{{{\text{ps}},\text{d}}} (a) - V_{{{\text{bis}},\text{d}}} }}{{\alpha \left( {\lambda_{\rm s,d}^{*} } \right)^{2} }} + \frac{{V_{{{\text{g/s}},\text{d}}}^{*} - V_{{{\text{ps}},\text{d}}} (a)}}{{\left( {\lambda_{\rm s,d}^{{}} } \right)^{2} }} = - \frac{q}{{\varepsilon_{\rm s,d} }}\rho_{\rm s,d} (a)\left( {\frac{{t_{\text{ox}} }}{{N_{\rm s,d} }}} \right)^{2}, $$

(26)

where $\lambda_{\rm s,d}^{{}} = \sqrt {\frac{{a_{\rm s,d}^{\prime } \varepsilon_{\rm s,d} }}{{2C_{{{\text{ox}}\,\rm s,d}} }}}$ and $V_{{{\text{g/s}},\text{d}}}^{*} = V_{\text{g}} - V_{{{\text{fb/s}},\text{d}}}$. The flat-band voltages of the extensions V_fb/s,d are defined by $V_{{{\text{fb/s}},\text{d}}} = \varPhi_{\text{m}} - \chi_{\rm s,d} - E_{{{\text{gs}},\text{d}}} + E_{{{\text{is}},\text{d}}} + V_{{{\text{bis}},\text{d}}} - V_{{{\text{qn}},\text{p}}}$. It is worth mentioning that the obtained expressions represent an approximated solution that might induce a consequent error in the tunneling current evaluation, especially for extensions with moderate doping, which yields deeper depletion and a more complex potential profile. Therefore, it is necessary to introduce a correction factor. The latter, denoted by α, is introduced into the denominator of the first term in Eq. (26); a value of 3 for both extensions was found to give good results. Furthermore, the use of Boltzmann statistics in the derivation of the channel potential expression [13] when Fermi–Dirac statistics are considered in the remaining device regions yields large errors during drain modulation. Thus, a correction is also applied to the channel potential as (V_c + V ^*_g )/2. Otherwise, a numerical solution of the 1D Poisson equation should be used.

3 Heterostructure band alignment

The band alignment in a heterostructure can be of three configurations or types, namely straddled, staggered, or broken gap. In this work, the affinity rule is used to determine the conduction and valence band discontinuity [14, 24]. The resulting definitions of this rule are:

$$ \left\{ {\begin{array}{*{20}l} {\Delta E_{\text{c}} = \chi_{\text{c}} - \chi_{\text{s}} } \hfill \\ {\Delta E_{\text{g}} = E_{\text{gs}} - E_{\text{gc}} } \hfill \\ {\Delta E_{\text{v}} = \Delta E_{\text{g}} - \Delta E_{\text{c}} } \hfill \\ {E_{\text{r}} = E_{\text{gc}} - E_{\text{ic}} + \chi_{\text{c}} } \hfill \\ \end{array} } \right. $$

(27)

The term E_r is defined as the energy reference from which the band alignment is calculated and refers to the smallest bandgap of the three regions. Overall, in most cases of n-type TFETs, E_r corresponds to the channel, and the drain energy reference of the same material is used for both regions to avoid any possible transport limitation of the heterojunction. In the opposite case, where E_gs> E_gc,d, the previous definitions and following development remain valid. As a consequence of the alignment, the built-in potential of the extensions and the potentials of the junctions are shifted by an amount defined as $\Delta V = E_{{{\text{is}},\text{d}}} - E_{{{\text{gs}},\text{d}}} - \chi_{\rm s,d} + E_{\text{r}},$ and the new values are computed by $V_{{{\text{bis}},\text{d}}}^{*} = V_{{{\text{bis}},\text{d}}} + \Delta V$ and $V_{{{\text{ps}},\text{d}}}^{*} = V_{{{\text{ps}},\text{d}}} + \Delta V$. Also, these latter definitions are involved in the calculation of the potentials of the junctions and the scaling lengths of the extensions. The electric fields can then be rewritten as $E_{{\parallel {\text{ps}},\text{d}}} (0) = \lambda_{\text{c}} \left( {V_{\text{c}} (0) - V_{{{\text{ps}},\text{d}}}^{*} (0)} \right)$ and $E_{{ \bot {\text{ps}},\text{d}}} (a) = \frac{{C_{\text{ox}} }}{{\varepsilon_{\text{c}} }}\left( {V_{\text{g}}^{*} - V_{{{\text{ps}},\text{d}}}^{*} (a)} \right)$, while the right-hand side (RHS) of the corresponding equations remains unchanged. Furthermore, Eq. (26) is redefined as

$$ \begin{aligned} & \frac{{V_{{{\text{ps}},\text{d}}}^{*} (a) - V_{{{\text{bis}},\text{d}}}^{*} }}{{\alpha \left( {\lambda_{\rm s,d}^{*} } \right)^{2} }} + \frac{{V_{{{\text{g/s}},\text{d}}}^{*} - V_{{{\text{ps}},\text{d}}}^{*} (a)}}{{\left( {\lambda_{\rm s,d}^{{}} } \right)^{2} }} \\ & = - \frac{q}{{\varepsilon_{\rm s,d} }}\rho_{\rm s,d} (a)\left( {\frac{{t_{\text{ox}} }}{{N_{\rm s,d} }}} \right)^{2}. \\ \end{aligned} $$

(28)

With the extraction of all necessary parameters, the valence and conduction bands (E_c = E_v + E_g) in the three regions are defined by

$$ E_{\text{vs}} = - V_{\text{bis}} - \left( {V_{\text{ps}} (a) - V_{\text{bis}} } \right)\exp \left( { - \frac{{zN_{\text{s}} }}{{\lambda_{\text{s}}^{*} t_{\text{ox}} }}} \right) - E_{\text{is}}, $$

(29)

$$ \begin{aligned} E_{\text{vc}} & = - V_{\text{c}} - \left( {V_{\text{ps}}^{*} (a) - V_{\text{c}} } \right)\exp \left( { - \lambda_{\text{c}} z} \right) - \left( {V_{\text{pd}}^{*} (a) - V_{\text{c}} } \right) \\ & \quad \exp \left( {\lambda_{\text{c}} z} \right)/\left( {2\sinh \left( {\lambda_{\text{c}} L} \right)} \right) - E_{\text{ic}}, \\ \end{aligned} $$

(30)

$$ \begin{aligned} E_{\text{vd}} & = - V_{\text{bid}} - \left( {V_{\text{pd}} (a) - V_{\text{bid}} } \right) \\ & \quad \exp \left( { - \frac{{\left( {z - L} \right)N_{\text{d}} }}{{\lambda_{\text{d}}^{*} t_{\text{ox}} }}} \right) - E_{\text{id}}. \\ \end{aligned} $$

(31)

The following figures show the energy band diagrams for such heterojunction TFETs with various choices of materials and doping (note that the definition of InAs in the Atlas software is different from the cubic III–V interpolation model set [14], yielding a staggered or nearly broken gap for the GaSb–InAs heterojunction while it should be broken). It is observed that the proposed model offers a good match with the numerical results. As pointed out previously, the main concern is the potential profile in the extensions for low doping concentrations, as showcased in Fig. 4. Obviously, this case is more critical, as the model may suffer from some anomalies in properly describing the electrostatic profile as a consequence of the assumptions made to solve Eq. (21).

Furthermore, it is important to emphasize that the numerical results shown in Figs. 3 and 4 are obtained without activation of the tunneling model. Indeed, the injection of carriers that results from the tunneling process creates charge dipoles which affect the electrostatic distribution near the tunneling junctions. Correct resolution of this problem would imply the use of an iterative scheme, which would increase the computation time. However, it is preferred in this study to make use of fitting parameters such as α in Eqs. (26, 28) to calibrate the tunneling current.

Fig. 3

The energy band diagrams of a GaSb–InAs and b AlSb–InAs for N_AS = 10²⁰ cm⁻³, V_gs = 1 V, and V_ds = 0.5 V

Fig. 4

The energy band diagrams of a GaSb–InAs and b GaAs–InAs for N_AS = 10¹⁹ cm⁻³, V_gs = 1 V, and V_ds = 0.5 V

4 Tunneling current model

As mentioned above, a nonlocal tunneling model is considered in this study. Thus, the tunneling current is evaluated for all possible electron tunneling paths between the valence band of the source and the conduction band of the channel in the case of the source junction. For the drain side, the evaluation is performed between the valence band of the channel and the conduction band of the drain. Therefore, the tunneling current density takes the form [14]

$$ \begin{aligned} J & = \frac{q}{\pi \hbar }\iint {T\left( E \right)\left[ {f_{\text{l}} \left( {E + E_{\text{T}} } \right)} \right.} \\ & \left. {\quad - \,f_{\text{r}} \left( {E + E_{\text{T}} } \right)\rho \left( {E_{\text{T}} } \right){\text{d}}E{\text{d}}E_{\text{T}} } \right], \\ \end{aligned} $$

(32)

where E and E_T are the lateral and transverse electron energy, respectively. ρ(E_T) represents the 2-D density of states that corresponds to the remaining transverse wavevectors and equals

$$ \rho \left( {E_{\text{T}} } \right) = \frac{{\sqrt {m_{\text{e}} m_{\text{h}} } }}{{2\pi \hbar^{2} }}, $$

(33)

where m_e and m_h are the electron and hole effective masses, including the tunneling contribution of each conduction-band valley (e.g., six for silicon) and both the light- and heavy-hole valence band. For an isotropic band structure, m_e and m_h equal the electron and hole density-of-states masses, respectively. For binary and ternary materials, the electron effective mass is related to the conduction-band valley corresponding to the minimum bandgap energy [14]. As this work is more qualitative than quantitative, the density-of-states definition is used for all materials, which is found to give a close result.

As discussed above, the Fermi occupancy difference accounts for the Landauer conduction formula and permits a null current to be obtained for a zero external applied voltage. The Fermi–Dirac distribution functions for the left or right side of the tunneling junction are defined as

$$ f_{\text{l,r}} \left( {E + E_{\text{T}} } \right) = \left( {1 + \exp \left( {\frac{{E + E_{\text{T}} - E_{\text{fl,r}} }}{KT}} \right)} \right)^{ - 1}. $$

(34)

Integrating Eq. (32) once with respect to the transverse energy from 0 to E_max = min(E_l − EE − E_r), which ensures the limitation of the total carrier energy (E + E_T) to the tunneling window, yields

$$ \begin{aligned} I_{\text{t}} & = \frac{qKT}{\pi \hbar }\rho \left( {E_{\text{T}} } \right)\int\limits_{0}^{a} {\int\limits_{{E_{\rm l} }}^{{E_{\rm r} }} {2\pi rT\left( E \right)\log } } \\ & \quad \left[ {\frac{{\left( {1 + \exp \left( {\frac{{E_{\text{fr}} - E}}{KT}} \right)} \right)\left( {1 + \exp \left( {\frac{{E_{{{\text{fl}}}} - E - E_{{\mathrm{max}} } }}{KT}} \right)} \right)}}{{\left( {1 + \exp \left( {\frac{{E_{\text{fl}} - E}}{KT}} \right)} \right)\left( {1 + \exp \left( {\frac{{E_{\text{fl,r}} - E - E_{{\mathrm{max}} } }}{KT}} \right)} \right)}}} \right]{\text{d}}E{\text{d}}r, \\ \end{aligned} $$

(35)

$$ T\left( E \right) = \exp \left( { - 2\int\limits_{{z_{1} }}^{{z_{2} }} {\kappa (z){\text{d}}z} } \right). $$

(36)

The tunneling probability T(E) is calculated using the WKB approximation. Normally, a valid dispersion relation that links the imaginary wavevectors in the two bands should be used, such as Kane’s widely adopted two-band model [14, 25, 26]. Nevertheless, analytical integral of such a relation is an intractable task. Therefore, the tunneling path is divided between the wavevectors associated with the valence and conduction band (κ_c and κ_v), with a branch point z₀ that should be carefully chosen with the aim of reproducing the original variation of the tunneling probability. It is worth mentioning that the branch point as used in this study does not capture all the physics inside the forbidden region, being rather a practical solution that yields acceptable results. The preceding equation can then be rewritten as

$$ T\left( E \right) = \exp \left( { - 2\left( {\int\limits_{{z_{1} }}^{{z_{0} }} {\kappa_{\text{v}} (z){\text{d}}z} + \int\limits_{{z_{0} }}^{{z_{2} }} {\kappa_{\text{c}} (z){\text{d}}z} } \right)} \right), $$

(37)

where $\kappa_{\text{c}} (z) = \frac{1}{\mathrm{i}\hbar }\sqrt {2m_{0} m_{\text{e}} (z)\left( {E - E_{\text{c}} (z)} \right)}$ and $\kappa_{\text{v}} (z) = \frac{1}{\mathrm{i}\hbar }\sqrt {2m_{0} m_{\text{h}} (z)\left( {E_{\text{v}} (z) - E} \right)}$with $m_{\text{e}} = \left( {m_{\text{l}} m_{t}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}}$ and $m_{\text{h}} = \left( {m_{\text{lh}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} + m_{\text{hh}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} } \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}.$

The parameters m₀, m_e(z), m_h(z), m_l, m_t, m_lh, and m_hh represent the electron rest mass, the position-dependent electron and holes effective masses (equivalent to the density-of-states ones), the lateral and transverse electron masses, and the light and heavy hole masses, respectively. Because the tunneling barrier is assumed to have an exponential profile in all regions of the device, the integral of the imaginary wavevector between the classical turning points z₁ and z₂ can be performed analytically. The latter are obtained by solving the equation E_c,v = E. Using the expressions for the valence and conduction bands in each region, the associated wavevectors can be written as

$$ \kappa (z) = \frac{1}{\mathrm{i}\hbar }\sqrt {2m_{0} m_{\text{e}} (z)\left( {A + B\exp (Cz)} \right)}. $$

(38)

Hence, the analytical integral of the wavevectors over any tunneling path gives

$$ \begin{aligned} \int\limits_{{z_{1} }}^{{z_{2} }} {\kappa (z){\text{d}}z} & = \frac{{\sqrt {2m_{0} m_{\text{e}} (z)} }}{\mathrm{i}\hbar } \\ & \quad \left[ {\frac{{\sqrt {A + B\exp (Cz)} - \sqrt A \tanh^{ - 1} \left( {\frac{{\sqrt {A + B\exp (Cz)} }}{\sqrt A }} \right)}}{C}} \right]_{{z_{1} }}^{{z_{2} }}. \\ \end{aligned} $$

(39)

The heterojunction TFET energy band diagram for a staggered or nearly broken gap (Fig. 5a) shows that the tunneling window must be divided into four regions or energy intervals, depending on the position of the turning points.

Fig. 5

a The energy band diagram and b tunneling probability distribution over the tunneling window of a staggered-gap GaAs_0.5Sb_0.5–InAs heterojunction TFETs with N_AS = 10²⁰ cm⁻³, V_gs = 1 V, and V_ds = 0.75 V

In the first region, the tunneling starts from the valence band of the source and ends at the conduction band of the junction. The branch point is located very close to the junction, and the tunneling probability in this case is dominated by the valence band wavevector as in Eq. (40a). In the second region, electrons tunnel from the valence band of the source to the conduction band of the channel. In contrast to other studies, in which the branch point is set exactly at the junction interface [4, 11, 12], a branch point located in the source side was found to give better results here; consequently, the probability includes three components as in Eq. (40b). The tunneling probability in the third region is dominated by wavevectors corresponding to the conduction band of the channel, thus the branch point is located close to the start turning point (40c). Finally, the tunneling in the fourth region occurs exclusively in the channel (40d). The branch point in this case is set at approximately 20 % of the tunneling distance from the starting turning point.

For $E \ge ( - V_{\text{ps}} (a) - E_{\text{is}} ) \, \& \, E \ge ( - V_{\text{ps}}^{*} (a) - E_{\text{ic}} + E_{\text{gc}} )$,

$$ \begin{aligned} T_{1} \left( E \right) & = \exp \left( { - 2\left( {\int\limits_{{z_{1} }}^{{z_{0} }} {\kappa_{\text{vs}} (z){\text{d}}z} + \int\limits_{{z_{0} }}^{{z_{2} }} {\kappa_{\text{cs}} (z){\text{d}}z} } \right)} \right) \\ & \quad {\text{and}}\quad \rho_{1} \left( {E_{\text{T}} } \right) = \frac{{\sqrt {m_{\text{es}} m_{\text{hs}} } }}{{2\pi \hbar^{2} }}. \\ \end{aligned} $$

(40a)

For $E \ge ( - V_{\text{ps}} (a) - E_{\text{is}} ) \, \& \, E < ( - V_{\text{ps}}^{*} (a) - E_{\text{ic}} + E_{\text{gc}} )$,

$$ \begin{aligned} T_{2} \left( E \right) & = \exp \left( { - 2\left( {\int\limits_{{z_{1} }}^{{z_{0} }} {\kappa_{\text{vs}} (z)\,{\text{d}}z} + \int\limits_{{z_{0} }}^{0} {\kappa_{\text{cs}} (z)\,{\text{d}}z} + \int\limits_{0}^{{z_{2} }} {\kappa_{\text{cc}} (z)\,{\text{d}}z} } \right)} \right) \\ & \quad {\text{and}}\quad \rho_{2} \left( {E_{\text{T}} } \right) = \frac{{\sqrt {m_{\text{ec}} m_{\text{hs}} } }}{{2\pi \hbar^{2} }}. \\ \end{aligned} $$

(40b)

For $E < ( - V_{\text{ps}} (a) - E_{\text{is}} ) \, \& \, E \ge ( - V_{\text{ps}}^{*} (a) - E_{\text{ic}} ),$

$$ \begin{aligned} T_{3} \left( E \right) & = \exp \left( { - 2\left( {\int\limits_{{z_{1} }}^{{z_{0} }} {\kappa_{\text{vc}} (z){\text{d}}z} + \int\limits_{{z_{0} }}^{{z_{2} }} {\kappa_{\text{cc}} (z){\text{d}}z} } \right)} \right) \\ & \quad {\text{and}}\quad \rho_{3} \left( {E_{\text{T}} } \right) = \frac{{\sqrt {m_{\text{ec}} m_{\text{hs}} } }}{{2\pi \hbar^{2} }}. \\ \end{aligned} $$

(40c)

For $E < ( - V_{\text{ps}} (a) - E_{\text{is}} ) \, \& \, E < ( - V_{\text{ps}}^{*} (a) - E_{\text{ic}} )$,

$$ \begin{aligned} T_{4} \left( E \right) & = \exp \left( { - 2\left( {\int\limits_{{z_{1} }}^{{z_{0} }} {\kappa_{\text{vc}} (z)\,{\text{d}}z} + \int\limits_{{z_{0} }}^{{z_{2} }} {\kappa_{\text{cc}} (z)\,{\text{d}}z} } \right)} \right) \\ & \quad {\text{and}}\quad \rho_{4} \left( {E_{\text{T}} } \right) = \frac{{\sqrt {m_{\text{ec}} m_{\text{hc}} } }}{{2\pi \hbar^{2} }}. \\ \end{aligned} $$

(40d)

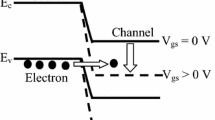
The total tunneling probability as a function of the tunneling path energy is then computed as $T\left( E \right) = \sum\limits_{i} {T_{i} \left( E \right)\left( {H\left( {E_{i}^{\text{u}} - E} \right) - H\left( {E_{i}^{\text{l}} - E} \right)} \right)}$, where H(E) is the Heaviside step function applied for each tunneling region indexed by i, comprised between the upper and lower energies E^u and E^l. Also, as each tunneling region has its proper density of states, $\rho \left( {E_{\text{T}} } \right)$ must be reinserted under the integral sign. On the other side, the drain tunneling junction is divided into two energy intervals. The first one evaluates the tunneling probability from the valence band of the channel to the conduction band of the drain, with a branch point located in the latter, while the second permits the computation of the tunneling probability in the drain extension. In fact, in a straddled-gap heterostructure configuration, a tunneling barrier results from the valence band discontinuity at the junction (Fig. 6a). The latter may further attenuate the current transport, which is dominated by the thermionic and field-emission mechanisms [27].

Fig. 6

a The energy band diagram and b tunneling probability distribution over the tunneling window of a straddled-gap GaAs–InAs heterojunction TFET with N_AS = 10²⁰ cm⁻³, V_gs = 1 V, and V_ds = 0.75 V

To avoid greater modeling complexity, the transport attenuation is included in an expression that reduces the tunneling probability in the fourth region by moving the branch point toward the conduction band, defined as

$$ z_{0} = z_{1} + 0.15\left( {1 + \Delta E_{\text{v}} } \right)L_{\text{t}} $$

(41)

with L_t being the tunneling distance. The following figures show the good agreement of the developed model with corresponding 2-D numerical simulations obtained by activating the nonlocal tunneling model with Fermi–Dirac statistics and the cubic III–V interpolation model. Note that the model was calibrated to cover a wide range of material configurations and parameters by applying a particular branch point position and tunneling probability coefficient for each tunneling region. Also, a relative error arises from the multiple assumptions in the potential model and tunneling probability expressions. In addition, simulations show that the electron and hole quasi-Fermi levels, particularly near the heterojunction interface, differ slightly from the assumed values (i.e., −V_d and −V_s). Consequently, the tunneling current is overestimated due to a larger occupancy factor.

By analyzing the source doping effect, Fig. 7 shows that an increase of the doping concentration moves the tunneling onset to lower gate voltages. This effect is common to all materials configurations and is a consequence of the elevation of the valence band of the source. Nevertheless, a very high degeneracy, i.e., E_vs − E_fs≫ 3KT, causes the tunneling onset to lie in energy states with a lower occupation factor. The variation of the current with respect to the gate voltage is therefore reduced, degrading the subthreshold slope [6].

Fig. 7

The transfer characteristic of a GaSb–InAs and b AlSb–InAs heterojunction TFETs for different source doping levels for V_ds = 1 V

The case of the GaSb–InAs heterojunction perfectly illustrates this effect (Fig. 7a), where a low doping level is preferable if a steep subthreshold slope and high current are desired. However, this performance is limited to a certain gate voltage interval. Considering also the ambipolar current, it is clear that low source doping can be advantageous only for small supplies. On the other hand, a moderate doping level of 5 × 10¹⁹ cm⁻³ offers a better compromise between the subthreshold slope and on-current.

In the case of straddled alignment, as in AlSb–InAs, the behavior is totally different. Indeed, it is observed that the tunneling current is then proportional to the source doping while the subthreshold slope remains unaffected for either high or moderate concentrations. This can be explained by the predominant contribution of the tunneling in the channel (T₄) to the total current (Fig. 6b). Also, such low doping depicts the case where the valence band lies below the Fermi level, leading to a narrowing of the tunneling window and a drastic degradation of the current.

Regarding the impact of the source material definition, it is observed that the broken-gap heterostructure provides the highest current with an almost 50 % increase in comparison with the straddled-gap heterostructure (Fig. 7). This is a direct consequence of the tunneling probability enhancement with a peak that approaches 1 in the first tunneling region (Fig. 8b). Nevertheless, this high tunneling probability, being located in states with low occupation, is attenuated. In such a case, use of a lower source doping shifts this peak to states with higher occupation, which explains the improvement observed in Fig. 7a.

Fig. 8

a The energy band diagram and b tunneling probability distribution over the tunneling window of a broken-gap GaSb–InAs heterojunction TFET with N_AS = 10²⁰ cm⁻³, V_gs = 1 V, and V_ds = 0.75 V

Also, the broken-gap alignment (as in GaSb–InAs) presents an energy region where the conduction and valence band discontinuities overlap (Fig. 8). Named a notch potential [3, 28], this region has a zero band-to-band tunneling probability, denoted as T_no. Nevertheless, for nonconfined systems, as in the present study, the combination of the high three-dimensional (3-D) density of states in the notch potential, even with a small scattering rate, results in a substantial off-state current while the subthreshold slope easily surpasses 60 mV/dec [3]. Because the actual model includes the ambipolar current, it can be assumed that it greatly exceeds the notch potential current, even for low drain supplies (I_off = 58 nA at V_ds = 0.2 V for GaAs–InAs). Thus, the notch potential current can be neglected.

For the nearly broken- and staggered-gap alignments, such as for GaAs_0.5Sb_0.5–InAs in Fig. 5, or GaSb–In_0.6Ga_0.4As and GaAs_0.5Sb_0.5–In_0.6Ga_0.4As in Fig. 9, the four tunneling regions are operational, with high tunneling probability. However, this tunneling probability and hence the current decrease with an increase of the As molar fraction as a consequence of the widening of the bandgap and the enhancement of the effective masses of the carriers. The tunneling current decreases further when moving towards a straddled-gap configuration. Besides the degradation of the tunneling probability (Fig. 6b), the current composition is reduced from four to two or three components, with predominance of the fourth one (T₄) (depending on the band alignment, the onset of the first component occurs for high gate biases and is generally negligible). This component yields the weakest tunneling probability and is further attenuated by the large valance band discontinuity, which acts to reduce further the drift of carriers from the source to channel. Also, Fig. 9 shows that the off-current increases as a consequence of the enhancement of the source tunneling current. On the other hand, the subthreshold slope is barely affected by the band alignment, as SS_min values of 67.66 and 66.38 mV/dec are obtained for As molar fractions of 0 and 1.

Fig. 9

The transfer characteristic of GaAs_ySb_1−y–In_0.6Ga_0.4As with different As molar fractions for N_AS = 10²⁰ cm⁻³ and V_ds = 1 V

The impact of the channel and drain material definition is depicted in Fig. 10. As expected, an inverse proportionality between the total current and the material bandgap is observed. Besides the decrease of the tunneling probability (longer tunneling distance and increased effective masses), a larger bandgap leads to a reduction of the heterojunction band discontinuity, and in the case of a staggered gap, to a tightening of the tunneling window of the first and third current components. Moreover, increasing the bandgap improves the subthreshold slope by reducing the ambipolar current. A SS_min value of 18.55 mV/dec is obtained for Ga molar fraction of 0.8 (E_g = 1.13 eV), while 66.44 mV/dec is found for a fraction of 0.4 (E_g = 0.67 eV). Furthermore, it is observed that materials with a low intrinsic density of states and to a lesser extent low permittivity can prolong the gate modulation to higher voltages. Therefore, thinner tunneling junctions can be formed with respect to the gate voltage variation, which ultimately yields smaller average subthreshold slopes; For instance, the average subthreshold slope, defined here as SS_avg = V_ds/[log₁₀(I_on/I_min)], takes values of 293.57 and 96.92 mV/dec for Ga molar fraction of 0.4 and 0.8, respectively, at V_ds = 1 V.

Fig. 10

Transfer characteristic of GaAs–In_1−xGa_xAs for different Ga molar fractions for N_AS = 10²⁰ cm⁻³ and V_ds = 1 V

Another approach to reduce the ambipolar current is simply to decrease the drain supply, as showcased in Fig. 11. By doing so, the tunneling window in the drain side is narrowed while the barrier is enlarged. Nevertheless, the gate modulation interval is also reduced, which attenuates the source tunneling current for higher gate voltages. This attenuation can vary in importance depending on the material properties. The combination of low drain voltage and narrow-bandgap materials reduces the gate modulation interval to less than 1 V. The current drop in such cases can exceed 50 %.

Fig. 11

Transfer characteristic of GaAs–In_0.4Ga_0.6As for different drain supplies with N_AS = 10²⁰ cm⁻³

A classic output characteristic of a TFET in the three operating regions is shown in Fig. 12. In comparison with conventional metal–oxide–semiconductor field-effect transistors (MOSFETs), the device operation on drain modulation is equivalent to the ohmic region. The current in the heterojunction TFET evolves with either a superlinear or sublinear slope, resulting in a variable on-resistance. This slope depends essentially on the type of alignment in the heterostructure and the source doping, such that they provide a high tunneling probability at highly occupied states. Note also that the disparity between the modeling and numerical results is a consequence of the channel potential solution, which is based on Boltzmann statistics.

Fig. 12

Output characteristic of GaAs–In_0.6Ga_0.4As for different gate voltages for N_AS = 10²⁰ cm⁻³

Likewise, the gate modulation that corresponds to the saturation region exhibits a very low output conductance, which is ideal for gain enhancement. On the other hand, the ambipolar conduction that behaves as a breakdown limits the device supply to very low values in comparison with conventional MOSFETs. This figure also depicts the delayed saturation that yields some issues for digital or analog applications (degradation of the noise margin and gain). An attenuation of the delayed saturation and ambipolar current is possible by enlarging the channel and drain bandgaps, at the expense of the saturation current.

Thus, the device material definitions can be used as a powerful tool to meet or even surpass actual and future technology requirements for low-power or high-performance applications. However, note that these results, especially the high on-current values, were obtained without considering mobility degradation or contact resistance limitations. Nevertheless, most III–V compounds are characterized by high mobility. Thus, the transport limitation of the channel should not be very important. Moreover, the lattice mismatch at the heterojunction interface is neglected. The resulting highly defective interface yields a substantial leakage current by means of trap-assisted tunneling and Shockley–Read–Hall generation, resulting in a much higher off-state current and subthreshold slope [5, 29]. Likewise, an interfacial layer might result from abrupt heterostructure formation, altering the band alignment and further degrading the device performance; indeed, formation of such a GaAs_0.022Sb_0.978 layer at the GaSb–InAs interface was reported in Ref. [30]. Furthermore, although Anderson’s rule applies well to abrupt heterojunctions in theory (especially in depletion [31]), many studies have demonstrated the oversimplification of the rule. Indeed, experimental measures of the band offset show variable and nonnegligible disparities with this model. The combination of the affinity rule and transport model error can reach critical levels. The case of a heterodiode confirms the limitation of the model, revealing a large disagreement between Anderson’s model and the experimental results in both quantitative and qualitative terms [27]. Therefore, the same conclusion can be transposed to the heterojunction TFET, particularly when considering the sensitivity of the tunneling current to the electrostatic distribution and the impact of charge dipole creation on the latter. Hence, a more realistic analysis of the device should be based on the experimental band alignment with an acceptable lattice mismatch.

5 Capacitance model

Device capacitances are essential to assess the performance in both analog and digital applications. Interest in this issue is more pronounced in the case of TFETs, as measurements and simulations have highlighted the large contribution of C_gd to the total gate capacitance and the resulting enhanced Miller effect [32]. However, the classical capacitance definitions for a MOSFET are no longer applicable, so proper expressions should be developed. Recall the general definition of capacitance:

$$ C_{ij} = \frac{{\partial Q_{i} }}{{\partial V_{j} }}, $$

(42)

where Q_i and V_j are the charge and potential associated with terminals i and j, respectively. As proposed in Ref. [33], the gate charge Q_g is composed of the channel inversion charge Q_c and an additional charge Q_if induced by the inner fringing fields from the drain junction. The former component is defined by the charge at the channel interface as

$$ Q_{\text{c}} = 2\pi aL^{\prime } C_{\text{ox}} \left( {V_{\text{g}}^{*} - V_{\text{c}} } \right), $$

(43)

where $L^{\prime } = L - \frac{1}{{\lambda_{\text{c}} }}\log \left( {\frac{{ - E_{\text{gc}} }}{{V_{\text{ps}}^{*} - V_{\text{c}} }}} \right)$; L′ accounts for the active channel length, i.e., without penetration of the tunneling junction into the channel. The penetration is defined as the distance at which the lateral electric field drops to a characteristic electric field that equals λ_c × E_gc. The inner fringing charge on the other hand can be expressed as

$$ Q_{\text{if}} = {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}\pi a^{2} \varepsilon_{\text{c}} E_{{{\text{pd}}\parallel }} (a). $$

(44)

The internal drain-to-gate capacitance $C_{\text{gd}}^{\prime }$ can now be obtained by differentiating the gate charge with respect to the drain voltage. This capacitance is placed in series with the active gate oxide capacitance as

$$ \begin{aligned} C_{\text{gd}} & = C_{\text{ox}}^{\prime } C_{\text{gd}}^{\prime } /\left( {C_{\text{ox}}^{\prime } + C_{\text{gd}}^{\prime } } \right) \\ & \quad {\text{where}}\quad C_{\text{ox}}^{\prime } = 2\pi aL^{\prime } C_{\text{ox}}. \\ \end{aligned} $$

(45)

As illustrated in Fig. 13, the proposed capacitance model offers an acceptable fit with the numerical results and thus for a large gate bias interval. As for the tunneling current during drain modulation, the error induced by the use of Boltzmann statistics in the derivation of the expression for the channel potential impacts on the inversion and inner fringing field charges. Similarly to the current, the use of the correction expression attenuates this error. Nevertheless, this model is sufficient to evaluate the capacitance in our range of interest. This figure also illustrates the impact of the channel material on the capacitance. It is observed that narrowing of the bandgap shifts the capacitance characteristic toward lower gate biases as a result of premature inversion charge formation. Moreover, a higher electric field arises at the drain junction interface, which slightly improves the inner fringing charge capacitance. Considering the importance of the gate-to-drain capacitance for both digital and analog circuits, the choice of the channel material is crucial for performance improvement.

Fig. 13

C_gd for a GaAs–In_x−1Ga_xAs heterojunction TFET for different molar fractions with N_AS = 10²⁰ cm⁻³ and V_ds = 1 V

The remaining device charge corresponds to the depletion charge of the source region. Using the expression for the potential to evaluate the depletion width, this charge is given by

$$ Q_{\text{s}} = q\pi a^{2} N_{\text{AS}} \left( {\frac{{\lambda_{\text{s}}^{*} t_{\text{ox}} }}{{4N_{\text{s}} }}} \right)\log \left( {\frac{{V_{\text{biS}} }}{{V_{\text{biS}} - V_{\text{ps}} }}} \right). $$

(4.46)

Differentiation of this charge with respect to the source potential gives the source capacitance. Also, an additional value of approximately 1 aF, which could correspond to the outer fringing capacitance, was found to be necessary to match the numerical results. Nonetheless, this definition of the capacitance is valid only when the source tunneling junction is active, as depicted in Fig. 14. In this case, the total channel charge is coupled to the drain terminal. For lower gate voltages and the ambipolar state, the channel charge is transferred to the source terminal. Hence, the definition of C_gd is transposed to the source junction. It is also observed that the composition of the channel material slightly affects the source capacitance by modifying the junction boundary potential and, by extension, the depletion charge. This attenuation effect is more pronounced for a lower Ga mole fraction, i.e., narrower bandgap, larger valence band discontinuity, and reduced gate modulation interval. Nevertheless, the variation of C_gs in the on-state is minor with respect to C_gd.

Fig. 14

C_gs for the GaAs–In_x−1Ga_xAs heterojunction TFET for different molar fractions with N_AS = 10²⁰ cm⁻³ and V_ds = 1 V

6 Conclusions

A new semianalytical model for an undoped heterojunction VSG TFET is developed, adopting an appropriate exponential approximation for the channel 2-D potential that is valid for long channels. Expressions for the junction potentials are derived based on both Fermi–Dirac and Boltzmann statistics to take into consideration the degeneracy in the extensions. Using the conformal representation technique, suitable expressions for the source and drain extensions and surface potential including the fringing field effect are developed. The band alignment in the heterostructure is computed using the affinity rule. The exponential potential profile over the whole device allows analytical integration of the tunneling probability using the WKB approximation. Adopting this nonlocal approach, a reasonable estimation of the tunneling current is obtained using an appropriate set of wavevectors and tunneling region contributions. The model is validated and calibrated against 2-D numerical simulations. The discussion showcases the tremendous possibilities provided by different material compositions and doping, which will enable enhancement of particular device features or an ensemble of performance parameters. The demonstrated validity of the model for a wide range of device material definitions and supplies will provide further insight into the physics occurring in heterojunction TFETs.