Normal edge-transitive Cayley graphs of Frobenius groups

Abstract

A Cayley graph for a group G is called normal edge-transitive if it admits an edge-transitive action of some subgroup of the holomorph of G [the normaliser of a regular copy of G in ${{\mathrm{Sym}}}(G)$]. We complete the classification of normal edge-transitive Cayley graphs of order a product of two primes by dealing with Cayley graphs for Frobenius groups of such orders. We determine the automorphism groups of these graphs, proving in particular that there is a unique vertex-primitive example, namely the flag graph of the Fano plane.

1 Introduction

Normal edge-transitive Cayley graphs were identified by the second author [1] in 1999 as a family of central importance for understanding Cayley graphs in general. Such graphs have an edge-transitive subgroup of automorphisms which normalises a copy of the group used to construct the Cayley graph. Moreover each normal edge-transitive Cayley graph was shown to have, as a ‘normal quotient’, a normal edge-transitive Cayley graph for a characteristically simple group. This raised the question of reconstructing normal edge-transitive Cayley graphs from a given normal quotient. In this paper we answer the question in the smallest case, where the normal quotient has prime order q and the group G of interest has order pq, where p also is prime.

Several cases for ‘small graphs’ of this type have been investigated. The case for groups of prime order was solved in [1] (see Example 2.1 below), and the case for abelian groups G of order pq was treated in the MSc thesis of Houlis [2]. After submitting this paper we were made aware that the normal edge-transitive Cayley graphs with 4p vertices, for p a prime, were classified by Darafsheh and Assari [3]. In this paper we complete the nonabelian case for |G| a product of two primes.

Theorem 1.1

Let $G_{pq}$ be a Frobenius group of order pq, where p and q are primes and $q<p$, and let $\varGamma$ be a connected normal edge-transitive Cayley graph for $G_{pq}$ and $Y={{\mathrm{Aut\,}}}\varGamma$. Then one of the following holds:

• (i) $\varGamma \cong C_q[\overline{K_p}]$, with $Y\cong S_p{{\mathrm{wr}}}D_{2q}, {{\mathrm{val}}}\varGamma = 2p$ if q is odd, and $Y\cong S_p {{\mathrm{wr}}}S_2, {{\mathrm{val}}}\varGamma = p$ if $q=2$;

• (ii) $\varGamma \cong K_p \times C_q$, with $Y\cong S_p \times D_{2q}, {{\mathrm{val}}}\varGamma = 2(p-1)$ if q is odd; or $K_p \times K_2$ with $Y = S_p\times \mathbb {Z}_{2}, {{\mathrm{val}}}\varGamma = p-1$ if $q=2$; or

• (iii) $\varGamma =\varGamma (pq,\ell ,i)$ as defined in Construction 2, for some proper divisor $\ell$ of $p-1$ with $\ell >1$, and either $(q,i)=(2,1)$ or $1\le i \le (q-1)/2$, and either

  $$\begin{aligned} Y\cong {\left\{ \begin{array}{ll} G_{pq}.\mathbb {Z}_{\ell } &{} \text { when } q=2 \text { or } q \not \mid \ell , \\ G_{pq}.\mathbb {Z}_{\ell }.\mathbb {Z}_{2} &{} \text { when } q\ge 3, q \mid \ell , \end{array}\right. } \end{aligned}$$

  with ${{\mathrm{val}}}\varGamma = 2\ell /\gcd (q,2)$; or $pq,\ell ,i, {{\mathrm{val}}}\varGamma , Y$ are as in one of the lines of Table 1.

In Table 1 and throughout, ${{\mathrm{val}}}\varGamma$ denotes the valency of $\varGamma$. Figures 1, 2 show examples arising from Constructions 1, 2 respectively, while Fig. 3 depicts a second graph from Construction 1 having the same number of vertices and the same valency as the graph in Fig. 1. The restriction to connected graphs is allowable as discussed in [1, p. 213, Remark 1]. Every Cayley graph $\varGamma ={{\mathrm{Cay\,}}}(G,S)$ admits as a subgroup of automorphisms the group $N :=\rho (G)\rtimes {{\mathrm{Aut\,}}}(G)_S$, where $\rho (G)$ is the group of right multiplication maps $\rho _g : x\mapsto xg$ (for $g\in G$) and ${{\mathrm{Aut\,}}}(G)_S$ is the setwise stabiliser in ${{\mathrm{Aut\,}}}(G)$ of S. The group N is the normaliser of $\rho (G)$ in ${{\mathrm{Aut\,}}}\varGamma$ (see for example [1, pp. 6–7]): if N is the full automorphism group then $\rho (G)$ is normal in ${{\mathrm{Aut\,}}}\varGamma$ and $\varGamma$ is called a normal Cayley graph. In Theorem 1.1 (iii), if $q\ge 3$ and $q\mid \ell$, then the group $G_{pq}$ is not normal in Y. Thus we have the following immediate corollary.

Table 1 Exceptional normal edge-transitive Cayley graphs for $G_{pq}$

Fig. 1

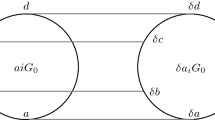
The graph $\varGamma (55,2,1)$ as in Construction 1

Fig. 2

The flag graph of the Fano plane [$\varGamma (7.3, 2,1)$ in the language of Construction 2]: the only vertex-primitive graph in the classification

Fig. 3

The graph $\varGamma (55,2,2)$ as in Construction 1

Corollary 1.1

Let $\varGamma$ be a connected normal edge-transitive Cayley graph for $G_{pq}$ as in Theorem 1.1. Then $\varGamma$ is a normal Cayley graph if and only if $\varGamma =\varGamma (pq,\ell ,i)$, for $q=2$, or $q\not \mid \ell$ as in Theorem 1.1 (iii), and $(pq,\ell ,i)$ are not as in Table 1.

Remark 1.1

• (i) There is a unique vertex-primitive, normal edge-transitive Cayley graph of a Frobenius group $G_{pq}$ of order pq, namely $\varGamma (7\times 3,2,1)$ as defined in Construction 2, and it is isomorphic to the flag graph of the Fano Plane (see Fig. 2; Proposition 4.1). The other three graphs in Table 1 are incidence graphs of the (11, 5, 2)-biplane, and the projective planes ${{\mathrm{PG}}}(2,2)$ and ${{\mathrm{PG}}}(2,8)$.

• (ii) If $q\mid \ell$ then $\varGamma (pq,\ell ,i)$ is a Cayley graph for $\mathbb {Z}_{p}\times \mathbb {Z}_{q}$ as well as a Cayley graph for $G_{pq}$ (see Proposition 3.1).

• (iii) The graphs $\varGamma (pq,\ell ,i)$ in Theorem 1.1 are arc-transitive if and only if $q=2$ or $q\mid \ell$. If q is odd and $q\not \mid \ell$ then apart from the exceptions in Table 1, $\varGamma (pq,\ell ,i)$ is edge-regular (often called half-arc-transitive in the literature).

• (iv) The normal edge-transitive Cayley graphs of order a product of two primes are now classified: they are the examples given in Theorem 1.1 (for $G_{pq}$), and those for abelian groups described in Sects. 3.1 and 3.3 (as originally given by Houlis [2]).

Section 2 presents essential results about permutation groups and the structure of normal edge-transitive Cayley graphs, and outlines the strategy for classification. In Sect. 3 we summarise Houlis’ classification of normal edge-transitive Cayley graphs for abelian groups of order a product of two primes (since his results are not published) and we classify the normal edge-transitive Cayley graphs for $G_{pq}$. In Sect. 4 we resolve questions of redundancy in our classification and determine the full automorphism groups of the graphs obtained.

2 Background and examples

For a subset S of a group G such that $1_G\notin S$ and S contains $s^{-1}$ for every $s\in S$, the Cayley graph $\varGamma ={{\mathrm{Cay\,}}}(G,S)$ has vertex set ${{\mathrm{V\Gamma }}}=G$, and edges the pairs $\{x,y\}$ for which $yx^{-1}\in S$. Each such graph admits the group $\rho (G)\cong G$, acting by right multiplication $\rho (g):x\mapsto xg$, as a subgroup of the automorphism group ${{\mathrm{Aut\,}}}\varGamma$, and $\varGamma$ is called normal edge-transitive if $N_{{{\mathrm{Aut\,}}}\varGamma }(\rho (G))$ (which is $\rho (G) \rtimes {{\mathrm{Aut\,}}}(G)_S$) is transitive on the edges of $\varGamma$ (see Sect. 2.1 or [1]).

Remark 2.1

Normal edge-transitivity is a property that depends upon the group G as well as the graph $\varGamma$. For example, for any group G, the graph ${{\mathrm{Cay\,}}}(G,G \setminus \{1\}) \cong K_{|G|}$ is always edge-transitive, but its normal edge-transitivity is not guaranteed.

Given a graph $\varGamma$ and a partition ${\fancyscript{P}}$ of the vertex set ${{\mathrm{V\Gamma }}}$, the quotient graph $\varGamma _{{\fancyscript{P}}}$ has vertex set ${\fancyscript{P}}$, with two blocks $B,B'$ adjacent if there exists a pair of adjacent vertices $\alpha , \alpha '\in {{\mathrm{V\Gamma }}}$ with $\alpha \in B$ and $\alpha '\in B'$. For an edge-transitive subgroup $A=\rho (G).A_0$ of $\rho (G).{{\mathrm{Aut\,}}}(G)_S$, a normal quotient of the Cayley graph $\varGamma ={{\mathrm{Cay\,}}}(G,S)$ is a quotient $\varGamma _{{\fancyscript{P}}}$, where ${\fancyscript{P}}$ is the set of orbits of an $A_0$-invariant normal subgroup M of G and is equal to ${{\mathrm{Cay\,}}}(G/M,SM/M)$ (see [1, Theorem 3]); we denote this quotient by $\varGamma _M$. The quotient $\varGamma _M$ admits an (unfaithful) normal edge-transitive action of A, with kernel $\rho (M).C_{A_0}(G/M)$. In particular each proper characteristic subgroup M of G is $A_0$-invariant, yielding a nontrivial normal quotient $\varGamma _M$ of $\varGamma$ which is a normal edge-transitive Cayley graph. The graph $\varGamma$ is called a normal multicover of $\varGamma _M$, since there is a constant k such that, for adjacent blocks $B, B'$ of $\varGamma _M$ each $\alpha \in B$ is adjacent in Gamma to exactly k vertices of $B'$.

The ‘basic’ members of the class of finite normal edge-transitive Cayley graphs were thus identified in [1] as Cayley graphs for characteristically simple groups H relative to a subgroup $A_0$ of ${{\mathrm{Aut\,}}}(H)$, leaving invariant no proper nontrivial normal subgroups of H.

To investigate the basic normal edge-transitive Cayley graphs, a natural starting point is $G=\mathbb {Z}_{q}$, with q a prime; normal edge-transitive Cayley graphs for these groups were described in [1, Example 2]. The result follows easily from Chao’s classification of symmetric (i.e. arc-transitive) graphs on q vertices [4]. The basic graphs are circulants (essentially, edge-unions of cycles). We discuss this case in more detail in Sect. 2.1.

With the simplest case complete, we look for multicovers of these most basic cases, but again we seek to identify a kind of ‘basic’ reconstruction. Suppose that $\varGamma ={{\mathrm{Cay\,}}}(G,S)$ is normal edge-transitive relative to $A=\rho (G)A_0$, where $A_0\leqslant {{\mathrm{Aut\,}}}(G)_S$, and that $\varGamma$ is a normal multicover of $\varGamma _N$, where N is an $A_0$-invariant normal subgroup of G. We say $\varGamma$ is a minimal normal multicover of $\varGamma _N$ relative to A if there is no way to get to $\varGamma _N$ in more than one step from $\varGamma$: that is, there is no $A_0$-invariant nontrivial normal subgroup of G properly contained in N.

Again we see that the smallest case is when the index |G : N| is prime, and G has order a product of two primes p, q. The groups G to consider are the abelian groups $\mathbb {Z}_{q^2}$ (with $p=q$) and $\mathbb {Z}_{p}\times \mathbb {Z}_{q}$, and the nonabelian Frobenius group $G_{pq}$, when $p\equiv 1 \pmod {q}$. The classification in the abelian cases was completed by Houlis in his MSc Thesis [2]. The classification in the final (nonabelian) case is completed in this paper, and since his thesis remains unpublished we also summarise Houlis’ results (see Sect. 3.1).

Our classification result for these minimal normal multicovers (which we prove in Sect. 3.3) is the following.

Proposition 2.1

Let $\varGamma$ be a connected normal edge-transitive Cayley graph for $G_{pq}$, where p, q are primes and q divides $p-1$. Let T be the Sylow p-subgroup of $G_{pq}$. Then $\varGamma$ is a normal multicover of $\varGamma _T\cong K_2$ if $q=2$ or $\varGamma _T\cong C_q$ if q is odd, and $\varGamma$ is one of the graphs listed in Theorem 1.1.

Remark 2.2

The automorphism groups of all connected normal edge-transitive Cayley graphs for $G_{pq}$ are determined in Proposition 4.1 and Theorem 4.1.

2.1 Normal edge-transitive Cayley graphs

Recall that $\rho (G)$ is the subgroup of ${{\mathrm{Sym}}}G$ consisting of all permutations $\rho (g): x\mapsto xg$ for $g\in G$, and that $N:=N_{{{\mathrm{Aut\,}}}\varGamma }(\rho (G))$ is $\rho (G).{{\mathrm{Aut\,}}}(G)_S$. Note that for normal edge-transitivity N need only be transitive on undirected edges, and may or may not be transitive on arcs (ordered pairs of adjacent vertices). Normal edge-transitivity can be described group-theoretically as follows. For $g\in G$ and $H\leqslant {{\mathrm{Aut\,}}}G$ we denote by $g^H=\{g^h\mid h\in H\}$ the H-orbit of g, and we write $g^{-H}=(g^{-1})^H$.

Lemma 2.1

([1], Proposition 1(c)) Let $\varGamma ={{\mathrm{Cay\,}}}(G,S)$ be an undirected Cayley graph with $S\ne \emptyset$, and $N=\rho (G).{{\mathrm{Aut\,}}}(G)_S$. Then the following are equivalent:

• (i) $\varGamma$ is normal edge-transitive;

• (ii) The set $S=T \cup T^{-1}$, where T is an ${{\mathrm{Aut\,}}}(G)_S$-orbit in G;

• (iii) There exists $H\leqslant {{\mathrm{Aut\,}}}(G)$ and $g\in G$ such that $S=g^H \cup g^{-H}$.

Moreover $\rho (G).{{\mathrm{Aut\,}}}(G)_S$ is transitive on the arcs of $\varGamma$ if and only if ${{\mathrm{Aut\,}}}(G)_S$ is transitive on S.

Hence every normal edge-transitive Cayley graph for a group G is determined by a (nonidentity) group element g and a subgroup H of ${{\mathrm{Aut\,}}}G$. This motivates the following definition:

Definition 2.1

For a group G, $g\in G\setminus \{1\}$ and $H\leqslant {{\mathrm{Aut\,}}}G$, define the normal edge-transitive Cayley graph

$$\begin{aligned} \varGamma (G,H,g):={{\mathrm{Cay\,}}}(G, g^{H} \cup g^{-H}). \end{aligned}$$

2.1.1 Use of symmetry in the analysis

A classification of normal edge-transitive Cayley graphs for a given group G is reduced to the study of the action of subgroups of ${{\mathrm{Aut\,}}}G$ on G. We employ this strategy in Sect. 4. For efficiency we use the following result to avoid producing too many copies of each example.

Lemma 2.2

Let $\sigma \in {{\mathrm{Aut\,}}}G$. Then $\sigma$ induces an automorphism from $\varGamma (G,H,g)$ to $\varGamma (G,H^{\sigma },g^{\sigma })$. In particular if $\sigma \in N_{{{\mathrm{Aut\,}}}G}(H)$, then $\varGamma (G,H,g)\cong \varGamma (G,H,g^{\sigma })$.

Proof

For any $x, y\in G$ we have $xy^{-1} \in S$ if and only if $x^{\sigma }(y^{\sigma })^{-1}=(xy^{-1})^{\sigma }\in S^{\sigma }$, and so $\{x,y\}\in {{\mathrm{E\Gamma }}}$ if and only if $\{x^{\sigma },y^{\sigma }\}\in {{\mathrm{E\Gamma }}}'$. $\square$

In particular for a given subgroup H, two elements of the same orbit in the action of $N_{{{\mathrm{Aut\,}}}G}(H)$ on H-orbits in G generate isomorphic graphs, and so we need only consider a single representative H-orbit from each $N_{{{\mathrm{Aut\,}}}G}(H)$-orbit.

2.2 Examples and constructions

First we describe how Lemma 2.2 can be used to classify all normal edge-transitive Cayley graphs of prime order p.

Example 2.1

Let G be the additive group of the ring $\mathbb {Z}_{p}$ of integers modulo a prime p, and ${{\mathrm{Aut\,}}}(G)=\mathbb {Z}_{p}^{*}= \langle m \rangle$, the multiplicative group of units, where m is a primitive element. For every even divisor $\ell$ of $p-1$, and for $\ell =1$ if $p=2$, there is a unique subgroup of ${{\mathrm{Aut\,}}}(G)$ of order $\ell$, namely

$$\begin{aligned} H_{\ell }:= \langle m^{(p-1)/\ell } \rangle . \end{aligned}$$

(2.1)

The graph $\varGamma (p,\ell ):=\varGamma (G, H_{\ell },1)$ is normal edge-transitive of valency $\ell$ and since ${{\mathrm{Aut\,}}}(G)$ normalises $H_{\ell }$ and is transitive on the $H_{\ell }$-orbits in $G\setminus \{0\}$, it follows from Lemma 2.2 that every normal edge-transitive Cayley graph for G is isomorphic to $\varGamma (p,\ell )$ for some $\ell$.

The notion of a product of two graphs may be defined in several ways: we present two here, each of which arises in our study (see Construction 1 and Lemma 3.3).

Definition 2.2

Given graphs $\varSigma , \varDelta$, the direct product $\varGamma =\varSigma \times \varDelta$ has vertex set ${{\mathrm{V\Sigma }}}\times {{\mathrm{V\Delta }}}$, with vertices $(\alpha _1, \beta _1), (\alpha _2, \beta _2)$ adjacent if both $\alpha _1$ is adjacent to $\alpha _2$ and $\beta _1$ is adjacent to $\beta _2$.

The direct product $\varSigma \times \varDelta$ is so named because the direct product ${{\mathrm{Aut\,}}}\varSigma \times {{\mathrm{Aut\,}}}\varDelta$ is contained in ${{\mathrm{Aut\,}}}(\varSigma \times \varDelta )$.

Definition 2.3

Given graphs $\varSigma , \varDelta$, the lexicographic product $\varGamma =\varSigma [\varDelta ]$ has vertex set ${{\mathrm{V\Sigma }}}\times {{\mathrm{V\Delta }}}$, with vertices $(\alpha _1, \beta _1), (\alpha _2, \beta _2)$ adjacent if either $\{\alpha _1 , \alpha _2\}\in {{\mathrm{E\Sigma }}}$, or both $\alpha _1=\alpha _2$ and $\{\beta _1 , \beta _2\}\in {{\mathrm{E\Delta }}}$.

If both $\varSigma$ and $\varDelta$ are regular, then their lexicographic product is regular with valency ${{\mathrm{val}}}\varDelta + |{{\mathrm{V\Delta }}}| {{\mathrm{val}}}\varSigma$. The lexicographic product has $({{\mathrm{Aut\,}}}\varDelta ){{\mathrm{wr}}}({{\mathrm{Aut\,}}}\varSigma )$ as a subgroup of automorphisms (which may be a proper subgroup: for example if $\varDelta =\varSigma =K_2$ then $\varGamma =\varSigma [\varDelta ]=K_4$ and $({{\mathrm{Aut\,}}}\varDelta ){{\mathrm{wr}}}({{\mathrm{Aut\,}}}\varSigma )=D_8 < S_4= {{\mathrm{Aut\,}}}K_4$).

The following result determines a sufficient condition for a Cayley graph to have a decomposition as a lexicographic product. If $\varGamma ={{\mathrm{Cay\,}}}(G,S)$ and $M \unlhd G$, then the normal quotient $\varGamma _M$ of $\varGamma$ is ${{\mathrm{Cay\,}}}(G/M, SM/M)$ (see [1, Theorem 3(b)]). For a graph $\varGamma$ and vertex $\alpha$ we denote by $\varGamma (\alpha )$ the set of vertices adjacent to $\alpha$ in $\varGamma$. Note that, in $\varGamma =\varGamma (G,H,g)$ we have $\varGamma (g)=Sg$, where $S=g^H\cup g^{-H}$.

Proposition 2.2

Let G be a group, M a normal subgroup with $m=|M|$, and let $\varGamma ={{\mathrm{Cay\,}}}(G,S)$ be a connected Cayley graph for G. Then $\varGamma \cong \varGamma _M[\overline{K_{m}}]$ if and only if S is a union of cosets of M.

Proof

Since $\varGamma _M={{\mathrm{Cay\,}}}(G/M,SM/M)$, by Definition 2.3 it follows that $\varGamma \cong \varGamma _M[\overline{K_{m}}]$ if and only if $\varGamma (1_G)=S$ is equal to SM, that is to say, S is a union of M-cosets. $\square$

Remark 2.3

If the graph $\varGamma$ in Proposition 2.2 is normal edge-transitive relative to $N\leqslant N_{{{\mathrm{Aut\,}}}\varGamma }(\rho (G))$, and if N normalises M, then $\varGamma _M$ is also normal edge-transitive, as it is a normal quotient of $\varGamma$ (see [1, Theorem 3]).

2.3 Permutation groups and group actions

We use the basic definitions and notation found in [5], and we assume G is a finite group acting on a set $\varOmega$. We denote by $\rho , \lambda ,\iota$, respectively, the right, left and conjugation actions of G on itself. We use extensively the following well-known result. The first assertions are due to Burnside, see [6, p. 1].

Proposition 2.3

Let G be a transitive permutation group of prime degree p. Then G is primitive, and either $G\leqslant {{\mathrm{AGL\,}}}(1,p)$, or G is almost simple and 2-transitive with socle T, where p, T and the Schur multiplier of T are as in one of the lines of Table 2.

The socle T of an almost simple group G is its unique minimal normal subgroup (which is a nonabelian simple group). The possibilities for p and T can be obtained from, for example, Cameron [6, Table 7.4]. Their classification depends on the finite simple group classification. The Schur multiplier M(T) is obtained from [7, Section 8.4].

Table 2 Simple normal subgroups T and Schur multipliers M(T) of almost simple 2-transitive groups of prime degree p

Our analysis in Sect. 4 deals, for the most part, with imprimitive groups. Given a transitive group G and a nontrivial system of imprimitivity ${\fancyscript{B}}$, the group G acts transitively on the set of blocks, inducing a subgroup $G^{{\fancyscript{B}}}$ of ${{\mathrm{Sym}}}{\fancyscript{B}}$. The setwise stabiliser $G_B$ of a block $B\in {\fancyscript{B}}$ in this action induces a transitive subgroup $G_B^B$ of ${{\mathrm{Sym}}}B$. These two actions play an important role in the structure of G; in particular for distinct blocks $B,B'\in {\fancyscript{B}}$ the induced groups $G_B^B$ and $G_{B'}^{B'}$ are permutationally isomorphic.

The kernel $K=G_{({\fancyscript{B}})}$ of the G-action on ${\fancyscript{B}}$ acts on each block $B\in {\fancyscript{B}}$. We say that the K-actions on B and $B'$ are equivalent if there exists a bijection $\varphi :B\rightarrow B'$ such that for every $\alpha \in B, k\in K$, we have $(\alpha ^{\varphi })^k=(\alpha ^k)^{\varphi }$. The following fact is useful; the proof is straightforward and omitted.

Lemma 2.3

Let ${\fancyscript{B}}=\{ B_1, B_2, \ldots , B_k\}$. Then the set $\varSigma :=\{ B_i \mid K^{B_i}\text { is}$ $\text {equivalent to }K^{B_1}\}$ is a block of imprimitivity for the action of G on ${\fancyscript{B}}$. In particular if G is primitive then $\varSigma = {\fancyscript{B}}$ or $\varSigma = \{{\fancyscript{B}}\}$.

3 The classification

3.1 The abelian case

In [2], Houlis classified the normal edge-transitive Cayley graphs for the groups $\mathbb {Z}_{p^2}, \mathbb {Z}_{p}\times \mathbb {Z}_{p}$ and $\mathbb {Z}_{p}\times \mathbb {Z}_{q}$, for primes p, q.

Recall from Proposition 2.1 and Definition 2.1 that every normal edge-transitive Cayley graph for a group G is equal to $\varGamma (G,H,g)={{\mathrm{Cay\,}}}(G, g^H\cup (g^{-1})^{H})$, where $H\leqslant {{\mathrm{Aut\,}}}(G)$ and $g\in G$. Note that when G is abelian, the inversion operation $\sigma$ lies in ${{\mathrm{Aut\,}}}(G)_S$, where $S= g^H \cup (g^{-1})^H$ [1, p. 217], so we may assume that $S=g^H$ and $\sigma \in H$. We summarise Houlis’ classification of the abelian case here by giving a representative H and g for each isomorphism class of graphs.

Recall the definition of $H_{\ell }= \langle m^{(p-1)/\ell } \rangle$ in (2.1) that, for a divisor $\ell$ of $p-1$, and note that $H_{\ell }$ contains the inversion operation if and only if $\ell$ is even (unless $p=2$, in which case inversion is trivial). This notation will be used throughout Sects. 3.1.1–3.1.3.

3.1.1 The case $G=\mathbb {Z}_{q}\times \mathbb {Z}_{q}$ ($p\ne q$)

Now ${{\mathrm{Aut\,}}}(\mathbb {Z}_{p}\times \mathbb {Z}_{q}) = \mathbb {Z}_{p}^* \times \mathbb {Z}_{q}^*$. Let m, y be primitive elements of $\mathbb {Z}_{p}^*, \mathbb {Z}_{q}^*$, respectively, and suppose that $d_2,d_1,d$ are integers satisfying the following conditions:

$$\begin{aligned} d_2 > 0, \quad d_2 \mid (q-1), \quad d_1 \mid (p-1), \quad 0\le d < d_1, \quad d_1d_2 \mid d(q-1) \end{aligned}$$

(3.1)

Define a subgroup of $\mathbb {Z}_{p}^* \times \mathbb {Z}_{q}^* = \langle m \rangle \times \langle y \rangle$ as follows:

$$\begin{aligned} H(d_2, d_1, d) := \langle (m^d, y^{d_2}),(m^{d_1},1) \rangle . \end{aligned}$$

Theorem 3.1

[2, Theorem 8.1.6] Let p, q be primes with $p\ne q$, let $G = \mathbb {Z}_{p}\times \mathbb {Z}_{q}$, and suppose that $\varGamma$ is a connected normal edge-transitive Cayley graph for G. Then there exist unique integers $d_2,d_1,d$ satisfying the conditions (3.1), with $\frac{q-1}{d_2}$ even if $q >2$ and $\frac{p-1}{\gcd (d,d_1)}$ even if $p > 2$, such that $\varGamma \cong \varGamma (G, H(d_2,d_1,d), (1,1))$. Moreover $\varGamma$ has valency $\frac{p-1}{d_1}\frac{q-1}{d_2}$.

Remark 3.1

It is not difficult to see that each subgroup of $\mathbb {Z}_{p}^* \times \mathbb {Z}_{q}^*$ is equal to $H(d_2,d_1,d)$ for some $d_2,d_1,d$ satisfying (3.1), see for example [2, Section 2.6]. However while every subgroup H of $\mathbb {Z}_{p}^*\times \mathbb {Z}_{q}^*$ yields a unique set of parameters $d_2,d_1,d$, this is not the only way of parametrising H: suppose that $H = H(d_1,d_2,d)$. If $d=0$, set $c_1:=d_2, c_2:=d_1$ and $c:=0$. If $d> 0$ then set

$$\begin{aligned} c_2 := \gcd (d,d_1), \quad c_1 := \frac{d_1d_2}{\gcd (d,d_1)}, \quad c:= \frac{c_1}{\gcd (c_1, \frac{p-1}{c_2})}. \end{aligned}$$

Then the parameters $c_2,c_1,c$ satisfy the conditions (3.1) with p and q interchanged, and $H= \langle (m^{c_2},y^c),(1,y^{c_1}) \rangle$. This yields another parametrisation of H (and hence of the normal edge-transitive Cayley graphs for G).

3.1.2 The case $G=\mathbb {Z}_{p}\times \mathbb {Z}_{p}$

When $p=q$, the automorphism group of G is larger than $\mathbb {Z}_{p}^* \times \mathbb {Z}_{q}^*$: namely G is a 2-dimensional $\mathbb {Z}_{p}$-vector space, and ${{\mathrm{Aut\,}}}(G)={{\mathrm{GL}}}(2,\mathbb {Z}_{p})$. There are two classes of subgroups $H\leqslant {{\mathrm{Aut\,}}}(G)$ to consider. Let $\ell$ be a divisor of $p-1$ which is even if $p>2$. Subgroups H in the first case have order $p\ell$, for such an $\ell$, and are conjugate to

$$\begin{aligned} H:=\left\{ \left( \begin{array}{cc} b &{} 0 \\ c &{} d \end{array}\right) \mid b\ne 0, d\in H_{\ell } \right\} \leqslant {{\mathrm{GL}}}(2,p). \end{aligned}$$

In this case the graph $\varGamma (G,H, (1,1))$ is the lexicographic product $\varGamma (\mathbb {Z}_{p},H_{\ell },1)[\overline{K_p}]$ (see [2, Definition 6.1.1(I), Theorem 6.1.5]).

In the second case H is a subgroup of the diagonal matrices, and hence is isomorphic to $H = H(d_2,d_1,d)$ for some parameters $d_2,d_1,d$ satisfying the conditions (3.1).

Theorem 3.2

[2, Theorem 6.1.5] Let p be a prime, let $G = \mathbb {Z}_{p}\times \mathbb {Z}_{q}$, and suppose that $\varGamma$ is a connected normal edge-transitive Cayley graph for G. Then one of the following holds:

• (i) $\varGamma \cong \varGamma (\mathbb {Z}_{p},H_{\ell },1)[\overline{K_p}]$, for $H_{\ell }$ as in Example 2.1, of valency $p\ell$, for some $\ell \mid (p-1)$, with $\ell$ even if $p >2$; or

• (ii) p is odd and there exist integers $d_2,d_1,d$ satisfying the conditions (3.1), with $\frac{p-1}{d_2}$ and $\frac{p-1}{\gcd (d,d_1)}$ even, such that $\varGamma \cong \varGamma (G, H(d_2,d_1,d), (1,1))$, of valency $\frac{(p-1)^2}{d_1d_2}$.

3.1.3 The case $G=\mathbb {Z}_{p^2}$

Theorem 3.3

[2, Theorem 7.1.3] Let p be a prime, let $G = \mathbb {Z}_{p^2}$, and suppose that $\varGamma$ is a connected, normal edge-transitive Cayley graph for G. Then there exists a divisor $\ell$ of $p-1$, with $\ell$ even if $p>2$, such that:

• (i) $\varGamma \cong \varGamma (\mathbb {Z}_{p}, H_{\ell },1)[\overline{K_p}]$, of valency $p\ell$; or

• (ii) p is odd and $\varGamma \cong {{\mathrm{Cay\,}}}(G,S)$ of valency $\ell$, where S is the unique subgroup of $\mathbb {Z}_{p^2}^*$ of order $\ell$.

3.2 The Frobenius group of order pq

A nonabelian group G of order pq, for primes p and q with $p > q \ge 2$, exists if and only if q divides $p-1$, and is a Frobenius group and unique up to isomorphism (see for example [8, Theorem 7.4.11]). In this section we construct such a group G as a subgroup of the 1-dimensional affine group ${{\mathrm{AGL\,}}}(1,p)$, and describe ${{\mathrm{Aut\,}}}G$.

The affine group $A:={{\mathrm{AGL\,}}}(1, p)$ consists of all affine transformations $x \mapsto xa + b$ of the field $\mathbb {Z}_{p}$ for $a, b \in \mathbb {Z}_{p}$, with $a\ne 0$. It is generated by

$$\begin{aligned} t:x \mapsto x+1, \quad m:x \mapsto xm, \end{aligned}$$

where m is a fixed primitive element of $\mathbb {Z}_{p}$. The element t has order $|t|=p$, and m has order $|m|=p-1$. The group $A=\langle m,t \rangle$ is the semidirect product $\langle t \rangle \rtimes \langle m \rangle$.

We use m to denote both the primitive element and the transformation induced by right multiplication by m: with this abuse of notation we have that $m^{-1}tm=t^m$, where the left-hand side denotes composition of maps (i.e. multiplication in the group A), and the right hand side denotes the mth power of the generator t. Each element of A may be uniquely expressed as $m^i t^j$, with $0\le i \le p-2$ and $0 \le j \le p-1$, and for $k \ge 0$ we have

$$\begin{aligned} (m^i t^j)^{t^k}=m^i t^{j+k(1-m^i)}, \quad (m^i t^j)^m = m^i t^{jm}. \end{aligned}$$

(3.2)

For a prime q dividing $p-1$ there is a unique subgroup $G_{pq}$ of ${{\mathrm{AGL\,}}}(1,p)$ of order pq; namely $G_{pq} := \langle z,t \rangle$, where $z = m^{(p-1)/q}$. Since $t^z: x\mapsto x+z$ and $z\ne 1$, it follows that $t^z\ne t$ and hence that $G_{pq}$ is not abelian. We identify the nonabelian group G of order pq with this subgroup $G_{pq}$, and denote the translation subgroup $\langle t \rangle$ by T. Note that

$$\begin{aligned} z^{-1}tz=t^{m^{(p-1)/q}}. \end{aligned}$$

(3.3)

In view of the role played by ${{\mathrm{Aut\,}}}G$ in our strategy for classifying normal edge-transitive Cayley graphs (see 2.1), we need to understand the automorphism group of $G_{pq}$ and its actions. Since $G_{pq}$ is the unique subgroup of A of order pq, it is a characteristic subgroup of A. Thus $G_{pq}$ is invariant under automorphisms of A and in particular under conjugation by elements of A. We denote by $\iota$ the conjugation action $A\rightarrow {{\mathrm{Aut\,}}}G_{pq}$, and with this notation $\iota (A)\leqslant {{\mathrm{Aut\,}}}G_{pq}$. In fact equality holds:

Lemma 3.1

Every automorphism of $G=G_{pq}$ is induced by conjugation by an element of $A={{\mathrm{AGL\,}}}(1,p)$, that is, ${{\mathrm{Aut\,}}}G = \iota (A) \cong A$.

Proof

It follows from (3.2) that $\ker \iota = C_{A}(G)$ is trivial, and so $\iota (A)\cong A$. The subgroup T of translations is the unique Sylow p-subgroup of $G:=G_{pq}$, and so is invariant under ${{\mathrm{Aut\,}}}G$. Thus there is an induced homomorphism $\varphi :{{\mathrm{Aut\,}}}G\rightarrow {{\mathrm{Aut\,}}}T$ which is onto since $\langle \varphi (\iota (m)) \rangle \cong {{\mathrm{Aut\,}}}T$, as both are cyclic of order $p-1$. An automorphism $\sigma \in \ker \varphi$ is uniquely determined by the image $z^{\sigma }$ of z. As $\langle t \rangle$ is normal in G, $ztz^{-1}\in T$ and hence is fixed by $\sigma$. Thus $(ztz^{-1})^{\sigma } = ztz^{-1}$.

Now $z^{\sigma }=z^x t^y$ for some x, y with $0\le x\le q-2, 0\le y\le p-1$. It follows that $(z^x t^y)t(z^x t^y)^{-1} = ztz^{-1}$ and so $t^{m^{x(p-1)/q}}=t^{m^{(p-1)/q}}$. Hence $m^{(x-1)(p-1)/q}\equiv 1 \pmod {p}$, or equivalently, $x\equiv 1 \pmod {q}$, as m is a primitive element of $\mathbb {Z}_{p}$. Since $0\le x\le q-2$ it follows that $x=1$ and $z^{\sigma }=z t^y$. This leaves at most p choices for $z^{\sigma }$ and so $|\ker \varphi |\le p$, and $|{{\mathrm{Aut\,}}}G|=(p-1)|\ker \varphi |\le p(p-1)=|\iota (A)|$. On the other hand $|{{\mathrm{Aut\,}}}G| \ge |\iota (A)|=p(p-1)$, and it follows that ${{\mathrm{Aut\,}}}G = \iota (A)$. $\square$

Recall that a normal edge-transitive Cayley graph $\varGamma (G,H,g)$ is connected if and only if $g^H$ generates G. In particular if G contains a proper characteristic subgroup which intersects $g^H$ nontrivially, then $g^H$ lies entirely in this subgroup, and $\varGamma$ is not connected (by [1, p. 213, Remark 1]). In the case of $G=G_{pq}$ this implies that the element g may not have order p, since all elements of order p lie in the characteristic subgroup T. It follows then that $o(g)=q$ and that the unique $\iota (H)$-invariant normal subgroup of G is T.

We investigate the subgroups of ${{\mathrm{Aut\,}}}G\cong {{\mathrm{AGL\,}}}(1,p)$ with a view to applying the strategy described in Sect. 2.1. Since T has prime order, a subgroup of ${{\mathrm{AGL\,}}}(1,p)$ either contains T or intersects it trivially. In the latter case H is cyclic, and we define, for $\ell \mid (p-1)$ and $0\le j\le p-1$,

$$\begin{aligned} H_{(\ell ,j)}:= \langle m^{(p-1)/\ell }t^j \rangle . \end{aligned}$$

(3.4)

Note that every element of ${{\mathrm{AGL\,}}}(1,p)\setminus T$ has order dividing $p-1$ and $|H_{(\ell ,j)}|=\ell$ for each j.

Under the natural action of ${{\mathrm{AGL\,}}}(1,p)$ on $G_{pq}$, the orbits are $\{1\}, T\setminus \{1\}$ and the left cosets $\{z^i T\mid 1\leqslant i \leqslant q-1\}$. The induced action of certain subgroups of ${{\mathrm{AGL\,}}}(1,p)$ on these orbits is of interest if we intend to apply Lemma 2.2, and is the subject of the following result.

Lemma 3.2

Let H be a nontrivial subgroup of ${{\mathrm{AGL\,}}}(1,p)$, acting by conjugation on itself. Then

• (i) if $T\subseteq H$, then for every $i\in \{1,\ldots p-1\}$, $\iota (H)$ fixes setwise and acts transitively on $m^iT$; and

• (ii) if $T \cap H = 1$ then $H= H_{(\ell , j)}$ for some $\ell , j$ with $\ell$ a divisor of $p-1$, $\ell > 1$, $0\le j\le p-1$, and for each $i\in \{1,\ldots ,p-1\}$, $\iota (H)$ fixes the coset $m^iT$ setwise and fixes a unique element of $m^iT$, namely $m^i t^k$ where $k\equiv j(m^i-1)(m^{(p-1)/\ell }-1)^{-1} \pmod {p}$. Moreover $\iota (H)$ permutes the other elements of $m^iT$ in $\frac{p-1}{\ell }$ orbits of size $\ell$, and $(m^iT)^{-1} \cap m^iT = \emptyset$.

Proof

For (i), let $m^i t^j \in m^i T$. By (3.2) it follows that $(m^i t^j)^h\in m^i T$ for all $h\in H$. Also $m^{-i}-1 \not \equiv 0 \pmod {p}$ as $1\le i \le q-1$. Setting $k\equiv -j(1-m^i)^{-1} \pmod {p}$ we have by (3.2), $(m^i t^j)^{t^k}=m^i t^{j+k(1-m^i)}=m^i$, and so T is transitive on the coset. Thus H fixes setwise and is transitive on $m^i T$.

For (ii), if $T \cap H = 1$ then H is cyclic and equal to $H_{(\ell , j)}= \langle m^{(p-1)/\ell } t^j \rangle$ for some $\ell , j$ with $\ell > 1$ since $H\ne 1$. It follows from (3.2) that $\iota (H)$ fixes $m^iT$ setwise and $(m^iT)^{-1}= m^{-i}T$ is disjoint from $m^iT$. An element $m^i t^k$ of $m^i T$ is fixed under conjugation by $m^{(p-1)/\ell } t^j$ if and only if $(m^i t^k)^{m^{(p-1)/\ell } t^j}=m^i t^k$, which, applying (3.2), is equivalent to $k\equiv j(m^i-1)(m^{(p-1)/\ell }-1)^{-1} \pmod {p}$. $\square$

Recall that $z=m^{(p-1)/q}$. It follows from Lemma 3.2 (ii) that $\iota (H_{(\ell ,j)})$ fixes a unique element of each orbit $z^iT$ for $0\le i\le q-1$, and these elements form a cyclic subgroup of $G_{pq}$ of order q.

Notation 1

Let $G=G_{pq}$ and $H=H_{(\ell , j)}$ as in (3.4) for some divisor $\ell$ of $p-1$, with $\ell \ne 1$ and $0\le j\le p-1$. Let X denote the set of elements of G fixed under conjugation by H, so that (by the remarks above) $X=\langle x \rangle$ is a cyclic subgroup of order q, where $x=zt^{j(z-1)(m^{(p-1)/\ell }-1)^{-1}}$. The cosets of X form a $\rho (G)\iota (H)$-invariant partition of G (recall that $\rho , \iota$ denote the actions of G on itself by right multiplication and conjugation, respectively), and $G=T\rtimes X$.

Recall that we define $\varGamma (G,H,g)={{\mathrm{Cay\,}}}(G, g^H \cup (g^{-1})^H)$.

Construction 1

Let p and q be primes with $p\equiv 1\pmod {q}$. Then define the graph

$$\begin{aligned} \varGamma (pq):= \varGamma (G_{pq}, T, z), \end{aligned}$$

of valency ${{\mathrm{val}}}\varGamma = 2p/\gcd (2,q)$, recalling that T is the translation subgroup of $G_{pq}\leqslant {{\mathrm{AGL\,}}}(1,p)$. The graph $\varGamma (pq)$ is isomorphic to the lexicographic product $C_q[\overline{K_p}]$ if q is odd and $K_2 [\overline{K_p}] = K_{p,p}$ if $q=2$.

Construction 2

Let p and q be primes with $q\equiv 1\pmod {p}$, let $\ell$ be a divisor of $p-1$ such that $\ell > 1$, and let i be an integer with $1\le i \le q-1$. Then define the graph

$$\begin{aligned} \varGamma (pq,\ell ,i):= \varGamma (G_{pq}, H_{(\ell ,1)}, z^i), \end{aligned}$$

of valency ${{\mathrm{val}}}\varGamma = 2\ell /\gcd (2,q)$, recalling that $H_{(\ell ,1)}=\langle m^{(p-1)/\ell }t \rangle$.

Remark 3.2

If $q\le 3$, then Construction 2 produces a unique graph $\varGamma (pq,\ell ,1)$ for each divisor $\ell >1$ of $p-1$ (since $1\le i\le (q-1)/2=1$). If $q\ge 5$ and $q\mid \ell$, then the graphs $\{\varGamma (pq,\ell ,i)\mid 1\le i \le (q-1)/2 \}$ are all isomorphic (see Proposition 3.1). If $q\ge 5$ and $q\not \mid \ell$ then these $(q-1)/2$ graphs are pairwise nonisomorphic (see Corollary 4.1).

Remark 3.3

When $q=2$, we have $i=1$ and $z=z^{-1}$. So $H=H_{(\ell ,1)}$ acts transitively on $S = z^H$, and $\varGamma (2p,\ell ,1)$ is $\rho (G)\iota (H)$-arc transitive of valency $\ell$, by Lemma 2.1.

Lemma 3.3

Let $\ell =p-1$, and let $\varGamma = \varGamma (pq,\ell ,i)$ as defined in Construction 2. Then $\varGamma , {{\mathrm{val}}}\varGamma$, and ${{\mathrm{Aut\,}}}\varGamma$ are as in Theorem1.1 (ii), and in particular ${{\mathrm{Aut\,}}}\varGamma$ has a system of imprimitivity consisting of p blocks of size q.

Proof

Set $H = H_{(p-1,1)} = \langle mt \rangle$, so $\varGamma = \varGamma (G,H,z^i)$. A vertex in $\varGamma =\varGamma (pq,p-1,i)$ is joined to the identity if and only if it is contained in the set $S=z^{iH}\cup z^{-iH}= (Tz^i \cup Tz^{-i})\setminus X$. Similarly $g\in G$ is joined to precisely $(Tz^ig \cup Tz^{-i}g)\setminus Xg$.

Consider the two partitions ${\fancyscript{P}}_T = \{Tg\mid g\in G\}$ and ${\fancyscript{P}}_X = \{Xg\mid g\in G\}$. The quotient graphs $\varGamma _{{\fancyscript{P}}_T}$ and $\varGamma _{{\fancyscript{P}}_X}$ are isomorphic to $C_q$ and $K_p$, respectively, and two vertices in $\varGamma$ are joined precisely when the corresponding vertices in the quotient graphs are joined. This is the definition of $K_p\times C_q$ (see Definition 2.2). Thus ${{\mathrm{Aut\,}}}\varGamma \geqslant {{\mathrm{Aut\,}}}K_p \times {{\mathrm{Aut\,}}}C_q = S_p \times D_{2q}$. It is not difficult to prove that equality holds, and so ${\fancyscript{P}}_X$ is ${{\mathrm{Aut\,}}}\varGamma$-invariant with blocks of size q. $\square$

3.3 Normal edge-transitive Cayley graphs for $G_{pq}$

3.3.1 Proof of Proposition 2.1

We divide the connected, normal edge-transitive Cayley graphs for $G_{pq}$ into two distinct classes. From now on we assume that $G=G_{pq}= \langle t,z \rangle$ as in Sect. 3.2, that $H\leqslant {{\mathrm{Aut\,}}}G=\iota ({{\mathrm{AGL\,}}}(1,p))$, and that $N=\rho (G)\iota (H)$ acts edge-transitively on a connected Cayley graph $\varGamma =\varGamma (G,H,g)={{\mathrm{Cay\,}}}(G,S)$ where $S=g^H \cup g^{-H}$ for some $g\in G\setminus \{1\}$. Recall that T is the unique $\iota (H)$-invariant normal subgroup of G and that, by Example 2.1, $\varGamma _T=\varGamma (q,a)$ for some $a\mid (q-1)$ with a even if $q>2$.

If $T\subseteq H \leqslant G$ then, by Lemma 3.2 (i), for some $i\in \{1,\ldots ,p-2\}$, the Cayley graph $\varGamma (G,H,g)={{\mathrm{Cay\,}}}(G,S)$ with $S= m^i T \cup m^{-i} T$, where $g\in m^i T$ and $g^H=m^i T$. Hence by Lemma 2.2, $\varGamma \cong \varGamma _{ T}[\overline{K_p}]$. The quotient graph $\varGamma _{T}$ is $K_2 =\varGamma (2,1)$ if $q=2$, or $C_q = \varGamma (q,2)$ if q is odd (since it has valency two). Moreover as $g^H=m^i T$ it follows from Proposition 2.1 that $\varGamma$ is normal edge-transitive relative to N. Thus we have proved the following.

Lemma 3.4

If p divides |H| then $\varGamma \cong \varGamma _T[\overline{K_p}]$, where $\varGamma _T=\varGamma (q,2)\cong C_q$ if q is odd, or $\varGamma (2,1)= K_2$ if $q=2$, and $\varGamma$ is normal edge-transitive relative to $\rho (G)\iota (H)$ of valency $2p/\gcd (2,q)$.

Note that this Lemma shows that all assertions of Proposition 2.1 hold if p divides |H|, and in this case $\varGamma$ is as in Theorem 1.1 (i). Also this Lemma implies $\varGamma (G,H,z)=\varGamma (G,T,z)$, and so if H contains T we assume without loss of generality that $H=T$. We now consider the second case where $H\cap T=1$, and hence $|H| \mid (p-1)$.

Lemma 3.5

Let $H=H_{(\ell , j)}\subseteq {{\mathrm{AGL\,}}}(1,p)$ (with $\ell > 1, \ell \mid p-1$), and let $g \in G:=G_{pq}$, and suppose that $\varGamma = \varGamma (G,H,g)$ is connected. If $\ell = |H|$ divides $p-1$ then $\ell > 1$ and $\varGamma \cong \varGamma (pq,\ell ,i)$ as in Construction 2 for some i.

Proof

By Lemma 3.2, $H=H_{(\ell ,j)}$ for some divisor $\ell$ of $p-1$ and some j where $0\le j\le p-1$, and we have $g = z^i t^k$ for some i, k. Using Eq. (3.2) it is straightforward to check that $y_1 := t^{k(m^{i(p-1)/q}-1)^{-1}}$ conjugates g to $z^i$ and conjugates $H_{(\ell , j)}$ to $H_{(\ell , j')}$ for some $j'$. Since $\varGamma$ is connected $\ell = |H| > 1$. If $j'\ne 0$ there exists r such that $j'm^r\equiv 1 \pmod {p}$ (interpreting m here as an element of $\mathbb {Z}_{p}$) and hence such that $(m^{(p-1)/\ell }t^{j'})^{z^r}=m^{(p-1)/\ell }t$. Thus $H_{(\ell ,j)}^{\iota (y_1 m^r)}=H_{(\ell ,j')}^{\iota (m^r)}=H_{(\ell ,1)}$, and $g^{\iota (y_1 m^r)} = (z^i)^{m^r} = z^i$ (since $z^i \in \langle m \rangle$)). So $\varGamma \cong \varGamma (G, H_{(\ell ,1)},z^i) = \varGamma (pq,\ell ,i)$.

If $j'=0$ then $H_{(\ell ,0)}$ centralises $z^i$ and hence $\varGamma \cong \varGamma (G,H_{(\ell ,0)}, z^i)={{\mathrm{Cay\,}}}(G,S)$ where $S=\{z^i, z^{-i}\}$ and so $\varGamma$ is isomorphic to $p.C_q$, contradicting the connectivity of $\varGamma$. $\square$

We now complete the proof of Proposition 2.1. By the remarks following Lemma 3.4 we may assume that $H\cap T = 1$, and by Lemma 3.5, we may further assume that $\varGamma = \varGamma (G_{pq}, H_{(\ell ,1)},z^i) = \varGamma (pq,\ell ,i)$ for some divisor $\ell$ of $p-1$ with $\ell \ne 1$ and with $1\le i\le q-1$. If q is odd then $\varGamma (G,H_{(\ell ,1)},z^i)=\varGamma (G,H_{(\ell ,1)},z^{q-i})$, since $(z^{q-i})^H\cup (z^{-{q-i}})^H=(z^{-i})^H\cup (z^{i})^H$. So if q is odd we may assume $1\le i \le \frac{q-1}{2}$. If $q=2$, then $i=1$.

If $\ell = p-1$, then by Lemma 3.3, $\varGamma$ is as in Theorem 1.1 (ii). In all other cases (that is, $1 < \ell < p-1$), $\varGamma$ is as in Theorem 1.1 (iii): the vertices of $\varGamma _T$ are the cosets of T, and in all cases $S = z^iH \cup z^{-i}H$, and so $ST = z^iT \cup z^{-i}T$. Thus the connection set of $\varGamma _T = ST/T = \{z^iT, z^{-i}T\}$, which has size 1 if $q=2$ and 2 if q is odd. Thus $\varGamma _T = K_2$ if $q=2$ and $C_q$ when q is odd. Proposition 2.1 is now proved.

3.3.2 Cayley graphs for $\rho (T)\times \lambda (X)$

The graphs of case (iii) all seem essentially ‘the same’ at first glance. However the structure of the graph differs fundamentally depending on the parameter $\ell$. This is because we sometimes, but not always, have a regular abelian subgroup of ${{\mathrm{Aut\,}}}\varGamma$ (see Lemma 3.6 below). In this case $\varGamma$ may be reinterpreted as a Cayley graph for an abelian group. Recall from Sects. 2.1 and 2.3 that $N=\rho (G){{\mathrm{Aut\,}}}(G)_S$ is the normaliser of $\rho (G)$ in ${{\mathrm{Aut\,}}}\varGamma$, and $\lambda (G)$ denotes the left regular action $\lambda _g : x \mapsto g^{-1} x$ of G.

Lemma 3.6

Let $\varGamma =\varGamma (pq,\ell ,i)$, and suppose q divides $\ell$. Then the following hold, for X as in Notation 1:

• (i) $X\leqslant H$;

• (ii) $\lambda (X) \leqslant N$;

• (iii) $\rho (T)\times \lambda (X)$ is a regular subgroup of ${{\mathrm{Aut\,}}}\varGamma$, and so $\varGamma$ is a Cayley graph for $\rho (T)\times \lambda (X)=\mathbb {Z}_{p}\times \mathbb {Z}_{q}$;

• (iv) As a Cayley graph for $\rho (T)\times \lambda (X)$, $\varGamma$ is normal edge-transitive.

Proof

Part (i) follows from the definition of X. For part (ii), observe that $\lambda (X) \leqslant \rho (X)\iota (X) \leqslant \rho (G)\iota (H)=N$. Part (iii) then follows easily.

For (iv), note that since $\rho (T){{\mathrm{char}}}\rho (G)\triangleleft N$, we have $\rho (T)\triangleleft N$, and since X is by definition fixed under $\iota (H)$, so is $\lambda (X)$. So $\lambda (X)$ is centralised by both $\iota (H)$ and $\rho (G)$, it is normal in the product, and so $\rho (T)\lambda (X) \triangleleft N$. Thus $N\subseteq N_{{{\mathrm{Aut\,}}}\varGamma }(\rho (T)\lambda (X))$, and so the normaliser is transitive on ${{\mathrm{E\Gamma }}}$. $\square$

When $q|\ell$ there is only one graph up to isomorphism: different choices of i give isomorphic graphs.

Proposition 3.1

If q divides $\ell$, then $\varGamma (pq,\ell ,i) \cong \varGamma (\mathbb {Z}_{p}\times \mathbb {Z}_{q}, \hat{H}, (1,1))$ where $\hat{H} = H(\frac{q-1}{2}, \frac{p-1}{\ell }, d)$ as in Sect. 3.1.1, and

$$\begin{aligned} d = {\left\{ \begin{array}{ll} 0 &{} \text { if } \quad \ell \text { is even; and }\\ \frac{p-1}{2\ell } &{} \text { if } \quad \ell \text { is odd}. \end{array}\right. } \end{aligned}$$

In particular $\varGamma (pq,\ell ,i)$ is independent of i up to isomorphism and has valency $2\ell /\gcd (2,q)$.

Proof

By Lemma 3.6, $L=\rho (T)\times \lambda (X)\leqslant {{\mathrm{Aut\,}}}\varGamma$. Since $\rho (T)$ is a characteristic subgroup of $\rho (G)$, we have that $\rho (T)$ is normalised by N. Since $\lambda (X)$ is centralised by $\rho (G)$ (the left and right regular actions centralise one another) and is centralised by $\iota (H)$ (since $X\leqslant H$ and H is cyclic), we have that $\lambda (X)$ is centralised by N. It follows that $N \leqslant N_{{{\mathrm{Aut\,}}}\varGamma }(L)$.

Now since (by Lemma 3.6) $\varGamma$ is a Cayley graph for L, we may identify the vertices of $\varGamma$ with the elements of L, and $\varGamma \cong {{\mathrm{Cay\,}}}(L,S)$ for some $S \subseteq L$ with $S = S^{-1}$. Then the automorphism $\varphi : x \rightarrow x^{-1}$ is an automorphism of L (since L is abelian) and it fixes the connection set S, and so $\varphi \in N_{{{\mathrm{Aut\,}}}\varGamma } (L)$. Set $\hat{N} = \langle N, \varphi \rangle$, and set $\hat{H} = \hat{N}_{1_G} = \langle \iota (H), \varphi \rangle$.

Now $\varGamma$ is normal edge-transitive as a Cayley graph for L (since $N\leqslant N_{{{\mathrm{Aut\,}}}\varGamma }(L)$ and N is edge-transitive). So $\hat{H}$ is transitive on the connection set S (since $\varphi$ switches an element with its inverse). Moreover we have $|\hat{H}| = |S| = 2\ell$, and $\hat{N}$ is transitive on the arcs of $\varGamma$.

We seek to determine the parameters $d_2,d_1,d$, such that $\hat{H} \cong \langle (x^d, y^{d_2}), (x^{d_1},1) \rangle \leqslant \mathbb {Z}_{p}^* \times \mathbb {Z}_{q}^* \cong {{\mathrm{Aut\,}}}(\rho (T)) \times {{\mathrm{Aut\,}}}(\lambda (X))$ (as in Theorem 3.1). Since $\iota (H)$ centralises $\lambda (X)$, the subgroup of ${{\mathrm{Aut\,}}}(\lambda (X))$ induced by the action of $\hat{H}$ is isomorphic to $\mathbb {Z}_{2}$, and so $d_2 = \frac{q-1}{2}$. Since $\iota (H)$ acts faithfully on $\rho (T)$, we have $\hat{H} \cap ({{\mathrm{Aut\,}}}(\rho (T)) \times 1) = \iota (H)$, and so $d_1 = \frac{p-1}{\ell }$.

Suppose that $d > 0$. Then the conditions in (3.1) give $0 < d \le d_1$ and $d_1 \mid 2d$ which implies that $d_1 = 2d$ is even. Thus $d = \frac{p-1}{2\ell }$. In this case the first generator of $\hat{H} = H(d_2,d_1,d)$ is $(x^{(p-1)/2\ell }, -1)$, which squares to the second generator $(x^{d_1},1)$. Thus $\hat{H}$ is cyclic and so $\varphi = (-1,-1)$ is the unique involution in $\hat{H}$. The only element in $\hat{H}$ with first entry $-1$ is $(x^{(p-1)/2\ell },-1)^{\ell } = (-1,(-1)^{\ell })$, and it follows that $\ell$ is odd.

Suppose now that $d=0$. Then $\hat{H}$ contains $(1,-1)$ and since $\hat{H}$ also contains $\varphi = (-1,-1)$, we have $(-1,-1)\in \hat{H} \cap ({{\mathrm{Aut\,}}}(\rho (T))\times 1) = \langle (x^{d_1},1) \rangle$. This implies that $\ell = |x^{d_1}|$ is even. $\square$

In the case $q\not \mid \ell$, however, the graphs in Proposition 2.1 are pairwise nonisomorphic (Corollary 4.1 below).

4 Redundancy and automorphisms

In this section we discuss the possibility of redundancy in our classification, that is, isomorphisms between the graphs $\varGamma (pq,\ell ,i)$ for different choices of parameters. In doing so we determine the automorphism groups of our graphs.

Recall the following: p and q are primes with q dividing $p-1$, $\ell$ is a proper divisor of $p-1$ with $\ell > 1$, i is an integer with $1\le i \le (q-1)/2$, $G=G_{pq}$, $H=H_{(\ell , 1)} = \langle m^{(p-1)/\ell }t \rangle$, and $N=\rho (G)\iota (H)$. Define $\varGamma (pq,\ell ,i)=\varGamma (G,H,z^i)$, and $Y={{\mathrm{Aut\,}}}\varGamma$. In this section we determine Y for most values of $(p,q,\ell ,i)$ (see Theorem 4.1), and decide when different sets of parameters yield isomorphic graphs (Corollary 4.1).

It is obvious that different primes p and q generate nonisomorphic graphs, as $\varGamma (pq,\ell ,i)$ has pq vertices. Each graph $\varGamma (pq,\ell ,i)$ has valency $\ell$ or $2\ell$, according as q is odd or even. Thus different choices for $\ell$ also yield nonisomorphic graphs. We therefore need only decide whether $\varGamma (pq, \ell , i)\cong \varGamma (pq, \ell , i')$ implies $i=i'$.

Theorem 4.1

Let $\varGamma =\varGamma (pq,\ell ,i)$ as defined in Construction 2, and let $Y={{\mathrm{Aut\,}}}\varGamma$. Then

$$\begin{aligned} Y={\left\{ \begin{array}{ll} \rho (G).\iota (H) &{} \text { when }\quad q=2 \text { or } q \not \mid \ell \text { and } \ell < p-1; \\ \rho (G).\iota (H).\mathbb {Z}_{2} &{} \text { when } \quad q\ge 3, q \mid \ell \text { and } \ell < p-1;\\ S_p \times \mathbb {Z}_{2} &{} \text { when }\quad \ell =p-1 \text { and } q=2; \text { and }\\ S_p \times D_{2q} &{} \text { when } \quad \ell =p-1 \text { and } q=3; \end{array}\right. } \end{aligned}$$

except in the cases $(p,q,\ell ,i)=(7,3,2,1), (7,2,3,1), (11,2,5,1)$ and (73, 2, 9, 1).

We prove Theorem 4.1 over the course of this section. First we give a proof of Theorem 1.1.

Proof

(Proof of Theorem 1.1 ) That $\varGamma$ satisfies one of Theorem 1.1 (i)–(iii) follows from Proposition 2.1, and the structure of $Y={{\mathrm{Aut\,}}}\varGamma$ follows from Theorem 4.1 in all cases except the four exceptional parameter sets of Theorem 4.1. The other automorphism groups can be calculated manually (using, for example, GAP [9]). $\square$

Next we deduce from Theorem 4.1 our claim about graph isomorphisms.

Corollary 4.1

Let $\varGamma (pq, \ell , i),\varGamma (pq,\ell ,i')$ be defined as in Construction 2, and suppose that $q\not \mid \ell$. Then $\varGamma (pq,\ell ,i)\cong \varGamma (pq,\ell ,i')$ if and only if $i=i'$.

Proof

Let $\varGamma =\varGamma (pq,\ell ,i),\varGamma '=\varGamma (pq,\ell ,i')$. If $q\le 3$ then $i=i'=1$, and so we assume without loss of generality that $q\ge 5$. An isomorphism $\varphi :\varGamma \rightarrow \varGamma '$ is a permutation of G such that ${{\mathrm{E\Gamma }}}^{\varphi }={{\mathrm{E\Gamma }}}'$. We may assume without loss of generality that $\varphi$ fixes the identity of G, since both graphs are vertex transitive.

Now $\varphi ^{-1}{{\mathrm{Aut\,}}}\varGamma \varphi ={{\mathrm{Aut\,}}}\varGamma '$, but by Theorem 4.1, ${{\mathrm{Aut\,}}}\varGamma ={{\mathrm{Aut\,}}}\varGamma '=\rho (G)\iota (H)$, and so $\varphi ^{-1}({{\mathrm{Aut\,}}}\varGamma )\varphi ={{\mathrm{Aut\,}}}\varGamma$. Hence $\varphi \in N_{1_G}=(N_{{{\mathrm{Sym}}}G}(\rho (G)\iota (H)))_{1_G}$.

Since N normalises $\rho (G)$, it is contained in the holomorph of G, namely $\rho (G).{{\mathrm{Aut\,}}}(G)$, and hence $N_{1_G} \subseteq {{\mathrm{Aut\,}}}(G)$. But by Formula (3.2), the action of ${{\mathrm{Aut\,}}}(G)$ fixes the cosets of T setwise. Now an isomorphism fixing $1_G$ must map $(z^{i})^{H}\cup (z^{-i})^{H}$ to $(z^{i'})^{H}\cup (z^{-i'})^{H}$, and if $q \ge 5,1\le i\le (q-1)/2$ then this is possible only if $i=i'$, as $(z^{i})^{H}\subseteq z^iT$. $\square$

Our first step in the proof of Theorem 4.1 is to identify one of the exceptional cases.

Proposition 4.1

Suppose $\varGamma =\varGamma (pq,\ell ,i)$ is vertex primitive. Then $(p,q,\ell ,i)=(7,3, 2,1)$ and $\varGamma$ is the flag graph $\varGamma _F$ of the Fano Plane (see Fig. 2), with automorphism group ${{\mathrm{PGL}}}(3,2).\mathbb {Z}_{2}$.

Proof

If $q=2$ then $\varGamma$ is bipartite, hence imprimitive. Also if $\ell = p-1$ then ${{\mathrm{Aut\,}}}\varGamma$ is imprimitive by Lemma 3.3. Thus $q\ge 3$, $p \ge 7$ since $q\mid p-1$, and $\ell$ is a proper divisor of $p-1$. The edge-transitive, vertex-primitive graphs of order a product of 2 primes are classified in [10, Table I, Table III], along with their valency and whether or not they are Cayley graphs. Requiring that $\varGamma$ be a Cayley graph, and that q and $\ell =\frac{{{\mathrm{val}}}\varGamma }{2}$ are divisors of $p-1$ with $1 < \ell < p-1$, we are left with the possibilities in Table 3:

Table 3 Possibilities in the proof of Proposition 4.1

The fact that $\ell > 1$ and $\ell$ divides $p-1$ rules out line 1 and in line 4 implies that $p=7$, $\ell =2$ and $q=3$. Thus we have exactly three $(p,q,\ell )$ to check further. Using Nauty [11] and the package GRAPE [12] for GAP [9], we constructed the graphs $\varGamma (pq, \ell ,i)$ for the three remaining possible $p,q,\ell$ as in the table (and for every $i\le (q-1)/2$) and computed their automorphism groups, finding that the automorphism group acts imprimitively for the graphs in lines 2 and 3 and that the graph $\varGamma (21,2,1)$ is vertex primitive and is the flag graph of the Fano plane as asserted. $\square$

4.1 Main case: Aut $\varGamma$ is imprimitive

By Proposition 4.1, if $(p,q,\ell )\ne (7,3,2)$ then ${{\mathrm{Aut\,}}}\varGamma$ is imprimitive. Throughout this section suppose $\varGamma =\varGamma (pq,\ell ,i)$ as defined in Construction 2, with either $(q,i)=(2,1)$ or q odd, $1\le i\le (q-1)/2$ and $(p,q,\ell )\ne (7,3,2)$, and let $Y={{\mathrm{Aut\,}}}\varGamma$. The case $\ell =p-1$ has been dealt with in Lemma 3.3, so we assume $1<\ell < p-1$. By our construction we know that $N:=\rho (G)\iota (H) \leqslant Y$; thus any Y-invariant partition of ${{\mathrm{V\Gamma }}}$ is also N-invariant. The following lemma describes the only N-invariant partitions, and so the only feasible Y-invariant partitions.

Lemma 4.1

Let $\varGamma =\varGamma (pq,\ell ,i)$ with $\ell < p-1$, and let $N=\rho (G).\iota (H)$. Then the following are the only nontrivial N-invariant partitions of ${{\mathrm{V\Gamma }}}$:

• (i) The partition of G into the right cosets of $T= \langle t \rangle$, consisting of q blocks of size p; and

• (ii) The partition into the right cosets of the subgroup X (see Notation 1). consisting of p blocks of size q.

Proof

Let B be a block of imprimitivity for N containing $1_G$. By [1, Theorem 3(a)], B is a subgroup of G. The setwise stabiliser of B in $\rho (G)$ is $\rho (B)$, and is a normal subgroup of $N_B$. Since $\iota (H) = N_{1_G}$ leaves B invariant (since $1_G \in B$), it follows that B is H-invariant. Conversely each H-invariant subgroup of G is a block for N.

Since T is normal in ${{\mathrm{AGL\,}}}(1,p)$ and $H \subseteq \iota ({{\mathrm{AGL\,}}}(1,p))$, T is H-invariant and so the cosets of T form an N-invariant partition as in (i). Any H-invariant subgroup L of G with $L\ne T$ has order q, and since by Formula (3.2) H fixes each coset of T setwise, H must centralise L. Thus by Lemma 3.2 there is only one other H-invariant subgroup, namely the subgroup $X= \langle x \rangle$, where $x= m^i t^{j(m^i-1)(m^{(p-1)/\ell }-1)^{-1}}$ (see Notation 1), as in (ii). $\square$

This gives us two possibilities for Y-invariant partitions of the vertex set: one into p blocks of size q and the other into q blocks of size p. We prove the following lemma in the course of the section:

Lemma 4.2

If $(p,q,\ell ,i)\ne (7,3,2,1)$ and $1<\ell < p-1$, then the cosets of T form a Y-invariant partition of ${{\mathrm{V\Gamma }}}$.

We begin by noting that in the case $q=2$, the cosets of T form a bipartition of $\varGamma$, and hence a system of imprimitivity. Now we assume:

$$\begin{aligned} q\ge 3 \text { and the cosets of } X \text {form a}\,\,Y\text {-invariant partition } {\fancyscript{P}}. \end{aligned}$$

(4.1)

If (4.1) does not hold, then by Lemma 4.1 the result is proved.

Lemma 4.3

Assume (4.1) holds, and let $s\in S=(z^{i})^{H} \cup (z^{-i})^{H}$. Then $|S \cap Xs|\in \{1,2\}$ and is independent of the choice of s.

Proof

Note first that $s\in S \cap Xs$, and so $|S\cap Xs|\ge 1$. Now suppose $|S\cap Xs| \ge 3$. Then since H has just two orbits on S, there exist distinct $s_1,s_2\in S\cup Xs$ with $s_1^h=s_2$ for some $h\in H$. Since $s_1,s_2\in Xs$, we have $s_1 s_2^{-1}\in X$, but on the other hand $s_1s_2^{-1}=s_1s_1^{-h}$, and since H fixes the cosets of T setwise it follows that $s_1s_2^{-1}\in T$. But $T\cap X = \{1\}$, and so $s_1=s_2$, contradiction.

If $|S \cap Xs| = 1$ for each $s\in S$ there is nothing more to prove, so suppose that $S\cap Xs = \{s, s'\}$ with $s\ne s'$. Then by the above argument $s'$ cannot be in $s^H$, and so $s'\in (s^{-1})^H$. So there exists $h\in H$ with $s'=s^{-h}$. Now choose $s_2\in S$; then $s_2$ is in the H-orbit of either s or $s'$. Suppose $s_2\in s^H$. Then for some $h'\in H$, $s_2=s^{h'}$. Then $s_2 s_2^{h} = s^{h'}s^{h'h} = (ss^h)^{h'} \in X^H = X$, so $Xs_2 = X s_2^{-h}$ and so $|S\cap Xs_2| =2$ for every $s_2\in S$. If $s_2 \in (s')^H$ then the same argument holds with $s'$ in place of s. $\square$

We now investigate the structure of the kernel $K=Y_{({\fancyscript{P}})}$ and its action on each member of the partition ${\fancyscript{P}}$ of (4.1). We assume for the moment that K is nontrivial. In this case K is transitive on every block (as $Y_B$ acts primitively on each block B and K is normal in $Y_B$, K is transitive). So if $K\ne 1$, the K-orbits are the cosets of X. Moreover since K acts transitively on each block Xg and each block has prime size q, by Proposition 2.3, $K^{Xg}$ is primitive.

Lemma 4.4

Assume (4.1) holds. Then the pointwise stabiliser $K_{(X)}$ is trivial, and so $K \cong K^{X}$.

Proof

If $K=1$ there is nothing to prove so assume $K\ne 1$. Let $s\in S$. Since $K_{(X)}$ fixes $1_G \in X$ it follows that $K_{(X)}$ fixes S setwise. Also $K_{(X)} < K = Y_{({\fancyscript{P}})}$ fixes the block X setwise and hence $K_{(X)}$ fixes $S \cap Xs$ setwise. By Lemma 4.3, $|S \cap Xs| \le 2 < q = |Xs|$, and hence $K_{(X)}$ is not transitive on Xs. Since K is primitive on Xs, its normal subgroup $K_{(X)}$ must therefore act trivially on Xs, and since this holds for all $s\in S$, it follows by connectivity that $K_{(X)} = 1$. $\square$

Lemma 4.5

Assume (4.1) holds, and that $K\ne 1$. Then either $K=\lambda (X)$ or $K= \lambda (X)\rtimes \mathbb {Z}_{2}\cong D_{2q}$, and in particular, $\lambda (X)\triangleleft Y$.

Proof

Let $s\in S$. Then $s\in S \cap Xs$ and by Lemma 4.3, $|S\cap Xs|\le 2$. Suppose first that $S\cap Xs=\{s\}$. Then $K_1$ fixes $S \cap Xs$ and so $K_1 \leqslant K_{s}$. Since all K-orbits have the same length, $K_1=K_s$, and this holds for every $s\in S$. By connectivity, $K_1=1$, and so $|K|=q$.

Now suppose $S\cap Xs = \{s,s'\}$. Since $K_1$ fixes $S\cap Xs$ setwise it follows that $|K_1 : K_{1,s} | \le 2$ and $K_{1,s} \subseteq K_{s,s'}$. Thus $|K_s : K_{s,s'}| \le 2$ and in particular if $K^{Xs}$ is 2-transitive then $q=3$ and $K^{Xs} = S_3 = {{\mathrm{AGL\,}}}(1,3)$. Thus by Proposition 2.3, in all cases $K^{Xs} \leqslant {{\mathrm{AGL\,}}}(1,q)$ and $K_{s,s'}$ fixes Xs pointwise. We therefore have $|K^{Xs}| = q|K_s : K_{s,s'}| \le 2q$.

Thus |K| is either q or 2q, and so K has a characteristic subgroup $K_0 \cong \mathbb {Z}_{q}$ and $K_0 \triangleleft Y$. We claim that $K_0=\lambda (X)$. Consider the subgroup $Y_0:=\langle K_0, \rho (T) \rangle$ of ${{\mathrm{Sym}}}(G)$. Now $\rho (T) \cap K_0 =1$ and $\rho (T)$ normalises $K_0$ and hence $|Y_0|=pq$. Since $p > q$, $\rho (T)$ is a normal subgroup of $Y_0$, and so $Y_0 = K_0 \times \rho (T)$ and $\rho (T)\leqslant C_{{{\mathrm{Sym}}}G}(K_0)$.

Now consider $\langle \rho (X), K_0 \rangle$. This group has order $q^2$ and so is abelian. In particular, $\rho (X)\subseteq C_{{{\mathrm{Sym}}}G}(K_0)$, and so $\rho (G) \leqslant C_{{{\mathrm{Sym}}}G}(K_0)$, as $\rho (G)=\langle \rho (T),\rho (X) \rangle$. This implies that $K_0\leqslant C_{{{\mathrm{Sym}}}G}(\rho (G))=\lambda (G)$. So $K_0=\lambda (X')$ for some subgroup $X'$ of G of order q, and since $K_0$ fixes X setwise we must have that $X'=X$. If $K=\lambda (X)\rtimes \mathbb {Z}_{2}$ then $K\cong D_{2q}$ as it cannot possibly be cyclic (all of its orbits have size q). $\square$

This yields three cases, according to K: it is either $D_{2q}, \mathbb {Z}_{q}$ or 1.

Lemma 4.6

Assume (4.1) holds. If $K\cong D_{2q}$ then the conclusion of Lemma 4.2 holds.

Proof

Observe that ${{\mathrm{Fix}}}K_1$ is a block of imprimitivity for Y in ${{\mathrm{V\Gamma }}}$. If $K\cong D_{2q}$ then by Lemma 4.4, K acts faithfully as $D_{2q}$ on every block in ${\fancyscript{P}}$, and so $K_1\cong \mathbb {Z}_{2}$ fixes a unique point in each of the p blocks. By Lemma 4.1, ${{\mathrm{Fix}}}K_1$ must be a coset of T and Lemma 4.2 is proved in this case. $\square$

Thus we may assume that $K=1$ or $K=\lambda (X)$. We consider these cases separately, investigating the quotient graph $\varGamma _{{\fancyscript{P}}}$ and the group $Y^{{\fancyscript{P}}}\cong Y/K$.

Lemma 4.7

Assume (4.1) holds. If $K=1$ then the conclusion of Lemma 4.2 holds.

Proof

Suppose that $K=1$. Then $Y\cong Y^{{\fancyscript{P}}}$, a primitive group of degree p which by Proposition 2.3 is affine or almost simple and 2-transitive. If $Y^{{\fancyscript{P}}} \cong Y$ is affine of degree p, then $Y \leqslant {{\mathrm{AGL\,}}}(1,p)$ and so $\rho (T) \triangleleft Y$ and the $\rho (T)$-orbits are blocks of imprimitivity for Y in $V\varGamma$, whence the conclusion of Lemma 4.2 holds. Thus we may suppose that Y is almost simple with socle L and $Y^{{\fancyscript{P}}}$ is 2-transitive with $L^{{\fancyscript{P}}}\cong L$ as in Table 2.

Since $Y^{{\fancyscript{P}}}$ is 2-transitive, the quotient graph $\varGamma _{{\fancyscript{P}}} \cong K_p$. Let $B\in {\fancyscript{P}}$ and $\alpha \in B$. Now $L^{{\fancyscript{P}}}$ is transitive, and if L is not transitive on ${{\mathrm{V\Gamma }}}$ then its orbits are blocks of imprimitivity for Y of size p and as before the conclusion of Lemma 4.2 holds. Thus we may assume that L is transitive on ${{\mathrm{V\Gamma }}}$, so $L_{\alpha } < L_{B} < L$, and $|L_B : L_{\alpha }|=q$. Since $q\ge 3$ and $q|(p-1)$, we have $p\ge 7$ and $q\le (p-1)/2$. We consider separately each line of Table 2. Note that, by Lemma 4.1, it is sufficient to prove either that Y has a block of imprimitivity of size p, or that $L_B$ has no subgroup of index q.

If $L=A_p$ with $p\ge 7$, then $L_B = A_{p-1}$ has no subgroup of index less than $p-1$. If $L={{\mathrm{PSL}}}(2,11)$ or $M_{11}$, with $p=11$, then $q=5$, so $\varGamma =\varGamma (55,\ell ,i)$, with $\ell =2$ or 5 and $i=1$ or 2. Using GAP we construct each graph and verify that none has an almost simple automorphism group. If $L=M_{23}$ then $q=11$ and $L_B=M_{22}$, which has no subgroups of index 11 (see [13, page 39]).

Thus $L={{\mathrm{PSL}}}(n,r)$, with $p=\frac{r^n-1}{r-1}$ and n prime, and $r=r_0^f$ with $r_0$ prime. First note that $n \ge 3$, for if $n=2$ then $p=r+1$ and so $p-1=r$ is even and so is a power of 2, and hence not divisible by q since $q\ge 3$.

Before seeking the subgroup $L_{\alpha }$ of index q in $L_B$ we obtain some further parameter restrictions. The subgroup $\rho (T)$, being cyclic of prime order $p=\frac{r^n-1}{r-1}$, is a Singer cycle of T, is self-centralising, and $N_Y(\rho (T)) \leqslant \rho (T).\mathbb {Z}_{n}.\mathbb {Z}_{f}$, so $|N_Y(\rho (T)) : \rho (T)|$ divides nf (see [14, Satz 7.3]). Since $\iota (H) \cong \mathbb {Z}_{\ell }$ normalises $\rho (T)$ it follows that $\ell$ divides nf and that ${{\mathrm{val}}}\varGamma \le 2nf$. Moreover since $\rho (T)$ is self-centralising, T does not contain $\lambda (X)$ and so, by Lemma 3.6, $q\not \mid \ell$. Now the number of $\varGamma$-edges with one vertex in B is $|B|{{\mathrm{val}}}\varGamma \le 2nfq$. On the other hand since $\varGamma _{{\fancyscript{P}}} = K_p$, this number is at least $p-1$, and hence

$$\begin{aligned} p-1\le 2nfq. \end{aligned}$$

(4.2)

Now $L_B = R\rtimes M \leqslant {{\mathrm{AGL\,}}}(n-1,r)$, where R is elementary abelian of order $r^{n-1}$, and ${{\mathrm{SL}}}(n-1,r) \leqslant M \leqslant {{\mathrm{GL}}}(n-1,r)$ with M of index $\gcd (n,r-1)$. The group $L_B^B$ is transitive of prime degree q, and hence primitive. Suppose first that $R^B \ne 1$. Since R is a minimal normal subgroup of $L_B$, R acts faithfully and transitively on B, and since R is abelian it follows that $R^B$ is regular and $q=r^{n-1}$, forcing $n=2$ and a contradiction. Thus $R^B=1$, and so $L_B^B=M^B$. Let $S={{\mathrm{SL}}}(n-1,r)\leqslant M$. If $S^B=1$ then $L_B^B$ is cyclic of order dividing |M : S|, which divides $r-1$. Hence by (4.2), $\frac{r(r^{n-1}-1)}{r-1} = p-1 \le 2nf(r-1) < 2nr(r-1)$ which implies $n=3$ (since n is prime) and so q divides $p-1 = r(r+1)$. Since also q divides $r-1$ it follows that $q=2$, a contradiction.

Thus $S^B \ne 1$, so $S^B$ is primitive of odd prime degree q. Suppose first that $(n,r)=(3,2)$ or (3, 3), so p is 7 or 13, respectively and $q=3$ is the only odd prime dividing $p-1$. Since $q\not \mid \ell$ we have only the following two cases: $(p,q,\ell ,i) = (13,3,2,1), (13,3,4,1)$ (since we are assuming that $(p,q,\ell )\ne (7,3,2)$). It is easy to verify (say, in GAP) that the automorphism groups of these graphs are as in Theorem 4.1, and in particular Y has a block of imprimitivity of size p so Lemma 4.2 holds. Thus we may assume that S is perfect and hence $S^B$ has ${{\mathrm{PSL}}}(n-1,r)$ as a composition factor. In particular $S^B$ is an insoluble primitive group of prime degree q and so by Proposition 2.3, $S^B \cong {{\mathrm{PSL}}}(n-1,r)$ and either $q=\frac{r^{n-1}-1}{r-1}$, or $(n,r,q)=(3,11,11),(3,5,5)$ or (3, 4, 5). In the last case $p = 1+4+16 = 21$ is not prime. In the previous two cases $Y = {{\mathrm{PSL}}}(3,r)$ does not contain a Frobenius group $G_{pq}$. Thus $q=\frac{r^{n-1}-1}{r-1}$. Since q is prime, also $n-1$ is prime, and since n is prime this implies $n=3$. Then $p=1+r+r^2$ and $q=1+r$. If $r=2$ we have the case excluded in Lemma 4.2. If $r > 2$ then q prime forces $r=2^a$ with a even, which implies that $p=1+r+r^2$ is divisible by 3, a contradiction. $\square$

Finally we consider the case $K=\lambda (X)$.

Lemma 4.8

Assume (4.1) holds. If $K= \lambda (X)$ then the conclusion of Lemma 4.2 holds.

Proof

Suppose $K=\lambda (X)$. Then Y / K acts faithfully on the partition${\fancyscript{P}}$, and so Y / K is a transitive group of degree p, and so by Proposition 2.3, is either affine or 2-transitive and almost simple.

If Y / K is affine, then $Y^{{\fancyscript{P}}}\leqslant {{\mathrm{AGL\,}}}(1,p)$, and so $\rho (T).K \triangleleft Y$. Since $\rho (T)$ centralises $K=\lambda (X)$, $\rho (T)$ is a characteristic subgroup of $\rho (T)K$ and hence $\rho (T) \triangleleft Y$. The $\rho (T)$-orbits in G are blocks of imprimitivity, and the conclusion of Lemma 4.2 holds. Thus we may assume that Y / K is almost simple with socle as in Table 2.

Let $K < L \leqslant Y$ be such that $L/K = {{\mathrm{Soc}}}(Y/K)$. We consider the derived group $L' \trianglelefteq L$. Since K has prime order, either $K \subseteq L'$ or $K \cap L' =1$.

Case 1 $K \cap L' =1$:

In this case K and $L'$ are normal subgroups which intersect trivially, and $L= L' \times K$. If $L'$ is intransitive then its orbits are blocks of size p, and the conclusion of Lemma 4.2 holds by Lemma 4.1. So we may assume that $L'$ is transitive. The argument in the proof of Lemma 4.7 shows that $L'={{\mathrm{PSL}}}(n,r)$ with n an odd prime and $p = \frac{r^n-1}{r-1}$. This time we have that $N_Y(\rho (T)) \leqslant (\lambda (X) \times \rho (T)).\mathbb {Z}_{n}.\mathbb {Z}_{f}$. So here we have that $\ell$ divides nfq (instead of nf).

Since $Y^{{\fancyscript{P}}}$ is 2-transitive, the quotient $\varGamma _{{\fancyscript{P}}} \cong K_p$. Moreover since ${\fancyscript{P}}$ is the set of $\lambda (X)$-orbits there is a constant c such that each vertex in B is joined to c vertices in each of the blocks distinct from B. Thus there are exactly $qc(p-1)$ edges of $\varGamma$ with one vertex in B. On the other hand this number is $|B|{{\mathrm{val}}}\varGamma = 2q\ell \le 2q^2nf$, and so again the inequality (4.2) holds: $p-1 \le 2nfq$.

Now the rest of the argument in the proof of Lemma 4.7 applies, ruling out all parameter values except possibly ${{\mathrm{PSL}}}(3,r)$ with $q=3$ and $(r,p) = (2,7)$ or (3, 13), for every $\ell$ dividing $p-1$ with $q\mid \ell$, and by assumption, $\ell < p-1$. This leaves only the parameters $(p,q,\ell ,i) = (7,3,3,1), (13,3,3,1),(13,3,6,1)$. A computer check of these graphs confirms that the conclusion of Lemma 4.2 holds in all cases.

Case 2 $K \subseteq L'$.

If $K \subseteq L'$ then L is a perfect central extension of L / K, and so (see [15, Chapter 5.1]), K is a subgroup of the Schur multiplier of L / K. Table 2 displays the Schur multipliers of the 2-transitive simple groups of prime degree: since q is an odd prime, we eliminate each case with a Schur multiplier of size less than 3. We are left with only two possibilities: $A_7$ and ${{\mathrm{PSL}}}(n,r)$. In the former case we have $p=7$, implying that $q=\ell =3$. Then the only parameter sets possible are (7, 3, 2, 1), (7, 3, 3, 1). The former yields the unique primitive example of Proposition 4.1, and the second is ruled out by computer search (as above in Case 1). In the latter case we have ${{\mathrm{PSL}}}(n,r)$, with $p=\frac{r^n-1}{r-1}$, in which case the Schur multiplier is cyclic of order $\gcd (r-1, n)$. Thus $q\mid r-1$ and $q\mid n$, and hence $p=1+r+\dots +r^{n-1} \equiv n\equiv 0 \pmod {q}$, but this implies $q \mid p$, which is a contradiction. $\square$

The proof of Lemma 4.2 now follows from Lemmas 4.5–4.8.

4.2 Blocks of size p

By Lemma 4.2, the partition ${\fancyscript{P}}=\{ Tg\mid g\in G\}$ is Y-invariant. Since by (3.2) $(z^{i})^{H} \subseteq z^i T$, the set $S \cap z^j T$ has order $\ell$ or 0, for any j. We dealt with the case $\ell =p-1$ in Lemma 3.3, and so we assume $\ell <{p-1}$. Recall that we also assume $(p,q,\ell )\ne (7,3,2)$.

Lemma 4.9

The quotient graph $\varGamma _{ T}$ is $K_2$ if $q=2$ and $C_q$ if q is odd, and $Y^{{\fancyscript{P}}}$ is $\mathbb {Z}_{2}$ or a subgroup of $D_{2q}$ containing $\mathbb {Z}_{q}$, respectively.

Proof

If $q=2$ then $\varGamma _{{\fancyscript{P}}} = K_2$ and $Y^{{\fancyscript{P}}}\cong \mathbb {Z}_{2}$, so assume that q is odd. Then $\varGamma _{{\fancyscript{P}}}={{\mathrm{Cay\,}}}(G/T, ST/T)$, and $|ST/T|=|((z^{i})^{H}T)/T|+|((z^{-i})^{H}T)/T|$. Since $\iota (H)$ fixes the cosets of T setwise, we have $((z^{i})^{H}T)/T= \{z^iT\}$, and so $|ST/T|=2$. So since $\varGamma _T$ is connected, it is a cycle. $\square$

Lemma 4.10

One of the following holds:

• (i) The kernel $K= Y_{({\fancyscript{P}})}$ is $\rho (T).\iota (H)$ with $\rho (T) \vartriangleleft Y$;

• (ii) $(p,q,\ell ,i) = (7,2,3,1), Y = {{\mathrm{PGL}}}(3,2).2$ and $\varGamma$ is the incidence graph of ${{\mathrm{PG}}}(2,2)$;

• (iii) $(p,q,\ell ,i) = (11,2,5,1), Y = {{\mathrm{PGL}}}(2,11)$ and $\varGamma$ is the incidence graph of the (11, 5, 2)-biplane; or

• (iv) $(p,q,\ell ,i) = (73,2,9,1), Y = {{\mathrm{P\Gamma L}}}(3,8).2$ and $\varGamma$ is the incidence graph of ${{\mathrm{PG}}}(2,8)$.

Proof

By Lemma 3.2 (i), $\iota (H)$ fixes each coset of T setwise, and so $\iota (H)\leqslant K$. Also since $T\triangleleft G$ it follows that $\rho (T)$ fixes each coset setwise, so $\rho (T)\leqslant K$. Thus it suffices to prove that either $|K|\leqslant p\ell$, or one of cases (ii)–(iv) holds.

Claim: $K\cong K^T$.

Let $T'$ be a block adjacent to T in $\varGamma _{{\fancyscript{P}}}$. The pointwise stabiliser $K_{(T)}$ is normal in K, and so $K_{(T)}^{T'} \triangleleft K^{T'}$, which is primitive (being transitive of prime degree) and is transitive or trivial. However $S \cap T'$ is fixed setwise by $K_{(T)}$, and $|S \cap T'| \le \ell < p$ so transitivity is impossible. Thus $K_{(T)}$ fixes $T'$ pointwise. Since $\varGamma$ is connected, we can repeat the same argument to show that $K_{(T)}$ acts trivially on every block, and so $K_{(T)}=1$, and hence $K\cong K^T$.

Since $\rho (T)\leqslant K$, K is transitive on each block of prime degree p, so by Proposition 2.3, this action is affine or 2-transitive and almost simple, and is given in Table 2. Assume first that the latter holds. Now each almost simple 2-transitive group has at most 2 inequivalent actions (see [6, Table 7.4]), and so if $q\ge 3$ then there exist at least two blocks on which K acts equivalently, and by Lemma 2.3, the actions of K on all blocks are equivalent.

If $q=2$ and the action of K on the two blocks T and Tz are inequivalent, then the only possibilities are $Y\leqslant {{\mathrm{PGL}}}(2,11)$ with $p=11$, or ${{\mathrm{PSL}}}(n,r)\leqslant Y \leqslant {{\mathrm{Aut\,}}}({{\mathrm{PSL}}}(n,r))$ with $p= \frac{r^n-1}{r-1}$ and n an odd prime. The former case can be checked by a GAP calculation, or by hand, for both $\ell = 2,5$: the graph $\varGamma (22,5,1)$ is the incidence graph of the (11, 5, 2)-biplane and $Y= {{\mathrm{PGL}}}(2,11)$, so part (iii) holds; and $K = \rho (T).\iota (H)$ holds for $\varGamma (22,2,1)\cong C_{22}$.

In the latter case $Y_{1}$ has orbits in Tz of sizes $\frac{r^{n-1}-1}{r-1}$ and $r^{n-1}$ and hence $\ell$ is one of these integers. Since $\ell$ divides $p-1$, we have $\ell = \frac{r^{n-1}-1}{r-1}$. However in this case a cycle of length $p = \frac{r^n-1}{r-1}$ in Y is a Singer cycle and the normaliser $N_Y(\rho (T))$ has size 2pnf, where $r=r_0^f$ with $r_{0}$ prime. So the stabiliser $(N)Y(\rho (T)))_1$ has size nf. Since this subgroup contains $\iota (H)$, it follows that $\ell$ divides nf. There are only two possible choices of parameters $(r_0,f,n)$ satisfying this constraint along with the constraint that $p=\frac{r^n-1}{r-1}$ is prime, namely $(r_0,f,n) = (2,1,3),(2,3,3)$. These sets produce the exceptional graphs $\varGamma (14,3,1)$ and $\varGamma (146,9,1)$, namely the incidence graphs of the Fano plane ${{\mathrm{PG}}}(2,2)$ and of ${{\mathrm{PG}}}(2,8)$, respectively, with $Y = {{\mathrm{P\Gamma L}}}(3,r).\mathbb {Z}_{2}$ so that part (iii) or (iv) holds, respectively. Assume now that none of parts (ii)–(iv) holds. Then (for all q) the K-actions on all blocks are equivalent. We now have that $K_1$ fixes a unique point $\alpha \in T'$. The set $T'\cap S$ of size $\ell$, where $1 <\ell < p-1$, is fixed setwise by $K_1$ and so $K_1 = K_\alpha$ is not transitive on $T' \setminus \{\alpha \}$. So $K^T$ is not 2-transitive, which is a contradiction.

This completes consideration of the case where $K^T$ is insoluble. Suppose now that $K^T \leqslant {{\mathrm{AGL\,}}}(1,p)$. Since $K^T$ is affine, all K-actions on blocks are equivalent and the stabiliser in $K^T$ of two points is trivial. Thus $K_1$ fixes a point $\alpha \in T'$, and $T \cap \varGamma (\alpha )$ is fixed setwise by $K_1$. Choose $\beta$ in this set: then the orbit-stabiliser theorem gives $|\beta ^{K_1}||K_{(1,\beta )}| = |K_1|$. But as $|\beta ^{K_1}| \le \ell$, we have $|K_1| \le \ell$, and so $|K| \le p\ell$ as required. $\square$

Proof

(Proof of Theorem 4.1 ) The four exceptional parameter sets are covered by Proposition 4.1 and Lemma 4.10, so we may assume that $(p,q,\ell ,i)\ne (7,3,2,1),(7,2,3,1), (11,2,5,1), (73,2,9,1)$. If $\ell = p-1$ the result follows from Lemma 3.3 so we may assume that $1 < \ell < p-1$. Then by Lemma 4.2, the cosets of T form a Y-invariant partition ${\fancyscript{P}}$ of $V\varGamma$, and by Lemmas 4.9 and 4.10, $Y^{{\fancyscript{P}}} \cong T/(\rho (T) \iota (H))$ is $\mathbb {Z}_{q}$ or $D_{2q}$. Thus $\rho (G)\iota (H)$ has index at most 2 in Y and hence is normal in Y.

Suppose first that $q\not \mid \ell$. Now $\rho (G)$ is characteristic in $\rho (G).\iota (H)$, as it is the unique Hall (p, q)-subgroup (since neither p nor q divides $\ell$), and hence $\rho (G) \triangleleft Y$, so Y is contained in the holomorph ${{\mathrm{Hol}}}(G)=\rho (G).{{\mathrm{Aut\,}}}(G)$ of G. If $Y^{\varGamma _T}$ were dihedral there would be an automorphism that fixes T and swaps the cosets $z^j T$ and $z^{-j}T$; but no such automorphism of G exists (see Lemma 3.1), and so $Y=\rho (G).\iota (H)$ in this case.

Now suppose that $q|\ell$. By Lemma 3.6 (iii), $\varGamma$ is a normal edge-transitive Cayley graph for the abelian group $\rho (T)\times \lambda (X)$. The map $\sigma : x\mapsto x^{-1}$ (where the vertex set of $\varGamma$ is identified with L) is an automorphism of L since L is abelian, and fixes $\varGamma (1)$ setwise. Moreover $\sigma$ is an automorphism of $\varGamma$. In fact it is in the normaliser $N_{Y}(\rho (L))$, but $\sigma$ is not contained in $\rho (G)\iota (H)$ as it swaps the cosets $Tz^i$ and $Tz^{-i}$ and fixes the subgroup T. So $\rho (G)\iota (H)$ has index 2 in Y and so $Y=\rho (G)\iota (H).\mathbb {Z}_{2}$.

$\square$