Multiparty Quantum Key Agreement Protocol with Entanglement Swapping

Abstract

Secure and fair multiparty quantum key agreement protocols demand all participants influence and negotiate the shared secret key with equal right and nobody can determine the shared secret key only by himself. To ensure the security and high efficiency, a novel multiparty quantum key agreement protocol based on entanglement swapping between Bell states and G-like states is proposed. This protocol makes full use of Bell states and G-like states as quantum resources and utilizes Bell measurement, Z-basis measurement and unitary operations to generate the shared secret key. It demonstrates that this proposed multiparty quantum key agreement protocol is secure and fair, and simpler with higher efficiency than some other protocols, especially when the number of participants in the protocol is big enough. Furthermore, the proposed protocol can be implemented with existing physical technologies.

1 Introduction

In the past few decades, quantum information technology has developed rapidly. With the development of quantum informatics, quantum cryptography has attracted more and more attention. Quantum cryptography exploits quantum informatics and other technologies to ensure unconditionally secure communications. Therefore, many kinds of quantum cryptographic protocols have been put forward, including quantum key distribution (QKD) [1,2,3,4,5,6], quantum oblivious transfer (QOT) [7, 8], quantum signature (QS) [9,10,11,12], quantum secret sharing (QSS) [13,14,15], quantum bit commitment (QBC) [16, 17], quantum secure direct communication (QSDC) [18,19,20], and so on.

Since the first quantum key distribution protocol was proposed by Bennett and Brassard in 1984 [1], quantum cryptography has made great progress. Recently, quantum key agreement (QKA) [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39] has become a new focus. Quantum key agreement protocol permits some parties to negotiate a classical shared secret key via public quantum channels. Moreover, each participant has a fair influence on the final key and the key can only be generated jointly by all participants.

The first quantum key agreement protocol [21] was proposed by Zhou et al. in 2004 by replacing a classical channel with a quantum one during quantum teleportation [40]. Inspired by this protocol, Hsueh and Chen put forward a QKA protocol with maximally entangled states in the same year [22]. However, Chong et al. believed that it was susceptible to participant attack [23]. In 2013, Yin et al. presented a tri-party QKA protocol with two-photon entanglement [27]. And in the same year, the first multiparty quantum key agreement protocol was proposed based on entanglement swapping without the help of a third party [24]. Liu et al. pointed out that the security of Shi’s protocol does not meet the actual requirement and then put forward a new multiparty quantum key agreement protocol with single particles [25]. Then Sun et al. improved Liu’s protocol based on unitary operations in 2013 [26]. Hereafter, a number of multiparty and two-party QKA protocols were proposed [29,30,31,32,33,34,35,36,37,38,39]. In 2017, Wang et al. put forward a circle-type multiparty QKA protocol to solve the problems of multiparty security communication and resist most common attacks [37]. In 2018, Cai et al. proposed a multi-party quantum key agreement protocol with five-qubit Brown states and single-qubit measurements, which weakens the hardware requirements of the participant but involving a large amount of calculations [38]. To counteract participants’ collusion attacks, Gong et al. proposed a novel multiparty quantum key agreement protocol with G-like states and Bell states in 2018 [39].

A new tri-party quantum key agreement protocol will be put forward based on entanglement swapping with Bell and G-like states. Furthermore, this proposed QKA protocol will be extended to a multiparty QKA protocol with a circle-type method. The proposed secure and fair protocol needs fewer calculations and is simpler than that in [38]. And the efficiency of the proposed protocol is higher than some other protocols when enough participants involve in the protocol. What’s more, the proposed protocol is feasible with real physical devices.

The structure of this paper is described as follows. In Section 2, the G-like and Bell states will be introduced. In Section 3, the tri-party QKA protocol with the seven-particle entangled state will be put forward. In Section 4, the multiparty QKA protocol extended by the tri-party QKA protocol will be proposed. In Section 5, the security and efficiency of this protocol will be analyzed. And in Section 6, a brief conclusion is provided.

2 Quantum States and Quantum Correlation Property

2.1 Bell States

Bell states are two-qubit entangled states. An EPR pair is one of the four Bell states and the four states are expressed as follows:

$$ \mid {\phi}^{+}\Big\rangle =\frac{1}{\sqrt{2}}\left(|00\Big\rangle +|11\Big\rangle \right), $$

(1)

$$ \mid {\phi}^{-}\Big\rangle =\frac{1}{\sqrt{2}}\left(|00\Big\rangle -|11\Big\rangle \right), $$

(2)

$$ \mid {\psi}^{+}\Big\rangle =\frac{1}{\sqrt{2}}\left(|01\Big\rangle +|10\Big\rangle \right), $$

(3)

$$ \mid {\psi}^{-}\Big\rangle =\frac{1}{\sqrt{2}}\left(|01\Big\rangle -|10\Big\rangle \right). $$

(4)

The entanglement swapping utilizing Bell measurements on Bell states was achieved by Shi et al. [24].

Suppose that ∣ϕ⁺〉₁₂ represents the entangled state ∣ϕ⁺〉 of particles 1 and 2 and ∣ψ⁺〉₃₄ indicates that particles 3 and 4 are in the entangled state ∣ψ⁺〉. If someone measures two particles 1 and 4 or 2 and 3 with the Bell basis, respectively, their measurement outcomes could be expressed as follows:

$$ {\displaystyle \begin{array}{c}\mid {\phi}^{+}\left\rangle {}_{12}\otimes \mid {\psi}^{+}\right\rangle {}_{34}=\frac{1}{\sqrt{2}}{\left(|00\Big\rangle +|11\Big\rangle \right)}_{12}\otimes \frac{1}{\sqrt{2}}{\left(|01\Big\rangle +|10\Big\rangle \right)}_{34}\\ {}=\frac{1}{2}{\left(|0001\Big\rangle +|0010\Big\rangle +|1101\Big\rangle +|1110\Big\rangle \right)}_{1234}\\ {}=\frac{1}{2}{\left(|0100\Big\rangle +|0001\Big\rangle +|1110\Big\rangle +|1011\Big\rangle \right)}_{1423}\\ {}=\frac{1}{2}\left(|{\phi}^{+}\Big\rangle {}_{14}|{\psi}^{+}\Big\rangle {}_{23}+|{\phi}^{-}\Big\rangle {}_{14}|{\psi}^{-}\Big\rangle {}_{23}+|{\psi}^{+}\Big\rangle {}_{14}|{\phi}^{+}\Big\rangle {}_{23}+|{\psi}^{-}\Big\rangle {}_{14}|{\phi}^{-}\Big\rangle {}_{23}\right)\end{array}} $$

(5)

If one encodes the states with the encoding rule such as: ∣ϕ⁺〉 → 00, ∣ϕ⁻〉 → 01, ∣ψ⁺〉 → 10 and ∣ψ⁻〉 → 11, then the correlation between the possible measurement results and the original Bell states can refer to [39]. If controlled-not (CONT) gates are utilized on their measurement outcomes, then the results will be

$$ {\displaystyle \begin{array}{c}\mid {\phi}^{+}\left\rangle {}_{12}\otimes \mid {\psi}^{+}\right\rangle {}_{34}=\frac{1}{\sqrt{2}}{\left(|00\Big\rangle +|11\Big\rangle \right)}_{12}\otimes \frac{1}{\sqrt{2}}{\left(|01\Big\rangle +|10\Big\rangle \right)}_{34}\\ {}=\frac{1}{2}{\left(|0001\Big\rangle +|0010\Big\rangle +|1101\Big\rangle +|1110\Big\rangle \right)}_{1234}\\ {}=\frac{1}{2}\mid 01\left\rangle {}_{14}\mid 00\right\rangle {}_{23}+\frac{1}{2}\mid 00\left\rangle {}_{14}\mid 01\right\rangle {}_{23}+\frac{1}{2}\mid 11\left\rangle {}_{14}\mid 10\right\rangle {}_{23}+\frac{1}{2}\mid 10\left\rangle {}_{14}\mid 11\right\rangle {}_{23}\end{array}}. $$

(6)

This shows that the result of the tensor product form of two Bell states can be separated into three systems. For example, these can be separated into two single particles and one pair of entangled particles.

2.2 GHZ-Like State

Quantum state $\mid G\Big\rangle =\frac{1}{2}\left(|001\Big\rangle +|010\Big\rangle +|100\Big\rangle +|111\Big\rangle \right)$ is called the GHZ-like state. It consists of a single particle and one EPR pair, that’s to say, the state ∣G〉 is obtained with the two states $\mid \varphi \Big\rangle {}_1=\frac{1}{\sqrt{2}}{\left(|0\Big\rangle +|1\Big\rangle \right)}_1$ and $\mid {\phi}^{+}\Big\rangle {}_{23}=\frac{1}{\sqrt{2}}{\left(|00\Big\rangle +|11\Big\rangle \right)}_{23}$. The specific process is

$$ {\displaystyle \begin{array}{c}\mid {G}_0\left\rangle {}_{123}=\mid \varphi \right\rangle {}_1\mid {\phi}^{+}\Big\rangle {}_{23}=\frac{1}{\sqrt{2}}{\left(|0\Big\rangle +|1\Big\rangle \right)}_1\otimes \frac{1}{\sqrt{2}}{\left(|00\Big\rangle +|11\Big\rangle \right)}_{23}\\ {}=\frac{1}{2}{\left(|000\Big\rangle +|011\Big\rangle +|100\Big\rangle +|111\Big\rangle \right)}_{123}\end{array}}, $$

(7)

where the subscript denotes the particle’s sequence number of the state ∣G₀〉. By performing controlled-not (CNOT) gate on ∣G₀〉₁₂₃, the result will be

$$ {\displaystyle \begin{array}{c}\mid {G}_0\Big\rangle {}_{123}=\frac{1}{2}{\left(|000\Big\rangle +|011\Big\rangle +|100\Big\rangle +|111\Big\rangle \right)}_{123}\\ {}=\frac{1}{\sqrt{2}}\left(|0\Big\rangle {}_1|{\phi}^{+}\Big\rangle {}_{23}+|1\Big\rangle {}_1|{\phi}^{+}\Big\rangle {}_{23}\right)\end{array}} $$

(8)

Similar to the Bell state, the GHZ-like state is divided into two systems, i.e., a single particle and an EPR pair.

3 Tri-Party QKA Protocol

Assume that U₀₀, U₀₁, U₁₀, U₁₁ indicate the four local unitary operations.

$$ {U}_{00}=\left(\begin{array}{cc}1& 0\\ {}0& 1\end{array}\right),{U}_{01}=\left(\begin{array}{cc}0& 1\\ {}1& 0\end{array}\right),{U}_{10}=\left(\begin{array}{cc}0& 1\\ {}-1& 0\end{array}\right),{U}_{11}=\left(\begin{array}{cc}1& 0\\ {}0& -1\end{array}\right). $$

(9)

∣0〉 and ∣1〉 form Z-basis, while ∣ + 〉 and ∣ − 〉 form X-basis, where $\mid \pm \Big\rangle =\frac{1}{\sqrt{2}}\left(|0\Big\rangle \pm |1\Big\rangle \right)$. All the transformations on the Bell states based on the four unitary operations are in Table 1.

Table 1 Transformations on Bell states

According to entanglement swapping and the specific correlation among the measurement results, a novel tri-party QKA protocol with Bell states and G-like states is proposed. The specific states used in this protocol are as follows:

$$ \mid {\phi}^{+}\left\rangle {}_{12}\mid G\right\rangle {}_{345}\mid {\phi}^{+}\Big\rangle {}_{67}=\frac{1}{4}{\left(|00\Big\rangle +|11\Big\rangle \right)}_{12}\otimes {\left(|001\Big\rangle +|010\Big\rangle +|101\Big\rangle +|110\Big\rangle \right)}_{345}\otimes {\left(|00\Big\rangle +|11\Big\rangle \right)}_{67} $$

(10)

By taking advantage of controlled-not (CNOT) gate on the particles 1, 3 and 6 of Eq. (10) and representing the decimal number with bold, Eq. (10) can be rewritten as:

$$ {\displaystyle \begin{array}{c}\mid {\phi}^{+}\left\rangle {}_{12}\mid G\right\rangle {}_{345}\mid {\phi}^{+}\left\rangle {}_{67}=\frac{1}{4}\right(\mid \mathbf{4}\left\rangle +\mid \mathbf{7}\right\rangle +\mid \mathbf{8}\left\rangle +\mid \mathbf{1}\mathbf{1}\right\rangle +\mid \mathbf{2}\mathbf{0}\left\rangle +\mid \mathbf{2}\mathbf{3}\right\rangle +\mid \mathbf{2}\mathbf{4}\left\rangle +\mid \mathbf{2}\mathbf{7}\right\rangle +\mid \mathbf{1}\mathbf{0}\mathbf{0}\Big\rangle \\ {}+\mid \mathbf{1}\mathbf{0}\mathbf{3}\left\rangle +\mid \mathbf{1}\mathbf{0}\mathbf{4}\right\rangle +\mid \mathbf{1}\mathbf{0}\mathbf{7}\left\rangle +\mid \mathbf{1}\mathbf{1}\mathbf{6}\right\rangle +\mid \mathbf{1}\mathbf{1}\mathbf{9}\left\rangle +\mid \mathbf{1}\mathbf{20}\right\rangle +\mid \mathbf{1}\mathbf{23}\left\rangle \right){}_{1234567}\\ {}=\frac{1}{4}\mid \mathbf{0}\left\rangle {}_{136}{\left(|\mathbf{2}\Big\rangle +|\mathbf{4}\Big\rangle \right)}_{2457}+\frac{1}{4}\mid \mathbf{1}\right\rangle {}_{136}{\left(|\mathbf{3}\Big\rangle +|\mathbf{5}\Big\rangle \right)}_{2457}\\ {}+\frac{1}{4}\mid \mathbf{2}\left\rangle {}_{136}{\left(|\mathbf{2}\Big\rangle +|\mathbf{4}\Big\rangle \right)}_{2457}+\frac{1}{4}\mid \mathbf{3}\right\rangle {}_{136}{\left(|\mathbf{3}\Big\rangle +|\mathbf{5}\Big\rangle \right)}_{2457}\\ {}+\frac{1}{4}\mid \mathbf{4}\left\rangle {}_{136}{\left(|\mathbf{10}\Big\rangle +|\mathbf{12}\Big\rangle \right)}_{2457}+\frac{1}{4}\mid \mathbf{5}\right\rangle {}_{136}{\left(|\mathbf{11}\Big\rangle +|\mathbf{13}\Big\rangle \right)}_{2457}\\ {}+\frac{1}{4}\mid \mathbf{6}\left\rangle {}_{136}{\left(|\mathbf{10}\Big\rangle +|\mathbf{12}\Big\rangle \right)}_{2457}+\frac{1}{4}\mid \mathbf{7}\right\rangle {}_{136}{\left(|\mathbf{11}\Big\rangle +|\mathbf{13}\Big\rangle \right)}_{2457}\end{array}} $$

(11)

Equation (11) can also be expanded with the Bell bases as follows:

$$ {\displaystyle \begin{array}{c}\mid {\phi}^{+}\left\rangle {}_{12}\mid G\right\rangle {}_{345}\mid {\phi}^{+}\left\rangle {}_{67}=\frac{1}{8}\mid \mathbf{0}\right\rangle {}_{136}\left(\mid {\phi}^{+}\right\rangle {}_{24}\mid {\psi}^{+}\left\rangle {}_{57}-\mid {\phi}^{+}\right\rangle {}_{24}\mid {\psi}^{-}\left\rangle {}_{57}+\mid {\phi}^{-}\right\rangle {}_{24}\mid {\psi}^{+}\left\rangle {}_{57}-\mid {\phi}^{-}\right\rangle {}_{24}\mid {\psi}^{-}\Big\rangle {}_{57}\\ {}+\mid {\psi}^{+}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}+\mid {\psi}^{+}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}+\mid {\psi}^{-}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}+\mid {\psi}^{-}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}\Big)\\ {}+\frac{1}{8}\mid \mathbf{1}\left\rangle {}_{136}\right(\mid {\phi}^{+}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}-\mid {\phi}^{+}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}+\mid {\phi}^{-}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}-\mid {\phi}^{-}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}\\ {}+\mid {\psi}^{+}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}+\mid {\psi}^{+}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}+\mid {\psi}^{-}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}+\mid {\psi}^{-}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}\Big)\\ {}+\frac{1}{8}\mid \mathbf{2}\left\rangle {}_{136}\right(\mid {\phi}^{+}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}-\mid {\phi}^{+}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}+\mid {\phi}^{-}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}-\mid {\phi}^{-}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}\\ {}+\mid {\psi}^{+}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}+\mid {\psi}^{+}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}+\mid {\psi}^{-}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}+\mid {\psi}^{-}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}\Big)\\ {}+\frac{1}{8}\mid \mathbf{3}\left\rangle {}_{136}\right(\mid {\phi}^{+}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}-\mid {\phi}^{+}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}+\mid {\phi}^{-}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}-\mid {\phi}^{-}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}\\ {}+\mid {\psi}^{+}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}+\mid {\psi}^{+}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}+\mid {\psi}^{-}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}+\mid {\psi}^{-}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}\Big)\\ {}+\frac{1}{8}\mid \mathbf{4}\left\rangle {}_{136}\right(\mid {\phi}^{+}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}-\mid {\phi}^{-}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}+\mid {\phi}^{+}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}-\mid {\phi}^{-}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}\\ {}+\mid {\psi}^{+}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}-\mid {\psi}^{+}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}+\mid {\psi}^{-}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}-\mid {\psi}^{-}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}\Big)\\ {}+\frac{1}{8}\mid \mathbf{5}\left\rangle {}_{136}\right(\mid {\psi}^{+}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}-\mid {\psi}^{-}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}+\mid {\psi}^{+}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}-\mid {\psi}^{-}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}\\ {}+\mid {\phi}^{+}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}-\mid {\phi}^{-}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}+\mid {\phi}^{+}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}-\mid {\phi}^{-}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}\Big)\\ {}+\frac{1}{8}\mid \mathbf{6}\left\rangle {}_{136}\right(\mid {\phi}^{+}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}-\mid {\phi}^{-}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}+\mid {\phi}^{+}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}-\mid {\phi}^{-}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}\\ {}+\mid {\psi}^{+}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}-\mid {\psi}^{+}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}+\mid {\psi}^{-}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}-\mid {\psi}^{-}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}\Big)\\ {}+\frac{1}{8}\mid \mathbf{7}\left\rangle {}_{136}\right(\mid {\psi}^{+}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}-\mid {\psi}^{-}\left\rangle {}_{24}\mid {\phi}^{+}\right\rangle {}_{57}+\mid {\psi}^{+}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}-\mid {\psi}^{-}\left\rangle {}_{24}\mid {\phi}^{-}\right\rangle {}_{57}\\ {}+\mid {\phi}^{+}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}-\mid {\phi}^{-}\left\rangle {}_{24}\mid {\psi}^{+}\right\rangle {}_{57}+\mid {\phi}^{+}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}-\mid {\phi}^{-}\left\rangle {}_{24}\mid {\psi}^{-}\right\rangle {}_{57}\Big)\end{array}} $$

(12)

According to Eq. (12), the state may collapse into any one of the 64 states with equal probability when the state is measured.

Assume that three participants, i.e., Alice, Bob and Charlie have to generate their own secret keys, i.e., K_A, K_B and K_C, respectively, and then they need to establish a shared secret key K.

$$ {K}_P=\left\{{k}_{P_i}|{k}_{P_i}\in \left\{0,1\right\},i=1,2,\dots, n.\right\},P\in \left(A,B,C\right). $$

(13)

$$ K={K}_A\oplus {K}_B\oplus {K}_C. $$

(14)

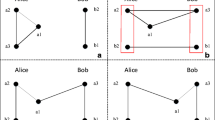
Then the tri-party quantum key agreement protocol as shown in Fig. 1 can be described as follows.

• Step 1 State preparation. State preparation is shown in Fig. 1a. (a) Alice prepares n entangled states ∣ϕ⁺〉₁₂ and divides these entangled states into two ordered states a₁ and a₂. (b) Bob generates n GHZ-like states in ∣G〉₃₄₅ and divides them into three ordered sequences b₁, b₂ and b₃. (c) Charlie produces n entangled Bell states as same as Alice, and also divides them into two ordered sequences c₁ and c₂.

• Step 2 Insertion of decoy states. Three participants randomly select enough decoy photons in the four states ∣0〉, ∣ 1〉, ∣  + 〉, ∣  − 〉. (a) Alice inserts some decoy states into a₂ at random and obtains ${a}_2^{\hbox{'}}$. (b) Bob randomly plugs some decoy states into b₂ and b₃ to produce ${b}_2^{\hbox{'}}$ and ${b}_3^{\hbox{'}}$, respectively. (c) Charlie also inserts some decoy states into c₂ at random to generate ${c}_2^{\hbox{'}}$ (Please refer to Fig. 1b.). (d) Subsequently, Alice (Bob) sends the mixed sequence ${a}_2^{\hbox{'}}$ (${b}_2^{\hbox{'}}$) to Bob (Alice), and Bob (Charlie) transmits the new sequence ${b}_3^{\hbox{'}}$ (${c}_2^{\hbox{'}}$) to Charlie (Bob) (Please refer to Fig. 1c.).

• Step 3 Channel security check. (a) After three participants confirm that all the sequences have received, they announce the positions of the decoy states and the corresponding preparation bases. (b) Then all the receivers measure the decoy states with the correct bases and tell the measurement outcomes to the corresponding sender. (c) All the senders and the corresponding receivers check the security of quantum channels by comparing the measurement results. Once the error rate exceeds the preset value, this round of communication should be aborted. Otherwise, they continue.

• Step 4 Bell measurement. Three participants pick out the decoy states in their state sequences and then Alice obtains the state sequence b₂, Bob gains the state sequences a₂ and c₂, Charlie obtains the state sequence b₃ (Please refer to Fig. 1d.). Then they perform the Bell measurement on their remaining sequences, respectively (Please refer to Fig. 1e.).

• Step 5 Bell measurement and insertion of decoy states. (a) Alice and Charlie perform a series of unitary operations chosen from {U₀₀, U₀₁, U₁₀, U₁₁} on each state in state sequences a₁ and c₁ and form new sequences ${a}_1^{\hbox{'}}$ and ${c}_1^{\hbox{'}}$. (b) Subsequently, Alice and Charlie insert enough decoy states randomly selected from the four states {| 0〉, | 1〉, | +〉, | −〉} into ${a}_1^{\hbox{'}}$ and ${c}_1^{\hbox{'}}$ to generate two new sequences ${a}_1^{\hbox{'}\hbox{'}}$ and ${c}_1^{\hbox{'}\hbox{'}}$ (Please refer to Fig. 1f.). (c) Alice (Charlie) sends sequence ${a}_1^{\hbox{'}\hbox{'}}$ (${c}_1^{\hbox{'}\hbox{'}}$) to Charlie (Alice) (Please refer to Fig. 1g.).

• Step 6 Channel security check. (a) After Alice (Charlie) acknowledges sequence ${c}_1^{\hbox{'}\hbox{'}}$ (${a}_1^{\hbox{'}\hbox{'}}$), Charlie (Alice) announces the positions of the decoy states and the corresponding preparation bases. (b) Subsequently, Alice (Charlie) measures the decoy states with the correct bases and tells the measurement results to Charlie (Alice). (c) Then two parties compare the measurement results. If the error rate exceeds the threshold, this round of communication must be abandoned. Otherwise, they continue.

• Step 7 Measurement and generation of shared key. (a) After removing the decoy states, Alice obtains sequence ${c}_1^{\hbox{'}}$ and Charlie gains sequence ${a}_1^{\hbox{'}}$. Then Alice and Charlie perform the Bell measurement on their sequences. (b) Bob performs the Z-basis measurement on every state in sequence b₁ and tells Alice and Charlie the measurement outcomes. (c) Apparently, Alice (Charlie) holds sequences b₂ and ${c}_1^{\hbox{'}}$ (${a}_1^{\hbox{'}}$ and b₃) and also knows the measurement results of b₁ while Bob possesses sequences b₁, a₂ and c₂ (Please refer to Fig. 1h.). (d) According to the measurement outcomes, each of the three participants can obtain the other two counterparts’ secret keys. Therefore, the three participants can compute the shared key as: K = K_A ⊕ K_B ⊕ K_C.

  Fig. 1

  

  Entanglement swapping of three parties

4 Multiparty QKA Protocol

For the multiparty case, circle-type multiparty quantum key agreement protocols are popular. To improve the efficiency significantly, the three participants in the proposed tri-party quantum key agreement protocol are regarded as a group to construct a new circle-type multiparty quantum key agreement protocol. The process of this multiparty QKA protocol is in the following.

• Step 1 Subkey generation. Assume that there are 3n participants, and all the participants are classified into three groups, i.e., A = {a_i| i = 1, 2, …, n}, B = {b_i| i = 1, 2, …, n} and C = {c_i| i = 1, 2, …, n}. (a) All the participants in groups A and C prepare Bell states, while all the participants in group B prepare the GHZ-like states. (b) All participants are regrouped into n groups and there are three participants (a_i, b_i, c_i) in each group. (c) Each group performs the tri-party quantum key agreement protocol described in Section 3 once to generate secret subkey, denoted by {K_i| i = 1, 2, …, n}.

• Step 2 Construction of circle-type MQKA protocol. All the participants from group A construct a circle-type multiparty QKA protocol at random, then the participants are randomly re-marked as R_i and R_i ∈ A. Every participant does not know who the two adjacent participants are. The circle-type multiparty QKA protocol is described in Fig. 2.

• Step 3 State preparation and insertion of decoy states. (a) Each participant in R_i prepares n Bell states and divides them into two ordered sequences s_i and l_i. Sequence s_i includes all the first particles of the EPR pairs, while sequence l_i includes all the second particles of the EPR pairs. (b) R_i randomly inserts enough decoy states in state ∣0〉, ∣1〉, ∣ + 〉 or ∣ − 〉 into s_i to obtain ${s}_i^1$. (c) R_i sends the mixed state sequence ${s}_i^1$ to R_i + 1.

• Step 4 Channel security check. (a) After R_i + 1 receives the state sequence ${s}_i^1$, R_i announces the positions of the decoy states and the corresponding measurement bases to R_i + 1. (b) Subsequently, R_i + 1 measures the decoy states with correct bases and tells R_i the measurement outcomes. (c) R_i and R_i + 1 check whether the measurement results are consistent with the initial states of the decoy states or not and calculate the error rate in the measurement outcomes. If the error rate exceeds the threshold, this protocol should be aborted. Otherwise, they continue.

• Step 5 Unitary operation and insertion of decoy states. (a) R_i + 1 picks out the decoy states to obtain the state sequence s_i and obtains the secret subkey K_i. (b) Subsequently, R_i + 1 performs a series of unitary operations chosen from {U₀₀, U₀₁, U₁₀, U₁₁} on each state in ${s}_i^1$. (c) Then R_i + 1 randomly selects and inserts enough decoy states in state ∣0〉, ∣1〉, ∣ + 〉 or ∣ − 〉 into ${s}_i^1$ to obtain ${s}_i^2$. (d) R_i + 1 sends the mixed sequence ${s}_i^2$ to R_i + 2.

• Step 6 Sequential operation. The participants R_i + 2, R_i + 3, …, R_i − 1 execute Step 4 and Step 5 in sequence in the same way as R_i. For security and simplicity, all participants should carry out the eavesdropping check first. Once the quantum channel is insecure, they give up this protocol. Otherwise, they perform specific unitary operations on ${s}_i^j$ and insert enough decoy photons into ${s}_i^j\left(j=0,1,\dots, n\right)$. After that, they send the mixed sequence to next participant.

• Step 7 Generation of secret key. When all the participants execute Steps 2–6, a round of circle communication is finished, and then sequence ${s}_i^n$ will return to participant R_i. R_i can generate the key K = K₁ ⊕ K₂ ⊕ … ⊕ K_n according to the quantum measurement results and the quantum entanglement property.

• Step 8 Intra-group transmission. Every group carries out transfer operation. Then the other two participants can also obtain the shared secret keys.

  Fig. 2

  

  The circle-type multiparty QKA protocol

5 Analysis and Discussion

What a quantum key agreement protocol needs to guarantee firstly is its security. So in this section, the ability of the proposed protocol against all kinds of attacks will be discussed.

5.1 Participant Attack

In order to ensure the security of the proposed tri-party QKA protocol, the delayed measurement technique [41] is adopted. In the multiparty QKA protocol, collusive attack with participants is the biggest security risk, since the dishonest participants may collaborate to predetermine the key without being detected [42]. In this protocol, however, it is impossible for R_i to find the corresponding dishonest participant because no participant knows the positions of other participant groups. Generally, a dishonest participant R_i may adopt three different methods to cheat other legal participants: (1) extracting all the subkeys’ information in the sequences and obtaining the final shared secret key before other participants. (2) announcing the wrong decoy positions to others to destroy this protocol. (3) finding the corresponding dishonest participants to obtain the final shared secret key.

For the first method, R_i cannot obtain the final shared secret key in advance. In fact, R_i must gain all the participants’ subkeys if he wants to obtain the final shared secret key. However, during the process of the proposed multiparty QKA protocol, each participant sends the state sequence with decoy particles, and all the participants sends their state sequence at the same time, so R_i cannot obtain the final shared secret key before other participants.

For the second method, if R_i announces the wrong positions of the decoy particles to other participants, the protocol must be abandoned. The state sequences that all the participants send to others are mixed state sequences. After each transmission of these state sequences, the receiver and the corresponding sender would check the channel by comparing the positions of decoy particles. If R_i announces the wrong positions of decoy particles, the corresponding sender will definitely find that R_i is dishonest and the protocol must be abandoned by other participants.

For the third method, R_i cannot find corresponding dishonest participants. From Step 2 in Section 4, it is known that every participant does not know who the two adjacent participants are, so even if R_i knows that there are other dishonest participants, he cannot find them since he does not know their positions.

5.2 Outsider Attack

5.2.1 Entangle-Measure Attack

If Eve makes use of entangle-measure attack, she intercepts the sequence transmitted in the quantum channel and entangles it with a pre-prepared intermediate state sequence, and then Eve resends the intercepted sequence to the corresponding participants. When the protocol is finished, Eve measures the intermediate state sequence, and then she will attempt to extract some useful information and obtain the final shared secret key. Assume that Eve intercepts the sequence sent from Alice to Bob, and she intercepts other sequences in the same way. Without loss of generality, Eve’s unitary operation U_e can be described as follows:

$$ {U}_{\mathrm{e}}\mid 0\left\rangle \mid E\right\rangle ={a}_e\mid 0\left\rangle \mid {e}_{00}\right\rangle +{b}_e\mid 1\left\rangle \mid {e}_{01}\right\rangle, $$

(15)

$$ {U}_{\mathrm{e}}\mid 1\left\rangle \mid E\right\rangle ={\mathrm{c}}_e\mid 0\left\rangle \mid {e}_{10}\right\rangle +{d}_e\mid 1\left\rangle \mid {e}_{11}\right\rangle, $$

(16)

where ∣e₀₀〉, ∣e₀₁〉, ∣e₁₀〉 and ∣e₁₁〉 are pure states and |a_e|² + |b_e|² = 1, |c_e|² + |d_e|² = 1. In the proposed protocol, all the decoy states are chosen from {| 0〉, | 1〉, | +〉, | −〉}, therefore the states ∣ + 〉 and ∣ − 〉 will become the following entangled states after Eve’s entanglement operations.

$$ {\displaystyle \begin{array}{l}\begin{array}{c}{U}_e\mid +\left\rangle \mid E\right\rangle =\frac{1}{\sqrt{2}}\left({a}_e|0\Big\rangle |{e}_{00}\Big\rangle +{b}_e|1\Big\rangle |{e}_{01}\Big\rangle +{c}_e|0\Big\rangle |{e}_{10}\Big\rangle +{d}_e|1\Big\rangle |{e}_{11}\Big\rangle \right)\\ {}=\frac{1}{2}\left\{+\Big\rangle \left({a}_e|{e}_{00}\Big\rangle +{b}_e|{e}_{01}\Big\rangle +{c}_e|{e}_{10}\Big\rangle +{d}_e|{e}_{11}\Big\rangle \right)\right\}\\ {}+\frac{1}{2}\left\{-\Big\rangle \left({a}_e|{e}_{00}\Big\rangle -{b}_e|{e}_{01}\Big\rangle +{c}_e|{e}_{10}\Big\rangle -{d}_e|{e}_{11}\Big\rangle \right)\right\}\end{array},\\ {}\kern2.16em \\ {}\kern2.28em \end{array}} $$

(17)

$$ {\displaystyle \begin{array}{c}{U}_e\mid -\left\rangle \mid E\right\rangle =\frac{1}{\sqrt{2}}\left({a}_e|0\Big\rangle |{e}_{00}\Big\rangle +{b}_e|1\Big\rangle |{e}_{01}\Big\rangle -{c}_e|0\Big\rangle |{e}_{10}\Big\rangle -{d}_e|1\Big\rangle |{e}_{11}\Big\rangle \right)\\ {}=\frac{1}{2}\left\{\mid +\Big\rangle \left({a}_e|{e}_{00}\Big\rangle +{b}_e|{e}_{01}\Big\rangle -{c}_e|{e}_{10}\Big\rangle -{d}_e|{e}_{11}\Big\rangle \right)\right\}\\ {}+\frac{1}{2}\left\{\mid -\Big\rangle \left({a}_e|{e}_{00}\Big\rangle -{b}_e|{e}_{01}\Big\rangle -{c}_e|{e}_{10}\Big\rangle +{d}_e|{e}_{11}\Big\rangle \right)\right\}\end{array}}. $$

(18)

If Eve guarantees no errors introduced in the eavesdropping check process, the general operation U_e must satisfy the conditions such as: a_e = d_e = 1, b_e = c_e = 0 and ∣e₀₀〉 =  ∣ e₁₁〉. So Eqs. (15) and (16) will become

$$ {U}_{\mathrm{e}}\mid 0\left\rangle \mid E\right\rangle =\mid 0\left\rangle \mid {e}_{00}\right\rangle, $$

(19)

$$ {U}_{\mathrm{e}}\mid 1\left\rangle \mid E\right\rangle =\mid 1\left\rangle \mid {e}_{11}\right\rangle . $$

(20)

From Eqs. (17)–(20), it is shown that iff the message qubits and decoy particles are both in the state ∣0〉 or ∣1〉, Eve may not be found when she attacks the proposed protocol. However, in the protocol, all the decoy particles are in the state ∣0〉, ∣1〉 ∣ + 〉 or ∣ − 〉 randomly. So it is easy for the participants to detect eavesdropper Eve and it is necessary for Eve to fail to obtain the final shared secret key by the entangle-measure attack strategy.

From Eqs. (15)–(20), it is clear that the error rate introduced by eavesdropper Eve will be: p_{e, 1} = 1 − |a_e|² or p_{e, 2} = 1 − |d_e|². Then the mutual information between Alice and Bob will be

$$ {I}_{e,1}\left(A,B\right)=1+{\left|{a}_e\right|}^2{\log}_2{\left|{a}_e\right|}^2+\left(1-{\left|{a}_e\right|}^2\right){\log}_2\left(1-{\left|{a}_e\right|}^2\right), $$

(21)

or

$$ {I}_{e,1}\left(A,B\right)=1+{\left|{d}_e\right|}^2{\log}_2{\left|{d}_e\right|}^2+\left(1-{\left|{d}_e\right|}^2\right){\log}_2\left(1-{\left|{d}_e\right|}^2\right). $$

(22)

If Eve utilizes the intermediate state sequence, Bob will gain the wrong measurement outcomes with the probability p_e,3 = |b_e|² + |c_e|², and the mutual information between Bob and Eve will be

$$ {I}_E\left(A,B\right)=1+\left({\left|{a}_e\right|}^2+{\left|{d}_e\right|}^2\right){\log}_2\left({\left|{a}_e\right|}^2+{\left|{d}_e\right|}^2\right)+\left({\left|{b}_e\right|}^2+{\left|{c}_e\right|}^2\right){\log}_2\left({\left|{b}_e\right|}^2+{\left|{c}_e\right|}^2\right). $$

(23)

Recalling Eqs. (21)–(23), one can obtain

$$ {I}_E\left(A,B\right)<{I}_{e,1}\left(A,B\right). $$

(24)

From Eq. (24), it is apparent that the mutual information with eavesdropping will be less than that without eavesdropping. So eavesdropper can be found easily by the participants.

Therefore, if Eve wants to gain the final shared secret key by making use of entangle-measure attack, she will be found by the participants easily, so she must fail and the protocol can effectively resist the entangle-measure attack.

5.2.2 Trojan Horse Attack

The multiparty QKA protocol may be insecure under the Trojan horse attack, since a certain number of particles are transferred more than once. Fortunately, a method to resist the Trojan horse attack was presented by Sun et al. [29] with circular quantum transmission [43, 44]. In the method, every participant should install a wavelength quantum filter to filter the invisible photons and the photon number splitters to discover the delay photons. If there is an irrational high rate of multi-photon signal, the eavesdropper can be detected. Therefore, it is impossible for the eavesdropper to obtain the final secret key by the Trojan horse attack, and the protocol can effectively resist the Trojan horse attack.

5.2.3 Intercept-Resend Attack

In the tri-party QKA protocol, Alice, Bob and Charlie need to send sequences to the other two participants. For instance, we just analyze the case that Alice sends state sequence ${a}_2^{\hbox{'}}$ to Bob and other state sequence transmissions are similar. When Alice sends the state sequence ${a}_2^{\hbox{'}}$ to Bob, assume that Eve can intercept state sequence ${a}_2^{\hbox{'}}$. All the states in sequence ${a}_2^{\hbox{'}}$ are as follows:

$$ {\rho}_{a_2^{\hbox{'}}}={\mathrm{tr}}_{a_1}\mid \varphi \left\rangle \right\langle \varphi \mid =\frac{1}{2}\left(\mid 0\right\rangle \left\langle 0|+|1\right\rangle \left\langle 1\mid \right). $$

(25)

Obviously, Eve can’t gain any information from the intercepted state sequence, for the state sequence ${a}_2^{\hbox{'}}$ is in the mixed state with decoy particles. For instance, Eve prepares an auxiliary state sequence and it is in the state ∣φ〉_e = α ∣ 0〉 + β ∣ 1〉 (|α|² + |β|² = 1). After intercepting ${a}_2^{\hbox{'}}$, Eve sends the auxiliary state sequence to Bob. But when Bob receives the state sequence, he will measure it by corresponding measurement bases from Alice. Assume that Alice informs Bob the positions of the decoy particles and Bob measures the decoy particles with computational bases {| 0〉, | 1〉}. After measuring the decoy particles, Bob can gain the measurement outcomes 0 or 1 with probability |α|² or |β|², which means the error rate with Eve is |α|² or |β|². Afterwards, Bob’s information can be expressed as [6]:

$$ {H}_e(B)=-{\left|\alpha \right|}^2{\log}_2{\left|\alpha \right|}^2-{\left|\beta \right|}^2{\log}_2{\left|\beta \right|}^2\le 1\ \mathrm{bit}, $$

(26)

where H denotes the Shannon entropy. According to the definition, the Shannon entropy can be expressed by:

$$ H(X)=-\sum \limits_x{p}_x{\log}_2{p}_x, $$

(27)

where X is a variable number and p_x is the presence probability of X [45]. From Eq. (26), it can be obtained that H_e(B) = 1 only if ${\left|\alpha \right|}^2={\left|\beta \right|}^2=\frac{1}{2}$. If eavesdropper Eve exists, the mutual information between Alice and Bob is

$$ {I}_e\left(A,B\right)={H}_e(B)-{H}_e\left(B|A\right)<{H}_e(B)\le 1\ \mathrm{bit}, $$

(28)

where H_e(B| A) denotes conditional entropy, and it is the expected entropy of Bob given the value of Alice and H_e(B| A) > 0.

According to the Holevo limit [45], if Eve does not exist, the mutual information is

$$ I\left(A,B\right)\le S\left(\rho \right)-\sum \limits_x{p}_xS\left({\rho}_x\right), $$

(29)

where S(ρ) =  − tr(ρlog₂ρ) is the von Neumann entropy of state $\rho =\sum \limits_x{p}_x{\rho}_x$. In the tri-party QKA protocol, $\mid {\phi}^{+}\Big\rangle {}_{12}=\frac{1}{\sqrt{2}}{\left(|00\Big\rangle +|11\Big\rangle \right)}_{12}$ is the maximal entangled state in sequences a₁ and a₂ (${a}_2^{\hbox{'}}$). Each particle in the state sequences a₁ and ${a}_2^{\hbox{'}}$ is

$$ {\rho}_{a_2^{\hbox{'}}}={\rho}_{a_1}=\frac{1}{2}\left(\mid 0\right\rangle \left\langle 0|+|1\right\rangle \left\langle 1\mid \right)=\frac{1}{2}\left[\begin{array}{l}0\ 1\\ {}1\ 0\end{array}\right]=\frac{1}{2}I. $$

(30)

So if there is no eavesdropper, the mutual information between Alice and Bob is

$$ I\left(A,B\right)=S\left(\rho \right)=-\sum \limits_x{\lambda}_x{\log}_2{\lambda}_x=1\ \mathrm{bit}, $$

(31)

where λ_x denotes the eigenvalue of state ρ. Combining Eq. (28) with Eq. (31), one obtains

$$ {I}_e\left(A,B\right)<I\left(A,B\right). $$

(32)

It is clear that the mutual information between Alice and Bob with eavesdropping will be less than that without eavesdropping. Therefore, if Eve wants to gain the shared secret key with the intercept-resend attack, Alice and Bob will easily find Eve’s interception attack.

For Eve’s interception attack, if Eve initially prepares Bell states instead of a state sequence with single particles, then Eve should send one state sequence of these EPR pairs and reserve the other state sequence. Suppose Alice also informs Bob to measure the decoy particles with computational bases {| 0〉, | 1〉, | +〉, | −〉}. There is no correlation between the state sequence received by Bob and Alice’s corresponding state sequence, therefore the probability that Bob’s measurement outcomes are same as Alice’s is 0.25. Statistically, the probability that the Bell state Eve prepared is $\mid {\phi}^{+}\Big\rangle =\frac{1}{\sqrt{2}}\left(|00\Big\rangle +|11\Big\rangle \right)$ is only 0.25. Therefore, the total probability that Eve is successfully found by Alice and Bob is ${p}_e=1-\frac{1}{16^n}$. In the tri-party QKA protocol, the transmission of six sequences is involved, so the total probability during the whole protocol that Eve is successfully found by Alice and Bob is ${p}_e=1-{\left(\frac{1}{16^n}\right)}^6$ and it is very difficult for Eve to obtain the shared secret key with this attack. Therefore, it is impossible for Eve to obtain the final shared secret key with the interception attack.

5.3 Efficiency Analysis

Cabello’s qubit efficiency η is defined as $\frac{c}{q+b}$, where c represents the total number of shared classical bits, q indicates the total amount of used qubits while b denotes the total number of classical bits exchanged for decoding the message. The qubit efficiency of our proposed multiparty QKA protocol is $\frac{2n}{\left(7n+\frac{N}{3}n\right)\frac{N}{3}}$, i.e., $\frac{18}{\left(21+N\right)N}$. The comparison with similar multiparty QKA protocols from the aspects of category, quantum resource and qubit efficiency are compiled in Table 2. From Table 2, it is obvious that the performance of this proposed multiparty QKA protocol is higher especially the number of participants in the protocol is big enough.

Table 2 Comparison with similar QKA protocols

6 Conclusion

Based on entanglement swapping between Bell states and G-like states, a novel multiparty quantum key agreement protocol is designed. It is composed of multiple tri-party quantum key agreement protocols and it can resist most of common attacks. The new multiparty quantum key agreement protocol is fair and secure, and it is simpler with few calculations. In addition, the proposed multiparty QKA protocol has better performance than some typical quantum key agreement protocols especially under enough participants in the protocol. The protocol can also be realized with current technology.