1 Introduction

With the development of quantum algorithm, the security of classical key agreement schemes based on computational complexity is confronted with severe challenges, especially since Shor [1] proposed two algorithms for quantum computation: discrete logarithms and factoring. Quantum cryptography is based on quantum mechanics, and its security is guaranteed by the fundamental principles of quantum mechanics. The main task of quantum cryptography is the quantum key distribution (QKD) which only one participant decides the private key and distributes it to the other ones. The first quantum key distribution protocol (QKD) was proposed by Bennett and Brassard in 1984 [2]. The BB84 is based upon a single particle carrier and non-orthogonal states which is easy to implement. In addition, BB84 utilized uncertainty principle and non-cloning theorem to ensure the security of QKD. Then, Shor et al. [3] proposed a protocol that proved the security of BB84 in 2000. In 1991, Ekert et al. [4] defined the delayed measurement at the first time. It is generally accepted that only non-orthogonal states can be used to design quantum cryptographic protocols because orthogonal states can be precisely cloned. However, Goldenberg et al. [5] proposed a protocol based on orthogonal states in 1995. Quantum cryptography had drawn considerable attention, and it has been developed quickly since the QKD protocols were proposed. Therefore, far many different types of quantum cryptographic protocols have been proposed, including quantum key agreement [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25], quantum secure direct communication [26,27,28], quantum secret sharing [29, 30], quantum key distribution [31,32,33,34], quantum signature [35,36,37,38] and so on.

Different from QKD, the QKA allows two or more parties to generate the shared key, and no one can determine the generated key alone. In 1976, Diffie and Hellman [6] presented the first key agreement protocol that involves two parties. Zhou et al. [7] first put forward a QKA protocol based on quantum teleportation in 2004. However, in 2009, Zhou et al.’s protocol was pointed out the existence of security defects by Tsai et al. [8]. That is, a participant can determine the shared key alone without being detected completely. In 2010, Chong and Hwang [9] proposed a QKA protocol based on BB84 that enables two participants to consult a shared key, and no one can determine the shared key alone. In 2011, Chong et al. [10] proposed a improvement QKA protocol based on maximally entangled states, and pointed out two security loopholes of Hsueh and Chen protocol [11]: (1) dishonest user can decide the shared key alone fully; (2) an eavesdropper can get the shared key without being detected. And they proposed a possible solution to avoid these attacks. In 2016, He and Ma [13] proposed a QKA based on four-particle entangled states about two parties. Since each particle was transmitted only once in quantum channel, the protocol can resist the Trojan horse attacks. But these QKA protocols [7,8,9,10,11,12,13,14,15,16] only involved two parties and can not to extend the multi-party case. Next, let us to focus on multi-party QKA protocols. In 2013, Shi and Zhong [18] first proposed a multi-party QKA protocol based on entanglement swapping. Unfortunately, Liu et al. [19] pointed out that Shi et al.’s protocol [18] is not secure that dishonest participant can completely determine the shared key. At the same time, Liu et al. [19] proposed a multi-party QKA with single particles which was the first safe multi-party QKA protocol. But, Sun et al. [20] pointed out that Liu et al.’s protocol is inefficient. And Sun et al. [20] proposed the improvements on Liu et al.’s protocol. The photo efficiency of Sun et al.’s protocol can be improved to \( \frac {1}{N(k + 1)} \), and the security is also improved. In 2014, Xu et al. [23] proposed a novel multiparty quantum key agreement protocol with GHZ states. In 2016, Liu et al. [25] pointed out that Xu et al.’s protocol is unjust that the participants can control the shared key to a certain degree since performing the eavesdropping detection. In view of this problem, Gu et al. [39] proposed improvement on Xu et al.’s protocol in 2017. In 2014, Huang et al. [21] first presented QKA protocol with blocks of EPR pairs and single-particle measurements. Chitra Shukl et al. [22] proposed protocols of quantum key agreement merely utilizing Bell states and Bell measurement the same year. However, Zhu et al. [24] pointed out Chitra Shukl et al.’s [22] protocol that the three-party protocol is not secure, and put forward a scheme to improve the three-party protocol in 2015. Recently, some multi-party quantum key agreement protocols [18,19,20, 23, 25, 40,41,42,43,44] were proposed.

In this paper, we put forward a multi-party quantum key agreement protocol with four-qubit symmetric W state. The shared key is generated by all participants; neither party can decide the shared key alone. The outsider eavesdropper and dishonest participants cannot obtain the shared key without introducing any error. This protocol is more efficient than other multi-party QKA protocols.

The rest of the paper is organized as follows. Section 2, we introduce our three-party and multi-party QKA protocol with four-qubit symmetric W state. Section 3, we give the security analysis. Section 4, efficiency analysis is discussed. Section 5, a short conclusion is given.

2 The Presented Multi-party Quantum key Agreement Protocol

First, we introduce the four Pauli gates:

$$\sigma^{0}=I=|0\rangle\langle0|+|1\rangle\langle1|,$$
$$\sigma^{1}=X=|0\rangle\langle1|+|1\rangle\langle0|,$$
$$\sigma^{2}=Z=|0\rangle\langle0|-|1\rangle\langle1|,$$
$$\sigma^{3}=iY=|0\rangle\langle1|-|1\rangle\langle0|.$$

Then, the four-qubit symmetric W state can be depicted as:

$$\begin{array}{ll} |\varphi_{a}\rangle_{1234}=\frac{1}{2}(|0001\rangle+|0010\rangle+|0100\rangle+|1000\rangle)_{1234}, \end{array} $$

where the subscripts 1, 2, 3, 4 denote the first particle, the second particle, the third particle and the fourth particle of the cluster states, respectively.

Assume that the initial state is \(|\varphi _{a}\rangle _{1234}=\frac {1}{2}(|0001\rangle +|0010\rangle +|0100\rangle +|1000\rangle )_{1234}\). When we perform unitary operation σi(i = 0, 1, 2, 3) on qubit 3 and qubit 4, the cluster state |φa〉1234 will be transformed into one of the following four cluster states [45]:

$$\begin{array}{ll} |\varphi_{a}\rangle_{1234}=&\frac{1}{2}(|0001\rangle+|0010\rangle+|0100\rangle+|1000\rangle)_{1234},\\ |\varphi_{b}\rangle_{1234}=&\frac{1}{2}(|0000\rangle-|0011\rangle-|0101\rangle-|1001\rangle)_{1234},\\ |\varphi_{c}\rangle_{1234}=&\frac{1}{2}(|0011\rangle+|0000\rangle+|0110\rangle+|1010\rangle)_{1234},\\ |\varphi_{d}\rangle_{1234}=&\frac{1}{2}(|0010\rangle-|0001\rangle-|0111\rangle-|1011\rangle)_{1234}. \end{array} $$

As shown in Table 1. In order to unify a secret key, let us to define the following encoding rules:

$$\begin{array}{ll} |\varphi_{a}\rangle_{1234}:00, |\varphi_{b}\rangle_{1234}:01, |\varphi_{c}\rangle_{1234}:10, |\varphi_{d}\rangle_{1234}:11. \end{array} $$
Table 1 shows the relationship of the unitary operations and the transformed states on the qubit 3 and qubit 4 of cluster state |φa〉1234
Full size table

2.1 The Three-Party Quantum Key Agreement Protocol

Suppose that three participants want to generate a shared key K. They are P1, P2 and P3. First, P1, P2 and P3 generate the bit strings K1, K2 and K3 randomly as their secret keys, respectively.

$$\begin{array}{ll} K_{1}=({k_{1}^{1}}, {k_{1}^{2}},\ldots, {k_{1}^{s}},\ldots, {k_{1}^{n}}),\\ K_{2}=({k_{2}^{1}}, {k_{2}^{2}},\ldots, {k_{2}^{s}},\ldots, {k_{2}^{n}}),\\ K_{3}=({k_{3}^{1}}, {k_{3}^{2}},\ldots, {k_{3}^{s}},\ldots, {k_{3}^{n}}). \end{array} $$

Therefore, the shared key \(K=K_{1}\oplus K_{2}\oplus K_{3}=({k_{1}^{1}}\oplus {k_{2}^{1}}\oplus {k_{3}^{1}}, {k_{1}^{2}}\oplus {k_{2}^{2}}\oplus {k_{3}^{2}},\ldots ,{k_{1}^{s}}\oplus {k_{2}^{s}}\oplus {k_{3}^{s}},\ldots ,{k_{1}^{n}}\oplus {k_{2}^{n}}\oplus {k_{3}^{n}})\). Where \({k_{1}^{s}}, {k_{2}^{s}}, {k_{3}^{s}} \in \{0, 1\}, s = 1, 2,\ldots ,n\) represent sth private information of Pi(i = 1, 2, 3). ⊕ denotes the addition module 2, and n is the length of secret bit string. Pi indicates ith participant. Next, we describe the three-party quantum key agreement protocol.

  1. 1

    The participant Pi(i = 1, 2, 3) prepares \(|\varphi _{a}\rangle _{1234}^{\otimes \frac {n}{2}}\), respectively. Pi divides these states into four sequences \({S_{i}^{1}}\), \({S_{i}^{2}}\), \({S_{i}^{3}}\) and \({S_{i}^{4}}\). Here, the sequence \({S_{i}^{l}}(l = 1, 2, 3, 4;i = 1, 2, 3)\) is composed of lth particle of the \(|\varphi _{a}\rangle _{1234}^{\otimes \frac {n}{2}}\). \({S_{i}^{l}}=(s_{i}^{l, 1},s_{i}^{l, 2},\ldots ,s_{i}^{l,j},\ldots ,s_{i}^{l,\frac {n}{2}})\), \(s_{i}^{l,j}(l = 1, 2, 3, 4;1\leq j \leq \frac {n}{2};i = 1, 2, 3)\) denotes jth particle of \({S_{i}^{l}}\). Then Pi prepares \(\frac {n}{2}\) decoy photos respectively which are randomly in {|0〉, |1〉, |+〉, |−〉} and \(|+\rangle =\frac {1}{\sqrt {2}}(|0\rangle +|1\rangle )\), \(|-\rangle =\frac {1}{\sqrt {2}}(|0\rangle -|1\rangle )\).

  2. 2

    The participant Pi randomly inserts these decoy photos into the two sequences \({S_{i}^{3}}\) and \({S_{i}^{4}}\), respectively. Then, Pi obtains the new sequence \(S^{t^{\prime }}_{i}(t = 3, 4;i = 1, 2, 3)\). Subsequently, Pi applies permutation operator \(({\prod }_{\frac {n}{2}})_{P_{i}}\) on \(S^{t^{\prime }}_{i}\) to create the new sequence \(({\prod }_{\frac {n}{2}})_{P_{i}}S^{t^{\prime }}_{i}=S^{t^{\prime \prime }}_{i}(t = 3, 4;i = 1, 2, 3)\), and sends \(S^{t^{\prime \prime }}_{i}(t = 3, 4;i = 1, 2, 3)\) to Pi+ 1. Here, + denotes the addition module 3, i.e., i + 1 = (i + 1) mod 3.

  3. 3

    After Pi confirms that Pi+ 1 has received the \(S^{t^{\prime \prime }}_{i}\). Pi announces the permutation operator \(({\prod }_{\frac {n}{2}})_{P_{i}}\). Then, Pi announces the positions and the corresponding bases of the decoy photos. Later, Pi+ 1 measures the decoy photos by utilizing the correct bases. Pi+ 1 publishes half of the measurement results randomly after the measurement. Then Pi publishes the initial states of the left half of the decoy photos. At last, they check whether the measurement results and the initial states are consistent. If they are consistent, Pi and Pi+ 1 declare that \({S_{i}^{3}}\) and \({S_{i}^{4}}\) are secure; otherwise, they discard the protocol.

  4. 4

    If all sequences \({S_{i}^{t}}(t = 3, 4)\) are secure. Pi+ 1 performs unitary operations \(\sigma ^{k_{i + 1}^{2j-1}}\) and \(\sigma ^{3{k_{i + 1}^{2j}}}\) on \(s_{i}^{3,j}\) and \(s_{i}^{4,j}\) respectively according to his secret keys \(k_{i + 1}^{2j-1}\) and \(k_{i + 1}^{2j}\), where \(j = 1, 2, 3, \ldots , \frac {n}{2}\). Then, they can get the two sequences \(S_{i,i + 1}^{3}\) and \(S_{i,i + 1}^{4}\). Then, he applies the decoy photos and permutation operator method that described in step 2 to generate the new sequence \(S^{t^{\prime \prime }}_{i,i + 1}(t = 3, 4)\) and sends it to the next participant Pi+ 2.

  5. 5

    The step is similar to step 3. After Pi+ 1 confirms that Pi+ 2 has received the \(S^{t^{\prime \prime }}_{i,i + 1}(t = 3, 4)\), Pi+ 1 announces the permutation operator \(({\prod }_{\frac {n}{2}})_{P_{i + 1}}\). Subsequently, Pi+ 1 announces the positions and the corresponding bases of the decoy photos. Later, Pi+ 2 measures the decoy photos by utilizing the correct bases. Pi+ 2 publishes half of the measurement results randomly after the measurement. Then Pi+ 1 publishes the left half of the initial decoy photos. At last, they check whether the measurement results and the initial states are consistent. If they are consistent, Pi+ 1 and Pi+ 2 declare that \(S^{t}_{i,i + 1}(t = 3, 4)\) is secure; otherwise, they discard the protocol.

  6. 6

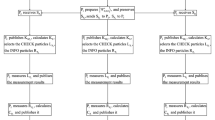
    The step is similar to step 4. If all the sequences \(S^{t}_{i,i + 1}(t = 3, 4)\) are secure. Pi+ 2 performs unitary operations \(\sigma ^{k_{i + 2}^{2j-1}}\) and \(\sigma ^{3{k_{i + 2}^{2j}}}\) on jth particle of sequences \(S_{i,i + 1}^{3}\) and \(S_{i,i + 1}^{4}\) respectively according to his secret key \(k_{i + 2}^{2j-1}\) and \(k_{i + 2}^{2j}\). Then, they can get two sequences \(S_{i,i + 2}^{3}\) and \(S_{i,i + 2}^{4}\). Then, he applies the decoy photos and permutation operator method that described in step (2) to generate the new sequence \(S^{t^{\prime \prime }}_{i,i + 2}(t = 3, 4)\) and sends it to the next participant Pi. Figure 1 shows the steps of transmitting photons.

  7. 7

    When Pi receives the two sequences \(S^{3^{\prime \prime }}_{i,i + 2}\) and \(S^{4^{\prime \prime }}_{i,i + 2}\), he detects eavesdropping with Pi+ 2. If all the sequences \(S^{t}_{i,i + 2}(t = 3, 4)\) are secure, Then Pi can obtain the two sequences \(S^{3}_{i,i + 2}\) and \(S^{4}_{i,i + 2}\). By performing W basis measurement on jth W state, Pi can get a measurement result. By Table 2, Pi can get the key Ki+ 1 ⊕ Ki+ 2. Then Pi an generate the final shared key K = Ki ⊕ Ki+ 1 ⊕ Ki+ 2.

Fig. 1
figure 1

The three-party quantum key agreement protocol steps of transmitting photons

Full size image
Table 2 shows the relationship of the unitary operations and the transformed states on the qubits 3 and 4 of cluster state |φa〉1234, |φb〉1234, |φc〉1234 and |φd〉1234
Full size table

2.2 The Multi-Party Quantum key Agreement Protocol

Suppose that m participants P1, P2, …, Pm want to generate a shared key K. They possess their own secret bit strings K1, K2, …, Km, respectively. Therefore, the shared key K = K1 ⊕ K2 ⊕⋯ ⊕ Km, wherein neither party can decide the shared key alone.

$$\begin{array}{ll} &K_{1}=({k_{1}^{1}},\ldots, {k_{1}^{s}},\ldots, {k_{1}^{n}}),\\ &\vdots\\ &K_{i}=({k_{i}^{1}},\ldots, {k_{i}^{s}},\ldots, {k_{i}^{n}}),\\ &\vdots\\ &K_{m}=({k_{m}^{1}},\ldots, {k_{m}^{s}},\ldots, {k_{m}^{n}}). \end{array} $$
  1. (1)

    Preparation: The participant Pi(i = 1, 2, …, m) prepares \(|\varphi _{a}\rangle _{1234}^{\otimes \frac {n}{2}}\), respectively. Pi divides these states into four sequences \({S_{i}^{1}}\), \({S_{i}^{2}}\), \({S_{i}^{3}}\) and \({S_{i}^{4}}\). \({S_{i}^{l}}=(s_{i}^{l, 1},s_{i}^{l, 2},\ldots ,s_{i}^{l,j},\ldots ,s_{i}^{l,\frac {n}{2}}) (l = 1, 2, 3, 4;1\leq j \leq \frac {n}{2};i = 1, 2,\ldots ,m)\), \(s_{i}^{l,j}\) denotes jth particle of \({S_{i}^{l}}\). Then he prepares \(\frac {n}{2}\) decoy states which are randomly in four states {|0〉, |1〉, |+〉, |−〉}.

  2. (2)

    Transmission: Similar to the second step in the three party agreement. Pi sends \(S^{t^{\prime \prime }}_{i}(i = 3, 4)\) to Pi+ 1. Here, + denotes the addition module m, i.e., i + 1 = (i + 1) mod m.

  3. (3)

    Detection: Similar to the third step in the three party agreement. If they are consistent, Pi and Pi+ 1 declare that \({S_{i}^{t}}(t = 3, 4)\) is secure; otherwise, they discard the protocol.

  4. (4)

    Encoding: If all sequences \({S_{i}^{t}}(t = 3, 4)\) are secure. Pi+ 1 performs unitary operations \(\sigma ^{k_{i + 1}^{2j-1}}\) and \(\sigma ^{3{k_{i + 1}^{2j}}}\) on jth particle of sequences \({S_{i}^{3}}\) and \({S_{i}^{4}}\) respectively according to his secret keys \(k_{i + 1}^{2j-1}\) and \(k_{i + 1}^{2j}\), where \(j = 1, 2,\ldots ,\frac {n}{2}\). Therefore, they can get two sequences \(S_{i,i + 1}^{3}\) and \(S_{i,i + 1}^{4}\). Then, Pi+ 1 applies the decoy photos and permutation operator method that described in step (2) to generate the new sequence \(S_{i,i + 1}^{t^{\prime \prime }}(t = 3, 4)\) and sends it to the next participant Pi+ 2.

  5. (5)

    The participants Pi+ 2, …, Pi− 1 perform the permutation operator, eavesdropping check and message encoding processes sequentially, just like steps (3) and (4). As shown in Fig. 2.

  6. (6)

    When Pi receives two sequences \(S_{i,i-1}^{3^{\prime \prime }}\) and \(S_{i,i-1}^{4^{\prime \prime }}\), he detects eavesdropping with Pi− 1. If all the sequences \(S_{i,i-1}^{t}(t = 3, 4)\) are secure, Then Pi can obtain two sequences \(S_{i,i-1}^{3}\) and \(S_{i,i-1}^{4}\). By performing W basis measurement on jth W state, Pi can get a measurement result. By Table 1, Pi can get the key \(K^{\prime }_{i}=\mathop {\oplus } \limits _{j, j \ne {i}} K_{j}\). Then Pi can generate the final shared key \(K=K_{i}\oplus K^{\prime }_{i}\).

Fig. 2
figure 2

The multi-party quantum key agreement protocol steps of transmitting photons

Full size image

3 Security Analysis

3.1 Participant Attack

Participant attack is a normal attack mode in the protocols that participants do not trust each other. Without loss of generality, we assume that Pi is the dishonest participant. If Pi gets the final key K ahead of time, where K is the bitwise of all parties. Pi wants to change the final shared key K to K∗. Then Pi encodes K∗⊕ K ⊕ Ki as his secret key instead of Ki when he performs the protocol. Other parties will regard K∗ as the final shared key because of K∗⊕ K ⊕ K = K∗. Thus, the multi-party agreement has a defect of fairness in this situation. To avoid the above unfairness, we demand that all participants must check eavesdropping. If all the sequences \({S_{i}^{t}}(t = 3, 4)\) are secure, they perform unitary operation by their own secret key in our protocol. Therefore, nobody can get the final shared key ahead of time, and all participants get the final generation key simultaneously. The dishonest participant Pi has no ability to change the final generate key as she expected. Therefore, it is impossible that a dishonest participant determines the final key alone by encoding a false secret to others.

3.2 Outsider Attack

Supposed that the outsider attacker is Eve. There are four kinds of attacks that Eve may use, including Trojan-horse attacks, Measure-resend attack, Intercept-resend attack and Entangle-measure.

3.2.1 Trojan-horse Attacks

Because our quantum protocol delivers the same photon more than once, it may be attacked by the Trojan horse attacks, such as the invisible-photon eavesdropping (IPE) attack and the delay-photon attack. A number of circular quantum transmission debated [47,48,49,50]. To avoid this type of attacks, participants can install a wavelength filter and the photon number splitters (PNS: 50/50). The photon number splitter (PNS: 50/50) which is used for dividing each signal into two pieces, should be introduced to defeat the delay-photon attack. If a multi-photon signal has an irrational high rate, an attack can be detected.

3.2.2 Measure-resend Attack

Eve may implement the measure-resend attack on the sequences \(S^{t^{\prime \prime }}_{i}, S^{t^{\prime \prime }}_{i,i + 1},\ldots ,S^{t^{\prime \prime }}_{i,i-1}(t = 3, 4)\) in steps (2), (4) and (5), respectively. Because Eve does not know the positions and the corresponding measurement bases of the decoy photos. The states of decoy photons will change when Eve performs measurement. Eve can be detected with the probability \(1-(\frac {3}{4})^{\frac {n}{2}}\) when the participants perform eavesdropping detection in step (3).

3.2.3 Intercept-resend Attack

First, Eve needs to forge some sequences. When Eve intercepts the sequences \(S^{t^{\prime \prime }}_{i}, S^{t^{\prime \prime }}_{i,i + 1},\ldots ,S^{t^{\prime \prime }}_{i,i-1}(t = 3, 4)\) in step (2), step (4) and step (5), she can send the forged sequences instead of \(S^{t^{\prime \prime }}_{i}, S^{t^{\prime \prime }}_{i,i + 1},\ldots ,S^{t^{\prime \prime }}_{i,i-1}(t = 3, 4)\) to the next participant. However, Eve cannot obtain any information about the decoy photos before Pi, Pi+ 1, …, Pi− 1 announce the positions and the corresponding bases of the decoy photos. Therefore, when the participants perform eavesdropping detection, Eve can be detected. Furthermore, Eve’s attack can be found with the probability of \(1-(\frac {1}{2})^{\frac {n}{2}}\) when \(\frac {n}{2}\) decoy photos are used for detecting this attack.

3.2.4 Entangle-measure Attack

Decoy photons are used for eavesdropping detection in the protocol. The decoy photons are |0〉, |1〉, |+〉, |−〉. Eve can only select a set of orthogonal bases to detect them, but she cannot distinguish which are the target photons and the decoy photons. Therefore, any eavesdropper will expose themselves by changing the quantum state. Without loss of generality, suppose the eavesdropper uses the operation \(\hat {U}_{E}\), and prepares an auxiliary system |ε〉E. We can get the following equations:

$$\begin{array}{@{}rcl@{}} \hat{U}_{E}|0\rangle|\varepsilon\rangle_{E}&=&a|0\rangle|\varepsilon_{00}\rangle_{E}+b|1\rangle|\varepsilon_{01}\rangle_{E},\\ \hat{U}_{E}|1\rangle|\varepsilon\rangle_{E}&=&c|0\rangle|\varepsilon_{10}\rangle_{E}+d|1\rangle|\varepsilon_{11}\rangle_{E},\\ \hat{U}_{E}|+\rangle|\varepsilon\rangle_{E}&=&\frac{1}{\sqrt{2}}(a|0\rangle|\varepsilon_{00}\rangle_{E}+b|1\rangle|\varepsilon_{01}\rangle_{E}+c|0\rangle|\varepsilon_{10}\rangle_{E}+d|1\rangle|\varepsilon_{11}\rangle_{E})\\ &=&\frac{1}{2}[|+\rangle(a|\varepsilon_{00}\rangle_{E}+b|\varepsilon_{01}\rangle_{E}+c|\varepsilon_{10}\rangle_{E}+d|\varepsilon_{11}\rangle_{E})+\\ &&|-\rangle(a|\varepsilon_{00}\rangle_{E}-b|\varepsilon_{01}\rangle_{E}+c|\varepsilon_{10}\rangle_{E}-d|\varepsilon_{11}\rangle_{E})],\\ \hat{U}_{E}|-\rangle|\varepsilon\rangle_{E}&=&\frac{1}{\sqrt{2}}(a|0\rangle|\varepsilon_{00}\rangle_{E}+b|1\rangle|\varepsilon_{01}\rangle_{E}-c|0\rangle|\varepsilon_{10}\rangle_{E}-d|1\rangle|\varepsilon_{11}\rangle_{E})\\ &=&\frac{1}{2}[|+\rangle(a|\varepsilon_{00}\rangle_{E}+b|\varepsilon_{01}\rangle_{E}-c|\varepsilon_{10}\rangle_{E}-d|\varepsilon_{11}\rangle_{E})+\\ &&|-\rangle(a|\varepsilon_{00}\rangle_{E}-b|\varepsilon_{01}\rangle_{E}-c|\varepsilon_{10}\rangle_{E}+d|\varepsilon_{11}\rangle_{E})]. \end{array} $$

where |a|2 + |b|2 = 1, |c|2 + |d|2 = 1. |ε〉E is the initial state of the ancilla E. {|ε00〉, |ε01〉, |ε10〉, |ε11〉} are pure ancilla states uniquely determined by \(\hat {U}_{E}\), so |ε00〉, |ε01〉, |ε10〉, |ε11〉 must satisfy \(\hat {U}_{E}\hat {U}_{E}^{+}=I\), i.e.:

$$\begin{array}{ll} \langle\varepsilon_{00}|\varepsilon_{00}\rangle+\langle\varepsilon_{01}|\varepsilon_{01}\rangle=&1,\\ \langle\varepsilon_{10}|\varepsilon_{10}\rangle+\langle\varepsilon_{11}|\varepsilon_{11}\rangle=&1,\\ \langle\varepsilon_{00}|\varepsilon_{01}\rangle+\langle\varepsilon_{10}|\varepsilon_{11}\rangle=&0,\\ \langle\varepsilon_{01}|\varepsilon_{00}\rangle+\langle\varepsilon_{11}|\varepsilon_{10}\rangle=&0. \end{array} $$

If Eve don’t to introduce error in the eavesdropping check, the \(\hat {U}_{E}|0\rangle |\varepsilon \rangle _{E}\), \(\hat {U}_{E}|1\rangle |\varepsilon \rangle _{E}\), \(\hat {U}_{E}|+\rangle |\varepsilon \rangle _{E}\), \(\hat {U}_{E}|-\rangle |\varepsilon \rangle _{E}\) can be denoted the following equations:

$$\begin{array}{ll} \hat{U}_{E}|0\rangle|\varepsilon\rangle_{E}=&a|0\rangle|\varepsilon_{00}\rangle_{E},\\ \hat{U}_{E}|1\rangle|\varepsilon\rangle_{E}=&d|1\rangle|\varepsilon_{11}\rangle_{E},\\ \hat{U}_{E}|+\rangle|\varepsilon\rangle_{E}=&\frac{1}{2}|+\rangle(a|\varepsilon_{00}\rangle_{E}+b|\varepsilon_{01}\rangle_{E}+c|\varepsilon_{10}\rangle_{E}+d|\varepsilon_{11}\rangle_{E}),\\ \hat{U}_{E}|-\rangle|\varepsilon\rangle_{E}=&\frac{1}{2}|-\rangle(a|\varepsilon_{00}\rangle_{E}-b|\varepsilon_{01}\rangle_{E}-c|\varepsilon_{10}\rangle_{E}+d|\varepsilon_{11}\rangle_{E}). \end{array} $$

Therefore, we can get the equations:

$$\begin{array}{@{}rcl@{}} b|1\rangle|\varepsilon_{01}\rangle_{E}&=&0,\\ c|0\rangle|\varepsilon_{10}\rangle_{E}&=&0,\\ a|\varepsilon_{00}\rangle_{E}-b|\varepsilon_{01}\rangle_{E}+c|\varepsilon_{10}\rangle_{E}-d|\varepsilon_{11}\rangle_{E}&=&0,\\ a|\varepsilon_{00}\rangle_{E}+b|\varepsilon_{01}\rangle_{E}-c|\varepsilon_{10}\rangle_{E}-d|\varepsilon_{11}\rangle_{E}&=&0. \end{array} $$

Then, we can get a = d = 1, b = c = 0, |ε00〉E = |ε11〉E. If Eve don’t to introduce error in the eavesdropping check, she cannot obtain any useful information. Therefore, the protocol can resist the outsider attack.

4 Efficiency Analysis

In this chapter, we will discuss the qubit efficiency of this protocol. A well-known measure of efficiency of secure quantum communication is known as qubit efficiency introduced by Cabello [46], which is given a

$$\eta=\frac{c}{q+b},$$

where c denotes the length of transmitted message bits (the length of the final key), q is the number of the used qubits, and b is the number of classical bits exchanged for decoding of the message (classical communication used for checking of eavesdropping is not counted). Hence, the qubit efficiency of our protocol can be computed \(\eta =\frac {n}{(2\cdot \frac {n}{2}+ 2\cdot \frac {n}{2})m}=\frac {1}{2m}\), where m is the number of participants. Table 3 shows that our protocol is more efficient than other multi-party QKA protocols.

Table 3 Comparison between proposed multi-party QKA protocols and ours
Full size table

5 Conclusion

In this paper, we present a multi-party quantum key agreement with four-qubit symmetric W state. By using the delayed measurement and decoy photos method, the security and fairness of the protocol are ensured. The m participants can get the final generation key fairly. And the result of security analysis shows that our protocol is safe in resisting both participant and outsider attacks. By utilizing block transmission technique and the dense coding method, the efficiency of the protocol is improved. Finally, we estimate its qubit efficiency. The efficiency analysis shows that the proposed protocol is more efficient than other multi-party QKA protocols.