1 Introduction

The observation of Type Ia Supernovae [27, 32] seems to support a universe undergoing a phase of accelerated expansion. In a universe composed mostly by matter, this feature is highly counterintuitive. Therefore to account for the acceleration, it is common to assume that the universe is made mostly (∼ 70%) by an exotic component, named dark energy (DE). The DE has an equation of state (EoS) ω ∼ −1 which justifies the present universe dynamics. In standard cosmology (or ΛCDM model), the DE is mathematically described by a cosmological constant (Λ) inserted in the Einstein’s field equations (FEs). However, the cosmological constant, coincidence and dark matter problems, missing satellites, hierarchy problem and other shortcomings (see [13] and references therein) arising from ΛCDM model, yield the consideration of alternative cosmological models.

Therefore we are led to search for some kind of matter fields which generates negative pressure enough to account for the cosmic acceleration. A scalar field which goes slowly down to its potential, making the potential term to dominate over the kinetic one, can produce sufficient negative pressure, and a cosmological scenario containing such a scalar field is named “quintessence” (check, for instance, [11, 24, 39]). As one can see in these references, it is also common to assume the universe dynamics is ruled by two (instead of one) scalar fields. In fact, in [24], such a two scalar field cosmological scenario has presented some advantages when compared to the one scalar field models, since it describes not only the accelerated phase of the universe, but also the phases in which the expansion decelerates, i.e., those for which the universe is dominated by radiation and matter.

Another alternative for the standard cosmology issues comes from the family of f(R) [16, 37] and f(R, T) [18] theories. The latter has been recently proposed as a theory in which the gravitational part of the action depends still on a general function of the Ricci scalar R, as the f(R) theories, but also on a function of T, the trace of the energy-momentum tensor. Such a novel dependence comes from the existence of imperfect fluids or quantum effects.

f(R, T) gravity has been applied to: anisotropic models [30, 35], scalar field models [36], extradimensional models [23, 25] and Λ(t) models [1, 33]. However, no application of the f(R, T) gravity to varying speed of light (VSL) scenarios [2, 3, 5, 21, 22] has been made so far.

Recently, some evidences that the electromagnetic fine structure constant α is, in fact, varying with cosmic time have been brought up [12, 26, 29, 40]. It is intuitive that if α changes with time, all of the fundamental constants should also change. Cosmological solutions in which low-energy fundamental constants are functions of time can be seen, for instance, in superstring theories [34]. In this work I will be interested in models for which a time variation of α is represented through a variation of c, the speed of light.

VSL scenarios have been used as an alternative to inflationary models [17, 20]. They were first inspired by the horizon problem. It is noted that photons emitted from opposite directions of the universe must have somehow communicated in the past, since the cosmic microwave background presents nearly the same temperature in all directions of the sky [19]. Such an issue can be solved from the idea of an exponential expansion the universe has passed through right after the Big-Bang, named “inflationary era”. On the other hand, a larger speed of light in the primordial universe could open up the horizons, providing an explanation for the large scale structures we see today. In [2], from VSL scenarios, the authors have solved the same cosmological puzzles inflation solves. Such puzzles have also been addressed from the perspective of VSL theories in [3]. Moreover, in contrast to the inflationary universe, a varying c may provide an explanation for the relative smallness of the cosmological constant [5].

Reasons for a search for alternatives to inflationary scenarios have been identified for a long time (check, for instance, [9, 41]) and still wait for convincing explanations. Moreover, it should be noted that a truly compelling microscopic foundation for inflation has yet to emerge.

Not only on VSL theories the alternatives to inflation are maintained. Non-inflationary models of universe can be found from different approaches and perspectives [4, 10, 14, 28]. Nevertheless, a VSL scenario will be in the scope of the present work.

With strong evidences supporting a varying fine structure “constant” together with the elegant replacement of inflation such models enable, VSL scenarios are expected to become more and more popular. However, as quoted above, they have not been approached in f(R, T) theories so far. Therefore it is worth checking the cosmology obtained from a VSL scenario in f(R, T) gravity, which is the aim of this work.

Note that VSL and f(R, T) theories are somehow complementary. A linear dependence on T for the functional form of f(R, T) (which will be assumed in the present work) brings no new information about a radiation-dominated universe, since for such an era, T = 0. On the other hand, VSL theories has much to offer at the primordial stages of the universe. According to them, there was no inflationary era, and a radiation-dominated universe with significant changes in the values of c is the proposed scenario. As time passes by, c(t) → c while the term proportional to T ≠ 0 becomes relevant. In this way, such a unification yields an optimistic alternative to describe different stages of the universe evolution.

2 A Variant Speed of Light Scenario in f(R, T) Gravity

In f(R, T) gravity, the gravitational part of the action is given by the following:

$$ S_{g}=\frac{c^{4}}{16\pi G}\int f(R,T)\sqrt{-g}d^{4}x, $$
(1)

with G being the gravitational constant, f(R, T) the general function of R and T, and g the determinant of the metric.

In this section I will reconstruct f(R, T) theory by allowing the speed of light c to vary with time, i.e., by making c → c(t). As proposed in [2], I will assume that a time-variable c does not introduce changes in the geometry of the universe through the FEs. To do so, the time coordinate of the model will be the comoving proper time. Moreover, by assuming a flat Friedmann-Robertson-Walker universe, there will be no spatial variations in c.

I am going to assume f(R, T) = R + 2λ T in (1), with λ a constant. This functional form, originally suggested by the f(R, T) gravity authors, has been broadly used in f(R, T) cosmological models (check, for instance, [23, 25, 31]). Even [18] have obtained from f(R, T) = R + 2λ T, a scale factor which describes a universe undergoing an accelerated expansion. Moreover, such a functional form benefits from the fact that one can recover general relativity (GR) just by letting λ to be null, which will be of fundamental importance in the proposed scenario.

Let me consider the matter source of the universe as a perfect fluid so that the matter lagrangian can be taken as \(\mathcal {L}_{m}=-p\), with p being the pressure of the universe. By allowing c to be a time variable, such a contribution to (1) yields, from the variation with respect to the metric, the following:

$$ G_{\mu\nu}=\frac{8\pi G}{c^{4}(t)}T_{\mu\nu}+\frac{G}{c^{4}(t)}[\lambda Tg_{\mu\nu}+2\lambda(T_{\mu\nu}+pg_{\mu\nu})], $$
(2)

for which T μ ν is the energy-momentum tensor of a perfect fluid. Note that, as addressed in [5], by treating the dynamics achieved from a variable c similarly as the one of a scalar field ψ,Footnote 1 the contribution \(\mathcal {L}_{\psi }\) must not contain the metric explicitly. In this way, it will not contribute to the energy-momentum tensor, so that the FEs do not acquire any new termsFootnote 2 when compared to the c = c t e scenario (check [23]).

By assuming a matter-dominated universe (p = 0) with a Friedmann-Robertson-Walker (+, −, −, −) geometry, (2) yields

$$ 3\left( \frac{\dot{a}}{a}\right)^{2}=\frac{8\pi G}{c^{4}(t)}(8\pi+3\lambda)\rho, $$
(3)
$$ 2\frac{\ddot{a}}{a}+\left( \frac{\dot{a}}{a}\right)^{2}=\frac{G}{c^{4}(t)}\lambda\rho, $$
(4)

with a being the scale factor, dots representing time derivatives and ρ the density of the universe.

In the next section, I will present cosmological solutions for (3)–(4).

3 f(R, T) Theory Cosmological Solutions for a Matter-Dominated Universe with c(t) = c 0 a n

In the calculations of the present and next sections, I will assume, as in [5], that

$$ c(t)=c_{0}a^{n}, $$
(5)

with c 0 representing the present value of the speed of light and n a constant. Moreover, for the sake of simplicity, I will work with natural units, so that c 0 = G = 1.

By substituting (5) in (3)–(4), one obtains:

$$ 3(\dot{a}a^{2n-1})^{2}=(8\pi+\lambda)\rho, $$
(6)
$$ 2\ddot{a}a^{4n-1}+(\dot{a}a^{2n-1})^{2}=\lambda\rho. $$
(7)

By manipulating (6)–(7), the following equation for the deceleration parameter \(q=-\ddot {a}a/\dot {a}^{2}\) is obtained:

$$ q=\frac{1}{2}\left( 1-\frac{3\lambda}{8\pi+3\lambda}\right). $$
(8)

Equation (8) reveals some interesting features. In order to account for the present acceleration of the universe, one must assume λ< −8π/3, since such a range allows negative values for q. Recall that I am assuming a matter-dominated universe (p = 0) and yet it is possible to obtain a negative q from (8).

It is well known that the matter-dominated universe in ΛCDM model, which is derived from GR, presents q = 1/2, i.e., a decelerated expansion. On the other hand, what allows the also matter-dominated universe of the present model to accelerate is the contribution from the term dependent on λ. Moreover, (8) retrieves standard predictions when λ = 0. According to [18], the condition λ = 0 must, indeed, allow the recovering of GR for such an f(R, T) functional form. Note that by taking λ = 0 in (8), one obtains q = 1/2.

4 A Radiation-Dominated Universe with Varying Speed of Light in f(R, T) Theory as an Alternative to Inflationary Era

It is valid to stress here that the c(t) = c 0 a n time evolution for the speed of light could indeed be extended to both matter and radiation-dominated universes, as demonstrated in [6].

In this way, let us see if the present model is also able to successfully describe a radiation-dominated universe. To do so, I will assume p = ρ/3 as the EoS to be used in (2).

The characterization above yields, for the FEs of the model, the following:

$$ 3(\dot{a}a^{2n-1})^{2}=8\left( \pi+\frac{\lambda}{3}\right)\rho, $$
(9)
$$ 2\ddot{a}a^{4n-1}+(\dot{a}a^{2n-1})^{2}=-\frac{4}{3}(2\pi+\lambda)\rho. $$
(10)

By dividing (9) by (10), one obtains the following equation for the deceleration parameter:

$$ q=\frac{1}{2}\left[\frac{3}{2}\left( \frac{2\pi+\lambda}{3\pi+\lambda}\right)+1\right]. $$
(11)

Remarkably, in (11), q = 1 when λ = 0. Once again, GR arises as a special case of the present model, since q = 1 is precisely the value of the deceleration parameter for a radiation-dominated universe in standard cosmology.

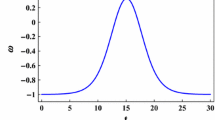
Moreover, from (9)–(10), it is possible to obtain the time evolution of the density ρ, as Fig. 1 below.

Fig. 1
figure 1

Time evolution of the density of the radiation-dominated universe with λ = 1 and n = −1.55

Full size image

The time evolution of ρ denoted in Fig. 1 above is in agreement with a non-inflationary universe. According to the solution obtained from (9)–(10) and the values of λ and n, ρ evolves as ∼ t −5. Recall that in VSL theories there is no inflationary era and no traces of an exponential expansion at primordial stages; therefore, the density of the universe needs to decay more rapidly than in standard case, in order to account for the absence of inflationary dynamics, yielding, at the same time scale as standard big-bang model, a transition from a radiation to a matter-dominated universe. This justifies the abrupt decreasing on the values of ρ during a small interval of time at the primordial stages of the universe shown in Fig. 1.

The reasons for the choice n = −1.55 in Fig. 1 are reported in the following. In [5], the author has argued that for a c(t) = c 0 a n evolution, if matter is described by the EoS p = (γ−1)ρ, the horizon problem may be solved if the condition n ≤ 0.5(2−3γ) is respected (from such an EoS, γ = 4/3 in the present case). Allied to this, still in [5], it was shown that n < −3/2 also solves the cosmological constant problem. One can see that n = −1.55 respects both constraints above.

There is another way of checking if the present model is capable of solving the cosmological puzzles here addressed. The comoving horizon progressively decomposes into more comoving causally connected regions as we go back into the past, which implies the horizon problem. As addressed in [2, 22], a larger speed of light in the early universe could open up the horizons. The comoving horizon is given by \(D_{h}=c/\dot {a}\). In this way, a solution to the horizon problem demands that D h decreased in the past so that the large regions we see today are causally connected. Therefore, mathematically, as addressed in [21], the condition

$$ \frac{\ddot{a}}{\dot{a}}-\frac{\dot{c}}{c}>0 $$
(12)

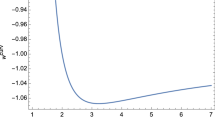
must be obeyed. By solving (9)–(10) for the scale factor, one is able to plot, with the help of (5), the lhs of (12) in Fig. 2 below.

Fig. 2
figure 2

Time evolution of the the relation \(\ddot {a}/\dot {a}-\dot {c}/c\) for λ = 1 and n = −1.55

Full size image

Figure 2 below confirms the obedience of relation (12) since it can be noted that its lhs is, indeed, restricted to positive values. Moreover,

$$ Lim_{t\rightarrow\infty}\left( \frac{\ddot{a}}{\dot{a}}-\frac{\dot{c}}{c}\right)=0, $$
(13)

so that \(\dot {c}/c\) tends to \(\ddot {a}/\dot {a}\) as time passes by, but never exceeds its value.

5 Discussion

Like inflationary scenarios, VSL theories are motivated by cosmological puzzles, such as the horizon and cosmological constant problems of standard Big-Bang cosmology.

In this work I have implemented a VSL model in the f(R, T) gravity. Such an implementation seems to be promising since it reveals relevant contributions from either T (in f(R, T)) or c(t) in different stages of the universe evolution.

I have showed that, as originally required in [18], GR predictions are retrieved when setting λ = 0 in f(R, T) = R + 2λ T. Such a retrieval indicates that f(R, T) gravity is allowed to encompass variations on c, since standard gravity is recovered only by setting λ = 0, with no need of assuming a constant c (note that solutions (8) and (11) for q are independent of n).

Apart from the evidences of a possible variation of the fine structure “constant” with time, what justifies the generalization of f(R, T) theories, allowing the speed of light to vary, is carefully described below. There are no specific informative contributions from f(R, T) theories when considering a primordial universe dominated by radiation. Since at such a stage of the universe, T = 0, the terms dependent on T on the FEs vanish.Footnote 3 On the other hand, the contribution from VSL models is highly relevant at the same epoch, since the rate for which c varies is considerably greater at this era.

As an argument, let us return to (2). When considering f(R, T) theory purely, one has c(t) → c in (2). If in such original FEs, one considers the EoS of the radiation-dominated universe p = ρ/3, and once again f(R, T) = R + 2λ T, the resulting deceleration parameter q ≠ 1 when λ = 0. This is not in accordance with the f(R, T) proposal, i.e., recovering GR when λ = 0. This is due to the apparent weakness f(R, T) theory manifests at the radiation-dominated stage of the universe. Note that by allowing c to vary, such a shortcoming vanishes and the theory successfully retrieves standard results, as described in Section 4.

Solution (11) recovers, then, the standard cosmology value when λ = 0, i.e., when standard gravity is recovered. In the general case (λ ≠ 0), the solution deviates from q = 1 since the primordial universe dynamics in a VSL scenario is far different from the one predicted by standard Big-Bang model. In VSL theories, for the description of the primordial universe, there is no invoking of the scalar field inflaton. In fact, the matter content of the universe is not changed. Instead, c is allowed to vary in a radiation-dominated universe. Since such a radiation-dominated universe is revealed earlier and with no trace of the inflaton dynamics, it is expected that q has some deviation from its standard behaviour, which, in this case, is described by the term dependent on λ.

Such a standard universe dynamics deviation also manifests in the evolution of ρ presented in Fig. 1. The time evolution for ρ diverges from the one obtained via standard cosmology, which is expected, since a non-inflationary universe decays more rapidly in a radiation-dominated scenario. Once such a radiation-dominated stage is longer than that of inflationary models and with no traces of an inflaton dynamics, the time evolution of ρ should be steeper than in ΛCDM model, which is confirmed in Fig. 1.

The choice for the value of n in Figs. 1 and 2 (n = −1.55) was not arbitrary. It respects bounds imposed by VSL theories when willing to solve the horizon and cosmological constant problems.

Furthermore, in what concerns the present accelerated dynamics of the universe, while in standard cosmology it is not possible to obtain an accelerated expansion from a matter-dominated universe, the present scenario is able to do so, just by requiring λ<−8π/3 in (8). Remarkably, such a cosmic feature is obtained without the need of invoking a cosmological constant or scalar fields responsible for the universe dynamics.

The consideration of a variable c seems to be an optimistic alternative to some issues surrounding the radiation-dominated universe in f(R, T) gravity. In such a universe stage, one of the foundations of f(R, T) = R + 2λ T model, i.e., recovering standard gravity when λ = 0, is not achieved. In order to successfully retrieves GR predictions, one should be encouraged to consider the approach in Section 4.

As a possible extension of this work, one might also consider variations in the gravitational constant G, as adressed, for instance, in [7, 8, 15, 38], allowing more general solutions to be obtained.