1 Introduction

Quantum cryptography allows higher security than classical cryptography as it is based on the laws of physics instead of some difficult mathematical problems. There are some quantum cryptography protocols been proposed, such as quantum key distribution (QKD) [1–6], quantum secret sharing (QSS) [7–12], quantum secure direct communication (QSDC) [13–17], quantum teleportation (QT) [18–21], and so on. Secure multiparty computation (SMPC) is an important and fundamental cryptographic protocol [22–29]. Unfortunately, it was shown by Mayers [24] and Lo-Chau [25] that deterministic two-party-setting computation was impossible, even with quantum means.

Quantum private comparison (QPC) is a interesting topic in quantum secure multiparty computation. It allows two distrustful parties, Alice and Bob, to determine whether their secret inputs are equal or not without disclosing their own secret information. In 2009, QPC was proposed by Yang et al. [30, 31] first. After these, some QPC schemes based on different states are proposed [32–41]. Since secure two-party-setting computation is impossible, a third party (TP) is needed in QPC to help Alice and Bob compare their private information. In some schemes, TP is required as at least a semi-honest participant. Recently, it was found that TP is not needed to be a semi-honest participant [40]. Hence, the QPC schemes presented previously have the following principles.

  1. 1.

    The QPC task is implemented with the help of a TP. TP will not be corrupted by others. He cannot learn any information about the players’ respective private inputs by means of various active and passive attacks.

  2. 2.

    No matter whether TP will know the positions of different bit value in the compared information or not, he/she will not be able to know the actual bit value of the information.

  3. 3.

    All outsiders and the two players should only know the result of the comparison (i.e., identical or different), but not the positions of the different information.

In this paper, we will propose a new QPC scheme based on phase encoding of single photons, and prove that it is secure in the above principles. This scheme is easy to be realized in current experiments as only some simple devices are used. It also can prevent some familiar attacks in practical setting.

The rest of this paper is constructed as follows. Section 2 proposes the QPC scheme based on phase encoding of single photons. In Section 3, we analyze the protocol’s correctness, security and the capability of fault-tolerate. Finally, a short conclusion is given in Section 4.

2 QPC Based on Phase Encoding of Single Photons

In this section, we give a QPC scheme based on phase encoding of single photons. Here are two participants, Alice and Bob, and a third party, Charlie who helps Alice and Bob to compare, but wants to know their private inputs by means of various active and passive attacks. Following the conclusions that a SMPC protocol should be insecure when less than a half of participants are honest [26], we suppose that TP should not be colluded by other dishonest parties.

Here, Alice and Bob have two private information M A and M B, respectively. The binary representations of \(F_{2^{N}}\) are \(\left ({{m^{A}_{1}}}, {{m^{A}_{2}}}, \ldots , {{m^{A}_{N}}}\right )\), \(\left ({{m^{B}_{1}}}, {{m^{B}_{2}}}, \ldots , {{m^{B}_{N}}}\right )\), where \({{m^{A}_{i}}}, {{m^{B}_{i}}}\in \{0,1\}\); \(M^{A}=\sum _{i=1}^{N}{{m^{A}_{i}}}\cdot {2^{i}}, M^{B}=\sum _{i=1}^{N}{{m^{B}_{i}}}\cdot {2^{i}}\).

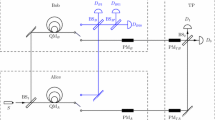
In this scheme, the single photon should be used with the technique block transmission, namely using an ordered particle sequence, which first proposed in Ref. [13]. They divide the N bits private information into some blocks including t bits, and fill the last block by some bits 0, then compare them one by one. When a pair of blocks are not identify, they know M A≠M B and stop the protocol. They accept M A=M B only when all of these blocks are identify. The specific steps of the scheme are described as follows. And the schematic of the scheme is shown in Fig. 1.

  1. 1.

    Charlie prepares photons sequence S=(s 1,s 1,⋯ ,s n′ ) which is composed by n ′ single photons and passes each of them through 50:50 beam splitter B S 1. The jth photon is split to two pulse waves \({{s^{a}_{j}}}\) and \({{s^{b}_{j}}}\). Then the state is

    $$ |\phi^{0}\rangle= \frac{1}{\sqrt{2}}(|0\rangle_{a}|1\rangle_{b}+i|1\rangle_{a}|0\rangle_{b}), $$
    (1)

    where |0〉 denotes the vacuum state, the subscripts a and b represent the paths towards Alice’s and Bob’s sites, respectively.

  2. 2.

    To the jth photon, Charlie randomly choose a phase \({{\theta ^{C}_{j}}}\) from the two basis sets of {0,π} and {π/2,3π/2}. Phase values 0 and π/2 represent \(k^{*C}_{j}=0\) and the other two represent \(k^{*C}_{j}=1\). Now Charlie has bits sequences \(K^{*C}=\left (k^{*C}_{1},k^{*C}_{1},\cdots ,k^{*C}_{n'}\right )\). He uses modulator introduce relative phase shift \({{\theta ^{C}_{j}}}\) to the pulse wave \({{s^{a}_{j}}}\) or \({{s^{b}_{j}}}\). The system state develops to

    $$\begin{array}{@{}rcl@{}} |\phi^{1}\rangle= \frac{1}{\sqrt{2}}\left(|0\rangle_{a}|1\rangle_{b}+ie^{i{{\theta^{C}_{j}}}}|1\rangle_{a}|0\rangle_{b}\right), \quad or \end{array} $$
    (2a)
    $$\begin{array}{@{}rcl@{}} |\phi^{1}\rangle= \frac{1}{\sqrt{2}}\left(e^{i{{\theta^{C}_{j}}}}|0\rangle_{a}|1\rangle_{b}+i|1\rangle_{a}|0\rangle_{b}\right). \end{array} $$
    (2b)

    Then he sends the two pulse waves sequences \(S^{A}=\left ({{s^{A}_{1}}},{{s^{A}_{1}}},\cdots , s^{A}_{n'}\right )\), \(S^{B}=\left ({{s^{B}_{1}}},{{s^{B}_{1}}},\cdots , s^{B}_{n'}\right )\) to Alice and Bob, respectively.

  3. 3.

    Alice and Bob insert a filter in front of her devices to filter out the photon signal with an illegitimate wavelength. They select l orders for detecting multi-photons as follows. They split each of these waves with a beam splitter followed by measuring the two signals with detectors. In an ideal scenario, only one detector would click for a same order. If the multi-photon rate is unreasonably high, they abort the protocol.

  4. 4.

    To the ith pulse wave, Alice and Bob randomly choose \({{\theta ^{A}_{j}}}\) and \({{\theta ^{B}_{j}}}\) from the two basis sets of {0,π} and {π/2,3π/2}. Phase values 0 and π/2 represent \(k^{*A}_{j}\) or \(k^{*B}_{j}=1\) and the other two represent \(k^{*A}_{j}\) or \(k^{*B}_{j}=0\). They use phase modulators to introduce relative phase shifts \({{\theta ^{A}_{j}}}\) and \({{\theta ^{B}_{j}}}\) to the pulse waves \({{s^{a}_{j}}}\) and \({{s^{b}_{j}}}\), respectively. Now Alice and Bob have two bits sequences \(K^{*A}=\left (k^{*A}_{1},k^{*A}_{1},\cdots ,k^{*A}_{n'}\right )\) and \(K^{*B}=\left (k^{*B}_{1},k^{*B}_{1},\cdots ,k^{*B}_{n'}\right )\), respectively. The system state develops to

    $$\begin{array}{@{}rcl@{}} |\phi^{2}\rangle&=& \frac{1}{\sqrt{2}}\left(e^{i{{\theta^{B}_{j}}}}|0\rangle_{a}|1\rangle_{b}+ie^{i({{\theta^{A}_{j}}}+{{\theta^{C}_{j}}})}|1\rangle_{a}|0\rangle_{b}\right)\\ &=&\frac{e^{i\left({{\theta^{C}_{j}}}+{{\theta^{A}_{j}}}\right)}}{\sqrt{2}}\left(e^{i({{\theta^{B}_{j}}}-{{\theta^{A}_{j}}}-{{\theta^{C}_{j}}})}|0\rangle_{a}|1\rangle_{b}+i|1\rangle_{a}|0\rangle_{b}\right), \quad or \end{array} $$
    (3a)
    $$\begin{array}{@{}rcl@{}}{} |\phi^{2}\rangle&=& \frac{1}{\sqrt{2}}\left(e^{i\left({{\theta^{B}_{j}}}+{{\theta^{C}_{j}}}\right)}|0\rangle_{a}|1\rangle_{b}+i\left(e^{i{{\theta^{A}_{j}}}}|1\rangle_{a}|0\rangle_{b}\right)\right.\\ {}&=&\frac{e^{i{{\theta^{A}_{j}}}}}{\sqrt{2}}\left(e^{i\left({{\theta^{B}_{j}}}+{{\theta^{C}_{j}}}-{{\theta^{A}_{j}}}\right)}|0\rangle_{a}|1\rangle_{b}+i|1\rangle_{a}|0\rangle_{b}\right), \end{array} $$
    (3b)

    where the overall factor \(e^{i\left ({{\theta ^{C}_{j}}}+{{\theta ^{A}_{j}}}\right )}\) and \(e^{i{{\theta ^{A}_{j}}}}\) could be omit. We denote the pulse waves after Alice and Bob’s phase shifts as \(s^{*A}_{j}\) and \(s^{*B}_{j}\).

    Then they send the two pulse waves sequences \(S^{*A}=\left (s^{*A}_{1},s^{*A}_{1},\cdots , s^{*A}_{n'}\right )\), \(S^{*B}=\left (s^{*B}_{1},s^{*B}_{1},\cdots , s^{*B}_{n'}\right )\) back to Charlie.

  5. 5.

    The two pulse waves are combined at the second beam splitters B S 2. The system state develops to

    $$\begin{array}{@{}rcl@{}} |\phi^{3}\rangle\,=\, \frac{1}{\sqrt{2}}\left(\left(e^{i\left({{\theta^{B}_{j}}}-{{\theta^{A}_{j}}}-{{\theta^{C}_{j}}}\right)}-1\right)|0\rangle_{c}|1\rangle_{d}+i\left(e^{i\left({{\theta^{B}_{j}}}-{{\theta^{A}_{j}}}-{{\theta^{C}_{j}}}\right)}+1\right)|1\rangle_{c}|0\rangle_{d}\right) \!\!\!\!\!\quad or\\ \end{array} $$
    (4a)
    $$\begin{array}{@{}rcl@{}} |\phi^{3}\rangle= \frac{1}{\sqrt{2}}\left(\left(e^{i\left({{\theta^{B}_{j}}}+{{\theta^{C}_{j}}}-{{\theta^{A}_{j}}}\right)}-1\right)|0\rangle_{C}|1\rangle_{d}+i\left(e^{i\left({{\theta^{B}_{j}}}+{{\theta^{C}_{j}}}-{{\theta^{A}_{j}}}\right)}+1\right)|1\rangle_{C}|0\rangle_{d}\right),\\ \end{array} $$
    (4b)

    which means the detector D 1 will click with probability \(\frac {1}{2}\left (1-\cos \left ({{\theta ^{B}_{j}}}-{{\theta ^{A}_{j}}}-\right .\right .\) \(\left .\left .{{\theta ^{C}_{j}}}\right )\right )\) or \(\frac {1}{2}\left (1-\cos \left ({{\theta ^{C}_{j}}}+{{\theta ^{B}_{j}}}-{{\theta ^{A}_{j}}}\right )\right )\), the detector D 2 will click with probability \(\frac {1}{2}\left (1+\cos \left ({{\theta ^{B}_{j}}}-{{\theta ^{A}_{j}}}-{{\theta ^{C}_{j}}}\right )\right )\) or \(\frac {1}{2}\left (1+\cos \left ({{\theta ^{C}_{j}}}+{{\theta ^{B}_{j}}}-{{\theta ^{A}_{j}}}\right )\right )\).

  6. 6.

    Alice, Bob and Charlie take turns to check whether the other two participants are honest or not. First, Alice selects a detecting photon and announces its order, let Bob announce his bit \(k^{*B}_{j}\), Charlie announce his bit \(k^{*C}_{j}\) and which detector clicked. Second, Bob selects a detecting photon and announces its order, let Alice announce his bit \(k^{*A}_{j}\), Charlie announce his bit \(k^{*C}_{j}\) and which detector clicked. Third, Charlie selects a detecting photon and announces its order, let Alice and Bob announce their bit \(k^{*A}_{j}\) and \(k^{*B}_{j}\). Then they come into another round of detecting process, till l ′ photons has been detected. They check dishonest participants with the following two restrains: In the two cases of (i) detector D 1 clicked and \(k^{*C}_{i}=1\) and (ii) detector D 2 clicked and \(k^{*C}_{j}=0\), it should be \(k^{*A}_{j}={{k^{B}_{j}}}\) with certainly; In the other two cases of (iii) detector D 1 clicked and \(k^{*C}_{i}=0\) and (iv) detector D 2 clicked and \(k^{*C}_{i}=1\), it should be \(k^{*A}_{j}=k^{*B}_{j}\) with probability 1/3 and \(k^{*A}_{j}\neq k^{*B}_{j}\) with probability 2/3. If all the checks passed, they go to the next step.

  7. 7.

    To the remaining m−l−l ′ orders, Charlie announces which orders are in the cases (iii) and (iv). In a half of these orders, Alice announces her bit \(k^{*A}_{j}\) following by Bob announces his bit \(k^{*B}_{j}\). In the other half of these orders, Bob announces his bit \(k^{*B}_{j}\) following by Alice announces her bit \(k^{*A}_{j}\). Same to the check process in step 5, it should be \(k^{*A}_{j}=k^{*B}_{j}\) with probability 1/3 and \(k^{*A}_{j}\neq k^{*B}_{j}\) with probability 2/3. If all the checks passed, they go to the next step.

  8. 8.

    We suppose the amount of the remaining orders is n. By eliminating the announced bits, Alice, Bob and Charlie still keep secret bit sequences \(K^{A}=\left ({{k^{A}_{1}}},{{k^{A}_{2}}},\ldots ,{{k^{A}_{n}}}\right )\), \(K^{B}=\left ({{k^{B}_{1}}},{{k^{B}_{2}}},\ldots ,{{k^{B}_{n}}}\right )\) and \(K^{C}=\left ({{k^{C}_{1}}},{{k^{C}_{2}}},\ldots ,{{k^{C}_{n}}}\right )\) orderly in bit sequences K ∗A, K ∗B and K ∗C, respectively.

  9. 9.

    Alice, Bob and Charlie select a [n,t] error-correcting code [42] which could use n bits codeword to encode t bits word by using generator matrix G(x t) and could correct t ′ codeword error bits using the error-correcting function D(y n).

  10. 10.

    Alice chooses a bits word \(R^{A}=\left ({{r_{1}^{A}}},{{r_{2}^{A}}},\ldots ,{{r_{t}^{A}}}\right )\) and calculates the corresponding bits codeword \(W^{A}=\left ({{w_{1}^{A}}},{{w_{2}^{A}}},\ldots ,{{w_{n}^{A}}}\right )\), i.e.,

    $$ W^{A}=R^{A} \cdot G, \quad and \quad R^{A}=W^{A} \cdot D. $$
    (5)

    Then she obtains bit string \(P^{A}=\left ({{p_{1}^{A}}},{{p_{2}^{A}}},\ldots ,{{p_{t}^{A}}}\right )\) by calculating \({{p_{j}^{A}}}={{r_{j}^{A}}}\oplus {{m_{j}^{A}}}\), bit string \(Q^{A}=\left ({{q_{1}^{A}}},{{q_{2}^{A}}},\ldots ,{{q_{n}^{A}}}\right )\) by calculating \({{q_{j}^{A}}}={{w_{j}^{A}}}\oplus {{k_{j}^{A}}}\). After these, she announces P A and Q A to Charlie.

  11. 11.

    Bob chooses a t bits word \(R^{B}=\left ({{r_{1}^{B}}},{{r_{2}^{B}}},\ldots ,{{r_{t}^{B}}}\right )\) and calculates the corresponding bits codeword \(W^{B}=\left ({{w_{1}^{B}}},{{w_{2}^{B}}},\ldots ,{{w_{n}^{B}}}\right )\), i.e.,

    $$ W^{B}=R^{B} \cdot G, \ \mbox{and}\ R^{B}=W^{B} \cdot D. $$
    (6)

    Then he obtains bit string \(P^{B}=\left ({{p_{1}^{B}}},{{p_{2}^{B}}},\ldots ,{{p_{t}^{B}}}\right )\) by calculating \({{p_{j}^{B}}}={{r_{j}^{B}}}\oplus {{m_{j}^{B}}}\), bit string \(Q^{B}=\left ({{q_{1}^{B}}},{{q_{2}^{B}}},\ldots ,{{q_{n}^{B}}}\right )\) by calculating \({{q_{j}^{B}}}={{w_{j}^{B}}}\oplus {{k_{j}^{B}}}\). After these, he announces P B and Q B to Charlie.

  12. 12.

    Charlie obtains bit string \(W^{C}=\left ({{w_{1}^{C}}},{{w_{2}^{C}}},\ldots ,{{w_{n}^{C}}}\right )\) by calculating \({{w_{j}^{C}}}={{q_{j}^{A}}}\oplus {{q_{j}^{B}}}\oplus {{k_{j}^{C}}}\). Then he uses the check matrix H of the [n,t] error-correcting code to check whether the number of error bits exceeds the threshold t ′. If it does, Charlie aborts the protocol and restarts from Step 1. Otherwise, he obtains t bits string R C by decoding W C with error-correcting function D(W C)=W C⋅D. He obtains \(R'^{C}=\left ({r'}_{1}^{C},{r'}_{2}^{C},\ldots ,{r'}_{t}^{C}\right )\) by calculating \({r'}_{j}^{C}={{p_{j}^{A}}}\oplus {{p_{j}^{B}}}\). If one or more bits are different between R C and R ′ C, Charlie announces X≠Y. Otherwise, he announces X=Y.

Fig. 1
figure 1

The schematic of QPC based on phase encoding of single photon (color online)

Full size image

3 Analysis

3.1 Correctness

For simpleness, we first prove that the protocol is correct in ideal scenario. Then we prove that the effect of limited noise will be removed by ECC in practical scenario.

3.1.1 Correctness in Ideal Scenario

Since there are \(l+l'+\frac {3(m-l-l')}{4}=\frac {3m+l+l'}{4}\) single photons used as detecting states which are not used in final comparison, we only consider the other n decoding single photons. In the protocol, up to step 8, it should be that

$$ K^{C}=K^{A}\tilde{\oplus} K^{B}, $$
(7)

where \(\tilde {\oplus }\) denotes that one bit string bitwise XOR another bit[r] string.Footnote 1 Obliviously, Charlie, Alice and Bob share some randomly bits from which one can know the other two parties’ bitwise XOR value.

At step 12, it should be that

$$\begin{array}{@{}rcl@{}} W^{C}&=&Q^{A}\tilde{\oplus} Q^{B}\tilde{\oplus} K^{C}\notag\\ &=&(W^{A}\tilde{\oplus} K^{A})\tilde{\oplus} (W^{B}\oplus K^{B})\tilde{\oplus} K^{C}\notag\\ &=&W^{A}\tilde{\oplus} W^{B}. \end{array} $$
(8)

Based on (5) and (6), we know that

$$ \begin{aligned} R^{A}\tilde{\oplus}R^{B}&=(W^{A}\tilde{\oplus}W^{B})\cdot D\\ &=W^{C}\cdot D. \end{aligned} $$
(9)

Since R C=W C⋅G, it should be that \(R^{C}=R^{A}\tilde {\oplus }R^{B}\).

After these, we consider the other bits string R ′ C which Charlie obtains at step 12 too. We know that

$$\begin{array}{@{}rcl@{}} R'^{C}&=&P^{A}\tilde{\oplus} P^{B}\notag\\ &=&(R^{A}\tilde{\oplus} M^{A})\tilde{\oplus} (R^{B}\tilde{\oplus} M^{B}). \end{array} $$
(10)

When M A=M B, it should be that

$$ R'^{C}=R^{A}\tilde{\oplus} R^{B}. $$
(11)

Otherwise, when M A≠M B, it should be that

$$ R'^{C}\neq R^{A}\tilde{\oplus} R^{B}. $$
(12)

In other words, Charlie knows whether M A=M B or not by comparing R C and R ′ C.

Therefore, the presented protocol is correct in an ideal scenario. We analyze it in practical scenario as follows.

3.1.2 Correctness in Practical Scenario

In practical scenario, noise might appear in all of quantum preparation setups, quantum channel and measurement equipments. Here we only consider their effect on the encoding states (i.e., the noise appear in the courses of obtaining K C) as the detecting photons will be discarded and not effect the correctness of comparison.

We denote the noise appear in the courses of obtaining K C as O=(o 1,o 2,…,o n ), where o i =0 or 1 representing error is existent or not in k i . So Charlie obtains bit string K ′ C as

$$\begin{array}{@{}rcl@{}} K'^{C}&=&K^{C}\tilde{\oplus}O \notag\\ &=&(R^{A}\tilde{\oplus}R^{B})\cdot G. \end{array} $$
(13)

Then (8) is replaced with

$$ W'^{C}=W^{A}\tilde{\oplus}W^{B}\tilde{\oplus} O. $$
(14)

When the error rate does not exceed a rational threshold, i.e., the number of 1 in bit string O does not exceed t ′, we have

$$\begin{array}{@{}rcl@{}} R^{A}\tilde{\oplus}R^{B}&=&(W^{A}\tilde{\oplus}W^{B}\tilde{\oplus} O)\cdot D\notag\\ &=&W^{C}\cdot D. \end{array} $$
(15)

replacing (9). Subsequently, noise will not effect (10)–(12). Namely, the present protocol is correct in practical scenario when noise has not exceed the used ECC’s ability.

3.2 Security

In QPC, every participant has more resources than outsider. With these resources, a dishonest participant has more strategies to cheat besides the strategies which outsider can perform. So the term “participant attack” [43–48] has attracted much attention in the cryptanalysis of quantum cryptography and should be paid more attention to. From the conclusions of QSMPC, we know that it should be insecure when less than a half of participants are honest [26]. Since QPC is a instance of QSMPC, it can only guarantee the secure when there is only one dishonest participant. So we will only analyze the attacks performed by Alice, Bob, and Charlie respectively, but not two colluded participants.

3.2.1 Alice’s (Bob’s) Attacks

In the proposed protocol, Alice’s position are equal to Bob’s completely. So we could only analyze the case that a dishonest Alice cheats Bob’s private information. Before the step 11, what Bob announced is about the detecting states which are not useful to extract Bob’s private information. And in the step 12, Charlie only announces the comparison result. So Alice must pay attention on the messages P B and Q B Bob announced at step 11. If Alice knows K B which is corresponding to Bob’s operations performed on the encoding states at step 3, she can extract Bob’s private information from P B and Q B as \(P^{B}=R^{B}\tilde {\oplus }M^{B}\), \(Q^{B}=W^{B}\tilde {\oplus }K^{B}\) and (6).

Since the encoding states travel between Charlie and Alice, Charlie and Bob respectively in the protocol, the Trojan horse attacks [49, 50] should be considered. With Trojan horse attacks, Alice might use invisible photon eavesdropping or delay-photon eavesdropping to cheat. Since a filter could filter out the photon signal with an illegitimate wavelength, invisible photon eavesdropping is prevented. With the use of multi-photon detection, enough number of delay-photon eavesdropping is prevented. If a few of bits in K B are extracted by Alice, she only can recover a few bits of W B. When the number of correct bits in W B is less than t, R B cannot be recovered with the error-correcting function correctly. Then the delay-photon eavesdropping is invalid.

Besides Trojan horse attacks, some other attacks [44–48] also could be used to cheat information from traveling states, such as intercept-resend attack, measurement-resend attack, and entanglement-measure attack [30, 31]. In these attacks, Alice first performs some operations on S B before step 3, such as entangles photons, replaces photon, then performs some measurements before it comes back to Charlie. However, these attacks will be detected by Charlie’s detection based on Alice and Bob’s announcements at step 6. In fact, the states used in this protocol is the four states which are similar as the four BB84 states. When \(\theta =\left \{0, \frac {\pi }{2}, \frac {\pi }{4}, \frac {3\pi }{4}\right \}\), the states \(\frac {1}{\sqrt {2}}\left (|0\rangle |1\rangle +ie^{i\theta }|1\rangle |0\rangle \right )\) are corresponding to BB84 states {|0〉,|1〉,|+〉,|−〉} respectively. Without the knowledge of the detecting photons’ positions, Charlie and Bob’s phase shifts, Alice might measure detecting states in incorrect bases. Then she will be detected for that the detecting states have been disturbed.

Therefore, the proposed protocol can resist all well known attacks performed by Alice and Bob.

3.2.2 Charlie’s Attacks

Now we consider the case that a dishonest Charlie cheats Alice and Bob’s private information. For extracting Alice and Bob’s private information, Charlie needs only cheat one of K A and K B as he know the value of \(K^{C}=K^{A}\tilde {\oplus }K^{B}\). So we only analyze the case that Charlie cheat Alice’s private information.

Similarly to the analysis in the above subsection, the two Trojan horse attacks will be prevented by Alice and Bob’s filter of illegitimate wavelength and the multi-photons detection.

In the other attacks, if Charlie cheats K A, he first performs some operations on S A at step 2, such as entangles photons, replaces photon, then performs some measurements on S ∗A as it was sent back to him. However, all of these attacks will be detected by the check process in which he is required to announce \({{k^{C}_{j}}}\) and the clicked detector first. Without the knowledge of the positions of detecting states, \({{k^{A}_{j}}}\) and \({{k^{B}_{j}}}\) before cheating, Charlie cannot make sure the detecting states’ bases. Then his any dishonest measurements or operations will disturb the detecting states. Subsequently, he will be detected.

Therefore, the proposed protocol can resist all well known attacks performed by Charlie.

3.3 The Capability of Limited Fault-Tolerate

In the presented scheme, ECC are used to prevent the limited noise which appears in non-ideal scenario, including quantum preparation setups, quantum channel and measurement equipments.

However, ECC’s capability of error-correcting is limited, so the protocol is appropriate for the scenario where the noise is limited. In the protocol, the error rate of noise must be less than t ′/n, otherwise, the scheme should be restarted. Then the participants should use another error-correcting code which has higher error-correcting capability to utilize the scheme.

4 Conclusion

In this paper, we propose a quantum private comparison scheme based on phase encoding. The analysis indicates that the scheme is secure which can prevent some familiar attacks. And this scheme is easy to be realized in current experiments as only some simple devices are used.