1 Introduction

The generalisation of the unique Schwarzschild exterior solution governing the behaviour of the gravitational field outside a spherically symmetric perfect fluid to include the effects of the electromagnetic field is given by the Reissner-Nordström spacetime. The standard Einstein’s equations are supplemented by Maxwell’s equation, and through an appropriate choice of gauge, only the electric contribution is significant. Interior spacetimes for charged spheres are not unique as the associated field equations reduce to a system of six partial differential equations in four unknowns. Theoretically there are 15 possible two element subsets of the six member set of geometrical and dynamical quantities that could serve as initial data for the problem. Ivanov [1] has compiled a comprehensive list of two member choices that have been treated historically. Recently an exact family of charged models with the Wyman-Adler metric was obtained by Fatema and Murad [2]; they provide a detailed motivation for the study of such objects and relevant references in the literature. In this regard, we also mention the investigations of Murad and Fatema [3], Gupta and Maurya [4] and Maurya and Gupta [5].

While the choice of the initial data appears ad hoc and guided largely by what functions allow for the complete solution of the Einstein-Maxwell system, systematic efforts have been followed by some researchers. For example, using a suitable change of coordinates Hansraj and Maharaj [6], Thirukkannesh and Maharaj [7, 8] have reduced the problem to a second order master differential equation in one of the space variables. The remaining gravitational potential and the electric field intensity may then be nominated in order to successfully integrate the master field equation. The method has proved useful in obtaining a physically relevant solution in the case of a charged analogue of the Durgapal and Bannerji star [9], and also the Finch and Skea star [10], which was been demonstrated to be consistent with the astrophysical theory of Walecka [11]. A similar approach was employed by Komathiraj and Maharaj [12] to produce a charged analogue of the Tikekar superdense star [13] with spheroidal geometry.

It must be noted that this is not the only approach that may be followed. A completely different attack is to impose ab initio some physical considerations on the system of equations. For example, an equation relating the (isotropic) pressure and energy density may be utilised. However, only limited success has been reported in the simplest case of a barotropic equation of state of the linear type where the pressure is proportional to the energy density. Another physically interesting case is the polytropic equation of state; however only a few exact solutions of this type have been discovered thus far. Numerical methods were applied by Nilsson and Uggla [14] to uncharged matter with a linear equation of state, and later the polytropic equation of state was considered by Nilsson and Uggla [15], when treating the case of a neutral ball of perfect fluid. Clearly the neutral case is more challenging than the charged version in view of the fact that there exists only one free variable to nominate at the outset. A different approach is to postulate a functional relationship between two other quantities, namely the electric field intensity and one of the metric potentials rather than an equation of state. This is the avenue we pursue in this article and we are able to report some new interesting solutions based on this approach.

Numerical methods have been utilised by Nduka [16] and Singh and Yadav [17] in order to electrify the Kuchowicz [18] neutral solution. An approximately linear equation of state is obtained. Ivanov [1] explained in detail the difficulty of imposing an equation of state in isotropic static spherical models. The field equations turn out to be not readily solvable. If we relax the condition of pressure isotropy to allow for both tangential and radial pressures, then the problem becomes simpler. Feroze and Siddiqui [19] and Maharaj and Mafa Takisa [20] reported new anisotropic models with a quadratic equation of state. These models contained particular isotropic models, and when the anisotropy parameter is set to zero, the familiar isotropic models of de Sitter and Einstein were regained. Thirukkanesh and Ragel [21] recently obtained a class of anisotropic solutions with a polytropic equation of state. In this paper we consider the more difficult case of isotropic pressures.

2 Einstein-Maxwell Field Equations

The differential equations governing models of spherically symmetric charged stars comprise the coupled Einstein-Maxwell field equations. This system is given by

$$\begin{aligned} G_{ab} =& M_{ab} + E_{ab} \end{aligned}$$
(1)
$$\begin{aligned} F_{ab;c} + F_{bc;a} + F_{ca;b} =& 0 \end{aligned}$$
(2)
$$\begin{aligned} F^{ab}{} {}_{;b} =& J^a \end{aligned}$$
(3)

where M ab =(ρ+p)u a u b +pg ab is the matter tensor, ρ is the energy density, p is the isotropic pressure, and u a is the timelike, unit four-velocity. The electromagnetic contribution to the total energy momentum tensor is given by

$$ E_{ab} = F_{ac}F_b{}^{c} - \frac{1}{4}g_{ab}F_{cd}F^{cd} $$
(4)

where the electromagnetic field tensor is defined by F ab =A b;a −A a;b and A a is the four-potential. The four-current density can be written as

$$ J^a=\sigma u^a $$
(5)

where σ is the proper charge density. Note that the four-potential is not uniquely determined by Maxwell’s equations but is constrained by gauge transformations.

In many physical situations it is reasonable to assume that the interior of the charged star is described by the line element

$$ ds^2 = -e^{2\nu(r)} dt^2 + e^{2\lambda(r)} dr^2 + r^2 \bigl(d\theta ^2 + \sin^2 \theta d\phi^2 \bigr) $$
(6)

where the functions ν(r) and λ(r) are gravitational potentials. The line element (6) is the most general for static spherically symmetric spacetimes. The Einstein-Maxwell equations (1) may be expressed as the system

$$\begin{aligned} \bigl[r\bigl(1-e^{-2\lambda}\bigr) \bigr]' =&r^2 \rho+ \frac{1}{2}r^2E^2 \end{aligned}$$
(7)
$$\begin{aligned} - \bigl(1-e^{-2\lambda} \bigr)+2\nu're^{-2\lambda} =& pr^2 -\frac{1}{2}r^2E^2 \end{aligned}$$
(8)
$$\begin{aligned} e^{-2\lambda} \biggl[\frac{\nu'}{r}-\frac{\lambda'}{r}+ \nu''-\nu '\lambda' + \nu'^2 \biggr] =&p+\frac{1}{2}E^2 \end{aligned}$$
(9)
$$\begin{aligned} \sigma =& \frac{1}{r^2} e^{-\lambda} \bigl( r^2 E \bigr) ' \end{aligned}$$
(10)

for the static spherically symmetric spacetime (6). We have introduced the electric field intensity E=e −(ν+λ) ϕ′(r) in the above. We have chosen the four-potential as A a =(ϕ(r),0,0,0) which gives the component F 01=e −(ν+λ) E(r). The conservation laws (M ab+E ab);b =0 reduce to the equation

$$\begin{aligned} p' + r (\rho+ p) \nu' = \frac{E}{r^2} \bigl[r^2 E \bigr]' \end{aligned}$$
(11)

which can be used in the place of one of the field equations (7)–(10).

Introducing a new coordinate x and two metric functions y(x) and Z(x) defined by

$$x = Cr^2,\qquad Z(x) = e^{-2\lambda(r)},\qquad y^2(x) = e^{2\nu(r)} $$

where C is constant, the Einstein-Maxwell field equations (7)–(10) assume the form

$$\begin{aligned} \frac{1-Z}{x}-2\dot{Z} =&\frac{\rho}{C}+\frac{E^2}{2C} \end{aligned}$$
(12)
$$\begin{aligned} \frac{Z-1}{x} + \frac{4Z\dot{y}}{y} =&\frac{p}{C}-\frac{E^2}{2C} \end{aligned}$$
(13)
$$\begin{aligned} 4x^2Z\ddot{y} + 2x^2\dot{Z}\dot{y}+ \biggl(\dot{Z}x-Z+1- \frac{E^2x}{C} \biggr)y =&0 \end{aligned}$$
(14)
$$\begin{aligned} \frac{\sigma^2}{C} =&\frac{4Z}{x} ( x\dot{E} + E )^2 \end{aligned}$$
(15)

where dots represent differentiation with respect to x. The transformed field equations are useful in generating new exact solutions as demonstrated by Thirukkanesh and Maharaj [22] for charged models with a linear equation of state and Mafa Takisa and Maharaj [23] with a polytropic equation of state. We have not imposed an equation of state in this study so other charged solutions are possible.

3 Physical Conditions

The system (12)–(15) admits an infinite number of exact solutions as there are more variables than equations. Unfortunately many of the solutions reported in the literature correspond to unrealistic distributions of charged matter (see the work of Delgaty and Lake [24] where a large number of neutral solutions were tested for physical applicability). Delgaty and lake [24] pointed out that only nine solutions so far are regular and well behaved. When analysing solutions of the Einstein-Maxwell system the following conditions are often imposed in order to obtain models of stellar configurations that are physically plausible:

  1. (a)

    Positivity and finiteness of pressure and energy density everywhere in the interior of the star including the origin and boundary:

    $$0 \leq p< \infty, \qquad 0<\rho<\infty $$
  2. (b)

    The pressure and energy density should be monotonically decreasing functions of the coordinate r. The pressure vanishes at the boundary r=R:

    $$\frac{dp}{dr}\leq0,\qquad\frac{d\rho}{dr}\leq0, \qquad p(R)=0 $$
  3. (c)

    Continuity of gravitational potentials across the boundary of the star. The interior line element should be matched smoothly to the exterior Reissner-Nordström line element at the boundary:

    $$e^{2\nu(R)}=e^{-2\lambda(R)}=1-\frac{2M}{R}+\frac{Q^2}{R^2} $$
  4. (d)

    The principle of causality must be satisfied, i.e., the speed of sound should be everywhere less than the speed of light in the interior:

    $$0\leq\frac{dp}{d\rho}\leq1 $$
  5. (e)

    Continuity of the electric field across the boundary:

    $$E(R)=\frac{Q}{R^2} $$
  6. (f)

    The metric functions e 2ν and e 2λ and the electric field intensity E should be positive and non-singular everywhere in the interior of the star.

  7. (g)

    The energy conditions: (weak ρ>0, ρ+p>0; strong ρ>0, ρ+3p>0; dominant ρ>0, ρ−p>0) should be satisfied.

  8. (h)

    The redshift value should be less that 2 to correspond to most observed stars.

The conditions (a)–(h) indicated above are not satisfied by all the solutions throughout the interior of the star. For example the Tolman V and VI solutions suffer the defect of being singular solutions, as they have infinite values of central density. Additionally, some of the above conditions may be overly restrictive. For example, observational evidence suggests that in particular stars the energy density ρ is not a strictly monotonically decreasing function (Shapiro and Teukolsky [25]).

4 A Solution Generating Algorithm

We elect to specify a functional relationship between the electric field intensity E(x) and the metric component Z(x). It is reasonable to expect that the strength of the electric field inside a charged star is position dependent. We invoke the prescription

$$ \dot{Z}x - Z + 1 = \frac{E^2}{C}x $$
(16)

The advantage of this choice is that it forces the second order differential equation in y to degenerate into a first order equation. It is worth observing that (14) has often been utilised for its value as a second order differential equation in y(x), however, it may also be rearranged as a first order differential equation in Z of the Riccati type. Such equations possess their own complications. With the choice (16), Eq. (14) becomes

$$ 2Z \ddot{y}+ \dot{Z}\dot{y} = 0 $$
(17)

which is essentially of first order in both Z or y. Solving for Z we get

$$ Z =\frac{1}{K(\dot{y})^2} $$
(18)

(K is an integration constant) which suggests that if we prescribe y then Z will follow trivially. Alternatively (17) has the general solution

$$ y = \int{\frac{K}{\sqrt{Z}}} dx + L $$
(19)

where L is another integration constant.

Now there are three distinct approaches in algorithmically constructing Einstein-Maxwell solutions based on the ansatz (16):

  • From (19) above we have obtained y in terms of Z. This means that if we pick suitable forms for Z then after integration we should be able to establish the function y(x). Then with the help of (16) we may obtain the form for the electric field intensity E. Thereafter the energy density ρ, the pressure p and the proper charge density σ may be found using (12), (13) and (15) respectively.

  • Alternatively using (18) we may choose a form for y and then find Z. On substituting into (16) we may obtain E. The remaining quantities may then be found as outlined above. A distinct advantage of this approach is that no integrations are called for. Therefore an infinite number of choices can be made for the metric potential y that will allow for the complete solution of the Einstein field equations.

  • A third approach is to specify the electric field intensity in (16). Then the metric function Z must be obtained by solving this linear differential equation (16). Finally we may substitute the Z into (19) to establish y. This method has the obvious drawback that, firstly, it may not be possible to find Z for a particular choice of E as the integration of Z may not be possible to complete. Secondly, even if we are able to find Z then there is still no guarantee that (19) can be integrated to yield y.

5 Specifying E

We explore the option of specifying the charge distribution and consider a variety of choices for the electric field quantity \({\frac {E^{2}}{C}}\). Then the algorithm operates as follows: We begin by nominating a form for the electric field intensity E and then solve (16) for Z. Thereafter the form for Z is substituted into (19) to give the metric potential y. The choice of E should allow for both Z and y to be obtained explicitly.

5.1 The Case \(\frac{E^{2}}{C} = \alpha\)

We commence by examining the simplest case \({\frac{E^{2}}{C} = \alpha}\) where α is a real parameter. Note that this implies a constant electric field. Equation (16) becomes

$$ \dot{Z}x-Z + (1-\alpha x) =0 $$
(20)

which has the solution

$$ Z(x)=C_1 x + 1 + \alpha x \log{x} $$
(21)

where C 1 is a constant. Substituting this form of Z into (19) we obtain

$$ y = \int{\frac{K}{\sqrt{C_1 x + 1 + \alpha x \log{x}}}} dx + L $$
(22)

which cannot be evaluated in closed form. We have commented on this case to indicate that the simplest case of a constant electric field intensity is non-trivial in general.

5.2 The Case \(\frac{E^{2}}{C} = \alpha x\)

With the above choice of E, (16) becomes

$$ \dot{Z} x - Z = \alpha x^2 - 1 $$
(23)

where α is an arbitrary constant, and it is solved by

$$ Z = 1 + C_3 x + \alpha x^2 $$
(24)

where C 3 is a constant of integration.

Substituting this form of Z into (19) we obtain

$$ y = \int{\frac{K}{\sqrt{1 + C_3 x + \alpha x^2}}} dx + C_2 $$
(25)

and performing the integration yields

$$ y=\frac{1}{\sqrt{\alpha}} \log \bigl( C_3 + 2\alpha x + 2 \sqrt {\alpha \bigl( 1 + C_3 x + \alpha x^2 \bigr)} \bigr)+C_2 $$
(26)

which establishes the remaining geometric potential.

The energy density ρ is given by

$$ \frac{\rho}{C}=-3C_3-\frac{11}{2}\alpha x $$
(27)

and its rate of change has the form

$$ \frac{d\rho}{Cdx}=-\frac{11}{2}\alpha $$
(28)

which is constant. The density is a monotonically decreasing function outwards from the centre. From (27) and (26) we note the conditions C 3<0 and \(\alpha> C_{3}^{2}/4\) for regularity at the centre. Note that our prescription E 2=αCr 2 then means that the model remains charged and there is no uncharged limit in this case.

The pressure p has the form

$$\begin{aligned} \frac{p}{C} =& C_3+\frac{3\alpha x}{2} \\ &{} +\frac{4\sqrt{\alpha}f^2_1 (x)}{f_1 (x) \log(C_3+2\alpha x+2\sqrt {\alpha(1+C_3 x)\log(c_3+2\alpha x+2\sqrt{\alpha} f_1(x))})} \end{aligned}$$
(29)

where we have introduced the function \(f_{1}(x) = \sqrt{1 + C_{3} x + \alpha x^{2}}\) to simplify the expressions. The rate of change of pressure is given by

$$\begin{aligned} \frac{dp}{dx} =&\frac{4\alpha}{\log(C_3+2\alpha x+2\sqrt{\alpha }(f_1(x))^2)} \\ &{}+ { 2\sqrt{\alpha} \biggl(\frac{(C_3+ 2\alpha x)(1+C_3 x)-\alpha ^2(2+C_3 x)\log(C_3+2\alpha x^2)\sqrt{\alpha}f_1 (x)}{(f_1(x))^3 \log (C_3+2\alpha x+2\sqrt{\alpha}f_1)} \biggr)} \end{aligned}$$

while the adiabatic sound speed index has the form

$$\begin{aligned} \frac{dp}{d\rho}=\frac{\alpha [(8+3\alpha)\sqrt{\alpha }f_1(x)+4(C_3+2\alpha x)\log [C_3+2\alpha x +2\sqrt{\alpha }f_1(x) ] ]}{44\sqrt{\alpha}f_1(x)} \end{aligned}$$

The following quantities

$$\begin{aligned} \frac{\rho- p}{C} =& -4C_3-7\alpha x \\ &{} -\frac{4}{\alpha} \bigl[\sqrt{\alpha}f_1(x) \log \bigl(C_3+2\alpha x+ 2\sqrt {\alpha\bigl(1+C_3 x +\alpha x^2\bigr)}\bigr) \bigr] \end{aligned}$$
(30)
$$\begin{aligned} \frac{\rho+ p}{C} =& -2C_3-4\alpha x \\ &{} +\frac{4}{\alpha} \bigl[\sqrt{\alpha}f_1(x) \log \bigl(C_3+2\alpha x+ 2\sqrt {\alpha\bigl(1+C_3 x +\alpha x^2\bigr)}\bigr) \bigr] \end{aligned}$$
(31)
$$\begin{aligned} \frac{\rho+ 3 p}{C} =& -\alpha x \\ &{} +\frac{12}{\alpha} \bigl[\sqrt{\alpha}f_1(x) \log \bigl(C_3+2\alpha x+ 2\sqrt{\alpha\bigl(1+C_3 x +\alpha x^2\bigr)}\bigr) \bigr] \end{aligned}$$
(32)

are useful when studying the energy conditions. These are all required to be positive within the stellar interior.

6 Specifying Z

We next consider exact solutions that may be derived by nominating the metric potential Z at the outset. Of course in view of the reciprocal of \(\sqrt{Z}\) in the integrand of (19), we expect only a small number of choices will result in a complete resolution of y.

6.1 Z=(1+x)n

This choice will lead to a Schwarzschild sphere in the absence of charge for the case n=1 as was demonstrated by Hansraj [26]. In other words this prescription will produce charged analogues of the Schwarzschild interior solution. This form also has the property of yielding solutions that are regular at the stellar centre. We obtain the electric field intensity in the form

$$ \frac{E^2}{C} =\frac{1+n x (1+x)^{n-1} -(1+x)^n}{x}. $$
(33)

With the choice of Z=(1+x)n, we obtain

$$ y = \frac{2}{2-n} (1+x )^{1-\frac{n}{2}}+C_4 $$
(34)

after integration using (19). Then the system of Einstein-Maxwell field equations is completely solvable. The density ρ and pressure p are given by

$$\begin{aligned} \frac{\rho}{C} =& \frac{1}{2} \biggl(\frac{1-(1+x)^n-5nx(1+x)^{n-1}}{x} \biggr) \end{aligned}$$
(35)
$$\begin{aligned} \frac{p}{C} =& \frac{2x(2-n+nx)(1+x)^{n-1}+(1+x)^n-1}{2 x} \end{aligned}$$
(36)

respectively. The rate of change of the energy density ρ and pressure p have the forms

$$\begin{aligned} \frac{d\rho}{C dx} =& \frac{-5 (-1+n) n x (1+x)^{-2+n}-6 n (1+x)^{-1+n}}{2 x} \\ &{} -\frac{1-5 n x (1+x)^{-1+n}-(1+x)^n}{2 x^2} \end{aligned}$$
(37)
$$\begin{aligned} \frac{dp}{C dx} =& \frac{1}{2 x^2 (1+x)^2}\bigl(1-(1+x)^n+2 n^2 x^3 (1+x)^n + x \bigl(2-2 (1+x)^n \\ &{} +n (1+x)^n\bigr)+x^2 \bigl(1- \bigl(5 - 9n + 2n^2\bigr) (1+x)^n \bigr)\bigr) \end{aligned}$$
(38)

which allows us to compute the sound speed parameter \(\frac{dp}{d\rho }\). This is given by

$$\begin{aligned} \frac{dp}{d\rho} =& x^2\biggl[ \frac{1}{2}-2n^2 - 2(2+n x) + (1+x)^n \\ & {} +\biggl(\frac{7}{2} x-\frac{3}{2} n x-n x^2-3 n^2 x^3\biggr) (1+x)^{n-2} \biggr] \\ & \big/ \bigl[-5n x^2(n-1) (1+x)^{n-2} - n x (1+x)^{n-1} + (1+x)^n -1\bigr] \end{aligned}$$
(39)

Finally the quantities \(\frac{\rho+ p}{C}\), \(\frac{\rho- p}{C}\), and \(\frac{\rho+3p}{C}\) are useful to study the energy conditions; these expressions follow immediately from (35) and (36). Since the above solution does not readily lend itself to an analytical treatment, we opt to generate plots of the dynamical and geometric quantities, with the help of Mathematica (Wolfram [27]) to obtain a qualitative view on the acceptability of these solutions to represent physical matter.

A consideration of the behaviour of our model at the stellar centre x=r=0 will assist in obtaining bounds for the various constants appearing in the solution. As x tends to zero we observe that both ρ and p have well defined limits. The positivity of central energy density and pressure require that

$$\rho_0 = -3nC > 0 ,\qquad p_0 = C \biggl(2- \frac{n}{2} \biggr) > 0 $$

where the subscript indicates central quantities. The adiabatic sound speed parameter at the centre is constrained by

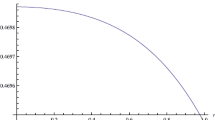
$$0 < \biggl( \frac{dp}{d\rho} \biggr)_0 = \frac{3n^2 - 15n + 8}{11n(n-1)} < 1 $$

and is satisfied in the intervals \(n < \frac{-1-\sqrt{17}}{4}\) or \(0 < n < \frac{-1+\sqrt{17}}{4}\) or n>1. Further if we take C>0 then the condition of positive central pressure and density as well as subluminal sound speed are satisfied for \(n < \frac{-1-\sqrt{17}}{4} \approx-1,28\). However, if we take C<0 (which is the case for the Schwarzschild interior metric), then all the physical constraints are satisfied for n>4. In view of the foregoing we consider the case n=−2 together with the choice of constants C=100 and C 4=2. These are compatible with a regular centre. Plots of the energy density, the pressure, the sound speed parameter as well as the energy conditions are generated, with the use of these values for the constants, in Figs. 1–4.

Fig. 1
figure 1

Plot of energy density versus radial coordinate

Full size image

From an investigation of Fig. 1, it is evident that the energy density is a positive, smooth and monotonically decreasing function. Additionally, the pressure profile in Fig. 2 is also positive and smooth, and importantly the pressure vanishes for a finite radius corresponding approximately at x=2 in geometric units. This hypersurface of zero pressure identifies the boundary of the star. This is an important requirement, the absence of which would indicate that our solution could only be used to model a cosmological fluid. The sound speed parameter in Fig. 3 is found to be less than unity everywhere in the interior so that our charged star model displays causal behaviour throughout the interior. Finally, it may be observed from Fig. 4 that all the energy requirements are satisfied everywhere within the star. Accordingly, our model may have merit in representing a realistic charged shell distribution of finite inner and outer radius.

Fig. 2
figure 2

Plot of pressure versus radial coordinate

Full size image
Fig. 3
figure 3

Plot of sound speed versus radial coordinate

Full size image
Fig. 4
figure 4

Plot of ρ−p,ρ+p,ρ+3p versus radial coordinate

Full size image

6.2 The Choice Z=(1+x 2)n

We substitute Z=(1+x 2)n in (19). This gives

$$ y = x{}_2F_1 \biggl[\frac{1}{2} , \frac{n}{2} , \frac{3}{2} , - x^2 \biggr] + L $$
(40)

where 2 F 1 is the hypergeometric series. The hypergeometric function is an infinite series in general and converges only in the range |x|<1. This means that the stellar model is only well behaved in an interval close to the centre. However for certain values of n, simple closed form solutions result; for these special cases the model is well behaved throughout the interior of the star. We tabulate some particular exact solutions in Table 1.

Table 1 Exact solutions
Full size table

From Table 1 we conjecture that the form for y, when n is an odd integer, involves a polynomial of order (n−2) in the numerator and a term \(( 1+ x^{2})^{\frac{n-2}{2}}\) in the denominator. The solutions appear to follow a pattern for certain values of n. It is remarkable that these solutions are simple rational polynomial type functions. They have ostensibly not been previously found using other approaches in the literature.

We now consider briefly the particular case where n=−2. From the table, when n=−2, we have \({y = x+\frac{x^{3}}{3}+C_{5}}\) and the electric field intensity is given by

$$ \frac{E^2}{C} = \frac{6x+3x^3+x^5}{(1+x^2)^3}. $$
(41)

The density and pressure are given by

$$\begin{aligned} \frac{\rho}{C} =&\frac{14x+3x^3+x^5}{2(1+x^2)^3} \end{aligned}$$
(42)
$$\begin{aligned} \frac{p}{C} =&\frac {12+39x^2-6x^3+17x^4+3x^5+2x^6+x^7}{x(3+x)(1+x^2)^3} \end{aligned}$$
(43)

respectively.

The rate of change of the energy density ρ and pressure p have the form

$$\begin{aligned} \frac{1}{C}\frac{d\rho}{dx} =&\frac{14-16x^2-4x^4-x^6}{2(1+x^2)^4} \end{aligned}$$
(44)
$$\begin{aligned} \frac{1}{C} \frac{dp}{dx} =& \bigl[36+24x+135x^2+132x^3+438x^4+92x^5+84x^6 \\ &{} +60x^7+10x^8+4x^9+x^{10} \bigr]\big/ \bigl[x^2(3+x)^2\bigl(1+x^2 \bigr)^4\bigr] \end{aligned}$$
(45)

which will allow us to compute the sound speed parameter which is given by

$$\begin{aligned} \frac{dp}{d\rho} =& \bigl[2\bigl(36+24x+135x^2+132x^3+438x^4+92x^5+84x^6+60x^7 \\ &{} +10x^8+4x^9+x^{10}\bigr)\bigr]\big/ \bigl[x^2(3+x) \bigl(-14+61x^2+4x^4+x^6 \bigr)\bigr] \end{aligned}$$
(46)

Finally the following expressions are useful when considering the energy conditions:

$$\begin{aligned} \frac{ \rho+p}{C} =&\frac {24+120x^2x^3+43x^4+9x^5-7x^6+3x^7}{2x(3+x)(1+x^2)^3} \end{aligned}$$
(47)
$$\begin{aligned} \frac{\rho-p }{C} =&\frac {24++36x^2-26x^3+25x^4+3x^5+x^6+x^7}{2x(3+x)(1+x^2)^3} \end{aligned}$$
(48)
$$\begin{aligned} \frac{ \rho+3p}{C} =&\frac {72+276x^2-22x^3+111x^4+21x^5+15x^6+7x^7}{2x(3+x)(1+x^2)^3} \end{aligned}$$
(49)

6.3 The Choice Z=1+x n

We substitute Z=1+x n in (19). Then the general solution for y is given by

$$ y=x_2F_1 \biggl[\frac{1}{2},\frac{1}{n}, \frac{n+1}{n},-x^2 \biggr] + L $$
(50)

in terms of the hypergeometric function 2 F 1. Observe that the case n=1 in the present function Z corresponds to n=1 for the previously treated Z=(1+x)n case. In the case n=2 the present function Z is equivalent to the choice n=1 in the case Z=(1+x 2)n also considered elsewhere in this article. Hence we do not consider these again. Empirical testing for exact models with n=3,4,5,… suggests that closed form solutions do not emerge. The forms for y turn out to involve elliptic functions. Accordingly we confine our attention to those cases which produce elementary forms for y on integration. In addition, fractional values of n appear to yield closed form solutions as do negative integral values of n. We tabulate some exact solutions that we have generated in Table 2.

Table 2 Exact solutions
Full size table

It is not surprising that these solutions all appear to be novel. They follow essentially because of our prescription of linking the electric field intensity to the gravitational potential Z. This approach has not previously been attempted. Therefore we find that the solutions reported in the previous two sections are new.

7 Specifying y(x)

Using \(Z = {\frac{\gamma}{\dot{y}^{2}}}\) we can nominate any form for y and then obtain Z via (18) and finally \({\frac {E^{2}}{C}}\) with the help of (16). The major advantage here is that the are no integrations to be performed. This means that any analytic function y will allow the complete integration of the Einstein field equations for this scheme. Recall the algorithm works subject to \(\frac{E^{2}}{C}x = \dot{Z} x - Z + 1\) which we prescribed. We give a simple example to illustrate this simple method of finding new exact solutions.

If we take y=1+x for example then we obtain Z=γ a constant using (18). Finally we get \({\frac{E^{2}}{C} = \frac {1 - \gamma}{x}}\) with the aid of (16). The density ρ and pressure p are given by

$$\begin{aligned} \frac{\rho}{C} =& \frac{1 - \gamma}{2 x} \end{aligned}$$
(51)
$$\begin{aligned} \frac{p}{C} =& \frac{9\gamma x+\gamma-x-1}{{2x(1+x)}} \end{aligned}$$
(52)

respectively. The rates of change of these dynamical quantities are given by

$$\begin{aligned} \frac{d\rho}{C dx} =& \frac{-(1-\gamma)}{2 x^2} \\ \frac{dp}{C dx} =& \frac{x^2(9\gamma-1)-(\gamma-1)(x+2)}{4x^2(1+x)^2} \end{aligned}$$

which in turn allows us to obtain the expression

$$\frac{dp}{d\rho}= \frac{(1+x)^2-\gamma (1+2 x+9 x^2 )}{(\gamma- 1) (1+x)^2} $$

which represents the adiabatic sound speed index. The expressions for the energy conditions are represented by the following equations:

$$\begin{aligned} \rho-p =&\frac{1-5\gamma x-\gamma}{x(1+x)} \\ \rho+p =& \frac{4\gamma-1}{x+1} \\ \rho+3p =& \frac{-(1+x-\gamma-13\gamma x)}{x(x+1)} \end{aligned}$$

We do not pursue any physical study of these quantities. We present them merely to illustrate the ease of finding new exact solutions using the method we have proposed. It is patently obvious that all the expressions above are singular at the stellar centre; for this model to correspond to realistic matter there will have to exist another core fluid which has finite density and pressure.

8 Conclusion

We have proposed an algorithmic method of generating models of static charged spherically symmetric distributions with perfect fluid. The construction involves specifying a functional dependence of the potential Z on the electric field intensity E. This is similar to specifying an equation of state relating the fluid pressure functionally with the density in either a barotropic or polytropic form. Our algorithm then requires the selection of certain source functions which will allow for a complete integration of the field equations. While some choices of the source functions are clearly restrictive—such as the algorithm involving integration of functions with square roots, at least one algorithm involves no integration at all. That is arbitrary potentials y may be selected and a complete solution of the Einstein-Maxwell system of partial differential equations may be achieved. We examine our solutions for physical palatability to see if they conform to observational evidence. We demonstrate a solution which does indeed display the qualitative features associated with realistic stars. In other cases, we list in tabular form new charged solutions not previously reported.