1 Introduction

In open quantum systems we have faced with interactions between system and its surrounding environment. These interactions which can led to decoherence, would cause the transition of system from pure quantum states to mixed ones and change the quantum properties, especially quantum correlations. Owing to their notable features in developing the idea of quantum computers, entanglement measures of concurrence and quantum discord which are two different faces of the quantum correlations have attracted much attention in recent years. Since quantum discord computation in systems with large dimensions is difficult, an alternative approach can be dissonance, a new quantum correlation introduced by K. Modi et al. [1] which is defined as a relative entropy between separable state and closest classical state that unlike discord excludes entanglement. Since all three of them (concurrence, discord and dissonance) have been realized to perform quantum information tasks, the investigation of decoherent dynamics of them is an important emerging field [2–8].

Recently, much attention has been paid to the quantum correlation in spin system, such as the Ising model and all kinds of Heisenberg models [9–13]. XXZ Heisenberg models can be supplemented with a magnetic term, the so-called Dzyaloshinskii-Moriya (DM) interaction that arises from spin-orbit coupling and is inevitably influenced by their spin environment. The coupling of spin systems with a spin bath often leads to strong non-Markovian behavior which has many physical importances in solid state, such as systems based on the nuclear spin of donors in semiconductors [14, 15] or on the electron spin in quantum dots [16]. In this paper, we consider the quantum discord, dissonance and concurrence within two spin qubit anisotropic XXZ Heisenberg model with antisymmetric DM interaction in the presence of the bath spin-\(\frac{1}{2}\) particles as environment. Since the dynamics of the system qubit in the model we study is highly non-Markovian, do not expect the use of traditional Markovian master equations.

Also, in this paper we discuss teleportation as one valuable features of quantum information theory that is based on non-local properties of entangled states. For studying teleportation, we have examined the problem of teleportation fidelity in the presence of DM interaction, bath-system coupling constant, temperature and magnetic field for entangled and separable states and considered the defined model as a channel for teleporting the quantum state. This paper is organized as follows: In Sect. 2 we introduce the Hamiltonian model with DM interaction coupled to an XY spin chain. In Sect. 3 we review the concept of concurrence, quantum discord and quantum dissonance and discuss the effects of the D z (the z-component of the DM interaction), g (the bath-system coupling constant), T (temperate) for initial entangle state and initial separable state on them. In Sect. 4 we consider this model as a channel to teleport the quantum state and show the effect of D z , g, μ 0 and T on fidelity. Conclusions are then presented in Sect. 5.

2 The Model and Its Solution

The quantum system we consider, consists of two spin-\(\frac{1}{2}\) anisotropic particles with DM interaction influenced by a local external magnetic field along the z-direction coupled to bath spin-\(\frac{1}{2}\) particles as the environment. Here the DM interaction is a supplemented magnetic term arising from any interaction with a particle’s spin with its motion, which can be represented in the form ∑ ij D ij .(S i ×S j ), where D is the DM vector coupling and the sum is over the pairs of spins. To see the effects of the DM interaction, we choose the z-component of the anisotropic parameter D. The total Hamiltonian is H tot =H s +H b +H sb , where H s and H b stand for the Hamiltonians of the system, bath spin respectively and H sb describes the interaction between the system and the bath. By considering interaction between the two anisotropic system-spin particles as a Heisenberg XXZ model, with DM interaction parameter D z , the Hamiltonian of the system is given by

$$ H_{s} = \varepsilon\bigl(S_{1s}^{z}+S_{2s}^{z} \bigr)+J_{z}S_{1s}^{z}S_{2s}^{z}+ J \bigl(S_{1s}^{+}S_{2s}^{-}+S_{1s}^{-}S_{2s}^{+} \bigr) +iD_{z}\bigl(S_{1s}^{+}S_{2s}^{-}-S_{1s}^{-}S_{2s}^{+} \bigr). $$
(1)

We restrict the interaction between the N-components of the bath spin and the system-bath so that it can be described by Heisenberg XY model as

(2)
(3)

For clarity, the (s) subscript refers to the system and (b) to the bath spin, where the parameter ε characterizes the intensity of the magnetic field applied along the z-axis and D z the z-component of the DM interaction. The coefficients J z , J, g 0 and g correspond to the real coupling constants with J z ,J>0 in the anti-ferromagnetic case and J z ,J<0 in the ferromagnetic case. By using the collective angular momentum operators \(J_{\pm}=\sum_{j=1}^{N}S_{jb}^{\pm}\) and the Holstein-Primakoff transformation as \(J_{+}=a^{\dag}(\sqrt{N-a^{\dag}a})\) and \(J_{-}=(\sqrt{N-a^{\dag}a})a\) with [a,a †]=1, the Hamiltonians of the bath spin H b and interaction H sb can be rewritten as

(4)
(5)

By considering the thermodynamic limit (i.e., N→∞) at a finite temperature, the above equations are reduced to

(6)
(7)

Observe that the bath spin is reduced into a single-mode bosonic thermal field with non-Markovian effects on the dynamics of our system. Since this thermal field will not stay in a thermal equilibrium state as usually assumed for an environment with very large degrees of freedom therefore, the master equation approach cannot be useful. Following the special operative technique introduced in [8], by tracing the degree of freedom of the environment from density matrix

$$ \rho_{tot}(t)=e^{-i H_{tot}t}\rho_{tot}(0)e^{i H_{tot}t}, $$
(8)

we can get the exact non-Markovian dynamics of reduced density matrix for the system at arbitrary finite temperatures. We assume that the initial density matrix for the total system can be described by a pure and separable states as ρ tot (0)=ρ s (0)⊗ρ b , where ρ b refers to the initial density operator of the single-mode bosonic thermal field which is represented in a thermal equilibrium by the Boltzmann distribution as \(\rho_{b}=\frac{1}{Z}\exp[-H_{b}/k_{B}T]\), with the partition function Z=(1−exp[−2g 0/k B T])−1, where k B is Boltzmann’s constant which we henceforth set to one. Two spin particles of the system are initially prepared in a normalized state with maximum quantum correlation as

$$ \bigl|\psi_{s}(0)\bigr\rangle= \alpha|00\rangle+ \beta|11\rangle, $$
(9)

it is easy to check that, the reduced density matrix for the system in the standard basis |00〉,|01〉,|10〉,|11〉 has the form:

(10)

By converting the time evolution equation of the system under the action of the total Hamiltonian in a set of coupled non-commuting operator variable equations introduced in [8] we can see that

$$ e^{-i H_{tot}t}|00\rangle= A(t)|00\rangle+B(t)|01\rangle+C(t)|10\rangle+D(t)|11 \rangle. $$
(11)

Where coefficients A(t),B(t),C(t) and D(t) are functions of operators a and a † and do not commute with each other. The Schrödinger equation for \(e^{-i H_{tot}t}|00\rangle\), is

$$ \frac{d}{dt}\bigl(e^{-i H_{tot}t}|00\rangle\bigr)=-i H_{tot} \bigl(e^{-i H_{tot}t}|00\rangle\bigr), $$
(12)

which by replacing Eq. (11), transforms to 4 coupled first-order differential equations of non-commuting operator variables as

(13)

From Eq. (11), the initial conditions are given by

$$ A(0)=1, \qquad B(0)=C(0)=D(0)=0. $$
(14)

Therefore, by finding the proper transformations of non-commuting operator variables, we can rewrite Eq. (13) as the coupled differential equations of complex-number variables. In this model, we can reach our goal by using transformations as

(15)

Where operator variables A 1(t),B 1(t),C 1(t) and D 1(t) are functions of \(\hat{n}=a^{\dag}a\), and commute with each other. Under these transformations the coupled differential equations of non-commuting operator variables change to the coupled differential equations of complex-number and commuting operator variables as

(16)

By solving Eq. (13) in the usual way with initial condition A 1(0)=1, and B 1(0)=C 1(0)=D 1(0)=0, we can evaluate the time evolution of the initial two spins state of |00〉. A similar analysis as above can be made if the two spins is initially prepared in |11〉 state. Let

$$ e^{-i H_{tot}t}|11\rangle= \tilde{A}(t)|00\rangle+\tilde{B}(t)|01\rangle+ \tilde{C}(t)|10\rangle+\tilde{D}(t)|11\rangle. $$
(17)

In this case, the proper transformations of non-commuting operator variables have the form:

(18)

Insertion of these transformations into Eq. (13) yields

(19)

We calculate all operations for initial state then add the DM interaction parameter D z and obtain transformed state or dynamics of this system in this case. So the density matrix with DM interaction is

$$ \rho_{s}(t)=\left ( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \rho_{11} &0 &0 &\rho_{14}\\ 0 &\rho_{22} &\rho_{23} &0\\ 0 &\rho_{32} &\rho_{33} &0\\ \rho_{14}^{*} &0 &0 &\rho_{44} \end{array} \right ), $$
(20)

where

(21)

3 Dynamics of Quantum Correlations

3.1 Concurrence

To investigate the entanglement dynamics of our bipartite system, we apply Wootters concurrence [17]. The concurrence can be calculated explicitly by the time-dependent density matrix ρ s (t) of the two spins. The quantum state Eq. (21) is entangled if and only if either ρ 22 ρ 33<|ρ 14|2 or ρ 11 ρ 44<|ρ 23|2. Both conditions cannot hold simultaneously [18]. The entanglement of this state is obtained as

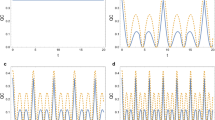
$$ C\bigl(\rho_{s}(t)\bigr)= \sqrt{\rho_{11} \rho_{44}}+|\rho_{14}|- \bigl|\sqrt{\rho_{11} \rho_{44}}-|\rho_{14}|\bigr|-2\rho_{22}. $$
(22)

In this section, we investigate concurrence for entangled state and demonstrate the properties of variable DM coupling parameter Dz on concurrence. In Fig. 1, we calculate concurrence with j z =j=0.0 and g 0=g=1.0 and figure out that by increasing the parameter D z , the concurrence increases.

Fig. 1
figure 1

The time evolution of the concurrence versus t for initial two-qubit state \(|\psi_{s}(0)\rangle=\frac{1}{\surd2}( |00\rangle+ |11\rangle)\) for J=0.0 and J z =0.0. Other parameters are ε=2.0,g 0=g=1.0, for D z =2.0,D z =0.3

Full size image

3.2 Quantum Discord

Quantum discord introduced independently by Ollivier with Zurek and Henderson with Vedral [2, 3] and it aims to capture all the non-classical correlations present in a system. So quantum discord defined as the difference between total correlation and classical correlation.

$$ D(\rho)=I_{tot}(\rho)-I_{cc}(\rho). $$
(23)

Here, I tot (ρ), total correlation in a bipartite quantum state ρ is measured by quantum mutual information given by

$$ I_{tot}(\rho)=S(\rho_{A})+S(\rho_{B})-S(\rho), $$
(24)

where \(S(\rho) = -\operatorname{Tr}(\rho \log \rho)\), is the von Neumann entropy, \(\rho_{A} = \operatorname{Tr}_{B}(\rho)\), and \(\rho_{B} = \operatorname{Tr}_{A}(\rho)\), are the reduced density operators for subsystems A and B, respectively. And I cc (ρ), classical correlation is measured by the following expression

$$ I_{cc}(\rho)=\sup_{\{\varLambda_{k}\}}I\bigl(\rho|\{\varLambda_{k} \}\bigr), $$
(25)

where the maximum is taken over all projective measurements performed locally on qubits, described by a set of orthogonal projectors {Λ k }=|i〉〈i|, k=1,2.

Conditional density operator ρ k associated with the measurement k state is:

$$ p_{k}:=\operatorname{Tr}\bigl[(I \otimes\varLambda_{k}) \rho(I \otimes \varLambda_{k})\bigr]. $$
(26)

In a bipartite quantum state with density matrix operator ρ s (t) that includes two parts and has the form of two-qubit X states [19]. With this, we obtain quantum discord for density matrix with DM interaction parameter D z Eq. (12) and investigate D z , g and the influence of temperature T on quantum discord. In Fig. 2, quantum discord for entangled state with given parameters versus t for different values of D z is plotted and it is found that by increasing D z the QD is increased but in Fig. 3, QD for separable state with given parameters versus t for different values of D z is plotted and it is figured out that by increasing D z , the QD is decreased and this implies that QD for entangled and separable states have inverse ratio. In Fig. 4, QD for entangled state with given parameters versus t for different values of g is plotted and it is found that by increasing g QD is increased. However in Fig. 5, QD for separable state with given parameters versus t for different values of g is plotted and it is seen that by increasing g, QD is decreased and we find out that QD for entangled and separable states have inverse ratio. In Fig. 6, QD for entangled state and in Fig. 7, QD for initial separable state with given parameters versus time and temperature T is plotted and it is found by increasing T, quantum discord is decreased.

Fig. 2
figure 2

The time evolution of the quantum discord versus t for initial two-qubit state \(|\psi_{s}(0)\rangle=\frac{1}{\surd2}( |00\rangle+ |11\rangle)\) for J=0.0 and J z =0.0. Other parameters are ε=2.0,g 0=g=1.0, T=2.0 for Dz=0.2,Dz=3.0

Full size image
Fig. 3
figure 3

The time evolution of the quantum discord versus t for initial two-qubit state |ψ s (0)〉=|00〉 for J=0.0 and J z =0.0. Other parameters are ε=2.0,g 0=g=1.0,T=2.0 for Dz=0.2,Dz=4.0

Full size image
Fig. 4
figure 4

The time evolution of the quantum discord versus t for initial two-qubit state |ψ s (0)〉=|00〉 for J=0.0 and J z =0.0. Other parameters are ε=2.0,g 0=1.0,T=2.0 and Dz=1.0 for g=0.2,g=2.0

Full size image
Fig. 5
figure 5

The time evolution of the quantum discord versus t for initial two-qubit state \(|\psi_{s}(0)\rangle=\frac{1}{\surd2}( |00\rangle+ |11\rangle)\) for J=0.0 and J z =0.0. Other parameters are ε=2.0,g 0=1.0 and Dz=1.0 for g=0.2 and g=2.0

Full size image
Fig. 6
figure 6

The time evolution of the quantum discord versus T and t for initial two-qubit state \(|\psi_{s}(0)\rangle=\frac{1}{\surd2}( |00\rangle+ |11\rangle)\) for J=0.0 and J z =1.0. Other parameters are ε=1.0,g 0=g=1.0 and Dz=0.5

Full size image
Fig. 7
figure 7

The time evolution of the quantum discord versus T and t for initial two-qubit state |ψ s (0)〉=|00〉 for J=0.0 and J z =1.0. Other parameters are ε=1.0,g 0=g=1.0 and Dz=0.5

Full size image

3.3 Quantum Dissonance

In this part, we study quantum correlation in separable systems called quantum dissonance that is based on relative entropy [1]. Dissonance as a measure of non-classical correlation without entanglement is defined as the distance from the closest separable state of the given state to the closest classical state of the separable state. According to the above definition, density matrix σ is said to be separable if it can be written as \(\sigma=\varSigma_{i}p_{i}\rho_{i}^{A}\otimes\rho_{i}^{B}\), Σ i p i =1, p i ≥0, so that the dissonance is defined as

$$ Q =\min_{\chi\in\sigma}S(\sigma\|\chi), $$
(27)

where \(\chi=\sum_{k_{n}}p_{k_{1}\ldots k_{n}}|k_{1}\ldots k_{n}\rangle\langle k_{1}\ldots k_{n} |=\sum_{\overrightarrow{k}}p_{\overrightarrow{k}}|\overrightarrow {k}\rangle\langle\overrightarrow{k}|\), is the closest separable state for N partite and \(\varSigma_{\overrightarrow{k}}|\overrightarrow{k}\rangle\langle \overrightarrow{k}|\), is complete set of projectors [20]. In this relation we use the quantum relative entropy:

$$ S(x\|y):=\operatorname{tr}(x\log x-x\log y). $$
(28)

Which is a measure of distinguishable between quantum states. It is also worth noting that the relative entropy function is asymmetric, that is, S(x∥y)≠S(y∥x).

In this paper, we investigate dissonance versus D z (the z-component of the DM interaction), g (the bath-system coupling constant), T (temperate), and for density matrix Eq. (12) the dissonance is equal to:

(29)

where

$$A=\sqrt{\rho_{14}\rho_{14}^{\ast}+4 \rho_{23}\rho_{32}-2\rho_{14}\rho _{33}+ \rho_{33}\rho_{33}^{\ast}}, $$

and

$$B=\sqrt{\rho_{11}\rho_{11}^{\ast}+4 \rho_{14}\rho_{41}-2\rho_{11}\rho _{44}+ \rho_{44}\rho_{44}^{\ast}}. $$

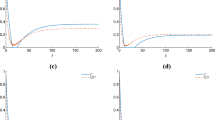
In order to represent the properties of variable DM coupling parameter D z on dissonance for entangled state (Fig. 8), is plotted versus t and it is found that by increasing D z dissonance first is increased then reduced to zero. In Fig. 9, dissonance versus t for different values of g is plotted for entangled state and it is inferred that by increasing g, the dissonance is increased and in Fig. 10, dissonance versus t and temperature T is plotted for entangled state that has a declining trend.

Fig. 8
figure 8

The time evolution of the quantum dissonance versus t for initial two-qubit state \(|\psi_{s}(0)\rangle=\frac{1}{\surd2}( |00\rangle+ |11\rangle)\) for J=0.0 and J z =0.0. Other parameters are ε=4.0,g 0=g=0.5 and Dz=0.2 and Dz=0.4

Full size image
Fig. 9
figure 9

The time evolution of the quantum dissonance versus t for initial two-qubit state \(|\psi_{s}(0)\rangle=\frac{1}{\surd2}( |00\rangle+ |11\rangle)\) for J=0.0 and J z =0.0. Other parameters are ε=4.0,g 0=0.5,D z =1 and g=0.2 and g=2.0

Full size image
Fig. 10
figure 10

The time evolution of the quantum dissonance versus T for initial two-qubit state \(|\psi_{s}(0)\rangle=\frac{1}{\surd2}( |00\rangle+ |11\rangle)\) for J=0.0 and J z =1.0. Other parameters are ε=2.0,g 0=g=0.5, and D z =1.0

Full size image

4 Teleportation of Qubit States via Two Coupled Spins

Quantum teleportation is about transferring quantum states from one particle to another at a distance. Bennett et al. have shown this process for the first time in about fifteen years ago [21]. For calculating teleportation we use a measure which is called fidelity. In this paper, we discuss the effects of the D z (the z-component of the DM interaction), g (the bath-system coupling constant), T (temperate) and μ 0 (magnetic field) on fidelity. By applying these parameters to fidelity we want to control the teleportation process by using of the noisy channel. We use the density matrix (11) as a channel to teleport the quantum state \(|\psi_{in}\rangle =\sin(\frac{\theta}{2})|0\rangle +e^{i\phi} \cos(\frac{\theta}{2})|1\rangle \). To do this, first we consider teleportation by using two-qubit state ρ x as a channel:

$$ \rho_{x}=\left ( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \rho_{11} &0 &0 &\rho_{14}\\ 0 &\rho_{22} &\rho_{23} &0\\ 0 &\rho_{32} &\rho_{33} &0\\ \rho_{41} &0 &0 &\rho_{44} \end{array} \right ). $$
(30)

In this case the output state is reduced to

$$ \rho_{out}=\operatorname{Tr}_{1,2}\bigl[U \rho_{in}\otimes \rho_{x} U^\dagger\bigr], $$
(31)

where U is a unitary operator. The fidelity of the quantum teleportation measures how much information is preserved and given by

$$ F=\langle\psi_{in}| \rho_{out}| \psi_{in}\rangle, $$
(32)

We get the fidelity for this channel in the following form:

(33)

In order to demonstrate the effects of different DM coupling parameters D z on fidelity, in Fig. 11, the quantum fidelity for initial two qubit entangled states versus t is plotted for different values of D z and the implication of this figure is that by increasing D z the number of oscillations is increased. In Fig. 12, fidelity for entangled state versus t for different values of g is plotted and it is found that by increasing g, amplitude of oscillation is increased but the number of oscillations is decreased. In Fig. 13, fidelity for entangled state versus t for different values of temperature T is plotted and it can be inferred that by increasing T, the amplitude of oscillations is decreased. Finally, the effect of μ 0 on fidelity is that by increasing μ 0 the number of oscillations is increased too much.

Fig. 11
figure 11

The fidelity versus t for initial two-qubit state \(|\psi_{s}(0)\rangle=\frac{1}{\surd2}( |00\rangle+ |11\rangle)\) for J=0.0 and J z =1.0. Other parameters are ε=4.0,g 0=g=2.0 and μ 0=0.5 for D z =0.1 and D z =0.1

Full size image
Fig. 12
figure 12

The fidelity versus t for initial two-qubit state \(|\psi_{s}(0)\rangle=\frac{1}{\surd2}( |00\rangle+ |11\rangle)\) for J=0.0 and J z =1.0. Other parameters are ε=2.0,g=0.5,μ 0=0.5 and D z =1.0 for g=1.0,g=3.0

Full size image
Fig. 13
figure 13

The fidelity versus t for initial two-qubit state \(|\psi_{s}(0)\rangle=\frac{1}{\surd2}( |00\rangle+ |11\rangle)\) for J=0.0 and J z =1.0. Other parameters are ε=6.0,g 0=g=1.0,μ 0=0.5 and D z =0.1 for T=0.2 and T=5.0

Full size image

5 Conclusions

In summary, we have investigated the quantum discord and entanglement measures of concurrence and quantum dissonance within two-qubit anisotropic XXZ Heisenberg model by antisymmetric DM interaction tunable parameter, such as D z influenced by a local external magnetic field along the z-direction in the presence of spin bath. We found that by increasing D z the value of concurrence, quantum discord and quantum dissonance increases for entangled state and decreases for separable state, and for g we get an inverse ratio for both entangled and separable states. In addition, we found that increasing the value of T (temperature) will reduce the amount of the concurrence, quantum discord and quantum dissonance. We propose that in open quantum systems that we cannot reduce the devastating effects of T and g by tuning J z and D z properly or exchanging the constituent material of the central spins can improve quantities of the concurrence, quantum discord and dissonance. Finally, we obtained the fidelity of this model and realized that D z , μ 0, g and T influenced on the amplitude and oscillations of fidelity.