Dynamics of non-equilibrium thermal quantum correlation in a two-qubit Heisenberg XYZ model

Abstract

The non-equilibrium thermal entanglement and quantum discord in a two-qubit Heisenberg XYZ model subjected to two thermal baths with different temperatures are investigated. The dynamical behaviors of entanglement and quantum discord under the influences of the initial states of the two-qubit system, the temperature of the thermal baths and the coupling constant $J_z$ are discussed. A special emphasis is devoted to study the effects of the thermal baths on the steady quantum correlation between the two qubits. Our results show that the temperature difference $\Delta T$ plays a key role for the appearance of steady quantum correlation, which can be enhanced by coupling constant $J_z$, DM interaction and non-uniform magnetic field.

1 Introduction

Quantum entanglement, as one of the most fascinating features of quantum mechanics, has been strongly affecting our conceptual implication on physics [1, 2]. It has no classical analog and is widely recognized as crucial resource in quantum computation and quantum information processing [3,4,5,6]. For the past two decades great effort has been devoted into the generation and investigation of entangled states. The main obstacle in preparing and preserving entanglement is decoherence induced by the interaction between the system and environment, since a real quantum system cannot be closed and it will unavoidably be influenced by the surroundings [7]. Therefore, the study of essential features of dynamical behaviors of entanglement under decoherence has attracted much attention in recent years [8,9,10,11,12,13,14,15,16,17]. Among these achievements, the most striking discovery is entanglement sudden death (ESD) [8], which describes the finite time disentanglement of two qubits coupled with two independent reservoirs. Shortly afterward, the authors in ref [10] have shown that the ESD of a two-qubit system is intimately linked to sudden birth of entanglement between two independent reservoirs. In addition, thermal effect always exists in any real environment, so studying the dynamics of quantum systems in environments at finite temperatures has practical significance [18,19,20,21,22].

Thermal entanglement, generally used to specify the amount of entanglement at thermal equilibrium state, has been extensively studied and exhibited its special characteristics [23,24,25,26,27,28]. It is usually studied by means of the Heisenberg model, which is a simple but effective description of magnetic systems. Besides that, numerous works have been devoted to non-equilibrium thermal entanglement in different Heisenberg models [29,30,31,32,33]. For example, ref [29] studied the non-equilibrium thermal entanglement of a two-qubit Heisenberg XXX model interacting with two heat baths at different temperatures. It proved the feasibility of a non-equilibrium enhancement-suppression transition behavior of the entanglement by temperature gradient. By virtue of the same model, ref [30] presented the analytical solution for the system dynamics, and the temperature dependence of the steady entanglement between the two qubits is analyzed. Huang [31] extended the study of non-equilibrium thermal entanglement to a three-qubit XX model with the help of effective Hamiltonian approach. Later the authors in ref [32] also took the three-spin interaction into account. Furthermore, non-equilibrium entanglement dynamics of a two-qubit Heisenberg XY model in the presence of inhomogeneous magnetic field and Dzyaloshinskii–Moriya (DM) interaction was also investigated [33].

Motivated by the previous investigations, we find the non-equilibrium thermal entanglement in the Heisenberg XYZ model has not been studied yet, so in this paper we will investigate the non-equilibrium entanglement dynamics of two qubits in a Heisenberg XYZ model with non-uniform external field and DM interaction. We consider the case that the two qubits interact with two independent thermal baths, respectively, and the temperature difference between the thermal baths always exists. Therefore, the entanglement between the two qubits is non-equilibrium thermal entanglement. On the other hand, recent works have revealed that entanglement is not the only type of quantum correlation because it does not account for all of the non-classical properties of quantum correlation, while quantum discord (QD), first introduced by Zurek [34], is supposed to have the ability to capture all non-classical correlations in a quantum system. Therefore, both the non-equilibrium thermal entanglement and quantum discord will be considered in this paper. In this respect, our study could be a beneficial supplement to the previous researches. Since real systems are not in equilibrium, it is practical significant to investigate the dynamical property of quantum correlation under non-equilibrium conditions. Beyond that, two coupled qubits in contact with different thermal baths are a system not only of theoretical interest but also an experimental issue [35, 36]. Our results show that the thermal effect can be depressed by the temperature difference of the two baths and the spin interaction between the two qubits; as a result, the steady entanglement and QD can be induced. Therefore, the present study would shed some light on understanding the dynamics of non-equilibrium quantum correlation in noisy environment.

The paper is organized as follows. In Sect. 2, we briefly review the concepts of the measures of quantum correlation, i.e., concurrence and QD. In Sect. 3, we present our model and derive the Markovian master equation describing the dynamics of the system. In Sect. 4, we give our numerical results and discussion in detail. Finally, we summarize the paper in Sect. 5.

2 Measurements of quantum correlation

To quantify the entanglement between two qubits we use the Wootters concurrence [37], defined as

$$\begin{aligned} C=\max \{0,\lambda _1-\lambda _2-\lambda _3-\lambda _4\}, \end{aligned}$$

(1)

where the quantities $\lambda _i$ $(i=1..4)$ are the square nonzero roots of eigenvalues for the matrix $\tilde{\rho }_{AB}=\rho _{AB}{\sigma _y\otimes \sigma _y }\rho _{AB}^*{\sigma _y\otimes \sigma _y}$ in descending order. The concurrence attains its maximum value $C = 1$ for maximally entangled states and vanishes for separate states.

For a bipartite quantum system, the QD is defined as [34]

$$\begin{aligned} D(\rho _{AB})=I(\rho _{AB})-\mathcal {C}(\rho _{AB}). \end{aligned}$$

(2)

where $I(\rho _{AB})=S(\rho _A)+S(\rho _B)-S(\rho _{AB})$ is the quantum mutual information and $\mathcal {C}(\rho _{AB})$ is the classical correlation between the two subsystems. $S(\rho _{AB})=-tr\rho _{AB}\log \rho _{AB}$ is the von Neumann entropy. The classical correlation is provided by $\mathcal {C}(\rho _{AB})=\max _{\{\Pi _k^A\}}[S(\rho _B)-\Sigma _kp_kS(\rho _{B|k})]$ where the maximum is taken over the set of projective measurements $\{\Pi _k^A\}$ on subsystem A and $\rho _{B|k}=tr_A(\Pi _k^A\rho _{AB}\Pi _k^A)/p_k$ with $p_k=tr_{AB}(\Pi _k^A\rho _{AB}\Pi _k^A)$. It is sufficient for us to evaluate the QD using the following set of projectors: $\{\Pi _k^A=|\psi _1\rangle \langle \psi _1|,|\psi _2\rangle \langle \psi _2|\}$, in which $|\psi _1\rangle =\cos \theta |g\rangle +e^{i\varphi }\sin \theta |e\rangle$ and $|\psi _2\rangle =-\cos \theta |e\rangle +e^{-i\varphi }\sin \theta |g\rangle$ with $\theta \in [0,\pi ]$ and $\varphi \in [0,2\pi ]$. We can obtain the QD via numerical optimization over the parameters $\theta$ and $\varphi$. QD can quantify all of the quantum correlation, including entanglement in a bipartite system. Consequently, QD is believed a new resource for quantum information [38, 39].

3 Model and formalism

The total Hamiltonian of a two-qubit system interacting with two separate bosonic baths at different temperatures is given by

$$\begin{aligned} {\widehat{H}}=\widehat{H}_S+\widehat{H}_{B1}+\widehat{H}_{B2}+\widehat{H}_{SB1}+\widehat{H}_{SB2}, \end{aligned}$$

(3)

where $\widehat{H}_S$ is the Hamiltonian of the two-qubit system described by a two-qubit Heisenberg XYZ model in non-uniform external field with Dzyaloshinskii–Moriya (DM) interaction along the z-direction [40]

$$\begin{aligned} \widehat{H}_S=-J_x\sigma _1^x\sigma _2^x-J_y\sigma _1^y\sigma _2^y-J_z\sigma _1^z\sigma _2^z-\frac{1}{2}D_z(\sigma _1^x\sigma _2^y-\sigma _1^y\sigma _2^x)-b_1\sigma _1^z-b_2\sigma _2^z.\nonumber \\ \end{aligned}$$

(4)

$\sigma _j^x$, $\sigma _j^y$ and $\sigma _j^z$ ($j=1,2$) are Pauli operators, $J_\mu (\mu =x,y,z)$ are real coupling coefficients between the two qubits, and $D_z$ is DM interaction along the z-direction. $b_{1(2)}$ indicates the z-component of the external magnetic field acting on the qubit 1(2). In the standard basis $\{|00\rangle ,|01\rangle ,|10\rangle ,|11\rangle \}$, the eigenvectors $|\varphi _i\rangle$ and eigenvalues $E_i$ of Hamiltonian $\widehat{H}_S$ are given by

$$\begin{aligned} |\varphi _1\rangle= & {} \cos \left( \frac{\theta _1}{2}\right) |00\rangle +\sin \left( \frac{\theta _1}{2}\right) |11\rangle ,\qquad E_1=-J_z+\sqrt{(b_1+b_2)^2+(J_-)^2},\nonumber \\ |\varphi _2\rangle= & {} \sin \left( \frac{\theta _1}{2}\right) |00\rangle -\cos \left( \frac{\theta _1}{2}\right) |11\rangle ,\qquad E_2=-J_z-\sqrt{(b_1+b_2)^2+(J_-)^2},\nonumber \\ |\varphi _3\rangle= & {} \cos \left( \frac{\theta _2}{2}\right) |01\rangle +e^{-i\varphi }\sin \left( \frac{\theta _2}{2}\right) |10\rangle ,E_3=J_z+\sqrt{(b_1-b_2)^2{+}D_z^2{+}(J_+)^2},\nonumber \\ |\varphi _4\rangle= & {} \sin \left( \frac{\theta _2}{2}\right) |01\rangle -e^{-i\varphi }\cos \left( \frac{\theta _2}{2}\right) |10\rangle ,E_4=J_z-\sqrt{(b_1-b_2)^2{+}D_z^2{+}(J_+)^2},\nonumber \\ \end{aligned}$$

(5)

with $J_\pm =J_x\pm J_y$ , $\tan (\theta _1)=-\frac{J_-}{b_1+b_2}$, $\tan (\theta _2)=\frac{\sqrt{D_z^2+(J_+)^2}}{b_1+b_2}$ and $\tan (\varphi )=\frac{D_z}{J_+}$.

The Hamiltonian for each bath is given by

$$\begin{aligned} \widehat{H}_{Bj}=\sum _n\omega _{n,j}\widehat{b}_{n,j}^{\dag }\widehat{b}_{n,j}, \end{aligned}$$

(6)

and the interaction between the jth spin and its bath can be written as

$$\begin{aligned} \widehat{H}_{SBj}=\widehat{\sigma }_j^+\sum _ng_n^{(j)}\widehat{b}_{n,j}+\widehat{\sigma }_j^-\sum _ng_n^{(j)*}\widehat{b}_{n,j}^{\dag }\equiv \sum _{\mu }\left( \widehat{V}_{j,\mu }^\dagger \widehat{f}_{j,\mu } +\widehat{V}_{j,\mu }\widehat{f}_{j,\mu }^\dagger \right) \end{aligned}$$

(7)

The operator $\widehat{V}_{j,\mu }$ is an eigenoperator of the system Hamiltonian satisfying $[\widehat{H}_S,\widehat{V}_{j,\mu }]=-\omega _{j,\mu }\widehat{V}_{j,\mu }$, and the $\widehat{f}_{j,\mu }$ act on the bath degrees of freedom. The index $\mu$ corresponds to transitions between eigenstates of the system induced by the baths. We assume that the jth bath is always in a thermal state at temperature $T_j$, i.e., $\widehat{\rho }_j=e^{-\beta _j\widehat{H}_{Bj}}/tr(e^{-\beta _j\widehat{H}_{Bj}})$ with $\beta _j=1/(k_BT_j)$. In this paper, we set $(k_B=\hbar =1)$ for simplicity.

With the help of general reservoir theory within Born–Markov and rotating wave approximation [7, 41, 42], the main equation for the reduced density matrix of the two-qubit system is as follows

$$\begin{aligned} \frac{\mathrm{d}\widehat{\rho }}{\mathrm{d}t}=-i[\widehat{H}_S,\widehat{\rho }]+\ell _1(\widehat{\rho })+\ell _2(\widehat{\rho }), \end{aligned}$$

(8)

where $\ell _j(\widehat{\rho })$ is the dissipative term due to the interaction between the jth qubit with its thermal bath given by

$$\begin{aligned} \ell _j(\widehat{\rho })=\sum _{\mu ,\nu }J_{\mu ,\nu }^{(j)}(\omega _{j,\nu })\{[\widehat{V}_{j,\mu },[\widehat{V}_{j,\nu }^{\dag },\widehat{\rho }]]-(1-e^{\beta _j\omega _{j,\nu }})[\widehat{V}_{j,\mu },\widehat{V}_{j,\nu }^{\dag }\widehat{\rho }]\}, \end{aligned}$$

(9)

where the spectral density of the jth bath is described as $J_{\mu ,\nu }^{(j)}(\omega _{j,\nu })=\int _0^{\infty }d\tau e^{i\omega _{j,\nu }\tau }\langle e^{-i\widehat{H}_{Bj}\tau }\widehat{f}_{j,\nu }^{\dag }e^{i\widehat{H}_{Bj}\tau }f_{j,\mu }\rangle _j.$ In the representation spanned by eigenvectors (5), the dissipative operator becomes

$$\begin{aligned} \ell _j(\widehat{\rho })= & {} \sum _{\mu =1}^4 J^{(j)}(-\omega _{\mu })(2\widehat{V}_{j,\mu }\widehat{\rho }\widehat{V}_{j,\mu }^{\dag }-\{\widehat{\rho },\widehat{V}_{j,\mu }^{\dag }\widehat{V}_{j,\mu }\}_+)+ J^{(j)}(\omega _{\mu })(2\widehat{V}_{j,\mu }^{\dag }\widehat{\rho }\widehat{V}_{j,\mu }\nonumber \\&-\{\widehat{\rho },\widehat{V}_{j,\mu }\widehat{V}_{j,\mu }^{\dag }\}_+), \end{aligned}$$

(10)

with transition frequencies

$$\begin{aligned} \omega _1= & {} E_3-E_1,\qquad \omega _2=E_4-E_1,\nonumber \\ \omega _3= & {} E_3-E_2,\qquad \omega _4=E_4-E_2, \end{aligned}$$

(11)

and transition operators

$$\begin{aligned} \widehat{V}_{j,1}= & {} a_{j,1}|\varphi _1\rangle \langle \varphi _3|,\qquad \widehat{V}_{j,2}=a_{j,2}|\varphi _1\rangle \langle \varphi _4|,\nonumber \\ \widehat{V}_{j,3}= & {} a_{j,3}|\varphi _2\rangle \langle \varphi _3|,\qquad \widehat{V}_{j,4}=a_{j,4}|\varphi _2\rangle \langle \varphi _4|, \end{aligned}$$

(12)

where

$$\begin{aligned} a_{1,1}= & {} \sin \left( \frac{\theta _1}{2}\right) \cos \left( \frac{\theta _2}{2}\right) +e^{-i\varphi }\cos \left( \frac{\theta _1}{2}\right) \sin \left( \frac{\theta _2}{2}\right) ,\nonumber \\ a_{2,1}= & {} \cos \left( \frac{\theta _1}{2}\right) \cos \left( \frac{\theta _2}{2}\right) +e^{-i\varphi }\sin \left( \frac{\theta _1}{2}\right) \sin \left( \frac{\theta _2}{2}\right) ,\nonumber \\ a_{1,2}= & {} \sin \left( \frac{\theta _1}{2}\right) \sin \left( \frac{\theta _2}{2}\right) -e^{-i\varphi }\cos \left( \frac{\theta _1}{2}\right) \cos \left( \frac{\theta _2}{2}\right) ,\nonumber \\ a_{2,2}= & {} \cos \left( \frac{\theta _1}{2}\right) \sin \left( \frac{\theta _2}{2}\right) -e^{-i\varphi }\sin \left( \frac{\theta _1}{2}\right) \cos \left( \frac{\theta _2}{2}\right) ,\nonumber \\ a_{1,3}= & {} -\cos \left( \frac{\theta _1}{2}\right) \cos \left( \frac{\theta _2}{2}\right) +e^{-i\varphi }\sin \left( \frac{\theta _1}{2}\right) \sin \left( \frac{\theta _2}{2}\right) ,\nonumber \\ a_{2,3}= & {} \sin \left( \frac{\theta _1}{2}\right) \cos \left( \frac{\theta _2}{2}\right) -e^{-i\varphi }\cos \left( \frac{\theta _1}{2}\right) \sin \left( \frac{\theta _2}{2}\right) ,\nonumber \\ a_{1,4}= & {} -\cos \left( \frac{\theta _1}{2}\right) \sin \left( \frac{\theta _2}{2}\right) -e^{-i\varphi }\sin \left( \frac{\theta _1}{2}\right) \cos \left( \frac{\theta _2}{2}\right) ,\nonumber \\ a_{2,4}= & {} \sin \left( \frac{\theta _1}{2}\right) \sin \left( \frac{\theta _2}{2}\right) +e^{-i\varphi }\cos \left( \frac{\theta _1}{2}\right) \cos \left( \frac{\theta _2}{2}\right) . \end{aligned}$$

(13)

In this paper, the bath is treated as an infinite set of harmonic oscillators, so the spectral density has such a form $J^{(j)}(\omega _{\mu })=\gamma _j(\omega _{\mu })n_j(\omega _{\mu })$, where $n_j(\omega _{\mu })=(e^{\beta _j\omega _{\mu }}-1)^{-1}$ is the mean thermal photon number of the jth bath at frequency $\omega _\mu$ and $J^{(j)}(-\omega _{\mu })=e^{\beta _j\omega _{\mu }}J^{(j)}(\omega _{\mu })$. For simplicity, let the coupling constant be independent of frequency, i.e., $\gamma _j(\omega _{\mu })=\gamma _j(-\omega _{\mu })=\gamma _j$.

After tedious calculation, we find that master equation (8) for diagonal elements decouple from non-diagonal ones in the basis $|\varphi _i\rangle$, so the differential equations for diagonal elements have the form $\frac{\mathrm{d}R(t)}{\mathrm{d}t}=BR(t)$, where $R(t)=(\rho _{11}(t),\rho _{22}(t),\rho _{33}(t),\rho _{44}(t))^T$ and the nonzero elements of $4\times 4$ matrix B can be written as follows

$$\begin{aligned} B_{11}= & {} -2\times (|a_{1,1}|^2J^{(1)}(\omega _1)+|a_{2,1}|^2J^{(2)}(\omega _1){+}|a_{1,2}|^2J^{(1)}(\omega _2){+}|a_{2,2}|^2J^{(2)}(\omega _2)),\nonumber \\ B_{13}= & {} 2\times (|a_{1,1}|^2J^{(1)}(-\omega _1)+|a_{2,1}|^2J^{(2)}(-\omega _1)),\nonumber \\ B_{14}= & {} 2\times (|a_{1,2}|^2J^{(1)}(-\omega _2)+|a_{2,2}|^2J^{(2)}(-\omega _2)),\nonumber \\ B_{22}= & {} -2\times (|a_{1,3}|^2J^{(1)}(\omega _3)+|a_{2,3}|^2J^{(2)}(\omega _3){+}|a_{1,4}|^2J^{(1)}(\omega _4){+}|a_{2,4}|^2J^{(2)}(\omega _4)),\nonumber \\ B_{23}= & {} 2\times (|a_{1,3}|^2J^{(1)}(-\omega _3)+|a_{2,3}|^2J^{(2)}(-\omega _3)),\nonumber \\ B_{24}= & {} 2\times (|a_{1,4}|^2J^{(1)}(-\omega _4)+|a_{2,4}|^2J^{(2)}(-\omega _4)),\nonumber \\ B_{31}= & {} 2\times (|a_{1,1}|^2J^{(1)}(\omega _1)+|a_{2,1}|^2J^{(2)}(\omega _1)),\nonumber \\ B_{32}= & {} 2\times (|a_{1,3}|^2J^{(1)}(\omega _3)+|a_{2,3}|^2J^{(2)}(\omega _3)),\nonumber \\ B_{33}= & {} -2\times (|a_{1,1}|^2J^{(1)}(-\omega _1)+|a_{2,1}|^2J^{(2)}(-\omega _1)\nonumber \\&+|a_{1,3}|^2J^{(1)}(-\omega _3)+|a_{2,3}|^2J^{(2)}(-\omega _3)),\nonumber \\ B_{41}= & {} 2\times (|a_{1,2}|^2J^{(1)}(\omega _2)+|a_{2,2}|^2J^{(2)}(\omega _2)),\nonumber \\ B_{42}= & {} 2\times (|a_{1,4}|^2J^{(1)}(\omega _4)+|a_{2,4}|^2J^{(2)}(\omega _4)),\nonumber \\ B_{44}= & {} -2\times (|a_{1,2}|^2J^{(1)}(-\omega _2)+|a_{2,2}|^2J^{(2)}(-\omega _2)+|a_{1,4}|^2J^{(1)}(-\omega _4)\nonumber \\&+|a_{2,4}|^2J^{(2)}(-\omega _4)). \end{aligned}$$

(14)

Furthermore, non-diagonal elements can be obtained easily by $\frac{\mathrm{d}\rho _{i,j}(t)}{\mathrm{d}t}=[-i(E_i-E_j)-C_{i,j}]\rho _{i,j}$ since they are not coupled. As a result, analytic solutions for non-diagonal elements have the simple form

$$\begin{aligned} \rho _{i,j}(t)=e^{-i(E_i-E_j)t-C_{i,j}t}\rho _{i,j}(0). \end{aligned}$$

(15)

where $C_{i,j}$ and $\rho _{i,j}(0)$ are determined by the system parameters and the initial states, respectively.

4 Results and discussion

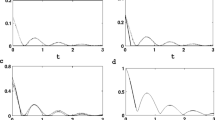
In Fig. 1, when the two qubits are initially in the maximally entangled state, the dynamics of non-equilibrium thermal entanglement and QD for different values of mean temperature $(T_M=\frac{T_1+T_2}{2})$ are shown. One can observe that entanglement and QD behave differently involving with time. Although both QD and entanglement first decrease and then increase to a steady value, the QD varies continuously and the entanglement experiences sudden death, which means the entanglement disappears suddenly and remains zero for a period time. The presence of mean temperature $T_M$ decreases entanglement and QD. With the increase in $T_M$, the steady values of entanglement and QD decrease and the death time for the entanglement is prolonged. In particular, when $T_M$ is large enough, such as $T_M=1$, the entanglement decays to zero at finite time eventually, but the QD still maintains nonzero steady value. Therefore, the mean temperature makes much stronger destructive effect on entanglement evolution. Figure 2 depicts the dynamics of non-equilibrium thermal entanglement and QD for a fixed mean temperature $T_M$ when temperature difference ($\Delta T=T_1-T_2)$ varies. We can find that when there is no temperature difference between the two baths $(\Delta T=0)$, the entanglement decays to zero at finite time and the QD converges to its steady value. Increasing $\Delta T$ has negligible impact on QD, but the steady entanglement can be induced. So the temperature difference is beneficial to obtain the steady entangled states. But we cannot conclude that the steady value of entanglement increases with increasing $\Delta T$, since the steady entanglement is almost not changed for a larger $\Delta T$.

Fig. 1

Dynamics of non-equilibrium thermal concurrence and QD for the initial system state $\widehat{\rho }(0)=\frac{1}{2}(|00\rangle +|11\rangle )(\langle 00|+\langle 11|)$. The parameters of the model are chosen to be $\gamma _1=\gamma _2=0.02$, $D_z=0$, $\Delta b=b_1-b_2=0.2$, $\bar{b}=\frac{b_1+b_2}{2}=0.4$, $J_x=J_y=0.6$, $J_z=0.1$, $\Delta T=T_1-T_2=0.4$. a $T_M=0.4$; b $T_M=0.6$; c $T_M=0.8$; d $T_M=1$

Fig. 2

Dynamics of non-equilibrium thermal concurrence and QD for the initial system state $\widehat{\rho }(0)=\frac{1}{2}(|00\rangle +|11\rangle )(\langle 00|+\langle 11|)$. The parameters of the model are chosen to be $\gamma _1=\gamma _2=0.02$, $D_z=0$, $\Delta b=0.2$, $\bar{b}=1$, $J_x=J_y=0.6$, $J_z=0.2$, $T_M=0.6$. a $\Delta T=0$; b $\Delta T=0.4$; c $\Delta T=0.8$; d $\Delta T=1.1$

Fig. 3

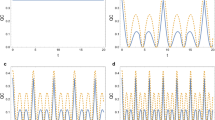
Dynamics of non-equilibrium thermal concurrence and QD for different initial states. The parameters of the model are chosen to be $\gamma _1=\gamma _2=0.02$, $D_z=0$, $\Delta b=0.2$, $\bar{b}=0.4$, $J_x=J_y=0.6$, $J_z=0.1$, $\Delta T=0.5$, $T_M=0.8$. a $\widehat{\rho }(0)=\frac{1}{2}(|00\rangle +|11\rangle )(\langle 00|+\langle 11|)$; b $\widehat{\rho }(0)=\frac{1}{2}(|01\rangle +|10\rangle )(\langle 01|+\langle 10|)$; c $\widehat{\rho }(0)=|00\rangle \langle 00|$; d $\widehat{\rho }(0)=|10\rangle \langle 10|$

Fig. 4

Dynamics of non-equilibrium thermal concurrence and QD for the initial system state $\widehat{\rho }(0)=\frac{1}{2}(|00\rangle +|11\rangle )(\langle 00|+\langle 11|)$. The parameters of the model are chosen to be $\gamma _1=\gamma _2=0.02$, $D_z=0$, $\Delta b=0.2$, $\bar{b}=0.4$, $J_x=J_y=0.6$, $\Delta T=0.4$, $T_M=1.3$

In Fig. 3, we give the plot of the dynamics of non-equilibrium thermal entanglement and QD for different initial states of the qubits. It can be seen that steady entanglement and QD can be established regardless of the initial states of the qubits. If the qubits are initially in non-symmetric states, i.e., $|10\rangle$ or $\frac{1}{\sqrt{2}}(|01\rangle +|10\rangle )$, the entanglement and QD exhibit intense oscillation with time. But there is no oscillation during the evolution of symmetric states, i.e., $|00\rangle$ or $\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )$. In the early time of the evolution, the values of QD are always larger than that of entanglement and the entanglement sudden birth occurs for the initial separate states. Besides, the steady values of QD and entanglement are independent of the choice of the initial state no matter whether the two qubits are initially in maximally entangled states or separate states. Here we also consider the case of initial mixed states, such as $0.5(|00> <00|+|11> <11|)$, which is a separate state only mixed. The result has almost the same characteristics as the initial separate state $|00> <00|$, so we do not give the details.

Figure 4 shows the dynamics of non-equilibrium thermal entanglement and QD for different values of $J_z$. We find that for the XY model, i.e., $J_z=0$, only steady QD can be observed, but the entanglement decays to zero at early time. As the absolute value of $J_z$ increases, the death time of entanglement will shortened slightly and the steady entanglement can be induced. Simultaneously, the presence of $J_z$ also enhances the steady QD, but its growth is not evident in comparison with the growth of entanglement. For example, when $J_z$ increases to $J_z=-0.9$, the steady entanglement increases greatly, while there is little change taking place for the steady QD. Therefore, we can obtain more nonzero or steady quantum correlation in XYZ model.

Fig. 5

The steady thermal concurrence as a function of the mean temperature $T_M$ for the initial system state $\widehat{\rho }(0)=\frac{1}{2}(|00\rangle +|11\rangle )(\langle 00|+\langle 11|)$. The parameters of the model are chosen to be $\gamma _1=\gamma _2=0.02$, $J_x=J_y=0.6$ $\Delta T=0.15$. a $D_z=0$, $\Delta b=0.2$, $\bar{b}=0.4$; b $J_z=-0.3$, $\Delta b=0.2$, $\bar{b}=0.4$; c $J_z=-0.3$, $D_z=0.5$, $\Delta b=0.2$; d $J_z=-0.3$, $D_z=0.5$, $\bar{b}=0.8$

Fig. 6

The steady thermal concurrence as a function of the temperature difference $\Delta T$ for the initial system state $\widehat{\rho }(0)=\frac{1}{2}(|00\rangle +|11\rangle )(\langle 00|+\langle 11|)$. The parameters of the model are chosen to be $\gamma _1=\gamma _2=0.02$, $J_x=J_y=0.6$, $T_M=1.5$. a $D_z=0.5$, $\Delta b=0.2$, $\bar{b}=0.6$; b $J_z=-0.1$, $\Delta b=0$, $\bar{b}=0.3$; c $J_z=-0.3$, $D_z=0.5$, $\Delta b=0.2$; d $J_z=-0.3$, $D_z=0.5$, $\bar{b}=0.8$

In the following we analyze the influences of the parameters related to Hamiltonian (4) and thermal baths on the steady non-equilibrium thermal entanglement and QD between the two qubits. First, we study the steady entanglement versus the mean temperature. As shown in Fig. 5, the steady entanglement decreases monotonically with increasing $T_M$ and it disappears when $T_M$ reaches the critical value $T_{MC}$, beyond which the steady entanglement is zero. It is clear to see that the steady entanglement for a fixed $T_M$ can be enhanced by increasing coupling constant $|J_z|$, DM interaction $D_z$ and field difference $\Delta b$; simultaneously, $T_{MC}$ can also be prolonged. But increasing mean field $\bar{b}$ significantly reduces the steady entanglement and shortens the size of $T_{MC}$. This means that more steady quantum correlation can be kept by inhomogeneously applying a weak magnetic. In addition, we also find that there is no steady entanglement when the mean field is strong enough at low mean temperature, but the steady entanglement can be created as $T_M$ increases. As to the variation of steady QD, we omit the details since the results are similar with the discussion about steady entanglement under the same conditions. But one point deserving mentioning here is that as is the case with equilibrium state mentioned in the previous section, the steady QD always decays with mean temperature asymptotically.

We continue to our study by considering the effects of the temperature difference on the steady quantum correlation. Here we also take the steady entanglement as an example, since we can obtain the same conclusion from the case of steady QD. In Fig. 6, we give the plot of the steady entanglement as a function of the temperature difference for different values of $J_z$, $D_z$, $\bar{b}$ and $\Delta b$. It is evident that the maximal steady entanglement is always located on the point where the temperature difference $\Delta T$ is nonzero. This indicates that the temperature difference benefits the steady quantum correlation. The trends of the steady entanglement with $\Delta T$ are almost similar for different parameters, i.e., the steady entanglement increases to its maximal value and then decreases with $\Delta T$ increasing. A proper value of $\Delta T$ can not only induce the steady entanglement but also enhance the steady entanglement in a great extent. By comparing these graphs, we find that when $\bar{b}$ is weak, $\Delta T$ will decrease the steady entanglement. But the enhancement of steady entanglement by $\Delta T$ is most obvious as $\Delta b$ varies, which means the temperature difference is essential to obtain steady quantum correlation between the two qubits under the non-uniform field.

Fig. 7

a Dynamics of the monogamic relation $E_{AE}$ for different values of mean temperature with $\Delta T=0.4$ and $J_z=0.1$; b dynamics of the monogamic relation $E_{AE}$ for different values of temperature difference with $T_M=0.6$ and $J_z=0.2$. The initial state is assumed to be $\widehat{\rho }(0)=\frac{1}{2}(|00\rangle +|11\rangle )(\langle 00|+\langle 11|)$, and the other parameters are chosen to be $\gamma _1=\gamma _2=0.02$, $D_z=0$, $\Delta b=0.2$, $\bar{b}=0.4$ and $J_x=J_y=0.6$

Fig. 8

a The steady monogamic relation $E_{AE}$ as a function of the mean temperature $T_M$ for different values of $J_z$ with $\Delta T=0.15$, $D_z=0$ and $\bar{b}=0.4$; b the steady monogamic relation $E_{AE}$ as a function of the temperature difference $\Delta T$ for different values of $J_z$ with $T_M=1.5$, $D_z=0.5$ and $\bar{b}=0.6$. The initial state is assumed to be $\widehat{\rho }(0)=\frac{1}{2}(|00\rangle +|11\rangle )(\langle 00|+\langle 11|)$, and the other parameters are chosen to be $\gamma _1=\gamma _2=0.02$, $\Delta b=0.2$ and $J_x=J_y=0.6$

As is known the decay of quantum correlation between the two qubits relates to the creation of quantum correlation between the qubits and the baths. In order to study the dynamics of quantum correlation between the thermal bath and one of the qubits, we use the monogamic relation between the entanglement of formation (EOF) and QD [43, 44]. As an effective measure of entanglement, the EOF can be described analytically in terms of concurrence for two qubits system as $E(\rho )=H[\frac{1+\sqrt{1-C^2(\rho )}}{2}]$ with $H(x)=-x\log _2x-(1-x)\log _2(1-x)$ [37]. Therefore, the monogamic relation gives

$$\begin{aligned} E_{AE}=D_{AB}+S_{A|B}, \end{aligned}$$

(16)

where $S_{A|B}=S(\rho _{AB})-S(\rho _B)$ is the conditional entropy. In Fig. 7, we show the dynamics of the monogamic relation $E_{AE}$ with the variations of $T_M$ and $\Delta T$. In comparison with Figs. 1 and 2, we find $E_{AE}$ exhibits adverse variation trend with time. For example, $E_{AE}$ first increases from zero and then decreases to a steady value. The higher the $T_M$ and $\Delta T$ are, the more steady $E_{AE}$ is obtained, which reveals that the quantum correlation contained in the qubit–qubit system is transferred to the qubit-bath system. Beyond that, from Fig. 8 we can find that the interaction $J_z$ between the qubits can preserve the steady quantum correlation between the qubits by restraining one qubit from building quantum correlation with the bath.

5 Conclusion

In summary, we have studied the non-equilibrium thermal quantum correlation, measured by quantum entanglement and QD, in a two-qubit XYZ Heisenberg model coupled with two thermal baths with different temperatures. We find the entanglement will experience sudden death, but the QD always keeps nonzero in finite time evolution. So the QD is more robust than the entanglement in resistance the decoherence induced by the thermal baths. However, both of them will may eventually converge to their steady values which is independent of the choice of initial states but depends on the temperature difference between the thermal baths. In comparison with the XY model, the two-qubit XYZ model can obtain more quantum correlation because the coupling constant $J_z$ can induce and enhance the steady entanglement and QD. In addition, the steady quantum correlation versus the mean temperature $T_M$ and the temperature difference $\Delta T$ are also investigated. Our results show that increasing coupling constant $J_z$, DM interaction $D_z$ and field difference $\Delta b$ can enhance the steady entanglement and prolong the regions of mean temperature where the steady entanglement is not zero. In particular, for a fixed value of mean temperature, a relative large steady entanglement can be obtained by introducing the temperature difference combining with $J_z$, $D_z$ and $\Delta b$. Finally, we also analyze the quantum correlation between one of the qubits and the thermal bath in terms of the monogamic relation.