1 Introduction

According to the modern observations (Riess et al. 1998) our universe is going through a phase of accelerated expansion that put new route in modern cosmology. A group of people is making attempts to accommodate this observational fact by choosing some exotic matter (known as Dark Energy) in the framework of general relativity. The purpose of modern cosmology is to determine the large-scale structure of the Universe. The astronomical observations of type-Ia supernovae experiments (Riess et al. 1998; Perlmutter et al. 1998, 1999, 2003; Hoftuft et al. 2009; Bennett et al. 2003; Spergel et al. 2003) suggest that the observable universe is undergoing an accelerated expansion. The recent observational data strongly indicate that our universe is dominated by a component with negative pressure, dubbed as dark energy (DE), which constitutes with 3/4 of the critical density. In order to explain the nature of dark energy and the accelerated expansion, there are several choices of the theoretical models namely the quintessence scalar field models (Wetterich 1988; Ratra and Peebles 1988), the phantom field (Caldwell 2002; Nojiri & Odinstov 2003a), K-essence (Chiba et al. 2000; Armendariz-Picon et al. 2000), tachyon field (Sen 2002; Padmanabhan & Chaudhury 2002), quintom (Elizalde et al. 2004; Anisimov et al. 2005), etc., also the dark energy models including Chaplygin gas (Kamenshchik et al. 2001; Bento et al. 2002) and so on. Also, Pawar and Solanke (2014), Samanta (2013a, b) and Pawar et al. (2014) has been investigated dark energy cosmological models in alternative theories of gravitation.

Einstein theory of gravitation was very much successful for constructing a cosmological model and explaining the origin and evolution of the universe. But Einstein theory fails to explain late time acceleration of modern cosmology. So copious attempts have been made to modify the gravity theory which is to gratify the present accelerated phase. A natural generalization is to choose a more general action in which the standard Einstein-Hilbert action is replaced by an arbitrary function of the Ricci scalar R (Nojiri and Odintsov 2003b) (i.e, f(R)) and is the name applied to f(R)-gravity. This modified theory may point this late time cosmic acceleration (Carroll et al. 2004). These f(R) models can satisfy local tests and integrate inflation with dark energy. For a brief review of f(R)-gravity one may refer to Nojiri and Odintsov (2003b), Carroll et al. (2004) and Capozziello et al. (2003). This modified gravity has recently been verified to explain the late-time accelerated expansion of the Universe. One of the interesting and prospective versions of modified gravity theory is the f(R, T) gravity proposed by Harko et al. (2011) where, the gravitational Lagrangian is given by an arbitrary function of the Ricci scalar R and the trace of the stress-energy tensor T. They have obtained the gravitational field equations in the metric formalism as well as the equation of motion for test particles, which follows the covariant divergence of the stress-energy tensor. Aktaş and Aygün (2017) have also discussed Magnetized strange quark matter solutions in f(R, T) gravity with a cosmological constant and it proves that the f(R, T) gravity models can explain the late time cosmic accelerated expansion of the Universe.

Recently, Samanta and Myrzakulov (2017) have studied imperfect fluid cosmological model in f(R, T)-gravity, Samanta et al. (2017) have studied Kaluza-Klein bulk viscous fluid cosmological models and the validity of the second law of thermodynamics in f(R, T) gravity. Also Keskin (2018), Sharif (2018), Chaubey and Shukla (2013), Samanta (2013a, b), and Reddy et al. (2012, 2013) have studied cosmological models in f(R, T) gravity in different Bianchi type space-times. Presently, Bianchi universes are playing important role in observational cosmology, since the WMAP data (Nojiri et al. 2008; Bamba et al. 2012) seem to require an addition to the standard cosmological model with positive cosmological constant that bears a likeness to the Bianchi morphology (Jamil et al. 2012a, b; Steigman & Turner 1983; Hinshaw et al. 2009). Katore et al. (2015) have discussed domain walls in f(R, T) theory. Agrawal and Pawar (2017a, b) have studied Bianchi type-V universe model with magnetized domain walls in f(R, T) theory. Also, Agrawal and Pawar (2017a, b) obtained plane symmetric cosmological model with quark and strange quark matter in f(R, T) theory of gravity.

Mostly the expansion of the universe is described within the framework of the homogeneous and isotropic Friedman–Robertson–Walker (FRW) cosmology. The reasons for this are purely technical. The simplicity of the field equations and the existence of analytical solutions in most of the cases have justified this over simplification for the geometry of space-time. However, there are no compelling physical reasons to assume the former before the inflationary period. To drop the assumption of homogeneity would make the problem intractable, while the isotropy of the space is something that can be relaxed and leads to anisotropy. Several authors (Jaffe et al. 2005, 2006; Campanelli et al. 2006, 2007) have studied particular cases of anisotropic models and found that the scenario predicted by the FRW model stand essentially unchanged even when large anisotropies were present before the inflationary period. Thus, the anisotropic Bianchi models become interesting in the academics. On this basis of this data, in the present study, Bianchi type-V space-time is taken into consideration. f(R, T) theory has attracted a lot of attention for the astrophysicist in recent times because of its ability to explain a lot of issues in cosmology and astrophysics (Barrow & Turner 1981; Sahoo et al. 2016a; Gron 1983a, b; Yousaf et al. 2017). Agrawal and Pawar (2017a, b) studied the f(R, T) theory in Bianchi Type V model. Pawar et al. 2016 also have analyzed two fluid axially symmetric cosmological models in f(R, T) Theory of Gravitation.

Recently, the dark energy models, which are inspiring many astrophysicists, are the holographic dark energy models. According to the holographic principle, the number of degrees of freedom in a bounded system should be finite and is related to the area of its boundary discussed by Sahoo et al. (2016b). It is argued that this model may solve the cosmological constant problem and some other issues. Several aspects of holographic dark energy have been investigated by Sahu et al. (2017) and Mishra et al. (2016). Also Gao et al. (2009) have proposed a HDE model, where the future event horizon is replaced by the inverse of the Ricci scalar curvature, and this model is named as “Ricci dark energy model” (RDE), that is, a holographic Ricci dark energy model, whose length scale is the inverse of the Ricci curvature scalar, i.e. \(L\approx \left| R \right| ^{\frac{-1}{2}}\). Granda and Oliveros (2008) suggested a new holographic Ricci dark energy model. Later, Chen and Jing (2009) and Cohen et al. (1999) and Hsu (2004) modified this model by assuming the density of dark energy contains the Hubble parameter H, the first order and the second order derivatives (i.e., \({\dot{H}} \hbox { and } {\ddot{H}})\). The expression of the energy density of dark energy is given by

$$\begin{aligned} \rho _\Lambda =3\eta _1 {\ddot{H}}{H}^{-1}+3\eta _2 {\dot{H}}+3\eta _3 H^{2} \end{aligned}$$

where \(\eta _1 , \eta _2 \hbox { and } \eta _{3} \) are three arbitrary dimensionless parameters.

Motivated by the above discussion, in the present paper, we consider spatially homogeneous and anisotropic Bianchi type-V universe filled with modified Holographic Ricci dark energy in f(R, T) theory of gravity. The geometrical and physical aspects of the models are also studied.

This work aims to study modified holographic Ricci dark energy under f(R, T) gravity and it is organized as follow.

In Section 2 we have described the f(R, T) model. In Section 3, we have studied the metric (Bianchi type-V) and field equations for MHRDE model in f(R, T) gravity. In Section 4, we have obtained the solutions of field equations. In Section 5, we have discussed the results obtained in the previous Sections. Finally, in Section 6, we have given conclusions of this work.

2 Gravitational field equation of f(R, T) modified gravity

The f(R, T) theory of gravity is the generalization or modification of General Relativity (GR). In this theory, the modified gravity action is given by

$$\begin{aligned} S=\frac{1}{2\kappa }\int {f(R,T)\sqrt{-g}d^{4}x+} \int {L_m \sqrt{-g}d^{4}x} \end{aligned}$$
(1)

which can be varied with respect to the metric tensor \(g_{ij} \)to obtain the gravitational field equation for f(R, T) gravity as

$$\begin{aligned}&f_R (R,T)R_{ij} -\frac{1}{2}f(R,T)g_{ij}\nonumber \\&\qquad +f_R (R,T)(g_{ij} \nabla ^{i}\nabla _i -\nabla _i \nabla _j )\nonumber \\&\quad =\kappa T_{ij} -f_T (R,T)T_{ij} -f_T (R,T)\theta _{ij} \end{aligned}$$
(2)

Where

$$\begin{aligned} \begin{array}{l} T_{ij} =T^{\prime }_{ij} +\overline{T_{ij} } \\ \theta _{ij} =g^{\alpha \beta }\frac{\partial T_{\alpha \beta } }{\partial g^{ij}}. \\ \end{array} \end{aligned}$$
(3)

Here \(f_R =\frac{\partial f(R,T)}{\partial R},f_T =\frac{\partial f(R,T)}{\partial T},\nabla _i \) is the covariant derivative. \(\kappa =\frac{8\pi G}{c^{4}}\), Where G and c are the Newtonian Gravitational constant and speed of light in vacuum respectively. \(T_{ij} \) is the standard matter energy-momentum tensor derive from the Lagrangian \(L_m \).

The energy-momentum tensor for pressureless matter and holographic dark energy are respectively given by

$$\begin{aligned} \begin{array}{l} {T^{{\prime }}}_{ij} =\rho _M u_i u_j ,i,j=1,2,3,4 \\ {{\overline{T}}} _{ij} =(\rho _\Lambda +p_\Lambda )u_i u_j +g_{ij} p_\Lambda \\ \end{array} \end{aligned}$$
(4)

where \(\rho _M \) is matter-energy density, \(\rho _\Lambda \) is the energy density of the modified holographic Ricci dark energy. \(u^{i}=(0,0,0,1)\) is the four-velocity vector in comoving coordinates which satisfies the condition \(u^{i}u_i =1\) and \(u^{i}\nabla _j u_i =0\).

The functional f(R, T) can be chosen in many ways corresponding to viable models. In the present work, we have considered the functional as \(f(R,T)=R+2f(T)\), where f(T) is an arbitrary function of the trace of the energy-momentum tensor. The corresponding field equations become,

$$\begin{aligned} R_{ij} -\frac{1}{2}Rg_{ij} {=}\kappa T_{ij} +2f_T T_{ij} +[f(T)+2p_\Lambda f_T ]g_{ij}\nonumber \\ \end{aligned}$$
(5)

Where \(f_T \) denotes the partial derivative of f with respect to T. Assuming \(f(T)=\lambda T,\lambda \) being constant.

Now, parameterizing, we have from Equation (4)

$$\begin{aligned} {{\overline{T}}} _j^i= & {} diag[-1,\omega _x ,\omega _y ,\omega _z ]\rho _\Lambda \nonumber \\= & {} diag[-1,\omega _\Lambda ,(\omega _\Lambda +\delta ),(\omega _\Lambda +\gamma )]\rho _\Lambda \end{aligned}$$
(6)

Here we have used the EoS parameter \(\omega \) given by

$$\begin{aligned} \omega _\Lambda \rho _\Lambda =p_\Lambda \end{aligned}$$
(7)

And \(\omega _x ,\omega _y ,\omega _z \) are the directional EoS parameters along x,y, z-axes respectively.

For simplicity we use \(\omega _\Lambda =1\).

3 Metric and field equations

We consider the spatially homogeneous and anisotropic Bianchi type-V space-time described by the line element,

$$\begin{aligned} ds^{2}=-dt^{2}+A^{2}dx^{2}+B^{2}e^{2x}(dy^{2}+dz^{2}) \end{aligned}$$
(8)

Where A and B are functions of cosmic time t only

Now using a co-moving coordinate system, the field equations (5) with the help of Equation (4) and Equation (6) for the metric (8), can be explicitly written as

$$\begin{aligned}&\frac{2{\ddot{B}}}{B}+\frac{\dot{B}^{2}}{B^{2}}-\frac{1}{A^{2}}=\lambda (8p_\Lambda +\rho _M )+p_\Lambda \end{aligned}$$
(9)
$$\begin{aligned}&\frac{{\ddot{A}}}{A}+\frac{{\ddot{B}}}{B}+\frac{\dot{A}{\dot{B}}}{AB}-\frac{1}{A^{2}}=\lambda (8p_\Lambda +\rho _M )+p_\Lambda \end{aligned}$$
(10)
$$\begin{aligned}&\frac{{\ddot{A}}}{A}+\frac{{\ddot{B}}}{B}+\frac{\dot{A}{\dot{B}}}{AB}-\frac{1}{A^{2}}=\lambda (8p_\Lambda +\rho _M )+p_\Lambda \end{aligned}$$
(11)
$$\begin{aligned}&\frac{2{\dot{A}}{\dot{B}}}{AB}+\frac{\dot{B}^{2}}{B^{2}}-\frac{3}{A^{2}}=\lambda (6p_\Lambda +3\rho _M +2\rho _\Lambda )\nonumber \\&\quad +p_\Lambda +\rho _M \end{aligned}$$
(12)
$$\begin{aligned}&\frac{{\dot{B}}}{B}-\frac{{\dot{A}}}{A}=0 \end{aligned}$$
(13)

Here an over head dot indicates differentiation with respect to cosmic time t.

We shall now define the dynamical parameters which will be useful in solving the field equations and in the physical discussion of the solution.

The average scale factor a(t) of the Bianchi type-V space-time is defined as

$$\begin{aligned} a(t)=(AB^{2})^{\frac{1}{3}} \end{aligned}$$
(14)

The spatial volume of the metric is

$$\begin{aligned} V=a^{3}(t)=AB^{2} \end{aligned}$$
(15)

The directional Hubble parameters are

$$\begin{aligned} H_x =\frac{\mathop A\limits ^{\bullet } }{A},H_y =H_z =\frac{\mathop B\limits ^{\bullet } }{B} \end{aligned}$$
(16)

The average Hubble parameter is

$$\begin{aligned} H=\frac{{\dot{a}}}{a}=\frac{1}{3}\frac{{\dot{V}}}{V}=\frac{1}{3}\left( {\frac{\mathop A\limits ^{\bullet } }{A}+2\frac{\mathop B\limits ^{\bullet } }{B}} \right) \end{aligned}$$
(17)

The dynamical scalar expansion \(\theta \) and shear scalar \(\sigma ^{2}\) are

$$\begin{aligned} \theta= & {} \frac{\mathop A\limits ^{\bullet } }{A}+2\frac{\mathop B\limits ^{\bullet } }{B}=3H \end{aligned}$$
(18)
$$\begin{aligned} \sigma ^{2}= & {} \frac{1}{2}\sigma ^{ij}\sigma _{ij} =\frac{1}{2}\left( {\frac{\mathop A\limits ^{\bullet } }{A}-\frac{\mathop B\limits ^{\bullet } }{B}} \right) ^{2} \end{aligned}$$
(19)

The average anisotropic parameter \(\Delta \) is defined as

$$\begin{aligned} \Delta =\frac{1}{3}\sum _{i=1}^3 {\left( {\frac{H_i -H}{H}} \right) } ^{2} \end{aligned}$$
(20)

Where \(H_i (i=1,2,3)\) represent the directional Hubble parameters.

We have chosen a system for \(\kappa =1\).

The deceleration parameter is

$$\begin{aligned} q=-1+\frac{d}{dt}\left( \frac{1}{H}\right) . \end{aligned}$$
(21)

4 A solution of field equations

Now the field equations (9)–(13) reduces to a system of four independent equations in five unknowns \(A,B,\rho _\Lambda ,p_\Lambda ,\rho _M \). Hence to find the determinate solution of the system we require one condition and this condition we get from Equation (13)

$$\begin{aligned} A=kB \end{aligned}$$

Where k is constant of integration and for simplicity we choose k=1.

$$\begin{aligned} \therefore A=B \end{aligned}$$
(22)

Now from Equations (9), (10) and (22) we obtain the metric potentials

$$\begin{aligned} A=B=c_1 +c_2 e^{t} \end{aligned}$$
(23)

Where \(c_1 ,c_2 \) are a (positive) constant of integration

Using equation (23), we can write the metric (8) in the form

$$\begin{aligned} ds^{2}= & {} -dt^{2}+(c_1 +c_2 e^{t})^{2}dx^{2}\nonumber \\&+(c_1 +c_2 e^{t})^{2}e^{2x}(dy^{2}+dz^{2}). \end{aligned}$$
(24)

5 Dynamical parameters and their physical discussion

Dynamical parameters are quite significant in the discussion of the physical properties of the cosmological model and to develop a cosmological theory in f(R, T) theory of gravity. We compute the following cosmological parameters for the model given by Equation (24)

The average scale factor a(t) found to be

$$\begin{aligned} a(t)=c_1 +c_2 e^{t} \end{aligned}$$
(25)

The spatial volume of the metric is

$$\begin{aligned} V=a^{3}(t)=(c_1 +c_2 e^{t})^{3} \end{aligned}$$
(26)

The directional Hubble parameters are

$$\begin{aligned} H_x =\frac{c_2 e^{t}}{c_1 +c_2 e^{t}}=H_y =H_z \end{aligned}$$
(27)

The average Hubble parameter is

$$\begin{aligned} H=\frac{c_2 e^{t}}{c_1 +c_2 e^{t}} \end{aligned}$$
(28)

The dynamical scalar expansion \(\theta \)and shear scalar \(\sigma \) are

$$\begin{aligned}&\theta = \frac{3c_2 e^{t}}{c_1 +c_2 e^{t}} \end{aligned}$$
(29)
$$\begin{aligned}&\sigma ^{2} = 0 \end{aligned}$$
(30)

The average anisotropic parameter \(\Delta \) is

$$\begin{aligned} \Delta =0 \end{aligned}$$
(31)

The deceleration parameter is

$$\begin{aligned} q=-\frac{c_1 +c_2 e^{t}}{c_2 e^{t}} \end{aligned}$$
(32)

Now from Equations (7), (9), (10) and (23) the modified holographic Ricci dark energy density and pressure is determined as

$$\begin{aligned}&\rho _\Lambda =\frac{1}{1+8\lambda }\left[ {\frac{-1+3c_2 ^{2}e^{2t}+2c_1 c_2 e^{t}}{(c_1 +c_2 e^{t})^{2}}} \right] \nonumber \\&\quad =p_\Lambda , \;\lambda \ne \frac{-1}{8} \end{aligned}$$
(33)

Also from Equations (7), (9), (10) and (33) we have the matter-energy density given by

$$\begin{aligned} \rho _M =\frac{-2}{1+3\lambda }\left[ {\frac{1+c_1 c_2 e^{t}}{(c_1 +c_2 e^{t})^{2}}} \right] ,\;\lambda \ne \frac{-1}{3} \end{aligned}$$
(34)
Fig. 1
figure 1

Variation of average scale factor against cosmic time for \(\hbox {c}_{1 }=0.1\), \(\hbox {c}_{2}=1\) with varying constant \(\lambda =0.14, 0.15, 0.16\), where \(t, a(t)\,and\,p_\Lambda \) all quantities are in arbitrary units.

Full size image
Fig. 2
figure 2

Variation of Ricci dark energy pressure against cosmic time for \(\hbox {c}_{1 }=0.1\), \(\hbox {c}_{2}=1\) with varying constant \(\lambda =0.14, 0.15, 0.16\), where \(t, a(t)\,and\,p_\Lambda \) all quantities are in arbitrary units.

Full size image
Fig. 3
figure 3

Variation of special volume against cosmic time for \(\hbox {c}_{1 }=0.1\), \(\hbox {c}_{2}=1\), where \(t, v\,and\,H\) all quantities are in arbitrary units.

Full size image

Above results are useful to discuss the behavior of the model (24). We have the following observations.

Fig. 4
figure 4

Variation of Hubble parameter against cosmic time for \(\hbox {c}_{1 }=0.1\), \(\hbox {c}_{2}=1\), where \(t, v\,and\,H\) all quantities are in arbitrary units.

Full size image
  1. 1)

    The model (24) represents an expanding, non-shearing, non-rotating and accelerating universe. The model (24) has no initial singularity. Since the metric potential of the universe A(t) and B(t) are constant at \(\hbox {t}=0\).

  2. 2)

    We observed that the positive value of the Hubble parameter and the deceleration parameter \(q=-\frac{c_1 +c_2 e^{t}}{c_2 e^{t}}\) (\(as\,t\rightarrow \infty ,q\rightarrow -1)\) throughout the evolution shows that the universe is expanding and accelerating exponentially.

  3. 3)

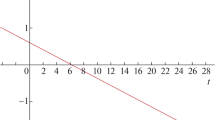
    The average scale factor increases with cosmic time increases (Figure 1), whereas Ricci dark energy pressure decreases with cosmic time increases (Figure 2).

  4. 4)

    The spatial volume (V) is finite at initial epoch and it increases with increase in cosmic time (Figure 3). The anisotropic parameter (\(\Delta \)) and shear scalar sigma (\(\sigma \)) are vanished. Since \(t\rightarrow \infty ,\left( {\frac{\sigma }{\theta }} \right) ^{2}\rightarrow 0\) the models approach isotropy for a large value of t.

Fig. 5
figure 5

Variation of dynamical scalar expansion against cosmic time for \(\hbox {c}_{1 }=0.1\), \(\hbox {c}_{2}=1\), where \(t, \theta \,and\,q\) all quantities are in arbitrary units.

Full size image
Fig. 6
figure 6

Variation of deceleration parameter against cosmic time for \(\hbox {c}_{1 }=0.1\), \(c_{2}=1\), where \(t, \theta \,and\,q\) all quantities are in arbitrary units.

Full size image

This shows that the model is isotropic throughout the evolution of the universe.

  1. 5)

    The directional Hubble parameter, average Hubble parameter (Figure 4), and dynamical scalar expansion (Figure 5) are finite at an initial epoch as well as at the infinite time. Also, it increases as cosmic time increases. Deceleration parameter decreases as cosmic time increases and it approaches to -1 for a large value of t. It shows that the universe is accelerating (Figure 6). Also, matter-energy density is an increasing function of t and it approaches zero for a large value of t (Figure 7).

Fig. 7
figure 7

Variation of Matter energy density against cosmic time for \(\hbox {c}_{1 }=0.1\), \(\hbox {c}_{2}=1\) with varying constant \(\lambda =0.14, 0.18, 0.22\), where \(t\,and\,\rho _M \) all quantities are in arbitrary units.

Full size image

6 Conclusion

We have studied the modified holographic Ricci dark energy model in f(R, T) theory of gravity by using anisotropy Bianchi type-V. In order to obtain the solutions of field equations, we used EoS \(\omega _\Lambda \rho _\Lambda =p_\Lambda \). The model we obtained has no physical singularity. It reveals that the universe starts its expansion with finite volume. The directional Hubble parameters, the mean generalized Hubble parameter H and the expansion scalar all these parameters are functions of the cosmic time t. These parameters are finite at the initial stage (\(\hbox {t} = 0\)), increase with increase in time t, and it becomes constant for a large value of t. Hence universe expand endlessly with the influence of dark energy. The negative value of the deceleration parameter and positive value of Hubble parameter throughout the evolution shows that the present universe is expanding and accelerating exponentially (This result match with Samanta et al. 2017; Mishra et al. 2016). We also observed result of Samanta and Myrzakulov (2017); they found the Hubble parameter is always positive and reduces as time increases but we have Hubble parameter is always positive, it increases as time increases and constant for infinite time.

The anisotropic parameter (\(\Delta \)) and shear scalar sigma (\(\sigma \)) are vanished. It is observed that the universe can approach to isotropy even in the presence of an anisotropic dark energy. It means an accelerated expansion period isotropizes both the expansion anisotropy and the anisotropy dark energy (This result match with Adhav et al. 2011). This shows that the model is isotropic throughout the evolution of the universe. Also modified holographic Ricci dark energy density and pressure is constant at an initial time and increases as time increases. Actually it tends to infinity as t tends to infinity. But dark matter density is constant at initial as well as in infinite time.