Multi-ML: Programming Multi-BSP Algorithms in ML

Abstract

bsp is a bridging model between abstract execution and concrete parallel systems. Structure and abstraction brought by bsp allow to have portable parallel programs with scalable performance predictions, without dealing with low-level details of architectures. In the past, we designed bsml for programming bsp algorithms in ml. However, the simplicity of the bsp model does not fit the complexity of today’s hierarchical architectures such as clusters of machines with multiple multi-core processors. The multi-bsp model is an extension of the bsp model which brings a tree-based view of nested components of hierarchical architectures. To program multi-bsp algorithms in ml, we propose the multi-ml language as an extension of bsml where a specific kind of recursion is used to go through a hierarchy of computing nodes. We define a formal semantics of the language and present preliminary experiments which show performance improvements with respect to bsml.

1 Introduction

Context of Work Nowadays, parallel programming is the norm in many areas but it remains a hard task. And the more complex the parallel architectures become, the harder the task of programming them efficiently is. As we moved from unstructured sequential code cluttered with goto statements towards structured code, there has been a move in parallel programming community to leave unstructured parallelism, with pairwise communications, in favour of global communication schemes [2, 6, 30] and of structured abstract models like bsp [2, 37] or of higher-level concepts like algorithmic skeletons [18].

Programming in the context of a bridging model, such as bsp, allows to simplify the task of the programmer, to ease the reasoning on cost and to ensure a better portability from one system to another [2, 25, 37]. However, designing a programming language [20, 24] for such a model requires to choose a trade-off between the possibility to control parallel aspects—necessary for predictable efficiency but which makes programs more difficult to write, to prove and to port—and the abstraction of such features, which makes programming easier but which may hamper efficiency and performance prediction.

With flat homogeneous architectures, like clusters of mono-processors, bsp has been proved to be an effective target model for the design of efficient algorithms and languages [39]: while its structured nature allows to avoid deadlocks and non-determinism with little care and to reason on program correctness [14, 15, 17] and cost, it is general enough to express many algorithms [2]. However, modern parallel architecture have now multiple layers of parallelism. For example, supercomputers are made of thousands of interconnected nodes, each one carrying several multi-cores processors. Communications between distant nodes cannot be as fast as communications among the cores of a given processor; Communications between cores, by accessing shared processor cache are faster than communications between processors through RAM.

Contribution of this Paper Those architectures specifics led to a new bridging model, multi-bsp [38], where the hierarchical nature of parallel architectures is reflected by a tree-shaped model describing the dependencies between memories. The multi-bsp model gives a more precise picture of the cost of computations on modern architectures. While the model is more complex to grasp than the bsp one, it keeps structured characteristics that prevents deadlock and non-determinism. We propose a language, multi-ml, which aims at providing a way to program multi-bsp algorithms so as bsml [16] is a way to program bsp ones. multi-ml combines the high degree of abstraction of ml (without poor performances because often, ml programs are as efficient as c ones) with the scalable and predictable performances of multi-bsp.

Outline The remainder of this paper is structured as follows. We first give in Sect. 2 an overview of previous works: the bsp model at Sect. 2.1 and then the bsml language at Sect. 2.2 following with the multi-bsp model at Sect. 2.3. Our language multi-ml is presented at Sect. 3. Its formal semantics and implementation, together with examples and benchmarks are given at Sect. 4. Section 5 discusses some related works and finally, Sect. 6 concludes the paper and gives a brief outlook on future work.

2 Previous Works

In this section, we briefly present the bsp and multi-bsp models and how to program bsp algorithms using the bsml language. We assume the reader is familiar with ml programming. We also give an informal semantics of the bsml primitives and some simple examples of bsml programs.

2.1 The BSP Model of Computation

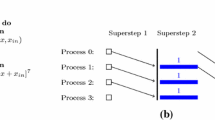
In the bsp model [2, 37], a computer is a set of ${\mathbf{p}}$ uniform processor-memory pairs and a communication network. A bsp program is executed as a sequence of super-steps (Fig. 1), each one divided into three successive disjoint phases: (1) each processor only uses its local data to perform sequential computations and to request data transfers to other nodes; (2) the network delivers the requested data; (3) a global synchronisation barrier occurs, making the transferred data available for the next super-step.

Fig. 1

A bsp super-step

This structured model enforces a strict separation of communication and computation: during a super-step, no communication between the processors is allowed, only requests of transfer; information exchanges only occur at the barrier. Note that a bsp library can send data during the computation phase of a super-step, but this is hidden from the programmers.

The performance of a bsp computer is characterised by 4 parameters: (1) the local processing speed $\mathbf{r}$; (2) the number of processors $\mathbf{p}$; (3) the time $\mathbf{L}$ required for a barrier; (4) and the time ${\mathbf{g}}$ for collectively delivering a 1-relation, i.e. every processor receives/sends at most one word. The network can deliver an h-relation in time ${\mathbf{g}} \times h$. To accurately estimate the execution time of a bsp program, these 4 parameters can be easily benchmarked [2]. The execution time (cost) of a super-step s is the sum of the maximal local processing time, the data delivery and the global synchronisation times. The total cost (execution time) of a bsp program is the sum of its super-steps’ costs.

2.2 BSP Programming in ML

bsml [16] uses a small set of primitives and is currently implemented as a library (http://traclifo.univ-orleans.fr/BSML/) for the ml programming language ocaml (http://caml.org). An important feature of bsml is its confluent semantics: whatever the order of execution of the processes, the final value will be the same. Confluence is convenient for debugging since it allows to get an interactive loop (toplevel); It also eases programming since the parallelisation can be done incrementally from an ml program. Last but not least, it is possible to reason about bsml programs using the coq (https://coq.inria.fr/) proof assistant [15, 17] and to extract actual bsp programs from proofs.

A bsml program is built as an ml one but using a specific data structure called parallel vector. Its ml type is . A vector expresses that each of the ${\mathbf{p}}$ processors embeds a value of any type . The processors are labelled with ids from 0 to ${\mathbf{p}}-1$. The nesting of vectors is not allowed. We use the following notation to describe a vector: $\langle v_0, v_1, \ldots , v_{{\mathbf{p}}-1} \rangle$. We distinguish a vector from a usual array because the different values, that will be called local, are blind from each other; it is only possible to access the local value $v_i$ in two cases: locally, on processor i (using a specific syntax), or after some communications.

Since a bsml program deals with a whole parallel machine and individual processors at the same time, a distinction between the 3 levels of execution that take place will be needed: (1) Replicated execution r is the default; Code that does not involve bsml primitive is run by the parallel machine as it would be by a single processor; Replicated code is executed at the same time by every processor, and leads to the same result everywhere; (2) Local execution l is what happens inside parallel vectors, on each of their components; Each processor uses its local data to do their own computations; (3) Global execution g concerns the set of all processors together as for bsml communication primitives. The distinction between local and replicated is strict: the replicated code cannot depend on local information. If it were to happen, it would lead to replicated inconsistency.

Table 1 Summary of the bsml primitives

Parallel vectors are handled through the use of different communication primitives. Table 1 shows their use. Informally, they work as follows: let be the vector holding everywhere (on each processor), the indicates that we enter a vector and switch to the local level. Replicated values are available inside the vectors. To access to local information within a vector, we add the syntax to read the vector and get the local value it contains. The ids can be accessed with the predefined vector . For example, using the toplevel for a simulated bsp machine with 3 processors:

The symbol is the prompt that invites the user to enter an expression to be evaluated. Then, the toplevel gives the evaluated value with its type. Thanks to bsml confluence, it is ensured that the results of the toplevel or of the distributed implementation are identical.

The primitive is the only way to extract local values from a vector. Given a vector, it returns a function such that, applied to the pid of a processor, the function returns the value of the vector at this processor. performs communications to make local values available globally and it ends the current super-step. For example, if we want to convert a vector into a list, we write:

where is the list of

.

The primitive is another communication primitive. It allows any local value to be transferred to any other processor. It is also synchronous, and ends the current super-step. The parameter of is a vector that, at each processor, holds a function of type returning the data to be sent to processor j when applied to j. The result of is a new vector of functions: at a processor j the function, when applied to i, yields the value received from processor i by processor j. For example, a could be written:

where the bsp cost is $({\mathbf{p}}-1)\times s\times {\mathbf{g}}+{\mathbf{L}}$ where s is the size of the biggest sent value.

Fig. 2

The difference between the multi-bsp and bsp models for a multi-core architecture

2.3 The multi-bsp Model for Hierarchical Architectures

The multi-bsp model [38] is another bridging model as the original bsp, but adapted to clusters of multi-cores. The multi-bsp model introduces a vision where a hierarchical architecture is a tree structure of nested components (sub-machines) where the lowest stage (leaf) are processors and every other stage (node) contains memory. Figure 2 illustrates the difference between both models for multi-cores. There exist other hierarchical models [29], such as d-bsp [1] or h-bsp [7], but multi-bsp describes them in a simpler way. An instance of multi-bsp is defined by $\mathbf {d}$ the depth of a tree and 4 parameters for each stage i:

• $\mathbf {p_i}$ is the number of components inside the i stage. We consider $\mathbf {p}_1$ as a basic computing unit where a step on a word is considered as the unit of time.

• $\mathbf {g_i}$ is the bandwidth between stages i and $i+1$: the ratio of the number of operations to the number of words that can be transmitted in a second (illustrated in Fig. 3).

• $\mathbf {L_i}$ is the synchronisation cost of all components of $i\!-\!1$ stage, but no synchronisation across above branches in the tree. Every components can execute codes but they have to synchronise in favour of data exchange. Thus, multi-bsp does not allow subgroup synchronisation as the d-bsp does: at a stage i there is only a synchronisation of the sub-components, a synchronisation of each of the computational units that manage the stage $i\!-\!1$.

• $\mathbf {m_i}$ is the amount of memory available at stage i.

Fig. 3

multi-bsp parameters

A node executes some code on its nested components (children), then waits for results, does the communications and synchronises the children. Considering $C_j^i\!=\!h_i\!\times \!\mathbf {g}_j\!+\!\mathbf {L}_j$, the communication cost of a super-step i at stage j with $h_i$ the size of the exchanged messages at step i, $\mathbf {g}_j$ the communication bandwidth with stage j and $\mathbf {L}_j$ the synchronisation cost. We can recursively express the cost of a multi-bsp algorithm as follows: $\sum _{i=0}^{N\!-\!1}w_i + \sum _{j=0}^{d\!-\!1}\sum _{i=0}^{M_j\!-\!1}C_j^i$ where N is the number of computational super-steps, $w_i$ is the cost of a single computation step and $M_j$ is the number of communication phases at stage j.

Fig. 4

bsml direct scan code

As a more evolved program, we can find an implementation of the standard direct scan in Fig. 4. This code builds the values to be communicated to all processes with a greater and it exchanges the values using the primitive. Then every processes maps the received values on their own data.

3 Design of the Multi-ML Language

multi-ml is based on the idea of executing a bsml-like code on every stage of the multi-bsp architecture, that is on every sub-machine. Hence, we add a specific syntax to ml in order to code special functions, called multi-functions, that recursively go through the multi-bsp tree. At each stage, a multi-function allows the execution of any bsml code. We first present the execution model that follows this idea; we then present the specific syntax and we finally give the limitations when using some advanced ocaml features.

3.1 Execution Model

A multi-ml tree is formed by nodes and leaves as proposed in multi-bsp with the difference that a node is not only a memory but has the ability to manage (coordinate) the values exchanged by its sub-machines. However, as common architectures do not have dedicated processors for each memory, one (or more, implementation dependent) selected computation unit has the responsibility to perform this management task, which is limited in practice. Because leaves are their own computing units, our approach coincides with multi-bsp if we consider that all the computations and memory accesses, at every nodes, are performed by one (or more) leaf: replicated codes (outside vectors) that takes place in nodes will be costlier than in leaves. This is why computations on nodes are reserved to the simple task of coordination. The multi-ml approach is also a bit more relaxed than multi-bsp regarding synchronisation. Unlike multi-bsp, we allow asynchronous codes in the sub-machines when only lower memories accesses are used. Of course, we do synchronise if a communication primitive is used. As suggested in [38], we also allow flat communications between nodes and leaves without using an upper level.

In a multi-ml tree, of type $'a\;tree$, every node and leaf contains a value of type $'a$ in its own memory. It is important to notice that the values contained in a tree are accessed by the corresponding node (or leaf) only. It is impossible to access the values of another component without using explicit communications. In multi-ml codes, we discern four strictly separated execution levels: (1) the level m (multi-bsp) is the upper one (outside trees) and is appropriate to call multi-functions and managing the trees; codes at this level are executed by all the computation units in a spmd fashion; (2) the level b (bsp) is used inside multi-functions and is dedicated to execute bsml codes on nodes; (3) level l (local) corresponds to the codes that are run inside vectors; (4) level s stands for standard ocaml codes finally executed by the leaves. It is to notice that it is impossible to communicate vectors or trees and, like in bsml, the nesting of parallelism (of vectors/trees) is forbidden.

The main idea of multi-ml is to structure the codes to control all the stage of a tree: we generate the parallelism by allowing a node to call recursively a code on each of its sub-machines (children). When leaves are reached, they will execute their own codes and produce values, accessible by the top node using a vector. As shown in Fig. 6, the data are distributed on the stages (toward leaves) and results are gathered on nodes toward the root node. Let us consider a code where, on a node, the following code is executed: . As shown in Fig. 5, the node creates a vector containing for each children i. As the code is run asynchronously, the execution of the node code will continue until reaching a barrier.

Fig. 5

Vector distribution

Fig. 6

Code propagation

3.2 The multi-ml Language

Table 2 shows the multi-ml primitives (without recall the bsml ones); their authorised level of execution and their informal semantics. n denotes the id of a node/leaf, i.e. its position in the tree encoded by the top-down path of positions in node’s vectors. For example, 0 stands for the root, 0.0 for its first child, etc. For the ith component of a vector at node n, the id is n.i. Figure 7 illustrates this naming. We now describe in details these primitives and multi-functions.

Table 2 Summary of the multi-ml primitives

Fig. 7

Node identifiers

The Let-Multi Construction The goal is to define a multi-function, i.e. a recursive function over the multi-bsp tree. Except for the tree’s root, when the code ends on a stage i, the computed value is made available to the upper stage $i-1$ in a vector. The let-multi construction offers a syntax to declare codes for two levels, one for the nodes (level b) and one for the leaves (level s):

are the arguments of the newly define multi-function . In the leaf block (i.e. level s), we find usual ml computations and most of the calculations should take place here. In the node block (i.e. level b), we find the code that will be executed at every stage of the tree but on the leaves. Typically, a node is charged to propagate the computations and the data using vectors (level l); to manage the sub-machine computations; and finally, gather the results using the (extraction of values from a vector). To go one step deeper in the tree, the node code must recursively call the multi-function inside a vector. This call must be done inside a vector in order to spread the computation all over the tree in the deeper stages. It is also to notice that a multi-function can only be called at m level of the code and values at this level are available throughout the multi-function execution. Figure 8 shows, as an example of how data moves through the multi-bsp tree, a simple program summing of the elements of a list.

Fig. 8

Sum multi-ml example

It works as follows: We define the multi-function (line 1); lines 2–5 give the code for the nodes and lines 6–7 give the code for the leaves; the list is scattered across each component i of the vector (line 3); on line 4, we recursively call the multi-function on the sub-lists (i.e. call in the contexts of the sub-nodes); we finally gather the results in line 5 ( is a bsml code that performs a to sum the $\mathbf {p}_n$ projected integers).

Tree Construction It is similar to the above multi-functions: instead of generating a single usual ml value, functions defined with build a tree of type $'a\;tree$. For this, a new constructor determines the values that are stored (keep) at each id and those that are ascended (up) to the upper stage—until now, the value returned by nodes and leaves was implicitly considered as the value given to the upper stage. This is the role of which works as follows: sends up the value and stores in the tree the value (thus replacing the previously stored value). The primitive returns the last value stored using or the default value initialised thanks to a construction. It is useful to update the tree.

Figure 9 shows the modifications that have to be added to in order to obtain a tree containing the list of partial sums on every leaves and the maximal sub-sums on each node—Thus, the root node contains the final sum. The code works as follows: We use a generic operator with an identity element and a list to be distributed (line 1); Then we traverse the tree two times (phases distinguished by a boolean flag): First to split the list and then to compute the partial sums. On the nodes, we split the list (line 6) and then we do a recursive call over the scattered lists to continue the splitting at lower levels and then recover the partial sums of children nodes (line 7), a bsp scan is used to transfer and compose these partial results from sibling nodes left to right ( could be replaced by any scan); Finally, we recall the multi-function (lines 8–10) to complete the partial sums with the communicated values and for this, we transmit down a list containing only the last value from each branch, keep it in the tree and give it to the upper level (line 11).

Fig. 9

Scan multi-ml example

When reaching the leaves the first time, we compute the partial sums (line 16) and, each time a value (communicated by other branches) comes down to a leaf, we add it to its own partial sums (line 17). Note that using two multi-functions, one to first split the list and another one to compute the partial sums, is surely easier, but using a one-shot multi-function, we exhibit more features of multi-ml.

Variables Accesses There are three different ways to access to variables in addition to the usual ml access. First, stands for reading the local value of a vector “” inside a vector (l level, as in bsml).

The second way is to read a value inside a vector which had been declared outside. As explained above, the values available on a node are not implicitly available on the child nodes. It is thus necessary to copy them from a node to its sub-machines. For example, the code is incorrect because “” is not available on children. It is imperative to use to copy the value of from the b level into the vector (l level).

The last way is for reading the value of a tree. Within the tree construction

(syntax explained below), stands for reading the value of “” at id n. Outside a vector (b level), accessing to a tree is done in the same way. Finally, is the predefined tree of nodes/leaves ids. When executed inside a vector (l level) at a level n, stands for the id n.i. However, inside a

code, it stands for the id of the current level. As expected, in a node (b level) or a leaf (s level), is the identifier at the corresponding level. However, at level m, it is the tree of level identifiers.

A Convenient Tree Construction For building a tree without using a multi-function (which induce communications), we add the

syntax. It allows to execute on every nodes and leaves. One can read the values of a previously defined tree using the access in the code of . In this way, using the predefined tree , we can execute different codes on each components of a tree without any need (and possibility) of communication between the stages.

A New Primitive For performances reason, we chose to add the new primitive . Indeed, in bsml a replicated code is duplicated on every processors, so it is not necessary to take care of data transfer in code like: where is a large list and a splitting function. With the multi-ml model, data are not distributed everywhere and we have to transfer data explicitly. One can write but it is not useful to copy the whole list on every children in order to extract a sub list and throw the rest. This is the reason why computes, first, values and then distributes them to the sub-machines, thus building a vector. This method is more expensive for the node n in terms of computation time, but it reduces drastically the amount of data transfers.

3.3 Current Limitations

Exceptions and Partially Evaluated Trees Exceptional situations are handled in ocaml with a system of exceptions. In parallel, this is at least as relevant: if one processor triggers an exception during a computation, bsml [16] as well as multi-ml have to deal with it, like ocaml would, and prevent a crash.

The problem is when an exception is raised locally (l level) on (at least) one processor whereas other processors continue to follow the execution stream, until they are stopped by the need of synchronisation. This happens when an exception escapes the scope of a parallel vector. Then, a crash can occur: a processor misses the global barrier. To prevent this situation, in [16], we introduce a specific handler of local exceptions that have not been caught locally. The structure catches any exception and handles it as usual in ocaml. To do this, when a barrier occurs, all exceptions are communicated to all processors in order to allow a global decision to be taken. Furthermore, any access to a vector that is in an incoherent state will raise, again, the exception.

For multi-ml, if an exception is not correctly handled in a stage, it must be propagated to the upper stage at the next barrier—as in bsml. If an exception is no handled in a multi-function, it must be thrown at the global level m as a standard ocaml exception. An exception thrown in a node of a tree leads this node in an incoherent state until the exception has been caught in a upper level. Any access to this tree must raise again the exception. This handling has not been implemented yet for multi-ml but the first author works on it.

An application case is partially evaluated trees. Take for example the following code: where is a multi-function. A part of the tree will never be instantiated. If a partially evaluated tree is accessed during a code execution an exception could be immediately thrown.

Type System The main limitation of our prototype is the lack of a type system. Currently, nesting of bsml vectors/trees are not checked. A type system for bsml exists [16] but has not been implemented yet. We are convinced that adding multi-functions will not fundamentally change the type system: it’s mainly a matter of adding just a new level of execution.

Other ml Features We have not yet studied all the interactions of all the ocaml features with the multi-function (as well in bsml). Objects, first-order modules and gadt are left as future works.

4 Semantics, Implementation and Examples

We present a formal semantics of multi-ml as well as two implementations. A semantics is useful as a specification of the language so as to simplify the design of the implementations. To get the assurance that both implementations are coherent, using the semantics, we first prove that multi-ml is confluent. We also give some examples and benchmarks to illustrates the usefulness of multi-ml. Our prototype is freely available at http://www.lacl.fr/vallombert/Multi-ML.

4.1 Operational Semantics

We give a big-step semantics of a core-language without tree creation to simplify the presentation. The syntax (Fig. 10) extends the popular core-ml.

Fig. 10

Syntax of core-multi-ml

Programs contain variables, constants (integers, etc.), operators ($\le$, $+$, etc.), pairing, $\mathbf{let}$, $\mathbf{if}$, $\mathbf{fun}$ statements as usual in ml, $\mathbf{rec}$ for recursive calls, the bsml primitives ($<\!\!e\!\!>$, $\mathbf{put}$, $\mathbf{proj}$), $\mathbf{mkpar}$, access $\$x\$$ to the local value of a vector x, local copy $\# x \#$ of a parent’s variable x, the vector of pid component and gid the tree of ids. Finally, we define let-multi as particular functions with codes for nodes and leaves.

The semantics is a big-step one with environments that represent the memories. We have a tree of memories (one per node and leaf) and we note them $\mathcal {E}$. $\Vert \mathcal {E}\Vert _n$ denotes the memory of $\mathcal {E}$ at n where n is the id of a node/leaf. $\{x \mapsto v\}$ denotes a binding of a variable x to a value v in the memory; $\in$ denotes a membership test and $\oplus$ denotes an update. Those operators have the subscript n that denotes the application in a specific memory.

$\mathcal {E} \vdash e \Downarrow v$ denotes the evaluation of e in the environment $\mathcal {E}$ to the value v. A value is a constant, an operator or a functional closure ( a function with its own environment of execution, denoted $\overline{({\mathbf{fun}}\,x\rightarrow e)[{\mathcal {E}}]}$). The rules of evaluation are defined by induction and given in Fig. 11. To simplify the reading of the rules, we count vector pids from 1 to $\mathbf {p}_n$ and not from 0 to $\mathbf {p}_n\!-\!1$. For core-ml the semantics are as usual.

Even if the semantics contains many rules, there is no surprise and it has to be read naturally. As explained before, there are 4 different levels of execution: level m for the execution on all computation units; bsp level b for bsml codes; Local level l for the codes inside a vector; and finally level s on the leaves. In this way, the evaluation $\Downarrow$ is upscripted by the level and can be subscripted by the id of the sub-machine.

The rules for the bsml primitives (Fig. 11) work as follows: (1) creating a new vector for the machine of id n is triggering $\mathbf {p}_n$ local evaluations, each with n.i as subscript since we are going one step deeper, in the $i\hbox {th}$ component; $\mathbf{proj}$ (2) and $\mathbf{put}$ (3) rules build the functions of exchanges; $\$\mathbf{pid}\$$ rule (4) returns i on child n.i; $\$x\$$ rule (5) read at n.i the ith value of the vector x available on node n; $\#x\#$ rule (6) read the value x at the node n from its child; the rule (7) is the evaluation of the core ml part (sequential); $\mathbf{mkpar}$ rule (8) creates the vector but first the node creates the values to be sent down.

Fig. 11

Operational big-step semantics rules of a core multi-ml

For the multi-functions, we have a rule to create them (9) and a rule (12) to initialise the recursion through the architecture from the root node. Then, inside the component i of a vector of sub-machine n, the recursive call of the multi-function generates an evaluation on n.i (rule 13), except if we reach a leaf, then the rule (14) says that the code is evaluated on leaf n.i with level s. The rule (10) is for the tree of ids. By induction, we can prove:

Lemma 1

(Confluence) $\forall \mathcal {E}$ if $\mathcal {E} \vdash e \Downarrow ^m v_1$ and $\mathcal {E} \vdash e \Downarrow ^m v_2$ then $v_1 \equiv v_2$

Co-inductive rules [28] $\Downarrow _\infty$ (for diverging programs) can be easily infered from the above rules. For sake of conciseness, we only present some typical examples:

We can then prove by co-induction the following lemma:

Lemma 2

(Mutually exclusive) $\forall \mathcal {E}$ if $\mathcal {E} \vdash e \Downarrow ^m v$ then $\lnot (\mathcal {E} \vdash e \Downarrow ^m_\infty )$

The result does not depend of the order of evaluation of the processes nor of the bsp sub-machines. All strategy work and return the same value, especially a sequential simulation and a distributed implementation. The former is fine for debugging whereas the latter is for benchmarking. We now present both.

4.2 Sequential Simulation and Distributed Implementation

Sequential Simulation We propose a sequential simulator that works as the ocaml toplevel. Given an architecture as a configuration file, the toplevel allows simulating multi-ml codes on a single core machine and printing the results. Currently, all the basic features of ocaml are available, without typing. To be executed, the multi-ml code is converted into a sequential code using a modified ocaml parser. The simulator creates a tree structure to represent the whole multi-bsp machine. Vectors are represented as arrays of data. A global hash table is used to simulate the memory available at each stage as suggested by the semantics. Figure 12 shows the result when using the toplevel for a simulated multi-bsp machine composed of 2 processors with respectively 2 cores.

Fig. 12

Example of the Toplevel

Distributed Implementation To be portable, our implementation is written to use various communication libraries. We have thus a modular approach and our implementation depends on a generic functor that requires the architecture configuration and some particular communication routines: asynchronous broadcasting and gathering for a group of processors, total exchange and building groups of processes. Our implementation of this module is currently based on mpi. We create one mpi process for every nodes and leaves of the architecture. Those processes are distributed over the physical cores and threads in order to balance the charge. As the code executed by nodes is, most of the time, a simple task of parallel management, this extra job is thus distributed over the leaves to reduce its impact.

Our implementation is based on a daemon running on each mpi process. Each daemon has 3 mpi communicators to communicate with its parent (upper node), its children (leafs) and its siblings (processes at the same sub-level). Each daemon is waiting for a task given by its parent. When a task is received, it is executed by the daemon, then the daemon returns to the waiting state until it receives a ”kill” signal, corresponding to the end of the program.

As the code is an spmd one, every processes know the entire code and they just need to receive a signal to execute a task. To do so, and to avoid serialising codes that are inside functional values (the closures) and known by all the nodes due to an spmd execution, when transmitting down values and thus creating parallel vectors, we identify the vectors by two kinds of identifiers: (1) a static identifier is generated globally for every vectors and references their computations through the execution; (2) when a node needs to create a parallel vector, it generates a dynamic identifier that represents the data on its children. Then, when a node executes some code using parallel values inside a vector, it just sends the static identifier (that references the code to execute) with the dynamic identifier (to substitute the distributed value) to its children which can then execute the correct tasks. The main advantage of this method is to avoid serialising unnecessary codes when creating vectors, and thus to reduce the size of the data exchanged by the processes. However, associating a value to a dynamic identifier can lead to a memory over-consumption, for example in loops. When the life cycle of a vector is terminated, we manually clean the memory by removing all the obsolete identifier and calling the garbage collector.

Shared Memory We propose an implementation to avoid some unnecessary copies of the transmitted data. Indeed, the ocaml memory is garbage collected and, to be safe, only a copy of the data can be transmitted. Using the standard posix “mmap” routine and some ipc functionalities (to synchronise the processes), the child (as daemons) can read asynchronously the transmitted serialised value in the mapping of the virtual address space of the father and synchronise with the father only, as the multi-bsp model suggest. As architectures can have different types of memory (distributed or shared), it is possible to mix executions schemes. Since the ocaml memory is garbage collected (currently with a global thread lock), we sadly cannot use pthreads as done in [39] to share values without performing first a copy. We are currently working on using some tricks to overcome this limitation but we leave it as future work.

4.3 Benchmarks

In this section we present the benchmarks of a simple scan with integer addition and a naive implementation of the sieve of Eratosthenes. A scan can be used to perform the sieve of Eratosthenes using a particular operator which implies more computations and communications than a simple list summing. The multi-bsp cost of the scan algorithm (Fig. 9) is as follows:

$$\begin{aligned} \sum \limits _{i\in [0\ldots \mathbf {d}[} V_{sp}(i) + \mathcal {O}(|l_{\mathbf {d}}|) + \sum \limits _{i\in [0\ldots \mathbf {d}[} C_i. \end{aligned}$$

where $\sum _{i\in [0\ldots \mathbf {d}[} V_{sp}(i)$ is the total cost of splitting the list toward the leaves (at depth $\mathbf {d}-1$); $\mathcal {O}(|l_{\mathbf {d}}|)$ is the time needed to compute the local sums in the leaves; and $\sum _{i\in [0\ldots \mathbf {d}[} C_i$ corresponds to the cost of diffusing partial sum back to leaves and to add these values to the values held by leaves. This diffusion is done once per node. $V_{sp}(i)$ is the work done at level i to split the locally held chunk $l_{i}$ and scatter it among children nodes. Splitting $l_{i}$ in $\mathbf {p}_{i}$ chunks costs $\mathcal {O}(|l_{i}|)$ where $|l_{i}|$, the size of $l_{i}$, is $n*\prod _{j\in [0...i[}\frac{1}{\mathbf {p_j}}$ where n is the size of the initial list holds by the root node. Scattering it among children nodes costs $\mathbf{p}_{\mathbf{i}}*\mathbf{g}_{\mathbf{i}-\mathbf{1}}+\frac{n_i}{\mathbf{p}_{\mathbf{i}}}+\mathbf{L}_{\mathbf{i}}$. The sequential list scan cost at leaves is $\mathcal {O}(|l_{d}|) = \mathcal {O}(n*\prod _{i\in [0...{\mathbf{d}}[}\frac{1}{\mathbf{p}_\mathbf{i}})$.

The cost $C_i$ at level i is the cost of a bsp scan, of the diffusion of the computed values toward the leaves, in addition to the sequential cost of a map on list held by leaves. Let s be the size of the partial sum, the cost of bsp scan at level i is $s*\mathbf {p_i}*\mathbf {g_{i-1}}+\mathbf {L_i}$, the diffusion cost is $\sum _{j\in ]i\ldots \mathbf {d}]}\mathbf {g_j}*s+l_{j}$ and the final map cost is $\mathcal {O}(s_{\mathbf{d}})$. The size s may be difficult to evaluate: for a sum of integers it will simply be the size of an integer, but for Eratosthenes sieve, the size of exchanged lists varies depending on which data are held by the node.

The sieve of Eratosthenes generates a list of prime numbers below a given integer n. From the list of all elements less than n, it iteratively removes elements that are a multiple of the smaller element of the list that has not been yet considered. We generate only the integers that are not multiple of the 4 first prime numbers, then we iterate $\sqrt{n}$ time (as it is known to be the maximum number of needed iterations). On our architectures Mirev2 and Mirev3 presented below, the direct and logarithmic scans are equally efficient.

Figure 4 gives the bsml code of the direct scan. We used the following functions:

which deletes from a list all the integers multiple of the given parameter;

iterates using elements from the first list to delete elements in the second;

which returns the list of integers between 2 bounds; and

which gives the $\sqrt{n}$ first prime numbers of a list.

For this naive example, we use a generic scan computation with as the $\oplus$ operator. In our computation, we also did extend the scan so that the sent values are first modified by a given function () to just send the $\sqrt{n}$ first prime numbers. The bsp methods is thus simple: each processor i holds the integers between $i \times \frac{n}{\mathbf {p}}+1$ and $(i+1) \times \frac{n}{\mathbf {p}}$. Each processor computes a local sieve (the processor 0 contains thus the first prime numbers) and then our is applied. We then eliminate on processor i the integers that are multiple of integers received from processors of lower identifier. Benchmark were done on two parallel architectures named Mirev2 and Mirev3. Here are the main specifications of these machines:

• Mirev2: 8 nodes with 2 quad-core (AMD 2376) at $2.3\,\hbox {Ghz}$ with $16\,\hbox {Gb}$ of memory per node and a $1\,\hbox {Gb/s}$ network.

• Mirev3: 4 nodes with 2 hyper-threaded octo-core (16 threads) (Intel XEON $E5-2650$) at $2.6\,\hbox {Ghz}$ with $64\,\hbox {Gb}$ of memory per node and a $10\,\hbox {Gb/s}$ network.

The multi-bsp and bsp model can be used to estimate the cost of an algorithm. We estimated the cost of transferring values and the sequential cost of summing lists of integers, then we used the multi-bsp parameters given in Table 3 in order to predict and compare the execution time of scan.

Table 3 Multi-BSP parameters of Mirev3 (left) and Mirev2 (right)

Table 4 Execution time (in sec.) of Eratosthenes using multi-ml and bsml on Mirev3

We measured the time to compute the sieve without the time to generate the initial list of values. The experiments have been done on Mirev2 and Mirev3 using bsml (mpi version) and multi-ml over lists of increasing size on an increasing number of processors. The processes have been assigned to machines in order to scatter as much as possible the computation among the machines, i.e. a 16 process run will use one core on each processor of the 8 machines of Mirev3. Tables 4 and 5 shows the results of our experimentations. We can see that the efficiency of multi-ml on small list is poor but as the list grows, multi-ml exceeds bsml. This difference is due to the fact that bsml communicates through the network at every super steps; while multi-ml is focusing on communications through local memories and finally communicates through the distributed level.

Table 6 gives the computation time of the simple scan using a summing operator. On the sum of integers, we can see that multi-ml introduces a small overhead due to the level management. However it is as efficient as bsml and concord to the estimated execution times. As the experiment shows, multi-ml out-performs bsml with communication intensive algorithms. The bsml program tends to saturate the network when all the processors start to communicate. On the contrary, the multi-ml algorithm avoid this bandwidth over consumption and takes advantage of the shared memory.

Table 5 Execution time (in sec.) of Eratosthenes using multi-ml and bsml on Mirev2

Table 6 Execution time (in sec.) and predictions of scan (sum of integers) on Mirev3

5 Related Work

There are a lot parallel languages or parallel extensions of sequential languages (functional, iterative, object-oriented, etc.). It would be too long to list all of them. We chose to point out those that were the most important to our mind. Notice that, except in [30], there is a lack of comparisons between parallel languages. It is difficult to compare them since many parameters have to be taken into account: efficiency, scalability, expressiveness, etc.

5.1 Programming Languages and Libraries for BSP Like Computing

Historically, the first library for bsp computing was the bsplib [24] for the c language; it has been extended in the pub library [4] by adding subgroup synchronisations, high performance operations and migration of threads. For the gpu architectures, a bsp library was provided in [26] with mainly drma primitives close to the bsplib’s ones. There is also MulticoreBSP [39] which proposes multi-bsp style programming features. For java, different libraries exist: the first one was [20], then in [12] a library has been designed with scheduling and migration of bsp threads—the scheduling is implicit but the migration can be explicit. The library hama [36] is implemented using a “mapreduce-like” framework. We can also highlight the work of neststep [27] which is c/java library for bsp computing, which brings nested computations capabilities in case of a cluster of multi-core but without any safety.

The bsml primitives were adapted for c++ [21]: the bsp++ library provides nested computation in the case of a cluster of multi-cores (mpi+open-mp). But it is the responsibility of the programmer to avoid harmful nested parallelism. bsml also inspired bsp-python [25] and bsp-haskell [33].

5.2 Functional Parallel Programming

A survey on parallel functional programming can be found in [23]. It has been used as a basis for the following classification with some updates.

Data-Parallel Languages The first functional one was nesl [3]. This language allows to create particular arrays and nested computations within these arrays. The abstract machine is responsible for the distribution of the data over the available processors. For ml, there is manticore [13], an extension of nesl with the dynamic creation of asynchronous threads and send/received primitives. For gpu architectures, an extension of ocaml, using a special syntax for the kernels has been developed in [5].

sac (Single Assignment c) [19] is a language (with a syntax close to c) for array processing. Some higher-order operations on multi-dimensional arrays are provided and the compiler is responsible for generating an efficient parallel code. A data-parallel extension of haskell has been done in [10] where the language allows to create data arrays that are distributed across the processors. And some specific operations permit to manipulate them.

The main drawback of all these languages is that cost analysis is hard to do since the system is responsible for the data distribution.

Explicit Process Creation We found two extensions of haskell in this category: eden [31] and gph [35]. Both use a small set of syntactic constructs for explicit process creation. Their fine-grain parallelism, while providing enough control to implement parallel algorithms efficiently, frees the programmer from the tedious task of managing low-level details of communications—which uses lazy shared data. Processes are automatically managed by sophisticated runtime systems for shared memory machines or distributed ones.

As above, cost analysis is hard to do and, sometimes, the runtime fails to distribute correctly the data [35]; it introduces too much communications and thus a lack of scalability. Another parallel language is hume [22]. The main advantage of this language is that it is provided with a cost analysis of the programs for real-time purpose but with limitations of the expressiveness.

Algorithmic Skeletons Skeletons are patterns of parallel computations [18]. They can be seen as high-order functions that provide parallelism. They thus fall into the category of functional extensions. They are many skeleton libraries [18]. For ocaml, the most known work is the one of [11].

Distributed Functional Languages In front of parallel functional languages, there are many concurrent extensions of functional languages such as erlang, clean or jocaml [32]. The latter is a concurrent extension of ocaml, which add explicit synchronisations of processes using specific patterns.

alice-ml [34] adds what is called a “future” for communicating values. A future is a placeholder for an undetermined result of a concurrent computation. When the computation delivers a result, the associated future is eliminated by globally replacing it by the result value. The language also contains “promises” that are explicit handles of futures. scala is a functional extension of java which provides concurrency, using the actor model: mostly, creation of agents that can migrate across resources. Two others extensions of ocaml are [8] and [9]. The former uses spmd primitives with a kind of futures. The latter allows migration of threads that communicate using particular shared data.

All these languages have the same drawbacks: they are not deadlock and race condition free; furthermore, they do not provide any cost model.

6 Conclusion and Future Work

6.1 Summary of the Contribution

The paper presents a language call multi-ml to program multi-bsp algorithms. It extends our previous bsml that has been designed for programming bsp algorithms. They both have the following advantages: confluent operational semantics; equivalence of the results for both toplevel and distributed implementation; cost model and efficiency.

The multi-bsp model extends the bsp one as a hierarchical tree of nested bsp machines. multi-ml extends bsml with a special syntax to define special recursive functions over this tree of nested machines, each of them programmed using bsml. In a tree, nodes contain codes to manage the sub-machines whereas leaves perform the largest part of the computation. In this work, we focus on the informal presentation of multi-ml, an operational semantics of a core-language and benchmarks of simple examples with a comparison with predicted performances associated with the multi-bsp cost model. We also compare multi-ml codes with bsml ones as well as the performances of both languages on a typical cluster of hyper-threaded multi-cores. As predicted, multi-ml codes run faster than bsml when the cores share the network: there is no bottleneck; And the multi-core synchronisations are cheaper.

Compared to bsml, multi-ml has several drawbacks. First, the codes, the semantics and the implementation are a bit more complex. Second, the cost model associated to the program is more difficult to grasp: designing multi-bsp algorithms and programming them in multi-ml is more difficult than using bsml only. However, from our experience, we can say that it is not so hard.

6.2 Future Work

In a near future we plan to axiomatise the multi-ml primitives inside coq, as we did for bsml in [15, 17], in order to prove the correctness of multi-bsp algorithms. We also consider to formally prove that the implementations follow the formal semantics. We also plan to benchmark bigger examples, we think of model-checking problems and algebraic computations that better follow high-level languages than intensive float operations can do.

The most important work to do is the implementation of a type system for multi-ml to ensure safety of the codes: forbid nesting of vectors, forbid data-races when imperatives features such as exceptions handling [16] are used. In the long term, the type system could be used to optimise the compiler. Indeed, currently, even in the case of a share-memory architecture, only serialised values are exchanged between nodes. We consider implementing a dedicated concurrent garbage collector.