Introduction

The equation of heat conduction is of the parabolic form, predicting infinite speeds of propagation for heat waves, and does not contain any elastic terms, according to the classical uncoupled theory of thermoelasticity. In order to solve the problem inherent in the traditional uncoupled hypothesis, Biot [1] defined the coupled thermoelasticity theory. To resolve this contradiction, a generalized theory with a finite speed of heat transfer in elastic solids (the hyperbolic heat transport equation) has been developed in recent years. Lord and Shulman (L–S) [2] provided this generalization theory, also referred to as the extended thermoelasticity theory, which only has one thermal relaxation time parameter. The first- and second-time derivatives of the strain are included in the Lord and Shulman energy equation. They considered a new law of heat conduction instead of the law of Fourier. Based on their theory, the linear correlation between temperature and heat flux includes temperature rate and thermal rates. According to this theory, the temperature propagation speed is finite due to the hyperbolic heat equation. Actually, as well known, the term “generalized” usually refers to thermodynamic theories based on hyperbolic (wave-type) heat equation, so that, a finite propagation speed for thermal signal is admitted. The generalized thermoelasticity has drawn extensive attention due to its applications in diverse fields, such as earthquake engineering, nuclear reactor design, and high-energy particle accelerators. Youssef [3] developed an isotropic elastic material with temperature-dependent mechanical and thermal properties that has a generalized thermoelasticity with the L–S theory. Bagri and Eslami [4] provide a one-dimensional generalized thermoelasticity model of a disk based on the L–S theory. L–S theory and linked theory were developed by Othman and Said [5, 6] to investigate the effects of rotation and a magnetic field on fiber-reinforced thermoelastic media. The L–S theory has lately been established in numerous studies covering a wide range of topics [7,8,9,10,11,12,13,14,15,16,17].

The nonlocal theory of elasticity was used to study applications in nano-mechanics including lattice dispersion of elastic waves, wave propagation in composites, dislocation mechanics, fracture mechanics, surface tension fluids, etc. Eringen [18] was interested in material bodies whose actions at any interior location depended on the conditions at all other sites within the body. The impact of harmonically fluctuating heat on FG nanobeams was demonstrated by Zenkour and Abouelregal [19] within the framework of a nonlocal two-temperature thermoelasticity theory. Yu et al. [20] examined size-dependent generalized thermoelasticity using Eringen's nonlocal model. In the context of the nonlocal theory, Ebrahimi et al. [21] examined the wave propagation properties in magneto-electro-elastic nanotubes while taking the shell model into consideration. The axisymmetric vibrational behavior of a size-dependent circular nano-plate with functionally graded material with different types of boundary conditions was investigated by Shariati et al. [22]. The authors Acharya and Mondal [23], Roy et al. [24], Zenkour [25], Bachher and Sarkar [26], Abouelregal and Mohammed [27], Zhou and Li [28], Kaur et al. [29], Gupta et al. [30], Said [31], Atta et al. [32], Yahya et al. [33], and Abouelregal et al. [34] have all published studies on nonlocal thermoelasticity.

Any study on the propagation waves in generalized thermoelasticity materials can be significant in structural engineering, geophysics, and seismology. Such a study becomes more realistic if the presence of gravity could be considered. In this study, a nonlocal thermoelastic solid with a moving internal heat source will be developed. Discussions covered location, temperature-dependent characteristics, and influences of the gravitational field. With the use of normal mode analysis, precise solutions to the physical field are obtained. The L–S theory was discussed in relation to the issue.

The Description of the Problem

A nonlocal thermoelastic solid that is affected by gravity field and has a moving internal heat source in the half-space \((\,x \ge 0\,)\,.\) The surface of the half-space is subjected to a thermal shock which is a function of \(x\) and \(z.\) Thus, all quantities are independent of \(y.\) The dynamic displacement \(\underline{u} = (u,0,\,w),\,\,\,v = 0,\,\,\,\,\,\,\,\,\frac{\partial }{\partial \,y} = 0\,.\)

The constitutive equations as presented by Hetnarski and Eslami [35] and Eringen [36]:

$$\left( {\,1 - \varepsilon^{2} \,\nabla^{2} } \right)\,\,\,\sigma_{ij} = \lambda \,e_{kk} \,\delta_{ij} + 2 \mu \,\,e_{ij} - \gamma \,\,\theta \,\delta_{ij\,} \,,$$
(1)

The heat conduction equation as Lord and Shulman [2]

$$K\,\,\nabla^{2} \theta = \left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\,\,\rho \,C_{E} \,\dot{\theta } + \gamma T_{0} \,\left( {1 + \tau_{0} \,\frac{\partial }{\partial t}} \right)\,\dot{e} - \left( {1 + \tau_{0} \,\frac{\partial }{\partial t}} \right)\,Q.$$
(2)

The equation of motion

$$\rho \,\ddot{u}_{i} = \sigma_{ji,\,j} + F_{i} ,$$
(3)

where \(F_{1} = \rho \,g\,\frac{\partial \,w}{{\partial \,x}},F_{2} = 0,F_{3} = - \rho \,g\,\frac{\partial \,u}{{\partial \,x}}.\)

According to Said [37]:

$$\mu = \mu_{0} \,(1 - \delta_{0} T_{0} )\,,\lambda = \lambda_{0} \,\,(1 - \delta_{0} T_{0} )\,,\gamma = \gamma_{0} \,\,(1 - \delta_{0} T_{0} )\,.$$
(4)

The case of the temperature-independent modulus of elasticity if \(\delta_{0} = 0\).

When Eqs. (1) and (4) are introduced in Eq. (3), we obtain

$$\,\rho \,(1 - \varepsilon^{2} \nabla^{2} )\,\,\ddot{u} = \,(1 - \delta_{0} T_{0} )\,\,\,\left( {(\lambda_{0} + 2\,\mu_{0} )\,\frac{{\partial^{{2}} u\,}}{{\partial \,x^{{2}} }} + (\lambda_{0} + \mu_{0} )\frac{{\partial^{{2}} w\,}}{\partial \,x\,\,\partial \,z\,} + \mu_{0} \,\,\frac{{\partial^{{2}} u\,}}{{\partial \,z^{{2}} }}} \right. - \left. {\gamma_{0} \,\,\frac{\partial \,\theta \,}{{\partial \,x}}} \right)\, + \,\rho g\,\,(1 - \varepsilon^{2} \nabla^{2} )\,\,\frac{\partial \,w\,}{{\partial \,x}},$$
(5)
$$\,\rho \,(1 - \varepsilon^{2} \nabla^{2} )\,\,\ddot{w} = \,\,(1 - \delta_{0} T_{0} )\,\left( {\,(\lambda_{0} + 2\,\mu_{0} )\,\frac{{\partial^{{2}} w\,}}{{\partial \,z^{{2}} }} + (\lambda_{0} + \mu_{0} )\frac{{\partial^{{2}} u\,}}{\partial \,x\,\,\partial \,z\,} + \mu_{0} \,\,\frac{{\partial^{{2}} w\,}}{{\partial \,x^{{2}} }}} \right.\left. { - \,\gamma_{0} \,\frac{\partial \,\theta \,}{{\partial \,z}}} \right)\,\, - \,\rho g\,\,(1 - \varepsilon^{2} \nabla^{2} )\,\,\frac{\partial \,u\,}{{\partial \,x}}.$$
(6)

We define the non-dimension variables as follows for convenience:

$$\begin{gathered} (x^{\prime},\,z^{\prime},\,\varepsilon^{\prime},\,u^{\prime},w^{\prime}) = \frac{1}{{l_{0} }}\,\,(x,\,z,\,\varepsilon ,u,\,w),g^{\prime} = \frac{{l_{0} }}{{d_{0}^{2} }}g,(t^{\prime},\,\tau_{0}{\prime} ) = \frac{{d_{0} }}{{l_{0} }}\,(t,\,\tau_{0} ),\theta^{\prime} = \frac{{\,\gamma_{0} \,\theta }}{{(\lambda_{0} + 2\mu_{0} )}}, \hfill \\ Q^{\prime} = \frac{{\,\gamma \,_{0} \,\,Q}}{{(\lambda_{0} + 2\mu_{0} )}},\sigma^{\prime}_{ij} = \frac{{\sigma_{ij} }}{{\mu_{0} \,(1 - \delta_{0} T_{0} )}}, \hfill \\ \end{gathered}$$
$$l_{0} = \sqrt {\frac{K}{{\rho \,C_{E} \,T_{0} \,\,}}} ,d_{0} = \sqrt {\frac{{\left( {\lambda_{0} + 2\mu_{0} } \right)\,\,(1 - \delta_{0} T_{0} )}}{\rho }} .$$
(7)

When Eqs. (7) are introduced in Eqs. (2), (5), and (6), we obtain

$$\,(1 - \varepsilon^{2} \nabla^{2} )\,\,\ddot{u} = \frac{{\partial^{{2}} u\,}}{{\partial \,x^{{2}} }} + \,(1 - \delta_{0} T_{0} )\,\,\left( {\frac{{\lambda_{0} + \mu_{0} }}{{\rho \,d_{0}^{2} }}\frac{{\partial^{{2}} w\,}}{\partial \,x\,\,\partial \,z\,} + \frac{{\mu_{0} }}{{\rho \,d_{0}^{2} }}\frac{{\partial^{{2}} u\,}}{{\partial \,z^{{2}} }}} \right) - \,\,\frac{\partial \,\theta \,}{{\partial \,x}} + \,\,g\,\,(1 - \varepsilon^{2} \nabla^{2} )\,\,\frac{\partial \,w\,}{{\partial \,x}},$$
(8)
$$\,\,(1 - \varepsilon^{2} \nabla^{2} )\,\,\ddot{w} = \,(1 - \delta_{0} T_{0} )\,\,\left( {\frac{{\mu_{0} }}{{\rho \,d_{0}^{2} }}\,\,\,\frac{{\partial^{{2}} w\,}}{{\partial \,x^{{2}} }} + \frac{{\lambda_{0} + \mu_{0} }}{{\rho \,d_{0}^{2} }}\frac{{\partial^{{2}} u\,}}{\partial \,x\,\,\partial \,z\,}} \right) + \frac{{\partial^{{2}} w\,}}{{\partial \,z^{{2}} }} - \frac{\partial \,\theta \,}{{\partial \,z}} - \,g\,\,(1 - \varepsilon^{2} \nabla^{2} )\,\,\frac{\partial \,u\,}{{\partial \,x}},\,$$
(9)
$$\,\nabla^{2} \theta = \frac{{\rho \,C_{E} \,d_{0\,} l_{0} }}{K}\,\,\left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\,\,\,\dot{\theta } + \frac{{\gamma^{2} \,T_{0\,\,} d_{0} \,l_{0} }}{K\,(\lambda + 2\mu )}\,\left( {1 + \tau_{0} \,\frac{\partial }{\partial t}} \right)\,\dot{e} - \frac{{l_{0}^{2} }}{K}\,\,\left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\,Q.$$
(10)

Normal Mode Analysis

The following normal modes can be used to decompose the solution of the physical variables under consideration:

$$\left( {\,u,w,\,\theta ,\,\sigma_{ij} \,} \right)\,\,(x,z,t) = \left( {\,u^{*} ,w^{*} ,\,\theta^{*} ,\,\sigma^{*}_{ij} \,} \right)\,\,(z)\exp \,\,\,\left( {mt + {\text{i}}\,\,a\,x} \right)\,,Q = \,Q^{*} \exp (m\,t + {\text{i}}\,a\,x),\quad Q^{*} = Q_{0} V_{0} ,$$
(11)

Introducing Eqs. (11) in Eqs. (8)–(10), we obtain

$$\left( {N_{1} \,D^{2} - N_{2} } \right)\,\,u^{*} + ia\,\left( { - g\,\varepsilon^{2} D^{2} + A_{1} D + N_{3} \,} \right)\,\,w^{*} - \,ia \, N_{4} \,\theta^{*} = 0,$$
(12)
$$ia\,\left( {g\,\varepsilon^{2} D^{2} + A_{1} D - N_{3} \,} \right)u^{*} + \,\left( {N_{5} \,D^{2} - N_{6} } \right)w^{*} - \,N_{4} D\,\theta^{*} = 0,$$
(13)
$$\,ia\,N_{7} u^{*} + N_{7} D\,w^{*} + \left( {N_{10} - \,D^{2} } \right)\theta^{*} = N_{9} ,$$
(14)

where \(\,D = \frac{d}{dz},\) \(N_{1} = \varepsilon^{2} m^{2} + \frac{{\mu_{0} \,(1 - \delta_{0} T_{0} )}}{{\rho \,d_{0}^{2} }},\) \(N_{2} = a^{2} + m^{2} (1 + a^{2} \varepsilon^{2} ),\) \(N_{3} = g\,(1 + a^{2} \varepsilon^{2} ),\) \(N_{4} = 1,\) \(N_{5} = \varepsilon^{2} m^{2} + 1,\) \(N_{6} = \frac{{\mu_{0} \,(1 - \delta_{0} T_{0} )}}{{\rho \,d_{0}^{2} }}\,\,a^{2} + m^{2} (1 + a^{2} \varepsilon^{2} ),\) \(N_{7} = \frac{{\gamma_{0}^{2} \,T_{0\,\,} d_{0} \,l_{0} }}{{K\,(\lambda_{0} + 2\mu_{0} )}}\,\,m\,(1 + m\tau_{0} ),\) \(N_{8} = \frac{{\rho \,C_{E} \,d_{0\,} l_{0} }}{K}m\,(1 + m\,\tau_{0} ),\) \(N_{9} = \frac{{Q_{0} \,V_{0} l_{0}^{2} }}{K}\,\,(1 + m\,\tau_{0} ),\) \(N_{10} = N_{8} + a^{2} .\)

By solving Eqs. (12)–(14), we obtain

$$\left( {D^{6} - C_{1} D^{4} + C_{2} D^{2} - C_{3} } \right)u^{*} (z) = - \frac{{iaN_{4} N_{6} N_{9} }}{{C_{0} }}.$$
(15)

The bound solution of Eq. (15) is:

$$u^{*} (z) = \sum\limits_{j = 1}^{3} {M_{j} } \,\exp ( - k_{j} z) + \frac{{iaN_{4} N_{6} N_{9} }}{{C_{0} C_{3} }}.$$
(16)

Similarly,

$$w^{*} (z) = \sum\limits_{j = 1}^{3} {H_{1j} \,M_{j} } \,\exp ( - k_{j} z) + \frac{{a^{2} N_{3} N_{4} N_{9} }}{{C_{0} C_{3} }},$$
(17)
$$\theta^{*} (z) = \sum\limits_{j = 1}^{3} {H_{2j} \,M_{j} } \,\exp ( - k_{j} z) + \frac{{a^{2} N_{3}^{2} N_{9} - N_{2} N_{6} N_{9} }}{{C_{0} C_{3} }}.$$
(18)

Using the above equations, we get

$$\sigma_{zz}^{*} (z) = \sum\limits_{j = 1}^{3} {H_{3j} \,M_{j} } \,\exp ( - k_{j} z) - C_{4} ,$$
(19)
$$\sigma_{xz}^{*} (z) = \sum\limits_{j = 1}^{3} {H_{4j} M_{j} } \,\exp ( - k_{j} z) + C_{5} ,$$
(20)

where \(k_{j}^{2} \,(\,j = 1,\,2,\,3\,)\) are the roots of the characteristic equation:\((\,k^{6} - C_{1} k^{4} + C_{2} k^{2} - C_{3} = 0\,).\)

$$C_{0} = g^{2} a^{2} \varepsilon^{4} - N_{1} N_{5} \,,C_{1} = \frac{1}{{C_{0} }}\left\{ \begin{gathered} \,2g\,N_{3} a^{2} \varepsilon^{2} + g^{2} a^{2} \varepsilon^{4} N_{10} + A_{1}^{2} a^{2} - N_{1} N_{4} N_{7} - N_{1} N_{6} - N_{2} N_{5} - \hfill \\ N_{1} N_{5} N_{10} \hfill \\ \end{gathered} \right\}\,,$$
$$C_{2} = \frac{1}{{C_{0} }}\left\{ \begin{gathered} \,2gN_{10} N_{3} a^{2} \varepsilon^{2} + 2A_{1} a^{2} N_{4} N_{7} + A_{1}^{2} a^{2} N_{10} + N_{3}^{2} a^{2} - N_{2} N_{4} N_{7} - \hfill \\ N_{2} N_{6} - N_{10} N_{1} N_{6} - N_{2} N_{5} N_{10} - a^{2} N_{4} N_{5} N_{7} \hfill \\ \end{gathered} \right\}\,,C_{3} = \frac{1}{{C_{0} }}\left\{ {\,N_{10} N_{3}^{2} a^{2} - N_{2} N_{6} N_{10} - a^{2} N_{4} N_{6} N_{7} } \right\}\,,$$
$$C_{4} = \frac{{N_{4} N_{9} (1 - \delta_{0} T_{0} )\,\,\left( {\lambda_{0} \,a^{2} N_{6} + (\lambda_{0} + 2\,\mu_{0} )(a^{2} N_{3}^{2} - N_{2} N_{6} )} \right)}}{{\mu_{0} \,C_{0} C_{3} (1 + \varepsilon^{2} a^{2} )}}\,,C_{5} = \frac{{i\,a^{3} N_{3} N_{4} N_{9} \,\,(1 - \delta_{0} T_{0} )\,}}{{\,C_{0} C_{3} (1 + \varepsilon^{2} a^{2} )}}\,,$$
$$H_{1j} = \frac{{N_{1} k_{j}^{3} - g\,a^{2} \varepsilon^{2} k_{j}^{2} + (a^{2} A_{1} - N_{2} )\,k_{j} + N_{3} a^{2} \,}}{{i\,a\,\,\left( {g\,\varepsilon^{2} k_{j}^{3} + (A_{1} - N_{5} )k_{j}^{2} - N_{3} k_{j} + N_{6} } \right)\,}}\,,H_{2j} = \frac{{N_{1} k_{j}^{2} - N_{2} + ia\,\,(\,N_{3} - A_{1} k_{j} - g\,\varepsilon^{2} k_{j}^{2} )\,\,H_{1j} }}{{i\,a\,N_{4} \,}}\,,$$
$$H_{3j} = \frac{{\,(1 - \delta_{0} T_{0} )\,\left[ {i\,a\,\lambda_{0} - (\,\lambda_{0} + 2\mu_{0} )\,\,\left( {k_{j} \,H_{1j} + N_{4} H_{2j} } \right)\,} \right]\,}}{{\mu_{0} \,\,(1 + \varepsilon^{2} a^{2} - \varepsilon^{2} k_{j}^{2} )}}\,,H_{4j} = \frac{{(1 - \delta_{0} T_{0} )\,\,(i\,a\,\,H_{1j} - k_{j} )}}{{1 + \varepsilon^{2} a^{2} - \varepsilon^{2} k_{j}^{2} }}\,.$$

The Boundary Conditions

In the physical problem, we should suppress the positive exponentials that are unbounded at infinity. To get the parameter \(M_{n} \,\,{(}n = {1,2,3)}\), the initial and regularity conditions are used to solve the present problem at \(\,z = 0,\) are

a. Thermal boundary condition that the surface of the half-space is subjected to a thermal shock

$$\theta = f_{1} f(x,\,t),$$
(21)

b. Mechanical boundary condition that the surface of the half-space is subjected to mechanical force

$$\sigma_{zz} = - f_{2} \,G(x,t),$$
(22)

c. Mechanical boundary condition that the surface of the half-space is traction-free

$$\sigma_{xz} = 0,$$
(23)

where \(f_{1} ,\,f_{2}\) are constants and \(f\,(x,\,t),\,\,G(x,\,t)\) are arbitrary functions.

We can find the following using Eqs. (18)–(20) in Eqs. (21)–(23):

$$\sum\limits_{j = 1}^{3} {\,H_{2j} M_{j} } = f_{1} \,,\sum\limits_{j = 1}^{3} {H_{3j} M_{j} } = - f_{2} + C_{4} ,\sum\limits_{j = 1}^{3} {H_{4j} M_{j} } = - C_{5} .$$
(24)

By solving the aforementioned system in Eq. (24), we obtain

$$\left( {\begin{array}{*{20}c} {M_{1} } \\ {M_{2} } \\ {M_{3} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {H_{21} } & {H_{22} } & {H_{23} } \\ {H_{31} } & {H_{32} } & {H_{33} } \\ {H_{41} } & {H_{42} } & {H_{43} } \\ \end{array} } \right)^{ - 1} \left( {\begin{array}{*{20}c} {f_{1} } \\ {C{}_{{_{4} }} - f_{2} } \\ { - C{}_{{_{5} }}} \\ \end{array} } \right).$$
(25)

We determine the values of the coefficients \(M_{j} (j = 1,\,2,\,3)\) by applying the inverse of the matrix approach of Eq. (25).

Validation and Applications

In the context of the L–S theory, we consider the numerical results for the physical constants as follows to compare the results for a nonlocal thermoelastic half-space solid with a moving internal heat source under the influence of the gravity field:

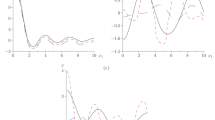
$$\begin{gathered} \lambda_{0} = 7.76 \times 10^{10} \,{\text{N m}}^{{ - {2}}} ,\quad \mu_{0} = 7.78 \times 10^{10} \,{\text{N m}}^{{ - {2}}} ,\quad \rho = 8954\,{\text{kg}} \times {\text{m}}^{{ - {3}}} ,\quad a = 0.5, \hfill \\ T_{0} = 293\,{\text{K,}}\quad C_{E} = 383.3\,{\text{J kg}}^{{ - {1}}} {\text{ K}}^{{ - {1}}} \,,\quad \alpha_{t} = 2.78 \times 10^{ - 3} {\text{ K}}^{ - 1} , \hfill \\ \end{gathered}$$
$$\begin{gathered} \tau_{0} = \,0.3\,{\text{s}},\quad f_{1} = 0.5{,}\quad f_{{2}} = 1.5;\quad K = 386\;{\text{w m}}^{{ - {1}}} {\text{ K}}^{{ - {1}}} {\text{ s}}^{{ - {1}}} {,}\quad m = m_{0} + i\xi {,} \hfill \\ m_{0} = - 0.3,\quad \xi = - 0.3,\quad Q_{0} = 3\,{\text{K}},\quad V_{0} = \,\,0.5\,{\text{m s}}^{ - 1} ,\quad x = - 0.5,\quad t = 0.5\,{\text{s}}\,{.} \hfill \\ \end{gathered}$$

Figures 1, 2, 3 and 4 display the vertical displacement distribution \(w,\) thermodynamic temperature distributions \(\theta ,\) and the stress components \(\sigma_{zz} ,\,\sigma_{xz}\) for the nonlocal thermoelastic media with different values of the gravity field \(g\). Figure 1 depicts the variation of vertical displacement distribution \(w\) begins with positive values. Values of \(w\) decrease in the range \(0 \le z \le 10\). With increasing the value of the gravity field \(g,\) values of \(w\) decrease. Figure 2 shows that the variation of thermodynmic temperature \(\theta\) begins with a positive value and obeys the boundary conditions. Values of \(\theta\) start with increasing attain their maximum values and then decrease. With increasing the value of \(g,\) values of \(\theta\) decrease. Figure 3 introduces that the variation of stress component \(\sigma_{zz}\) begins with a negative value and satisfies the boundary conditions. Values of \(\sigma_{zz}\) increase in the range \(0 \le z \le 10\). With increasing the value of \(g,\) values of \(\sigma_{zz}\) increase. Figure 4 depicts that the variations of stress component \(\sigma_{xz}\) begin from a zero value at \(z = 0\) and satisfy the boundary conditions. With increasing the value of \(g,\) values of \(\sigma_{xz}\) decrease.

Fig. 1
figure 1

Vertical displacement distribution \(w\) for different values of the gravity field

Full size image
Fig. 2
figure 2

Thermal temperature distribution \(\,\theta\) for different values of the gravity field

Full size image
Fig. 3
figure 3

Distribution of stress component \(\,\sigma_{zz}\) for different values of the gravity field

Full size image
Fig. 4
figure 4

Distribution of stress component \(\,\sigma_{xz}\) for different values of the gravity field

Full size image

Figures 5 and 6 display the horizontal displacement components \(u\) and thermodynamic temperature distributions \(\theta\) for the nonlocal thermoelastic media with different values of an empirical material constant \(\delta_{0} .\) Figure 5 depicts that the variation of horizontal displacement distribution \(u\) starting with positive values. Values of \(u\) decrease attain their minimum values in the range \(0 \le z \le 3\) and then increase in the range \(3 \le z \le 10\). With increasing the value of \(\delta_{0} ,\) values of \(u\) increase and then decrease. Figure 6 depicts that the variation of thermodynamic temperature \(\theta\) starting with a positive value. Values of \(\theta\) decrease in the range \(0 \le z \le 10\). With increasing the value of \(\delta_{0} ,\) values of \(\theta\) increase and then decrease.

Fig. 5
figure 5

Horizontal displacement distribution \(u\) for different values of an empirical material constant

Full size image
Fig. 6
figure 6

Thermal temperature distribution \(\,\theta\) for different values of an empirical material constant

Full size image

Figures 7 and 8 display the horizontal displacement components \(u\) and stress component \(\sigma_{xz}\) distributions for the thermoelastic media with different values of a nonlocal parameter \(\varepsilon .\) Figure 7 depicts that the variation of horizontal displacement distribution \(u\) starting with decreasing to reach its maximum values and then increases. The increasing of the value of \(\varepsilon\) causes decreasing values of \(u\) and then increases. Figure 8 depicts that the variations of stress component \(\sigma_{xz}\) begin from a zero value and obey the boundary conditions. The values of \(\sigma_{xz}\) attain their minimum values in the range \(0 \le z \le 0.5,\) then increase attain their maximum values in the range \(0.5 \le z \le 4,\) and again decrease. The increasing of the value of \(\varepsilon\) causes decreasing values of \(\sigma_{xz} .\) Figures 9 and 10 display 3D distributions of the non-dimensional thermal temperature \(\theta\) and stress component \(\sigma_{xz} .\) These figures are very important to study the dependence of these physical quantities on the vertical component of distance.

Fig. 7
figure 7

Horizontal displacement distribution \(u\) for different values of a nonlocal parameter

Full size image
Fig. 8
figure 8

Distribution of stress component \(\,\sigma_{xz}\) for different values of a nonlocal parameter

Full size image
Fig. 9
figure 9

Thermal temperature distribution \(\,\theta\) in three-dimensional

Full size image
Fig. 10
figure 10

Distribution of stress component \(\,\sigma_{xz}\) in three-dimensional

Full size image

Conclusion

The present theoretical results may provide interesting information and a mathematical foundation for working on the subject, because the increasing interest in the theory of thermoelasticity has many applications in such diverse fields as geophysics, acoustic wave damping in a magnetic field, machine element design of such equipment as heat exchangers, boiler tubes, nuclear devices emitting electromagnetic radiations, the development of magnetometers that are high in sensitivity and are super-conducting, the engineering of electrical power, plasma physics, etc. The new generalized nonlocal thermoelasticity model predicts novel characteristics for temperature, displacement, stresses, and strain. The conversations that have been held have led to the following conclusions:

  1. a.

    The nonlocal parameter plays a big part in how the physical fields are distributed.

  2. b.

    The distributions of the physical fields are significantly influenced by the gravity field.

  3. c.

    This impression supports the notion that the L–S theory is unquestionably a theory of generalized thermoelasticity.

  4. d.

    The physical fields are significantly impacted by the temperature-dependent characteristics.

  5. e.

    The physical fields are significantly impacted by the vertical distance.

  6. f.

    Even if a nonlocal thermoelastic medium is switched out for a thermoelastic one, the technique is still valid.