BLUP(REMQL) estimation of a correlated random effects negative binomial hurdle model

Abstract

Bed days is a potentially useful metric of efficiency in clinical studies involving the hospital admission decision. However, this metric involves excess zeros, possible overdispersion, and possible clustering (in multi-site studies). A random effects negative binomial hurdle model can account for each of these issues. We extend this model to include site-level correlation between the two component parts and implement best linear unbiased prediction-type estimation with restricted maximum quasi-likelihood. This approach offers computational advantages over maximum likelihood in a generalized linear mixed model setting. Simulations show that the proposed approach performs well for fixed effects and variance components under a plausible range of bivariate correlation. The Emergency Department Community Acquired Pneumonia study motivates this work and illustrates the methods.

1 Introduction

Community-acquired pneumonia (CAP) is a common, costly, and often fatal illness with more than 4 million episodes in the United States each year (Hsu et al. 2010). Providing quality and cost-effective care in patients with CAP has important economic and public health implications. The direct medical care costs of treating pneumonia are almost $10 billion per year, with the cost of inpatient treatment being 20 times higher than that of outpatient treatment (Fine et al. 2000; Niederman et al. 1998). Because inpatient cost is comprised mainly of the cost of hospitalizations, reducing the admission rate of low risk patients and reducing the length of stay (LOS) for inpatients with CAP could contribute substantially to medical care cost savings and efficient health care utilization (Fine et al. 2000). Measures of efficiency of care include the probability of outpatient treatment and LOS (Brown et al. 2003). An alternative measure of efficiency that includes both components is “bed days”, defined as zero for outpatients and LOS for inpatients, where LOS is the difference between discharge and admission dates (Wang et al. 2002). Bed days has problematic statistical characteristics, including excess zeros and possible overdispersion. In addition, clustering may be present, as in multi-site studies or repeat hospitalizations.

Finite mixture models, including zero-inflated models and hurdle models, commonly are used to allow for excess zeros. In a g-component Poisson mixture model, the number of components must be estimated (Schlattmann et al. 1996; Wang et al. 1996). For bed days, the number of components is known to be two, i.e., inpatients and outpatients. Although the zero-inflated and hurdle models accommodate counts with excess zeros (Cunningham and Lindenmayer 2005; Min and Agresti 2002; Ridout et al. 1998; Welsh et al. 1996), we will not consider zero-inflated models here because the zero-inflated model presumes that zeros can occur in both component distributions. Hurdle models have been used in economic applications and health care services (Arulampalam and Booth 1997; Gurmu 1998; Pohlmeier and Ulrich 1995). A hurdle model is a two-component mixture with a binomial part (probability of passing the “hurdle”) and a Poisson or negative binomial part. A hurdle model is more appropriate than a zero-inflated model for the outcome of bed days, because all patients are at risk for hospitalization when they present to a site (hospital), but zero bed days occur only among outpatients.

The hurdle model has been extended to account for clustering (e.g., by site) using maximum likelihood (ML) estimation in a generalized linear mixed model (GLMM) framework. ML estimation integrates out random effects from the joint likelihood using numerical approximations (Min and Agresti 2005). Although efficient, ML involves intensive computing and may not converge. In addition, ML can give biased estimates of variance components for random effects. An alternative method to estimate variance components in the GLMM setting, best linear unbiased prediction (BLUP)-type estimation with restricted maximum quasi-likelihood (REMQL), requires less integration and produces less biased estimates of variance components relative to ML (McGilchrist 1994; McGilchrist and Yau 1995). Although the BLUP(REMQL) approach has been used to estimate random effects in some finite mixture models (including zero-inflated models), it has not been implemented for the random effects hurdle model. A Bayesian approach also has been implemented to reduce small-sample bias and avoid asymptotic approximations or estimation of functions of parameters (Neelon et al. 2010). However, the Bayesian approach still is computationally intensive.

In this paper, we develop BLUP(REMQL) estimation for a correlated random effects hurdle model. We consider Poisson and negative binomial hurdle models and allow the binomial and count components to be correlated at the site level. In Sect. 2, we develop a procedure to estimate the fixed effect parameters. Estimation of the variance components is described in Sect. 3, and the scale parameter estimation is derived in Sect. 4. In Sect. 5, we apply the method to analyze bed days in the multi-site Emergency Department Community Acquired Pneumonia (EDCAP) study (Yealy et al. 2004, 2005). We describe a simulation study to investigate the validity of the proposed estimation procedure for the negative binomial hurdle model in Sect. 6. Section 7 concludes with a discussion.

2 Hurdle model with correlated random effects

Let Y _j (j = 1, 2, …, n) be the number of bed days for patient j, where the total number of patients is n. Because the Poisson hurdle model is a special case of the negative binomial hurdle model, we describe the negative binomial hurdle model here (Pohlmeier and Ulrich 1995).

$$ P(Y_{j} = 0) = p_{j}, $$

(1)

$$ P(Y_{j} = y_{j}|y_{j}>0) = (1-p_j)\cdot \frac{f(y_{j})}{1-f(0)}, $$

where p _j indicates the conditional probability of not passing the hurdle (i.e., not being hospitalized) given patient j is at risk for hospitalization and f is a negative binomial distribution.

This model was extended by Min and Agresti (2005) to include random effects. Let $Y_{ij}\; (i=1,2,\ldots,m;\; j=1,2,\ldots,n_i)$ be the number of bed days of patient j at site i, when m is the number of sites, n _i is the number of patients at site i, and the total number (n) of patients is ∑ ^m _i=1 n _i . Then, the negative binomial hurdle model with random effects is:

$$ P(Y_{ij} = 0) = p_{ij}, $$

(2)

$$ \begin{aligned} P(Y_{ij} = y_{ij}|y_{ij}>0) &= (1-p_{ij})\cdot \frac{f(y_{ij})}{1-f(0)} \\ &= (1-p_{ij}) \left(\begin{array}{l} y_{ij}+k-1 \\ y_{ij} \end{array}\right) \frac{t_{ij}^k(1-t_{ij})^{y_{ij}}}{1-t_{ij}^k}, \\ \end{aligned} $$

where p _ij indicates the conditional probability of not passing the hurdle given patient j at site i is at risk for hospitalization, μ _ij is the mean of the underlying negative binomial distribution, $y_{ij}!= y_{ij}\times (y_{ij}-1)\times \cdots \times 1, t_{ij} = ({k}/{k+\mu_{ij}})$, and k is the scale parameter (which is equal to 1/dispersion parameter). Note that the probability (p _ij ) can be modeled by logistic regression and f(y _ij )/1 − f(0) can be regarded as a truncated negative binomial distribution. When k goes to infinity, the negative binomial hurdle model reduces to the Poisson hurdle model. In the regression setting, both logit(p _ij ) and log(μ _ij ) are assumed to depend on linear functions of covariates. Following notation for the two-component mixture model in Wang et al. (2007), the linear predictors ξ _ij and η _ij are defined by

$$ {\rm logit}(p_{ij}) = \xi_{ij} = \user2{w}_{ij}^T\varvec{\alpha}+u_{i}, $$

(3)

$$ {\rm log}(\mu_{ij}) = \eta_{ij} = \user2{x}_{ij}^T\varvec{\beta}+v_{i}, $$

where $\user2{w}_{ij}$ and $\user2{x}_{ij},$ respectively, are vectors of covariates for the logistic and the negative binomial distributions, and $\varvec{\alpha}$ and $\varvec{\beta}$ are the corresponding vectors of coefficients. Here, u _i and v _i denote site-level random effects ($i=1,\ldots,m$), where $\user2{r}_{i}^T=(u_i, v_i)^T$ is assumed to be distributed as $N({\bf 0}, \user2{D})$ (i.e., a random intercept model). Given the site-level random effects, the two components (binomial part and negative binomial part) are assumed to be independent.

We introduce correlation between the binomial and count components through the covariance matrix $\user2{D}$ of $\user2{r}_i^T$ where

$$ \user2{D}= \left(\begin{array}{ll} \sigma_{u}^2& \rho\sigma_{u}\sigma_{v} \\ \rho\sigma_{u}\sigma_{v} & \sigma^2_{v} \end{array}\right), \qquad i=1,2,\ldots,m $$

(4)

and $\varvec{\rho}$ denotes a bivariate correlation between the random effects. In the case of uncorrelated random effects, ρ = 0, $\user2{u}$ and $\user2{v}$ are assumed to be independently distributed as N(0, σ ² _u I _m ) and N(0, σ ² _v I _m ) respectively, where I _m denotes an m × m identity matrix. In the uncorrelated case, the logistic regression and negative binomial regression components can be estimated separately. Estimation must be done jointly in the correlated case.

We adapt the framework of McGilchrist (1994) and McGilchrist and Yau (1995) to develop BLUP(REMQL) estimation of the negative binomial hurdle model with random effects and correlated components. The joint BLUP-type loglikelihood of Y _ij and $\user2{r}_i$ can be written as $\ell(\user2{y}, \user2{r}) = \ell_1(\user2{y}|\user2{r}) + \ell_2(\user2{r})$, where

$$ \begin{aligned} \ell_1(\user2{y}|\user2{r}) =& \sum_{i=1}^m \sum_{j=1}^{n_i} [ {\rm I}(y_{ij}=0){\rm log} (p_{ij}) + (1-{\rm I}(y_{ij}=0)){\rm log}(1-p_{ij}) \\ &+ (1-{\rm I}(y_{ij}=0)) \{ {\rm log} \frac{\Upgamma (y_{ij}+k)}{\Upgamma (y_{ij}+1) \Upgamma (k)}+k {\rm log} (t_{ij}) \\ &+ y_{ij} {\rm log}(1-t_{ij})-{\rm log}(1-t_{ij}^k) \} ], \\ \ell_2(\user2{r}) =& {\rm constant}-\frac{1}{2}\sum_{i=1}^m\left[ {\rm log}(|\user2{D}(\varvec{\phi})|)+\user2{r}_i^T \user2{D}(\varvec{\phi})^{-1} \user2{r}_i \right], \\ \end{aligned} $$

(5)

and ${\rm I}(\cdot)$ represents a binary indicator function, $\user2{y}$ denotes a vector of y _ij , and $\user2{r} = (\user2{r}_1^T,\user2{r}_2^T,\ldots,\user2{r}_m^T)$. Here, $\ell_1(\user2{y}|\user2{r})$ is the loglikelihood function when the random effects are conditionally fixed and $\ell_2(\user2{r})$ indicates the penalty function for the conditional loglikelihood. First, coefficients ($\varvec{\alpha},\varvec{\beta}$) in the linear predictors are estimated for fixed variance components and fixed scale parameter by maximizing (5). Then, the variance component parameters $\varvec{\phi} = (\sigma_{u},\sigma_{v},\rho$) can be estimated using REMQL estimating equations. The scale parameter k, which is assumed to be given in estimation of the regression coefficients ($\varvec{\alpha}, \varvec{\beta}$), also is obtained and updated by maximizing a profile loglikelihood with the current estimates. Estimation can be done iteratively via the Newton–Raphson (N–R) algorithm. Suppose $\varvec{\xi} = \user2{W}\varvec{\alpha} + \user2{R}\user2{u}$ and $\varvec{\eta} = \user2{X}\varvec{\beta} + \user2{R}\user2{v}$ where $\varvec{\theta} = (\varvec{\alpha}^T,\varvec{\beta}^T,\user2{r}^T)^T$ is the vector of unknown parameters of interest, and $\user2{R}$ is a design matrix for the random components. In the initial step, coefficients in the linear predictor ($\varvec{\alpha},\varvec{\beta},\user2{r}$) are estimated given initial values $\varvec{\theta}_0$ by

$$ \hat{\varvec{\theta}} = \varvec{\theta}_0 + \user2{V}^{-1} \frac{\partial\ell}{\partial\varvec{\theta}}, \qquad \user2{V} = - \frac{\partial^2\ell}{\partial\varvec{\theta}\partial\varvec{\theta}^T}, $$

(6)

where $\user2{V}$ denotes the negative second derivatives of the BLUP-type loglikelihood (ℓ) with respect to $\varvec{\theta}.$ Details of these derivations are given in Appendix 1. The inverse of the matrix of negative second derivatives of the BLUP-type loglikelihood $\user2{V}^{-1}$ can be written as

Asymptotic variances of $\hat{\varvec{\alpha}}$ and $\hat{\varvec{\beta}}$ are obtained from the corresponding components $\user2{V}_{\varvec{\alpha}}^*$ and $\user2{V}_{\varvec{\beta}}^*$ of $\user2{V}^{-1}.$

3 Variance component estimation

When the N–R algorithm was used to estimate linear predictors in Sect. 2, the variance components were assumed to be known. Actually, they need to be estimated and updated in each iteration of the N–R algorithm. The approximate REMQL estimators ($\hat{\varvec{\phi}}_{REMQL}$) of variance components can be obtained by solving the REMQL estimating equation (McGilchrist and Yau 1995) as follows:

$$ tr \left(\user2{A}^{-1} \frac{\partial\user2{A}}{\partial\varvec{\phi}} \right) + tr\left( \user2{V}_{\user2{r}}^*\frac{\partial\user2{A}^{-1}}{\partial\varvec{\phi}} \right) + \user2{r}^T \user2{r}\frac{\partial\user2{A}^{-1}}{\partial\varvec{\phi}} = 0. $$

(7)

Note that

$$ \frac{\partial\user2{D}}{\partial\sigma_u} = \left(\begin{array}{ll} 2\sigma_u &\rho\sigma_v \\ \rho\sigma_v & 0 \end{array}\right), \qquad \frac{\partial\user2{D}}{\partial\sigma_v} = \left(\begin{array}{ll} 0 & \rho\sigma_u \\ \rho\sigma_u & 2\sigma_v \end{array}\right), \qquad \frac{\partial\user2{D}}{\partial\rho} = \left(\begin{array}{ll} 0 & \sigma_u\sigma_v \\ \sigma_u\sigma_v & 0, \end{array}\right), \\ $$

(8)

and

$$ \begin{aligned} \frac{\partial\user2{D}^{-1}}{\partial\sigma_u} &= \frac{1}{\sigma_u^3 \sigma_v^2 (1-\rho^2)}\left(\begin{array}{ll} -2\sigma_v^2 & \rho\sigma_u\sigma_v \\ \rho\sigma_u\sigma_v & 0 \end{array}\right), \\ \frac{\partial\user2{D}^{-1}}{\partial\sigma_v} &= \frac{1}{\sigma_u^2 \sigma_v^3 (1-\rho^2)}\left(\begin{array}{ll} 0 & \rho\sigma_u\sigma_v \\ \rho\sigma_u\sigma_v & -2\sigma_u^2 \end{array}\right), \\ \frac{\partial\user2{D}^{-1}}{\partial\rho} &= \frac{1}{\sigma_u^2 \sigma_v^2 (1-\rho^2)^2}\left(\begin{array}{ll} 2\rho\sigma_v^2 & -(1+\rho^2)\sigma_u\sigma_v \\ -(1+\rho^2)\sigma_u\sigma_v & 2\rho\sigma_u^2 \end{array}\right). \end{aligned} $$

(9)

After substituting with (8) and (9) in (7), the exact equations for the variance components (σ _u , σ _v , ρ) are:

$$ \begin{aligned} &\sum_{i=1}^m [ 2\sigma_u^2 \sigma_v^2(1-\rho^2)-2\sigma_v^2 v_{ii,11} + \sigma_u\sigma_v\rho(v_{ii,12}+v_{ii,21}+2u_i v_i)-2\sigma_u^2 u_i^2 ] = 0, \\ &\sum_{i=1}^m [-2\sigma_u^2 \sigma_v^2 (1-\rho^2)-2\sigma_u^2 (v_{ii,22}+v_i^2) +\sigma_u\sigma_v\rho(v_{ii,12}+v_{ii,21}+2u_i v_i) ] = 0, \\ &\sum_{i=1}^m [-2\sigma_u^2 \sigma_v^2 \rho(1-\rho^2)+2\rho\sigma_v^2 v_{ii,11} +2\sigma_u^2 (v_{ii,22}+u_i^2+v_i^2)- \sigma_u\sigma_v(1+\rho^2)(v_{ii,12}\\ &\quad +v_{ii,21}+2u_i v_i) ] = 0, \\ \end{aligned} $$

(10)

where v _ii denotes the 2 × 2 block matrix portion of $\user2{V}_{\user2{r}}^*$ corresponding to $\user2{r}_i$ and $v_{ii}=\left(\begin{array}{ll} v_{ii,11} & v_{ii,12} \\ v_{ii,21} & v_{ii,22} \end{array}\right).$ The variance components can be estimated using the N–R algorithm.

4 Scale parameter estimation

The estimation via the N–R algorithm in Sect. 2 assumed that the scale parameter k was known. In practice, k is updated and estimated in each iteration in accordance with the updated estimates of $\varvec{\alpha}, \varvec{\beta}, \user2{r}, \sigma_u, \sigma_v$ and ρ by maximizing the profile loglikelihood function:

$$ \begin{aligned} \ell_k &= \sum_{i=1}^m \sum_{j=1}^{n_i} \left[ {\rm I}(y_{ij}=0){\rm log}(p_{ij})+(1-{\rm I}(y_{ij}=0)){\rm log}(1-p_{ij}) \right.\\ &+ (1-{\rm I}(y_{ij}=0)) \left\{ {\rm log}\frac{\Upgamma (y_{ij}+k)}{\Upgamma (y_{ij}+1) \Upgamma(k)} + k{\rm log}(t_{ij}) + y_{ij}{\rm log}(1-t_{ij}) \right.\\ &\left. \left.-{\rm log}(1-t_{ij}^k) \right\}\right]. \\ \end{aligned} $$

(11)

The asymptotic variance of $\hat{k}$ can be obtained by $Var(\hat{k}) = (-\frac{\partial^2\ell_k}{\partial k^2})^{-1};$ details are given in Appendix 2.

5 Application to the EDCAP study

We illustrate the models by analyzing bed days in the 32-site EDCAP study (Yealy et al. 2004, 2005). EDCAP is a cluster-randomized trial in CT and PA to assess the effectiveness and safety of 3 guideline implementation interventions of low (8 sites), moderate (12 sites), and high (12 sites) intensity to increase the proportion of low risk patients who were treated as outpatients. Risk was ascertained using a validated measure of pneumonia severity, the Pneumonia Severity Index (PSI) (Yealy et al. 2005), with low risk defined as PSI ≤ 3 without hypoxemia.

In the EDCAP study, we examine whether the distribution of bed days varies by intervention arm and PSI risk class among 1,877 low risk patients with clinical and radiographic evidence of pneumonia. Among eligible low risk patients, 57 % (n = 1,061) were treated as outpatients and 43 % (n = 816) were treated as inpatients; 37 % of patients had PSI = 1, 37 % of patients had PSI = 2, and 26 % of patients had PSI = 3 (Table 1). Relatively fewer low risk patients at the low intensity intervention sites were treated as outpatients (38 % vs. 62 % at the moderate intensity and 63 % at the high intensity intervention sites).

Table 1 Probability of outpatient, mean and median of inpatients and overall bed days by PSI risk class and by intervention arm for 1,877 eligible low risk patients

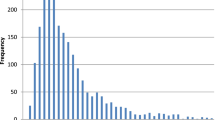
Figure 1 shows the empirical distribution of bed days for patients in each PSI risk class by intervention arm. The spikes at zero bed days represent outpatients; in each intervention arm, the prevalence of outpatient care decreases with increasing risk class. The distributions at the moderate and high intensity intervention sites are right skewed; both had more outpatients and fewer inpatient bed days than did the low intensity intervention sites.

Fig. 1

Bed days by intervention arm and PSI risk class

In the modeling of bed days, the patient-level PSI risk class and the site-level intervention arm were included as dummy variables; with PSI2 = 1 if PSI = 2; 0 else, PSI3 = 1 if PSI = 3; 0 else, Mod = 1 if moderate intensity intervention; 0 else, and High = 1 if high intensity intervention; 0 else. The Poisson/negative binomial hurdle model with random effects is:

$$ \begin{aligned} {\rm logit}(p_{ij}) &= \alpha_0 + \alpha_1 \cdot {\rm PSI}2 + \alpha_2 \cdot {\rm PSI}3+ \alpha_3 \cdot {\rm Mod} + \alpha_4 \cdot {\rm High} + u_i, \\ {\rm log}(\mu_{ij}) &= \beta_0 + \beta_1 \cdot {\rm PSI}2 + \beta_2 \cdot {\rm PSI}3 + \beta_3 \cdot {\rm Mod} + \beta_4 \cdot {\rm High} + v_i, \\ \end{aligned} $$

(12)

where (u _i , v _i )^T is assumed to be distributed as $N({\bf 0},\user2{D})$ when the covariance matrix $\user2{D}$ is defined in (4) with $i=1,\ldots,32$.

Table 2 summarizes the ML and BLUP(REMQL) estimates for the random effects Poisson hurdle model. The fixed effects estimates and standard errors (SE) are almost identical between the two estimation methods for both components of the model. The estimated bivariate correlation between the two components is low (−0.01 for ML; −0.04 for BLUP(REMQL)).

Table 2 Correlated random effects Poisson hurdle model estimates based on (a) ML and (b) BLUP(REMQL) estimation

ML and BLUP(REMQL) estimates for the negative binomial hurdle model are shown in Table 3. Except possibly for k, these estimates are quite similar to each other for both components. The log odds ratio (log OR) of outpatient care decreases significantly with increasing risk class, with log ORs of −1.47 and −2.51 for PSI2 and PSI3, respectively, and increases significantly for the moderate and high intensity intervention sites, with log ORs of 0.97 and 0.91, respectively. The scale parameter (k = 2.71) indicates significant overdispersion relative to the Poisson distribution. The estimated bivariate correlation is modest (−0.10). The P values for the PSI parameters in the count component of the model are less significant in the negative binomial hurdle model than in the Poisson hurdle model, due to the correction for overdispersion.

Table 3 Correlated random effects negative binomial hurdle model estimates based on (a) ML and (b) BLUP(REMQL) estimation

Figure 2 illustrates the better fit of the negative binomial hurdle model than the Poisson hurdle model to the EDCAP data. To identify unusual sites based on the random effects negative binomial hurdle model, the predicted site-level random effects are plotted for the logistic and the negative binomial parts in Fig. 3. Site 25 appears to be unusual in that it is a moderate intensity intervention site with a low predicted probability of treating low risk patients as outpatients. In addition, Fig. 3 indicates that there is more site-level variation in the logistic part (i.e., hospitalization decision) than in the negative binomial part (i.e., LOS).

Fig. 2

Observed vs predicted distribution of bed days by intervention arm. Distributions are predicted based on the Poisson hurdle model (dots) and negtive binomial hurdle model (dashed line)

Fig. 3

Site specific predicted random effects for the logistic and negative binomial parts of the negative binomial hurdle model for the low (open circle), moderate (closed triangle), and high (closed circle) intensity intervention sites

6 Simulation study

We conducted simulation studies to compare the performance of the proposed BLUP(REMQL) to ML in the correlated random effects negative binomial hurdle model with a plausible range of bivariate correlations. We imitated the unbalanced cluster-randomized structure of the EDCAP data and included patient-level (PSI1, PSI2, PSI3) and site-level covariates (Low, Mod, High). PSI1 and Low intensity intervention served as the reference levels. For each of the m = 32 sites, n _i patients were randomly generated from a Poisson distribution. Based on the estimates in Table 3, $\varvec{\alpha}$ was specified as (0.8, −1.5, −2.5, 1.0, 0.9), $\varvec{\beta}$ was specified as (1.3, 0.1, 0.4, −0.1, 0.1), k = 2.6, σ _u  = 0.6, σ _v  = 0.2, and ρ took one of the following values (−0.1, −0.3, −0.5, −0.7). We used 1,000 replications for each of the four simulated settings.

In Table 4, we summarized one randomly chosen simulated dataset to show how well our simulated data replicated the EDCAP data structure summarized in Table 1. Figure 4 confirms that the cumulative distributions of observed and simulated bed days are almost identical.

Table 4 Probability of outpatient, mean and median of inpatients bed days, and mean and median of overall bed days by PSI risk class and by intervention arm for one simulated dataset (N = 1,823)

Fig. 4

Cumulative density function of bed days by EDCAP data (closed circle) and one simulated dataset (open circle) with ρ = −0.1

Results of the simulation studies (Table 5) verify the performance of the proposed BLUP(REMQL) estimation in the negative binomial hurdle model. We report the average bias, the bias relative to the true parameter (Percent), SE, mean square error (MSE), and coverage probability (CP) of the 95 % confidence interval over 1,000 replications for each value of ρ considered. The biases in the estimated fixed effects generally were small (≤3.0 %) for both ML and BLUP(REMQL) for both the logistic and negative binomial components of the model for all values of ρ considered. The exceptions were somewhat larger biases (4.0–8.5 %) in some of the ML and/or BLUP(REMQL) estimated site-level parameters (i.e., Mod or High) in the negative binomial component when ρ = −0.5 or −0.7. Biases in the estimated fixed effects generally (but not always) were smaller for ML than for BLUP(REMQL). The SEs and the corresponding MSEs of the estimated fixed effects were similar for ML and BLUP(REMQL), and the CPs were generally at least as good, if not better, for BLUP(REMQL) relative to ML.

Table 5 Simulation results using correlated random effects negative binomial hurdle model based on ML and BLUP(REMQL) estimation with 1,000 replications and a plausible range of bivariate correlation (ρ = −0.1, −0.3, −0.5, −0.7)

The BLUP(REMQL) estimates of the random effects (σ _u and σ _v ) and ρ have much smaller biases than the corresponding ML estimates; for example, the percent bias is 1.5 % vs. 6.5 % for σ _u , 1.5 % vs. 11.0 % for σ _v , and 3.0 % vs. 63.0 % for ρ, Table 5a. However, the BLUP(REMQL) estimate of the scale parameter (k) in the negative binomial component has larger bias than the corresponding ML estimate (e.g., 8.8 % vs. 1.5 % in Table 5a), and poorer CP (e.g., 0.90 vs. 0.96). Similar patterns were observed for the other values of ρ.

In summary, these simulation results demonstrate that BLUP(REMQL) estimation in the negative binomial hurdle model with correlated random effects performs well relative to ML for the fixed effects and variance components considered, but not for the scale parameter. All replications converged for BLUP(REMQL), while some did not converge for ML (i.e., 10/1000 replications at ρ = −0.3; 26/1000 replications at ρ = −0.5; 91/1000 replications at ρ = −0.7). BLUP(REMQL) ran in about 3/7 the time as ML for these simulated data. We used the SAS procedure NLMIXED to fit the model with ML, and R to obtain the BLUP(REMQL) estimates.

7 Discussion

We have proposed a BLUP(REMQL) approach to estimate a negative binomial hurdle model with correlated random effects. We also illustrated the application of this model to a potentially useful efficiency metric in health services studies, bed days. This model appropriately accounts for excess zeros and overdispersion relative to the Poisson distribution, and allows for site-level correlation between the binary and count components of the model. This model gives an overall assessment of the effect on an intervention on two aspects of care, e.g., admission and LOS in the EDCAP study. While the interventions in EDCAP were designed to influence the admission decision and recommended processes of care in the ED, there was no intervention to influence inpatient LOS. Our results confirmed that the intervention was significantly associated with reduced hospitalization but not with LOS. The small negative bivariate correlation indicates some tendency for shorter inpatient LOS at sites with relatively low admission rates for low risk patients. Although not well-illustrated by the EDCAP study, our proposed approach could give more efficient estimates of random effects in a similarly-designed study with interventions that affected both components of the model.

In this paper, we have accounted for correlated random effects at the site level that could be associated with both the hospitalization decision and inpatient LOS. The EDCAP intervention was limited to low-risk patients, so that the predominant factors driving the hospitalization decision in these patients are site-level (e.g., practice patterns, guideline compliance, quality and/or efficiency of care) rather than patient level characteristics. We can extend this model to patient-level correlated random effects by defining a multivariate normal distribution of random effects.

For the scenarios considered, our simulation study indicated that the BLUP(REMQL) approach provides less biased estimates of variance components than ML, and estimates similar to ML for the fixed effects. However, BLUP(REMQL) estimation yields somewhat larger bias in the estimated scale parameter relative to ML. This issue requires further investigation. BLUP(REMQL) estimation remains attractive because it ran faster than ML for these data and had better convergence properties. For either BLUP(REMQL) or ML, the choice of initial values affects convergence rates and computation time. To guarantee the convergence and reduce computation time, we initialized parameter estimates by fitting fixed effect hurdle models. Our simulations mimicked the structure of the EDCAP data and that additional simulations would need to be done to assess the sensitivity of (BLUP)REMQL to initial values.

We can implement ML simply using SAS. In the absence of generally available software, adapted R code is required to obtain the BLUP(REMQL) estimates considered here. A flexible alternative is Bayesian estimation, which can be implemented using WinBUGS (Neelon et al. 2010).

In summary, the proposed BLUP(REMQL) estimation in these hurdle models appears to be promising. The computational advantages may facilitate application of this approach to more complex versions of these models, such as a 3-level model defined by patient, medical provider, and site.

Appendices

Appendix 1: First and second derivatives of the joint BLUP-type loglikelihood

From the joint BLUP-type loglikelihood, we can obtain:

$$ \begin{aligned} \frac{\partial\ell}{\partial\varvec{\alpha}} &= \user2{W}^T\frac{\partial\ell_1}{\partial\varvec{\xi}},\qquad \frac{\partial\ell}{\partial\varvec{\beta}}=\user2{X}^T\frac{\partial\ell_1}{\partial\varvec{\eta}},\qquad \frac{\partial\ell_1}{\partial\user2{u}}=\user2{R}^T\frac{\partial\ell_1}{\partial\varvec{\xi}},\qquad \frac{\partial\ell_1}{\partial\user2{v}}=\user2{R}^T\frac{\partial\ell_1}{\partial\varvec{\eta}}, \\ \frac{\partial\ell}{\partial\user2{r}} &= \left(\begin{array}{ll} \frac{\partial\ell_1}{\partial\user2{u}} \\ \frac{\partial\ell_1}{\partial\user2{v}} \end{array}\right) \user2{G} -\user2{A}^{-1}\user2{r}, \\ \end{aligned} $$

(13)

where a 2m × 2m matrix (G) satisfies $\left(\begin{array}{ll} \user2{u} \\ \user2{v} \end{array}\right) G = \user2{r}$ and $\user2{A}=[\user2{D},\user2{D},\ldots,\user2{D}]$ denotes a 2m × 2m block diagonal matrix. Now,

$$ \begin{aligned} \frac{\partial\ell_1}{\partial\xi_{ij}} &= {\rm I}(y_{ij}=0)-\frac{e^{\xi_{ij}}}{1+e^{\xi_{ij}}}, \\ \frac{\partial\ell_1}{\partial\eta_{ij}} &= (1-{\rm I}(y_{ij}=0)) \left\{ y_{ij}\frac{k}{k+e^{\eta_{ij}}} - \frac{k(1-\frac{k}{k+e^{\eta_{ij}}})}{1-(\frac{k}{k+e^{\eta_{ij}}})^k} \right\}. \end{aligned} $$

(14)

The second derivatives of the joint BLUP-type loglikelihood are obtained as follows:

$$ \begin{aligned} \frac{\partial^2\ell}{\partial\varvec{\alpha}\partial\varvec{\alpha}} &= \user2{W}^T\frac{\partial^2\ell_1}{\partial\varvec{\xi}\partial\varvec{\xi}^T}\user2{W}, \\ \frac{\partial^2\ell}{\partial\varvec{\beta}\partial\varvec{\beta}^T}&=\user2{X}^T\frac{\partial^2\ell_1}{\partial\varvec{\eta}\partial\varvec{\eta}}\user2{X}, \\ \frac{\partial^2\ell}{\partial\varvec{\alpha}\partial\varvec{\beta}^T} &= \user2{W}^T\frac{\partial^2\ell_1}{\partial\varvec{\xi}\partial\varvec{\eta}^T}\user2{X}, \\ \end{aligned} $$

(15)

$$ \begin{aligned} \frac{\partial^2\ell}{\partial\varvec{\alpha}\partial\user2{r}^T} &= \left( \user2{W}^T\frac{\partial^2\ell_1}{\partial\varvec{\xi}\partial\varvec{\xi}^T}\user2{R}, \user2{W}^T\frac{\partial^2\ell_1}{\partial\varvec{\xi}\partial\varvec{\eta}^T}\user2{R} \right)\user2{G}, \\ \frac{\partial^2\ell}{\partial\varvec{\beta}\partial\user2{r}^T} &= \left( \user2{X}^T\frac{\partial^2\ell_1}{\partial\varvec{\xi}\partial\varvec{\eta}^T}\user2{R}, \user2{X}^T\frac{\partial^2\ell_1}{\partial\varvec{\eta}\partial\varvec{\eta}^T}\user2{R} \right)\user2{G}, \\ \frac{\partial^2\ell}{\partial\user2{r}\partial\user2{r}^T} &= \user2{G}^T \left(\begin{array}{ll} \user2{R}^T\frac{\partial^2\ell_1}{\partial\varvec{\xi}\partial\varvec{\xi}^T}\user2{R} & \user2{R}^T\frac{\partial^2\ell_1}{\partial\varvec{\xi}\partial\varvec{\eta}^T}\user2{R}, \\ \user2{R}^T\frac{\partial^2\ell_1}{\partial\varvec{\xi}\partial\varvec{\eta}^T}\user2{R} & \user2{R}^T\frac{\partial^2\ell_1}{\partial\varvec{\eta}\partial\varvec{\eta}^T}\user2{R} \end{array}\right)\user2{G}-\user2{A}^{-1}, \\ \end{aligned} $$

where

$$ \frac{\partial^2\ell_1}{\partial\varvec{\xi}\partial\varvec{\xi}^T} = \hbox {Diag} \left[ -\frac{e^{\xi}}{(1+e^{\xi})^2} \right], $$

(16)

$$ \begin{aligned} \frac{\partial^2\ell_1}{\partial\varvec{\eta}\partial\varvec{\eta}^T} &= \hbox {Diag} \left[ -(1-{\rm I}(\user2{y}=0))t(1-t)\left\{ \user2{y} - \frac{k^2(1-t)t^{k-1}-k(1-t^k)}{(1-t^k)^2} \right\} \right], \\ \frac{\partial^2\ell_1}{\partial\varvec{\xi}\partial\varvec{\eta}^T} &= 0. \\ \end{aligned} $$

Appendix 2: First and second derivatives of the profile loglikelihood

Following Lee et al. (2003), suppose $A(k) = \sum_{y_{ij}>0} {\rm log} \frac{\Upgamma (y_{ij}+k)}{\Upgamma (y_{ij}+1) \Upgamma (k)},$ and $f(\tau)= \# \left\{ y_{ij}\geq\tau, \forall i,j \right\}$ be the number of patients whose observed count is greater than or equal to τ, then the first and second derivatives of A(k) are derived as:

$$ \begin{aligned} \dot{A(k)} &= \sum_{\tau=1}^{max(y_{ij})-1} \frac{f(\tau)}{k+\tau}, \\ \ddot{A(k)} &= -\sum_{\tau=1}^{max(y_{ij})-1} \frac{f(\tau)}{(k+\tau)^2}. \\ \end{aligned} $$

(17)

Then, the first and second derivatives of ℓ _k can be expressed in terms of $\dot{A(k)}$ and $\ddot{A(k)}{:}$

$$ \begin{aligned} \frac{\partial\ell_k}{\partial k} &= \dot{A(k)} + \sum_{y_{ij}>0} { \frac{B_{ij}}{1-t_{ij}^k} - \frac{y_{ij}t_{ij}}{k} }, \\ \frac{\partial^2\ell_k}{\partial k^2} &= \ddot{A(k)} + \sum_{y_{ij}>0} \frac{\dot{B_{ij}}(1-t_{ij}^k)+B_{ij}^2 t_{ij}^k}{(1-t_{ij}^k)^2} +\frac{y_{ij}t_{ij}^2}{k^2}, \\ \end{aligned} $$

(18)

where

$$ B_{ij} = {\rm log}(t_{ij}) + 1 - t_{ij} \qquad \hbox {and} \qquad \dot{B_{ij}} = \frac{(1-t_{ij})^2}{k}. $$

(19)