Regression modeling of one-inflated positive count data

Abstract

This paper extends regression modeling of positive count data to deal with excessive proportion of one counts. In particular, we propose one-inflated positive (OIP) regression models and present some of their properties. Also, the stochastic hierarchical representation of one-inflated positive poisson and negative binomial regression models are achieved. It is illustrated that the standard OIP model may be inadequate in the presence of one inflation and the lack of independence. Thus, to take into account the inherent correlation of responses, a class of two-level OIP regression models with subjects heterogeneity effects is introduced. A simulation study is conducted to highlight theoretical aspects. Results show that when one-inflation or over-dispersion in the data generating process is ignored, parameter estimates are inefficient and statistically reliable findings are missed. Finally, we analyze a real data set taken from a length of hospital stay study to illustrate the usefulness of our proposed models.

1 Introduction

Related to the structure of count data, several regression models, such as the negative binomial (NB) and its zero-inflated version (e.g., Yau et al. 2003; Garay et al. 2011) are introduced in the literature. In practical applications, the positive poisson (PP) regression model is also being used to analyze positive, or zero-truncated, count outcomes (e.g., Matthews and Appleton 1993; Xie and Aickin 1997; Zuur et al. 2009). A useful modeling strategy in the presence of over-dispersion in zero-truncated data is addressed by Sampford (1955) and then is extended by many others, such as Gurmu (1991). Some properties of the positive negative-binomial (PNB) distribution is given by Lee et al. (2003). Other count regression models are also introduced to allow over-dispersion caused by unobserved heterogeneity and excess zeros produced by rare event occurrences. Various popular approaches to deal with these issues are often verified based on zero-inflated poisson (Lambert 1992) and zero-inflated NB models (e.g., Yau et al. 2003). Recently, Lim et al. (2014) propose a zero-inflated poisson mixture model for heterogeneous count data with excess zeros. An extensive review of the related literature on the NB model including a number of applications taken from a wide variety of disciplines is provided by Hilbe (2011).

The application of count data has been extensively discussed by many authors and variety of regression models are proposed to analyze certain real-life count data sets (e.g., Gschlößl and Czado 2008; Cordeiro et al. 2012). In our knowledge, in almost all proposed cases, there is currently a gap in the existing research literature when the count response exhibits excess frequency of ones while analyzing positive outcomes. These features have motivated the introduction of new regression models for count data. Thus, we first introduce an alternative regression model, namely the one-inflated positive poisson (OIPP), to deal with occurrence of excess ones. It is discussed that over-dispersion may be the result of excess ones or some other causes. If extra variation remains even after handling excess ones, we then introduce the one-inflated positive negative-binomial (OIPNB) regression model. This model allows the variance to be larger than the mean through an additional parameter to handle over-dispersion. In general, the proposed models are shown to be constructed by a mixed strategy such that it mixes a distribution degenerated at one with a baseline PP or a NB distribution. Hence, this paper provides a useful approach in modeling positive count outcomes focusing mainly on data that exhibits over-dispersion.

In fitting zero-truncated count models, one-inflation and the lack of independence may exist simultaneously as a consequence of the inherent correlation structure and the underlying heterogeneity. Thus, this paper introduces a two-level OIP regression model as an alternative to handle clustered observations. This extension is motivated by methodologies addressed in fitting zero-inflated models (e.g., Hall 2000; Wang et al. 2002; Hur et al. 2002).

A simulation study is conducted to illustrate the importance of modeling strategies for one-inflation in positive counts and to show the impact of models mis-specification. The simulation is designed for two OIPP and OIPNB models. The average root mean squared error (RMSE) is used to assess the overall performance of estimates, while the average model bias is used to assess the impact of correctly identifying the OIPP or the OIPNB models on statistical inference.

The data set we re-analyze in this paper is originally taken from the US national Medicare inpatient hospital database which is prepared yearly from hospital filing records. Several researchers used these count data and fitted some models mainly without any concern on the positiveness of counts. In specific, Hardin and Hilbe (2007) and Hilbe (2011) fitted poisson and NB models. They also analyzed the data set using the zero-truncated version of poisson and NB models. In the present paper we fit the proposed OIPP and OIPNB regression models and report that these are better fitted to the data.

The rest of paper is organized as follows. Section 2 introduces the OIP distribution and highlights some of its properties. Specifically, we derive the probability mass function of the OIP distribution in general, and find its corresponding recursive formula. Specific properties of the OIPP and OIPNB distributions are provided as special cases. Section 3 introduces OIP regression models and derives associated likelihood equations. Also, the stochastic hierarchical form of the OIPP and OIPNB distributions are achieved. Section 4 proposes a two-level OIP regression model with heterogeneity effects to address fitting of correlated data. A simulation study for large samples is conducted in Sect. 5 to highlight theoretical aspects. Section 6 aims to analyze length of stay in hospital data.

2 The specification of OIP distributions

Motivation to introduce OIP distributions arises originally from the fact that a variety of positive or zero-truncated count data involves excess ones. Here, the one and subsequent counts are generated by different mechanisms.

Definition 1

Let for each subject Y, a Bernoulli trial be used to determine two data generating processes for only a one response, with probability p, and a positive distribution, with probability 1$-$ p, for subsequent counts. This introduces the probability mass function (pmf) of OIP random variable as

$$\begin{aligned} f_{\textit{OIP}}\left( 1\right)= & {} p+\left( 1-p\right) f_{P}\left( 1\right) , \nonumber \\ f_{\textit{OIP}}\left( Y=y\right)= & {} \left( 1-p\right) f_{P}\left( y\right) ,~~\ \ \ \ y=2,3,\cdots , \end{aligned}$$

(1)

where $f_{P}\left( y\right) =P(Y=y)$ denotes the pmf of a positive count at point y.

In general, the pmf of a positive count is derived in terms of its underlying un-truncated distribution. That is, for a given un-truncated pmf, $f\left( y\right)$, we have $f_{P}\left( y\right) =\pi f\left( y\right)$ for $y=1,2,\cdots$, where $\pi =(1-f(0))^{-1}$ with $\pi >1$. Putting this in Eq. (1) gives the OIP pmf. The OIP poisson and OIP NB distributions are two special cases of the family of OIP distributions though the OIPNB can be thought to arise as an extension of either the PNB or the OIPP distributions.

The pmf of an OIPP random variable Y is defined by setting $f_{P}(\cdot )$ in Eq. (1) to

$$\begin{aligned} f_{\textit{PP}}\left( y\right) =\pi _{P}\frac{\exp \left( -\mu \right) ~\mu ^{y}}{y! },~~y=1,2,\cdots , \end{aligned}$$

(2)

where $\pi _{P}=(1-\exp \left( -\mu \right) )^{-1}$. We denote $Y\sim \textit{OIPP}(\mu , p)$.

Similarly, for the pmf of an OIPNB we set $f_{P}(\cdot )$ in (1) to

$$\begin{aligned} f_{\textit{PNB}}\left( y\right) =\pi _{\textit{NB}}\frac{\Gamma (y+\kappa )}{\Gamma (\kappa )\Gamma (y+1)} t^{\kappa }\left( 1-t\right) ^{y},~~y=1,2,\cdots , \end{aligned}$$

(3)

where $t =\frac{\kappa }{\kappa +\mu }$, $\pi _{\textit{NB}}=\left( 1-t^{\kappa }\right) ^{-1}$, and $\mu$ denotes the mean of corresponding NB distribution. We denote $Y\sim \textit{OIPNB}(\kappa ,\mu , p)$.

Let Y follows an OIP distribution. Some basic properties of the family of OIP distributions are shown below in which any clear proof is omitted.

• i. The cumulative distribution function (cdf) is

  $$\begin{aligned} F_{\textit{OIP}}(y) = p + (1-p) \pi \left\{ F(y)-F(0) \right\} , \end{aligned}$$

  (4)

  where $F\left( \cdot \right)$ is the cdf of un-truncated count distribution.

• ii. Let M(r) be a moment generating function (mgf) which exists for all values r and $F\left( 0\right)$ be a probability at zero of a un-truncated count distribution. Then the mgf is

  $$\begin{aligned} M_{\textit{OIP}}\left( r\right) = pe^{r} +\left( 1-p\right) \pi \left\{ M\left( r\right) -F\left( 0\right) \right\} . \end{aligned}$$

  (5)

• iii. Provided that $M_{\textit{OIP}}\left( r\right)$ exists in a neighbourhood of $r=0$, the m-th moment of Y is given by

  $$\begin{aligned} E_{\textit{OIP}}\left( Y^{m}\right)= & {} p+\left( 1-p\right) \pi E\left( Y^{m}\right) ,~\ \ \ \ \ \ m=1,2,3,\cdots , \end{aligned}$$

  (6)

  where it is assumed that $E\left( Y^{m}\right) <\infty$.

• iv. For all values r which the expected value exists, the probability generating function (pgf) G of Y is defined as follows

  $$\begin{aligned} G_{\textit{OIP}}\left( r\right) = pr+\left( 1-p\right) \pi \left\{ G\left( r\right) -F\left( 0\right) \right\} , \end{aligned}$$

  (7)

  where $G\left( r\right)$ is the pgf of un-truncated count distribution.

• v. Provided that $G_{\textit{OIP}}\left( r\right)$ exists in a neighbourhood of $r=1$, the m-th factorial moment is given by

  $$\begin{aligned} E_{\textit{OIP}}\left\{ \left( Y\right) _{m}\right\}= & {} {\left\{ \begin{array}{ll} p+\left( 1-p\right) \pi E\left( Y\right) ,~\ \ \ \ \ \ m=1 \\ \left( 1-p\right) \pi E\{ \left( Y\right) _{m}\} ,~\ \ \ \ \ \ m=2,3,\cdots , \end{array}\right. } \end{aligned}$$

  (8)

  showing that there is a linear relationship between $E_{\textit{OIP}}\{\left( Y\right) _{m}\}$ and the m-th factorial moment of the un-truncated distribution, e.g. $E\left\{ \left( Y\right) _{m}\right\} =\mu ^{m}$ for poisson and $E\left\{ \left( Y\right) _{m}\right\} =\frac{\Gamma \left( \kappa +m\right) }{\Gamma \left( \kappa \right) }\left( \frac{\mu }{\kappa }\right) ^{m}$ for the NB distribution.

• vi. Let the recursive equation for an un-truncated distribution be

  $$\begin{aligned} f\left( y+1\right) =C\left( \varvec{\theta }, y\right) f\left( y\right) , ~~y=0,1,\cdots , \end{aligned}$$

  (9)

  where $\varvec{\theta }$ denotes corresponding parameters vector and $C\left( \varvec{\theta } ,y\right)$ be a known function of $\varvec{\theta }$ and y. Then,

  $$\begin{aligned} f_{P}\left( y+1\right) =C(\varvec{\theta } ,y)f_{P}\left( y\right) , \end{aligned}$$

  for $y=1,2,\cdots$. Similarly

  $$\begin{aligned} f_{\textit{OIP}}\left( y+1\right) =C(\varvec{\theta } ,y)f_{\textit{OIP}}\left( y\right) , \end{aligned}$$

  (10)

  for $y=2,3,\cdots$. To see this, for $y=1,2,\cdots$, multiplying Eq. (9) by $\pi$ gives a recursive equation of positive random variable. For $y=2,3,\cdots$, multiplying Eq. (9) by $\pi \left( 1-p\right)$ gives a recursive equation of the OIP random variable.

• vii. The expectation and variance are shown to be

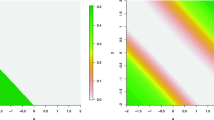
  $$\begin{aligned} E_{\textit{OIP}}\left( Y\right)= & {} p+\left( 1-p\right) ~\pi E\left( Y\right) , \nonumber \\ Var_{\textit{OIP}}\left( Y\right)= & {} p+\left( 1-p\right) \pi \left\{ Var\left( Y\right) +E^{2}\left( Y\right) \right\} -E_{\textit{OIP}}^{2}\left( Y\right) , \end{aligned}$$

  (11)

  where E(Y) and Var(Y) are, respectively, the mean and variance of the underlying un-truncated distribution, e.g., $E(Y)=Var(Y)=\mu$ for poisson and $E(Y)=\mu$, $Var\left( Y\right) =\mu \left\{ 1+\frac{\mu }{\kappa }\right\}$ for the NB distribution. In Fig. 1 we have provided a comparison between the variance and expectation of the OIP models to illustrate evidence of how they deal with over-dispersion or under-dispersion. Figures display the difference $d_{\textit{OIP}}\left( p\right) =Var_\mathbf{OIP }\left( Y\right) -E_{\textit{OIP}}\left( Y\right)$, as a function of p, for the OIPP and OINB distributions. When the quantity $d_{\textit{OIP}}\left( p\right)$ is positive (negative) then the OIP distribution carries out over-dispersion (under-dispersion). Specifically, Fig. 1a indicates that the quantity $d_{\textit{OIP}P}\left( p\right)$ is positive for some values of $\mu$ over the interval $p\in (p_{0},p_{1}]$ for some $p_{0}$ and $p_{1}$, which shows over-dispersion, whereas is negative outside of these intervals showing under-dispersion. In our case, using some numerical approaches to solve $d_{\textit{OIPP}}\left( p\right) =0$ we obtain $p_{0}=0.142,0.036$ and $p_{1}=0.749, 0.890$ for $\mu =3,4$, respectively. Also, Fig. 1a illustrates that the OIPP may always handle under-dispersion for some values of $\mu$, e.g., 2. We also observe in Fig. 1a that as p tends to 0 the OIPP becomes equivalent to the PP model which is known to display under-dispersion (Winkelmann (2008). chap. 5). Besides, Fig. 1b confirms that the OIPNB cannot always cover over-dispersion while the proportion of ones, p, gets some large values.

Fig. 1

Differences between the variance and expectation of a the OIPP and b the OIPNB distributions

Example 1

Suppose that Y follows an OIPP distribution then we obtain

$$\begin{aligned} G_{\textit{OIPP}}\left( r\right) =pr+\left( 1-p\right) \frac{\exp (\mu r) -1}{\exp (\mu )-1}, \end{aligned}$$

(12)

and

$$\begin{aligned} f_{\textit{OIPP}}\left( y+1\right) =\frac{\mu }{y+1}f_{\textit{OIPP}}\left( y\right) , ~y=2,3,\cdots .\ \end{aligned}$$

(13)

Example 2

Let Y be distributed as an OIPNB then

$$\begin{aligned} G_{\textit{OIPNB}}\left( r\right) =pr+\left( 1-p\right) \pi _{\textit{NB}} t^{\kappa }\left\{ \frac{1}{\left[ 1-r\left( 1-t\right) \right] ^{\kappa }}-1\right\} , \end{aligned}$$

(14)

for $\left| r\right| <\frac{1}{1-t}$. Also,

$$\begin{aligned} f_{\textit{OIPNB}}\left( y+1\right) =\frac{\left( \kappa + y \right) \mu }{\left( \mu +\kappa \right) \left( y+1\right) }f_{\textit{OIPNB}}\left( y\right) , ~y=2,3,\cdots . \end{aligned}$$

(15)

Proposition 1

The OIPNB reduces to the OIPP distribution as $\kappa \rightarrow \infty$.

Proof

Tending $\kappa$ to infinity, we obtain $\pi _{\textit{NB}}\rightarrow \pi _{P}~$, where $\pi _{\textit{NB}}$ and $\pi _{P}$ are previously defined. Also, the pmf of $\textit{NB}\left( \kappa ,\frac{\kappa }{\kappa +\mu }\right)$ tends to $f_{pois}\left( \mu \right)$. Then Proposition (1) is proved. $\square$

Thus the OIPP is a special case of the OIPNB distribution. Figure 2a confirms the result for $p=0.5$ and $\mu =1$. Using the graphical techniques we provide more comparisons between two distributions. Figure 2b shows the difference $d(y) =$ $f_{\textit{OIPNB}}(y)$ $-f_{\textit{OIPP}}( y)$, for $\kappa =0.5, 1, 2$, $\mu =1$ and $p=0.5$. The comparison is performed for same means, i.e., a re-parametrization is done accordingly to make means equal. We see that the sign pattern of d$\left( y\right)$ is$~\{+,-,+\}$ as y  increases on its support. The inequality $f_{\textit{OIPNB}}\left( 1\right)$ $> f_{\textit{OIPP}}\left( 1\right)$ holds showing that for a large number of ones the OIPNB density is more appropriate than the OIPP density with the same mean. Similar pattern was additionally seen for other different values of parameters. An expectation was illustrated for $\kappa$ closed to zero showing that the third sign was closer to zero.

Fig. 2

a Probability mass functions of the OIPNB and OIPP b Differences between the OIPNB and OIPP densities, d(y) c Probability of an one outcome as p increases d Probability of an one outcome as $\mu$ increases

The influence of other parameters on the probability of an one outcome is illustrated as follows. Let Y be distributed as OIPP or OIPNB, then an increase in $\mu$ reduces the probability of an one outcome and an increase in p increases the probability of an one outcome. These results were obtained readily by the differentiation of $f_{\textit{OIPNB}}\left( 1\right)$ (or $f_{\textit{OIPP}}\left( 1\right)$) with respect to all model parameters. Figure 2c, d confirm these results. By setting $\mu =\kappa =1$, Fig. 2c shows that as p increases the probability of an one outcome increases. Similarly by putting $p=0.5$ and $\kappa =1$, Fig. 2d shows that as $\mu$ increases the probability of an one outcome decreases.

3 The specification of OIP regression models

Let the $Y_{i}$ ($i=1,2,\cdots ,n$) be independent responses, distributed as OIP and the i-th subject is associated with a m-dimensional vector $\mathbf {x}_{i}$ of covariates. In fitting related regression models, covariates are typically incorporated using the link function $log\left( \mu _{i}\right) =\mathbf{x}_{i}^{\prime }{\varvec{\beta }}$, where ${\varvec{\beta }}$ is an m-dimensional vector of coefficients. Also a logistic scheme is used to account for predicting $p_{i}$, i.e. $log\left( \frac{p_{i}}{1-p_{i}}\right) =\mathbf{w}_{i}^{\prime }\varvec{\gamma }$, where $\mathbf w_{i}$ and $\varvec{\gamma }$ denote k-dimensional vectors of covariates and coefficients, respectively. Note that the logistic models answer the question that how a covariate which induces change in $\mu _{i}$ affects the probability of one. The complete data likelihood is given by

$$\begin{aligned} L\left( \varvec{\theta ,\gamma ;y}\right) =\prod \limits _{y_{i}=1}\left\{ p_{i}+\left( 1-p_{i}\right) f_{P}\left( y_{i}\right) \right\} \prod \limits _{y_{i}>1}\left( 1-p_{i}\right) f_{P}\left( y_{i}\right) , \end{aligned}$$

(16)

where $\varvec{\theta }$ denotes a parameter vector of the associated positive distribution which includes $\varvec{\beta }$. Under independent sampling scheme, taking the first derivative of the log-likelihood function gives the likelihood equations

$$\begin{aligned} \frac{\partial l\left( \varvec{\theta ,\gamma ;y}\right) }{\partial \varvec{\gamma }}=\sum _{i=1}^{n}\frac{1-f_{P}\left( 1\right) }{p_{i}+\left( 1-p_{i}\right) f_{P}\left( 1\right) } p_{i}\left( 1-p_{i}\right) \mathbf{w}_{i}-\sum _{i=1,y_{i}>1}^{n}p_{i}\mathbf{w}_{i}, \end{aligned}$$

(17)

and

$$\begin{aligned} \frac{\partial l\left( \varvec{\theta ,\gamma ;y}\right) }{\partial \varvec{ \theta }}=\sum _{i=1}^{n}\frac{S_{P}\left( \varvec{\theta } ,1\right) }{p_{i}+\left( 1-p_{i}\right) f_{P}\left( 1\right) }+\sum _{i=1,y_{i}>1}^{n}\frac{ S_{P}\left( \varvec{\theta } ,y_{i}\right) }{f_{P}\left( y_{i}\right) }, \end{aligned}$$

(18)

where $S_{P}\left( \varvec{\theta } ,\cdot \right)$ denotes the first partial derivative of the pmf with respect to $\varvec{\theta }$, and P denotes any positive distribution, such as poisson and the NB. The above likelihood equations are given generally for every underlying distribution of the OIP count outcomes. Deriving the maximum likelihood estimates (MLEs) of model parameters from Eqs. (17) and (18) requires implementing advanced numerical techniques, such as Newton-Raphson. To obtain local maxima, the Hessian matrix, i.e., the matrix of second derivatives, has to be negative definite. After some algebraic operations are performed, the second derivatives of the log-likelihood, $\frac{\partial ^{2}l\left( \varvec{\theta ,\gamma ;y}\right) }{\partial {\varvec{\theta }}{\varvec{\theta }^\prime }}$, $\frac{\partial ^{2}l\left( \varvec{\theta ,\gamma ;y}\right) }{\partial \varvec{\theta }\partial \varvec{\gamma }}$ and $\frac{\partial ^{2}l\left( \varvec{\theta ,\gamma ;y}\right) }{\partial {\varvec{\gamma }}^{2}}$ can readily be obtained but they are not tractable and available in closed forms. Thus details are omitted to save space. To solve likelihood equations simultaneously we recommend the use of optimization procedures in statistical software packages, such as NLP or NLIN in SAS, or, NLM in R. They are capable to report parameter estimates, their standard errors, and further statistical measures.

Corollary 1

Under independent sampling scheme and setting the PP density to $f_{P}$ in (16), the MLE of $\varvec{\beta }$ is found by solving Eq. (18) and putting

$$\begin{aligned} S_{Pois}\left( \varvec{\beta },y_{i}\right) =\left( y_{i}-{\mu _{i}\pi _{i,P}}\right) \mathbf{x}_{i}. \end{aligned}$$

Corollary 2

Denote P in (16) the PNB distribution and let $\varvec{\theta }=\left( \varvec{\beta },\kappa \right)$. Under independent sampling scheme likelihood equations are derived by setting

$$\begin{aligned} S_{\textit{NB}}\left( \kappa , y_{i} \right) =\frac{\left( 1-t_{i}\right) ^{2}}{\mu _{i} }\left\{ \sum _{j=0}^{y_{i}-1}\left( j+\kappa \right) ^{-1}+\frac{\kappa }{t_{i}}-\frac{y_{i}}{1-t_{i}}+\pi _{i,\textit{NB}}\kappa t_{i}^{\kappa -1}\right\} , \end{aligned}$$

(19)

for parameter $\kappa$ and

$$\begin{aligned} S_{\textit{NB}}\left( \varvec{\beta }, y_{i} \right) =\left\{ y_{i}t_{i}-\pi _{i,\textit{NB}}\kappa \left( 1-t_{i}\right) \right\} \mathbf{x}_{i}, \end{aligned}$$

(20)

for parameter $\varvec{\beta }$.

Letting a logistic regression model for predicting $p_{i}$ the use of advanced numerical maximization methods are required to solve the first order conditions for $\mathbf \beta ,\gamma$ and $\kappa$.

Proposition 2

Let the $Y_{i}$ ($i=1,2,\cdots ,n$) be independent count variables that each follows the OIPP or OIPNB distribution. Then an increase in the covariate $\mathbf {x}_{i}$ reduces the probability of an one outcome provided that the associated regression coefficient, $\varvec{\beta }$, is positive, and increases it otherwise. Also, the covariate $\mathbf {z}_{i}$ in the logit model is directly related to the probability of an one outcome. That is, as the value of $\mathbf {z}_{i}$ increases (decreases) the probability of an one outcome increases (decreases) for positive $\varvec{\gamma }$.

Proof

In the OIPP model

$$\begin{aligned} \frac{\partial }{\partial \mu _{i}}f_{\textit{OIPP}}\left( 1\right) =\left( 1-p_{i}\right) {\pi _{i,P}^{2}}~exp{ \left( -\mu _{i}\right) }\left\{ 1-\mu _{i}-\exp (-\mu _{i})\right\} , \end{aligned}$$

(21)

and in the OIPNB model

$$\begin{aligned} \frac{\partial }{\partial \mu _{i}}f_{\textit{OIPNB}}\left( 1\right) =\left( 1-p_{i}\right) t_{i}^{\kappa } (1-t_{i})\pi ^2_{i,\textit{NB}}\left\{ t_{i}\left( \kappa +1\right) -t_{i}^{\kappa +1}-\kappa \right\} . \end{aligned}$$

(22)

To show the effect of a change in covariate ${\mathbf {x}}_{i}$ when $\mu _{i}=\exp \left( \mathbf {x}_{i}^{\prime }\varvec{\beta }\right)$, we use the chain rule which obliged the above expressions to be multiplied by $\frac{\partial }{\partial x_{ij}}\mu _{i}=\mu _{i}\beta _{j}$, where $\beta _{j}$ is an element in the vector $\varvec{\beta }$ corresponding to $\mathbf {x}_{i}$. Equations (21) and (22) are negative thus the effect at the probability of one is negative. An increase in $x_{ij}$ reduces the probability of an one outcome if $\beta _{j}>0$, and increases it otherwise. Similarly, the derivative with respect to the covariate $z_{ij}~$ for the OIPP regression model is given by

$$\begin{aligned} \frac{\partial }{\partial z_{ij}}f_{\textit{OIPP}}\left( 1\right) =\left\{ 1-\pi _{i,P}~\mu _{i}\exp {\left( -\mu _{i}\right) }\right\} \frac{\exp \left( -\varvec{z}_{i}^{\prime }\varvec{\gamma }\right) }{\left\{ 1+\exp \left( -\varvec{z}_{i}^{\prime }\varvec{\gamma }\right) \right\} ^{2}}\gamma _{j}, \end{aligned}$$

(23)

and for the OIPNB model is

$$\begin{aligned} \frac{\partial }{\partial z_{ij}}f_{\textit{OIPNB}}\left( 1\right) =\left\{ 1-\pi _{i,\textit{NB}}\kappa t_{i}^{\kappa }\left( 1-t_{i}\right) \right\} \frac{\exp \left( -\varvec{z}_{i}^{\prime }\varvec{\gamma }\right) }{\left\{ 1+\exp \left( -\varvec{z}_{i}^{\prime }\varvec{\gamma }\right) \right\} ^{2}}\gamma _{j}, \end{aligned}$$

(24)

where $\gamma _{j}$ is an element in $\varvec{\gamma }$. Since signs of expressions (23) and (24) are positive thus $\gamma _{j}$ has a positive effect on the probability of one. That is, an increase in $z_{ij}$ increases the probability of an one outcome when $\gamma _{j}$ $>0$, and reduces it otherwise. $\square$

In below we introduce new stochastic hierarchical representations for both OIPP and OIPNB models. These are shown to be mixtures of known distributions that assist researchers to generate variants of these models or enable them to use in Bayesian approaches.

Theorem 1

Let the $Y_{i}$, $i=1,...,n$, be independent counts. Consider the hierarchical representation

$$\begin{aligned}&Y_{i}|\omega _{i},u_{i}\overset{ind}{\sim }poisson\left( \mu _{i}\left( 1-\omega _{i}\right) +\log \left( 1-u_{i}\mu _{i}^{*}\right) \right) , \end{aligned}$$

(25)

$$\begin{aligned}&\omega _{i}\overset{iid}{\sim }Bern\left( p\right) , \end{aligned}$$

(26)

$$\begin{aligned}&u_{i}\overset{iid}{\sim }Unif\left( 0,1\right) , \end{aligned}$$

(27)

where $u_{i}$ and $\omega _{i}$ are mutually independent and $\mu _{i}^{*}=1-\exp \left\{ -\mu _{i}\left( 1-\omega _{i}\right) \right\}$. Then the shifted count variable $Y_{i}+1$ is distributed as $OIPP\left( \mu _{i},p\right)$.

Proof

By integrating out the $u_{i}$ from the joint density of $\left( Y_{i},\omega _{i},u_{i}\right)$ we can directly show that

$$\begin{aligned} f\left( y_{i}|\omega _{i}\right) =\frac{\left\{ \mu _{i}\left( 1-\omega _{i}\right) \right\} ^{y_{i}+1}e^{-\mu _{i}\left( 1-\omega _{i}\right) }}{ \left( y_{i}+1\right) !\mu _{i}^{*}},~~y_{i}=0,1,\cdots . \end{aligned}$$

(28)

Furthermore,

$$\begin{aligned} f\left( y_{i}\right) =pf\left( y_{i}|\omega _{i}=1\right) +\left( 1-p\right) f\left( y_{i}|\omega _{i}=0\right) . \end{aligned}$$

It is easy to show that $f\left( y_{i}|\omega _{i}=1\right)$ takes 1 for $y_{i} = 0$ and zero otherwise and $f\left( y_{i}|\omega _{i}=0\right)$ is of the form (28) with $\mu _{i}^{*} = 1-\exp \left( -\mu _{i}\right)$. Then the proof is completed after simple statistical calculations are made. $\square$

Theorem 2

Suppose that the $Y_{i}$, $i=1,...,n$, are independent counts. Consider the hierarchical stochastic representation

$$\begin{aligned}&Y_{i}|\nu _{i},\omega _{i},u_{i},\lambda _{i}\overset{ind}{\sim }Pois\left( \nu _{i}+\log \left( 1-u_{i}\nu _{i}^{*}\right) \right) , \nonumber \\&\nu _{i}|\lambda _{i},\omega _{i}\overset{ind}{\sim }Gamma\left( \kappa +1,\lambda _{i}+\xi _{i}\right) , \\&\lambda _{i}|\omega _{i}\overset{ind}{\sim }F\left( \lambda _{i}|\omega _{i}\right) , \nonumber \\&\omega _{i}\overset{ind}{\sim }Bern\left( p\right) , \nonumber \\&u_{i}\overset{iid}{\sim }Unif\left( 0,1\right) , \nonumber \end{aligned}$$

(29)

where $u_{i}$ and $\omega _{i}$ are mutually independent, $\xi _{i}=\frac{\kappa }{\mu _{i}\left( 1-\omega _{i}\right) }$, $\nu _{i}^{*}=1-\exp \left( -\nu _{i} \right)$, and

$$\begin{aligned} F\left( \lambda _{i}|\omega _{i}\right) =\frac{1-\left( 1+\frac{\lambda _{i}}{\xi _{i}}\right) ^{-\kappa }}{1-\left( 1+\frac{1}{\xi _{i}}\right) ^{-\kappa }},~~0<\lambda _{i}<1, \end{aligned}$$

is the cdf of $\lambda _{i}$ given $\omega _{i}$. Then the shifted count variable $Y_{i}+1$ is distributed as $\textit{OIPNB}\left( \kappa ,\mu _{i},p\right)$.

Proof

The marginal pmf for each $Y_{i}$, for $i=1,\cdots ,n$, is obtained directly from the joint density of variables $\left( Y_{i},\nu _{i},\lambda _{i}, u_{i}, \omega _{i} \right)$ by integrating out $\nu _{i}$, $\lambda _{i}$, $u_{i}$, and summing over the binary variable $\omega _{i}$. First, the integration over $u_{i}$ gives the explicit solution

$$\begin{aligned} f\left( y_{i}|\nu _{i},\omega _{i},\lambda _{i}\right) =\frac{\nu _{i}^{y_{i}+1}e^{-\nu _{i}}}{\left( y_{i}+1\right) !\nu _{i}^{*}},~~y_{i}=0,1,\cdots . \end{aligned}$$

Then the conditional pmf of $Y_{i}$ given $\omega _{i}$ is derived by integrating with respect to the distribution functions of $\nu _{i}$ and $\lambda _{i}$ as

$$\begin{aligned} f\left( y_{i}|\omega _{i}\right)= & {} \int _{0}^{1}\int _{0}^{\infty }f\left( y_{i}|\nu _{i},\omega _{i},\lambda _{i}\right) dF\left( \nu _{i}|\omega _{i},\lambda _{i}\right) dF\left( \lambda _{i}|\omega _{i}\right) \nonumber \\= & {} \frac{\Gamma \left( y_{i}+\kappa +1\right) }{\Gamma \left( y_{i}+2\right) \Gamma \left( \kappa \right) }\frac{1}{1-t_{i}^{\kappa }}t_{i}^{\kappa }\left( 1-t_{i}\right) ^{y_{i}+1}, \end{aligned}$$

(30)

for $y_{i}=0,1,\cdots$, where $t_{i}=\frac{\kappa }{\kappa +\mu _{i}\left( 1-\omega _{i}\right) }$. Finally, we have

$$\begin{aligned} f\left( y_{i}\right) =pf\left( y_{i}|\omega _{i}=1\right) +\left( 1-p\right) f\left( y_{i}|\omega _{i}=0\right) . \end{aligned}$$

It is straightforward to show that $f\left( y_{i}|\omega _{i}=1\right) =0$ for $y_{i}=1,2,\cdots$ and $f\left( 0|\omega _{i}=1\right) =1$. Also, $f\left( y_{i}|\omega _{i}=0\right)$ is of the form (30), where $t_{i}$ reduces to $\frac{\kappa }{\kappa +\mu _{i}}$. After some simple algebraic operations are done we readily show that the shifted count variable $Y_{i}+1$ follows $\textit{OIPNB}\left( \kappa ,\mu _{i} ,p\right)$. $\square$

Hierarchical representation (29) is useful to generate variants from the OIPNB model since one can simply generate variants from all known distributions in (29). In addition, one may use the inverse transform sampling to generate $\lambda _{i}$ or apply the transformation $\lambda _{i}=\frac{\left( b_{i}-1\right) \kappa }{\mu _{i}\left( 1-\omega _{i}\right) }$, where $b_{i}$ follows the upper-truncated Pareto distribution with parameters $\kappa$, 1 and $1+\frac{\mu _{i}\left( 1-\omega _{i}\right) }{\kappa }$ (e.g. Aban et al. 2006).

4 A two-level OIP regression model

One main motivation to extend an OIP model is in the case when correlation exists between outcomes. Correlation due to clustering raises challenges. Clustering may be due to similarities among subjects. One inflation and lack of independence may occur simultaneously, which render the standard OIP model inadequate. To account the inherent correlation of subjects, we introduce a class of two-level OIP regression models with the heterogeneity effects.

Let the $Y_{ij}$ ($i=1,2,\cdots ,n$, $j=1,2,\cdots ,n_{i}$ and $\sum \nolimits _{i=1}^{n}n_{i}=N$ gives the total number of subjects) be OIP distributed random variables of the j-th subject in the i-th cluster. In the regression setting, both $logit(p_{ij})$ and $log\left( \mu _{ij}\right)$ are assumed to be linear functions of covariates. The covariates appearing in these two parts are not necessarily the same. In addition, random heterogeneity effects $\nu _{i}$ and $u_{i}$ for $i=1,2,\cdots ,n$ are introduced into the linear predictors to account for possible correlation between subjects within the same cluster. These random components control unexplained variations in the model. The linear predictors are defined as

$$\begin{aligned} \log \left( \mu _{ij}\right) =\mathbf {x}^{\prime }_{ij}\varvec{\beta }+u_{i}, \end{aligned}$$

(31)

and

$$\begin{aligned} \log \left( \frac{p_{ij}}{1-p_{ij}}\right) =\mathbf {z}_{ij}^{\prime }\varvec{\gamma }+\nu _{i}, \end{aligned}$$

(32)

where $\mathbf {x}_{ij}$ and $\mathbf {z}_{ij}$ are vectors of covariates, $\varvec{\beta }$ and $\varvec{\gamma }$ are the corresponding vectors of regression coefficients. Let $\mathbf {u}=\left( u_{1},u_{2},\cdots ,u_{n}\right) ^{\prime }$ and $\varvec{\nu =}\left( \nu _{1},\nu _{2},\cdots ,\nu _{n}\right) ^{\prime }$. Usual assumptions are that the effects $\mathbf {u}$ and $\varvec{\nu }$ are independent and distributed, respectively, as $N\left( \mathbf{{0}},\sigma _{u}^{2}\mathbf{{I}}_{n}\right)$ and $N\left( \mathbf{{0}},\sigma _{\nu }^{2}\mathbf{{I}}_{n}\right)$, where $\mathbf{{I}}_{n}$ denotes an $n\times n$ identity matrix. Although other distributions such as log-gamma can be adopted, but normally distributed random effects are the preferred choice in many applications. In order to capture the possible dependence between the two processes, we let the effects $\mathbf{{b}}_{i}=(u_{i},\nu _{i})$ be drawn from a bivariate distribution with density function $h(\cdot )$. The likelihood function is

$$\begin{aligned} L\left( \cdot \right) =\prod \limits _{i=1}^{n} \int _{ \mathbb {R}^2} \prod \limits _{j=1}^{n_{j}}f_{\textit{OIP}}\left( y_{ij}|\mathbf {b}_{i}\right) h\left( \mathbf {b}_{i}\right) d\mathbf {b}_{i} \end{aligned}$$

(33)

No closed form solution of the underlying integral is available. With modern computing power, direct computation by numerical approximations are quite straightforward. In particular, an appropriate approximation technique to numerically evaluate the integral involved in the marginal likelihood is Gauss-Hermite quadrature. This is adopted as a useful tool in mixed modeling contexts (e.g. Liu and Pierce 1994) when a normal density is specified to the random-effects. There are several reliable procedures in standard statistical packages, such as SAS and R, to provide Gauss–Hermite quadrature calculations. Between them, proc nlmixed in SAS includes adaptive Gaussian quadrature by default to allow exact likelihood computation.

5 A simulation study

Now we conduct a simulation study to highlight the importance of accounting for one-inflation and to illustrate the impact of mis-specification on model fitting. The simulation is conducted as follows. The data set is sampled by one of the OIPNB or OIPP regression models. A total number of 1000 data sets with 500 subjects has been generated. The covariates $X_{1}$ and Z are generated independently from standard normal distributions and $X_{2}$ from a Bernoulli $\left( 0.5\right)$ distribution. For each subject, $i=1,2,\cdots ,500$, $\mu _{i}$ $=$ $exp( \beta _{0}$ $+$ $\beta _{1}X_{1i}$ $+$ $\beta _{2}X_{2i})$ was calculated by fixing $\beta _{0}=0.5$ and $\beta _{2}=-\beta _{1}=1$ for all experiments. Also let $logit(p_{i}) =\gamma _{0}+\gamma _{1}Z_{i},$ and set $\gamma _{0}=-0.5$ and $\gamma _{1}=0.5$. When the data generating process is according to the regression model OIPNB, we set four different values for $\kappa$, 0.2, 0.6, 1 and 2. We know as $\kappa$ becomes large the OIPNB tends to OIPP and as p takes small values the distribution becomes close to the PNB distribution. Also, when simultaneously p takes small values and $\kappa$ gets large then the OIPNB becomes close to the PP distribution. However, in practical applications one may fit any of these models to positive one-inflated count data incorrectly and thus it is required to investigate the impact of this mis-specification. This importance is illustrated below.

For each replication, data are simulated according to the chosen regression model and all parameters are estimated using the PNB, PP and OIPP or OIPNB as alternative regression models. The average bias and the RMSE of estimates are obtained. Results of the simulation are summarized in Tables 1, 2, 3.

Table 1 Bias and RMSE of model parameters under fitted models when the true model is OIPP

Table 2 Bias and RMSE of model parameters under fitted models when the true model is OIPNB

Estimation results are reported in Table 1 when the true model is specified as OIPP. Here, based on RMSE, the PP and PNB models perform poorly relative to OIPP and OIPNB models. The estimate of $\kappa$ under the OIPNB is very large ($>$4E7) showing that the OIPNB reduces to the OIPP. Thus two OIPP and OIPNB models perform equally well and they have lower estimated biases with the RMSEs less than the alternative models. In overall, the average biases indicate that ignoring the one-inflated nature of data may result in under-estimation of the intercept and under- or over-estimation of the other parameters which may lead to non-significant findings.

Estimation results for the OIPP, PNB and PP fitted models are reported in Table 2 when the true model is specified as OIPNB. In this case, no alternative model is selected as the best fitted model by using the RMSE criterion. The RMSE indicates that the OIPP, PNB and PP models perform unsatisfactory relative to the OIPNB model. The bias and RMSE for all parameters of OIPP and PP models decrease when $\kappa$ increases. These models under-estimated $\beta _{2}$ and over-estimated $\beta _{0}$ and $\beta _{1}$, whereas the PNB model over-estimated $\beta _{2}$ and under-estimated $\beta _{0}$ and $\beta _{1}$ in overall. The PNB model produces the most bias and RMSE for $\kappa$ and the constant term. Also, in this model, for a large value of $\kappa$, the bias and RMSE of parameters (except intercept) become large. The Akaike information criterion, AIC $\, =-2\log L( \widehat{\mathbf {\theta }}) +2p$, and the Bayesian information criterion, BIC $\, =-2\log L( \widehat{\mathbf {\theta }}) +p$ $\log n$, where $L( \widehat{\mathbf {\theta }})$, p, and n denote the likelihood, number of parameters, and sample size, respectively, are used to select the best fitted model. Smaller values of these criteria indicate better fit. In the comparison of all models, the AIC and BIC values are computed and shown in Table 3. It is seen that the previous results are confirmed by using these criteria. In fact, the OIPP and OIPNB models are comparable in fitting the OIPP model but not in the OIPNB model. This finding does suggest the importance of identifying the over-dispersion for the un-truncated distribution. Also findings indicate that the PNB and PP models are not suitable in comparison to the OIPNB and OIPP models. That is, ignoring one-inflated nature of data leads to an erroneous significant finding.

Table 3 Information criterion values for various fitted models

6 An empirical application with two modeling strategies

As already mentioned, the data are taken from the US national Medicare inpatient hospital database. It is emphasized in previous studies that the length of stay (LOS) in hospital is a key element in the consumption of hospital resources and very important for hospital planning. Thus, the response variable is considered as the LOS in which, regardless of how little time a patient has spent in hospital, at least one day is credited. The data set consists 1495 observations on patients registered to a Health maintenance organization (Hmo), patient identifies themselves as Caucasian (White), patient died (Died) and type of admission (Type) variables. Type is a factor variable with three levels, elective admission (Type1), urgent admission (Type2), emergency admission (Type3). We set Type1 as the reference category. In below we report results of two regression modeling strategies to highlight the theoretical methodologies. The first is undertaken within the framework of cross-sectional data analysis which assumes that count responses are independent. The second strategy is organized through the two-level modeling setting to take into account the correlation between subjects.

6.1 Cross-sectional data analysis

We adopt the following log-linear link function

$$\begin{aligned} \log \left( \mu _{i}\right) =\beta _{0}+\beta _{1}\text {Type2}_{i}+\beta _{2} \text {Type3}_{i}+\beta _{3}\text {Hmo}_{i}+\beta _{4}\text {Died}_{i}, \end{aligned}$$

and the logit function

$$\begin{aligned} \log \left( \frac{p_{i}}{1-p_{i}}\right) =\gamma _{0}+\gamma _{1}\text {Type2} _{i}+\gamma _{2}\text {Type3}_{i}+\gamma _{3}\text {Hmo}_{i}+\gamma _{4}\text { Died}_{i}, \end{aligned}$$

for $i=1,2,\cdots ,1495$. The variance of the LOS variable is 78.022 which is significantly larger than the mean 9.854. A fit of the PP model gives the variance 9.841 and the mean 9.854. Also the observed proportion of one counts is equal to 8.43 % while the PP model predict it in average 0.15 % which is notably less than actually observed in the data. The OIPP model predicts the probability of ones more than the PP model, however it does not account for the extra variation by receiving the variance 15.731 and the mean 9.856. For the PNB model, the estimate of the dispersion parameter $\kappa$ is equal to $0.533~ (se=0.0293)$ with the corresponding p value $<0.001$ which indicates strong evidence of over-dispersion. This suggests that employing the OIPNB model may be suitable to fit the data.

We fit the OIPNB regression model and make comparison to the OIPP, PP and PNB models. Table 4 shows the parameter estimates and their standard errors in fitting various models. Model performance is evaluated by using four criteria. The Hannan–Quinn information criterion, HQIC $\, =-2\log L( \widehat{\mathbf {\theta }})$ $+$ $2 p log\left\{ log(n)\right\}$, and the consistent Akaike information criterion, CAIC $=$ $-2\log L( \widehat{\mathbf {\theta }})$ $+$ $p\left\{ \log (n)+1\right\}$, where $L( \widehat{\mathbf {\theta }})$, p, and n denote the likelihood, number of parameters, and sample size, respectively, are also used to select the best fitted model. Smaller values of these criteria indicate better fit. We also report BIC and AIC values for each fitted model. Results show that the PP model performs very poor relative to the other models since it accommodates only positive data while the OIPNB is the preferred model as it fairly deal with extra variation of positive and one-inflated data.

Table 4 Estimates and criteria values of the OIPNB, OIPP, PNB and PP regression models

In this analysis, the regression coefficients of the Hmo and the patient died are not statistically significant while the type of hospital admission is positively significant. Thus, patients admitted to the urgent and emergency have longer length of stay than those with the elective admission. The sign of estimates in these models is important since it can determine not only the influence of covariates on the length hospital stay in days but also can control whether a specific patient stays in hospital one day or more. This helps hospital managers to predict the number of beds at hospital. The sign of estimates for admitted patients to the urgent and emergency is positive in model part whereas is negative in the logit part. These reasonable findings show that these admitted patients stay in hospital longer than one day in comparison to those patients admitted elective. Also, the estimate of $\gamma$ is positively significant in the logit part illustrating that the number of days for patient who died approaches to one day at hospital.

6.2 A two-level one-inflated regression model

The original data set includes 54 different insurance providers. All patients are nested into these providers. It is possible that some providers may provide facilities that tend to keep the length of hospital stay long. Thus, we may fit one-inflated models to take into account the correlation of patients with the same insurance provider. We also aim to see if extra variation is caused by correlation due to the existence of the provider heterogeneity in models. Table 5 presents results of fitting two-level regression models. In fitting OIP models we observed that the scale parameter of the provider heterogeneity effect in the logit part insignificant. Thus, only a random provider effect was arranged in the first part of the model. That is, for $i=1,2,...,1495$ and $j=1,2,...,$54,

$$\begin{aligned} \log \left( \mu _{ij}\right) =\beta _{0}+\beta _{1}\text {Type2}_{ij}+\beta _{2}\text {Type3}_{ij}+\beta _{3}\text {Hmo}_{ij}+\beta _{4}\text {Died} _{ij}+u_{i}, \end{aligned}$$

where $u_{i}$ $\sim$ $N\left( 0,\sigma _{u}^{2}\right)$ and

$$\begin{aligned} \log \left( \frac{p_{ij}}{1-p_{ij}}\right) =\gamma _{0}+\gamma _{1}\text { Type2}_{_{ij}}+\gamma _{2}\text {Type3}_{_{ij}}+\gamma _{3}\text {Hmo}_{ij}+\gamma _{4}\text {Died}_{_{ij}}. \end{aligned}$$

Table 5 Estimates and criterion values from the two-level regression models

Results suggest that the two-level OIPNB model fits better than other mentioned models. In this model, the patient died is negatively significant showing that patients who died had less length of stay to persistent patients. The effect of covariates on the LOS and one day stay, or more, are rather similar to those obtained under the cross-sectional regression models while the standard errors for some of covariates are slightly increased. It appears that there is indeed an excess correlation of responses within insurance providers which takes into account extra variation. Finally, the estimate of $\sigma _{u}^2$ illustrates considerable heterogeneity in providers.

7 Concluding remarks

Traditional regression models for the analysis of count data are often unfitting in the presence of over-dispersion and zero-truncation issues. In the present paper, the positiveness and the one-inflation are addressed by utilizing some OIP regression models. These proposed models allow two separate mechanisms to the prediction of one-inflated counts by adopting a logit function and to the generation of subsequent counts by implementing discrete distributions, such as poisson or NB. A two-level OIP regression model is also introduced to take into account the correlation between subjects and to model excess one counts. These OIP models can provide insight into the source of excess ones and extra variation. They perform attractive alternative to zero-truncated models for count data since the corresponding marginal likelihoods are available in closed forms while the MLE of model parameters require the implementation of advanced numerical methods. The extension of our methodology straightforwardly can be applied further to various applications of count data that directly employ mixed poisson distributions with different mixing priors, such as the log-normal (e.g. Izsák 2008) or the inverse-Gaussian (Dean et al. 1989; Rigby et al. 2008). In these cases the associated marginal likelihoods are complex and need further work to make statistical inference. Moreover, hierarchical stochastic representations of two proposed models OIPP and OIPNB allow to utilize substituting enhanced estimation approaches, such as Gibbs sampling in a Bayesian perspective, that are computationally simpler than the marginal likelihood technique. These are topics of our future research.