Interval-Valued Intuitionistic Fuzzy WASPAS Method: Application in Reservoir Flood Control Management Policy

Abstract

Interval-valued intuitionistic fuzzy sets (IVIFSs) are very flexible tool to cope with the uncertainty arises in multi-criteria decision making (MCDM) problems. In recent times, MCDM problems with interval-valued intuitionistic fuzzy information have achieved more attention from researchers in different areas and consequently, several MCDM methods have been extended for IVIFSs. In this paper, a novel approach based on WASPAS method is developed under IVIFSs. The developed method is based on the operators of IVIFSs, some amendments in the classical WASPAS method and a new process for calculation of criteria and decision experts’ weights. In process for calculating weights, new procedures is propoesd to compute the decision experts’ weights and criteria weights based on interval-valued intuitionistic fuzzy information measures (entropy, divergence and similarity measures) to achieve more realistic weights. Innovative information measures are developed based on the exponential function for IVIFSs to determine the weights of the criteria and decision experts. Since the uncertainty is an unavoidable feature of MCDM problems, the developed method can be a constructive tool for decision-making in an uncertain environment. Further, an uncertain decision making problem of reservoir flood control management policy is implemented with interval-valued intuitionistic fuzzy information, which reveals the effectiveness and reliability of the proposed IVIF-WASPAS method. To validate the result, comparative analysis with existing methods and sensitivity analysis are presented under interval-valued intuitionistic fuzzy environment.

1 Introduction

Today, because of increasing competitions, it is noticed that the decision making has achieved as one of the fastest emergent research topic related to real life problems. Multi-criteria decision making (MCDM) is one of the significant part of decision making process to rank the alternatives over set of multiple conflicting criteria and then select the optimal one. As the criteria are conflicting with each other, therefore, it may not have a unique solution satisfying all the criteria concurrently. Nowadays, various MCDM approaches have been developed to get more reasonable decision results. In recent times, due to uncertainty and complexity of human thought, fuzzy sets (FSs) developed by Zadeh (1965), have received more attraction from decision experts in the field of decision making. FSs are characterized by a membership function, which can be widely associated in various fields such as image processing, disease diagnosis, pattern recognition and so on. Later on, FSs have been extended to interval-valued fuzzy sets (IVFSs) (Zadeh 1975), intuitionistic fuzzy sets (IFSs) (Atanassov 1986), interval-valued intuitionistic fuzzy sets (IVIFSs) (Atanassov and Gargov (1989), vague sets (VSs) (Gau and Buehrer (1993), hesitant fuzzy sets (HFSs) (Torra 2010) etc. Atanassov (1986) explained the notion of IFSs, which are highly useful to cope with the uncertainty of MCDM problems. Since IFSs are categorized by the membership and non-membership functions, therefore, many decision making methods and problems have been presented within the context of IFSs [Xia and Xu 2012; Vahdani et al. (2013); Mishra et al. 2017b]. Due to complexity of socio-economic environment and lack of knowledge or data, the doctrine of IVIFSs commenced by Atanassov and Gargov (1989), are characterized by the membership and non-membership functions in the form of intervals rather than real numbers. As the extension of IFSs, IVIFSs have received much attention in different areas and numerous issues related to decision making have been discussed under interval-valued intuitionistic fuzzy environment (Xu 2007a; Rani et al. 2018b).

The studies of information measures (entropy, divergence and similarity measures) in different fuzzy environments are one of the interesting topics of research. Zadeh (1969) firstly developed the notion of fuzzy entropy measure to handle the uncertainty between FSs. The axiomatic description of fuzzy entropy has been defined by De Luca and Termini (1972), to quantify the degree of uncertainty associated with a fuzzy set. Later on, the idea of entropy measure has been developed to various extension of FSs such as IVFSs, IFSs and HFSs (Pal and Pal 1989; Szmidt and Kacprzyk 2001; Hung and Yang 2006; Mishra 2016; Mishra et al. 2016a, b, c, 2017a, b, c; Mishra and Rani 2017; Ansari et al. 2018; Rani and Jain 2017; Rani et al. 2018a; Mishra et al. 2018a, b, d). Based on Szmidt and Kacprzyk’s (2001) entropy measure for IFSs, Liu et al. (2005) firstly proposed the axiomatic requirements of entropy measure for IVIFSs. In recent times, various entropy measures have been presented for IVIFSs (Chen et al. 2010; Wei et al. 2011; Wei and Zhang 2015; Meng and Chen 2016; Rani et al. 2018b; Mishra and Rani 2018; Mishra et al. 2018c). Divergence measure is a fundamental tool to appraise the degree of discrimination between objects and it has been implemented various disciplines such as image processing, pattern recognition, disease diagnosis and so on. Motivated by probabilistic divergence measure, Bhandari and Pal (1993) introduced the idea of fuzzy divergence measure. Later on, many divergence measures have been pioneered for FSs (Montes et al. 2002, 2015). Analogous to FSs, many researches have been discussed various divergence measures for IFSs and applied for different purposes (Vlachos and Sergiadis 2007; Xia and Xu 2012; Mishra et al. 2016c, 2017a, b; Ansari et al. 2018; Mishra and Rani 2017). Afterward, few studies on the divergence measure for IVIFSs have been presented in the literature (Zhang et al. 2010; Ye 2011; Meng and Tang 2013; Gupta et al. 2015; Meng and Chen 2015). Similarity measure, as an important topic in information measures, has obtained a great deal of interest by researchers. Firstly, Li and Cheng (2002) proposed the notion of similarity measure for IFSs and their findings have been used in pattern recognition problems. Furthermore, different intuitionistic fuzzy similarity measures have been developed by copious authors (Hung and Yang 2004, 2008; Mishra 2016; Mishra et al. 2017c, 2018b). To quantify the degree of similarity between IVIFSs, Xu and Chen (2008) developed the notion of interval-valued intuitionistic fuzzy similarity measure and extended lots of similarity measures to IVIFSs, and applied in pattern recognition. Various authors have paid attention on the similarity measures for IVIFSs (Xu 2007b; Wei and Zhang 2015; Meng and Chen 2016; Rani et al. 2018b).

Generally, the MCDM approaches have some common points as decide the goal; determine the alternative and criterion sets; compute the criteria on as well as decision experts’ weights; assess the alternatives over the criteria and aggregate the decision matrix; rank the alternatives and select the desirable one. In the MCDM process, the criterion weight determination is an important issue for the accuracy of evaluation results, for this reason, various weight-determining methods have been developed by many authors (Xu 2007b, Xu and Chen 2008). At a time, FSs and its extensions have gained more attentiveness in the field of decision making because of increasing intricacy and limitation of time, so that, different MCDM methods such as TOPSIS (Chen 2000), ELECTRE (Benayoun et al. 1966), TODIM (Gomes and Lima 1991), VIKOR (Opricovic 1998), PROMETHEE (Brans 1982), WASPAS (Zavadskas et al. 2012) and many others have been generalized under uncertain decision atmosphere with diverse weight-determination approaches.

In recent times, the MCDM approaches have been divided into two groups: utility theory based approaches and outranking approaches. The VIKOR method is one of the well-known MCDM utility theory based method, which determines the compromise solution by ranking and selecting the optimal alternative concerning many conflicting criteria. One of the new utility theory based approach named as weighted aggregated sum product assessment (WASPAS), pioneered by Zavadskas et al. (2012), is an integration of weighted sum model (WSM) and weighted product model (WPM). The WASPAS method enables to assess and rank the alternatives with higher order of reliability. This approach has been extended for many decision making problems under different fuzzy doctrines. For instance, Zavadskas et al. (2014) extended the WASPAS method for MCDM problems with interval-valued intuitionistic fuzzy information. Turskis et al. (2015) presented a combination of WASPAS and AHP (Analytic Hierarchy Process) under fuzzy environment and applied to select the best the shopping centre construction site. Ghorabaee et al. (2016) developed the WASPAS method for MCDM problems based on operators of interval type-2 fuzzy sets. Mardani et al. (2017) presented a systematic review of methodologies and applications with recent fuzzy developments of two new MCDM utility determining approaches including Step-wise Weight Assessment Ratio Analysis (SWARA) and the WASPAS and fuzzy extensions which discussed in recent years. Peng and Dai (2017) proposed three novel methods to solve hesitant fuzzy soft decision making problem by Multi-Attributive Border Approximation area Comparison (MABAC), WASPAS and COPRAS methods. Mishra et al. (2018b) implemented intuitionistic fuzzy weighted aggregated sum and product assessment (IF-WASPAS) method to compare the performance of telecom service providers (TSPs) in Madhya Pradesh circle India.

At present, due to increasing intricacy of socio-economic surroundings, IVIFSs have widely been applied in many practical decision-making problems, as a result, the present study focuses within the environment of IVIFSs. The outcomes of this paper are as follows:

• 1. New entropy, divergence and similarity measures are proposed for IVIFSs.

• 2. As the classical WASPAS method is extended to handle the MCDM problems, the classical WASPAS method is modified under interval-valued intuitionistic fuzzy environment.

• 3. In the proposed methodology, a new formula is developed to find the weights of the decision experts based on the proposed similarity measure.

• 4. Corresponding to Xia and Xu (2012), an approach is discussed to determine the weights of the criteria based on the proposed divergence and entropy measures.

• 5. An MCDM problem of reservoir flood control management policy evaluation is presented to exemplify the applicability and validity of the proposed methods.

2 Preliminaries

In this section, some fundamental concepts related to IVIFSs are presented.

Definition 2.1

(Atanassov and Gargov 1989). Let $Z = \,\left\{ {z_{1} ,\,z_{2} ,\, \ldots ,\,z_{n} } \right\}$ be a fixed universal set. Then an IVIFS $P$ in $Z$ is an object having the following form:

$$ P\, = \,\left\{ {\left\langle {z_{i} ,\,b_{P} (z_{i} ),\,n_{P} (z_{i} )} \right\rangle \,:\,z_{i} \, \in \,Z} \right\}, $$

where $b_{P} ,\,n_{P} \,:\,Z\, \to \,\left[ {0,\,1} \right]$ satisfy the condition $\sup (b_{P} (z_{i} ))\, + \,\sup (n_{P} (z_{i} ))\, \le \,1.$ Here, $b_{P} (z_{i} )$ and $n_{P} (z_{i} )$ denote the interval-valued membership and the non-membership functions of the element $z_{i}$ to the set $Z,$ respectively. For convenience, if $b_{P} (z_{i} )\, = \,\left[ {b_{P}^{ - } (z_{i} ),\,b_{P}^{ + } (z_{i} )} \right]$ and $n_{P} (z_{i} )\, = \,\left[ {n_{P}^{ - } (z_{i} ),\,n_{P}^{ + } (z_{i} )} \right]$ such that $b_{P}^{ + } (z_{i} )\, + \,n_{P}^{ + } (z_{i} )\, \le \,1$ for all $z_{i} \, \in \,Z.$ The interval $\left[ {1 - b_{P}^{ + } (z_{i} ) - n_{P}^{ + } (z_{i} ),\,1 - b_{P}^{ - } (z_{i} ) - n_{P}^{ - } (z_{i} )} \right]$ abridged by $\left[ {\pi_{P}^{ - } (z_{i} ),\,\pi_{P}^{ + } (z_{i} )} \right]$ and symbolized by $\pi_{P} (z_{i} )$ and called as the hesitancy degree of $z_{i}$ to $P.$ Clearly, if $b_{P} (z_{i} )\, = \,b_{P}^{ - } (z_{i} )\, = \,b_{P}^{ + } (z_{i} )$ and $n_{P} (z_{i} )\, = \,n_{P}^{ - } (z_{i} )\, = \,n_{P}^{ + } (z_{i} )$ then the given IVIFSs $P$ is reduced to ordinary IFSs.

As per the Definition 2.1, an IVIFS is characterized by an interval-valued membership and an interval-valued non-membership functions and expressed as an ordered pair. For a given $z_{i} \, \in \,Z,$ the pair $\left( {b_{P} (z_{i} ),\,n_{P} (z_{i} )} \right)$ is called an interval-valued intuitionistic fuzzy number (IVIFN) (Xu 2007a). For ease, an IVIFN is usually simplified as $P\, = \,\left( {\left[ {\alpha ,\,\beta } \right],\,\left[ {\gamma ,\,\delta } \right]} \right),$ where $\left[ {\alpha ,\,\beta } \right]\, \subset \,\left[ {0,\,1} \right],\,\,\left[ {\gamma ,\,\delta } \right]\, \subset \,\left[ {0,\,1} \right]$ and $\beta \, + \,\delta \, \le \,1.$

Dymova and Sevastjanov (2016) analyzed the Definition 2.1, developed by Atanassov and Gargov (1989) and proposed new constructive definition of IVIFSs.

Definition 2.2

(Dymova and Sevastjanov 2016) An IVIFS $P$ in $Z$ is an object having the following mathematical form:

$$ P\, = \,\left\{ {\left\langle {z_{i} ,\,b_{P} (z_{i} ),\,n_{P} (z_{i} )} \right\rangle \,:\,z_{i} \, \in \,Z} \right\}, $$

where $b_{P} ,\,n_{P} \,:\,Z\, \to \,\left[ {0,\,1} \right]$ satisfy the condition $\sup (b_{P} (z_{i} ))\, + \,\inf (n_{P} (z_{i} ))\, \le \,1$ and $\inf (b_{P} (z_{i} ))\, + \,\sup (n_{P} (z_{i} ))\, \le \,1.$ Here, $b_{P} (z_{i} )$ and $n_{P} (z_{i} )$ denote the interval-valued membership and the interval-valued non-membership functions of the element $z_{i}$ to the set $Z,$ respectively.

Definition 2.3

(Atanassov and Gargov 1989) Assume $P,\,Q\, \in \,IVIFSs\left( Z \right),$ then some operations can be explained as follows:

• 1. $P\, \subseteq \,Q$ iff $b_{P}^{ - } (z_{i} )\, \le \,\,b_{Q}^{ - } (z_{i} ),\,\,b_{P}^{ + } (z_{i} )\, \le \,\,b_{Q}^{ + } (z_{i} ),\,\,n_{P}^{ - } (z_{i} )\, \ge \,n_{Q}^{ - } (z_{i} )$ and $n_{P}^{ + } (z_{i} )\, \ge \,n_{Q}^{ + } (z_{i} )$ for each $z_{i} \in \,Z;$

• 2. $P\, = \,Q$ iff $P\, \subseteq \,Q$ and $P\, \supseteq \,Q;$

• 3. $P^{c} \, = \,\left\{ {\left\langle {z_{i} ,\,\left[ {n_{P}^{ - } (z_{i} ),\,n_{P}^{ + } (z_{i} )} \right],\,\left[ {b_{P}^{ - } (z_{i} ),\,b_{P}^{ + } (z_{i} )} \right]} \right\rangle \,:\,\,z_{i} \, \in \,Z} \right\};$

• 4. $P \cup \,Q\, = \,\left\{ {\left\langle \begin{aligned} z_{i} ,\,\left[ {b_{P}^{ - } (z_{i} )\, \vee \,b_{Q}^{ - } (z_{i} ),\,b_{P}^{ + } (z_{i} )\, \vee \,b_{Q}^{ + } (z_{i} )} \right], \hfill \\ \,\,\,\,\,\,\left[ {n_{P}^{ - } (z_{i} )\, \wedge \,n_{Q}^{ - } (z_{i} ),\,\,n_{P}^{ + } (z_{i} )\, \wedge \,\,n_{Q}^{ + } (z_{i} )} \right] \hfill \\ \end{aligned} \right\rangle \,:\,z_{i} \, \in \,Z} \right\};$

• 5. $P \cap \,Q\, = \,\left\{ {\left\langle \begin{aligned} z_{i} ,\,\left[ {b_{P}^{ - } (z_{i} )\, \wedge \,b_{Q}^{ - } (z_{i} ),\,b_{P}^{ + } (z_{i} )\, \wedge \,b_{Q}^{ + } (z_{i} )} \right], \hfill \\ \,\,\,\,\,\,\left[ {n_{P}^{ - } (z_{i} )\, \vee \,n_{Q}^{ - } (z_{i} ),\,\,n_{P}^{ + } (z_{i} )\, \vee \,\,n_{Q}^{ + } (z_{i} )} \right] \hfill \\ \end{aligned} \right\rangle \,:\,z_{i} \, \in \,Z} \right\}.$

Definition 2.4

(Xu 2007a) Consider $P = \left\langle {\left[ {\alpha ,\,\,\beta } \right],\left[ {\gamma ,\,\,\delta } \right]\,} \right\rangle$ be an IVIFN and $\xi \in {\mathbb{R}}$ be an arbitrary positive real number, then

$$ \xi P = \left\langle {\left[ {1 - \left( {1 - \alpha } \right)^{\xi } ,\,\,1 - \left( {1 - \beta } \right)^{\xi } } \right],\left[ {\gamma^{\xi } ,\,\,\delta^{\xi } } \right]\,} \right\rangle . $$

(1)

On the basis of (1), we have implemented Xu (2007a) definition as follows:

Let $P = \left\{ {P_{1} ,P_{2} , \ldots ,\,P_{t} } \right\}$ be the set of ‘t’ IVIFNs such that $P_{k} = \left\langle {\left[ {\alpha_{k} ,\,\,\beta_{k} } \right],\left[ {\gamma_{k} ,\,\,\delta_{k} } \right]\,} \right\rangle ,\,\,k = 1,2, \ldots ,t.$ Then, the weighted arithmetic operator of IVIFNs is defined as follows:

$$ \sum\limits_{k = 1}^{t} {\xi_{k} P_{k} } = \left\langle {\left[ {1 - \prod\limits_{k = 1}^{t} {\left( {1 - \alpha_{k} } \right)^{{\xi_{k} }} } ,\,\,1 - \prod\limits_{k = 1}^{t} {\left( {1 - \beta_{k} } \right)^{{\xi_{k} }} } } \right],\left[ {\prod\limits_{k = 1}^{t} {\left( {\gamma_{k} } \right)}^{{\xi_{k} }} ,\,\,\prod\limits_{k = 1}^{t} {\left( {\delta_{k} } \right)}^{{\xi_{k} }} } \right]\,} \right\rangle . $$

(2)

Definition 2.5

(Xu 2007a) Consider $P = \left\langle {\left[ {\alpha ,\,\,\beta } \right],\left[ {\gamma ,\,\,\delta } \right]\,} \right\rangle$ be an IVIFN. Then

$$ {\mathbb{S}}\left( P \right) = \frac{1}{2}\left( {\alpha + \beta - \gamma - \delta } \right),\,\,\hbar \left( P \right) = \frac{1}{2}\left( {\alpha + \beta + \gamma + \delta } \right), $$

are called the score and the accuracy functions of the IVIFN $P,$ respectively. Here, ${\mathbb{S}}\left( P \right) \in \left[ { - 1,1} \right]$ and $\hbar \left( P \right) \in \left[ {0,1} \right]$ can be considered as the score and the accuracy degrees, respectively.

Since ${\mathbb{S}}\left( P \right) \in \left[ { - 1,1} \right],$ when several score functions are aggregated with linear weighted summation method and it may be appear that positive score functions are offset by negative score functions. Therefore, Xu et al. (2015) defined a new score function of IVIFNs as follows:

Definition 2.6

(Xu et al. 2015) Let $P = \left\langle {\left[ {\alpha ,\,\,\beta } \right],\left[ {\gamma ,\,\,\delta } \right]\,} \right\rangle$ be an IVIFN. Then

$$ {\mathbb{S}}^{*} \left( P \right) = \frac{1}{2}\left( {{\mathbb{S}}\left( P \right) + 1} \right),\quad \hbar^{^\circ } \left( P \right) = 1 - \hbar \left( P \right), $$

are called the normalized score and the uncertainty functions, respectively. Obviously, ${\mathbb{S}}^{*} \left( P \right) \in \left[ {0,1} \right]$ and $\hbar^{^\circ } \left( P \right) \in \left[ {0,\,\,1} \right].$

Let $P_{1} = \left\langle {\left[ {\alpha_{1} ,\,\,\beta_{1} } \right],\left[ {\gamma_{1} ,\,\,\delta_{1} } \right]\,} \right\rangle$ and $P_{2} = \left\langle {\left[ {\alpha_{2} ,\,\,\beta_{2} } \right],\left[ {\gamma_{2} ,\,\,\delta_{2} } \right]\,} \right\rangle$ be the IVIFNs. Then, a system can be derived easily to compare any two IVIFNs, which is based on the normalized score function ${\mathbb{S}}^{*} \left( P \right)$ and the uncertainty function $\hbar^{^\circ } \left( P \right)$ which as

• (i) If ${\mathbb{S}}^{*} \left( {P_{1} } \right) > {\mathbb{S}}^{*} \left( {P_{2} } \right),$ then $P_{1} > P_{2} ,$

• (ii) If ${\mathbb{S}}^{*} \left( {P_{1} } \right) = {\mathbb{S}}^{*} \left( {P_{2} } \right),$ then

  • (a) if $\hbar^{^\circ } \left( {P_{1} } \right) > \hbar^{^\circ } \left( {P_{2} } \right),$ then $P_{1} < P_{2} ;$

  • (b) if $\hbar^{^\circ } \left( {P_{1} } \right) = \hbar^{^\circ } \left( {P_{2} } \right),$ then $P_{1} = P_{2} .$

Definition 2.7

(Liu et al. 2005) An interval-valued intuitionistic fuzzy entropy measure $H:\,\,IVIFS(Z)\, \to \,\left[ {0,\,1} \right]$ is a real valued function which satisfies the following axiomatic requirements:

• (E1). $H\left( P \right)\, = \,0$ iff $P$ is a crisp set;

• (E2). $H\left( P \right)\, = 1$ iff $\left[ {b_{P}^{ - } (z_{i} ),\,b_{P}^{ + } (z_{i} )} \right]\, = \,\left[ {n_{P}^{ - } (z_{i} ),\,n_{P}^{ + } (z_{i} )} \right],$ for all $z_{i} \in \,Z;$

• (E3). $H\left( P \right)\, = \,H\left( {P^{c} } \right);$

• (E4). $H(P)\, \le \,H(Q)$ if $P\, \subseteq \,Q$ when $b_{Q}^{ - } (z_{i} )\, \le \,n_{Q}^{ - } (z_{i} )$ and $b_{Q}^{ + } (z_{i} )\, \le \,\,n_{Q}^{ + } (z_{i} )$ for each $z_{i} \in Z$ or $Q\, \subseteq \,P$ when $b_{Q}^{ - } (z_{i} )\, \ge \,n_{Q}^{ - } (z_{i} )$ and $b_{Q}^{ + } (z_{i} )\, \ge \,n_{Q}^{ + } (z_{i} )$ for each $z_{i} \in Z.$

Definition 2.8

(Montes et al. 2015) A mapping $D_{v} \,:\,IVIFSs(Z)\, \times \,IVIFSs(Z)\, \to {\mathbb{R}}$ is said to be a divergence measure for IVIFSs if it satisfies the following axioms:

• (A1). $D_{v} \left( {P,Q} \right)\, = \,D_{v} \left( {Q,\,P} \right);$

• (A2). $D_{v} \left( {P,\,Q} \right)\, = \,0$ if and only if $P\, = \,Q;$

• (A3). $D_{v} \left( {P \cap \,R,\,Q\, \cap \,R} \right)\, \le \,D_{v} \left( {P,\,Q} \right)$ for every $R\, \in \,IVIFS(Z);$

• (A4). $D_{v} \left( {P \cup \,R,\,Q\, \cup \,R} \right)\, \le \,D_{v} \left( {P,\,Q} \right)$ for every $R\, \in \,IVIFS(Z).$

Definition 2.9

(Xu and Chen 2008) A real-valued function $\Delta \,:IVIFSs(Z) \times IVIFSs(Z) \to [0,\,\,1]$ is said to be a similarity measure on $IVIFSs(Z),$ if it satisfies the following conditions:

• (C1). $0 \le \Delta \left( {P,\,Q} \right) \le 1;$

• (C2). $\Delta \left( {P,\,Q} \right) = 1 \Leftrightarrow P\, = \,Q;$

• (C3). $\Delta \left( {P,\,Q} \right) = \Delta \left( {Q,\,P} \right);$

• (C4). If $P\, \subseteq \,Q \subseteq \,R,$ then $\Delta \left( {P,\,R} \right) \le \Delta \left( {P,\,Q} \right)$ and $\Delta \left( {P,\,R} \right) \le \,\Delta \left( {Q,\,R} \right),$ for all $P,\,Q,\,R\,\, \in IVIFSs(Z).$

3 Information Measures for Interval-Valued Intuitionistic Fuzzy Sets (IVIFSs)

In this section, a new entropy, divergence and similarity measures are developed for IVIFSs and compared with some existing measures for IVIFSs.

3.1 Entropy Measure

Based on Mishra et al. (2017a), for each $P \in IVIFS(Z),$ entropy measure for IVIFSs is denoted by $H\left( P \right)$ and defined as

$$ \begin{aligned} H\left( P \right) & = \tfrac{1}{{n\,\sqrt e \left( {\sqrt e - 1} \right)}}\sum\limits_{i = 1}^{n} {\,\left[ {e - \,\left( {\tfrac{{\left( {b_{P}^{ - } (z_{i} ) + \,b_{P}^{ + } (z_{i} )} \right) + 2 - \left( {n_{P}^{ - } (z_{i} ) + \,n_{P}^{ + } (z_{i} )} \right)}}{4}} \right).\,e^{{\left( {\tfrac{{\left( {b_{P}^{ - } (z_{i} ) + \,b_{P}^{ + } (z_{i} )} \right) + 2 - \left( {n_{P}^{ - } (z_{i} ) + \,n_{P}^{ + } (z_{i} )} \right)}}{4}} \right)}} } \right.} \\ & \left. {\quad - \left( {\tfrac{{\left( {n_{P}^{ - } (z_{i} )\, + \,\,n_{P}^{ + } (z_{i} )} \right) + 2 - \left( {b_{P}^{ - } (z_{i} ) + b_{P}^{ + } (z_{i} )} \right)}}{4}} \right)e^{{\left( {\tfrac{{\left( {n_{P}^{ - } (z_{i} )\, + \,\,n_{P}^{ + } (z_{i} )} \right) + 2 - \left( {b_{P}^{ - } (z_{i} ) + b_{P}^{ + } (z_{i} )} \right)}}{4}} \right)}} } \right]. \\ \end{aligned} $$

(3)

Theorem 3.1

The function $H\left( P \right),$ defined by (3), is an entropy measure for IVIFS ($Z$).

Proof

Measure $H\left( P \right),$ is valid entropy measure for IVIFSs because it satisfies the requirements (E1)–(E4) of Definition 2.7.

Remark 3.1

If an IVIFS reduces to be an IFS, then the entropy measure defined by (3) diminishes to the intuitionistic fuzzy entropy measure defined by Mishra et al. (2017a).

3.1.1 Comparison with Existing Measures

Let $P\, \in IVIFS(Z).$ Here, some existing entropies are depicted as follows:

Chen et al. (2010):

$$ H_{C} \left( P \right)\, = \, - \frac{1}{n\,\ln 4}\sum\limits_{i = 1}^{n} {\left[ \begin{aligned}& b_{P}^{ - } (z_{i} )\,\ln b_{P}^{ - } (z_{i} )\, + \,b_{P}^{ + } (z_{i} )\,\ln b_{P}^{ + } (z_{i} )\, + \,n_{P}^{ - } (z_{i} )\,\ln n_{P}^{ - } (z_{i} ) \hfill \\ &\quad + \,n_{P}^{ + } (z_{i} )\,\ln n_{P}^{ + } (z_{i} )\, - \,(1 - \pi_{P}^{ - } (z_{i} ))\,\ln (1 - \pi_{P}^{ - } (z_{i} )) - \,\pi_{P}^{ - } (z_{i} )\ln 2 \hfill \\ &\qquad\quad - \,(1 - \pi_{P}^{ + } (z_{i} ))\,\ln (1 - \pi_{P}^{ + } (z_{i} )) - \,\pi_{P}^{ + } (z_{i} )\ln 2 \hfill \\ \end{aligned} \right]} . $$

(4)

Wei et al. (2011):

$$ H_{W} \left( P \right) = \,\frac{1}{n}\,\sum\limits_{i = 1}^{n} {\left( {\tfrac{{\hbox{min} \{ b_{P}^{ - } (z_{i} ),\,n_{P}^{ - } (z_{i} )\} + \hbox{min} \{ b_{P}^{ + } (z_{i} ),\,n_{P}^{ + } (z_{i} )\} \, + \pi_{P}^{ - } (z_{i} ) + \,\pi_{P}^{ + } (z_{i} )}}{{\hbox{max} \{ b_{P}^{ - } (z_{i} ),\,n_{P}^{ - } (z_{i} )\} + \hbox{max} \{ b_{P}^{ + } (z_{i} ),\,n_{P}^{ + } (z_{i} )\} \, + \pi_{A}^{ - } (z_{i} ) + \,\pi_{A}^{ + } (z_{i} )}}} \right)} . $$

(5)

Wei and Zhang (2015):

$$ H_{WZ} \left( P \right) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\cos } \left( {\tfrac{{\left( {\left| {b_{P}^{ - } (z_{i} ) - n_{P}^{ - } (z_{i} )} \right| + \left| {b_{P}^{ + } (z_{i} ) - n_{P}^{ + } (z_{i} )} \right|} \right)\,\pi }}{{2\left( {2 + \,\pi_{P}^{ - } (z_{i} ) + \,\pi_{P}^{ - } (z_{i} )} \right)}}} \right), $$

(6)

Meng and Chen (2016):

$$ H_{MC} \left( P \right) = \,\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\tfrac{{\hbox{min} \left\{ {b_{P}^{ - } (z_{i} ),\,n_{P}^{ - } (z_{i} )} \right\} + \hbox{min} \left\{ {b_{P}^{ + } (z_{i} ),\,n_{P}^{ + } (z_{i} )} \right\}}}{{\hbox{max} \left\{ {b_{P}^{ - } (z_{i} ),\,n_{P}^{ - } (z_{i} )} \right\} + \hbox{max} \left\{ {b_{P}^{ + } (z_{i} ),\,n_{P}^{ + } (z_{i} )} \right\}}}} \right)} , $$

(7)

Rani et al. (20118a, 2018b):

$$ \begin{aligned} H_{R} (P) & = \,\tfrac{1}{{n\left( {\sqrt e \, - 1} \right)}}\sum\limits_{i = \,1}^{n} {\left[ {\left( \begin{aligned} \tfrac{1}{4}\left\{ {\left( {b_{P}^{ - } (z_{i} ) + b_{P}^{ + } (z_{i} )} \right) + 2} \right. \hfill \\ \left. { - \left( {n_{P}^{ - } (z_{i} ) + \,n_{P}^{ + } (z_{i} )} \right)} \right\} \hfill \\ \end{aligned} \right)\,e^{{\left( \begin{aligned} \tfrac{1}{4}\left\{ {\left( {n_{P}^{ - } (z_{i} ) + \,n_{P}^{ + } (z_{i} )} \right) + \,2} \right. \hfill \\ \left. { - \,\left( {b_{P}^{ - } (z_{i} ) + b_{P}^{ + } (z_{i} )} \right)} \right\} \hfill \\ \end{aligned} \right)}} } \right.} \\ & \quad + \left. {\left( \begin{aligned} \tfrac{1}{4}\left\{ {\left( {n_{P}^{ - } (z_{i} ) + \,n_{P}^{ + } (z_{i} )} \right) + \,2} \right. \hfill \\ \left. { - \,\left( {b_{P}^{ - } (z_{i} ) + b_{P}^{ + } (z_{i} )} \right)} \right\} \hfill \\ \end{aligned} \right)\,e^{{\left( \begin{aligned} \tfrac{1}{4}\left\{ {\left( {b_{P}^{ - } (z_{i} ) + b_{P}^{ + } (z_{i} )} \right) + \,2} \right. \hfill \\ \left. { - \,\left( {n_{P}^{ - } (z_{i} ) + \,n_{P}^{ + } (z_{i} )} \right)} \right\} \hfill \\ \end{aligned} \right)}} - 1} \right]. \\ \end{aligned} $$

(8)

Example 3.1

Let us compute entropy measures for the following IVIFSs:

$$ \begin{aligned} & P_{1} \, = \left\{ {\left\langle {z_{i} ,\,[0.1,\,0.2],\,[0.5,\,0.6]} \right\rangle :\,z_{i} \, \in \,Z} \right\},\,P_{2} \, = \left\{ {\left\langle {z_{i} ,\,[0.2,\,0.3],\,[0.4,\,0.6]} \right\rangle :\,z_{i} \, \in \,Z} \right\}, \\ & P_{3} \, = \left\{ {\left\langle {z_{i} ,\,[0.3,\,0.4],\,[0.5,\,0.6]} \right\rangle :\,z_{i} \, \in \,Z} \right\}.\,\,{\text{and}}\,\,P_{4} \, = \left\{ {\left\langle {z_{i} ,\,[0.2,\,0.2],\,[0.2,\,0.3]} \right\rangle :\,z_{i} \, \in \,Z} \right\}. \\ \end{aligned} $$

The above mentioned entropy measures (4)–(8) satisfy the set of requirements in Definition 2.7. Table 1 represents the values of the different entropy measures.

Table 1 Comparison results of different entropy measures

It can be interpreted that the closer the membership degree to the non-membership degree, the higher the value of interval-valued intuitionistic fuzzy entropy. And hence, from Table 1, it can be constructed that the measures are satisfied the following order:

$$ \begin{aligned} & H_{C} (P_{1} )\, < \,H_{C} (P_{2} )\, < H_{C} (P_{3} )\, < \,H_{C} (P_{4} ),\,H_{W} (P_{1} )\, < \,H_{W} (P_{2} )\, < H_{W} (P_{3} )\, < \,H_{W} (P_{4} ), \\ & H_{WZ} (P_{1} )\, < \,H_{WZ} (P_{2} )\, < H_{WZ} (P_{3} )\, < \,H_{WZ} (P_{4} ),\,H_{MC} (P_{1} )\, < \,H_{MC} (P_{2} )\, < H_{MC} (P_{3} )\, < \,H_{MC} (P_{4} ), \\ & H_{R} (P_{1} )\, < \,H_{R} (P_{2} )\, < H_{R} (P_{3} )\, < \,H_{R} (P_{4} )\,{\text{and}}\,\,H(P_{1} )\, < \,H(P_{2} )\, < H(P_{3} )\, < \,H(P_{4} ). \\ \end{aligned} $$

Thus, the obtained result of the proposed interval-valued intuitionistic fuzzy entropy measure (3) is in accordance with existing measures.

3.2 Divergence Measure for IVIFSs

Based on Mishra et al. (2017b), we propose the following Jensen-Shannon divergence measure for IVIFSs as follows:

$$ \begin{aligned} D_{v} \left( {P,\,Q} \right) & = \frac{ - 1}{{n\sqrt e \left( {\sqrt e - 1} \right)}}\sum\limits_{i = 1}^{n} {\left[ {\tfrac{\begin{subarray}{l} \left( {b_{P}^{ - } (z_{i} ) + b_{Q}^{ - } (z_{i} )} \right) + \left( {b_{P}^{ + } (z_{i} ) + b_{Q}^{ + } (z_{i} )} \right) + 4 \\ \,\,\,\,\,\,\,\, - \left( {n_{P}^{ - } (z_{i} ) + n_{Q}^{ - } (z_{i} )} \right) - \left( {n_{P}^{ + } (z_{i} ) + n_{Q}^{ + } (z_{i} )} \right) \end{subarray} }{8}\,\exp \left( {\tfrac{\begin{subarray}{l} \left( {b_{P}^{ - } (z_{i} ) + b_{Q}^{ - } (z_{i} )} \right) + \left( {b_{P}^{ + } (z_{i} ) + b_{Q}^{ + } (z_{i} )} \right) + 4 \\ \,\,\,\,\,\,\,\, - \left( {n_{P}^{ - } (z_{i} ) + n_{Q}^{ - } (z_{i} )} \right) - \left( {n_{P}^{ + } (z_{i} ) + n_{Q}^{ + } (z_{i} )} \right) \end{subarray} }{8}} \right)} \right.} \\ & \quad + \,\tfrac{\begin{subarray}{l} \left( {n_{P}^{ - } (z_{i} ) + n_{Q}^{ - } (z_{i} )} \right) + \left( {n_{P}^{ + } (z_{i} ) + n_{Q}^{ + } (z_{i} )} \right) + 4 \\ \,\,\,\,\,\,\,\, - \left( {b_{P}^{ - } (z_{i} ) + b_{Q}^{ - } (z_{i} )} \right) - \left( {b_{P}^{ + } (z_{i} ) + b_{Q}^{ + } (z_{i} )} \right) \end{subarray} }{8}\exp \left( {\tfrac{\begin{subarray}{l} \left( {n_{P}^{ - } (z_{i} ) + n_{Q}^{ - } (z_{i} )} \right) + \left( {n_{P}^{ + } (z_{i} ) + n_{Q}^{ + } (z_{i} )} \right) + 4 \\ \,\,\,\,\,\,\,\, - \left( {b_{P}^{ - } (z_{i} ) + b_{Q}^{ - } (z_{i} )} \right) - \left( {b_{P}^{ + } (z_{i} ) + b_{Q}^{ + } (z_{i} )} \right) \end{subarray} }{8}} \right) \\ & \quad - \,\frac{1}{2}\left\{ {\tfrac{{\left( {b_{P}^{ - } (z_{i} ) + b_{P}^{ + } (z_{i} )} \right) + 2 - \left( {n_{P}^{ - } (z_{i} ) + \,n_{P}^{ + } (z_{i} )} \right)}}{4}\,\exp \left( {\tfrac{{\left( {b_{P}^{ - } (z_{i} ) + b_{P}^{ + } (z_{i} )} \right) + 2 - \left( {n_{P}^{ - } (z_{i} ) + \,n_{P}^{ + } (z_{i} )} \right)}}{4}} \right)} \right. \\ & \quad + \,\tfrac{{\left( {n_{P}^{ - } (z_{i} ) + n_{P}^{ + } (z_{i} )} \right) + 2 - \left( {b_{P}^{ - } (z_{i} ) + b_{P}^{ + } (z_{i} )} \right)}}{4}\,\exp \left( {\tfrac{{\left( {n_{P}^{ - } (z_{i} ) + n_{P}^{ + } (z_{i} )} \right) + 2 - \left( {b_{P}^{ - } (z_{i} ) + b_{P}^{ + } (z_{i} )} \right)}}{4}} \right) \\ & \quad + \,\tfrac{{\left( {b_{Q}^{ - } (z_{i} ) + b_{Q}^{ + } (z_{i} )} \right) + 2 - \left( {n_{Q}^{ - } (z_{i} ) + n_{Q}^{ + } (z_{i} )} \right)}}{4}\,\exp \left( {\tfrac{{\left( {b_{Q}^{ - } (z_{i} ) + b_{Q}^{ + } (z_{i} )} \right) + 2 - \left( {n_{Q}^{ - } (z_{i} ) + n_{Q}^{ + } (z_{i} )} \right)}}{4}} \right) \\ & \quad \left. {\left. { + \tfrac{{\left( {n_{Q}^{ - } (z_{i} ) + n_{Q}^{ + } (z_{i} )} \right) + 2 - \left( {b_{Q}^{ - } (z_{i} ) + b_{Q}^{ + } (z_{i} )} \right)}}{4}\exp \left( {\tfrac{{\left( {n_{Q}^{ - } (z_{i} ) + n_{Q}^{ + } (z_{i} )} \right) + 2 - \left( {b_{Q}^{ - } (z_{i} ) + b_{Q}^{ + } (z_{i} )} \right)}}{4}} \right)} \right\}} \right]. \\ \end{aligned} $$

(9)

Theorem 3.2

The mapping $D_{v} (P,\,Q),$ defined by (9), is a valid divergence measure for IVIFSs.

Proof

In order for (9) to be qualified as a valid divergence measure for IVIFSs, it must satisfy the axioms (A1)–(A4) of Definition 2.8.

• (A1). It is evident from (9) that $D_{v} (P,\,Q)\, = \,D_{v} (Q,\,P).$

• (A2). If $P\, = \,Q,$ then we can easily obtain that $D_{v} \left( {P,\,Q} \right)\, = \,0.$

• (A3). For every $P,\,Q,\,R\, \in \,IVIFSs\left( Z \right).$ To prove (A3), we partition $Z$ into the following eight subsets:

  $$ \begin{aligned} Z & = \left\{ {z_{i} \in Z|\,P\left( {z_{i} } \right) \le Q\left( {z_{i} } \right) = R\left( {z_{i} } \right)} \right\} \cup \left\{ {z_{i} \in Z|\,P\left( {z_{i} } \right) = R\left( {z_{i} } \right) \le Q\left( {z_{i} } \right)} \right\} \\ & \quad \cup \left\{ {z_{i} \in Z|\,P\left( {z_{i} } \right) \le Q\left( {z_{i} } \right) < R\left( {z_{i} } \right)} \right\} \cup \left\{ {z_{i} \in Z|\,P\left( {z_{i} } \right) \le R\left( {z_{i} } \right) < Q\left( {z_{i} } \right)} \right\} \\ & \quad \cup \left\{ {z_{i} \in Z|\,Q\left( {z_{i} } \right) < P\left( {z_{i} } \right) \le R\left( {z_{i} } \right)} \right\} \cup \left\{ {z_{i} \in Z|\,Q\left( {z_{i} } \right) \le R\left( {z_{i} } \right) < P\left( {z_{i} } \right)} \right\} \\ & \quad \cup \left\{ {z_{i} \in Z|\,R\left( {z_{i} } \right) < P\left( {z_{i} } \right) \le Q\left( {z_{i} } \right)} \right\} \cup \left\{ {z_{i} \in Z|\,R\left( {z_{i} } \right) < Q\left( {z_{i} } \right) < P\left( {z_{i} } \right)} \right\}, \\ \end{aligned} $$

  which are denoted by $\delta_{1} ,\,\delta_{2} ,\, \ldots ,\delta_{8} .$ From Montes et al. (2002), for each $\delta_{j} ;\,\,j = 1,\,2,\, \ldots ,\,8,\,$

  $$\begin{aligned} &\left| {\left( {P \cup R} \right)\left( {z_{i} } \right) - \left( {Q \cup R} \right)\left( {z_{i} } \right)} \right| \le \left| {P\left( {z_{i} } \right) - Q\left( {z_{i} } \right)} \right|\\ &\quad \,\,{\text{and}}\,\left| {\left( {P \cap R} \right)\left( {z_{i} } \right) - \left( {Q \cap R} \right)\left( {z_{i} } \right)} \right| \le \left| {P\left( {z_{i} } \right) - Q\left( {z_{i} } \right)} \right|.\end{aligned} $$

  This implies that $D_{v} \left( {P \cup R,\,Q \cup R} \right) \le D_{v} \left( {P,\,Q} \right)$ for every $R \in IVIFS\left( Z \right).$

• (A4). The proof is similar as (A3).

Proposition 3.1

Let $P,\,Q,\,R \in \,IVIFSs(Z).$ The measure, defined by (9), satisfies the following postulates:

• (i) $0\, \le \,D_{v} \left( {P,\,Q\,} \right)\, \le \,\,1;$

• (ii) $D_{v} \left( {P,\,Q} \right)\, = \,D_{v} \left( {P^{c} ,\,Q^{c} } \right);$

• (iii) $D_{v} \left( {P,\,Q^{c} } \right)\, = \,D_{v} \left( {P^{c} ,Q} \right);$

• (iv) $D_{v} \left( {P,P^{c} } \right) = \,1$ if and only if $P$ is a crisp set;

• (v) $D_{v} \left( {P,\,P^{c} } \right) = \,0$ if and only if $b_{P} (z_{i} ) = \,n_{P} (z_{i} )$ for all $z_{i} \in \,Z;$

• (vi) $D_{v} \left( {P \cap Q,\,P \cup Q} \right)\, = \,D_{v} \left( {P,\,Q} \right);$

• (vii) $D_{v} \left( {P,\,Q} \right) \le \,D_{v} \left( {P,\,R} \right)$ and $D_{v} \left( {Q{,}R} \right) \le \,D_{v} \left( {P,\,R} \right)$ for $P\, \subseteq \,Q \subseteq \,R.$

3.3 Similarity Measures for IVIFSs

Let $P{,}Q\, \in IVIFSs(Z).$ Corresponding to Hung and Yang (2004), a new interval-valued intuitionistic fuzzy similarity measure is defined as

$$ \Delta (P,\,Q) = 1 - \tfrac{{1 - \exp \left[ { - \frac{1}{4n}\sum\limits_{i = 1}^{n} {\left( {\left| {b_{P}^{ - } (z_{i} )\, - \,b_{Q}^{ - } (z_{i} )} \right| + \left| {b_{P}^{ + } (z_{i} )\, - \,b_{Q}^{ + } (z_{i} )} \right|\,\, + \left| {n_{P}^{ - } (z_{i} )\, - \,n_{Q}^{ - } (z_{i} )} \right| + \left| {n_{P}^{ + } (z_{i} )\, - \,n_{Q}^{ + } (z_{i} )} \right|} \right)} } \right]}}{1 - \exp ( - 1)}. $$

(10)

Lemma 3.1

If $h(\lambda ) = 1 - \frac{1 - \exp ( - \lambda )}{1 - \exp ( - 1)},$ then

$$ \mathop {\hbox{max} }\limits_{\lambda \in [0,\,n]} h(\lambda ) = h(0) = 1\,\,{\text{and}}\,\,\mathop {\hbox{min} }\limits_{\lambda \in [0,\,n]} h(\lambda ) = h(n) = 0. $$

Proof

Since $h^{'} (\lambda ) = - \frac{\exp ( - \lambda )}{1 - \exp ( - 1)} < 0,\,\,\forall \,\lambda \in [0,\,\,n],$ therefore, $h\left( \lambda \right)$ is decreasing in $[0,\,n].$

Theorem 3.3

The function $\Delta \left( {P,\,Q} \right),$ defined by (10), is a valid similarity measure for IVIFSs.

Proof

To proof this theorem, we must have to satisfies the conditions (C1)–(C4) of Definition 2.9.

• (C1). Consider $P,\,Q\, \in \,IVIFSs(Z)$ and

  $$ \lambda \, = \,\frac{1}{4n}\sum\limits_{i = 1}^{n} {\left( {\left| {b_{P}^{ - } (z_{i} )\, - \,b_{Q}^{ - } (z_{i} )} \right| + \left| {b_{P}^{ + } (z_{i} )\, - \,b_{Q}^{ + } (z_{i} )} \right|\,\, + \left| {n_{P}^{ - } (z_{i} )\, - \,n_{Q}^{ - } (z_{i} )} \right| + \left| {n_{P}^{ + } (z_{i} )\, - \,n_{Q}^{ + } (z_{i} )} \right|} \right)} . $$

  Since $\lambda \, \in \,\left[ {0,\,n} \right],$ therefore, $\Delta \left( {P,\,Q} \right)\, = \,h\left( \lambda \right).$ Hence, using Lemma 3.1, we have $0\, \le \,\Delta \left( {P,\,Q} \right)\, \le \,1.$

• (C2). Suppose $P\, = \,Q$ that means $\left[ {b_{P}^{ - } (z_{i} ),\,b_{P}^{ + } (z_{i} )} \right] = \,\left[ {n_{P}^{ - } (z_{i} ),\,\,n_{P}^{ + } (z_{i} )} \right].$ Then, it is evident from (10) that $\Delta \left( {P,\,Q} \right)\, = 1.$

  Let $\Delta \left( {P,\,Q} \right)\, = 1.$ From (10), we obtain

  $$ 1 - \tfrac{{1 - \exp \left[ { - \frac{1}{4n}\sum\limits_{i = 1}^{n} {\left( {\left| {b_{P}^{ - } (z_{i} )\, - \,b_{Q}^{ - } (z_{i} )} \right| + \left| {b_{P}^{ + } (z_{i} )\, - \,b_{Q}^{ + } (z_{i} )} \right|\,\, + \left| {n_{P}^{ - } (z_{i} )\, - \,n_{Q}^{ - } (z_{i} )} \right| + \left| {n_{P}^{ + } (z_{i} )\, - \,n_{Q}^{ + } (z_{i} )} \right|} \right)} } \right]}}{1 - \exp ( - 1)}\, = 1,\,\forall \,z_{i} \, \in \,Z. $$

  It implies that

  $$\begin{aligned} &\left| {b_{P}^{ - } \left( {z_{i} } \right) - \,b_{Q}^{ - } \left( {z_{i} } \right)} \right|\, + \,\left| {b_{P}^{ + } \left( {z_{i} } \right) - \,b_{Q}^{ + } \left( {z_{i} } \right)} \right|\\ &\quad + \,\left| {n_{P}^{ - } \left( {z_{i} } \right) - \,n_{Q}^{ - } \left( {z_{i} } \right)} \right|\, + \,\left| {n_{P}^{ + } \left( {z_{i} } \right) - \,n_{Q}^{ + } \left( {z_{i} } \right)} \right|\, = \,0,\,\forall \,z_{i} \, \in \,Z.\end{aligned} $$

  Hence $P\, = \,Q.$

• (C3). It is clear from the definition that $\Delta \left( {P,\,Q} \right)\, = \,\Delta \left( {Q,\,P} \right).$

• (C4). Given that $P\, \subseteq \,Q\, \subseteq \,R,$ then

  $$ \begin{aligned} & b_{P}^{ - } \left( {z_{i} } \right)\, \le \,b_{Q}^{ - } \left( {z_{i} } \right)\, \le \,b_{R}^{ - } \left( {z_{i} } \right),\,\,b_{P}^{ + } \left( {z_{i} } \right)\, \le \,b_{Q}^{ + } \left( {z_{i} } \right)\, \le \,b_{R}^{ + } \left( {z_{i} } \right), \\ & n_{P}^{ - } \left( {z_{i} } \right)\, \ge \,n_{Q}^{ - } \left( {z_{i} } \right)\, \ge n_{R}^{ - } \left( {z_{i} } \right)\,\,{\text{and}}\,\,n_{P}^{ + } \left( {z_{i} } \right)\, \ge \,n_{Q}^{ + } \left( {z_{i} } \right)\, \ge n_{R}^{ + } \left( {z_{i} } \right),\,\forall \,z_{i} \, \in \,Z. \\ \end{aligned} $$

  Then,

  $$ \begin{aligned} \lambda_{1} & = \frac{1}{4}\sum\limits_{i = \,1}^{n} {\left( {\left| {b_{P}^{ - } (z_{i} ) - \,b_{Q}^{ - } (z_{i} )} \right| + \left| {b_{P}^{ + } (z_{i} ) - \,b_{Q}^{ + } (z_{i} )} \right| + \left| {n_{P}^{ - } (z_{i} ) - \,n_{Q}^{ - } (z_{i} )} \right| + \left| {n_{P}^{ + } (z_{i} ) - \,n_{Q}^{ + } (z_{i} )} \right|} \right)} \\ & \le \,\lambda_{2} = \frac{1}{4}\sum\limits_{i = \,1}^{n} {\left( {\left| {b_{P}^{ - } (z_{i} ) - \,b_{R}^{ - } (z_{i} )} \right| + \left| {b_{P}^{ + } (z_{i} ) - \,b_{R}^{ + } (z_{i} )} \right| + \left| {n_{P}^{ - } (z_{i} ) - \,n_{R}^{ - } (z_{i} )} \right| + \left| {n_{P}^{ + } (z_{i} ) - \,n_{R}^{ + } (z_{i} )} \right|} \right)} ,\,\forall \,z_{i} \, \in \,Z. \\ \end{aligned} $$

As a consequence, by means of Lemma 3.1, we get $\Delta \left( {P,\,Q} \right)\, = \,h\left( {\lambda_{1} } \right) \ge \,\,h\left( {\lambda_{2} } \right)\, = \,\Delta \left( {P,\,R} \right).$ In the similar manner, we can prove that $\Delta \left( {Q,\,R} \right)\, \ge \,\Delta \left( {P,\,R} \right).$

With the similar manner, similarity measure between two matrices is proposed.

Definition 3.1

Let $P = \left( {p_{ij} } \right)$ and $Q = \left( {q_{ij} } \right),\,\,i = 1,\,2,\, \ldots ,\,m,j = 1,\,2,\, \ldots ,\,n$ be two matrices such that $p_{ij} = \left\langle {\left[ {\alpha_{ij}^{1} ,\,\,\beta_{ij}^{1} } \right],\left[ {\gamma_{ij}^{1} ,\,\,\delta_{ij}^{1} } \right]\,} \right\rangle$ and $q_{ij} = \left\langle {\left[ {\alpha_{ij}^{2} ,\,\,\beta_{ij}^{2} } \right],\left[ {\gamma_{ij}^{2} ,\,\,\delta_{ij}^{2} } \right]\,} \right\rangle$ are IVIFNs. Then, the similarity measure between $P$ and $Q$ is defined as below:

$$ \Delta \left( {P,Q} \right) = 1 - \frac{{1 - \exp \left[ { - \frac{1}{4\,m\,n}\sum\limits_{i\, = 1}^{m} {\sum\limits_{j\, = 1}^{n} {\left( {\left| {\alpha_{ij}^{1} - \alpha_{ij}^{2} } \right| + \left| {\beta_{ij}^{1} - \beta_{ij}^{2} } \right|\,\, + \left| {\gamma_{ij}^{1} - \gamma_{ij}^{2} } \right| + \left| {\delta_{ij}^{1} - \delta_{ij}^{2} } \right|} \right)} } } \right]}}{1 - \exp ( - 1)}. $$

(11)

4 Interval-Valued Intuitionistic Fuzzy WASPAS (IVIF-WASPAS) Method for MCDM Problems

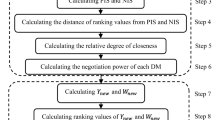
In this section, the interval-valued intuitionistic fuzzy WASPAS (IVIF-WASPAS) method is discussed for evaluating and ranking the alternatives based on set of different criteria. The procedure for IVIF-WASPAS method is given as follows (see Fig. 1):

Fig. 1

The framework of proposed IVIF-WASPAS method

Algorithm 1: IVIF-WASPAS method

Step 1 Formulate the alternative and criteria.

In the process of decision making, our main goal is to select the most appropriate alternative among set of $m$ alternatives $V = \left\{ {V_{1} ,\,V_{2} , \ldots ,\,V_{m} } \right\}$ with respect to the criterion set $F = \left\{ {F_{1} ,\,F_{2} , \ldots ,\,F_{n} } \right\}.$ Assume that a committee (group) of $t$ decision experts $B = \left\{ {B_{1} ,\,B_{2} , \ldots ,\,B_{t} } \right\}$ has been constituted to determine the most suitable alternative(s).

Step 2 Compute the weights of decision experts.

Due to uncertain information and imprecise human knowledge, decision expert $B_{k}$ cannot easily estimate an exact value to alternative $V_{i}$ with respect to criterion $F_{j} .$ The decision experts express their opinions in terms of IVIFN because of its capability to handle the uncertainty. Let $P_{k} = \left( {p_{ijk} } \right)$ be the decision matrix of $k{\text{th}}$ decision expert such that $p_{ijk} = \left\langle {\left[ {b_{ijk}^{ - } ,\,b_{ijk}^{ + } } \right],\left[ {n_{ijk}^{ - } ,\,n_{ijk}^{ + } } \right]\,} \right\rangle ,$ $k = 1,\,2,\, \ldots ,\,t$ is an IVIFN. Next, we construct preference selection matrix $P_{*} = \left( {p_{ij*} } \right)$ such that preference selection value is $p_{ij*} = \left( {{1 \mathord{\left/ {\vphantom {1 t}} \right. \kern-0pt} t}} \right)\sum\nolimits_{k = 1}^{t} {p_{ijk} } ,$ and by using (2), we obtain

$$ p_{ij*} = \left\langle {\left[ {1 - \prod\limits_{k = 1}^{t} {\left( {1 - b_{ijk}^{ - } } \right)^{{{1 \mathord{\left/ {\vphantom {1 t}} \right. \kern-0pt} t}}} } ,\,1 - \prod\limits_{k = 1}^{t} {\left( {1 - b_{ijk}^{ + } } \right)^{{{1 \mathord{\left/ {\vphantom {1 t}} \right. \kern-0pt} t}}} } } \right]} \right.,\,\left. {\left[ {\prod\limits_{k = 1}^{t} {\left( {n_{ijk}^{ - } } \right)^{{{1 \mathord{\left/ {\vphantom {1 t}} \right. \kern-0pt} t}}} } ,\,\prod\limits_{k = 1}^{t} {\left( {n_{ijk}^{ + } } \right)^{{{1 \mathord{\left/ {\vphantom {1 t}} \right. \kern-0pt} t}}} } } \right]} \right\rangle . $$

(12)

where $p_{ij*} = \left\langle {\left[ {b_{ij*}^{ - } ,\,b_{ij*}^{ + } } \right],\left[ {n_{ij*}^{ - } ,\,n_{ij*}^{ + } } \right]\,} \right\rangle$ is an IVIFN.

During the process of decision making, computation of weight of a decision expert is a necessary step. In this method, we apply the doctrine of similarity measure to obtain the decision experts’ weight. The higher the similarity index of decision matrix $B_{k}$ form preference selection matrix has the higher importance for $B_{k} .$ Hence, based on similarity measure, we evaluate overall preference value of the decision matrix of $B_{k}$ and preference selection matrix $P_{*} ,$ which is given as follows:

$$ {\mathbb{C}}\left( {P_{k} ,\,P_{*} } \right) = \frac{{\Delta \left( {P_{k} ,\,P_{*} } \right)}}{{\Delta \left( {P_{k} ,\,P_{*} } \right) + \Delta \left( {P_{k} ,\,P_{*}^{c} } \right)}}, $$

(13)

where $P_{*}^{c}$ is the complement of preference selection matrix $P_{*} ,$ $\Delta \left( {P_{k} ,\,P_{*} } \right)$ and $\Delta \left( {P_{k} ,\,P_{*}^{c} } \right)$ denote the similarity measures between $P_{k}$ and $P_{*}$, and $P_{k}$ and $P_{*}^{c} ,$ respectively.

Subsequently, based on overall preference value, the decision experts’ weights are determined as follows:

$$ \varpi_{k} = \frac{{{\mathbb{C}}\left( {P_{k} ,\,P_{*} } \right)}}{{\sum\limits_{k = 1}^{t} {{\mathbb{C}}\left( {P_{k} ,\,P_{*} } \right)} }},\,\,k = 1,\,2,\, \ldots ,\,t. $$

(14)

Evidently, $\varpi_{k} \ge 0$ and $\sum\nolimits_{k = 1}^{t} {\varpi_{k} = 1.}$

Step 3 Determine the aggregated interval-valued intuitionistic fuzzy decision matrix.

In order to aggregate all the individual decisions and create single group decision, we have to create aggregated interval-valued intuitionistic fuzzy decision matrix. For this, let $P = \left( {p_{ij} } \right) = \left\langle {\left[ {b_{ij}^{ - } ,\,b_{ij}^{ + } } \right],\,\left[ {n_{ij}^{ - } ,\,n_{ij}^{ + } } \right]} \right\rangle ,$ $i = 1,\,2,\, \ldots ,\,m,$ $j = 1,\,2,\, \ldots ,\,n$ be the aggregated interval-valued intuitionistic fuzzy decision matrix, where $P = \sum\nolimits_{k = 1}^{t} {\varpi_{k} P_{k} }$ and

$$ p_{ij} = \left\langle {\left[ {1 - \prod\limits_{k = 1}^{t} {\left( {1 - b_{ijk}^{ - } } \right)^{{\varpi_{k} }} } ,\,1 - \prod\limits_{k = 1}^{t} {\left( {1 - b_{ijk}^{ + } } \right)^{{\varpi_{k} }} } } \right]} \right.,\,\left. {\left[ {\prod\limits_{k = 1}^{t} {\left( {n_{ijk}^{ - } } \right)^{{\varpi_{k} }} } ,\,\prod\limits_{k = 1}^{t} {\left( {n_{ijk}^{ + } } \right)^{{\varpi_{k} }} } } \right]} \right\rangle . $$

(15)

Step 4 Calculate the weights of the criteria.

To determine the relative importance of each criterion, we have developed the following formula with the help of entropy and divergence measures:

$$ \wp_{j} \, = \,\tfrac{{\sum\limits_{i = \,1}^{m} {\left[ {\tfrac{1}{m\, - 1}\sum\limits_{k = \,1}^{m} {D_{v} \left( {\eta_{ij} ,\,\eta_{kj} } \right)\, + \left( {1\, - \,H\left( {\eta_{ij} } \right)} \right)} } \right]} }}{{\sum\limits_{j = \,1}^{n} {\sum\limits_{i = \,1}^{m} {\left[ {\tfrac{1}{m\, - 1}\sum\limits_{k = \,1}^{m} {D_{v} \left( {\eta_{ij} ,\,\eta_{kj} } \right)\, + \left( {1\, - \,H\left( {\eta_{ij} } \right)} \right)} } \right]} } }},\,\,j\, = 1,\,2,\, \ldots ,\,n. $$

(16)

Here, $D_{v} \left( {\eta_{ij} ,\,\eta_{kj} } \right)$ denotes the divergence measure between $\eta_{ij}$ and $\eta_{kj} ,$ and $H\left( {\eta_{ij} } \right)$ denotes the entropy measure of $\eta_{ij} .$

Step 5 Compute the measures of weighted sum model (WSM) $S_{i}^{(1)}$ for each alternative using the formula

$$ S_{i}^{(1)} \, = \,\sum\limits_{j = \,1}^{n} {\wp_{j} \,\eta_{ij} } . $$

(17)

Step 6 Compute the measures of weighted product model (WPM) $S_{i}^{(2)}$ for each alternative by using the following formula

$$ S_{i}^{(2)} \, = \,\prod\limits_{j\, = 1}^{n} {\wp_{j} \,\eta_{ij} } . $$

(18)

Step 7 Calculate the aggregated measure of the WASPAS method for each alternative, which as

$$ S_{i} \, = \,\lambda \,S_{i}^{(1)} \, + \,\left( {1 - \,\lambda } \right)\,S_{i}^{(2)} . $$

(19)

where $\lambda$ is the aggregating coefficient of decision precision. It is developed to estimate the accuracy of WASPAS based on initial criteria exactness and when $\lambda \in \left[ {0,\,\,1} \right]$ (when $\lambda = 0,$ and $\lambda = 1,$ WASPAS is transformed to the WPM and the WSM, respectively). It has been proven that the accuracy of the aggregating methods is higher than the accuracy of single ones.

Step 8 Rank the alternatives according to decreasing values (i.e., crisp score values) of $S_{i} .$

Step 9 End.

5 Application of the Proposed Method for Reservoir Flood Control Management

In this section, to exemplify the efficacy of the IVIF-WASPAS method, an evaluation problem of reservoir flood control management is presented (Hashemi et al. 2014).

Due to huge critical potency and high prevalence, the flood calamity is one of the most serious natural hazard for civilization and hence, a flood control management policy is required to reduce the flood calamity and at the same time, maintains the water intensity of the reservoir as low as possible at the ending of this flood. Usually, the reservoir flood control management is very complicated in nature as it depends on several uncertain factors arises due to environmental, political and social impacts. Here, we consider a decision making problem of reservoir flood control management policy, where the decision experts express their estimations with interval-valued intuitionistic fuzzy information. In the intial step, a team of five decision experts $B_{1} ,$ $B_{2} ,$ $B_{3} ,$ $B_{4}$ and $B_{5}$ is created to perform the assessment of management policies of reservoir flood control under IVIFSs.

The proposed IVIF-WASPAS method is applied to evaluate an optimal reservoir flood control management. The procedural steps are as follows:

Step 1 With the preliminary screening, the skillful group offers five possible management policy alternatives $V_{1} ,$ $V_{2} ,$ $V_{3} ,$ $V_{4}$ and $V_{5} ,$ and these policies are evaluated with respect to the following criteria: (i) Flood control storage between the design flood level and the highest level of reservoir during reservoir routing (F₁), The storage between the terminal level of reservoir and the desired terminal level (F₂), The spillover volume beyond the limit of discharge for power generation (F₃), Flood control risk of the protected downstream area (F₄), Flood control risk of the reservoir (F₅), Sediment load in reservoir area (F₆), Risk of failure of the dam and its structures (F₇), Flood peak discharge at downstream (F₈), Drainage area (F₉), Sediment transport (F₁₀), Trap efficiency (F₁₁) and Dead storage level (F₁₂).

Here, Table 2 presents the linguistic ratings in terms of IVIFNs for the importance of criteria and the alternatives. Tables 3, 4, 5, 6 and 7 show the linguistic ratings by five decision experts for the criteria performances of given alternatives.

Table 2 Linguistic scale for the importance of criterion and the alternatives

Table 3 Linguistic ratings for criteria performances of alternatives from decision expert $B_{1}$

Table 4 Linguistic ratings for criteria performances of alternatives from decision expert $B_{2}$

Table 5 Linguistic ratings for criteria performances of alternatives from decision expert $B_{3}$

Table 6 Linguistic ratings for criteria performances of alternatives from decision expert $B_{4}$

Table 7 Linguistic ratings for criteria performances of alternatives from decision expert $B_{5}$

Step 2 The construction of preference selection matrix is necessary to determine the weights of the decision experts. Thus, with the help of (13), the preference selection matrix for the team of decision experts is calculated in Table 8.

Table 8 Preference selection matrix for decision experts’ weights

Using (10) and (13) in (14), the weight of the decision expert is computed and expressed in Table 9.

Table 9 Weights of decision experts

Step 3 With the use of (15), the aggregated interval-valued intuitionistic fuzzy decision matrix is estimated based on the decision experts’ opinions and thus, the result is shown in Table 10.

Table 10 Aggregated interval-valued intuitionistic fuzzy decision matrix

Step 4 In order to determine the weights of the criteria, use formula (16) in view of (3) and (9), hence, we obtain

$$ \begin{aligned} & \wp_{1} \, = \,0.1405,\,\,\wp_{2} \, = \,0.1092,\,\,\wp_{3} \, = \,0.0795,\,\,\wp_{4} \, = \,0.0549,\,\,\wp_{5} \, = \,0.0797,\,\,\wp_{6} \, = \,0.1367,\,\,\wp_{7} \, = \,0.0865, \\ & \wp_{8} \, = \,0.1447,\,\,\wp_{9} \, = \,0.0155,\,\,\wp_{10} \, = \,0.0216,\,\,\wp_{11} \, = \,0.0652\,\,{\text{and}}\,\,\wp_{12} \, = \,0.0660. \\ \end{aligned} $$

Step 5 With the use of formula (17), the calculated measures of weighted sum model (WSM) $S_{i}^{(1)}$ for each alternative.

Step 6 Using formula (18), the measures of weighted product model (WPM) $S_{i}^{(2)}$ for each alternative.

Step 7 The aggregated measure of the WASPAS method for each alternative is computed using formula (19) for $\lambda = 0.5.$

Table 11 presents the calculated measures of weighted sum model (WSM) $S_{i}^{(1)} ,$ weighted product model (WPM) $S_{i}^{(2)}$ and the aggregated measure of the WASPAS method for each alternative. From Table 11, the ranking of reservoir flood control operation management policy alternatives is $V_{3} \, \succ \,V_{2} \, \succ \,V_{5} \, \succ \,V_{4} \, \succ \,V_{1}$ and thus, $V_{3}$ is the best reservoir flood control operation management.

Table 11 The overall computational evaluation of IVIF-WASPAS method

6 Comparative Study and Sensitivity Analysis

In this section, the outcomes of the proposed IVIF-WASPAS method are demonstrated based on a comparison and a sensitivity analysis. Some MCDM methods have been introduced in recent years within the context of reservoir flood control operation management policy and different uncertain environment. Each of these methods has characteristics and steps which differentiate it from the others. Here, we have considered some methods for the comparison which have good efficiency in the literature and could be applicable in the considered multi-criteria decision-making problem. In the literature survey, Hameshi et al. (2015), Chitsaz and Banihabib (2015) and Zhu et al. (2016, 2018) proposed IVIF-VIKOR methods are selected for the comparative analysis. First, with the analysis on the same decision making problem mentioned in Sect. 5, we select the extended IVIF-VIKOR method to facilitate the comparative analysis.

6.1 Comparison with IVIF-VIKOR Method

The classical VIKOR method developed by Opricovic (1998), is a proficient approach to solve the MCDM problems with conflicting and noncommensurable criteria. This method helps to determine a compromise solution based on the particular measure of closeness to the ideal solution. The key concept of VIKOR method is to attain the compromise solution(s) corresponding to $L_{p}$-metric, which are used as an aggregating function in the compromise programming method. In point of fact, the compromise solution is a pareto optimal solution, nearest to the ideal solution based on the particular measure.

In the proposed method, the $L_{p}$-metric over the alternatives $V_{i} \,\left( {i\, = \,1,\,2,\, \ldots ,\,m} \right)$ for compromise programming is assessed on the basis of proposed divergence measure, which is given as

$$ L_{p,\,i} = \left( {\sum\limits_{j = \,1}^{n} {\left( {\wp_{j} \,\frac{{D_{v} \left( {\eta_{j}^{ + } ,\,\eta_{ij} } \right)}}{{D_{v} \left( {\eta_{j}^{ - } ,\,\eta_{j}^{ + } } \right)}}} \right)^{p} } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} ,\,\,1 \le \,p\, \le \,\infty ,\quad i\, = \,1,\,2,\, \ldots \,m, $$

(20)

where $\wp_{j}$ denotes the weights of the criteria, $\eta_{i}^{ + } \, = \,\mathop {\hbox{max} }\limits_{i} \,\eta_{ij}$ and $\eta_{i}^{ - } \, = \,\mathop {\hbox{min} }\limits_{i} \,\eta_{ij}$ are the ideal and anti-ideal points, respectively. The VIKOR method provides a maximum “group utility” for the “majority” and a minimum “individual regret” for the opponent, which are formulated by the metrics $L_{1,i}$ and $L_{\infty ,i} ,$ respectively. Due to rapid development of social economy, IVIFSs have been received considerable attention in the field of decision making. So, in this section, we have extended the classical VIKOR method to handle the MCDM problems under IVIFSs. Now, the procedure for interval-valued intuitionistic fuzzy VIKOR (IVIF-VIKOR) method has been given as in following steps:

Algorithm 2: IVIF-VIKOR Method

Steps 1–4 Steps 1–4 are same as Algorithm 1.

Step 5 Evaluate the ideal and anti-ideal points.

The ideal and anti-ideal points denoted by $\eta_{j}^{ + }$ and $\eta_{j}^{ - } ,$ respectively, are calculated on the basis of the following expressions:

$$ \eta_{j}^{ + } \, = \,\left\langle {\left[ {b_{j + }^{ - } ,\,b_{j + }^{ + } } \right],\,\left[ {n_{j + }^{ - } ,\,n_{j + }^{ + } } \right]} \right\rangle \, = \,\left\langle {\left[ {\mathop {\hbox{max} }\limits_{i} \,b_{ij}^{ - } ,\,\mathop {\hbox{max} }\limits_{i} b_{ij}^{ + } } \right],\,\left[ {\mathop {\hbox{min} }\limits_{i} \,n_{ij}^{ - } ,\,\mathop {\hbox{min} }\limits_{i} n_{ij}^{ + } } \right]} \right\rangle , $$

(21)

$$ \eta_{j}^{ - } \, = \,\left\langle {\left[ {b_{j - }^{ - } ,\,b_{j - }^{ + } } \right],\,\left[ {n_{j - }^{ - } ,\,n_{j - }^{ + } } \right]} \right\rangle \, = \,\left\langle {\left[ {\mathop {\hbox{min} }\limits_{i} \,b_{ij}^{ - } ,\,\mathop {\hbox{min} }\limits_{i} b_{ij}^{ + } } \right],\,\left[ {\mathop {\hbox{max} }\limits_{i} \,n_{ij}^{ - } ,\,\mathop {\hbox{max} }\limits_{i} n_{ij}^{ + } } \right]} \right\rangle . $$

(22)

Step 6 Determination of group utility, individual regret and compromise measure.

Compute the values of group utility, individual regret and compromise measure of the alternatives $V_{i} \,(i = \,1,\,2,\, \ldots ,\,m),$ respectively, using the relations

$$ \varLambda_{i} \, = \,L_{1,\,i} \, = \,\,\sum\limits_{j\, = 1}^{n} {\wp_{j} \,\frac{{D_{v} \left( {\eta_{j}^{ + } ,\,\eta_{ij} } \right)}}{{D_{v} \left( {\eta_{j}^{ - } ,\,\eta_{j}^{ + } } \right)}}} , $$

(23)

$$ \varPsi_{i} \, = \,L_{\infty ,\,i} \, = \,\mathop {\hbox{max} }\limits_{1\, \le \,j\, \le \,n} \left( {\wp_{j} \,\frac{{D_{v} \left( {\eta_{j}^{ + } ,\,\eta_{ij} } \right)}}{{D_{v} \left( {\eta_{j}^{ - } ,\,\eta_{j}^{ + } } \right)}}} \right), $$

(24)

$$ \varTheta_{i} \, = \,\varsigma \,\frac{{\left( {\varLambda_{i} - \,\varLambda^{ + } } \right)}}{{\left( {\varLambda^{ - } \, - \,\varLambda^{ + } } \right)}} + \,\left( {1 - \,\varsigma } \right)\,\frac{{\left( {\varPsi_{i} - \,\varPsi^{ + } } \right)}}{{\left( {\varPsi^{ - } \, - \,\varPsi^{ + } } \right)}}, $$

(25)

where $\varsigma$ denotes the coefficient of decision mechanism or weight of the decision making strategy of “the majority of criteria or the maximum group utility”.

Step 7 Rank the alternatives by sorting the values of $\varLambda_{i} ,\,\varPsi_{i}$ and $\varTheta_{i}$ in decreasing order.

Step 8 Find the best or compromise solution.

Uniqueness of final alternatives is satisfied by the following conditions:

Condition (1)

Acceptable advantage:

$$ \varTheta (V^{(2)} ) - \varTheta (V^{(1)} )\, \ge \,\frac{1}{(m - 1)}, $$

(26)

where $m$ is the number of alternatives, $V^{(1)}$ and $V^{(2)}$ are the alternatives with the first and second positions in the ranking list, respectively.

Condition (2)

Adequate stability: the alternative $V^{(1)}$ must also be the finest ranked by $\varLambda_{i}$ and $\varPsi_{i} .$ This compromise solution is stable within a decision making process which can be selected with “voting by majority rule $(\varsigma > 0.5)$” or “by consensus $(\varsigma \approx \,0.5)$” or “by veto $(\varsigma < \,0.5)$”.

If the Condition (1) is not fulfilled, then the maximum value of $M$ should be inspected by the following relation:

$$ \varTheta (V^{(M)} ) - \varTheta (V^{(1)} )\, < \,\frac{1}{(m - 1)}. $$

(27)

Thus, all the alternatives $V^{(i)} \,(i\, = 1,\,2,\, \ldots ,\,m)$ are the compromise solutions.

The alternatives $V^{(1)}$ and $V^{(2)}$ are compromise solutions in case of condition (2) is not satisfied.

Step 9 End.

Flowchart of the proposed IVIF-VIKOR method is depicted in Fig. 2.

Fig. 2

Schematic representation of proposed IVIF-VIKOR method

In the following steps, the proposed VIKOR method is applied to evaluate the suitable management policy for reservoir flood control:

Steps 1–4 Similar to Algorithm 1.

Step 5 The ideal and anti-ideal points are computed with the help of (21) and (22). Table 12 presents the result.

Table 12 Ideal and anti-ideal points

Step 6 Using (23)–(25), the values of group utility, individual regret and compromise measures of the alternatives $V_{i} \,\left( {i\, = 1,\,2,\,3,\,4,\,5} \right)$ are calculated in Table 13.

Table 13 Values of the $\varLambda_{i} ,$$\varPsi_{i}$ and $\varTheta_{i}$

Step 7 According to the decreasing values of $\varLambda_{i} ,\,\varPsi_{i}$ and $\varTheta_{i} \,\left( {\varsigma \, = \,0.5} \right),$ three ranking results are presented as below:

$$ \begin{aligned} & \varLambda_{3} \, \succ \,\varLambda_{4} \, \succ \,\varLambda_{5} \, \succ \,\varLambda_{2} \, \succ \,\varLambda_{1} , \\ & \varPsi_{3} \, \succ \,\varPsi_{5} \, \succ \,\varPsi_{4} \, \succ \,\varPsi_{1} \, \succ \,\varPsi_{2} , \\ \end{aligned} $$

and

$$ \varTheta_{3} \, \succ \,\varTheta_{4} \, \succ \,\varTheta_{5} \, \succ \,\varTheta_{2} \, \succ \,\varTheta_{1} . $$

Step 8 Corresponding to the decreasing values of $\varTheta_{i} ,$ the ranking order of the management policies is $V_{3} \, \succ \,V_{4} \, \succ \,V_{5} \, \succ \,V_{2} \, \succ \,V_{1}$ and hence, the alternative $V_{3}$ is the compromise solution. Since $\varTheta (V^{(2)} ) - \varTheta (V^{(1)} )\, = \,0.5252\, > \,\frac{1}{(5 - \,1)}\, = 0.25,$ therefore, the alternative $V_{3}$ assures both the conditions (1) and (2). Thus, the alternative $V_{3}$ is an optimal management policy for reservoir flood control and it is stable within a decision making process for different values of weight $\varsigma \,\,\left( {0.0\, \le \,\varsigma \, \le \,1.0} \right).$

To provide a better view of the comparison results, we put the results of the ranking of alternatives obtained by the IVIF-WASPAS and IVIF-VIKOR approaches into Fig. 3. From Fig. 3, we clearly know that the ranking orders of alternatives obtained by these two methods are remarkable different (optimal alternative $V_{3}$ is identical). Using the IVIF-WASPAS and IVIF-VIKOR methods, the best suitable recommended alternative in the above decision problem is $V_{3} .$

Fig. 3

The representation of the IVIF-COPRAS and IVIF-VIKOR methods rankings

To compare the results of the proposed approach with the other existing methods, we use the Spearman’s rank correlation coefficient $\left( {r_{G} } \right).$ Table 14 shows the interpretation of different values of $r_{G}$ (Walters 2009). According to this table, when the value of $r_{G}$ is greater than 0.6, it can be said that there is high statistical dependency between results. The results of comparison between the proposed method and the existing methods are represented in Table 15. As can be seen in this table, most of correlation coefficients are greater than 0.7 except correlation coefficient between proposed method and Zhu et al. (2016), which is 0.3; therefore, the relationships between ranking results are strong and/or very strong. With respect to this analysis, we can say that the result of the proposed approach is consistent with the other methods.

Table 14 Classification of Spearman coefficient of correlation (Walters 2009)

Table 15 Comparison of ranking of the alternatives with different existing methods

Also, if we compare the IVIF-score values of reservoir flood control management policy alternative from the ideal solution (IVIF-IS) and anti-ideal solution (IVIF-AIS), it is obvious that $V_{3}$ should superior to rest of the reservoir flood control management policy alternative because the optimal option(s) is the one with the shortest distance from the ideal solution and the farthest distance from the anti-ideal solution (see Fig. 4). Hence, to summarize, reservoir flood control management policy alternative $V_{3}$ is the optimal one.

Fig. 4

Comparisons of score values among each alternatives with IVIF-IS and IVIF-AIS

6.2 Sensitivity Analysis

This subsection attempts to conduct sensitivity analysis to validate the proposed method and results in reservoir flood control management policy case. The aim of the first sensitivity analysis is to investigate the impact of various settings of the precision parameter $\lambda .$ For different values of precision coefficient $\lambda ,$ Table 16 reveals that the corresponding results of the IVIF-WASPAS method and the ultimate rankings of the reservoir flood control management policy. Additionally, the results of the sensitivity analysis for various $\lambda$ values are presented graphically in Figs. 5 and 6. More specifically, Figs. 5 and 6 depict the comparison results of IVIF-WASPAS method among reservoir flood control management policy under different settings of the parameter $\lambda .$ As indicated in Table 16 and Figs. 5 and 6, the values of $V_{i} :\,\,i\, = \,1,\,2,\,3,\,4,\,5$ increase when the $\lambda$ value increases from 0 to 1. In particular, the five ranking results are determined as $V_{3} \succ V_{5} \succ V_{2} \succ V_{1} \succ V_{4} ,$ $V_{3} \succ V_{5} \succ V_{2} \succ V_{4} \succ V_{1} ,$ $V_{3} \succ V_{2} \succ V_{4} \succ V_{1} \succ V_{5} ,$ $V_{3} \succ V_{2} \succ V_{5} \succ V_{4} \succ V_{1} ,$ $V_{3} \succ V_{2} \succ V_{4} \succ V_{5} \succ V_{1}$ in the cases of $\lambda = 0.0,$ $\lambda = 0.1,0.2,0.4,$ $\lambda = 0.3,0.9,$ $\lambda = 0.5,0.6,0.7,0.8$ and $\lambda = 1.0.$ Moreover, in all cases reservoir flood control management policy alternative $V_{3}$ is the optimal alternative.

Table 16 Score Values of IVIF-WASPAS method for reservoir flood control management policy problem

Fig. 5

Rank acceptability indices of alternatives with respect to decision mechanism coefficient

Fig. 6

Impact of different values of weight parameter on the alternatives (IVIF-WASPAS)

Next, we also perform a sensitivity analysis of IVIF-VIKOR method to see the impact of the coefficient of decision mechanism or weight $\varsigma$ on the ranking results of the reservoir flood control management policy alternative given in Table 13. From Table 13, it can be examined that if the weight $0.0\, \le \,\varsigma \, \le \,0.2,$ then the optimal management policy is $V_{3}$ and the ranking order of the policies is $V_{3} \, \succ \,V_{5} \, \succ \,V_{4} \, \succ \,V_{1} \, \succ \,V_{2} .$ If the weight $0.3\, \le \,\varsigma \, \le \,0.4,$ then the optimal policy is same but the ranking order of the policies is slightly different and it is $V_{3} \, \succ \,V_{4} \, \succ \,V_{5} \, \succ \,V_{1} \, \succ \,V_{2} .$ The optimal management policy is again $V_{3}$ for $0.5\, \le \varsigma \, \le \,1.0$ and the ranking order is $V_{3} \, \succ \,V_{5} \, \succ \,V_{4} \, \succ \,V_{2} \, \succ \,V_{1} .$ Thus, from above analysis, we recommend that the alternative $V_{3}$ is the most optimal reservoir flood control management policy. Figure 7 depicts the sensitivity analysis results at different values of $\varsigma .$

Fig. 7

Impact of different values of weight on the alternatives (IVIF-VIKOR)

7 Conclusions

This paper extends the classical WASPAS method for IVIFSs to evaluate and rank the alternatives. In the present decision making method, the performance ratings of the alternatives and the criteria are evaluated in terms of linguistic variables and then translated into IVIFNs. Based on the proposed similarity measure, the relative importance of each decision expert is determined in the proposed approach. Further, a formula for the determination of criteria weights is developed on the basis of divergence and entropy measures. To determine the decision experts’ and criteria weights, new entropy, divergence and similarity measures are proposed for IVIFSs and an illustrative example is evaluated to verify the reliability of the proposed entropy measure.

To demonstrate the validity and practicability of the proposed method, a decision making problem of reservoir flood control management policy is presented with interval-valued intuitionistic fuzzy information. A sensitivity analysis of the results is discussed to see the impact of the different values of precision parameters on the decision result, which also determines the applicability of the proposed WASPAS method. Finally, a comparative study with existing and proposed VIKOR methods verifies the stability of an optimal alternative. The main advantages of the proposed approach are the simplicity of computation in IVIF environment and using a procedure for obtaining more realistic weights of criteria and decision experts and increasing the stability of method. The proposed method can be applied for any issues that have the common structure of MCDM problems and use IVIF information. In future, we suggest using different envirionment and application of the proposed method in different MCDM problems.