1 Introduction

Due to hazardous consequences of slope instability, the evaluation of slope stability is one of the challenging issues in rock and geotechnical engineering. The factor of safety (FOS) based on an appropriate geotechnical model as an index of stability, is required in order to evaluate slope stability. Many variables are involved in slope stability evaluation and the calculation of the FOS requires physical data on the geologic materials, information on pore-water pressures, geometrical data and their shear-strength parameters, etc. Traditionally, the methods available to solve the FOS of a given slope are classified into the categories including: limit equilibrium method (LEM) (Cheng et al. 2007a; Gu et al. 2015; Qi et al. 2016; Yu et al. 1998; Zhu et al. 2003), material point method (MPM) (Bhandari et al. 2016; Wang et al. 2016), finite element method (FEM) (Duncan 1996; Griffiths and Fenton 2004; Griffiths and Lane 1999; Luo et al. 2016), discontinuous deformation analysis for rock failure (DDARF) (Li et al. 2018), probabilistic stability analysis (Zhu and Yang 2018), multiple regression analysis (Marrapu and Jakka 2017), finite element limit analysis (Tschuchnigg et al. 2015), finite difference method (Sun et al. 2014), FEM-based shear strength reduction (Kaya 2017), discrete element method (Babanouri and Sarfarazi 2018), numerical limit analysis methods (Lim et al. 2015), boundary element method (Martel and Muller 2000), strength reduction FEM (Jiang et al. 2015) and numerical back analysis (Salmi and Hosseinzadeh 2015). Previously, several techniques for calculating the safety factor have been developed. Two well-known methods which were extensively used for SF analysis include numerical methods (NM) and LEM (Duncan1996). Nevertheless, these methods (LEMs and NMs) are complex and need repetitive operations. Additionally, they sometimes require a well-fitted constitutive model and real mechanical parameters which are difficult to be determined precisely. Recently, soft computing methods have been successfully applied to predict slope stability as a complex, non-linear and multivariate problem (Cheng et al. 2007b; Ercanoglu and Gokceoglu 2002; Fattahi 2017; Gao 2015; Gelisli et al. 2015; Hoang and Pham 2016; Kahatadeniya et al. 2009; Kang et al. 2016, 2017; Koopialipoor et al. 2019; Lu and Rosenbaum 2003; McCombie and Wilkinson 2002; Pradhan 2010; Qi and Tang 2018; Rukhaiyar et al. 2018; Saboya Jr et al. 2006; Sakellariou and Ferentinou 2005; Suman et al. 2016; Tun et al. 2016; Wang et al. 2005; Yang et al. 2004; Zolfaghari et al. 2005). Although, soft computing techniques have been successfully employed for prediction of slope stability, the main problem of most these techniques is that they are black box. This means that they don’t give a transparent model which shows the relationship between input and output parameters.

In recent years, Bayesian methods have attracted researchers (Cao et al. 2016; Chiu et al. 2012; Zhou et al. 2014) because of their ability to model and analyze complex problems that were previously difficult or impossible to solve. The growth in use of the Bayesian methods can be attributed mainly to two reasons. The first reason for the growth in use of Bayesian statistics is the development of the computer-based Markov chain Monte Carlo (MCMC) simulation methods, which allow Bayesian analysis to be performed flexibly and for very complex models (Herath 2018). The second reason for the growth in the Bayesian statistics is that traditional data analysis methods (classical statistics or frequentist statistics) which rely on null hypothesis significant testing have known problems (Cashen and Geiger 2004; Kruschke et al. 2012). In Bayesian statistics, parameters are viewed as unobserved realizations of the random processes or random variables with probability distributions. That is, before obtaining data, a prior distribution is chosen to represent all available information regarding the possible value of the parameter. Then information regarding the parameter is updated using observed data and is represented by the posterior distribution, which is used to estimate parameter values and quantify uncertainty. Bayesian analysis is hence a more versatile estimation approach because it uses not only the available data but also existing knowledge about model parameters (Herath 2018). In this paper a methodology based on Bayesian MCMC method using free software package, WinBUGS (Adoko et al. 2017; Fattahi and Zandy Ilghani 2019a, b; Lunn et al. 2000; Spiegelhalter et al. 2002)) aimed at identifying the most appropriate models to predict FOS among several selected candidate models, is proposed. To validate the performance of the models proposed, it is applied to field data given in open source literatures.

2 Methodology

2.1 Markov Chain Monte Carlo (MCMC) Simulation Approach

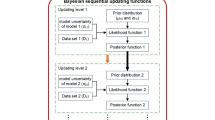
Typical statistical problems involve estimating a vector of parameters, θ, using the available data. The classical approach assumes that the parameters are fixed, but have unknown values to be estimated. Classical maximum likelihood estimates generally provide a point estimate of the parameter of interest. The Bayesian approach assumes that the parameters themselves have some unknown distribution. The approach is based upon the idea that the experimenter begins with some prior beliefs about the system, and then updates these beliefs on the basis of observed data. Using Bayes’ Theorem, the posterior distribution of the parameters given the data π(θ|data) has density proportional to the product of the likelihood of the data given the parameters L(data|θ) and the prior distribution of the parameters π(θ): π(θ|data) ∝L(data|θ) × π(θ) (Gimenez et al. 2009).

The Bayesian approach does this through integration using the MCMC algorithm. The high-dimensional integral associated with the posterior density is actually estimated using appropriate Monte Carlo integration, which consists of constructing a Markov chain with stationary distribution equal to the posterior distribution of interest (Gimenez et al. 2009). Then, once the chain has converged, realizations can be regarded as a dependent sample from this distribution. WinBUGS implements powerful ways of constructing these chains, adapting to a wide range of target (posterior) distributions and therefore allowing a large number of possible models to be fitted. Further details on Bayesian modeling using MCMC algorithms can be found in Brooks et al. (2011). Also for more information about Bayesian modeling using WinBUGS can be found in Ntzoufras (2011).

2.2 MCMC Simulation Software

There are numerous kinds of software, both open source and proprietary, that can be used to implement Bayesian analysis using Bayesian MCMC simulation. The popular WinBUGS software is an interactive Windows program for Bayesian analysis of complex statistical models (Herath 2018). It uses BUGS [Bayesian inference Using Gibbs Sampling (Chun 2008)], and samples are drawn from their conditional (posterior) distribution instead of the marginal posterior distributions. The standard MCMC software such as WinBUGS uses the Gibbs sampling algorithm, the Metropolis–Hastings (MH) algorithm (Hastings 1970), or a hybrid of both. In addition, the reversible-jump MCMC algorithm is gaining acceptance. In order to overcome the inefficiencies in Gibbs sampling and MH algorithms, ideas from physics have been used develop the newer and more robust Hamiltonian Monte Carlo (HMC) algorithm, which can be used independently (continuous parameters) or combined with Gibbs sampling and the MH algorithm for discrete parameters (Herath 2018). This paper uses the open source software WinBUGS to derive the posterior distributions. The WinBUGS software is currently freely available at https://www.mrc-bsu.cam.ac.uk/software/bugs/the-bugs-project-winbugs/.

3 The Features of the Database

The main scope of this work was to implement the methodology in the problem of slope stability estimation. To achieve this, datasets given in previous papers are borrowed (Fattahi 2017; Madzic 1988; Sah et al. 1994). The parameters that were selected were related to the geometry and the geotechnical properties of each slope. More specifically, the parameters utilized for circular failure were slope angle (β), pore pressure ratio (ru), angle of internal friction (φ), height (H), cohesion (C) and unit weight (γ) (Fig. 1). The output layer composed of a single output parameter (FOS). The data set consisted of 62 case studies of the slopes analyzed for the circular critical failure mechanism. Partial dataset used in this study are presents in Table 1. Also, descriptive statistics of the all data sets are shown in Table 2.

Fig. 1
figure 1

The parameters utilized for circular failure

Full size image
Table 1 Partial dataset used for constructing the models (Fattahi 2017; Madzic 1988; Sah et al. 1994)
Full size table
Table 2 Statistical description of dataset utilized for construction of models
Full size table

4 Bayesian Models: Inference, Selection and Prediction

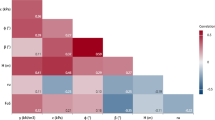
First of all, the database containing 62 datasets were divided into two. The first part representing 75% of the total datasets (i.e. containing 47 datasets) was used to establish the model while the second part served for the model performance evaluation. Based on the training database, a Bayesian predictive model was proposed. Firstly, a preliminary correlation analysis was performed to investigate the possible type of relationships between the FOS (dependent) and each of the independent variable (γ, C, φ, β, H and ru) in order to explore the potential candidate terms in developing the correlation for FOS. The following candidates are used:

$${\text{Model}}\;\# 1\;FOS = \frac{{a_{1} (\gamma^{{b_{1} }} \cdot C^{{b_{2} }} ) + a_{2} (H^{{b{}_{3}}} \cdot \cos r_{u} ) + a_{3} }}{{a_{4} \cos (b_{4} \rho + b_{5} \beta + b_{6} r_{u} ) + a_{5} }}$$
(1)
$${\text{Model}}\;\# 2\;FOS = \frac{{a_{1} (\gamma^{{b_{1} }} \cdot C^{{b_{2} }} ) + a_{2} (H^{{b{}_{3}}} \cdot \cos r_{u} ) + a_{3} }}{{a_{4} \cos (b_{4} \rho + b_{5} \beta ) + a_{5} }}$$
(2)
$${\text{Model}}\;\# 3\;FOS = \frac{{a_{1} (\gamma^{{b_{1} }} \cdot C^{{b_{2} }} ) + a_{2} (\rho^{{b{}_{3}}} \cdot \beta^{{b_{4} }} ) + a_{3} }}{{a_{4} H^{{b_{5} }} + a_{5} \cos r_{u} + a_{6} }}$$
(3)
$${\text{Model}}\;\# 4\;FOS = \frac{{a_{1} \gamma^{{b_{1} }} + a_{2} C^{{b_{2} }} + a_{3} H^{{b_{3} }} + a_{4} r_{u}^{{b_{4} }} + a_{5} }}{{a_{6} \rho^{{b_{5} }} + a_{7} \beta^{{b_{6} }} + a_{8} }}$$
(4)
$${\text{Model}}\;\# 5\;FOS = \frac{{a_{1} \gamma^{{b_{1} }} + a_{2} C^{{b_{2} }} + a_{3} H^{{b_{3} }} + a_{4} r_{u}^{{b_{4} }} + a_{5} }}{{a_{6} \sin \rho + a_{7} \cos \beta + a_{8} }}$$
(5)
$${\text{Model}}\;\# 6\;FOS = a_{1} \gamma + a_{2} C + a_{3} \rho + a_{4} \beta + a_{5} H + a_{6} r_{u} + a_{7}$$
(6)
$${\text{Model}}\;\# 7\;FOS = \frac{{a_{1} \gamma^{{b_{1} }} + a_{2} C^{{b_{2} }} + a_{3} H^{{b_{3} }} + a_{4} r_{u}^{{b_{4} }} + a_{5} }}{{a_{6} \sin \rho + a_{7} \sin \beta + a_{8} }}$$
(7)
$${\text{Model}}\;\# 8\;FOS = \frac{{a_{1} \gamma^{{b_{1} }} + a_{2} C^{{b_{2} }} + a_{3} H^{{b{}_{3}}} + a_{4} \cos r_{u} + a_{5} }}{{a_{6} \cos (c_{1} \rho + c_{2} \beta ) + a_{7} }}$$
(8)
$${\text{Model}}\;\# 9\;FOS = \frac{{a_{1} (\gamma^{{b_{1} }} \cdot H^{{b_{2} }} ) + a_{2} (C^{{b{}_{3}}} \cdot \cos r_{u} ) + a_{3} }}{{a_{4} \cos (c_{1} \rho + c_{2} \beta ) + a_{5} }}$$
(9)
$${\text{Model}}\;\# 10\;FOS = a_{1} \gamma^{{b{}_{1}}} + a_{2} C^{{b_{2} }} + a_{3} \rho^{{b_{3} }} + a_{4} \beta^{{b_{4} }} + a_{5} H^{{b_{5} }} + a_{6} r_{u}^{{b_{6} }} + a_{7}$$
(10)
$${\text{Model}}\;\# 11\;FOS = a_{1} \gamma^{{b{}_{1}}} + a_{2} C^{{b_{2} }} + a_{3} \sin \rho + a_{4} \cos \beta + a_{5} H^{{b_{3} }} + a_{6} r_{u}^{{b_{4} }} + a_{7}$$
(11)
$${\text{Model}}\;\# 12\;FOS = \frac{{a_{1} \gamma^{{b_{1} }} + a_{2} C^{{b_{2} }} + a_{3} H^{{b_{3} }} + a_{4} r_{u}^{{b_{4} }} + a_{5} }}{{a_{6} \sin (c_{1} \rho + c_{2} \beta ) + a7}}$$
(12)
$${\text{Model}}\;\# 13\;FOS = \frac{{a_{1} (\gamma^{{b_{1} }} \cdot \rho^{{b_{2} }} ) + a_{2} (C^{{b{}_{3}}} \cdot \beta^{{b_{4} }} ) + a_{3} }}{{a_{4} H^{{b_{5} }} + a_{5} \cos r_{u} + a_{6} }}$$
(13)
$${\text{Model}}\;\# 14\;FOS = a_{1} \gamma^{{b{}_{1}}} + a_{2} C^{{b_{2} }} + a_{3} \cos \rho + a_{4} \sin \beta + a_{5} H^{{b_{3} }} + a_{6} r_{u}^{{b_{4} }} + a_{7}$$
(14)
$${\text{Model}}\;\# 15\;FOS = a_{1} \gamma^{{b{}_{1}}} + a_{2} C^{{b_{2} }} + a_{3} \sin \rho + a_{4} \sin \beta + a_{5} H^{{b_{3} }} + a_{6} r_{u}^{{b_{4} }} + a_{7}$$
(15)
$${\text{Model}}\;\# 16\;FOS = \frac{{a_{1} (\gamma^{{b_{1} }} \cdot r_{u}^{{b_{2} }} ) + a_{2} (C^{{b{}_{3}}} \cdot H^{{b_{4} }} ) + a_{3} }}{{a_{4} \cos (c_{1} \rho + c_{2} \beta ) + a_{5} }}$$
(16)
$${\text{Model}}\;\# 17\;FOS = a_{1} \gamma^{{b{}_{1}}} + a_{2} C^{{b_{2} }} + a_{3} \cos \rho + a_{4} \cos \beta + a_{5} H^{{b_{3} }} + a_{6} r_{u}^{{b_{4} }} + a_{7}$$
(17)
$${\text{Model}}\;\# 18\;FOS = \frac{{a_{1} \gamma^{{b_{1} }} + a_{2} C^{{b_{2} }} + a_{3} H^{{b_{3} }} + a_{4} r_{u}^{{b_{4} }} + a_{5} }}{{a_{6} \cos \rho + a_{7} \sin \beta + a_{8} }}$$
(18)
$${\text{Model}}\;\# 19\;FOS = a_{1} \gamma^{{b{}_{1}}} + a_{2} C^{{b_{2} }} + a_{3} \sin (c_{1} \rho + c_{2} \beta ) + a_{4} H^{{b_{3} }} + a_{5} r_{u}^{{b_{4} }} + a_{6}$$
(19)
$${\text{Model}}\;\# 20\;FOS = \frac{{a_{1} \gamma^{{b_{1} }} + a_{2} C^{{b_{2} }} + a_{3} H^{{b_{3} }} + a_{4} r_{u}^{{b_{4} }} + a_{5} }}{{a_{6} \cos \rho + a_{7} \cos \beta + a_{8} }}$$
(20)

In this study, the unknown parameters of the different candidate models are considered as random variables. The aim of this study as stated previously is to identify objectively the most suitable models that fit best the FOS datasets using a Bayesian framework where the inference of model parameters is conducted in WinBUGS software based on Bayesian MCMC methods. Therefore, one of the essential tasks in this study is to sample values of the unknown parameters from their conditional posterior distribution given the stochastic nodes that have been observed, after having specified the model as a full joint distribution on all quantities for both parameters and observables.

5 Modeling and Results

After specifying the models in WinBUGS language at the logical nodes, normal (or lognormal or other distributions) were selected at the stochastic nodes for γ, C, φ, β, H and ru respectively. Subsequently, the first group of the datasets was loaded and the models compiled and the MCMC sampler was applied to compute the model parameters. A trial-and error approach was used to identify the optimal settings of the modeling. It can be seen that for Model #2, the mean values of the unknown parameters a1, a2,…, a5 and b1, b2, …, b5 are 24.04, 10.32, − 5.941, − 1.974, 3.888, − 2.058, 0.8093, − 0.05221, − 3.596 and 4.243 respectively. These values are the most probable the model parameters would take for the predicted FOS to have maximum accuracy since those values correspond to the peak of the posterior distributions which are plotted in Fig. 2. The summaries of the different models are provided in Table 3.

Fig. 2
figure 2

Posterior distributions of the model parameters (a1, a2,…, a5 and b1, b2, …, b5) corresponding to Model #2

Full size image
Table 3 Summary statistics for the Model #2 parameters computed with WinBUGS
Full size table

As the models contain a maximum number of 20, checking the convergence for every parameter could be afforded and were monitored. If the trace plots move around the mode of the distribution and do not show a trend in the sample space, then the model has converged as shown in Fig. 3. As seen from Fig. 3, an example of the dynamic traces of the model parameters corresponding to Model #2 indicating convergence.

Fig. 3
figure 3

Dynamic trace of the model parameters (a1, a2,…, a5, b1, b2, …, b5) corresponding to Model #2

Full size image

The dynamic trace plots of the sample values versus iteration suggested that the simulation appears to have stabilized.

To verify the performance of the models, four statistical criteria viz. mean squared error (MSE) and squared correlation coefficient (R2) were chosen to be the measure of accuracy (Fattahi et al. 2019). Let tk be the actual value and \(\hat{t}_{k}\) be the predicted value of the kth observation and n be the number of observations, then MSE and R2 could be defined, respectively, as follows:

$$MSE = \frac{1}{n}\sum\limits_{k = 1}^{n} {(t_{k} - \hat{t}_{k} )^{2} }$$
(21)
$$R^{2} = 1 - \frac{{\sum\nolimits_{k = 1}^{n} {(t_{k} - \hat{t}_{k} )^{2} } }}{{\sum\nolimits_{k = 1}^{n} {t_{k}^{2} } \frac{{\sum\nolimits_{i = 1}^{n} {\hat{t}_{k}^{2} } }}{n}}}$$
(22)

With the purpose of evaluating the prediction performance of the model, the datasets (training and testing datasets) were used to assess the optimal model. Performance analysis of 20 models for training and testing datasets is shown in Table 4 and Fig. 4.

Table 4 A comparison between the results of models for training and testing datasets
Full size table
Fig. 4
figure 4

A comparison between the results of models for a training datasets b testing datasets

Full size image

In general, the results indicated that the proposed model (Model #2) could be used to predict the FOS. Finally, the Model #2 is ranked the best candidate while Model #20 is the worst candidate for predicting the FOS using the training and testing datasets. It is evident that the prediction model constructed in this research is open for more development if more data are available.

6 Conclusions

Slope stability assessment is a critical research area in civil engineering. Disastrous consequences of slope collapse necessitate better tools for predicting their occurrences. In this paper, a new methodology based on Bayesian inference was implemented to identify the most appropriate models for estimating the FOS among several candidate models that had been analyzed using the WinBUGS software. The input of the predictive model included the γ, C, φ, β, H and ru. Overall, the results suggest that the proposed models FOS possess satisfactory predictive performance. Based on the R2 and MSE, the model #2 was the most adequate model (among those considered) which was in agreement with performance indices. This study shows that the Bayesian MCMC method can be applied as a powerful tool for modeling of some problems involved in rock and soil engineering.