1 Introduction

Acoustic emission (AE) is defined (ASTM E1316-10c) by the sudden redistribution of energy in a solid caused by the activation and/or development of one or more localized sources, which are typically part of irreversible processes related to deformation and damage across materials including fracture, slip activity, twinning, phase transformations, and delaminations (Chung and Kannatey-Asibo 1992; Koslowski et al. 2004; Lamark et al. 2004; Lockner et al. 1991; Lou et al. 2007; Mathis et al. 2006; Miguel et al. 2001; Richeton et al. 2006; van Bohemen et al. 2003; Vanniamparambil et al. 2015; Wisner et al. 2015). More specifically, AE is generated when the energy stored in a material or structure is released and dissipated in the form of transient elastic waves that typically have frequencies in the ultrasonic regime depending on the source size and duration of the damage process, as recently demonstrated by the authors (Cuadra et al. 2015).

In the case of crack initiation, a significant amount of the energy stored in the region near the notch/crack tip eventually is expended in the formation of new crack surfaces, which has been analytically, experimentally and computationally described in several fracture mechanics formulations (Boyce et al. 2014; Nguyen et al. 2001; Owen et al. 1998; Ravi-Chandar 2004). In this incremental view of the crack initiation process, the energy release that occurs can further excite transient dynamic motion as well as multispectral (e.g. thermal) energy dissipation, which are both part of the associated energy redistribution (Döll 1984; Ernst et al. 1979; Gross et al. 1993; Sharon et al. 1996). In this context, the experimental work by Döll and Gross et al. suggested that most of the stored energy is dissipated as heat and that only a fraction (approximately 3 %) of the total fracture energy could be associated with AE (Döll 1984; Gross et al. 1993; Hack et al. 1989). In other investigations, such energy considerations concepts have been applied experimentally to detect the fracture process zone size by using energy measures and density of AE events which were used to provide critical regions for crack detection (Muralidhara et al. 2013). Other research efforts relied on the use of the AE experimental methodology to characterize the fracture related energy release and reported limitations to quantify specific energy amounts e.g. related to stress wave propagation, due to inherent restrictions placed for example by the sensors. Nevertheless, such efforts provided empirical relations which were used to describe damage initiation and severity by several AE-defined features (Boler 1990; Bosia et al. 2008; Jungk et al. 2006; King et al. 1981; Sause et al. 2012). The generation of AE from the fracture process has also been described based on the different types of produced waves. For example, in semi-infinite media, Rayleigh waves have been estimated to carry about 67 % of the energy radiated from the damage source in perfectly isotropic materials, while the shear and longitudinal waves contain 26 and 7 %, respectively (Achenbach 1973).

Fig. 1
figure 1

a Compact tension (CT) model geometry; b applied boundary and loading conditions; c material law extracted by performing tension experiments using dog-bone specimens, and d cohesive-based XFEM traction separation law used in the finite element model

Full size image

In the context of fracture mechanics, the early studies related to fracture were also based on associated energy concepts. Specifically, the work by Griffith (1921) aimed at describing the energy release rate, which in its simplest form may be associated with the rate of change in potential energy near the crack, which provided a way to characterize and quantify crack formation. Griffith’s criterion was built upon the condition that sufficiently high applied loads at the continuum scale are related to similar ones at the microscale in order to predict fracture initiation (Anderson 2005). Several investigations followed Griffith’s approach including the work by Rice (1965), in which an energy balance for the fracture process was derived for both linear elastic and plastic materials. Rice’s investigations were not only an extension of Griffith’s work but provided a broader overview of the energy quantities associated with crack formation by defining two concomitant equilibrium states before and after crack advance. Furthermore, this energy balance was not a priori imposed; instead it was derived using continuum formulations of the energy at each state, disregarding microstructural effects at the atomic or meso-scales which are not adequately described by continuum mechanics theories. In addition to the energy balance formulation, Rice (1968) developed a path independent integral, known as J-integral, to characterize the energy associated with the fracture process. These findings were later used to construct the so-called HRR singularity (Hutchinson 1968; Rice and Rosengren 1968) by deriving a formulation for the singular stress and strain field at the crack tip for a power law hardening material. The J-integral is not only a measure of the stress intensity in ductile materials but it can also be used as a criterion for crack initiation and to some extent for crack growth.

In this article, an attempt is made to quantify the energy associated with AE by considering both Rice’s energy balance approach and an energy flux approach frequently used in the field of wave mechanics to account for transient effects that are associated with AE. The main contribution of this investigation is therefore a direct estimation, for the first time to the authors’ best knowledge, of the amount of energy associated with the generation and propagation of transient elastic waves, which are responsible for the dissipation of a portion of the energy that is released due to the formation of a new crack increment in ductile fracture. To accomplish this goal, a 3D computational model that has been calibrated by experimental information is developed and used both for static and dynamic calculations.

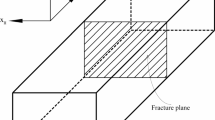
2 Methodology

2.1 Computational model

The integrated method developed previously by the authors Cuadra et al. (2015) is utilized in this paper to extract experimental parameters that are used as inputs to a 3D computational model capable to link static to dynamic simulations. Furthermore, the approach followed in this article differs from prior analytical and computational approaches in the area of AE modeling (Hora et al. 2013; Sause and Richler 2015; Uhnáková et al. 2010), primarily because it does not impose a damage source for the generation of the fracture-related stress waves. The geometry investigated is that of a compact tension (CT) specimen of an aluminum alloy (Al2024) with 6 mm thickness and subjected to Mode I loading, as shown in Fig. 1a, b. The eXtended finite element method (XFEM) in ABAQUS (2013) was adopted to model the crack initiation and its concomitant dynamic response. The analysis was carried out using the implicit solver, achieving the use of a single computational model that satisfies equilibrium at each time step. The parameters for the XFEM fracture criteria were directly extracted from targeted experiments, as described previously by the authors (Cuadra et al. 2015). The computational parameters that are directly related to experimental inputs include: (1) the XFEM damage initiation criterion, and (2) the XFEM damage evolution related softening curve for crack growth. In this article, these model parameters were adjusted by comparing numerically computed reaction forces to the load measured by experiments, and by calibrating FEM nodal displacements and strains in Fig. 1b with digital image correlation (DIC)-defined full field deformation fields. The initial step in this process consisted of building a phenomenological traction-separation law (TSL) using the DIC data, as previously implemented in other similar investigations via inverse or optimization methods (e.g. Gain et al. 2011; Shen and Paulino 2011; Zhu et al. 2009). In the methodology applied herein and to minimize inconsistencies, tractions and opening displacements were defined near the notch tip. The selected power law for the TSL can be written as (Feih 2006)

$$\begin{aligned} T(\delta )=\left\{ {{\begin{array}{l@{\quad }l} {\left[ {1-\left( {\frac{\delta _c -\delta }{\delta _c }} \right) ^{\alpha }} \right] \sigma _{\max }, }&{} {0\le \delta <\delta _c, } \\ {0, }&{} {\delta =\delta _c, } \\ \end{array} }} \right. \end{aligned}$$
(1)

where \(\delta \) represents the separation (opening displacement), while the variables \(\sigma _{\max }, \delta _c\) and a are curve fitting variables.

Furthermore, in order to construct the TSL, a stress-strain curve was necessary. For this reason, a tension test for a dog-bone specimen of the same aluminum 2024 alloy was performed in accordance with the procedure described by Moosbrugger (2002). A continuous piecewise function was then defined using the true strain and stress, as follows

$$\begin{aligned} \sigma \left( \varepsilon \right) =\left\{ {{\begin{array}{l@{\quad }l} {73.1\cdot 10^{3}\varepsilon , }&{} {0<\varepsilon \le 0.0036, } \\ {52.61 \ln \left( \varepsilon \right) +568.42,}&{} {0.0036<\varepsilon \le 0.21, } \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$
(2)

where the stress \(\sigma \) is in MPa. The corresponding curve with both logarithmic and nominal values is shown in Fig. 1c. Based on this curve, the Young’s Modulus was calculated from a linear fit, while the Poisson’s ratio was obtained from the ratio of the experimentally calculated full-field average transversal and longitudinal strains. The stress-strain relationship was essential to assign the material law in the FEM model, including the elastic and plastic regimes. In the case of the TSL in Fig. 1d, an array of measuring points close and ahead of the crack tip were extracted (Cuadra et al. 2015). The strain component in the loading direction at these sites was then converted to a stress value by neglecting all shear components. Such array of points was extracted at different time instances in order to understand the state of deformation related to crack initiation at several stages of loading. Specifically, an array of fifteen experimentally obtained DIC measurement points ahead of the crack tip was used to obtain the crack opening displacement and strain values. In addition, displacement values directly above and below the crack were measured for each point in the selected DIC stages in order to calculate the crack opening displacements. These experimental data points were used to fit the three-parameter power law function given in Eq. (1), formulated based on the requirement to preserve the fracture energy. Note that based on the procedure described herein, the critical displacement value for crack initiation was determined to be equal to \(80\,\upmu \hbox {m}\). Accordingly, the power law fitting function yielded a tensile strength value of \(\sigma _{\max } =480\,\hbox { MPa}\), while the exponent \(\alpha \) was set to 19, for a fracture energy estimate \(G_0 =1490.7\, \hbox { J/m}\) (see also Cuadra et al. 2015).

Fig. 2
figure 2

a DIC and b XFEM \(\varepsilon _{yy}\) strain contours at the crack initiation state. c Load-displacement response compared to experimental results

Full size image

In order to optimize the state of stress at crack initiation, it was necessary to calibrate the XFEM model using the critical displacement for fracture initiation defined in the TSL in Fig. 1c. Consequently, further DIC analysis and evaluation of the FEM boundary conditions were required. To this aim, two-point calculations using the DIC data were performed and averaged using neighboring points at the plastic wake and at the crack tip as shown in Fig. 2a. Although displacement values were identified in this way, the failure initiation criterion was based on the maximum nominal strain, as shown in Fig. 2b. Furthermore, a mesh convergence study was conducted to investigate the effect of mesh size in the load-displacement response of the XFEM model, as shown in Fig. 2c. After identifying the optimum mesh size, the model was calibrated by adjusting the maximum nominal strain. Once mesh convergence was achieved, to calibrate the fracture initiation criterion the state during which the crack tunnels to the surface, which is characteristic of a displacement jump and occurs at the critical opening displacement of \(80 \,\upmu \hbox {m}\), was computed. This calibration process further included the steps of implementing the appropriate boundary conditions and adjusting the maximum nominal strain for crack initiation using the values in Table 1.

Table 1 Input values for the XFEM model
Full size table
Fig. 3
figure 3

Von Mises stress contour plots at the surface and through thickness: a before and c after crack initiation. b Wave propagation visualized using out-of-plane velocity contour plots at different time instances following crack initiation

Full size image

This procedure provided a computational model suitable to investigate both the static crack initiation and the subsequent dynamic stress wave generation and propagation. The XFEM model was further validated against experimental load-displacement data, as shown in Fig. 2.

2.2 Energy calculations

Several approaches were implemented in this article to quantify the various parts involved in the energy redistribution due to ductile crack initiation and are presented next.

2.2.1 Energy balance

Based on static simulations only, this approach was used herein to estimate the amount of energy associated with the formation of the new crack surfaces during the first increment of fracture in a ductile material, which could be also considered an upper bound of the energy dissipation that occurs between the equilibrium states before and after crack initiation. As previously mentioned, this approach was first introduced by Rice (1965) and was an extension to the work presented by Griffith (1921). Specifically, Rice described an energy balance approach for crack extension in linear elastic and ductile materials, while he further discussed the role of surface energy and work hardening. This concept is schematically illustrated in Fig. 3 (using actual FEM results from the computational model introduced in Sect. 2.1 and discussed later in Sect. 3), and demonstrates the equilibrium states before (Fig. 3a) and after (Fig. 3c) crack initiation, as well as the transient states (Fig. 3b) during which the generated stress waves propagate until equilibrium is reached. Given the schematic representation of the crack initiation process in Fig. 3, the energy dissipation occurring due to AE is related to the release of waves visualized in this figure by the out-of-plane velocity wavefronts which are produced at the crack initiation location and radiate away from the source as a function of time until they completely dissipate. As shown next, the energy balance approach could provide only an upper bound estimate of this energy dissipation, as it does not account for any transient effects. However, for model verification purposes this approach was implemented first to evaluate the capability of the computational model to provide quantitative metrics related to the energy redistribution that occurs during the first crack increment that occurs in a ductile material.

Considering a pseudo-static loading process, the energy before crack propagation is described by the external work which is equal to the internal stored energy, as described in Eq. (3).

$$\begin{aligned} \int _\Gamma {f_i^c u_i dA} =\int _V {\sigma d\varepsilon _{ij}^{el} dV} +\int _V {\sigma d\varepsilon _{ij}^{pl} dV}, \end{aligned}$$
(3)

where \(\Gamma \) is the surface area (in this model at the pins where Mode I type loading is applied) and V is the volume, while f represents the tractions associated to the externally imposed displacement \(u_i \). The right hand side of Eq. (3) is composed of the elastic strain energy and plastic dissipation terms, for which the assumed strain decomposition is denoted by the subscripts “el” and “pl”, respectively. Following Rice (1968), this derivation ignores any thermal-mechanical coupling. After an incremental crack growth of size \(\Delta \alpha \) has occurred (shown in Fig. 3c), the energy balance must account for an additional term related to the crack extension. The energy associated to the crack formation, denoted here as \(E_{crack}\), is obtained by using Green’s theorem and applying the corresponding boundary conditions, i.e.

$$\begin{aligned} E_{{crack}}= & {} \int _V\left( \int _{a}^{b}\sigma _{ij}d\varepsilon _{ij}^{el}\right) dV + \int _{V}\left( \int _{a}^{b}\sigma _{ij}d\varepsilon _{ij}^{pl}\right) dV\nonumber \\&-\int _{\Gamma } {\Delta f_{i}^{c} \Delta u_{i} dA}. \end{aligned}$$
(4)

In Eq. (4), the limits “a” and “b” denote the states before and after energy release due to crack growth and “\(\Delta \)” refers to the change in imposed tractions or displacements between the two states. Essentially, Eq. (4) represents the difference in the total (mechanical) energy, which refers to the external work minus the internal (stored) energy for the two equilibrium states. Note that as it will be also shown next, both elastic and plastic energy terms in Eq. (4) are negative (due to the energy release that occurs at crack initiation and statically computed at state “b”). In addition, the external work term is also negative since there is a load drop the moment the crack advances. Hence, \(E_{crack}\) in Eq. (4) is positive based on the way the terms in this equation have been arranged. Furthermore, this notation is consistent with the fact that the external work decreases the total energy in this ductile fracture process, as it would be shown next.

By calculating the difference between the two states, one obtains:

$$\begin{aligned} E_{crack}= & {} \sum _{elems} \left[ \int _{V_{elem}}\left( \int _{a}^{b}\sigma _{ij}d\varepsilon _{ij}^{el} \right) dV_{elem}\right. \nonumber \\&\left. +\int _{V_{elem}}\left( \int _{a}^{b}\sigma _{ij}d \varepsilon _{ij}^{pl}\right) dV_{elem} \right] -\Delta E_{ext},\nonumber \\ \end{aligned}$$
(5)

where “elem(s)” refers to the finite elements so that the internal energy is the sum of the elastic strain energy and plastic dissipation in all elements, while \(\Delta E_{ext} \) is the change in external work done in the system calculated from the imposed force/displacement boundary conditions. It can be observed that Eq. (5) is only valid for two states associated with a single crack growth increment, where \(E_{crack} \) denotes the corresponding energy associated with the formation of crack including all transient portions of energy that in this approach are not explicitly quantified.

Fig. 4
figure 4

Illustration of contours and terms associated with the J-integral approach

Full size image

2.2.2 J-integral

A direct method to estimate the energy release due to ductile crack initiation is the J-integral. A convenient formulation of the J-integral can be obtained by applying Reynolds transport and divergence theorems to a fixed contour with a given area A and a moving contour with a fixed size, \(\Gamma \), which moves along with the crack. A 2D representation of the constituents for obtaining the energy release is depicted in Fig. 4.

The J-integral for a 2D case and a crack increment along the horizontal (x-direction) can be expressed as (Cherepanov 1967; Rice 1968),

$$\begin{aligned} J=\mathop {\lim }\limits _{\varGamma \rightarrow 0}\int _{\varGamma }\left[ W\delta _{1j}-\sigma _{ji}\frac{\partial u_{i}}{\partial x} \right] n_{j}d\Gamma , \end{aligned}$$
(6)

where W is the internal energy density, n is the outer unit normal to the closed contour \(\Gamma \), while the Kronecker \(\delta \) represents the crack direction. The energy release per unit of crack area is evaluated herein for an elastoplastic constitutive model with incremental plasticity in contrast to an idealized nonlinear material law. It is important to note that in Eq. (6) a linear unloading path based on the deformation theory of plasticity and steady state crack growth under dynamic loading conditions with negligible kinetic energy are assumed. Furthermore, the limit of \(\varGamma \) to zero allows for the line integral to be independent of the shape of the contour itself. Equation (6) has also been introduced as a surface integral and subsequently derived for the FEM framework by using a smooth function, q. In this case, the energy per unit of crack area can be expressed as (Li et al. 1985)

$$\begin{aligned} J= & {} \sum _{V} {\sum _{p=1}^{m} {\left\{ {\left[ {\left( {\sigma _{ij} \frac{\partial u_j }{\partial x_1 }-W\delta _{1i} } \right) \frac{\partial q}{\partial x_i }} \right] \det \left( {\frac{\partial x_j }{\partial \xi _k }} \right) } \right\} _p \omega _p } }\nonumber \\&-{\mathop {\mathop {\sum }\limits _{crack}}\limits _{faces}} {\left( {\sigma _{2j} \frac{\partial u_j }{\partial x_1 }q} \right) \omega }, \end{aligned}$$
(7)

where \(\{\,\}_p\) and subscript “p” represent the quantities evaluated at the Gaussian points, \(\omega \) is the Gaussian weighting factor, m is the number of Gaussian points per element, and \(\xi \) are the natural coordinates (i.e. FEM isoparametric coordinates). Moreover, the smooth function q, can be represented in terms of the shape functions \(N_I\) and the nodal values by interpolating within an element, such that,

$$\begin{aligned} q\left( {x_i } \right) =\sum _{i=1}^p {N_I q_I }, \end{aligned}$$
(8)

where p is the number of nodes per finite element. Consequently, the energy per unit of crack area is calculated in this study using Eq. (7) for the computational model in order to characterize and quantify its energy state before and after the onset of crack growth under both equilibrium and transient dynamic conditions.

Fig. 5
figure 5

a Two different contour sizes, C3 and C17 (area of node groups) at the center of the model through the thickness. b Contour size convergence for integral calculation. c Mesh dependence study of the contour integral calculation compared to analytical expression. d XFEM precrack with corresponding mesh. e Contour integral results comparison for a seam crack or an XFEM model

Full size image

For the Mode I loading assumed in this work the J-integral can be conveniently formulated by separating the elastic and plastic displacements, which is valid if unloading does not occur. Thus, in a load-controlled formulation

$$\begin{aligned} J= & {} J_{el} +J_{pl} =\int _{0}^{P}\frac{\partial \delta }{\partial a}\bigg |_{p}dP\nonumber \\= & {} \int _{0}^{P}\frac{\partial \delta _{el}}{\partial a}\bigg |_{p}dP+\int _{0}^{P}\frac{\partial \delta _{pl}}{\partial a}\bigg |_{p}dP, \end{aligned}$$
(9)

where \(\delta _{el} \) and \(\delta _{pl} \) are the elastic and plastic components of the displacement which are assumed to follow an additive decomposition, a is the crack length and P the force per unit of length (thickness). Intuitively, the elastic part can be related to Linear Elastic Fracture Mechanics using Griffith’s formulation of the energy release rate, where \(J_{el} =G\). The plastic part can then be derived by dimensional analysis assuming that the plasticity is confined to the characteristic length of the uncracked ligament, \(b_o \), for any medium containing a crack. A second assumption regarding the dimensional integrand states that separation of variables can be applied (Ernst et al. 1979; Merkle and Corten 1974). Moreover, it was later shown that the geometrical parameters associated to J can be estimated empirically for a compact tension specimen (Clarke and Landes 1979). Thus, the plastic part of J-integral can be written in terms of the plastic work \(A_{pl} \) (i.e. the area under the nonlinear part of the load-displacement curve), in which case

$$\begin{aligned} J=\frac{K_I^2 (1-\nu ^{2})}{E}+\frac{2A_{pl} }{b_n b_o }+\frac{0.522A_{pl} }{b_n w}, \end{aligned}$$
(10)

where w is the specimen’s width and \(b_n \) is the specimen’s thickness.

This analytical form of J-integral can be used to validate the contour integral formulation presented in Eq. (7). This analytical formulation is part of the ASTM E1820 standard, which is used for the experimental measurement of fracture toughness. This calculation relies on an experimental record of the load and displacement for a specific crack size with the expectation that no unloading occurs. In summary, once the energy release rate is validated for a stationary crack using Eq. (10) then the energy difference between the two states before and after crack growth can be defined. From this difference, the associated energy release due to crack initiation can be calculated for a given crack increment area since the J-integral is expressed in terms of energy per unit of area.

To compute the J-integral using the FEM approach in this article, a mesh sensitivity investigation was conducted, as shown in Fig. 5. Two different meshes, one coarse and one fine, were evaluated for the same contour calculation size and compared to the analytical expression (Eq. 10). The results showed excellent agreement for both mesh sizes. To further demonstrate the convergence of contour integral calculations, various contour sizes (shown in Fig. 5a) were utilized. The first contour includes only one point, the crack front, and every additional contour is expanding to the adjacent finite element nodes. The integral involved in this approach was transformed from a line integral to a surface integral formulation (see also Parks 1977; Shih et al. 1986). However, there was a limit to the size that could be used since other geometrical features, such as the CT specimen pins, could cause divergence of the integral calculation. Another important factor about the size of the contour was to assure that the plastic process zone was completely included in order to account for all dissipation around the crack tip (Brocks et al. 2001; Carka and Landis 2010). The calculations for different contour sizes are shown in Fig. 5b. The corresponding results for all contour sizes show that at the eighth contour (C8) the calculation converges. This result suggested that C8 comprised most of the plastic zone and can be used to accurately determine the J-integral as a function of loading increments. In order to confirm this convergent result, the integral calculation was compared to that of the analytical form using the load-displacement response of the model (Eq.  10). The results show excellent agreement between the contour integral calculation and the analytical expression regardless of the mesh size and configuration (Fig. 5c). The analytical form was further utilized to calculate the J-integral for the experimental data obtained using the DIC method.

Fig. 6
figure 6

Schematic of a confined cylindrical volume close to crack tip and generic configuration of the Poynting vector

Full size image

All of the above integral calculations were performed using a stationary seam (i.e. duplicating nodes on top and bottom crack surfaces) to simulate in accordance with the experimental measurements. However, the model is based on an enriched-type crack, as illustrated in Fig. 5d. Specifically, the XFEM model relies on a Heaviside step function and a search algorithm to determine if an element is separated, while the location of such separation can be found without the need to explicitly create nodes on the mesh of the precrack. In contrast, the seam methodology uses a stationary crack which needs to be predefined before running the FEM analysis. Therefore, a hybrid methodology which takes under consideration the contour integral for a growing enriched crack was necessary to quantify the J-integral as a function of loading increments.

In Fig. 5e, a comparison between the different analyses using the seam and XFEM crack models is shown. All seam crack methods converged regardless of the analysis type in the FEM formulation. However, the XFEM crack results differ from each other. Further, the default XFEM method in ABAQUS (2013) is also limited to a stationary crack with small strain (i.e. infinitesimal FEM formulation) and overestimates the J-integral compared to the seam crack. Consequently, a user-defined hybrid methodology to calculate it was necessary. Such methodology relied in manually defining the crack front by specifying nodes close to the enriched crack tip, which were within an element as shown in Fig. 5d. The second step was to set the direction of the energy release using the global coordinate system. This methodology definitely has limitations and, as seen in the results of Fig. 5e, still overestimates the energy release, although less than the XFEM default method.

2.2.3 Energy flux

Motivated by the fact that the J-integral describes the energy release due to crack initiation but does not explicitly account transient energy effects, part of which is also the dissipation that occurs because of acoustic emission, the concept of energy flux was further explored. This concept has been widely investigated in the fields of Electromagnetism and Acoustics (see Achenbach 1973; Auld 1973) and relies on the evaluation of the Poynting vector over the boundary of an arbitrary control volume inside which the source exists, which therefore represents a measure of the rate at which the mechanical energy is transferred. The main idea in this approach is that the energy released by the crack source can be evaluated by computing the energy leaving a given volume that surrounds the crack tip in a specified time window so that bulk and surface wave effects are allowed to propagate while prohibiting incoming waves due, for example, to boundary reflections. This concept is graphically illustrated in Fig. 6, in which the energy radiates from region “1” (inside) to “2” (outside a cylindrical surface enclosing the crack tip).

Fig. 7
figure 7

a Load drop response due to crack growth. b Total energy calculation as a function of applied displacement that denotes the onset of plasticity. c Plastic dissipation and elastic strain energy calculations as a function of applied displacement

Full size image

In this scheme, the Poynting vector is represented by the product \({\varvec{\upsigma }} \cdot {\dot{\mathbf{u}}}\), while the external normal to the surface \(A_c \) of the cylindrical surface is denoted with n. Essentially, the energy radiated is associated to the tractions (i.e. \({\varvec{\upsigma }} \cdot \mathbf{n})\) and the corresponding velocity vectors, \({\dot{\mathbf{u}}}\), for which the power balance becomes

$$\begin{aligned} -\frac{\partial (\sigma _{ji} \dot{u}_i )}{\partial x_j }=\rho \ddot{u}_i \dot{u}_i +\sigma _{ji} \frac{\partial (\dot{u}_i )}{\partial x_j }+\dot{u}_i \cdot f_i^{AE}, \end{aligned}$$
(11)

where \(f_i^{AE}\) are the tractions related to the AE source and \(\ddot{u}\) denotes acceleration. Following the classical derivation of Poynting’s theorem (see Auld 1973, Chapter 5C), the application of the divergence theorem and integration over time allow the energy radiated, \(E_R\), to be expressed as

$$\begin{aligned} E_R= & {} \int _{0}^{t}\oint _{A_{c}}(-\sigma \cdot \dot{u})\cdot \hat{n}dA_{c}d\tau \nonumber \\= & {} - \int _{0}^{t} {\left( {\int _{V} {\sigma :\dot{\varepsilon }^{{el}} \,dV} } \right) d\tau }\nonumber \\&- \int _{0}^{t} {\left( {\int _{V} {\sigma :\dot{\varepsilon }^{{pl}} \,dV} } \right) d\tau }\nonumber \\&-\int _{0}^{t} \left( \int _{V}\rho \ddot{u}_{i} \dot{u}_{i}dV\right) d\tau + E_{{external}}, \end{aligned}$$
(12)

i.e. the radiated energy corresponds to the surface integral of the Poynting vector over \(A_c \) and over time, which is equal to the difference of the total energy over time including the kinetic energy (which was ignored in Eqs. (4) and (6), i.e. in the previous two formulations presented in this section). Equation (12) can be expressed in a finite elements’ approximation scheme, e.g. employing a trapezoidal quadrature rule, as

$$\begin{aligned} E_R= & {} \sum _{i=1}^N \frac{t_{i+1} -t_i }{2}A_{ eff}^j \left[ \left( {\sum _{j=1}^M {\left( {-\dot{u}^{j}\cdot \sigma ^{j}} \right) \cdot \hat{{n}}^{j} } } \right) _{i+1}\right. \nonumber \\&\left. +\left( {\sum _{j=1}^M {\left( {-\dot{u}^{j}\cdot \sigma ^{j}} \right) \cdot {\hat{n}}^{j} } } \right) _i \right] , \end{aligned}$$
(13)

where “i” represents the number of energy rate data points (related to number of time increments in the FEM) and “j” is the number of nodes belonging to the effective surface area of each node, \(A_{ eff}\). Hence, energy “exits” from the confined area defined by the cylindrical region and is approximated to be equal to the area defined by each finite element (i.e. for a \(400 \,\upmu \hbox {m}\) mesh size, a 2D area of \(0.16\,\hbox { mm}^{2}\) is obtained). In summary, Eqs. (12) and (13) provide a method to quantify the energy from the source which is radiated in a time period of duration t, as the stress waves propagate through the volume. In comparison, the energy flux approach does provide the means to directly evaluate the energy dissipation via Acoustic Emission and its use is validated in this article by the results obtained by the other two approaches.

Fig. 8
figure 8

a Crack fronts utilized for the J-integral calculations. b J-integral values for various perpendicular directions to each of the two crack fronts. c Detail showing the drop in the J-integral

Full size image

3 Results and discussion

The three methods described previously, were implemented in this work in conjunction with the fracture-induced AE model and the corresponding results are presented in this section.

3.1 Energy balance

The critical stage for the onset of crack growth was necessary to be defined to link the static to the dynamic model in order to accurately simulate the AE source generation and propagation (Cuadra et al. 2015). In addition to providing the conditions for the AE source, such critical stage serves as the equilibrium state before crack initiation in a corresponding energy balance approach. Consequently, the static equilibrium solution right after crack initiation was used to calculate the difference in total energy related always to the first crack increment. This means that although the computational model could be used to simulate crack growth, the focus in this article was only on the first crack increment.

Fig. 9
figure 9

Energy flux calculation calculated using the dynamic solution

Full size image

In equilibrium the external work is equal to the internal energy (i.e. stored energy). Computationally although the total energy could be nonzero due to several numerical effects, the equilibrium state could still be computed since the FEM formulation solves for the first energy variation to be zero. Specifically, the computational model used in this article contains two mechanisms that could create nonzero equilibrium energy states, which include the incremental plasticity and crack growth (i.e. stress relaxation due to newly created surfaces) formulations. Consequently, the onset of crack growth can be identified by the results shown in Fig. 7. A load drop of \(\sim 200\hbox { N}\) was calculated at crack initiation, when a new crack increment of total area \(\Delta \alpha \) equal to \(2.32\hbox { mm}^{2}\) was created, as shown in Fig. 7a (the insert shows more clearly the load drop in the force versus load line displacement trend line). The total energy calculation in Fig. 7b shows the onset of plasticity by the amount of energy beyond the original zero-energy equilibrium state. The total energy evolution as a function of applied displacement at the pin location of the computational model is also capable to denote the onset of crack growth, by the sudden drop in accordance with the explanation provided earlier in Sect. 2, related to the work done to create the new crack surfaces. This drop was calculated to be approximately 3.86 mJ. As explained earlier, this amount of energy is considered to be the crack formation energy \(E_{crack}\), as represented in Eq. (5). This energy drop can be further seen by the drop in the elastic strain energy (which is intimately related to the energy dissipation via AE) and the increase in plastic dissipation terms shown in Fig. 7c. As mentioned earlier, the energy drop can be considered an upper bound of the energy dissipated via AE since the AE part is only a portion of this energy that is distinct and different from the energy expended to form the crack. Hence, the \(E_{crack} \) in this approach includes both the energy to form the crack area \(\Delta a\) and the energy that dissipated due to the formation of elastic waves, which justifies the need for additional ways to energetically describe the process of the first crack increment formation in a ductile material, as shown next.

3.2 J-integral

Following the investigation described in Sect. 2.2, the J-integral formulation was applied for two crack fronts as shown in Fig. 8a, and two corresponding normal directions, using the XFEM user-defined approach producing the results shown in Fig. 8b. After performing a contour size convergence study for each of the four calculations, the evolution of the J-integral showed a sudden drop when the crack initiated in all directions. The change in the J-integral value for the stages before and after crack growth was calculated and then multiplied by the newly created crack surface area to obtain the final value of the energy release. The results for the x-direction in CF1 are plotted in Fig. 8c to demonstrate this process. The first drop of the J-integral value was found to be equal to \(1.11\,\hbox { kJ/m}^{2}\) for \(\alpha \Delta \alpha = 2.24\, \hbox {mm}^{2}\) which gives an energy release value equal to 2.48 mJ. This value is 35 % different from the corresponding estimate provided by the energy balance approach, however both methods produce results of the same order of magnitude, which validates the approach followed. The advantage of the J-integral approach is that it can be computed for specific directions taking specific crack fronts into account and therefore it could be considered an improvement towards estimating the energy release due to the first crack increment. A further improvement of this approach would be to use a computational method to account for e.g. the kinetic energy and include it in a J-integral formulation for dynamic conditions, which could then be used to also demonstrate the effect of transient behavior due to acoustic emission.

3.3 Energy flux

To make the proper calculations for wave propagation due to crack growth, the Poynting vector formulation was implemented, as described in Eq. (13). A model with a refined mesh around the crack tip, which excluded the residual stresses was utilized to recalculate the radiated energy from the AE source. Two volumes sizes equal to 384 and \(864\,\hbox {mm}^{3}\) were used, as shown in Fig. 9a. The two volume sizes were sufficiently large to include the crack tip and plastic zone. In order to numerically evaluate the integral in Eq. (13), the normal vector corresponding to each surface was approximated to be in the direction of the standard basis vectors of the global coordinate system, e.g. the top surface elements have a [0 1 0] direction (i.e. they lie in the direction of the y-axis) quantified by their normal vector. The results of the calculated radiated energy along with the energy from the AE source are shown in Fig. 9b, c, respectively. The energy radiated was calculated using the dynamic stresses to account only for the energy associated to the propagating stress waves. The accumulated stresses from the static solution were also included in the calculations, while the velocity values used included those from the dynamic solution. It can be seen in the results in Fig. 9 that the radiated energy reaches a plateau to a value between 12–14 nJ at around \(5\, \upmu \hbox {s}\). Furthermore, the total energy due to crack initiation is calculated by adding the elastic strain energy, plastic dissipation and kinetic energy to the radiated energy as derived in Eq. (12). Based on Fig. 9c, the AE source energy also reaches a plateau at around \(5 \,\upmu \hbox {s}\) to the value of 2.24 mJ.

Table 2 Summary of computed estimates of energy release and acoustic emission
Full size table

It is important to note here that the radiated energy computed by the energy flux approach is a more comparable parameter to what the energy dissipation due to AE is, as it corresponds to the portion of the energy that is transiently transferred away from the crack source. As the calculations presented in this article demonstrate in Table 2, the energy dissipation that occurs due to Acoustic Emission although it is almost negligible compared to other parts of the energy redistribution due to the first increment in a ductile fracture process, is however present and can be estimated based on a careful consideration of contributing factors to what is referred to as energy release. From a magnitude perspective, it is understood that depending on the size of the crack increment and given the properties of the elastoplastic strain accumulation at the crack tip, the amount of energy associated with the dissipation via acoustic emission would vary.

4 Concluding remarks

A computational methodology was introduced to provide an estimate of the energy dissipation that occurs in the form of acoustic emission during the energy release from the first increment of fracture in a ductile material. To compute this energy dissipation a 3D finite element model was created and was calibrated by using full field deformation experimental measurements on a compact tension specimen subjected to Mode I loading. As the energy dissipation that occurs because of acoustic emission is of transient nature, three different approaches were used to provide estimates for this effect. The first one, called energy balance, accounted for the difference in total energy measured numerically by the model, and it was pointed out that it could only provide an upper bound estimate as it does not account for any transient effects. The second one involved the use of the J-integral applied for equilibrium states and provided an estimate of the total energy release which agreed with the energy balance approach, however it again could not account for any transient effects using the form implemented in this article. The final approach, called energy flux, was based on the Poynting vector. This method was capable to provide both an estimate of the energy release by evaluating the steady-state of a transient estimate of the energy release obtained by integrating over time for the rate of change to the total energy which in this case included kinetic effects. This last approach was further capable to provide an estimate of the radiated energy through two control volumes surrounding the crack tip. The comparison of the energy flux with the first two approaches validated its use in estimating the energy release occurring due to crack initiation, while it further provided an estimate of the energy dissipation due to acoustic emission. This investigation showed that the dissipation is a small fraction of the total energy redistributions that occurs at the time of fracture. Comments were made regarding the role of the AE source which in this article was the first increment of ductile frature, such as its size and elastoplastic strain accumulation in defining the magnitude of such energy dissipation. Although this investigation was theoretical in nature, it is believed by the authors to be the first attempt to provide a computational continuum level methodology to estimate the specific portion of energy that dissipates due to the release of transient elastic waves from direct simulations of crack initiation. Therefore, it is expected that the presented results could assist in the interpretation of relevant nondestructive information as well as in the design of next generation of sensing technologies.