1 Introduction

Impact loadings, as well as accidental or malicious explosions, may impose high loading rates to engineering structures [36]. Therefore, dynamic behavior of a material, which can significantly differ from its static one [8], is essential in applications such as collision, explosion, ballistic impact, high-speed machining, and metal forming. As the choice of the constitutive model and the identification of model parameters are vital [72], a large number of research studies that investigated the dynamic response of materials focused on establishing a plastic constitutive model. Plastic constitutive models can be divided into two categories: Microstructure-based physical models and empirical phenomenological models [50]. In addition, plastic constitutive models can be categorized as rate-independent models or rate-dependent models. Interested readers on rate-independent constitutive models are referred to recent articles by Siddiq [83], Asim et al. [5], and Fu et al. [32]. On the other hand, rate-dependent constitutive models are discussed more in detail in the following paragraphs.

Zerilli and Armstrong [101] model is an example of microstructure-based physical model. The model is based on dislocation mechanics and the constitutive equations were developed for body-centered-cubic (BCC) and face-centered-cubic (FCC) materials. Later, Voyiadjis and Abed [95] discussed the derivation of Zerilli–Armstrong constitutive equations and they proposed a model that accounts for the evolution of mobile dislocation density. Various models that consider the effect of dislocation density evolution on the response of different crystal structures are available in the literature (see, e.g., [7, 34, 52, 80, 81, 94]). A widespread use of microstructure-based physical models is limited, as they generally involve a large number of parameters [85].

An example of empirical phenomenological model is Johnson and Cook [43] model. Johnson and Cook [43] presented a constitutive model that primarily aims to ease numerical implementation. The model includes five material constants, and the authors provided the numerical values of these constants for twelve different materials. Another example of empirical phenomenological model was proposed by Khan and Liang [48] based on the experimental results of three BCC metals (tantalum, tantalum alloy with 2.5% tungsten, and AerMet 100 steel). This model has been subjected to several modifications based on the observations on the mechanical responses of polycrystalline materials during nearly two decades [45, 50]. In addition to those mentioned, numerous phenomenological models have been proposed in the literature (see, e.g., [65, 82, 92]). Interested readers are referred to Sung et al. [89], Huh et al. [42], and Tanimura et al. [90], where a summary and comparison of several strain rate (and temperature)-dependent constitutive models are presented.

Material failure models can be divided into physically based models and empirical phenomenological models as well. Additionally, they can be divided into two categories as coupled models and uncoupled models. The former approach couples the constitutive model and the fracture criterion, that is, damage accumulation is incorporated into the constitutive model. A well-known example of this class is the Gurson model [37]. Gurson model, developed for porous ductile materials, is based on the void growth mechanics and has been subjected to modifications to account for realistic values (see, e.g., [91]) as well as shear dominated stress states (see, e.g., [67] for shear modification and [69] for further extension). Interested readers are referred to Benzerga et al. [11] for a comprehensive review of Gurson-based models. Moreover, variational methods have been utilized as well in order to model damage accumulation (see, e.g., [75,76,77, 84]). On the other hand, the latter approach decouples damage accumulation and the constitutive model, that is, fracture criterion and the constitutive model act independent from each other. Hancock–Mackenzie model [40] can be given as an example for this class.

In contrast to the plastic constitutive models, only a small portion of studies (that investigated the dynamic response of materials) focused on establishing a ductile fracture criterion for dynamic loading conditions. More than three decades ago, Johnson and Cook [44] proposed a strain rate (and temperature)-dependent fracture criterion based on the results of a series of tensile tests on three different metals (OFHC copper, Armco iron, and 4340 steel). Although the original version is still used in the literature, Johnson–Cook fracture model has been exposed to modifications as well (see, e.g., [15]). Other strain rate-dependent ductile fracture criteria have been proposed in addition to Johnson–Cook-based failure criteria. Kim et al. [54] proposed two failure criteria (using the effective strain or damage parameters) as a function of Zener–Holloman parameter [100] to predict the fracture behavior of magnesium alloy sheets. The proposed criteria are based on observations and deep drawing experiments of AZ31 sheets were conducted in order to validate the proposed criteria. Khan and Liu [51] proposed an empirical strain rate (and temperature)-dependent fracture criterion, based on the magnitude of stress vector criterion [49], and the criterion was calibrated for Al2024–T351 alloy. Liu and Sun [59] proposed a dynamic ductile fracture model that involves the effect of hydrostatic pressure, Lode angle, and the strain rate. The criterion was applied to determine the material parameters of Al–7075 alloy. Roth and Mohr [79] proposed an empirical extension of the Hosford–Coulomb model [63] to include the strain rate effect on fracture initiation. The expression was calibrated and validated using the experimental results of DP590 steel and TRIP780 steel. Although a comprehensive review on dynamic ductile fracture lacks, interested readers are referred to Molinari et al. [64] for dynamic necking and fragmentation, and dynamic damage by microvoiding with applications to spalling and dynamic crack growth.

Currently, the original [44] or slightly modified versions (see, e.g., [15]) of Johnson–Cook fracture criterion is commonly used to account for the effect of strain rate (and temperature). However, Johnson–Cook fracture criterion and its modifications experience fundamental shortcomings as presented in the following. Firstly, Johnson–Cook criterion is based on stress triaxiality only; therefore, it cannot capture the difference between different stress states of same triaxiality. Nevertheless, experimental studies have shown that the Lode angle/parameter (that is, the third stress invariant) plays an important role (in addition to stress triaxiality) in ductile fracture process (see, e.g., [9, 10, 20, 97]). Hence, both parameters need to be taken into account to predict ductile fracture accurately. Although researchers have modified Johnson–Cook criterion in order to include the Lode angle dependency, this results in extra material constant(s), which requires additional experiment(s) to calculate these new constant(s) (see, e.g., [29]). Secondly, Johnson–Cook fracture criterion exhibits mesh size dependency [56]. Thirdly, Johnson–Cook-based fracture criteria as well as aforementioned fracture criteria are empirical, and an analytical strain rate-dependent ductile fracture criterion still lacks. Therefore, the aim of the current study is to develop an analytical strain rate-dependent criterion on ductile fracture initiation at the continuum scale. This relationship is obtained by further developing the energy balance concept [47]. The energy-based criterion to be developed includes the stress triaxiality and the Lode angle dependencies inherently, without the necessity of extra material constants, by considering the stress state as a whole. Moreover, as the criterion to be developed introduces a characteristic length, use of characteristic length as a mesh size removes mesh dependency. The novelty of the current research is development of a rate-dependent ductile fracture criterion (of tensile mode) that is physically based, mesh independent and encompasses stress triaxiality and Lode angle/parameter dependencies inherently.

Dynamic loading here and thereafter corresponds to non-cyclic loading cases, that is, fatigue loading is beyond the scope of the current investigation and studied elsewhere (see, e.g., [3, 4, 58, 68]). The article is organized as follows. The ductile fracture criterion is derived in Sect. 2, and implemented into two example applications in Sect. 3. The results are presented and discussed in Sect. 4. Finally, a summary with conclusion remarks are given in Sect. 5.

2 Ductile fracture criterion for dynamic loading

In this section, an analytical strain rate-dependent criterion on ductile fracture initiation at the continuum scale is developed. This relationship is obtained by further developing the energy balance concept [47] and the focus is given only tensile mode (i.e., Mode I) fracture.

Conservation of energy principle requires the sum of the rate of work done on a body by external forces and all other energy rates being equal to the time rate of change of the internal energy and the kinetic energy [31]. In the following, the case where the work done on the system is only by external forces is considered, that is, no other external energy enters the system. It is also assumed that there are no pre-existing cracks or damage at the continuum scale. Moreover, elastic deformation (i.e., elastic strain energy) can be ignored as ductile fracture usually associated with large strains where plastic deformation dominates. The mechanical work increment per unit volume, dw, then takes the form of

$$\begin{aligned} \hbox {d}w=\hbox {d}u+\hbox {d}k=\sigma _{ij}\hbox {d}\varepsilon _{ij}+\rho v_{i}\hbox {d}v_{i} \end{aligned}$$
(1)

where du and dk represent the plastic work increment and the kinetic energy increment per unit volume, respectively. Also, \(\sigma _{ij}\) are the components of true stress tensor, \(\hbox {d}\varepsilon _{ij}\) are the components of (plastic) strain increment tensor, \(\rho \) is the mass density of the material, and \(v_{i}\) are the components of velocity vector.

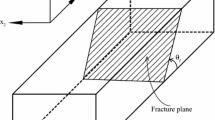
Let consider an isotropic continuous medium in a rectangular Cartesian coordinate system subjected to uniform state of stress before fracture. Suppose that this medium has the current dimensions of \(l_\mathrm{{I}}\), \(l_\mathrm{{II}}\), and \(l_\mathrm{{III}}\) in the principal directions of \(x_\mathrm{{I}}\), \(x_\mathrm{{II}}\), and \(x_\mathrm{{IIII}}\), respectively. The volume element with a potential fracture plane is presented in Fig. 1.

Fig. 1
figure 1

Volume element and potential fracture plane

Full size image

The mechanical work increment per unit volume of the unfractured medium can be written in terms of principal values as

$$\begin{aligned} \hbox {d}w=\sigma _\mathrm{{I}}\hbox {d}\varepsilon _\mathrm{{I}}+\sigma _\mathrm{{II}}\hbox {d}\varepsilon _\mathrm{{II}}+\sigma _\mathrm{{III}}\hbox {d}\varepsilon _\mathrm{{III}}+\rho \left( v_\mathrm{{I}}\hbox {d}v_\mathrm{{I}}+v_\mathrm{{II}}\hbox {d}v_\mathrm{{II}}+v_\mathrm{{III}}\hbox {d}v_\mathrm{{III}} \right) \end{aligned}$$
(2)

where \(\sigma _\mathrm{{I}}\ge \sigma _\mathrm{{II}}\ge \sigma _\mathrm{{III}}\). Also, the natural strain components in the principal directions are defined as

$$\begin{aligned} \hbox {d}\varepsilon _\mathrm{{I}}=\hbox {d}l_\mathrm{{I}}/l_\mathrm{{I}} , \hbox {d}\varepsilon _\mathrm{{II}}=\hbox {d}l_\mathrm{{II}}/l_\mathrm{{II}} , \hbox {d}\varepsilon _\mathrm{{III}}=\hbox {d}l_\mathrm{{III}}/l_\mathrm{{III}}. \end{aligned}$$
(3)

Integrating Eq. (3) yields

$$\begin{aligned} \varepsilon _\mathrm{{I}}=\ln \frac{l_\mathrm{{I}}}{l_{\mathrm{{I}},0}} , \varepsilon _\mathrm{{II}}=\ln \frac{l_\mathrm{{II}}}{l_{\mathrm{{II}},0}} , \varepsilon _\mathrm{{III}}=\ln \frac{l_\mathrm{{III}}}{l_{\mathrm{{III}},0}} \end{aligned}$$
(4)

where \(l_{i,0}\) and \(l_{i}\) are the initial and the current length components of the volume element, respectively. Now, let take the time derivative of Eq. (4)

$$\begin{aligned} \dot{\varepsilon _\mathrm{{I}}}=\frac{1}{l_\mathrm{{I}}}\frac{\hbox {d}l_\mathrm{{I}}}{\mathrm{{d}}t} , \dot{\varepsilon _\mathrm{{II}}}=\frac{1}{l_\mathrm{{II}}}\frac{\hbox {d}l_\mathrm{{II}}}{\mathrm{{d}}t} , \dot{\varepsilon _\mathrm{{III}}}=\frac{1}{l_\mathrm{{III}}}\frac{\hbox {d}l_\mathrm{{III}}}{\mathrm{{d}}t} \end{aligned}$$
(5)

where \(\dot{\varepsilon _\mathrm{{I}}}\), \(\dot{\varepsilon _\mathrm{{II}}}\), \(\dot{\varepsilon _\mathrm{{III}}}\) are the true strain rates in the principal directions.

Rigid body translational or rotational velocities are not considered (in the calculation of kinetic energy increment) as they do not make any contribution to fracture process. In other words, the ‘effective/active’ velocity is \(v_{i}=\hbox {d}l_{i}/\hbox {d}t\) not \(v_{i}=\hbox {d}x_{i}/\hbox {d}t\), with \(x_{i}\) representing the components of position vector. Hence, the velocity components can simply be written as

$$\begin{aligned} v_\mathrm{{I}}=l_\mathrm{{I}}\dot{\varepsilon _\mathrm{{I}}} , v_\mathrm{{II}}=l_\mathrm{{II}}\dot{\varepsilon _\mathrm{{II}}} , v_\mathrm{{III}}=l_\mathrm{{III}}\dot{\varepsilon _\mathrm{{III}}}. \end{aligned}$$
(6)

Equation (6) is in accordance with the true strain rate definition given by Dieter [26]. Differentiating both sides of Eq. (6) yields

$$\begin{aligned} {\hbox {d}v}_\mathrm{{I}}= & {} l_\mathrm{{I}}\hbox {d}\dot{\varepsilon _\mathrm{{I}}}+\dot{\varepsilon _\mathrm{{I}}}\hbox {d}l_\mathrm{{I}}\nonumber \\ {\hbox {d}v}_\mathrm{{II}}= & {} l_\mathrm{{II}}\hbox {d}\dot{\varepsilon _\mathrm{{II}}}+\dot{\varepsilon _\mathrm{{II}}}\hbox {d}l_\mathrm{{II}}\nonumber \\ {\hbox {d}v}_\mathrm{{III}}= & {} l_\mathrm{{III}}\hbox {d}\dot{\varepsilon _\mathrm{{III}}}+\dot{\varepsilon _\mathrm{{III}}}\hbox {d}l_\mathrm{{III}}. \end{aligned}$$
(7)

It is presumed that the strain rate remains nearly constant during an increment, that is, \(\hbox {d}\dot{\varepsilon _\mathrm{{I}}}=\hbox {d}\dot{\varepsilon _\mathrm{{II}}}=\hbox {d}\dot{\varepsilon _\mathrm{{III}}}=0\). Hence, Eq. (7) reduces to

$$\begin{aligned} {\hbox {d}v}_\mathrm{{I}}=\dot{\varepsilon _\mathrm{{I}}}{\hbox {d}l}_\mathrm{{I}} , {\hbox {d}v}_\mathrm{{II}}=\dot{\varepsilon _\mathrm{{II}}}{\hbox {d}l}_\mathrm{{II}} , {\hbox {d}v}_\mathrm{{III}}=\dot{\varepsilon _\mathrm{{III}}}{\hbox {d}l}_\mathrm{{III}}. \end{aligned}$$
(8)

Substituting Eq. (3) into Eq. (8) yields

$$\begin{aligned} {\hbox {d}v}_\mathrm{{I}}=l_\mathrm{{I}}\dot{\varepsilon _\mathrm{{I}}}\hbox {d}\varepsilon _\mathrm{{I}} , {\hbox {d}v}_\mathrm{{II}}=l_\mathrm{{II}}\dot{\varepsilon _\mathrm{{II}}}\hbox {d}\varepsilon _\mathrm{{II}} , {\hbox {d}v}_\mathrm{{III}}=l_\mathrm{{III}}\dot{\varepsilon _\mathrm{{III}}}\hbox {d}\varepsilon _\mathrm{{III}}. \end{aligned}$$
(9)

Finally, substituting Eqs. (6) and (9) into Eq. (2), and multiplying by the current volume yield the mechanical work increment of the unfractured medium, dW

$$\begin{aligned} \hbox {d}W=l_\mathrm{{I}}l_\mathrm{{II}}l_\mathrm{{III}}\left\{ \left[ \sigma _\mathrm{{I}}+\rho \left( l_\mathrm{{I}}\dot{\varepsilon _\mathrm{{I}}} \right) ^{2} \right] \hbox {d}\varepsilon _\mathrm{{I}}+\left[ \sigma _\mathrm{{II}}+\rho \left( l_\mathrm{{II}}\dot{\varepsilon _\mathrm{{II}}} \right) ^{2} \right] \hbox {d}\varepsilon _\mathrm{{II}}+\left[ \sigma _\mathrm{{III}}+\rho \left( l_\mathrm{{III}}\dot{\varepsilon _\mathrm{{III}}} \right) ^{2} \right] \hbox {d}\varepsilon _\mathrm{{III}} \right\} . \end{aligned}$$
(10)

This expression, i.e., Eq. (10), provides the necessary amount of energy increment for the system to deform without fracture; that is, dE. On the other hand, the necessary amount of energy increment for the system to fracture, \(\hbox {d}E^{*}\), includes an additional energy that is required to create new surfaces [47], that is

$$\begin{aligned} \hbox {d}E^{*}=\left( {\Gamma }_\mathrm{{I}}\times A \right) \hbox {d}\varepsilon _\mathrm{{I}}+\hbox {d}W^{*} \end{aligned}$$
(11)

where

$$\begin{aligned} \hbox {d}W^{*}=l_\mathrm{{I}}l_\mathrm{{II}}l_\mathrm{{III}}\left\{ \left[ \sigma _\mathrm{{I}}^{*}+\rho \left( l_\mathrm{{I}}\dot{\varepsilon _\mathrm{{I}}^{*}} \right) ^{2} \right] \hbox {d}\varepsilon _\mathrm{{I}}^{*}+\left[ \sigma _\mathrm{{II}}^{*}+\rho \left( l_\mathrm{{II}}\dot{\varepsilon _\mathrm{{II}}^{*}} \right) ^{2} \right] \hbox {d}\varepsilon _\mathrm{{II}}^{*}+\left[ \sigma _\mathrm{{III}}^{*}+\rho \left( l_\mathrm{{III}}\dot{\varepsilon _\mathrm{{III}}^{*}} \right) ^{2} \right] \hbox {d}\varepsilon _\mathrm{{III}}^{*} \right\} . \end{aligned}$$
(12)

Here, \({\Gamma }_\mathrm{{I}}\) denotes the critical effective energy release rate per unit surface area of the fracture plane (of tensile mode fracture) and \(dW^{*}\) is the mechanical work increment of the fractured medium. Tensile mode fracture plane and its area, which is \(A=l_\mathrm{{II}}l_\mathrm{{III}}\), are shown in Fig. 1. Also, all stress, strain, and strain rate quantities denoted by star are associated with the fractured medium. Moreover, the critical effective energy release rate \(({\Gamma })\) is a material property for a particular fracture mode [47], and it can be a function of strain rate and temperature.

The rate of energy change of the unfractured medium is initially less than the fractured medium, as the system maintains the minimum energy state. In other words, the system, seeking the minimum energy state, will fracture if the necessary energy increment for the fractured state becomes less than the necessary energy increment for the unfractured state. Therefore, the critical state is reached when the rate of energy change of these two states becomes equal [47]. Hence, mathematical representation of the critical state is

$$\begin{aligned} \hbox {d}E=\hbox {d}E^{*} \end{aligned}$$
(13)

with principal stresses and strains, and strain rates maintained consistent with the boundary conditions, that is

$$\begin{aligned}&\sigma _\mathrm{{II}}^{*}\hbox {d}\varepsilon _\mathrm{{II}}^{*}=\sigma _\mathrm{{II}}\hbox {d}\varepsilon _\mathrm{{II}},\left( \dot{\varepsilon _\mathrm{{II}}^{*}} \right) ^{2}\hbox {d}\varepsilon _\mathrm{{II}}^{*}=\left( \dot{\varepsilon _\mathrm{{II}}} \right) ^{2}\hbox {d}\varepsilon _\mathrm{{II}}\nonumber \\&\sigma _\mathrm{{III}}^{*}\hbox {d}\varepsilon _\mathrm{{III}}^{*}=\sigma _\mathrm{{III}}\hbox {d}\varepsilon _\mathrm{{III}},\left( \dot{\varepsilon _\mathrm{{III}}^{*}} \right) ^{2}\hbox {d}\varepsilon _\mathrm{{III}}^{*}=\left( \dot{\varepsilon _\mathrm{{III}}} \right) ^{2}\hbox {d}\varepsilon _\mathrm{{III}}. \end{aligned}$$
(14)

As the increment in strain is concentrated in the fracture zone, \(\hbox {d}\varepsilon _\mathrm{{I}}^{*}\) suddenly drops to zero; hence, the first term (in the parenthesis) of Eq. (12) vanishes. Therefore, the critical state condition, i.e., Eq. (13), takes the following form

$$\begin{aligned} l_\mathrm{{I}}l_\mathrm{{II}}l_\mathrm{{III}}\left[ \sigma _\mathrm{{I}}+\rho \left( l_\mathrm{{I}}\dot{\varepsilon _\mathrm{{I}}} \right) ^{2} \right] \hbox {d}\varepsilon _\mathrm{{I}}=\left( {\Gamma }_\mathrm{{I}}\times A \right) \hbox {d}\varepsilon _\mathrm{{I}}. \end{aligned}$$
(15)

Substituting \(A=l_\mathrm{{II}}l_\mathrm{{III}}\) into Eq. (15) and simplifying it yields

$$\begin{aligned} l_\mathrm{{I}}\left[ \sigma _\mathrm{{I}}+\rho \left( l_\mathrm{{I}}\dot{\varepsilon _\mathrm{{I}}} \right) ^{2} \right] ={\Gamma }_\mathrm{{I}}. \end{aligned}$$
(16)

Now, let define

$$\begin{aligned} C_\mathrm{{I}}=\frac{{\Gamma }_\mathrm{{I}}}{l_{\mathrm{{I}},0}}. \end{aligned}$$
(17)

Finally, substituting Eqs. (4) and (17) into Eq. (16) yields the critical state for tensile mode fracture

$$\begin{aligned} e^{\varepsilon _\mathrm{{I}}}\left[ \sigma _\mathrm{{I}}+\rho \left( l_\mathrm{{I}}\dot{\varepsilon _\mathrm{{I}}} \right) ^{2} \right] =\mathrm {C}_\mathrm{{I}}. \end{aligned}$$
(18)

As presented above, \(l_{\mathrm{{I}},0}\) and \(l_\mathrm{{I}}\) are the initial and the current length of the volume element, respectively, in the maximum principal stress/strain direction. Use of a material feature (e.g., a characteristic length) for \(l_{\mathrm{{I}},0}\) such that the stress state within the volume element remains uniform at the continuum scale is suggested. Hence, in this case, \(\mathrm {C}_\mathrm{{I}}\) is a material property, and can be a function of strain rate and temperature. Physically, \(\mathrm {C}_\mathrm{{I}}\) represents the specific surface energy density as it refers to critical effective energy release rate per unit (characteristic) length [47].

The critical state condition given by Eq. (18) does not include any terms that take the history of state of stress or strain into consideration. Hence, this form of the equation is suggested to be utilized for proportional loading conditions. On the other hand, a slight improvement to Eq. (18) that can be used for non-proportional loading cases is proposed in the following

$$\begin{aligned} e^{\int _{0}^{\varepsilon _\mathrm{{eq}}^{f}} \left( 1/\zeta _\mathrm{{I}} \right) \hbox {d}\varepsilon _\mathrm{{eq}}}\left[ \sigma _\mathrm{{I}}+\rho \left( l_\mathrm{{I}}\dot{\varepsilon _\mathrm{{I}}} \right) ^{2} \right] =\mathrm {C}_\mathrm{{I}} \end{aligned}$$
(19)

where

$$\begin{aligned}&\zeta _\mathrm{{I}}=\sqrt{\frac{2}{3}\left[ 1+\left( \frac{\hbox {d}\varepsilon _\mathrm{{II}}}{\hbox {d}\varepsilon _\mathrm{{I}}} \right) ^{2}+\left( \frac{\hbox {d}\varepsilon _\mathrm{{III}}}{\hbox {d}\varepsilon _\mathrm{{I}}} \right) ^{2} \right] } \end{aligned}$$
(20)
$$\begin{aligned}&\hbox {d}\varepsilon _\mathrm{{eq}}=\sqrt{\frac{2}{3}\left[ \left( \hbox {d}\varepsilon _\mathrm{{I}} \right) ^{2}+\left( \hbox {d}\varepsilon _\mathrm{{II}} \right) ^{2}+\left( \hbox {d}\varepsilon _\mathrm{{III}} \right) ^{2} \right] }. \end{aligned}$$
(21)

Here, plastic incompressibility is assumed and \(\zeta _\mathrm{{I}}\) is assumed to remain constant during an increment. \(\hbox {d}\varepsilon _\mathrm{{eq}}\) denotes the equivalent (plastic) strain increment with \(\varepsilon _\mathrm{{eq}}\) denoting the equivalent (plastic) strain. The integral term in Eq. (19) takes the deformation history into account; hence, use of Eq. (19) is suggested for non-proportional loading cases. Accordingly, use of the integral term \(\int _{0}^{\varepsilon _\mathrm{{eq}}^{f}} \left( 1/\zeta _\mathrm{{I}} \right) \hbox {d}\varepsilon _\mathrm{{eq}}\) is suggested in the graphical illustration of fracture locus (instead of equivalent plastic strain itself (\(\varepsilon _\mathrm{{eq}}))\) for non-proportional loading cases. If the loading is proportional, \(\zeta _\mathrm{{I}}\) remains constant throughout loading and Eq. (19) reduces to Eq. (18).

There is not sufficient time for appreciable heat flow to occur at high rates of deformation [26] due to sudden and abrupt nature of the crack nucleation process [18]. Therefore, in high loading cases, where the plastic work cannot be totally dissipated, there will be temperature increase in the material. Although a temperature term does not explicitly appear in the critical state equation (Eq. 19), the effect of temperature increase should be included implicitly by determining the current temperature after each increment, and updating the values of temperature-dependent terms, particularly \(\sigma _\mathrm{{I}}\) (i.e., the constitutive equations) and \(C_\mathrm{{I}}\), accordingly. The increase in temperature, \({\Delta }T\), can be computed by

$$\begin{aligned} {\Delta }T=\frac{\beta }{\rho c_{V}}\int {\sigma _{ij}\hbox {d}\varepsilon _{ij}} \end{aligned}$$
(22)

where \(\beta \) is the fraction of the plastic work contributing to temperature increase, and \(c_{V}\) is the specific heat capacity at constant volume. Here, the thermal energy term is considered to be only generated by mechanical work; however, extraneous heat sources may exist in the system that are not purely mechanical (see, e.g., Rittel, 2014 for details). Additionally, the reason for the use of the specific heat capacity at constant volume is that the plastic flow is essentially isochoric [46].

3 Example applications

Numerous experimental studies have been conducted in order to explore the effect of dynamic loading on fracture behavior of metals, including various types of steels [1, 2, 14, 16, 23, 30, 35, 53, 57, 62, 93], aluminum alloys [13, 21, 22, 28, 73, 87], magnesium alloys [28, 98], titanium alloys [12, 28, 41, 96, 102], nickel alloys [86], tungsten alloys [78], and tantalum [27]. In addition, fracture behavior of additively manufactured metals is a rising topic of research interest (see, e.g., [24, 88, 99]) thanks to rapid development of 3D-printing technology. However, in this section, the experimental results of Bobbili et al. [13] and Bobbili and Madhu [12] are utilized, as the articles were published recently and the authors provided enough data of interest (i.e., true fracture strain values for various stress states and strain rates) to investigate the application of the proposed criterion.

The von-Mises equivalent stress in terms of principal stresses is defined as

$$\begin{aligned} \sigma _\mathrm{{eq}}=\sqrt{\frac{1}{2}\left[ \left( \sigma _\mathrm{{I}}-\sigma _\mathrm{{II}} \right) ^{2}+\left( \sigma _\mathrm{{II}}-\sigma _\mathrm{{III}} \right) ^{2}+\left( \sigma _\mathrm{{III}}-\sigma _\mathrm{{I}} \right) ^{2} \right] }. \end{aligned}$$
(23)

Also, for a given stress state, it is convenient to express the equivalent stress in terms of maximum principal stress, that is

$$\begin{aligned} \sigma _\mathrm{{eq}}=\xi _\mathrm{{I}}\sigma _\mathrm{{I}} \end{aligned}$$
(24)

with \(\xi _\mathrm{{I}}\) takes the following form for the axisymmetric stress state [47]

$$\begin{aligned} \xi _\mathrm{{I}}=\frac{3}{2+3\eta } \end{aligned}$$
(25)

where \(\eta \) is the stress triaxiality.

Moreover, the flow rule is expressed as [25]

$$\begin{aligned} {\hbox {d}\varepsilon }_\mathrm{{I}}= & {} \frac{2}{3}\lambda \left[ \sigma _\mathrm{{I}}-\frac{1}{2}\left( \sigma _\mathrm{{II}}+\sigma _\mathrm{{III}} \right) \right] \nonumber \\ {\hbox {d}\varepsilon }_\mathrm{{II}}= & {} \frac{2}{3}\lambda \left[ \sigma _\mathrm{{II}}-\frac{1}{2}\left( \sigma _\mathrm{{I}}+\sigma _\mathrm{{III}} \right) \right] \nonumber \\ {\hbox {d}\varepsilon }_\mathrm{{III}}= & {} \frac{2}{3}\lambda \left[ \sigma _\mathrm{{III}}-\frac{1}{2}\left( \sigma _\mathrm{{I}}+\sigma _\mathrm{{II}} \right) \right] \end{aligned}$$
(26)

where \(\lambda \) is a non-negative scalar factor and may vary throughout loading.

Bobbili et al. [13] and Bobbili and Madhu [12] conducted tensile tests on Al–4.8Cu–1.2Mg alloy and Ti–10V–2Fe–3Al alloy to investigate the fracture behavior of these alloys at different loading rates. They provided experimental data for four different stress triaxialities at four strain rates. However, as there was no explicit information on the fracture mode of the smooth specimens, only the data of notched specimens (i.e., three data points for each strain rate) are considered here, that is, \(\eta =0.5153\), \(\eta =0.6209\), and \(\eta =0.7387\). Moreover, the authors did not provide any data for strain rate beyond 1000 \(\hbox {s}^{\mathrm {-1}}\) for Al-4.8Cu-1.2 Mg alloy and 1500 \(\hbox {s}^{\mathrm {-1}}\) for Ti–10V–2Fe–3Al alloy. Hence, Johnson–Cook fracture criterion [44] is used to calculate the approximate fracture strains at any loading case beyond these strain rates. The fracture strain values at these loading cases are calculated for the same three stress triaxialities. Furthermore, although proportional loading is not generally the case in actual experiments, it is assumed that the stress triaxiality remains nearly constant throughout loading, as the authors did not provide any experimental data on the evolution of stress triaxiality. Hence, for the proportional loading case, as mentioned above, \(\zeta _\mathrm{{I}}\) remains constant throughout loading with \(\zeta _\mathrm{{I}}=1\) for the axisymmetric case [47].

Johnson–Cook constitutive model [43] is used to represent the constitutive behavior of Al–4.8Cu–1.2Mg and Ti–10V–2Fe–3Al alloys, as Bobbili et al. [13] and Bobbili and Madhu [12] used Johnson–Cook constitutive model as well, and they provided the material constants of the model. The authors also proposed a slightly modified version of Johnson–Cook constitutive equation to improve the prediction accuracy of the flow behavior of the materials of interest at high strain rates and temperatures [12, 13]. However, the original Johnson–Cook constitutive equation, given in the following, is used here as it describes the flow behavior of the materials of interest fairly well, as well.

$$\begin{aligned} \sigma _\mathrm{{eq}}=\left[ A_{1}+A_{2}\varepsilon _\mathrm{{eq}}^{n} \right] \left[ 1+A_{3}\ln \left( \frac{\dot{\varepsilon }}{\dot{\varepsilon _{0}}} \right) \right] \left[ 1-\left( \frac{{T-T}_\mathrm{{room}}}{T_\mathrm{{melt}}-T_\mathrm{{room}}} \right) ^{m} \right] \end{aligned}$$
(27)

where \(\sigma _\mathrm{{eq}}\), \(\varepsilon _\mathrm{{eq}}\), \(\dot{\varepsilon }\), and \(\dot{\varepsilon _{0}}\) are the equivalent stress, equivalent plastic strain, strain rate, and reference strain rate, respectively. Also, T, \(T_\mathrm{{room}}\), and \(T_\mathrm{{melt}}\) are the actual material temperature, room temperature and the melting temperature of the material, respectively. Moreover, there are five material constants \((A_{1}, A_{2}, A_{3}, n, m)\) to be determined. Different strategies on the calculation of these material parameters were extensively discussed by Gambirasio and Rizzi [33] and the material constants were determined for three materials (i.e., DH36 structural steel, a commercially pure niobium and an AL-6XN stainless steel) using the published experimental data.

3.1 Example 1: Tensile mode fracture of Al–4.8Cu–1.2Mg

Bobbili et al. [13] conducted tensile tests on Al–4.8Cu–1.2Mg alloy at four different strain rates: 0.01 \(\hbox {s}^{\mathrm {-1}}\), 0.1 \(\hbox {s}^{\mathrm {-1}}\), 1 \(\hbox {s}^{\mathrm {-1}}\), 1000 \(\hbox {s}^{\mathrm {-1}}\). Nevertheless, the specific surface energy density, \(\mathrm {C}_\mathrm{{I}}\), is determined for three additional strain rates as well, i.e., for 5000 \(\hbox {s}^{\mathrm {-1}}\), 20,000 \(\hbox {s}^{\mathrm {-1}}\), 50,000 \(\hbox {s}^{\mathrm {-1}}\). The approximate fracture strains at these strain rates are calculated by using Johnson–Cook fracture criterion, given by Bobbili et al. [13] as

$$\begin{aligned} \bar{\varepsilon _{f}}=\left[ 0.05+1.281e^{-3.5\eta } \right] \left[ 1+0.138\ln \left( \frac{\dot{\varepsilon }}{\dot{\varepsilon _{0}}} \right) \right] . \end{aligned}$$
(28)

Again, as mentioned previously, Eq. (28) is used to determine the fracture strains only for three stress triaxialities in order to obtain the approximate value of \(\mathrm {C}_\mathrm{{I}}\) at strain rates beyond 1000 \(\hbox {s}^{\mathrm {-1}}\).

Moreover, the following constitutive equation, whose material constants are provided by Bobbili et al. [13], is used to predict the flow behavior of Al–4.8Cu–1.2Mg alloy

$$\begin{aligned} \sigma _\mathrm {{eq}}=\left[ 380+482\varepsilon _\mathrm {{eq}}^{0.51} \right] \left[ 1+0.0128\ln \left( \frac{\dot{\varepsilon }}{\dot{\varepsilon _{0}}} \right) \right] \end{aligned}$$
(29)

with the reference strain rate is taken as \(\dot{\varepsilon _{0}}=1\) \(\hbox {s}^{\mathrm {-1}}\).

There is no published data on mass density or average spacings of large inclusions of Al–4.8Cu–1.2Mg alloy, to the authors’ best knowledge. Additionally, although the temper designation of the Al alloy is provided as T6, its commercial name is not known (personal communication with Dr. Bobbili through e-mail). However, the copper and magnesium contents of Al–4.8Cu–1.2Mg alloy remains within the chemical composition range of Al 2024 and Al 2124 alloys [19]. Therefore, properties of these two alloys are considered to approximate the mass density and characteristic length of Al–4.8Cu–1.2Mg alloy.

Mass densities of Al 2024 and Al 2124 alloys are 2770 kg/\(\hbox {m}^{\mathrm {3}}\) [6]; hence, the mass density of Al–4.8Cu–1.2Mg alloy is taken as \(\rho =2770\) kg/\(\hbox {m}^{\mathrm {3}}\). Even though center to center spacing of inclusions for Al 2024 and Al 2124 alloys with T6 temper condition are not provided in the open literature (to the authors’ best knowledge), Hahn and Rosenfield [39] provided center to center spacing of inclusions for Al 2024 and Al 2124 alloys with T851 temper condition. Hence, considering the average value of (center to center spacing of inclusions for) Al 2024-T851 and Al 2124-T851 alloys gives a characteristic length of \(l_{\mathrm{{I}},0}\approx 8 \quad \upmu \)m. Despite the fact that temper condition of the alloy of interest is different than those considered in the prediction of the characteristic length, \(l_{\mathrm{{I}},0}\approx 8\) \(\upmu \)m is a reasonable approximation, as it is on the order of inclusion spacing of other 2xxx Al alloys as well, for instance, Al 2014-T6 alloy (see, e.g., [39]).

3.2 Example 2: Tensile mode fracture of Ti–10V–2Fe–3Al (Ti–1023)

Bobbili and Madhu [12] conducted tensile tests on Ti–10V–2Fe–3Al (also called Ti-10-2-3) alloy at four different strain rates as well: 0.01 \(\hbox {s}^{\mathrm {-1}}\), 500 \(\hbox {s}^{\mathrm {-1}}\), 1000 \(\hbox {s}^{\mathrm {-1}}\), 1500 \(\hbox {s}^{\mathrm {-1}}\). Again, the specific surface energy density, \(\mathrm {C}_\mathrm{{I}}\), is determined for three additional strain rates, i.e., for 5000 \(\hbox {s}^{\mathrm {-1}}\), 20,000 \(\hbox {s}^{\mathrm {-1}}\), 50,000 \(\hbox {s}^{\mathrm {-1}}\), and the approximate fracture strains at these strain rates are calculated by using Johnson–Cook fracture criterion. The expression was given by Bobbili and Madhu [12] as

$$\begin{aligned} \bar{\varepsilon _{f}}=\left[ -0.04+0.46e^{0.21\eta } \right] \left[ 1+0.027\ln \left( \frac{\dot{\varepsilon }}{\dot{\varepsilon _{0}}} \right) \right] . \end{aligned}$$
(30)

Again, Eq. (30) is used to determine the fracture strains only for three stress triaxialities in order to obtain the approximate value of \(\mathrm {C}_\mathrm{{I}}\) at strain rates beyond 1500 \(\hbox {s}^{\mathrm {-1}}\).

In addition, the following constitutive equation, whose material constants are provided by Bobbili and Madhu [12], is used to predict the flow behavior of Ti–10V–2Fe–3Al alloy

$$\begin{aligned} \sigma _\mathrm {{eq}}=\left[ 842+754\varepsilon _\mathrm {{eq}}^{0.42} \right] \left[ 1+0.021\ln \left( \frac{\dot{\varepsilon }}{\dot{\varepsilon _{0}}} \right) \right] \end{aligned}$$
(31)

with the reference strain rate is taken as \(\dot{\varepsilon _{0}}=1\) \(\hbox {s}^{\mathrm {-1}}\).

Mass density of Ti–10V–2Fe–3Al alloy is \(\rho =4650\) kg/\(\hbox {m}^{\mathrm {3}}\) [17]. Moreover, the defect spacing (only inclusions and pores that participated in the fracture process are included) of Ti–10V–2Fe–3Al alloy was provided in Figure 15 of Moody et al. [66] for various samples that were subjected to different processing conditions. Taking an average value of these data gives a characteristic length of \(l_{\mathrm{{I}},0}\approx 12 \quad \upmu \)m.

4 Results and discussion

The specific surface energy densities of Al and Ti alloys of interest for a wide range of strain rates are presented in Figs. 2 and 3, respectively. Red circles are determined using the critical state equation (with actual experimental data or data obtained through Johnson–Cook fracture criterion) and a curve fit of red circles are presented as a blue solid line. The data used for the lowest four strain rates are the experimental data, whereas Johnson–Cook data are used for the remaining three strain rates. The equation of the curve fit (blue solid line) takes the form of \(C_\mathrm{{I}}=999.5+2.5\times {10}^{-7}\left[ 2.86+\log \left( \frac{\dot{\varepsilon }}{\dot{\varepsilon _{0}}} \right) \right] ^{11.4}\) for the Al–4.8Cu–1.2Mg alloy (see Fig. 2), and \(C_\mathrm{{I}}=1011+6.5\times {10}^{-7}\left[ 2.98+\log \left( \frac{\dot{\varepsilon }}{\dot{\varepsilon _{0}}} \right) \right] ^{11.6}\) for the Ti–10V–2Fe–3Al alloy (see Fig. 3).

Fig. 2
figure 2

Specific surface energy density of Al–4.8Cu–1.2Mg alloy for various strain rates

Full size image
Fig. 3
figure 3

Specific surface energy density of Ti–10V–2Fe–3Al alloy for various strain rates

Full size image

As can be seen from Figs. 2 and 3, the specific surface energy density (hence, the critical effective energy release rate) remains nearly constant at low strain rates. The specific surface energy density for the Al–4.8Cu–1.2Mg and Ti–10V–2Fe–3Al alloys at low strain rates are determined as on the order of \(C_\mathrm{{I}}^{Al}\approx 1000\) MPa and \(C_\mathrm{{I}}^{Ti}\approx 2000\) MPa, respectively. These values correspond to critical effective energy release rates of \({\Gamma }_\mathrm{{I}}^{Al}\approx 8\) kJ/\(\hbox {m}^{\mathrm {2}}\) and \({\Gamma }_\mathrm{{I}}^{Ti}\approx 24\) kJ/\(\hbox {m}^{\mathrm {2}}\) for Al–4.8Cu–1.2Mg alloy and Ti–10V–2Fe–3Al alloy, respectively. The determined critical effective energy release rates are consistent with the energy release rates of Al and Ti alloys provided by Hahn et al. [38].

On the other hand, the specific surface energy density (hence, the critical effective energy release rate) increases dramatically at high strain rates, that is, the specific surface energy density and the critical effective energy release rate are highly dependent on the loading rate at high strain rates. The trend of increase in critical effective energy release rate with strain rate, particularly at high strain rates, agrees with the results reported in the literature. Both experimental (see, e.g., [71]) and numerical (see, e.g., [70]) studies showed that the effect of loading rate on energy release rate is little at small loading rates, whereas energy release rate is found to increase dramatically at high loading rates. Actually, the second term in Eqs. (18) and (19) explains the reason behind these observations. As can be seen from these equations, the second term is proportional to square of the strain rate and it does not contribute to the response very much until it approaches on the order of maximum principal stress (\(\sigma _\mathrm{{I}})\). In other words, the specific surface energy density (hence, the critical effective energy release rate) does not change significantly until a critical strain rate (at which the second term approaches on the order of maximum principal strain) and then increases dramatically as the second term in the critical state equation is proportional to the square of the strain rate. Physically, material rate sensitivity and the material microstructure were found to be the main governors of this response [70]. The critical state equation is in accordance with this finding as well. In the equation, the maximum principal stress \((\sigma _\mathrm{{I}})\) represents the material rate sensitivity, whereas the material microstructure is represented by the characteristic length (\(l_{\mathrm{{I}},0}\)).

Fracture loci of Al and Ti alloys of interest for three different strain rates are shown in Figs. 4 and 5, respectively. Fracture loci curves for \(\dot{\varepsilon }=20{,}000\) \(\hbox {s}^{\mathrm {-1}}\) are determined by evaluating the data obtained by Johnson–Cook fracture criterion, whereas the remaining two curves are obtained by evaluating experimental data presented by Bobbili et al. [13] and Bobbili and Madhu [12]. Newton–Raphson method is used to solve the critical state equation.

An interesting observation from Figs. 4 and 5 is that the fracture locus loses its nonlinear characteristic as the strain rate increases and it turns into nearly linear at ultra-high strain rates (the classification of strain rates in this article is based on the classification proposed by Piao et al. [74]) as can be seen from red dash-dot lines. However, determined fracture strains for the highest strain rate considered (i.e., \(\dot{\varepsilon }=20{,}000\) \(\hbox {s}^{\mathrm {-1}})\) do not agree well with the fracture strains estimated by Johnson–Cook criterion. The main reason for this disagreement is believed to be the fact that Johnson–Cook fracture criterion is an empirical criterion and may not produce accurate results for strain rates much higher than the strain rates used to determine the model parameters. Moreover, proportional loading assumption, neglecting temperature increase and the use of Johnson–Cook constitutive model are believed to slightly contribute to this disagreement as well.

Fig. 4
figure 4

Fracture locus of Al–4.8Cu–1.2Mg alloy for various strain rates

Full size image
Fig. 5
figure 5

Fracture locus of Ti–10V–2Fe–3Al alloy for various strain rates

Full size image

As stated before, proportional loading is not generally the case in actual experiments, and the temperature of the material increases at high loading rates. Nevertheless, neither loading history nor temperature changes throughout loading are considered in the example applications presented here, as no data on the history of stress/strain state were provided by Bobbili et al. [13] and Bobbili and Madhu [12]. However, both loading history and temperature changes should be considered for the proper application of the critical state equation. The values of temperature-dependent terms, particularly \(\sigma _\mathrm{{I}}\) (i.e., the constitutive equations) and \(C_\mathrm{{I}}\), should be updated accordingly, in every increment. Moreover, the choice of constitutive model is crucial as well, as strain hardening, strain rate, and temperature sensitivity of the material need to be accurately modeled for the appropriate and correct use of the developed fracture criterion.

Furthermore, as Bobbili et al. [13] and Bobbili and Madhu [12] did not provide any data on local strain rates, global strain rates are used for the example applications considered. However, local strain rate can be different than global strain rate and it is location dependent [81]. Therefore, use of local strain rate is suggested for the appropriate application of the proposed criterion.

5 Conclusions

The energy balance concept developed by Karr and Akçay [47], which is based on continuum modeling of energy release rates, is further developed to include the effect of dynamic loading into consideration. The formulation introduces a material length scale \((l_{\mathrm{{I}},0})\) and a material property \((C_\mathrm{{I}})\) that is a function of strain rate and temperature. \({C}_\mathrm{{I}}\) is a material property only in the case of use of a material feature (e.g., a characteristic length) for \(l_{\mathrm{{I}},0}\) such that the stress state within the volume element remains uniform at the continuum scale. Physically, \({C}_\mathrm{{I}}\) represents the specific surface energy density as it refers to critical effective energy release rate per unit (characteristic) length [47].

The proposed ductile fracture criterion is implemented into two example applications, Al–4.8Cu–1.2Mg alloy and Ti–10V–2Fe–3Al alloy, whose experimental data were published by Bobbili et al. [13] and Bobbili and Madhu [12]. The fracture loci of these two alloys at various strain rates, and the specific surface energy densities as a function of strain rate are determined. The fracture locus is found to lose its nonlinear characteristic as the strain rate increases, and it turns into nearly linear at ultra-high strain rates (see [74] for the classification of strain rates). Moreover, the specific surface energy densities (hence, the critical effective energy release rates) of the considered alloys are found to be highly dependent on the loading rate, particularly at high strain rates. The trend of increase in critical effective energy release rate with strain rate, particularly at high strain rates, is in accordance with the results reported in the literature (see, e.g., [70, 71]). Moreover, determined critical effective energy release rates of Al–4.8Cu–1.2Mg alloy and Ti–10V–2Fe–3Al alloy are consistent with the energy release rates of Al and Ti alloys provided by Hahn et al. [38].

On the other hand, the fracture criterion proposed in this article is applicable to tensile mode (i.e., Mode I) ductile fracture only. However, in practical applications, fracture may not be pure tensile mode; shear mode fracture, i.e., Mode II fracture (see, e.g., [55, 60]), as well as mixed mode fracture (see, e.g., [61]) has been observed commonly at high strain rates. Therefore, development of a companion ductile fracture criterion of shear mode for dynamic loading conditions is vital and an avenue of continuing study.