1 Introduction

Fracture prediction depends on the fracture criterion [1]. However, the classical fracture theories, such as the maximum tangential stress criterion [2], the minimum strain energy density criterion [3] and the maximum energy release rate criterion [4], work well only for predicting a new born crack initiation from a crack tip. These well-known classical fracture theories cannot yet be used to predict some other potential fracture behaviours, such as the crack branching etc. Similar cases can be found in the other methods [5,6,7,8,9,10,11].

Planar crack propagation under pure Mode-I loading is generally stable and will become unstable with the superposition of a Mode-III loading [12, 13]. An initially flat parent crack segments into an array of daughter cracks that rotate towards a direction of maximum tensile stress [14]. Numerical simulations of mixed Mode-I/III brittle fracture using a continuum phase field method [15,16,17] indicated that planar crack propagation is linearly unstable against helical deformations of the crack front. During growth evolution, facets gradually coarsen in striking analogy with the coarsening of finger patterns observed in non-equilibrium growth phenomena. However, the crack initiation behaviour and its mechanism for a well-defined mixed Mode-I/III crack are still foundational issues which govern the subsequent potential evolution of the crack surface.

Fracture criterion should have predicted various potential fracture behaviours, such as the crack propagation and branching. As the crack branching can be observed not only at the Mode-I crack tip, but also at the Mode-II and mixed Mode-I/II crack tips, it is therefore reasonable to speculate that the similar fracture behaviour should happen at the mixed Mode-I/III crack tip. Usually, if a crack tip split into two or more crack tips, the stress intensity factors for the newborn cracks are smaller in varying degrees than that for the original crack [18], which may change the crack growth behaviours. The fracture mechanism also plays a major role in the engineering applications, such as the formation of the hydraulic crack system during hydraulic fracturing. A good understanding on crack propagation, branching conditions and mechanism is important to explain and predict the complex fracture phenomenon.

Recently, a two-dimensional energy-based modelling had been suggested to simulate the physics process involved in multiple cracks initiation from a crack tip under Mode-I, Mode-II and mixed Mode-I/II loading [19,20,21,22,23]. In present article, this modelling has been extended to three-dimensional one and used to formulize the multiple cracks initiation from a crack tip under mixed Mode-I/III loading. Some potential fracture configurations, including the mixed Mode I/III crack tri-branching, symmetrical-branching, side-branching, kinking and extension, are investigated in detail. The possible crack initiation angles, the associated energy-based configuration driving forces and the K-based effective fracture toughness are found within the framework of the linear elastic fracture mechanics.

2 Three-dimensional geometrical and fracture modelling

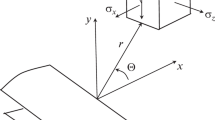
Figure 1 shows a cracked solid subjected to mixed Mode-I/III loading. The x3-axis is along the crack front, and x2 is normal to the crack surface. A plate-shaped segment, bounded by two planes paralleling to the x1-x2 plane at unit distance from each other and a longitudinal closed surface, can be detached from the cracked solid as shown in Fig. 1a, c and d, which will be used as a three-dimensional modelling to formulized the physical process of energy release for potential multiple cracks initiation from the local boundary around crack tip.

Fig. 1
figure 1

Geometrical modelling of multiple cracks initiation from a crack tip (in case of m = 3) when s→0. a A cracked solid under mixed Mode-I/III loading \((r_{o} \to 0^{ + } )\). b Typical local integral surfaces within the K-dominant region. c Multiple-notches model for boundaries \(A_{i}\) (i = 1, 2, 3) shifting. d Model for multiple cracks initiation

Full size image

Multiple cracks initiation from a boundary within the K-dominant region can be geometrically considered as multiple boundaries shifting in different directions as shown in Fig. 1c. When the local crack surfaces \(A_{i} = s_{i}\) × 1 shift in vi-direction (i = 1, 2, 3,…, m), m notches should be formed and will degenerate into m cracks with the width \(s = s_{1} + s_{2} + \cdot \cdot \cdot + s_{m} \to 0\) as shown in Fig. 1d in the case of \(m = 3\). Then, from the local boundary surface \(A = A_{1} + A_{2} + \cdot \cdot \cdot + A_{m} \to 0\), a three-dimensional geometrical modelling for multiple cracks initiation in m directions can be proposed and sketched in Fig. 1d. This modelling is actually the three-dimensional extension from the two-dimensional one [19,20,21,22,23,24]. For the geometrical configuration of boundary shifting as shown in Fig. 1c, d, the energy release rate can be given by [19,20,21,22,23,24]

$$G = \mathop {\lim }\limits_{A \to 0} \iint\limits_{A} {{\text{we}}_{i} n_{i} d\Omega } = \sum\limits_{l = 1}^{m} {\left( {\mathop {\lim }\limits_{{s_{l} \to 0}} \iint\limits_{{A_{l} }} {{\text{we}}_{i} n_{i} d\Omega }} \right)} ,$$
(1)

where \(e_{i} = \cos \alpha_{i}\) and \(\alpha_{i}\) is the angle between shifting direction \(v_{l}\) of the boundary \(A_{l}\) and \(x_{i}\)-axis illustrated in Fig. 1c; \(n_{i}\) is the unit normal vector of the boundary \(A_{l}\). By using the three-dimensional conservation law [24, 25], Eq. (1) may be expressed by

$$G = \sum\limits_{l = 1}^{m} {\left\{ {J_{1} \left( {A_{l} } \right)|_{{A_{l} \to 0}} \cos \left( {\alpha_{1} } \right)_{l} + J_{2} \left( {A_{l} } \right)|_{{A_{l} \to 0}} \cos \left( {\alpha_{2} } \right)_{l} + J_{3} \left( {A_{l} } \right)|_{{A_{l} \to 0}} \cos \left( {\alpha_{{3}} } \right)_{l} } \right\}} ,$$
(2)

where

$$J_{j} \left( {A_{l} } \right)|_{{A_{l} \to 0}} = \mathop {\lim }\limits_{{A_{l} \to 0}} \iint\limits_{{A_{l} }} {wn_{j} d\Omega } = \iint\limits_{{\left( {A_{in} } \right)_{l} }} {\left( {wn_{j} - T_{i} u_{i,j} } \right)d\Omega },j = {1},{ 2},{ 3}$$
(3)

and \(\left( {A_{in} } \right)_{l}\), (l = 1, 2…m), is an integral surface within the solids; \(\left( {A_{{{\text{in}}}} } \right)_{l} - A_{l}\) becomes a closed one. The \(J_{j} \left( {A_{l} } \right)|_{{A_{l} \to 0}}\) in Eq. (3) is the energy release rate when the boundary \(A_{l}\) shifts in \(x_{j}\)-direction.

Unlike the applications of the classical fracture criterion, when Eq. (2) is applied to formulize the multiple cracks initiation, the integral subintervals for Jj-integrals should be determined first. Then, the maximized energy release rate for multiple cracks initiation can be found based on the positive/negative features of \(J_{j} \left( {A_{l} } \right)|_{{A_{l} \to 0}}\)-integrals. It should be indicated that when the local boundary surface \(A_{l}\) moves inward to solids, \(J_{j} \left( {A_{l} } \right)|_{{A_{l} \to 0}}\) may be positive or negative. If \(J_{j} \left( {A_{l} } \right)|_{{A_{l} \to 0}}\) > 0.0, the cracking induced by \(A_{l}\) moving inward to solids will lead strain energy release, which may occur naturally. If \(J_{j} \left( {A_{l} } \right)|_{{A_{l} \to 0}}\) < 0.0, the so-called cracking should lead to energy absorbing, which is impossible to happen naturally. Then, Eq. (2) must include all the contributions of the positive energy release for the \(A_{l}\), (l = 1, 2…m), shifting inward to solids in order to maximize the energy release rate. The negative \(J_{j} \left( {A_{l} } \right)|_{{A_{l} \to 0}}\) should be excluded from Eq. (2), because which violates the principle of energy release [12,13,14,15,16]. In this case, the maximized energy release rate becomes a real energy-based configuration driving force, which exhibits a fracture modelling to capture the physical process of multiple cracks initiation.

3 Positive/negative features on \(J_{j}\)-integrals

The positive/negative features of the \(J_{j}\)-integrals can be easily revealed by analysing its integrands, based on which the number m of the subintervals can be found.

3.1 \(J_{j}\)-integrals

A well-defined crack tip can be enlarged as a U-turn-shaped crack surface with unit width and \(r_{o} \to 0^{ + }\) as shown in Fig. 1b. When \(\left( {A_{in} } \right)_{l} = \sum\nolimits_{i = 1}^{5} {A_{i} }\), where \(A_{{1}}\) is a cylindrical surface within the K-dominant region, from Eq. (3), the \(J_{j}\)-integrals over \(A_{l}\) can be given by

$$J_{j} \left( {A_{l} } \right)|_{{A_{l} \to 0}} = \mathop {\lim }\limits_{{A_{l} \to 0}} \iint\limits_{{A_{l} }} {wn_{j} d\Omega } = \iint\limits_{{\sum\limits_{i = 1}^{5} {A_{i} } }} {\left( {wn_{j} - T_{i} u_{i,j} } \right)d\Omega }\mathop = \limits^{{r \to r_{o} }} \iint\limits_{{A_{1} }} {\left( {wn_{j} - T_{i} u_{i,j} } \right)d\Omega },j = {1},{ 2},{\text{ and 3}}.$$
(4)

For any local crack surface \(A_{l} = \left\{ {A\left| {r_{o} \to 0^{ + } ,\theta \in \left[ {\theta_{0} ,\theta } \right],x_{3} \in \left[ { - 0.5,0.5} \right]} \right.} \right\}\) as shown in Fig. 1b, substituting the stress and displacement within the K-dominant region into Eq. (4), the \(J_{j}\)-integrals over the surface \(A_{l}\) can be found, respectively, as

$$J_{1} \left( {A_{l} } \right) = \frac{{1 - \mu^{2} }}{2\pi E}\int_{{\theta_{{0}} }}^{\theta } {\left[ {K_{I}^{{2}} \left( {1 - \cos 2\theta } \right) + \frac{1}{1 - \mu }K_{III}^{{2}} } \right]d\theta } ,$$
(5)
$$J_{2} \left( {A_{l} } \right) = \frac{{1 - \mu^{2} }}{2\pi E}\int_{{\theta_{{0}} }}^{\theta } {\left( { - K_{I}^{2} \sin 2\theta } \right)d\theta }$$
(6)

and

$$J_{{3}} \left( {A_{l} } \right) = {0}{\text{.}}$$
(7)

It should be noted that as \(J_{{3}} \left( {A_{l} } \right) = {0}\), the newborn crack surface or crack tip does not move in x3-direction, which means that the new crack tip still remains in the x1-x2 plane. Additionally, Eq. (6) does not contain any contribution of KIII, which implies that the behaviours of \(J_{2} \left( {A_{l} } \right)\)-integral are similar to the case of pure Mode-I deformation [22].

For convenience of subsequent analysis, introduce a normalized parameter

$$\varphi = \frac{2}{\pi }\arctan \frac{{K_{I} }}{{K_{III} /\sqrt {{1 - }\mu } }},$$
(8)

which varies from 0.0 for pure Mode-III deformation to 1.0 for pure Mode-I and may completely describe the relative strength of \(K_{I}\) and \({\text{K}}_{{{\text{III}}}}\). By using Eq. (8), Eqs. (5) and (6) become

$$J_{1} \left( {A_{l} } \right) = \frac{{\left( {1 - \mu^{2} } \right)\left( {K_{I}^{2} + K_{III}^{2} /(1 - \mu )} \right)}}{{{2}\pi E}}\int_{{\theta_{{0}} }}^{\theta } {\left( {1 - \sin^{2} \frac{\pi \varphi }{2}\cos {2}\theta } \right)d\theta }$$
(9)

and

$$J_{2} \left( {A_{l} } \right) = \frac{{\left( {1 - \mu^{2} } \right)\left( {K_{I}^{2} + K_{III}^{2} /(1 - \mu )} \right)}}{2\pi E}\int_{{\theta_{0} }}^{\theta } { - \sin^{2} \frac{\pi \varphi }{2}\sin 2\theta d\theta } .$$
(10)

Equation (9) shows that the integrand of the normalized \(J_{1} \left( {A_{l} } \right)\)-integral always takes on positive value, i.e. \({1 - }\sin^{2} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } {2}}} \right. \kern-0pt} {2}}} \right)\cos 2\theta \ge 0\) on \({ - }\pi \le \theta \le \pi\) as illustrated in Fig. 2, which means the energy release when any local boundary \(A_{l}\) shifts in \(x_{1}\)-direction. Unlike Eq. (9), Eq. (10) shows that the integrand of the normalized \(J_{2} \left( {A_{l} } \right)\)-integral may take on both positive and negative values as shown in Fig. 3.

Fig. 2
figure 2

Integrand of normalized \(J_{1}\)-integral

Full size image
Fig. 3
figure 3

Integrand of normalized \(J_{2}\)-integral

Full size image

3.2 \(J_{2}\)-integral

For a cracked solid under mixed Mode-I/III loading, five intersection points of the integrand of normalized \(J_{2}\)-integral and θ-axis can be found by setting \(\sin^{2} ({{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2})\sin 2\theta = 0\), i.e.

$$\theta_{k} = \frac{k\pi }{2},k\, = \,0,\, \pm \,{1},\, \pm \,{2}.$$
(11)

As sketched in Fig. 3, these intersection points should divide the interval [π, −π] into four subintervals, i.e. [0, π/2] and [π/2, π] for the upper crack surface, [−π, −π /2] and [−π /2, 0] for the lower crack surface, which is similar to the case of the pure Mode-I deformation [20, 22]. Figure 3 indicates that the integrand of the normalized \(J_{2} \left( {A_{l} } \right)\)-integral \(- \sin^{2} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)\sin 2\theta \le 0\) on [0, π/2] and [−π, −π /2]; \(- \sin^{2} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)\sin 2\theta \ge 0\) on [π/2, π] and [−π /2, 0]. The \(J_{2} \left( {A_{l} } \right)\)-integral over the four subintervals takes on either positive or negative value and is summarized in Table 1.

Table 1 Normalized \(J_{j} \left( {A_{l} } \right)\)-integrals
Full size table

The physical meanings of the positive and negative \(J_{2}\)-integrals are different, which determine the division of the integral subintervals and the distribution of energy-based driving forces. For the upper half a crack tip boundary, \(A_{1} = \left\{ {A\left| {r_{o} ,\theta \in \left[ {0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}} \right],x_{3} \in \left[ { - 0.5,0.5} \right]} \right.} \right\}\) and \(A_{2} = \left\{ {A\left| {r_{o} ,\theta \in \left[ {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2},\pi } \right],x_{3} \in \left[ { - 0.5,0.5} \right]} \right.} \right\}\), \(J_{2} \left( {A_{1} } \right) < 0\) and \(J_{2} \left( {A_{{2}} } \right) > 0\) theoretically indicate that if the boundary \(A_{1}\) moves in x2-direction, the cracked solids will absorb or increase strain energy, which actually is impossible to occur naturally; if the \(A_{2}\) moves in the x2-direction, the solid will release the energy. So, viewed from maximizing energy release rate, the contribution of \(J_{2} \left( {A_{{1}} } \right)\) should be excluded from Eq. (2) with the aid of the reasonable division of subintervals. For the boundaries \(A_{3} = \left\{ {A\left| {r = r_{o} ,\theta \in \left[ { - \pi ,{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0pt} 2}} \right],x_{3} \in [ - 0.5,0.5]} \right.} \right\}\) and \(A_{4} = \left\{ {A\left| {r = r_{o} ,\theta \in \left[ {{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0pt} 2},0} \right],x_{3} \in \left[ { - 0.5,0.5} \right]} \right.} \right\}\) for the lower half a crack tip surface, when \(A_{{3}}\) moves in the opposite x2-direction, the energy release rate \({ - }J_{2} \left( {A_{{3}} } \right) > 0\), which means that a crack initiation from \(A_{{3}}\) as a wing crack is possible; when \(A_{{4}}\) moves in the opposite x2-direction, \({ - }J_{2} \left( {A_{{4}} } \right) < 0\) implies that this form of boundary moving will cause energy-absorbing and is not going to happen. The potential energy-based driving forces acting, respectively, on \(A_{1}\), \(A_{2}\), \(A_{{3}}\) and \(A_{{4}}\) and the potential crack initiation angles are shown in Fig. 4. It should be noted that the energy-based driving force has three basic elements, such as the point of application, direction and magnitude.

Fig. 4
figure 4

Division of subintervals, energy-based driving forces and the fracture trends. (ro → 0+)

Full size image

The analysis of this section implies that the subinterval number m should be no larger than 4.

4 Multiple-cracks initiation from a mixed Mode-I/III crack tip

The above analysis implies that when the energy-based driving forces acting, respectively, on the four subintervals reach the critical value, the concerned local boundaries around a crack tip will fracture. Any real fracture configuration is one of the potential fracture configurations, which may be a triggered new born crack or the combination of multiple new born cracks under proper conditions.

For a mixed Mode-I/III crack, there are five basic potential fracture configurations, i.e. the crack tri-branching (-shaped fracture), branching (-shaped symmetrical fracture), side-branching (-shaped fracture) as shown in Fig. 5, kinking and extension. The detailed analysis will be given in this section.

Fig. 5
figure 5

Basic fracture configurations for multiple cracks initiation

Full size image

4.1 Configuration driving force and fracture angles for mixed Mode-I/III crack tri-branching

Based on the discussions in Sect. 3.2, the fracture configuration of crack tri-branching may be created when boundaries \(A_{2}\) and \(A_{{3}}\) move inward to solid as two wing cracks and \(A_{1}\) + \(A_{{4}}\) moves together in x1-direction in form of the original crack extension as illustrated in Figs. 4, 5a and 6. In this regard, the whole boundary around crack tip is actually divided to three subboundaries (m = 3), i.e. \(A_{2}\), \(A_{{3}}\) and \(A_{1}\) + \(A_{{4}}\), on which there are three energy-based driving forces acting, respectively, as shown in Fig. 4. By using the symmetry of the tri-fractures configuration, the concerned energy release rate can be given by

$$G^{{{\text{tri}} - b}} = {2}\left( {J_{1} \left( {A_{1} } \right)\cos \alpha_{1} + J_{1} \left( {A_{2} } \right)\cos \alpha_{2} + J_{2} \left( {A_{{2}} } \right)\sin \alpha_{{2}} } \right)$$
(12)
Fig. 6
figure 6

The geometrical sketch on three cracks initiation from a Mode-I/III crack tip

Full size image

from Eq. (2). By substituting the results in Table 1 into Eq. (12), the following expression can be found.

$$G^{{{\text{tri}} - b}} = \frac{{\left( {1 - \mu^{2} } \right)\left( {K_{I}^{2} + K_{III}^{2} /(1 - \mu )} \right)}}{2E}\left\{ {\cos \alpha_{1} + \sqrt {1 + \left( {4/\pi^{2} } \right)\sin^{4} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)} \cos \left( {\alpha_{{2}} { - }\beta } \right)} \right\},$$
(13)

where

$$\beta = \tan^{ - 1} \left[ {\left( {2/\pi } \right)\sin^{2} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)} \right]\deg .$$
(14)

To find the maximised energy release rate, we set \(\frac{{\partial G^{{{\text{tri}} - b}} }}{{\partial \alpha_{i} }} = 0\), i = 1 and 2, and obtain \(\sin \alpha_{1c} = 0\) and \(\sin \left( {\alpha_{{{2}c}} { - }\beta } \right) = 0\), which give

$$\alpha_{1c} = \alpha_{{{4}c}} = 0\;{\text{deg}}.$$
(15)

and

$$\alpha_{{{2}c}} = - \alpha_{3c} = \beta \,{\text{deg}}.,$$
(16)

where \(\alpha_{1c}\) and \(\alpha_{2c}\), schematically shown in Figs. 4 and 7, are the theoretical expected critical crack initiation angles at which \(G_{{}}^{tri - b}\) reaches its maximum value and can be given by

$$G_{\max }^{{{\text{tri}} - b}} = \frac{{\left( {1 - \mu^{2} } \right)\left( {K_{I}^{2} + K_{III}^{2} /(1 - \mu )} \right)}}{E}\frac{{1 + \sqrt {1 + \left( {4/\pi^{2} } \right)\sin^{4} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)} }}{2}.$$
(17)
Fig. 7
figure 7

Critical crack initiation angle α2c

Full size image

Equation (17) denotes an energy-based configuration driving force for mixed Mode-I/III crack tri-branching as shown in Figs. 5a and 6. It indicates that when

$$G_{\max }^{{{\text{tri}} - b}} = G_{C}^{{{\text{tri}} - b}} ,$$
(18)

the mixed Mode-I/III crack will theoretically fracture in the form of crack tri-branching.

4.2 K-based effective fracture toughness for Mode-I/III crack tri-branching

For the cracked brittle solids, the Griffith’s criterion [26] states that a crack will initiate when the driving force or applied \(G_{\max }\) reaches its critical value \(G_{C}\) [26, 27], i.e.

$$G_{\max } = G_{C} .$$
(19)

For pure Mode-I deformation, when \(G_{\max } = G_{C}\), we have

$$G_{C} = \frac{{\left( {1 - \mu^{2} } \right)K_{IC}^{2} }}{E}.$$
(20)

When the mixed Mode-I/III crack tri-branching is triggered, as discussed in Sect. 4.1, the energy-based driving force acting on \(A_{2}\) or \(A_{3}\) can be found as

$$G_{\max }^{{A_{2} - {\text{wing}}}} = \frac{{\left( {1 - \mu^{2} } \right)\left( {K_{I}^{2} + K_{III}^{2} /(1 - \mu )} \right)}}{E}\frac{{\sqrt {1 + \left( {4/\pi^{2} } \right)\sin^{4} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)} }}{4}.$$
(21)

The energy-based driving force triggering A1 + A4 to fracture as a form of crack extension can be expressed by

$$G_{\max }^{{A_{1} + A_{4} - {\text{ext}}}} = \frac{{\left( {1 - \mu^{2} } \right)\left( {K_{I}^{2} + K_{III}^{2} /(1 - \mu )} \right)}}{E}\frac{1}{2}.$$
(22)

From Eqs. (19)-(22), it is not difficult to find the K-based fracture toughness

$$K_{{{\text{eff}} - C}}^{{A_{2} - {\text{wing}}}} = \frac{2}{{\left[ {1 + \left( {4/\pi^{2} } \right)\sin^{4} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)} \right]^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}} }}K_{{{\text{IC}}}}$$
(23)

for wing crack, where the effective stress intensity factor \(K_{{{\text{eff}}}} = \sqrt {K_{I}^{2} + K_{III}^{2} /(1 - \mu )}\), and

$$K_{{{\text{eff}} - C}}^{{A_{1} + A_{4} - {\text{ext}}}} = {1}{\text{.41}}K_{{{\text{IC}}}}$$
(24)

for main crack extension as shown in Fig. 8. Then, from Eqs.(17) and (18), the critical energy release rate for crack tri-branching can be found as

$$G_{C}^{{{\text{tri}} - b}} = \frac{{\left( {1 - \mu^{2} } \right)\left( {K_{{{\text{eff}} - C}}^{{{\text{tri}} - b}} } \right)^{2} }}{E}\frac{{1 + \sqrt {1 + \left( {4/\pi^{2} } \right)\sin^{4} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)} }}{2},$$
(25)
Fig. 8
figure 8

Normalized fracture toughness \({{K_{{{\text{eff}} - C}}^{{A_{2} - {\text{wing}}}} } \mathord{\left/ {\vphantom {{K_{{{\text{eff}} - C}}^{{A_{2} - {\text{wing}}}} } {K_{{{\text{IC}}}} }}} \right. \kern-0pt} {K_{{{\text{IC}}}} }}\) and \({{K_{eff - C}^{{A_{i} - ext}} } \mathord{\left/ {\vphantom {{K_{eff - C}^{{A_{i} - ext}} } {K_{IC} }}} \right. \kern-0pt} {K_{IC} }}\) for local boundaries

Full size image

where \(K_{{{\text{eff}} - C}}^{{{\text{tri}} - b}}\) is the K-based effective fracture toughness for crack tri-branching and can be written as

$$K_{{{\text{eff - }}C}}^{{{\text{tri}} - b}} = \max \left\{ {K_{{{\text{eff}} - C}}^{{A_{2} - {\text{wing}}}} , \, K_{{{\text{eff}} - C}}^{{A_{1} + A_{4} - {\text{ext}}}} } \right\} = K_{{{\text{eff}} - C}}^{{A_{2} - {\text{wing}}}} .$$
(26)

The relationship between \(G_{\max }^{{A_{2} - wing}}\), \(G_{\max }^{{A_{1} + A_{4} - ext}}\) and \(G_{\max }^{tri - b}\) may be schematically shown in Fig. 9. The K-based criterion for Mode-I/III crack tri-branching can be found as:

$$K_{{{\text{eff}}}} = K_{{{\text{eff}} - C}}^{{{\text{tri}} - b}} .$$
(27)
Fig. 9
figure 9

The relationship between \(G_{\max }^{{A_{2} - {\text{wing}}}}\), \(G_{\max }^{{A_{1} + A_{4} - {\text{ext}}}}\) and \(G_{\max }^{tri - b}\)

Full size image

4.3 Another case of mixed Mode-I/III crack tri-branching

Taking some non-idealized crack tips or the other disturbance into consideration, such as a notch tip, a new-born crack should initiate only from the subboundary \(A_{1}\) or \(A_{{4}}\) as a form of extension as shown in Fig. 10. In this case, a potential fracture configuration of crack tri-branching, i.e. three new-born cracks initiation from sub boundaries \(A_{1}\), \(A_{{2}}\) and \(A_{{3}}\), respectively, should be triggered. Then, another form of mixed Mode-I/III crack tri-branching may be formed. By using the same way in Sects.  4.1–4.2, the energy-based configuration driving force for mixed Mode-I/III crack tri-branching can be given by

$$G_{\max }^{tri - b} = \frac{{\left( {1 - \mu^{2} } \right)\left( {K_{I}^{2} + K_{III}^{2} /(1 - \mu )} \right)}}{E}\frac{{1 + {2}\sqrt {1 + \left( {4/\pi^{2} } \right)\sin^{4} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)} }}{{4}}.$$
(28)
Fig. 10
figure 10

Another form of Mode-I/III crack tri-branching

Full size image

The energy-based driving force for crack initiation from \(A_{1}\) in a form of crack extension can be found as

$$G_{\max }^{{A_{1} - ext}} = \frac{{\left( {1 - \mu^{2} } \right)\left( {K_{I}^{2} + K_{III}^{2} /(1 - \mu )} \right)}}{E}\frac{1}{{4}}.$$
(29)

From Eqs. (19), (20) and (29), the K-based fracture toughness of the local boundary \(A_{1}\) can be found as.

$$K_{{{\text{eff}} - C}}^{{A_{1} - {\text{ext}}}} = 2K_{{{\text{IC}}}} .$$
(30)

Then, from Eqs. (18) and (28), the critical energy release rate for mixed Mode-I/III crack tri-branching can be found as

$$G_{C}^{tri - b} = \frac{{\left( {1 - \mu^{2} } \right)\left( {K_{eff - C}^{tri - b} } \right)_{{}}^{2} }}{E}\frac{{1 + {2}\sqrt {1 + \left( {4/\pi^{2} } \right)\sin^{4} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)} }}{{4}},$$
(31)

where the K-based effective fracture toughness can be expressed by

$$K_{{eff{ - }C}}^{tri - b} = \max \left\{ {K_{eff - C}^{{A_{2} - wing}} , \, K_{eff - C}^{{A_{1} - ext}} } \right\} = K_{eff - C}^{{A_{1} - ext}} = {2}K_{IC}^{{}} ,$$
(32)

which is schematically shown in Fig. 8.

4.4 Mixed Mode-I/III crack side-branching

There are theoretically three forms of potential mixed Mode-I/III crack side-branching as shown in Fig. 11. By using the same way discussed in Sects.  4.1 and 4.2, the energy-based configuration driving forces and K-based effective fracture toughness for mixed Mode-I/III crack side-branching can be found and listed in Table 2.

Fig. 11
figure 11

The geometrical sketch on the three potential forms of mixed Mode-I/III crack side-branching

Full size image
Table 2 The normalized energy-based configuration driving forces and K-based effective fracture toughness for mixed Mode-I/III crack side-branching
Full size table

4.5 Mixed Mode-I/III crack branching and kinking

When two cracks initiate, respectively, from boundaries \(A_{{2}}\) and \(A_{{3}}\) inward to solids as two wing cracks, the potential and classical crack branching should be formed as shown in Figs. 5b and 12a. In this case, the concerned energy-based configuration driving force can be expressed as

$$G_{\max }^{sym - b} = \frac{{\left( {1 - \mu^{2} } \right)\left( {K_{I}^{2} + K_{III}^{2} /(1 - \mu )} \right)}}{E}\frac{{\sqrt {1 + \left( {{4 \mathord{\left/ {\vphantom {4 {\pi^{2} }}} \right. \kern-0pt} {\pi^{2} }}} \right)\sin^{4} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)} }}{2}.$$
(33)
Fig. 12
figure 12

The geometrical sketch on the enlarged mixed Mode-I/III crack symmetrical branching and kinking

Full size image

The K-based effective fracture toughness for mixed Mode-I/III crack branching can be given by

$$K_{{{\text{eff - }}C}}^{{{\text{sym - }}b}} = K_{{{\text{eff}} - C}}^{{A_{2} - {\text{wing}}}} = \frac{2}{{\left[ {1 + \left( {4/\pi^{2} } \right)\sin^{4} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)} \right]^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}} }}K_{IC} .$$
(34)

If only one wing crack initiates from \(A_{{2}}\) or \(A_{{3}}\) as a form of crack kinking as shown in Fig. 12b, the concerned energy-based configuration driving force becomes

$$G_{\max }^{{{\text{kinking}}}} = \frac{{\left( {1 - \mu^{2} } \right)\left( {K_{I}^{2} + K_{III}^{2} /(1 - \mu )} \right)}}{E}\frac{{\sqrt {1 + \left( {{4 \mathord{\left/ {\vphantom {4 {\pi^{2} }}} \right. \kern-0pt} {\pi^{2} }}} \right)\sin^{4} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)} }}{4}.$$
(35)

The K-based effective fracture toughness for mixed Mode-I/III crack kinking can be given by

$$K_{{\text{eff - C}}}^{kinking} = K_{{{\text{eff}} - C}}^{{A_{2} - {\text{wing}}}} = \frac{2}{{\left[ {1 + \left( {4/\pi^{2} } \right)\sin^{4} \left( {{{\pi \varphi } \mathord{\left/ {\vphantom {{\pi \varphi } 2}} \right. \kern-0pt} 2}} \right)} \right]^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}} }}K_{IC} .$$
(36)

4.6 On mixed Mode-I/III crack extension

As shown in Fig. 13, when the moving of the whole boundary \(A\) = \(A_{1}\) + \(A_{{2}}\) + \(A_{{3}}\) + \(A_{{4}}\) in x1-direction as a form of crack extension is triggered, from Table 1, the corresponding energy-based driving force can be found

$$G_{\max }^{A - ext} = \frac{{\left( {1 - \mu^{2} } \right)\left( {K_{I}^{2} + K_{III}^{2} /(1 - \mu )} \right)}}{E},$$
(37)
Fig. 13
figure 13

Crack extension under mixed Mode-I/III loading

Full size image

which is consistent with the classical J-integral method. Then, from Eqs. (19), (20) and (37), the K-based effective fracture toughness for mixed Mode-I/III crack extension can be given by.

$$K_{{\text{eff - IC}}}^{{A - {\text{ext}}}} = K_{{{\text{IC}}}} .$$
(38)

When the local boundary \(A_{1}\), \(A_{1}\) + \(A_{{4}}\)(or \(A_{1}\) + \(A_{{2}}\)) or \(A_{1}\) + \(A_{{3}}\) + \(A_{{4}}\) moves in x1-direction, from Table 1 and Eqs.(19), (20), (22), (24) and (29) and by using the same way, it is not difficult to get the K-based effective fracture toughness

$$K_{{\text{eff - IC}}}^{{A - {\text{ext}}}} = \left\{ \begin{gathered} {2}K_{IC} , \, A_{1} {\text{ moving and }}A = A_{1} \hfill \\ \sqrt {2} K_{IC} , \, A_{1} + A_{4} {\text{ moving and }}A = A_{1} + A_{{4}} {\text{ or }}A_{{1}} + A_{{2}} \, \hfill \\ \left( {{{2} \mathord{\left/ {\vphantom {{2} {\sqrt {3} }}} \right. \kern-0pt} {\sqrt {3} }}} \right)K_{IC} , \, A_{1} + A_{{3}} + A_{4} {\text{ moving and }}A = A_{1} + A_{{3}} + A_{{4}} \hfill \\ \end{gathered} \right..$$
(39)

Equations (38) and (39) indicate that there are four potential K-based effective fracture toughness for crack straight propagation under mixed Mode-I/III loading, which is similar to the case of the pure Mode-I deformation [28].

5 Triggering for mixed Model-I/III crack multiple-branching

As discussed in the above sections, for a cracked solid under mixed Mode-I/III loading, there are many forms of the potential fracture configurations. Obviously, the real fracture configuration may be one of them, which is triggered under proper conditions. There are many factors that affect the fracture behaviours, including the geometrical shape of the crack/flaw tip [16], the way of loading [15] and the disturbance from a weak Mode-II loading [21], etc. Taking the notch tip for example, if the width of which is narrow enough, the mixed Mode-I/III stress fields are approximately correct and the fracture configurations as shown in Figs. 11a and 12 are most likely to be triggered because A1 and A4 cannot move together in x1-direction. Moreover, as the difference between the driving forces \(G_{\max }^{{A_{2} - {\text{wing}}}}\) and \(G_{\max }^{{A_{{1}} - {\text{ext}}}}\), only wing crack/cracks in form of the crack kinking/branching as shown in Fig. 12 will be triggered under quasi-static mixed Mode-I/III loading. Additionally, if increasing loading rate or even impulse mixed Mode-I/III loading, the \(G_{\max }^{{A_{2} - {\text{wing}}}}\) and \(G_{\max }^{{A_{{1}} - {\text{ext}}}}\) may reach the critical values simultaneously or in a enough short time period. Then two cracks, respectively, initiate from the local boundaries A1 and A2. The potential mixed Mode-I/III crack multiple-branching, such as the crack side-branching as shown in Fig. 11a, should be triggered similar to the cases of pure Mode-I [22] and pure Mode-II deformation [23].

The dynamical nature of the crack branching has been one of the focuses in fracture mechanics. Yoffe [29] argued that the maximum \(\sigma_{\theta \theta }\) stress acted normal to lines that make an angle of 60° with the direction of crack propagation when the crack velocity exceeded 60% of the shear wave speed. Therefore, she suggested that this fact might cause the crack to branch whenever the crack velocity exceeded that value. Ravi-Chandar and Knauss [30] suggested that crack branching is a natural evolution from a "cloud" of micro-cracks that accompany and lead the main crack. Present analysis, including the works [21,22,23], provides an alternative energy-based fracture mechanism for crack multiple-branching.

6 Experimental observations on cracked specimen under mixed Mode-I/III loading

A new test configuration called the edge notched disc bend specimen (ENDB) [31,32,33,34,35,36] had been recently suggested to investigate the fracture behaviour of a cracked solid under mixed Mode-I/III loading as shown in Fig. 14. This disc-shaped specimen with radius R and thickness t is subjected to three-point bend loading. An edge narrow notch of depth a is created through the disc diameter. The crack plane makes an inclination angle of α relative to the loading rollers. The extensive three-dimensional finite element analyses and experimental fracture investigations were performed for different geometrical parameters and loading conditions to introduce full combinations of mixed Mode-I/III ranging from pure Mode-I to pure Mode-III [31,32,33,34,35,36] by changing the crack inclination angle α. Then, the effectiveness of the ENDB specimen had been verified.

Fig. 14
figure 14

Geometry and loading sketch of the ENDB specimen

Full size image

Usually, different KI, KII and KIII values can be expected along the notch tip front as shown in Fig. 14. However, because the x1-x2 plane is an antisymmetric plane of Mode-II deformation, KII tends to zero when x3 → 0, which creates a stable condition of mixed Mode-I/III loading around x3 = 0. Numerical results [29] indicated that at the mid-section of the ENDB specimen, the effective stress intensity factor will reach its maximum value and the local notch front around x3 = 0 will fracture first. It should be noted that the fracture configuration at x3 = 0 presents a form of crack extension because of the antisymmetric Mode-II deformation, which is also a typical underlying fracture configuration predicted by present method and is the most energetically favourable in this case. Then the critical load can be used to investigate the fracture behaviours of a cracked solid under mixed Mode-I/III loading [31,32,33,34,35,36].

In order to get the fracture toughness of PUR foams, a series of experiments had been conducted [32]. Some typical fracture configurations of the tested ENDB polyurethane specimens under different Mode mixities are shown in Fig. 15 [32]. The theoretical normalized effective fracture toughness predicted by present method and experimental values are listed in Table 3 and sketched in Fig. 16, which indicate that the theoretical values are basically the same with the experimental values. From Fig. 15, it is not difficult to observe that the local fracture configuration of tested polyurethane ENDB specimens at z = 0 is obviously the form of crack extension.

Fig. 15
figure 15

Typical fracture configurations for polyurethane ENDB specimens under typical Mode mixities [32]

Full size image
Table 3 The theoretical and experimental normalized effective fracture toughness (μ = 0.333) [32]
Full size table
Fig. 16
figure 16

Theoretical and experimental K-based effective fracture toughness

Full size image

Similar fracture configuration had been observed from the ENDB specimens made of hot mix asphalt (HMA) composites [33]. The theoretical and experimental normalized effective fracture toughness values are listed in Table 4 and schematically shown in Fig. 16.

Table 4 The theoretical and experimental normalized effective fracture toughness (μ = 0.35) [33]
Full size table

7 Conclusions

A three-dimensional modelling has been proposed to formulize the physical process of multiple cracks initiation from a crack tip under mixed Mode-I/III loading. Present analysis indicates that at the onset of fracture, the moving of the new-born cracks remains in the plane perpendicular to x3-axis (crack front) because of the \(J_{3} = 0.0\). Based on the present energy-based modelling, in order to maximize the energy release rate, it is reasonable that the whole boundary around a crack tip should be theoretically divided into four subintervals. Then the four energy-based driving forces can be found, which will drive the four sub boundaries to fracture in form of either wing cracks or extension. The energy-based driving forces have three basic elements, i.e. the point of application, direction and magnitude. So the potential fracture configurations for cracked solids under the mixed Mode-I/III loading, such as the crack tri-branching, symmetrical branching, side-branching, kinking and extension, can be theoretically predicted from the combinations of the new triggered cracks. The present investigations should refresh the understanding on the complex fracture phenomena in the specimen and the engineering structures, such as the hydraulic fracturing for getting more abundant hydraulic crack system.

The physical nature of the experimental fracture phenomenon can be easily recognized based on the present modelling. By comparing the experimental fracture configurations with the potential fracture configurations predicted by present method, which form of the underlying fracture configuration and the fracture mechanism, such as crack side-branching, kinking and extension, can be identified. Then, the corresponding energy-based configuration driving force, K-based effective fracture toughness and fracture criterion can be clearly known.

The experimental observations on the ENDB specimens made of PUR foams and HMA composites under mixed Mode-I/III loading indicate that the fracture configuration in form of the crack extension at the mid-section x3 = 0 of the specimen has been verified, which is one of the typical potential fracture configurations predicted by present modelling. The normalized K-based effective fracture toughness predicted in this article agree well with the experimental values.

From the present investigations, there are four potential K-based fracture toughness for crack extension. It is therefore reasonable to speculate that the experimental data should be scattered from an infinitely sharp crack to a blunt notch, which is similar to the additive effect of crack-tip damage zones [37].