Optimal production and corrective maintenance in a failure-prone manufacturing system under variable demand

Abstract

Failure-prone manufacturing systems facing dynamical market conditions that result in demand variations are considered. The combined production and corrective maintenance optimization problem for a one-machine-one-product system is addressed. Repairing the machine after the failure, the manager has to solve the dilemma: to choose an inexpensive (but lower) repair rate, or to use the higher, (but more expensive) repair rate. The former decision seems to be appropriate when there is no risk of inventory shortage, while the latter one has to be used in critical (stock shortage) situations. Precise solution to this problem presented in the paper is theoretically instructive and valuable for practitioners. Optimality conditions in the form of time-dependent Hamilton–Jacoby–Bellman equations are obtained and a novel numerical approach is proposed for solving these equations for the case of periodically time-varying demand. The optimal policy is shown to be the hedging-curve-policy, that extends the hedging-point-policy to the case of varying level of safety stock. The simulation results show that the optimal policies have an important property of anticipating the future demand evolutions and making the optimal decisions relevant to such dynamic conditions. In particular, it has been shown that in the large domain of the system parameters it is advantageous to use the lower (and inexpensive) repair rate when the stock is approaching the hedging level and especially when the demand level is near its bottom edge.

1 Introduction

This paper is devoted to the combined optimization of production and corrective maintenance in the dynamic environment, namely under the varying market demand. Dynamic conditions often appear in practical applications, but are replaced by stationary ones for simplifications required by existing solution methodologies. Demand variations in time occur for several reasons and are often partitioned into fast random component and slower systematics component. The former is usually unpredictable, while the latter may follow different patterns. Most important among them are the trend-type and oscillatory behaviors. The former are mainly due to increasing sales along the period when the product is new on the market, then the demand usually stabilizes and finally declines close to the end of the product life cycle. The latter are usually due to the seasonal variations in market price and environmental or logistical factors.

The behavior of the systems under varying demand was often addressed in scientific literature using the framework of economic order quantity (EOQ) (Tripathi 2011), especially when the trend-type demand variations are considered. The inventory control problem for the systems under non-stationary stochastic demand are considered in Leo et al. (2011) and Prak et al. (2016) with particular interest to interactions between demand forecasting and safety stock calculation. Ramp-type varying demand model is used in Mishra and Singh (2011) and Wang and Huang (2014) for the cost analysis of inventory in the systems with deteriorating items. Seasonal demand variations were addressed in Kleber et al. (2002) and Minner and Kleber (2001), in the context of the systems that use remanufacturing in the production process. In these papers, the system under consideration was supposed to be fully reliable, both demand and return rates were represented by periodically varying functions and optimal control technique was used to determine the production policies.

Production optimization of failure-prone manufacturing systems have been addressed in numerous works (Boukas and Haurie 1990; Sethi and Zhang 1994; Gershwin 2011). For the system that contains one machine and manufactures one product type, the analytical solution has been obtained in Akella and Kumar (1986), were the demand was set constant and the flows of failures and repairs were described as stochastic Markov processes with fixed rates.

Considering the corrective maintenance as a controlled activity was proposed in Boukas et al. (1996) and Boukas (1998). This approach constitutes an important extension to the production optimization problem with fixed repair rate formulated and solved in Akella and Kumar (1986). In Boukas (1998) the repair rate is supposed to belong to an interval from minimal to maximal rate, with a particular value of this rate chosen by the decision maker at the expense of the repair cost proportional to the chosen rate. The term corrective maintenance is designated to such activity in contrast to the term repair used when the rate is fixed. The proposed approach was further developed in Kenne et al. (2003), where the case of multi-machine manufacturing system producing several product types was addressed through numerical implementation of optimality conditions in the form of Hamilton–Jacoby–Bellman (HJB) equations.

It is important to consider the corrective maintenance with controlled rate in order to resolve the trade-off between the direct repair cost and the cost attributed to the machine downtime. Considering the role of downtime cost in relations with maintenance activity is not new, although it is appear sparsely in the literature. It worth mentioning in this context two papers: Saranga (2004) and Saltoglu et al. (2016). The former paper proposes the generic downtime cost model in order to optimize the maintenance cost using opportunistic approach (and genetic algorithm technique). The latter paper addresses the problem of aircraft maintenance optimization considering the combined direct maintenance cost and downtime cost to characterize the performance. It is of particular importance to address the trade-off between explicit repair costs and implicit downtime cost the dynamic situation: when the demand rate changes in time the impact of the machine downtime varies (higher demand rate results in faster decrease of stock level leading to stock shortage). This makes the timely decision about the maintenance rate critical for system performance, and determines the relevance of our study to industrial practice.

It worth emphasizing that we consider in this work only corrective maintenance as opposed to preventive maintenance —an important concept often studied in the context of deteriorating systems and subject of numerous researches. We outline below few important results obtained in this direction. In Chelbi and Ait-Kadi (2004) periodical preventive maintenance was considered and optimal safety stock level to hedge against stochastic flow of failures and random durations of repair and maintenance actions. In Dehayem Nodem and Kenne (2011) authors studied the deteriorating systems and determined the joint optimal production and preventive maintenance policy using stochastic dynamic programming framework and numerical approach to solve underlying HJB equations. Further results for the systems that deteriorates both in quality and reliability were obtained in Rivera-Gomez et al. (2013) and for the systems that make use of overhaul (maintenance) and subcontracting strategy—in Rivera-Gomez et al. (2016).

It worth noticing the connection between controlled corrective maintenance and subcontracting activity. In Rivera-Gomez et al. (2016) subcontracting option was used to supplement the limited production capacity of the system in spite of its higher cost. Maintenance option was used to cope with deterioration. In a similar way, company may consider subcontracting option for repair and maintenance. Namely, it may an in-house repair team used for ordinary repair/maintenance with usually acceptable repair time and relatively low cost. However, in critical situations such as major failure, necessitating specific qualifications, or failure occurring at the moment of high demand (with risk of costly backlog or loss of sale), subcontracting the repair activity to insure short downtime in spite of higher direct cost may turn out to be advantageous.

Evolutionary stochastic optimization procedure for one-machine-multiple-product systems characterized by short-run cost functions was proposed in Mok and Porter (2005), where the behavior of corresponding short-run hedging points is investigated for the various initial inventory and demand levels. Proposed methodology allowed to adapt the hedging point strategy to to uncertain or varying demand level. Similar approach based on discrete-event simulations is used in Sajadi et al. (2011) to address the production optimization problem for a network of multiple machines with restrictions imposed on the values of intermediate inventory buffers. The systems with impatient customers characterized by backlog-dependent demand are considered in Wang et al. (2014) where optimality of hedging-point policy is investigated analytically and numerically.

The results of previous works in the context of the problem in hand can be summarized as follows: the combined optimal production and corrective maintenance policy is of hedging point type, namely there exist a production hedging level (PHL) and a maintenance hedging level (MHL) such that (1)—maximal production rate is to be used below PHL, and zero production rate is to be used above PHL, and (2)—maximal repair rate is to be used below MHL, and minimal repair rate is to be used above MHL.

We address in this work the situation when the system is facing time-varying demand and propose the solution to the problem of combined optimization of production and corrective maintenance for failure-prone manufacturing systems. To the best of authors’ knowledge this problem has not been addressed in the literature.

An additional aspect of the problem that has not attracted sufficient attention in the previous works is the relative position of the hedging levels determining production (PHL) and corrective maintenance (MHL) policies. For example in Boukas (1998) the presented production and maintenance policies are such that the PHL is below the MHL, thus making MHL barely useful, since the system can not reach MHL level under the proposed optimal policy. This aspect is important for practitioners as directly affecting the structure of optimal policy; it also is significant in the context of this study because the demand variation affects two hedging points (PHL and MHL) differently, thus changing their relative position.

The remainder of the paper is organized as follows: in Sect. 2 the detailed problem formulation is given. Theoretical basis for the proposed approach is given in Sect. 3. Section 4 is devoted to the method guidelines and the production optimization in one-machine-on-product system. The main results about combined production and corrective maintenance optimization are described in Sect. 5. In Sect. 6 we present the results about the comparison of the policies taking into account the demand variation with those based on the average demand level. We continue in Sect. 7 with more general discussion of our contributions, assumptions and limitations. Conclusions and future works are addressed in Sect. 8.

2 Problem formulation

Before providing the detailed problem description we summarize in the next section the notations used throughout the paper.

2.1 Notations

$\alpha$:

State of the machine

x:

Serviceable inventory level

$u_1$:

Production rate

$U_1$:

Maximal production rate

$u_2$:

Corrective maintenance rate

$U_2^+$:

Maximal corrective maintenance rate

$U_2^-$:

Minimal corrective maintenance rate

$D_m$:

Average demand rate

$D_a$:

Amplitude of change of the demand rate

$\omega$:

Frequency of the demand rate evolutions

$\phi$:

Initial phase of the demand rate evolutions

$c^+$:

Unitary holding cost

$c^-$:

Unitary backlog cost

$C^-_r$:

Cost of slow maintenance (per time unit)

$C^+_r$:

Cost of fast maintenance (per time unit)

$c_r(u_2)$:

Maintenance cost as a function of maintenance rate

$h(\cdot )$:

Instantaneous holding and maintenance cost (per time unit)

$\rho$:

Discount factor

p:

Machine failure rate

$\xi$:

Random state of the machine

Q:

Generator (transition rate) matrix

$q_{\alpha \beta }$:

Transition rate form state $\alpha$ to state $\beta$

$\varGamma (\alpha )$:

Admissible control set at state $\alpha$

$J(\cdot )$:

Total expected cost

$V(\cdot )$:

Value function (minimal expected cost)

Let us formulate the problem of policy optimization for manufacturing system under random perturbations and facing varying demand, by extending the conventional model to encompass the demand behavior.

2.2 System dynamics

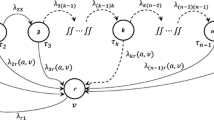
The system under consideration is composed of one failure-prone machine manufacturing one product type stored in the inventory used to service the market demand, which varies in time. The schematics of the system is shown in Fig. 1. It emphasizes that the system is under variable rate market demand, and that in order to control the process performance, the decision maker regulates production rate ($u_1$) and corrective maintenance rate ($u_2$).

We would like to emphasize that the term machine is used here for simplicity; it may actually designate the production unit of any size, as soon as we may consider its activity as production process.

The system dynamics is hybrid, it contains a continuous (evolutions of inventory level x(t)) and a discrete (switching between failure and operational states) components.

Fig. 1

Manufacturing system schematics

The continuous system dynamics can be described by the following equation:

$$\begin{aligned} \dot{x}(t) = u_1(t) -D(t) \end{aligned}$$

(1)

Equation (1) states that the variation of the stock level (at any instance t) equals to the difference between production and demand rates.

The following generic demand will be considered in this study:

$$\begin{aligned} &D=F(\omega t), \quad t \in [0,\infty ] \\ & 0< F(\omega t) \le F^+, \quad \Vert F^{\prime}(\omega t) \Vert \le f^d (2^a ) \end{aligned}$$

(2)

where $F(\cdot )$ is a strictly positive continuously differentiable bounded function with bounded derivative, $\omega$ is a small parameter responsible of the pace of the temporal evolution of the demand rate.

In other words demand rate is a slowly varying function, and its derivative over t is small of the order $O(\omega )$. Both $\omega$ and $F(\cdot )$ are known and therefore can be used in the design of optimal control policy.

As the system performance is characterized by its behavior over the infinite horizon (the details are described in the next (sub)section), an assumption about knowing in advance the demand rate for infinitely long period of time seems rather limiting. This leads to considering an important particular class of the demand varying periodically, in which case only the behavior along the finite time interval—demand period—is needed.

We therefore consider below (and use for the numerical simulations) the demand varying periodically in time. This is often the case for repeatable seasonal demand variations (see Minner and Kleber 2001 for the examples). As an example of the demand of this type we chose the following model

$$\begin{aligned} D(t) =D_m+D_a \cos (\omega t - \phi ) \end{aligned}$$

(3)

Here $D_m$ naturally corresponds to the average demand level, $D_a$—to the amplitude of periodical variations, $\omega$—to the frequency of variation and $\phi _0$—to the initial phase. By setting $D_m>D_a$, we also ensure that the demand remains positive and bounded. and therefore model (3) satisfies the generic conditions (2).

At each moment t the machine is either in operational state $\xi (t) =1$ or in failure state $\xi (t) =2$, randomly switching between these states according to Poisson process (time intervals between failures and repair time intervals both have exponential distributions).

Discrete stochastic dynamics is described by the transition matrix

$$\begin{aligned} Q = \{q_{ij}\} = \left( \begin{array}{cc} -p &{} p\\ u_2 &{} -u_2 \end{array} \right) \end{aligned}$$

(4)

Here $q_{12}=p$ is the (constant) transition probability from operational to failure state (failure rate), $q_{21}=u_2$ is the transition probability from failure to operational (repair rate) which can vary between lower and upper limits in order to optimize the system behavior (decision variable).

The set $\varGamma (\cdot )$ of admissible control policies ${\mathbf{u}}=(u_1(.),$

$u_2(.))$ at state $\alpha$ is defined as follows :

$$\begin{aligned} \varGamma (\alpha ) = \left\{ \begin{array}{l} {\mathbf{u}}=u_1(.), u_2(.):\\ 0 \le u_1(.) \le U_1 \, Ind_1(\alpha )\\ U_2^- \le u_2(.) \le U_2^+\\ \end{array} \right\} , \;\; \alpha =1,2 \end{aligned}$$

(5)

where $Ind_k(\alpha )= \left\{ \begin{array}{ll} 1 &{} \text{ if } k=\alpha \\ 0 &{} \text{ otherwise. } \end{array} \right.$

The instantaneous cost is:

$$\begin{aligned} h(x,{\mathbf{u}},\alpha ) = c^+ x^+ + c^-x^- + c_r (u_2)Ind_2(\alpha ) \end{aligned}$$

(6)

where most of parameters are defined in Sect. 2.1, $x ^+ = \max (0,x), \, x ^- = \max (0, - x)$, corrective maintenance (repair) cost function $c_r(u_2)$ is defined by a generic linear expression over $u_2$:

$$\begin{aligned} c_r(u_2) = C_r^-+ (u_2-U_2^-) \frac{C_r^+-C_r^-}{U_2^+-U_2^-} \end{aligned}$$

(7)

One can see that expression (7) linearly interpolates the maintenance cost onto all admissible maintenance rates $u_2\in [U_2^-,U_2^+]$ as per expressions (4), from the costs corresponding to the extremal rates $U_2^-$ and $U_2^+$.

2.3 Objective function and optimality conditions

The objective is to determine production and corrective maintenance policies $u_1(\cdot ),\,u_2(\cdot )$ in order to minimize the expected discounted cost, that is defined on the time interval $(t,\infty )$ as follows:

$$\begin{aligned} J (x_0, {\mathbf{u}},t,\alpha ) & = E \Big \{ \int _{t}^{\infty }e^{-\rho s} h(x(s),{\mathbf{u}}(s) ds \mid \\&\quad x(0)=x_0, \xi (0) =\alpha , {\mathbf{u}} \in \varGamma (\alpha ) \Big \} \end{aligned}$$

(8)

The value functions are conventionally defined as follows (Boukas and Haurie 1990):

$$\begin{aligned} V(x,t,\alpha ) =\inf _{{\mathbf{u}} \in \varGamma (\alpha )} \{J(x,{\mathbf{u}},t,\alpha ) \}, \alpha =1,2 \end{aligned}$$

(9)

As we consider the time-varying demand rate D(t), the optimality conditions will be represented by the set of non-stationary Hamilton–Jacobi–Bellman (HJB) equations which are similar to the conventional stationary case derived in Boukas and Haurie (1990), Boukas (1998) and Kenne and Gharbi (2004), but contains an additional value-function-time-derivative term.

$$\begin{aligned} \rho \,V(x,t,\alpha ) &= \frac{\partial V(x,t,\alpha )}{\partial t} + \min _{{\mathbf{u}} \in \varGamma (\alpha )} \Big \{ (u_1 Ind_1(\alpha ) -D(t))\cdot \\&\frac{\partial V(x,t,\alpha )}{\partial x} + h(x,{\mathbf{u}},\alpha ) \\&\quad + q_{\alpha \beta }(u_2) \cdot (V(x,t,\beta ) - V(x,t, \alpha )) \Big \},\; \beta \ne \ \alpha \end{aligned}$$

(10)

It is worth noting that deriving expressions (5), (6) and (10) we have rectified the mathematical formulation of the problem given previously in the literature, and defined a more general maintenance cost (7) comparing to Boukas and Haurie (1990), Boukas (1998) and Kenne and Boukas (1997).

3 Analysis of non-stationary HJB equations using asymptotic expansion methodology

In case of constant demand rate, in order to determine the optimal policy one needs to find the stationary solution of HJB equations (10). For time-varying demand rate D(t)—it is not the case, the solutions of HJB equations will be also time-varying. Below we show how to exploit an assumption that demand rate variation [according to (2) or (3)] is slow ($\omega$ is small) and apply asymptotic expansion methods (Vasil’eva and Butuzov 1973) for constructing an approximate solutions to (10).

Let us perform the time transformation to slow time $\tau =\omega t$, we get

$$\begin{aligned} \rho \,V(x,\tau ,\alpha ) &= \omega \frac{\partial V(x,\tau ,\alpha )}{\partial \tau } + \min _{{\mathbf{u}} \in \varGamma (\alpha )} \Big \{ (u_1 Ind_1(\alpha ) -D(\tau ) )\cdot \\&\quad \frac{\partial V(x,\tau ,\alpha )}{\partial x}+ h(x,{\mathbf{u}},\alpha )+ \\&\quad q_{\alpha \beta }(u_2)\cdot (V(x,\tau ,\beta ) - V(x,\tau , \alpha )) \Big \}, \; \beta \ne \alpha \end{aligned}$$

(11)

For the case of $D(\tau )$ determined by model (3) we can equivalently define it by differential equations:

$$\begin{aligned} dD / d \tau &=S \\ dS / d \tau &=-D \end{aligned}$$

(12)

Since small parameter $\omega$ multiplies the time-derivative term in (11) the system (11, 12) is a singularly perturbed system of differential equations. As one can see, setting $\omega =0$ transforms equations (11) into conventional HJB equations without value-function-time-de- rivative term (as in Kenne et al. 2003), which depends on $D(\tau )$ as parameter. Let us denote this solution (value function) called degenerate solution by $V^{(0)}(x, 0 ,\alpha ,D(\tau )).$

For non-zero value of $\omega$, the solutions $V(x, \tau ,\alpha ,D(\tau )$ of (11,12), according to Tikhonov theorem Vasil’eva and Butuzov (1973), converge to the degenerate solution $V^{(0)}(x, 0 ,\alpha ,D(\tau )$, for $\tau >0$:

$$\begin{aligned} V(x, \tau ,\alpha ,D(\tau ) \rightarrow \text{ when } \omega \rightarrow 0 \end{aligned}$$

This convergence is not uniform near $\tau =0$—there exists a thin layer $0<\tau <\tau ^p (\omega )$—boundary layer, shrinking to zero when $\omega \rightarrow 0$, in which solutions differ significantly $V(x, \tau ,\alpha ,D(\tau )) \ne V^{(0)}(x, 0 ,\alpha ,D(\tau ))$.

Based on Tikhonov theorem and using two-scale expansion the full asymptotic expansion series for the solutions for (11, 12) can be constructed. Description of this technique goes beyond the scope of this paper. Also, in line with conventional arguments for computing stationary solution of HJB equations, we are not interested in transient component tightly related to the solution within by boundary layer—technically most challenging part of the asymptotic expansion technique. We rather need to better approximate the slow-varying long term component of the solution. The following result describes an approximated solution of (11) up to second order (over $\omega$):

$$\begin{aligned} V(x, t,\alpha ,D(\omega t))=V^{(1)}(x, t, \alpha ,D(\omega t)) +\epsilon _2(x, t, \omega ) \end{aligned}$$

(13)

where $\epsilon _2(x, t, \omega )= O(\omega ^2); \; V^{(1)}(x, t ,\alpha ,D(\tau ))$ is a solution of

$$\begin{aligned} \rho \,V^{(1)}(\cdot ,\alpha ) &= \frac{\partial V^{(0)}(\cdot , \alpha )}{\partial t} + \min _{{\mathbf{u}} \in \varGamma (\alpha )} \Big \{ (u_1 Ind_1(\alpha ) -D(\omega t) ) \cdot \\&\quad \frac{\partial V^{(1)}(\cdot ,\alpha )}{\partial x}+ h(\cdot , \alpha ) \\&\quad + q_{\alpha \beta } \cdot (u_2)(V^{(1)}(\cdot ,\beta ) - V^{(1)}(\cdot , \alpha )) \Big \}, \;\beta \ne \alpha \end{aligned}$$

(14)

where $V^{(0)}(\cdot , \alpha )=V^{(0)}(x, 0 ,\alpha ,D)$ is a degenerate solution to (11) with $\omega =0$ (without time-derivative term)

Recall that $V^{(0)}(x, 0 ,\alpha ,D)$ only approximates V(x, 

$t,\alpha ,D(\omega t))$ with first (over omega) oder of accuracy:

$$\begin{aligned} V(x, t,\alpha ,D(\omega t))=V^{(0)}(x, 0, \alpha ,D(\omega t)) +\epsilon _1(x,t, \omega ) \end{aligned}$$

(15)

where $\epsilon _1(x, t, \omega )= O(\omega )$.

Therefore, we have obtained a better approximation (13) for an (unknown) exact solution, but at the expense of solving modified HJB equations (14).

In the remaining part of the paper we develop a numerical procedure that implements the proposed approach. This implementation is based primarily on the fact, that the powerful numerical method exists for solving the stationary HJB equations (proposed in Kushner and Dupuis (1992), and that this method can extended for solving modified HJB (14). Kushner method belongs to the class of policy iteration algorithms, it uses discrete representation $V_h(x_k,\alpha )$ of value functions $V(x,\alpha )$ over the grid (with the step h in inventory space x. It was successfully used in numerous works, e.g. (Boukas and Haurie 1990; Boukas et al. 1996; Dehayem Nodem and Kenne 2011). Algorithm allows to iteratively compute the new set of value functions on the basis of the set computed previously. Successful utilization of this grid-based method for solving contitnuous problem is essentially based on the convergence theorem (Boukas and Haurie 1990; Boukas et al. 1996), asserting that $V_h(x_k,\alpha ) \rightarrow V(x,\alpha )$ when $h \rightarrow 0$ here $(x_{k+1}-x_k=h, k=1,2,\dots )$.

4 One-machine-one-product system with fixed failure/repair rates

To validate the methodology proposed for dealing with the case of varying demand rate we consider in this section the one-machine-one-product system (M1P1) with fixed transition rates, for which the analytical solution has been obtained in Akella and Kumar (1986) under assumptions that the demand rate is constant. Applying the proposed approach to the benchmark M1P1-system allows to highlight the key algorithmic issues and to get the insight used later in the analysis of more general problems. Our main contribution—the combined production and corrective maintenance optimization under varying demand is presented in Sect. 5.

We consider the demand model is described by equation (3) and demand range is $\bar{D}=[D_m-D_a, D_m+D_a]$, although the results hold for generic demand model (2). For any value $D(t) \in \bar{D}$ one can compute a “ stationary” solution of HJB equation (10) with time-derivative term $\frac{\partial V({\mathbf{x}},t,\alpha )}{\partial t}$ being neglected. However, considering the obtained solutions for a whole set of demand rates one will find out that the solutions depend on D(t), which itself varies in time according to equations (3). Therefore, neglecting the time derivative term, although does provide an approximation (since D(t) varies slowly in time), but introduces an error that is often not acceptable. This error can be rectified by retroactively estimating the neglected term based on approximative solution), and recomputing the solution with this term taken into account.

We describe below a four-step procedure that implements the outlined approach and allows to find the suboptimal policy for the case of varying demand rate.

• 1. Our first step consists of dividing the segment D into N intervals $I_j=[d^j,d^{j+1}], \; j=1,\dots , N;\; d^1=D_m-D_a, \; d^N=D_m+D_a$. Larger is N, more precise is the result, but more is the computational burden.

• 2. Next step consists of computing the solutions of conventional HJB equations (without non-stationary terms) for discrete demand levels $D=d^j$ (taken at times $t_j$), and thus obtain numerically the series of value functions $V^j(x, \alpha )$ ($\alpha = 1,2$ with $\alpha =1$ standing for operational state and $\alpha = 0$—for failure state). Note that we may also use an analytical solution found in Akella and Kumar (1986) instead of the numerical one. It is important that the demand model (2) determines the mapping from the demand level $d^j$ to the time domain $t_j$, namely $t_j=t_j(d^j)$ when $D(t_j)=d^j$. For each $d^j$ there are two time-points $t_j^{1,2}(d^j)$ for each period, except the extremal levels $d^j= D_m-D_a$ or $d^j= D_m+D_a$ where there is only one point $t_j^1= t_j^2$.

• 3. Third step consists of computing the numerical estimates for the time-derivative term using value functions for consecutive j (obtained for two consecutive demand levels $d^j$ and $d^{j+1}$):

  $$\begin{aligned} \frac{\partial V^j (x, \alpha )}{\partial t} \simeq \frac{V^{j+1}(x, \alpha )-V^j(x, \alpha )}{t_{j+1}(d^{j+1})-t_j(d^j) } \end{aligned}$$

• 4. The last step consists of recomputing the numerical solutions of the HJB equations with the time-derivative terms integrated into the grid data. The conventional algorithm (Kushner and Dupuis 1992; Boukas and Haurie 1990) is modified in a way that the time-derivative terms (approximated with the ratio of finite differences) are calculated using the “previous” value functions for all grid-points, then these terms are added to the conventional grid-based expressions and used for computing the newly updated value functions.

Table 1 First set of parameters used for simulations

Fig. 2

Value function (operational state) for various demand levels

The described approach has been implemented, and the results obtained numerically for the system parameters given in Table 1 are illustrated in Figs. 2, 3, 4, 5 and 6. We recall that repair rate is constant and denoted by q. The guidelines for the choice of parameters are the following:

• the maximal production rate $U_1$ sufficiently exceeds the maximal demand rate $D_m+D_a$;

• for Poisson type failure and repair flows with average rates p and q respectively, the mean-time-to-failure (MTTF) and mean-time-to-repair (MTTR) are 1 / p and 1 / q respectively, and are chosen to satisfy the natural constraint $MTTF \gg MTTR$ and to respect feasibility condition $(U_1-D_m-D_a) MTTF > (D_m+D_a) MTTR$;

• the demand half-period $\pi /\omega$ (full range evolution time) is sufficiently large comparing to a  tenfold discount decay time ($\pi /\omega > 2.3/\rho$).

In Fig. 2 the value functions for operational mode (V(x, 1) are shown for different ”frozen” demand levels (from $D_m-D_a=0.17$ to $D_m+D_a=0.21$). The corresponding hedging-point-policies are shown in Fig. 3, and value functions for failure state (V(x, 0))—in Fig. 4.

Fig. 3

Policy switching for various demand levels

Fig. 4

Value function (failure state) for various demand levels

Observing the figures one can come to the following conclusions: operational state value functions are moving consistently up when the demand rate increases (Fig. 2). The curves are located in the following (bottom–up) order : D = 0.17 (marked as 1), D = 0.18 (marked as 2), D = 0.19 (marked as 3) D = 0.2 (marked as 4), D = 0.21 (marked as 5). The inventory level where the value function attains its minimum (hedging level) consistently increases when the demand rate increases (this is clearly visible in Fig. 3, and also in Fig. 2—the points of minimum of higher located curves are located further to the right and up). Failure state value functions are located above the operational state value functions for each particular value of demand rate. This property, however, does not hold globally—for example the failure state value function for the lower demand level (e.g $d=0.17$, marked as 1 in Fig. 4) is below the operational state value function for the higher demand level (e.g $d=0.21$ marked as 5 in Fig. 2).

Fig. 5

Value function for varying (decreasing/stable/increasing demand rate

Fig. 6

Evolutions of hedging points for periodically varying demand

Figure 5 illustrates the results obtained after taking into account the demand variation in the neighborhood of a particular demand rate level ($D =0.19$ in this case), not only the level itself. One can observe 3 curves representing operational state value-functions and corresponding to the frozen demand (1), increasing demand (2) and decreasing demand (3) respectively.

When the demand rate varies, the hedging level also varies, namely it increases (respectively decreases) when the demand rate increases (respectively decreases)—that is also observable on Fig. 5. However, there is an additional anticipatory effect: namely the hedging level increases (respectively decreases) more and earlier then it would do if we just compare two corresponding demand rate levels. The rational behind this property is that the hedging point “reacts” not only on the demand level, but also on the pace of evolutions and the direction of change.

The evolution of the hedging point along the whole period of the demand evolution is illustrated in Fig. 6. The curve $z_s(t)$ corresponds to the different “frozen” levels of the demand. The curve $z_{ns}(t)$ corresponds to the ”non-stationary” hedging level obtained when local variations of the demand (increase or decrease) are taken into account; the curve on the bottom of the plot is shown to illustrate the corresponding demand evolutions). One can clearly see the anticipatory effect in $z_{ns}(t)$vs$z_s(t)$: the increases and decreases of the curve $z_{ns}(t)$ are advanced with respect to those of $z_s(t)$. But near the extremal points of the demand, where it varies slower—both curves get close ($z_{ns}(t) \simeq z_s(t)$) to each other.

The results above were obtained for the periodic demand model (3). The technique is fully applicable to more general demand model (2) and the main results will hold. Also, it worth mentioning that as far as discounted cost is used to evaluate the performance, the demand rate in the distant future is negligible (highly discounted), and therefore the generic demand function ($F(\omega t )$) can be, without loss of generality, set to zero for $t\ge T$ with large enough T, or replaced by a periodic function with large enough period (small enough $\omega$). Thus model (3) is a representative example of generic model (2) when discounted cost is used for performance evaluation.

Presented analysis of the M1P1-problem under varying demand allowed us to validate the key elements of our methodology, to gain the insight about the behavior of the numerical scheme, and to target potentially important features of the solutions such as an anticipatory property. In the next section we apply the developed methodology to the main subject of our study—the combined production and maintenance optimization problem.

5 Combined production and maintenance optimization under varying demand

In order to address the problem in hand—combined production and maintenance under time-varying demand—we proceed in a way similar to the one developed in Sect. 4. Namely, we apply the proposed 4-steps procedure: (1) discretize the demand interval, (2) compute the solutions of HJB equations for each demand level, (3) compute the estimates for the derivative terms and (4) recompute the solutions of modified HJB equations. The main difference with the simper problem addressed in Sect. 4 consists in that no analytic solution of HJB-equations is available, and solving them is numerically more involved, because the admissible control set $\varGamma$ is 2-dimensional. We describe below the algorithmic aspects that we had to address along the implementation.

5.1 Algorithmic aspects

Compute the series of value functions for the series of “frozen” demand levels (N = 18 has been chosen for the numerical examples discussed below). These demand levels are obtained from the points in time domain distributed uniformly along the segment $[\phi /\omega ,(\pi +\phi )/\omega ]$. This results in more dense distribution of discretization points within the region where demand rate changes faster.

Save these 2(N + 1) = 38 functions (number is doubled because value functions for both operational and failure states are needed) in the memory to make them available for subsequent computations.

Using adjacent value functions, compute the finite difference terms approximating the time derivative of value functions (attributed to the middle point between two adjacent demand levels stored in memory); compute additional value functions for “frozen” middle layers (18 in current implementation). This step is based on the chain rule for derivatives of composite functions

$$\begin{aligned} \frac{dV}{dt}= \frac{dV}{dD}\cdot \frac{dD}{dt}\simeq \frac{V^{j+1}-V^j}{\varDelta D}\frac{\varDelta D}{\varDelta t}= \frac{(V^{j+1}-V^j) \omega N}{\pi } \end{aligned}$$

Compute the modified value functions corresponding to increasing (positive time derivative terms) and decreasing (negative time derivative terms) demand rate respectively for both operational and failure states ($72=18 \times 2 \times 2$ in total). Operational state value functions used further to compute optimal the hedging curves determining optimal production and maintenance policies.

5.2 Numerical examples

We present here the series of the results obtained by numerical simulations. The set of the parameters used for numerical simulations is shown in Table 2.

Table 2 Second set of parameters used for simulations

Figures 7 and 8 illustrate these results. The curves 1 and 2 in Fig. 7 show production and corrective maintenance hedging levels (respectively PHL and MHL) obtained for“frozen” (constant) demand levels. One can see that for low demand level (indexes 1–10 and 27–36) the MHL is below the PHL, and therefore belongs to the operational area (optimal policy does not allow inventory to grow above the PHL). The zones with MHL below PHL are marked by larges (yellow) stripes. When demand gets to higher values, two HLs first coincide (indexes 10-15 and 23-28), and then MHL gets higher than PHL, thus leaving the area where the real system may operate.

Next, we analyze what are the changes that are obtained when we take into account the dynamic effects of the demand variation. Corresponding curves are 3 and 4 (also marked with crosses for production and stars for maintenance HLs). One can see that in the low demand areas the “dynamic” and “frozen” curves almost coincide (1 with 3 and 2 with 4), so the previous conclusions hold. For higher demand area the anticipatory effect is clearly observable for both maintenance and production HLs: “dynamic” curves (3 and 4) grow and descend earlier than “frozen” ones (1 and 2), .

Obtained result is important from managerial point of view and can be formulated as the following “rule”: the use of lower (less costly) maintenance rate is advantageous in a low demand zone and for inventory levels close to the production HL (between maintenance and production HLs).

Figure 8 illustrates the behavior discussed above in the time domain (instead of indexed demand rate domain). The demand evolution is also shown to illustrate that anticipatory effect [“dynamic” curves (3 and 4) with respect to “frozen” curves (1 and 2)] is synchronized with the intervals of rapidly changing demand.

It is important to ensure that the “representative time” of demand evolution (half-period : $\pi / \omega \simeq 314$) is of the same order of magnitude as the “representative time” (tenfold decay) of the total cost due to discount effect ($2.3/\rho \sim 230$).

Fig. 7

Hedging levels for stationary and varying demand

Fig. 8

Hedging levels’ time evolutions for stationary and varying demand

In Figs. 9 and 10 we illustrate the case corresponding to a different set of parameters exemplifying the different relative location of MHL and PHL (data set 3). Namely, the mean repair times (both) and the cost of fast repair are higher (respectively rates are lower): c ($U_2^-=0.12, \;U_2^+ =0.5, \;C_r^+=12$; average demand and backlog cost are slightly lower $d_m=0.2, \;c^-=50$. Other parameters were left intact. In Fig. 9 the phenomena are studied in terms of the (enumerated) demand levels (indexes 1–18 correspond to the demand increasing from 0.15 to 0.25, and indexes 19–36—to the demand decreasing from 0.25 to 0.15). In Fig. 10 the phenomena are studied in time domain.

For constant demands at all levels the corrective maintenance HL (curve 2) is located consistently lower than production HL (curve 1). This suggests using the slow repair rate in the inventory layer between the curves 1 and 2 and within the whole domain of demand. One can observe that this layer is larger for low demand rates (0.15, indexes 1-12, 25-36) and narrower for high demand rate (0.25, indexes 13–24).

When the demand dynamics is taken into account, the situation is different: it depends on whether the demand is increasing or decreasing. For increasing demand both hedging points increase faster comparing to the case of “frozen” demand, but MHL (curve 4) remains below the PHL (curve 3). However, when the demand decreases, the layer, where the slow (and less costly) repair rate is suggested disappears until the demand level sufficiently decreases (at the time $t \simeq 400$, see Fig. 10). Here, the layer between two hedging levels PHL and MHL starts growing again and gets large ($\simeq 0.5$) by the time when the demand reaches its minimum (at the time $t\simeq 600$).

Fig. 9

Hedging points for leveled and varying demand

Fig. 10

Hedging points’ evolution in time

Figures 11 and 12 illustrate the production (Fig. 11) and corrective maintenance (Fig. 12) policies for frozen and time-varying demand in terms of 3D plots. The higher surface (marked with 1) corresponds to the time-varying case, the lower one (marked with 2)—to the frozen case. The former was explicitly shifted up to show their distinct shapes.

Fig. 11

Production policies for fixed and varying demand

Fig. 12

Corrective maintenance policies for fixed and varying demand

6 Performance comparison

We present in this section an approach that allows to compare the performance of the system under different policies that are computed through the optimization procedures that use different demand models. Conventional approach for comparing the systems that use for example constant and varying demand models would consist of directly computing their performance under corresponding assumptions. This does not allow the fair comparison, because one system actually functioning under varying demand, while another—under constant demand. We propose to put the systems in the same conditions—let say apply the varying demand—but consider the decision making policies computed by using different assumptions leading to different models (that may match the reality up to higher or lower degree).

The same is true for comparing the systems with fixed and controlled return rate as it has been done in Kenne and Boukas (1997). It is natural that the system with corrective maintenance (that uses controlled repair rate) has better performance than the system with slow repair rate—since it has higher availability. It would be of more interest to compare system with corrective maintenance (controlled repair rate) to the system with fast but fixed repair rate. To get better performance in this case we must show that slowing the repair rate might be sometime advantageous due to cost saving.

For a fair comparison of the policies under study, the systems have to be functioning in the identical environment, but the models used for decision making might be different. Thus for comparing the constant and varying demand models we consider the systems that use 3 different decision making procedures:

• policy 1 uses the model described by equations (3) and full methodology described in Sect. 5;

• policy 2 uses the model described by equations (3), but takes into account the frozen demand levels for decision making (neglecting its instantaneous rate of change);

• policy 3 uses the average demand level $D=Dm$ for decision making, completely neglecting the demand variations.

All three instances of the system (under different policies) are exposed to the demand that actually follows the model (3).

In order to evaluate the system performance we solve the HJB equations using conventional numerical approach (Kushner and Dupuis 1992), but use one of the methods itemized above to compute the policy on each iteration, instead of minimizing over the whole admissible policies $\varGamma (\cdot )$ as it is conventionally done for solving HJB equations. In other words: the system under policy 1 uses optimal production and maintenance policies based on the solution of HJB equations (10) with an approach described in Sect. 5.

The system under policy 2 uses conventional methods Kenne and Boukas (1997) and Kenne et al. (2003) applied for several “frozen” demand rate levels and ignores that this levels changes in time (thus neglecting the time-derivative terms in HJB equations). These policies are computed and applied to calculate the value functions through the series of iterations until they converge.

The system under policy 3 totally ignores the demand rate variations and uses the average demand rate $D_m$ to compute the maintenance and production hedging levels and corresponding policies, that are for this case (see Kenne and Boukas 1997; Kenne et al. 2003).

$$\begin{aligned} u_1 &= \left\{ \begin{array}{ll} U_1 &{} \text{ if } x< Z_p\\ D_m &{\text{ if}}\; x=Z_p\\ 0 &{ \text{ otherwise}} \end{array} \right. \end{aligned}$$

(16)

$$\begin{aligned} u_2 &= \left\{ \begin{array}{ll} U_2^+ &{ \text{ if}}\; x< Z_m\\ U_2^- &{ \text{ otherwise}} \end{array} \right. \end{aligned}$$

(17)

here $Z_p$ and $Z_m$ are production and maintenance hedging point respectively.

We present below 2 figures to illustrate the comparison of the policies 1 and 2 that we call adaptive policies against the policy 3 that we call fixed policy. In Fig. 13 we show value functions computed for an adaptive policy (1 or 2) shown as solid curve and a fixed policy 3 shown as dashed curve. We apply the demand close to the maximal range $D_m+D_a$. Note that in this case systems that use either one of adaptive policies (1 or 2) provide similar results, because the time-derivative terms are small near the maximum of the demand.The system performance under fixed policy is worse, namely, one can see that the value function for the system under policy 3 has consistently higher value in the whole inventory space, and near the minimum ($x\simeq 3$, corresponding to the hedging point), it is $\sim 3.7$ times worse.

Figure 14 illustrates the comparison of adaptive policies (1 and 2) against fixed policy using the ratio $R^{(i)}=(V^{(3)}-V^{(i)})/V^{(i)},$$i=1,2,$ computed for the increasing demand interval (from $D_m-D_a$ to $D_m+D_a$), and averaged along the operational area of inventory space. Solid curve corresponds to $i=1$ (fully adaptive policy), dashed curve—to $i=2$ (frozen demand). One can see that under the fixed policy the system behaves poorly against both adaptive policies, especially for the large demands. In other words: using the average demand when it is actually below average (overestimation) is acceptable, but using it when demand is actually above average (underestimation) is not. We can also see that fully adaptive time-varying policy 1 outperforms the frozen demand policy 2 in the domain of large demand (above the average $D_m$—level indexes from 9 to 18), while for the demand levels below average they are comparable (but both outperform the system under policy 3 by $\sim 10 \%$)

Fig. 13

Value functions for fixed and adaptive production policies

Fig. 14

Relative quality of fixed control against adaptive control

7 Generalization to non-exponential repair time distributions

In the previous sections a system subject to failures and repairs with exponentially distributed time between failures and time to repair. In the real manufacturing systems, an assumption about exponential inter-event time may not hold: the machine up and down time often follows more general distribution.

First it worth mentioning that within stochastic production control framework along the last 40 years no methods have been developed for optimal control of manufacturing systems subject to non-Poisson type failure and repair flows. Optimality conditions (Sect. 2) are derived based on exponentially distributed inter-failures and repair times, and without such assumption the optimality condition in the form of HJB equations (or similar) are difficult (if ever possible) to obtain.

Indeed, the industrial practice requires to circumvent this situation and the following approach, coupling optimization and simulation methods has been repeatedly used starting (Kenne and Gharbi 2000) and various application problems have been successfully addressed (Gharbi et al. 2006; Hlioui et al. 2017).

In Kenne and Gharbi (2000) authors study the benchmark M1P1 problem solved by Akella and Kumar in Akella and Kumar (1986) (see also Sect. 4) and compare analytical solution, numerical solution based on HJB equation (in both cases the time-between-failures and repair time are exponentially distributed), and the series of solutions obtained using simulations based on design of experiments (DOE) and response surface methodology (RSM) for differently distributed time-between-failures and repair times. DOE and RSM utilize the parametric representation of the control policy inspired by the structure of the optimal policy obtained under more restrictive (exponential time distribution) assumptions. Comparing wide range of distributions (Gamma, Weibull, Lognormal) with same means and variances against the exponential distribution with the same mean, it was shown that (1) the safety threshold (hedging point) for exponential distribution is the highest among all other cases, (2) the incurred cost for exponential distribution is also the highest, (3) the threshold and the incurred costs obtained for other distributions are rather close (for the same means and variances). The reason behind this result is that the hedging point determines the level of stock needed to protect the system against the shortage-related penalty. This level depends on the mean-time-to-failure (MTTF) and mean-time-to-repair (MTTR)—more frequent are failures and longer are the repairs—higher is the threshold. But it also depends on the variability of underlying flows. Namely, higher is the variability, more frequent are the repair times much longer than average, and more frequent are the undesirable couplings of “long repair times” with short up-times between them.

To illustrate in more detail how the general failure/repair distribution affects the behavior of the system with variable demand described in previous sections, we analyze in this section the case of non-exponen- tial repair time using direct numerical simulations. We have kept the exponential distribution for time-between- failures since according to the literature (Kieckhafer et al. 2000) this distribution is most often close to exponential, while the repair time in real applications rarely holds this property.

The numerical experiments are set up as follows (1) the sequence of failures separated by exponentially distributed time-intervals with average value (MTTF) $1/q_{12}$ has been generated, (2) the sequence of repair time-intervals following Weibull-distributions and Gam- ma-distributions with the mean $1/q_{21}$ and various standard deviations $\sigma (k)$ (k is the shape parameter) have been generated, (3) the sequence of exponentially distributed repair time-intervals with the mean $1/q_{21}$ has been generated and used for comparison. Production and maintenance policies based on hedging curves determined in Sect. 5.2 are used (see Fig. 10).

Representative results are shown in Figs. 15, 16 and 17. In Fig. 15 the stock dynamics within the system affected by the series of failures with exponentially distributed inter-arrival times, and the series of exponentially distributed repair times is presented. In Fig. 16 the system with the identical series of failures, but repair times distributed according to Weibull distribution with shape parameter $k=3$ and scale parameter $\lambda _{weib}=\lambda _{exp} \varGamma (1+1/k)$ (last expression serves to adjust the Weibull MTTR to exponential MTTR, $\lambda _{exp} =q_{21}\simeq 0.15$). Comparing Figs. 15 and 16 one can observe several instances of long repairs leading to shortage/backlog ($t\simeq 55,160,\dots$ etc.). However, for the exponential repair case these shortage/backlogs are much more pronounced than for Weibull case ($\simeq 0.3$ for Weibull and $\simeq 1$ for exponential). Observed behavior is due to higher variability of exponential distribution (vs. Weibull distribution). Characterizing variability by the standard deviation we get $\sigma _{exp}=1/\lambda _{exp}\simeq 6.67, \; \sigma (3)\simeq 2.423$ (last value is computed according to analytic expression available for Weibull distribution). These results are consistent with the result reported in Kenne and Gharbi (2000) that exponential distribution is the most unfavorable one. As a particular event illustrating the distinctive behaviors for the two cases under study one can observe the “third long repair” in Fig. 15 that leads to significant shortage in exponential case (time $t\simeq 250$), but in Weibull case (Fig. 16) the stock level remains positive (an event occurs earlier $t \simeq 200$ due to shorter repair times occurred beforehand).

Note that we have mentioned above only one value $q_{21}$ of repair rate, but in fact, it is a control variable taking two values $U_2^+$ and $U_2^-$ according to maintenance policy (determined by the lower (hedging) curve shown as dashed line in Figs. 15, 16). So, actually, 2 sets of repair times have been generated (for both exponential and Weibull cases). Also, the lower panels in Figs. 15 and 16 show the resulting production rates (doubled in scale and shifted down for better visibility) for both exponential (Fig. 15) and Weibull (Fig. 16) cases.

In Fig. 17 the evolution of incurred costs for 5 different cases are shown for comparison. The highest curve corresponds to exponential distribution of repair times. Next two closely located curves correspond to Weibull distribution with $k=2$ (dashed curve) and Gamma distribution with $k\simeq 3.66$ (solid curve) that have same variances. Remaining two curves correspond to Weibull with $k=3$ (dotted curve), and $k=5$ (dash-dotted curve) respectively. We my characterize each curve be the ratio of the standard deviation (std) of corresponding distribution to the std of exponential distribution (variability ratio. The results are summarized in Table 3 together with the final incurred cost for each case.

Table 3 Cost and variability ratio

Figure 17 and Table 3 clearly illustrate that higher is the variability of the distribution—higher is the incurred cost (MTTR are the same). Exponential repair distribution is the worst case, in full agreement with Kenne and Gharbi (2000).

Obtained results show that the optimal policies computed using exponentially distributed repairs are usable in general case and provide “conservative overestimate” (Kieckhafer et al. 2000) comparing to other distributions with lower variability. That means that for such distributions, lower hedging value (hedging curve in case of variable demand considered here) may further lower the expected costs. In order to compute such policies, the full implementation of DOE/RSM methodology (Kenne and Gharbi 2000; Gharbi et al. 2006) based on adequate parametrization of hedging curves is needed—a non trivial problem that will be addressed in our future work.

Fig. 15

Stock trajectory for exponentially distributed repair times

Fig. 16

Stock trajectory for Weibullp-distributed repair times

Fig. 17

Cost comparison for exponential and non-exponential repairs

8 Discussion: contributions and limitations

We continue with the discussion of the contribution made in this paper as well as existing limitations.

The main contribution of the paper can be divided in two parts. The first part concerns a particular problem studied in this paper, namely: combined production and corrective maintenance policy optimization for the systems under slow periodically varying demand. The optimal production policy can be characterized as extended hedging point policy. It requires to apply maximal production rate until the inventory reaches the hedging level, then switches to on-demand production in order to follow the hedging level that varies in time due to demand evolutions. The optimal maintenance policy is also of extended hedging point-type. Switching from low to high maintenance rate occurs along the hedging level, which also varies in time due to demand evolutions.

One of important features revealed by our study is an anticipatory effect: considering the extended hedging point evolutions in time, it is shown that the hedging level rises and descends earlier then in the system under “frozen”demand (computed by neglecting time-derivative terms). Another result concerns the relative position of production and corrective maintenance hedging levels (HLs). This is of particular importance, because the maintenance HL is only valid when it is located within the operational area of the system below the production HL, and since both HLs vary in time, their relative position may change in time in a nontrivial way.

The second part of our contribution concerns the generic problem of policy optimization for failure-prone manufacturing systems under time-varying demand.

Proposed methodology is based on the approximated solution of non-stationary Hamilton–Jacobi–Bellman equations using asymptotic expansion framework. The methodology is implemented numerically as a four steps procedure that consists of (1) discretizing the demand range, (2) solving the conventional optimization problem for several frozen (discrete) demand levels (using HJB equations), (3) estimation of non-stationary terms in HJB equations using finite difference approximation, and (4) solutions of modified HJB equations upgraded with the non-stationary terms estimates.

We consider in this study a single-machine-single-product system. Concerning this limitation the following aspects needs to be emphasized. An approach, coupling optimization and simulation methods based on design of experiments (DOE) and response surface methodology (RSM) outlined in previous section in the context of studying non-Poisson failure/repair flows has been also successfully used for production control optimization of multi-machine systems. In Kenne et al. (2003), Gharbi et al. (2006) and Hlioui et al. (2017) the multi-machine multi-product systems were analyzed that addressed controlled corrective maintenance, setups and combined optimization of supplier selection, production and replenishment respectively.

In all systems considered in the above papers, the policy structure inspired by the optimal policy computed under simplified assumptions (one machine, exponentially distributed up and down times, etc.) is para- metrized, then DOE/RSM simulation-based approach is used to find optimal parameters and to determine suboptimal policies. Rather complex systems containing several machines were successfully analyzed: five machines in Gharbi et al. (2006) and two-machines, two suppliers, four products in Hlioui et al. (2017). This proves that simulation-based approach that makes use of DOE/ RSM methods is well suited for addressing multi-machine systems subject to general failure/repair time distributions.

We can therefore expect that this approach can be used to address the multi-machine systems under variable demand. This will allow to extend the prosed me- thodology and to make it applicable to a wider class of manufacturing systems. As a first example of such extension it worth mentioning production optimization problem for hybrid manufacturing–remanufacturing systems under variable demand and return has been addressed in Polotski et al. (2018). The system studied in that paper is of more complex structure (two machines), but no maintenance option is considered.

The main difficulty that can be envisioned in application of DOE/RSM simulation-based approach to the system under variable demand is that the optimal policy is determined by hedging curve instead of hedging point. The parametrization of such curves may constitute a challenging task. A novel approach to approximation of complex systems by a simpler model, based on the concept of intrinsic variability ratio and on thorough analysis of the system bottlenecks was proposed in Wu and McGinnis (2012) and further developed in Wu et al. (2016). Although developed within queuing system framework, an approach may be applicable to constructing adequate parametrization of the production policy in the complex systems, for further analysis using DOE/RSM methodology. Investigation of this approach is the subject of our future work.

In this study, the demand rate is variable and known (this is the case of expected rump-up, seasonal changes, etc.). We describe an approach that allows to decision maker to determine the combined optimal production and maintenance policy under such varying but known conditions. Considering the stochastic demand models is an alternative approach used by several authors and also utilized in Ouaret et al. (2013). This approach differs from the one pursued in the current study in that the solution that is optimal in average over all possible realizations of stochastic demand is targeted. Our approach aims at utilizing the known evolutions of the demand rate in order to account for them in optimization procedure.

In the context of the presented study the demand evolution frequency $\omega$ is supposed to be small. This is rather natural: we describe the method that is dedicated to capture the demand variation based on the solution obtained by neglecting the time-derivative of value function (first step of proposed procedure). Such step is only meaningful if this term is small in some sense. When the demand rate varies slowly in time the above mentioned term is actually small—it is proven in the paper by considering the system behavior in slow time ($\omega t$). When HJB equations are re-written in slow time, the value-function-time-derivative gets multiplied by ($\omega$), leading to singularly perturbed HJB. Its degenerate solution (corresponding to $\omega =0$) corresponds to a conventional stationary solution of the HJB equations, which differs from the exact solution by an $\omega$-proportional term. Proposed approach and corresponding algorithm allows to construct better approximation (of second order over $\omega$) of the exact solution. Our approach may not be suitable to the system with very large variation of the demand because it inherently considers them as small. But conventional assumption about constant demand rate are even less suitable. Our approach aims at capturing the known variations in order to include them into the model and account for them in optimization algorithm.

9 Conclusion

We have described in this work a novel approach to optimization of failure-prone manufacturing systems under time-varying demand. The results are based on the numerical solution of non-stationary Hamilton–Jacobi–Bellman equations. We have first validated our methodology by analyzing a one-machine-one-product manufacturing system under varying demand, and then used the proposed approach for studying the combined productive and corrective maintenance optimization problem under dynamic market conditions (demand variation). The solution of this problem obtained earlier in the literature for the constant demand is known to be of hedging-point type for both production and maintenance policies. Maintenance switching level (from low to high rate and back) is only relevant, from managerial point of view, if it belongs to the system’s operational zone (is located below the production hedging level).

When the time-varying demand is considered, the relative position of maintenance and production hedging points varies in time making the combined control problem challenging from the theoretical point of view. Solution of this problem is important for the practitioners who need to adjust the managerial decision based to varying market conditions.

Another important aspect encountered in the case of varying demand is that the on-demand production mode in which the system keeps the required safety stock level necessitates the production rate that varies in time in a nontrivial way. Even if the production rate is not adjusted instantly (to keep stock on the optimal level) the decision maker may adjust the production rate periodically, following the hedging point evolutions under varying market conditions.

In the future works we plan to address some limitations related to the assumptions made in this study. In particular, an assumption about slow varying demand (formalized through small frequency $\omega$) needs be quantified in order to simplify the assessment of applicability of the proposed approach in practical situations.

Another important issue is the extension of the proposed methodology in order to study more complex systems. As a step in this direction it worth mentioning the recent study of manufacturing-remanufacturing systems under varying demand and return (Polotski et al. 2018). To analyze the multi-machine systems, the integration of the proposed numerical procedure with the simulation approach based on design-of-experiments and response-surface-methodology (Gharbi et al. 2006) is planned. This will likely necessitate the parametrization of the hedging curves that are currently computed only numerically.