Integrated production and maintenance control policies for failure-prone manufacturing systems producing perishable products

Abstract

The problem of integrated production and maintenance control of unreliable manufacturing systems evolving in a stochastic and dynamic environment is studied in this paper. The considered system is subject to degradation and the produced products are perishable with random shelf-lives. The literature of operations management for perishable products reports a correlation between the shelf-life of the product and the machine degradation. In fact, the latter results in shelf-lives reduction. Ignoring this correlation effect may result in inaccurate values of the shelf-lives and inefficient control policies. The objective of this paper is to develop a joint production and maintenance control policy that minimizes the total cost composed of backlog, inventory holding, disposal, and maintenance costs. The proposed parametrized joint control policy combines a multi hedging point policy and an age-based preventive maintenance policy. The optimization of the parameters of the proposed joint control policy is obtained using a simulation-based optimization approach and sensitivity analyses are provided to confirm its robustness. The obtained results show that the correlation between machine degradation and shelf-life reduction has a major influence on the control parameters and that preventive maintenance interventions can lead to increasing the shelf-life of products and minimizing the total cost. The proposed joint control policy is then compared to three other polices for a wide range of system and cost data. The obtained results show that the proposed joint control policy outperforms the other polices in terms of total incurred costs.

1 Introduction

From the inventory control for perishable products side, product’s shelf-life is generally estimated regardless of the manufacturing system condition and the degradation of the machine. However, in practice, there is a correlation between the shelf-life of perishable products and machine degradation [1, 2]. Indeed, the degradation of the machine results in a decrease in shelf-lives. Finding production and maintenance control policies for manufacturing systems of perishable products independently of this correlation, as it is often considered in the literature, may lead to higher costs. In fact, perishable products represent a big part of the market and poorly estimating the shelf-life can lead to major loss in terms of costs [3]. This is due to the limited shelf-life characteristics and the fact that they must be disposed from inventory passed their expiration date. Examples of perishables products are fruits, vegetables, medications, seafood, poultry, and dairy products.

In manufacturing industries, the maintenance actions are considered a priority and are at the center of industrial concerns given their crucial role in minimizing failure occurrences. Manufacturing systems aim to find a trade-off between maximizing its availability on the one hand, and minimizing the costs for maintenance activities on the other hand. As the manufacturing systems are prone to breakdowns depending on many factors such as fatigue, cracks, and corrosion, the interest in finding efficient strategies for maintenance interventions is increasing every day. Moreover, in the case of failure-prone manufacturing systems producing perishable products, maintenance activities can play a crucial role into minimizing incurred costs as they can lead to increasing the shelf-life of products. Consequently, it is important for manufacturing system managers to revise their strategies by adopting a joint maintenance and production control policy that take into consideration the characteristics of perishable products and the relationship between machine degradation and shelf-life reduction in order to minimize the total incurred cost.

Undeniably, manufacturing systems are subject to multiple sources of uncertainties such as random failure and repair times and the different interactions that may exist between system parameters. In this context, research questions can be presented as follows: (i) How can we quantify the correlation between shelf-life reduction and machine degradation? (ii) How does this correlation affect the maintenance and production control policies? (iii) What is the best joint maintenance and production control policy to adopt to minimize the total incurred cost? Accordingly, in this paper, we aim to develop a joint maintenance and production control policy for failure-prone manufacturing systems while taking into consideration the perishable nature of products and the related variation of the shelf-life. We also take into consideration the impact of machine degradation on the shelf-life of finished products. The objective is to find the optimal maintenance and production control policies that minimizes the total cost composed of backlog, inventory holding, disposal and maintenance costs.

The remainder of this paper is structured as follows: Sect. 2 represents a literature review. Section 3 is dedicated to the system description and problem formulation. The proposed joint production and maintenance control policy is detailed in Sect. 4. The adopted resolution approach is presented in Sect. 5. The simulation–optimization method used to obtain the optimal control parameters is presented in Sect. 6. Sensitivity analysis is provided in Sect. 7. A comparative study between the proposed joint policy and other policies adapted from the literature is provided in Sect. 8. Managerial insights and implementation issues are discussed in Sect. 9. Finally, the conclusion is presented in Sect. 10.

2 Literature review

In this section, we represent a literature review related to our study. A summary of the reviewed studies is categorized into three groups and is presented in Table 1. The first group is dedicated to production and control policies for failure prone manufacturing systems. The second group reviews work dealing with production control policies for perishable products. The third group presents perishable product models that integrate the effect of machine degradation on the shelf-lives of the product. Table 1 summarizes relevant articles based on key criteria in terms of whether or not perishability is considered, and if so, the type of shelf-life (random or not), whether the shelf-life is dependent on the machine degradation, unreliable manufacturing systems, and the consideration of maintenance control policies and production control policies.

Table 1 Summary of relevant literature

The first group of the literature review is related to integrated policies for maintenance and production control. According to Berthaut et al. [4], in a manufacturing context, the shutdowns of production units due to maintenance interventions reduce the availability of the system and can lead to shortages. Hence comes the interest in integrating joint maintenance and production policies. This combination makes it possible to optimize the control parameters related to the production control policies and to the preventive maintenance control policies simultaneously, and at the same time study the variations in inventory levels depending on maintenance interventions [5]. In this context, Gharbi et al. [6] combined in their work the hedging point policy (HPP) with an age-based preventive maintenance policy for unreliable manufacturing systems composed of a single machine producing one family type of finished products. For the same manufacturing system, Dhouib et al. [7] determined the critical age for preventive maintenance interventions and the optimal inventory level. In the same context, the work of Kouedeu et al. [8] deals with integrated maintenance and production control policies for unreliable systems and consider that failures are operation dependent. The work of Amelian et al. [9] studies also a maintenance and production control problem for failure-prone systems and uses simulation techniques for the resolution approach. In the same sense, integrated production and maintenance control policies were studied in Nourelfath et al. [10] and Cheng et al. [11]. Kang and Subramaniam [12] studied as well integrated policies for deteriorating manufacturing systems. Also, Rivera-Gómezi et al. [13] studied an optimization problem of integrated production and maintenance control policies while considering a dynamic sampling strategy. Hajej et al. [5] studied also a degrading manufacturing system in order to determine a joint maintenance and production control policy with dynamic inspection. The literature laid out thus far deals with integrated production and maintenance control policies for failure-prone manufacturing systems and highlights the importance of considering joint policies. However, it does not include the case where the products are of perishable nature and the fact that they must be removed from inventory passed their shelf-life. This brings us to the next group of this literature review, which deals with production control policies for manufacturing systems producing perishable products.

Studying control problems for unreliable manufacturing systems has been in the center of research for decades with a focus on feedback control policies especially the class of the HPP. Many researchers were prompted to develop several extensions based on the concept of HPP to study different system configurations for multiple manufacturing contexts, one of whom is the perishability of products. In this area, there has been relatively little work that consider perishability issues in dynamic stochastic systems. We cite the work of Bounkhel and Tadj [14] dealing with perishable products with a deterministic shelf-life while using the classical HPP but for a reliable manufacturing system. [15] studies also control problems for reliable manufacturing systems for perishable products having a deterministic shelf-life and a random demand rate. As for work that include machine failure, we cite Sajadi et al. [16] and Tavan and Sajadi [17] that applied the classical HPP for perishable products with a deterministic shelf-life. The work of Malekpour et al. [18] and Hatami-Marbini et al. [19] deal with production control problems for unreliable manufacturing systems composed of a network of machines where the final product perishable. In their work, the shelf-life is deterministic and the classical HPP is used for production control. In the same context, the work of Polotski et al. [20] deals with a production control problem of failure-prone manufacturing systems for perishable products having a deterministic shelf-life. We see that, when dealing with perishable products for a failure-prone manufacturing system, there is always limitation regarding the shelf-life (deterministic shelf-life). Moreover, the aforementioned work that deal with feedback control policies for perishable product used the classical HPP without developing suitable policies that take into consideration the specificities of perishable products and the variability of the shelf-lives. Furthermore, all these studies did not consider any maintenance control policies. Therefore, there is no previous study that combines maintenance control policies with production control policies and take into consideration the perishable nature of products and failure prone manufacturing systems simultaneously in a stochastic and dynamic context. Yet, many researchers highlight that there is a correlation between the shelf-life of perishable products and the degradation of the machine and how the latter can result in a decrease of shelf-lives.

The third group of the literature review focuses on studies related to perishable products and the factors that can affect the value of shelf-lives. One of these main factors is machine degradation. This relationship is confirmed throughout many industrial contexts. For instance, in the work of Barry-Ryan and O'beirne [21], they confirm that the blades used for slicing carrots degrade over time thus decreasing the products’ shelf-lives. Many other studies concentrate on the relationship between machine degradation and shelf-life reduction such as the work of Martinez‐Romero et al. [22] explaining how shelf-lives of fruits can be extended if the machine providing a certain dosage is well maintained; the work of Labuza and Breene [2] dealing with a packaging machine for vegetables and highlighting the fact that when the machine ages, the glue nozzle gets less effective which leaves air bubbles in each packed product and leading to a decrease in shelf-life,Ali et al. [23] studying tomato fruit,and Kittur et al. [24] studying bananas and mangos. This relationship is also discussed in studies related to quality control and how machine degradation can lead to a decrease in products’ quality and this result, in practice, in shelf-life reduction [25]. This statement is also mentioned in the work of Eskin and Robinson [26]. However, to the best of our knowledge, all these studies spoke about a qualitative relationship between machine degradation and shelf-life reduction and no quantitative relationship has been established. As can be noted, more studied are required to fully integrate maintenance and production activities in a joint control policy that incorporate a quantitative relationship between machine degradation and shelf-life reduction.

To sum up, according to the literature review provided, we see that most manufacturing system models dealing with both maintenance and production control policies do not consider the perishability of products. In addition, the research that deal with manufacturing system models for perishable products does not integrate preventive maintenance policies. Moreover, even though numerous studies confirm that machine degradation can result in a decrease in shelf-life, no quantitative relationship has been proposed to this matter.

In the present paper, our objective is to fill the gap in the literature by proposing a joint maintenance and production control policy for a failure-prone manufacturing system producing perishable products having a random shelf-life that decreases as the machine degrades. In the same sense, we propose a quantitative relationship linking the shelf-life of the product with the age of the machine. The proposed joint policy allows the decision maker to jointly decide on both maintenance and production activities to determine how to control the production rate and when it is convenient to execute preventive maintenance activities. The proposed joint policy aims to increase product’ shelf-lives and decrease the occurrence of failures in order to minimize the total incurred cost composed of backlog, holding, disposal and maintenance (corrective and preventive) costs.

3 System description and problem formulation

The notations used are presented and the studied system is described in this section.

3.1 Notations

The notations used in this study are defined as follows:

xi (t)	Inventory level at time t for the portion of stock being at state i at time t
di	Demand rate for the portion of stock
D	Total demand rate (product/unit of time)
u (t)	Production rate at time t (product/unit of time)
um	Maximum production rate (product/unit of time)
α(.)	Age of machine since the last maintenance action
A	Critical PM age of the machine
${C}_{i}^{+}$	Holding cost for the portion of stock being at state i ($ (product/unit of time)
${C}_{i}^{-}$	Backlog cost of portion of stock being at state i ($ (product/unit of time)
Cp	Disposal cost date of perishability ($/ product)
Cpm	Cost of preventive maintenance (PM) operation ($/ PM operation)
Ccm	Cost of corrective maintenance (CM) operation ($/ CM operation)
TTF	Time to failure
MTTF	Main time to failure
TTR	Time to repair
MTTR	Mean time to repair
TPM	Time of preventive maintenance
MTPM	Mea time of preventive maintenance
SL(.)	Shelf life mean of the product
σ(.)	Variability of the shelf life of the product
ωp	Binary variable that is equal to 1 if PM is conducted and 0 otherwise
πi	Limiting probability at mode i
J(.)	Cost function

3.2 System description

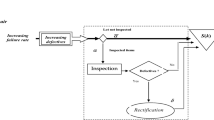
The considered manufacturing system is composed of a single machine producing one type of finished products having a limited and random shelf-life. Figure 1 illustrates the structure of the manufacturing system. The machine degrades over time and is prone to random failure and repair times. It can undergo two types of maintenance: corrective maintenance (CM) and preventive maintenance (PM).

Fig. 1

Studied manufacturing system

CM interventions are executed upon each failure in order to restore the machine to operational mode however without changing its age. Meaning CM actions restore the machine to “as-bad-as-old” condition. However, to preventively cope with machine degradation, PM interventions are performed to restore the machine to “as-good-as-new” condition. Meaning, PM actions restore the age of the machine to zero. These assumptions are considered for multiple manufacturing systems in which maintenance interventions can include the replacement of degrading or failed parts [13].

The finished product is of perishable nature having a random and limited shelf-life. Products are stored in inventory before satisfying demand. If the age of a product exceeds its shelf-life while still in inventory, it must be disposed. The shelf-life of the product is related to the degradation of the machine. Basically, when the machine degrades, the shelf-life decreases. This relationship between the shelf-life reduction and machine degradation is detailed in Sect. 3.3. Products passed their shelf-life incur a disposal cost. We consider a holding cost as well for each product in inventory. Also, due to machine failure and repair times, unsatisfied demand is delayed with a backlog cost. In addition, each maintenance activity (preventive or corrective) incurs a maintenance cost.

3.3 Problem formulation

In this paper, the system behavior is described by a hybrid state comprising both a continuous component (stock of products) and a discrete component (modes of the machine). The discrete component is represented by a stochastic process $\xi \left(t\right)$ describing the dynamics of the machine. The continuous components consist of the age of the machine $a(t)$ and the stock of produced parts into several sub-stocks ${x}_{i}$.

The dynamics of the machine is described at time $t$ by the stochastic process $\xi \left(t\right)$ with value in $B = \{1, 2, 3\}$, such that:

$$\xi\left(t\right)=\left\{\begin{array}{l}1\;machine\;is\;operational\\2\;machine\;is\;under\;CM\;activities\\3\;machine\;is\;under\;PM\;activities\end{array}\right.$$

The manufacturing system is subject to PM interventions using the decision variable ${\omega }_{p}(.)$ that allows the transition of the machine from an operational mode (mode 1) to PM mode (mode 3). Let us define ${\omega }_{p}(.)$ representing a binary variable indicating if PM interventions are executed (equal to 1) or not (equal to 0). The age of the machine $a\left(t\right)$ is measured using the cumulative number of produced parts from the last maintenance. It is described by the following differential equation:

$$\dot{a}\left(t\right)=k.u\left(.\right)$$

(1)

where $u\left(.\right)$ is the production rate and $k$ is a given positive constant.

The decision variables in this problem are the production rate $u(.)$ of the manufacturing system and the decision of PM interventions ${\omega }_{p}(.)$. Regarding the dynamic of inventory, we discretize the total stock into several sub-stocks ${x}_{i}$ each representing a part of the total stock with a specific state $i$ representing the sub-stock’s age.

As we see in Fig. 2, the machine operates with a production rate $u(.)$ manufacturing a product with a limited shelf-life with mean $SL$. The first sub-stock is ${x}_{1}$ which represents the newest stock. As time advances, the stock that is not pulled by demand from that first sub-stock gets older and passes to the next sub-stock ${x}_{2}$ and so on to the next sub-stock ${x}_{3}$ reaching the maximum shelf-life and the product is disposed. In this case, the sub-stock ${x}_{3}$ represents perished products. The time that products remains in each sub-stock is denoted ${\alpha }_{i}.$ At this point, we introduce the two rates ${u}_{1}^{p}$ and ${u}_{2}^{p}$ that denote the rate at which products exit each sub stock. They are expressed by the following equations:

$${u}_{1}^{p }= \frac{ {x}_{1}^{+} }{{\alpha }_{1}}$$

(2)

$$u_2^p=\frac{x_2}{\alpha_2}$$

(3)

The meaning of ${x}_{1}^{+}= \mathrm{max} ({x}_{1}, 0)$ is to express allowing backlog only in the first sub-stock. In fact, the total demand $D$ is also divided into multiple ${D}_{i}$ that each one pulls from the corresponding sub-stock ${x}_{i}$ with 0 $\le {D}_{i}\le$ $D$ and $D ={\sum }_{i}{D}_{i}$. The demand is set in a way that it pulls from the oldest stock ${x}_{2}$ until it becomes empty and then moves on to newest stock ${x}_{1}$. When the latter becomes empty, demand is backlogged.

Fig. 2

Modeling perishable products

The dynamic of the stock levels is expressed by the following differential equations:

$$\dot{x_1}=u-u_1^p-D_1,\quad\quad\quad\quad\quad x_1(0)=x_1^0$$

$$\dot{x_2}=u_1^p-u_2^p-D_2,\quad\quad\quad x_2(0)=x_2^0$$

(4)

with ${x}_{1}^{0}$ and ${x}_{2}^{0}$ denote the levels of each sub-stock at the initial time.

As stated above, the demand is set in a way to allow a certain queuing policy that allows the products that have the shortest remaining shelf-life to be pulled from inventory. This is expressed with the following equations:

$${D}_{2}=\left\{\begin{array}{l}D \quad\quad\quad\quad\ if\; {x}_{2} > 0\\ {u}_{1}^{p }\quad\quad\quad\quad if\; {x}_{2} = 0\\ 0 \quad\quad\quad\quad\ otherwise\end{array}\right.$$

(5)

$${D}_{1}=\left\{\begin{array}{l}0 \quad\quad\quad\quad\quad\quad\quad\quad if\; {x}_{2} > 0\\ D-{u}_{1}^{p } \quad\quad\quad\quad\quad\ if\; {x}_{2} = 0\\ D \quad\quad\quad\quad \quad\quad\quad\; otherwise\end{array}\right.$$

(6)

Here, we aim to establish a quantitative relationship between products’ shelf-life and machine degradation represented by its age. This is based on the work of [25] establishing the link between the shelf-life and the quality of the product. It is also based on the work of [27] establishing the link between the quality of the products and machine degradation in function of the machine’s age. The relationship between product’s shelf-life and the age of the machine is expressed by Eq. (7).

$$SL\left(a\right)= {SL}_{w}+ \eta \; exp(-\lambda {a}^{\delta })$$

(7)

where ${SL}_{w}$ is the smallest shelf-life a product can have. $\lambda$ and $\delta$ are given positive constants generally found from historical data and $\eta$ is the boundary considered for shelf-life reduction. Figure 3 represents the variation of the product’s shelf-life in function of the machine’s age based on Eq. (7). As we can see, when the machine is new, the shelf-life is at its biggest. As the machine ages, the shelf-life starts to decrease, and when the system is old, the shelf-life reaches its worst value ${SL}_{w}$. From these observations, ${SL}_{w}$ is the worst shelf-life value when the system is old, and (${SL}_{w}$+ $\eta$) represents the biggest shelf-life value, when the system is new. $\lambda$ and $\delta$ are used to change the scale and the shape of the model defined in Eq. (7). The latter is commonly used in the literature [28, 29] [13] apply the same model and highlight this “S” shape or, in our case, this “S reversed” shape (Fig. 3) by drawing it from simulation results. The authors note that this formulation is widely used and is considered general since it can represent many cases. Moreover, this model as well as parameters could be fitted based on historical data using different techniques such as Bayesian approaches and maximum likelihood [30]. Figure 3 shows also the effect of the parameter $\delta$ on the shape of the mean of the shelf-life. When $\delta$ (Fig. 3a) or $\lambda$ (Fig. 3b) increase, the shelf-life tend to reach its worst value.

Fig. 3

Mean of shelf-life decrease with the machine’s age. (a) Effect of variation of $\updelta$ ($\uplambda =1.5.{10}^{-4}$). (b) Effect of variation of $\uplambda$ ($\updelta =1.1)$

The variability of the shelf-life increases with the increase of machine’s age. In the same sense, we model the variability of the shelf-life by the following equation:

$$\sigma \left(a\right)= {\sigma }_{b}+ \mathsf{y} \; (1-exp\left(-\beta {a}^{r}\right))$$

(8)

where ${\sigma }_{b}$ is the smallest shelf-life variability accorded to a product when the machine’s age $a(t)$ is low. $\beta$ and $r$ are given positive constants obtained from historical data and $\mathsf{y}$ is the boundary considered in the shelf-life variability increase. We show in Fig. 4 the effect of machine’s age on the shelf-life variability and its variation when varying $r$ (Fig. 4a) and $\beta$ (Fig. 4b). As we can see, when the age of the machine is small, the variability is at its lowest value, and as the machine ages, it increases. The model described by Eq. (8) is based on the work of [13] by using the same “S” shape. By changing the values of $\beta$ and $r$, we could change the shape of the model. When $r$ and $\omega$ increase, the shelf-life variability increases as well.

Fig. 4

Shelf-life variability increase with the machine’s age. (a) Effect of variation of $r$($\upbeta =2.{10}^{-4}$). (b) Effect of variation of $\upbeta$ ($r=1.2$)

Based on the theory of probability [31], we use the set of Eq. (9) to compute the limiting probability at each mode.

We should note at this point that computing the probability for the different modes of the manufacturing system can lead to creating some fuzziness since knowing the exact number is difficult [32, 33]. However, and in order to alleviate any fuzziness created, we compute the limiting probability at each mode to insure the feasibility of the manufacturing system, as illustrated by the feasibility constraint (Eq. 11). Upon that, simulation techniques will be used to model the studied manufacturing system and optimize the decision variables. The use of simulation techniques can help avoid the fuzziness created since it uses probability distribution to model the behavior of the system.

$$\left\{\begin{array}{c}{(\pi}_1\;\pi_2\;\pi_3).\;Q=0\\\pi_1+\pi_2+\pi_3=1\end{array}\right.$$

(9)

where ${\pi }_{i}$ is the limiting probability at mode i (i $\epsilon B$) and $Q$ representing the transition rates matrix given by:

$$\mathrm{Q}=\left(\begin{array}{ccc}-(\frac{1}{\mathrm{MTTF}\left(a\right)}+{\omega }_{p}\left(.\right))& \frac{1}{\mathrm{MTTF}\left(a\right)}& {\omega }_{p}\left(.\right)\\ \frac{1}{\mathrm{MTTR}}& -\frac{1}{\mathrm{MTTR}}& 0\\ \frac{1}{\mathrm{MTPM}}& 0& -\frac{1}{\mathrm{MTPM}}\end{array}\right)$$

With $\mathrm{MTTF}\left(a\right)={q}_{1}+ {q}_{2} (1-exp\left(-{q}_{3} a\right))$ illustrated in Fig. 5 for given positive constants ${q}_{1}$, ${q}_{2}$, and ${q}_{3}$. This model describes the machine degradation as its age increases according to a model often used in the literature (Rivera-Gomez et al. [, 34, 35].

Fig. 5

Variation of MTTF with the machine’s age

Upon resolving Eq. (9), the limiting probability at each mode given by the following expressions:

$$\left\{\begin{array}{l}\pi_1(a)=\frac{MTTF(a)}{MTTF(a)+MTTR+\omega_p(.)MTTF(a).MTPM}\\\pi_2\left(a\right)=\frac{MTTR}{MTTF\left(a\right)}\pi_1\left(a\right)\\\pi_3\left(a\right)=\omega_p\left(.\right).MTPM.\pi_1\left(a\right)\end{array}\right.$$

(10)

At any time $t$, the machine must satisfy the feasibility constraint expressed by the following Eq. (11).

$${U}_{m}*{\pi }_{1}\left(a\right)>D+ {u}_{2}^{p}$$

(11)

where ${u}_{2}^{p}$ defines the rate of disposal as expressed in Eq. (3).

We note that when there is no preventive maintenance (${\omega }_{p}\left(.\right)$ = 0), the value of the limiting probability at the operational mode is ${\pi }_{1}(a)$ $=\frac{\mathrm{MTTF}(a)}{\mathrm{MTTF}(a)+\mathrm{MTTR}}$ (see Eq. (10)) that decreases when the age of the machine increases. We represent in Fig. 5 the evolution of $\mathrm{MTTF}(a)$ when the machine’s age increases. We see that MTTF decreases as the machine ages. Consequently, from a certain age, the system may become infeasible according to Eq. (11). That is why PM interventions are needed to restore the manufacturing system to “as-good-as-new” condition. Moreover, at the completion of the PM interventions, the shelf-life is restored to its highest value as discussed above.

We denote $\Gamma$ (.) the domain of admissible decisions:

$$\begin{aligned}\Gamma\;\left(a\right)=&\{u\left(a,.\right),\omega_p\left(a,.\right)\vert0\leq u\leq U_m\;\mathrm{Ind}\;\left\{\alpha=1\right\}\\ &,\omega_p\in\{0,1\}\}\;\mathrm{with}\;\xi\left(t\right)=\alpha\end{aligned}$$

(12)

First, we define the cost rate function $g(.)$ to be able to penalize the costs of inventory holding, disposal, backlog, and maintenance (corrective and preventive) as follows:

$$\begin{aligned}g\left({\alpha,x}_1,x_2,a,u,\omega_p\right)=&C_1^+\cdot x_1^++C_1^+x_2\cdot C_1^-\cdot x_1^-+C_p\cdot u_2^px_2\\ &+C_{cm}\cdot E_{\mathrm{cm}}+C_{pm}\cdot E_{\mathrm{pm}}\end{aligned}$$

(13)

Where:

$$x_1^+=\max\;\left(0,x_1\right),x_1^-=\max\;({-x}_1,0)$$

And,

$$E_{\mathrm{cm}}=\begin{pmatrix}1\;if\;\xi\left(t\right)=2\\0\;{otherwise}\end{pmatrix},\quad\quad\quad\quad\quad\quad\quad\quad E_{\mathrm{pm}}=\begin{pmatrix}1\;if\;\xi\left(t\right)=3\\0\;{otherwise}\end{pmatrix}$$

Having defined the admissible domain in (12) and based on the instantaneous cost defined in Eq. (13), we define the overall cost function $J\left(.\right)$ over a finite horizon given in Eq. (14) as in [20].

$$J\left({\alpha,x}_1,x_2,a,u,\omega_p\right)=\lim_{\mathrm T\rightarrow\infty}\frac1TE\left\{\int_0^{\mathrm T}g\left(.\right)\;\mathrm{dt}\;\vert x_1(0)=x_{1\;},x_2\left(0\right)=x_2\;,\xi\left(0\right)=\alpha,\right\},\;\forall\;\alpha\;\in\;\mathrm B$$

(14)

The objective is to minimize a long-run average cost $J(.)$ defined in (14) over (α) and under constraints given by Eqs. (1) to (11). Hence, we have to proceed with the definition of ${J}^{*}\left(.\right)$ as a minimizer of $J\left(.\right)$ as follows: ${J}^{*}\left(.\right)=$ $\underset{{(u,\omega }_{p}) \in\Gamma \left({\alpha }\right)}{\mathrm{Inf}}J\left({\alpha , x}_{1},{x}_{2}, a,u,{\omega }_{p}\right)$.

The determination of the cost ${J}^{*}\left(.\right)$ and the associated joint optimal policy ${(u,\omega }_{p})$ is considered complex in the work of Polotski et al. [20] with respect to optimization approaches based on stochastic optimal control theory centered on dynamic programming techniques. In their study, the shelf-lives of the products were considered deterministic. However, in this study, we consider a dynamic and stochastic environment: random failures and repair times, random shelf-lives, evolutions of shelf-life variability, interactions between shelf-lives, and machine’s age. Hence, these factors make the resolution process much more complicated. Therefore, we adopt a resolution approach based on simulation technique, design of experiment and response surface methodology. The resolution approach is detailed in Sect. 5.

4 Proposed joint production and maintenance control policy

We propose a joint production and maintenance control policy for manufacturing systems subject to random failure and repair times producing perishable products where the shelf-life decreases with the machine’s degradation.

4.1 Production control policy

The production control policy adopted in this study is inspired from the literature. In fact, the considered manufacturing system is unreliable with random failure and repair times. In this case, the class of the hedging point policies is considered efficient. That is why we propose to extend the classical (HPP) to a multi-hedging point policy (MHPP) for the case of perishable products. The proposed production control policy is based on the work of [36] dealing with a failure prone manufacturing system producing two product types (${x}_{1}$ and ${x}_{2}$). Ben Salem et al. 2015 also proposed a MHPP for a failure prone manufacturing system respecting environmental regulations. We propose the structure of production control policy described by Eqs. (15) to (17). It consists of building and maintaining safety stocks of each sub-stock (${x}_{1}$ and ${x}_{2}$) based on multiple hedging levels. The objective of the proposed production control policy is to allow the system to satisfy demand during the non-operational times of the machine on one hand, and to minimize the number of perished products on the other hand. The production rate in Eqs. (15) to (17) is determined based on the dynamics of the stock expressed in Eq. (4) and the value of the demand expressed in Eqs. (5) and (6).

$$If\;x_2\geq Y$$

$$u \; (1,.)=\left\{\begin{array}{l}{U}_{\mathrm{m}} \quad\quad\quad\quad\quad if \; {x}_{1} (t) < {Z}_{1} \\ {u}_{{Z}_{1}}^{P } \quad\quad\quad\quad\:\; if\; {x}_{1} (t) = {Z}_{1} \\ 0 \quad\quad\quad\quad\quad \;\; if \; {x}_{1} (t) > {Z}_{1} \end{array}\right.$$

(15)

where ${u}_{{Z}_{1}}^{P }= \frac{{Z}_{1}}{{\alpha }_{1}}$

$${If}\;0<{x}_{2}<{{Y}}$$

$$u \; (1,.)=\left\{\begin{array}{c}{U}_{\mathrm{m}}\quad\quad\quad\quad\quad if \; {x}_{1} (t) < {Z}_{2} \\ {u}_{{Z}_{2}}^{P } \quad\quad\quad\quad\quad if\; {x}_{1} (t) = {Z}_{2} \\ 0\quad\quad\quad\quad\quad\;\; if \; {x}_{1} (t) > {Z}_{2} \end{array}\right.$$

(16)

where ${u}_{{Z}_{2}}^{P }= \frac{{Z}_{2}}{{\alpha }_{2}}$

$$If \; {x}_{2}=0$$

$$u \; (1,.)=\left\{\begin{array}{l}{U}_{\mathrm{m}} \quad\quad\quad\quad\quad if \; {x}_{1} (t) < {Z}_{2} \\ D \quad\quad\quad\quad\quad\ if \; {x}_{1} (t) = {Z}_{2} \\ 0 \quad\quad\quad\quad\quad\;\; if \; {x}_{1} (t) > {Z}_{2} \end{array}\right.$$

(17)

With ${\alpha }_{1}$ and ${\alpha }_{2}$ positive constants and ${Z}_{1}$ $\le$ ${Z}_{2}$, $u(2,.)$ = $u(3,.)$ = 0.

4.2 Maintenance policy

As for the maintenance policy, we propose an age-based PM policy. This choice is motivated by the fact that machine degradation is dependent on its age and the fact that products’ shelf-life decreases as the machine degrades. The structure of the maintenance policy is based on the work Rivera-Gómez et al. [37] and Berthaut et al. [38] and is governed by two control parameters: $A$ and ${Z}_{PM}$. The structure of the proposed maintenance policy is expressed by Eq. (18). In this case, the machine is maintained upon reaching a predetermined age $A$ and when the inventory on hand is bigger than ${Z}_{PM}$. Indeed, $A$ is a threshold of cumulative number of produced products called also the critical PM age. ${Z}_{PM}$ denotes the critical products’ threshold that must be in inventory in order to execute PM activities. This parameter aims to minimize the risk of backlog and is based on the work of Berthaut et al. [38] who deals with the case of a single type of finished product. We propose to use the sum of instantaneous inventories of the two sub-stocks of finished products (${x}_{1} (t)$+${x}_{2} (t)$) to control the preventive interventions. Here, the decision variable called ${\omega }_{p}\left(t\right)$ is defined by a binary function equal to 1 if a preventive maintenance action is performed, and equal to 0 if not.

$${\omega }_{p}\left(3,.\right)= \left\{\begin{array}{l}1 \quad\quad \left(if \; a\left(t\right)\ge A\right)\; and \; ({x}_{1}\left(t\right)+ {x}_{2}\left(t\right))\ge {Z}_{PM} \\ 0 \quad\quad\quad otherwise\end{array}\right.$$

(18)

The optimization problem consists of finding the optimal control parameters (${Z}_{1}$, ${Z}_{2}$, $Y, A$, ${Z}_{PM}$) of the joint production and maintenance control policy called hereinafter perishable production maintenance policy (PPMP) to minimize the expected total cost expressed by Eq. (14). It includes backlog, inventory holding, disposal, and maintenance costs.

5 Resolution approach

This section details the main steps of the resolution approach adopted. We should note that it is difficult to find the analytical solution for complex problem evolving in a dynamic and stochastic context. Therefore, in order to optimize the control parameters that minimizes the total cost in Eq. (14), a simulation-based optimization method is adopted. This method combines simulation modeling, design of experiment (DOE), and a response surface methodology (RSM). The adopted method is frequently used in the resolution of complex problems such [37]. The resolution steps are illustrated in Fig. 6.

Fig. 6

Proposed resolution approach

5.1 Step 1: Structure of joint policy

In this step, the studied manufacturing system is described, and the problem is formulated. Afterwards, the structure of the proposed joint control policy is defined. The control parameters represent inputs of the simulation model (see Sects. 3 and 4).

5.2 Step 2: Simulation model

In order to imitate the system dynamics under the proposed joint policy, a simulation model is built. The control parameters of the proposed joint control policy are considered inputs for multiple experiments in order to evaluate the performance of the system (see Sect. 6.1).

5.3 Step 3: Optimization using design of experiment (DOE) and response surface methodology (RSM)

In this step, the objective is to find the optimal control parameters that minimizes the total incurred cost. DOE is used to define the inputs for the simulation runs. RSM is applied on the total cost obtained with the simulation to establish the effect of significant control parameters, their interactions, and their quadratic effects on the total incurred cost. The total cost is then minimized to determine the optimal control parameters. Section 6.2 details this step.

5.4 Step 4: Sensitivity analysis

In this step, multiple sensitivity analyses are conducted for a wide range of cost and system data (backlog disposal variability of shelf-life…) to observe the behavior the proposed joint maintenance and production control policy and to confirm the robustness of the resolution approach (see Sect. 7).

5.5 Step 5: Comparative study

This step aims to conduct a comparative study between the proposed joint control policy and other policies. The comparison is carried out for a wide range of system and cost parameters to determine the policy that offers the lowest incurred total cost (see Sect. 8).

5.6 Step 6: Implementation of the control policy

In Sect. 9, the implementation of the proposed joint control policy is established. The objective here is to provide the decision maker with insights to help him effectively implement the proposed joint control policy. An example is provided to guide the manager step by step through the implementation process.

6 Simulation-based optimization method

The control problem formulated above has constraints and is stochastic. The stochastic events are the correlated shelf-lives of the product with the age of the machine, and the random failure and repair times of the machine. When dealing with complex systems with dynamic and stochastic settings, obtaining analytical solutions is difficult. Therefore, a simulation-based optimization method is used in order to evaluate the economic performance of the proposed joint control policy. It combines simulation, DOE, and RSM in order to determine the optimal control parameters. This approach is very commonly used for problem resolution of complex manufacturing systems’ problems [39, 40].

6.1 Simulation model and its validation

The simulation model developed using Arena software combines discrete and continuous events. The advantage of using simulation modeling technique lies in its capacity to imitate the actual operating conditions under which the manufacturing system evolves. The block diagram of the simulation model is presented in Fig. 7. The structure of the model consists of several events interacting with each other such as arrival of demand, the control policies, etc.

Fig. 7

Block diagram of the simulation model

The first block (block 1) is the initialization of input variables (demand rate, maximum production rate, shelf-life, control parameters, …). Then, the manufacturing system (block 2) prone to failure and repair times (block 5) is governed by the joint production and maintenance control policy. The production control policy (block 3) allows the manufacturing system to determine the production rate based on the different inventory levels following Eqs. (15) to (17). The preventive maintenance control policy (block 4) is responsible for providing changes in the state of the system based on the two control parameters: age of the machine and the level of inventory. The manufacturing system aims to satisfy the demand (block 6) that directly affects the inventory level of both sub-stocks of finished products. Then, the level of inventory (block 7) is updated accordingly. Indeed, the variation in inventories depends on machine production rates, demand rate, and the disposal of perished products. (Block 8) represents the evolution of stock due to their perishable nature and is linked to (block 5) since that the value of the shelf-life varies in function of the machine’s age. In this step, the age of inventory is checked; if the product exceeds its shelf-life, then it must be disposed and if not, then it satisfies demand (block 6). Before the end of the simulation run, the total cost (block 9) is calculated taking into consideration the cost of disposal of perishable products, backlog, inventory holding, and maintenance costs (PM and CM).

To validate the simulation model, a numerical example was executed for a manufacturing system governed by the joint control policy PPMP. We show in Fig. 8 the variation of different system parameters. Figure 8 shows in (arrow ①, Fig. 8a) the increase of level of inventory ${x}_{1}$ with a rate (${U}_{m} - {u}_{1}^{p }- {D}_{1}$) as the machine operates at maximum capacity. The inventory level allows the satisfaction of demand first. As for the remaining products, they are used to build the hedging level${Z}_{2}$. When reaching ${Z}_{2}$ (arrow ②, Fig. 8a), the production rate is set to a value equal to ${u}_{2}^{p }=\frac{{Z}_{2}}{{\alpha }_{2}}$. Given that the age of products is continuously growing, the level of ${x}_{2}$ increases according to (${u}_{1}^{p}$ − − ${u}_{2}^{p}{D}_{2}$) as shown in Fig. 8b. Also, the perishable products increase as well as shown in Fig. 8c. When a failure event occurs (Fig. 8d), its impact is first seen in inventory ${x}_{2}$ as it decreases until reaching zero (arrow ③, Fig. 8b). In fact, since the demand is set in way to follow Eqs. (5) and (6), products are pulled from the oldest inventory ${x}_{2}$ until it is empty then it starts pulling from${x}_{1}$. At that time, ${x}_{1}$ starts decreasing (arrow ④, Fig. 8a) with a rate equal to ($- {u}_{1}^{p }- {D}_{1}$). In (arrow ⑤, Fig. 8a), backlog occurs and the stock level of ${x}_{1}$ decreases bellows zero, at that time ${x}_{2}$ is equal to zero. In (arrow ⑥, Fig. 8b), the inventory level ${x}_{2}$ reaches the threshold which means that the manufacturing system has enough inventory to reduce the production rate. In such a situation, the threshold level of the sub-stock ${x}_{1}$ decreases to ${Z}_{1}$ (arrow ⑦, Fig. 8a) and the production rate is reduced to ${u}_{1}^{p}$= $\frac{{Z}_{1}}{{\alpha }_{1}} .$ When a failure occurs, the machine undergoes repair interventions (Fig. 8d), and is restored to an “as-bad-as-old” condition (arrow ⑪, Fig. 8e). As for the preventive maintenance interventions (arrow ⑧, Fig. 8d), when the machine’s age reaches the critical age $A$ (arrow ⑨, Fig. 8e), the manufacturing system checks the quantity of inventory on hand and compares it to the critical threshold ${Z}_{PM}$ and only executes PM interventions if inventory is enough (${x}_{1}\left(t\right)+ {x}_{2}\left(t\right)\ge {Z}_{PM}$). As we explained in previous sections, the shelf-life of products is highly dependent on the machine’s age. Upon a PM intervention, the machine is restored to “as-new-condition,” which means the shelf-life increases. That is why we notice that the slope of the perishable products’ variation (Fig. 8c) decreases (arrow ⑩, Fig. 8c).

Fig. 8

Variations of system parameters when PPMP is used. (a) Evolution of inventory. (b) Evolution of inventory ${x}_{2}$. (c) Perished products ${x}_{3}$. (d) Machine operation and shut down. (e) Age of machine

The following section is dedicated to the optimization of the control parameters and the approximation of the total cost incurred.

6.2 RSM model and optimization

We present in this section the optimization step of the control parameters for the proposed joint policy to minimize the total cost incurred. The objective is to obtain the equation of the optimal total cost and the control parameters and see their interaction and effect on the total cost. In this sense, a numerical example is considered in order to illustrate the experimental approach combining simulation, DOE, and RSM. The data used are summarized in Table 2 and are fixed based on the literature related to maintenance strategies and control policies. For instance, the TTF, TTR, and TPM are chosen based on the work of [41] following a log-normal distribution.

Table 2 Parameters for the numerical example

Here, it is important to mention that ${Z}_{PM}$ must be smaller than ${Z}_{2}$. In fact, ${Z}_{PM}$ represents the threshold of the total inventory and ${Z}_{2}$ represent the highest threshold the inventory can reach. In this case, we can say that ${Z}_{PM}$ can be written as a function of ${Z}_{2}$: ${Z}_{PM}$ = $\tau$ ${Z}_{2}$ with 0 ≤ $\tau$ ≤ 1. In this case, the control parameters to optimize (${Z}_{1}$, ${Z}_{2}$, $Y$, $A$, τ).

For the proposed policy PPMP, a dependent variable (total cost) and five independent variables (${Z}_{1}$, ${Z}_{2}$, $Y$, $A$, $\tau$) are considered. In this sense, we adopt the full factorial designs at three levels 3⁵ for the PPMP control policy. This kind of designs allows that each interaction is estimated separately which leads to more accurate results [42]. Given the number of independent variables (n = 5), 2 replications were executed for each factor’s combination, involving the performance of 486 (3⁵ ∗ 2) simulation runs. Regarding the duration of the simulation model, it is fixed at 500,000 U.T in order to reach steady state.

The effect of each independent variables (${Z}_{1}$, ${Z}_{2}$, $Y$, $A$ and $\tau )$, their interactions, and their quadratic effect on the total cost are obtained using a multifactorial ANOVA. Figure 9 represents the pareto plot of the proposed policy. It shows the level of significance of each control parameters, their interactions, and their quadratic effect as well as ${R}_{\mathrm{adjusted}}^{2}$ (the adjusted correlation coefficients). Figure 9 shows that at the exception of the interactions ${(Z}_{1}*Y, {Z}_{1}*\tau , Y*\tau )$ and the quadratic effect ${Z}_{1}^{2}$, all the main factors (${Z}_{1}$, ${Z}_{2}$, $Y$, $A$ and $\tau$), the other interactions and quadratic effects are significant at a level of significance of 95%.

Fig. 9

Standardized pareto plot for the proposed policy. P = 0.05. ${R}_{\mathrm{adjusted}}^{2}$ = 96.01%

Also, we see that the correlation coefficient ${R}_{\mathrm{adjusted}}^{2}$ is equal to 96.01%. We can say that the response surface model (Eq. 19) explains more than 95% of the variability observed on the total estimated cost [42]. Also, Statgraphics software allowed us also to perform other statistical analysis such as the homogeneity of the variance and the analysis of the normality of the residuals which allowed us to verify the conformity of our model.

A response surface methodology is carried out to find the optimal control parameters. The response surface model is given by Eq. (19).

$$\begin{aligned}\widehat{{Cost}_{PPMP}} =& 1164.49 -585.61 \; {10}^{-2}{Z}_{1}- 826.29 \; {10}^{-2}{.Z}_{2}\\ &- 121.28 \; {10}^{-2}.Y- 65.9 \; {10}^{-2}.A - 593.24\;\;.\tau \\ &+ 206.32 \; {10}^{-5}{.Z}_{1}\;\;{Z}_{2}- 99.80 \; {10}^{-5}{.Z}_{1} .Y\\ &- 82.27\;{10}^{-5} \; {.Z}_{1}.A-61.6\;{10}^{-2} {.Z}_{1}.\;\tau \\ &+ 76.36\;{10}^{-4}.{Z}_{2}.Y-19.2 \; {10}^{-5} {.Z}_{2}.A\\ &+714.69 \; {10}^{-2}{.Z}_{2.}\; \tau + 8.2\;{10}^{-5} .Y \;.A\\ &-36.2\;{10}^{-2}.Y\; .\tau +21.7 \; {10}^{-2}.A.\tau \\ &- 31.88\;{10}^{-5} {Z}_{1}^{2}+ 762.18\;{10}^{-5} {Z}_{2}^{2}+ 109 \; {10}^{-4} {Y}^{2}\\ &+ 15.1 \; {10}^{-5} {A}^{2}+ 603.3 \; {10}^{1} \; {\tau }^{2} + \varepsilon\end{aligned}$$

(19)

By optimizing Eq. (19), the obtained results are as follows: ${\mathrm{Cost}}_{PPMP}^{*} =$ 4608.60, ${Z}_{1}^{*}=$ 419,${Z}_{2}^{*}=$ 802, ${Y}^{*}=$ 358, ${A}^{*}$ = 5711, $\tau$ = 0.53 (${Z}_{PM}$ = 425). Figure 10 represents the estimated total cost contour plot.

Fig. 10

The estimated total cost contour surface plot

The response surfaces corresponding to the total cost function (Eq. 19) are presented in Fig. 10. In addition, to cross-check the validity of the developed model, we compute the confidence interval that is obtained based on an additional 50 simulation runs using as input the optimal parameters. Results confirm that the optimal total cost approximated ${\mathrm{Cost}}_{\mathrm{PPMP}}^{*} =$ 4608.60 falls within the 95% confidence interval [4589.18, 4659.27].

7 Sensitivity analyses

The effectiveness of the proposed joint policy PPMP is verified by examining the effect of different system and cost parameters on the control policy parameters and on the total cost incurred.

7.1 Effects of cost variation

In Table 3, we present different cases of cost parameters variations and their effect on the control parameters (${Z}_{1}$, ${Z}_{2}$, $Y$,$A$, ${Z}_{PM}$). We did not include the holding costs (${{{C}}}_{1}^{+},\boldsymbol{ }{{{C}}}_{2}^{+}$) because it has no significant effect on the control policy parameters.

• Effect of the Backlog cost ${{{C}}}_{1}^{-}$: By increasing the backlog cost ${C}_{1}^{-}$, the manufacturing system reacts by increasing the hedging levels ${Z}_{1}$, ${Z}_{2}$, and $Y$ which allows a higher stock level in the system, thus, minimizing the risk of backlog. Here, we notice an increase of the level of inventory of the second sub-stock. In fact, by increasing $Y$, the model guaranties that the level of inventory of the first sub-stock is maintained at the highest threshold ${Z}_{2}$ for a longer time, so the system has more inventory, and this decreases the risk of backlog. When the thresholds increase, the machine produces more which means that the age of the machine increase. This leads to an increase in the frequency of PM by decreasing the critical age $A$ and the critical threshold ${Z}_{PM}$ in order to minimize the occurrence of failures. In this case, the non-operational times of the machine are shorter, so the system risks less backlog. Also, by executing more PM actions, each time the mean value of shelf-life increases, and the variability decreases so less perished products, and the system risks less backlog.

• Effect of the Disposal cost ${{{C}}}_{P}$: In the case of disposal cost variation, we can observe two different and opposite phenomena. First, for the case study 3 and 4, the variation of ${C}_{p}$ affects mainly the hedging level ${Z}_{1}$ that decreases when ${C}_{p}$ increases. Here, the system tries to minimize the risk of having perishable products by reducing the value of ${Z}_{1}$ related to the first sub-stock. As for the variation of ${Z}_{2}$, it decreases as well but slowly compared to ${Z}_{1}$. However, the risk of backlog becomes higher since there are not enough products to satisfy demand. That is why we observe a relatively small increase for the value of $\mathrm{Y}$ to serve against backlog. In the same sense, to hedge against this backlog, the system reacts by increasing the PM parameters ($A, {Z}_{PM})$ in order to increase the operational time of the machine. In this case, the control parameters are set in a way to avoid a more expensive cost of backlog. However, we can observe another system behavior if we set a high value of the disposal cost (case 5). Here, the manufacturing system behaves in a way to minimize the more expensive cost of disposal. First, we observe that the system wants to execute more PM interventions by reducing ${Z}_{PM}$ and $A$ in order to increase the shelf-life of the products. Also, to avoid the risk of disposal, the production control parameters ${Z}_{1}$, ${Z}_{2}$, and $Y$ decreases.

Table 3 Sensitivity analysis for the proposed policy

• Effect of the PM intervention cost ${{{C}}}_{pm}$: When the cost of PM increases, the critical age $A$ and the threshold ${Z}_{PM}$ to execute PM interventions increase to avoid PM actions that cost more. In this case, the risk of failures increases, hence the need to increase the threshold levels ${Z}_{1}$, ${Z}_{2}$, and $Y$ to avoid backlog.

• Effect of the CM intervention cost ${{{C}}}_{cm}$: Compared to the variation in the cost of PM, the influence of the cost of corrective maintenance ${C}_{cm}$ has the opposite effect on the control parameters. Indeed, when ${C}_{cm}$ increase, the system tends to execute more PM interventions by reducing the critical $A$ and the threshold ${Z}_{PM}$ in order to avoid more CMs over time. In this case, the system risks more backlog hence the increase of the thresholds ${Z}_{1}$, ${Z}_{2}$, and $Y.$

7.2 Effect of shelf-life parameters

The lognormal distribution is widely used to approximate the shelf-life of many perishable products. For this section, we are interested in varying the mean value of the shelf-life by varying $\delta$ in Eq. (7). Also, we studied the effect of shelf-life variability on the control parameters by varying $r$ in Eq. (8).

We show in Fig. 11 the effect of varying $\delta$ on the control policy parameters (${Z}_{1}$, ${Z}_{2}$, $Y$,$A$, ${Z}_{PM}$). As we presented in Sect. 3, when $\delta$ increase, the mean value of the shelf-life decreases faster in function of the machines’ age.

Fig. 11

Effect of the variation of shelf life mean on the oprimal control parameters (variation of δ). a Variations of the thresholds (${Z}_{1}$, ${Z}_{2}$, $Y$). b Variation of the critical age A and the threshold Z_PM

We notice that the variation of $\delta$ affects significantly the values of the control parameters. The threshold ${Z}_{1}$, ${Z}_{2}$, and $Y$ (Fig. 11a) increase as $\delta$ increases. In fact, when the mean value of the shelf-life value decreases (as $\delta$ increases), the number of perished products increases as well and so does the corresponding cost component. Moreover, when the number of perished products increase, the less there is to satisfy demand which means more backlog. In this case, the system find itself increasing the value of the control parameters to protect itself from high costs especially those due to backlog. The opposite effect is observed on the PM parameter. The critical age $A$ to execute PM interventions decreases when $\delta$ increases (Fig. 11b). In this case, the system reacts in way to execute more PM actions in order to restore the machine to “As-good-as-New” condition thus increasing the shelf-life. That is why we also observe a decrease in the value of the threshold ${Z}_{PM}$ (Fig. 11b). This decrease gets gradually higher as $\delta$ increases in order to guaranty a more frequent PM interventions that restore the shelf-life to its best value.

We show in Fig. 12 the effect of varying $r$ on the control policy parameters (${Z}_{1}$, ${Z}_{2}$, $Y$,$A$, ${Z}_{PM}$). As we presented in Sect. 3, As $r$ increase, as the shelf-life variability increase faster in function of the machines’ age. Here, we draw the same conclusions as in Fig. 11. The threshold ${Z}_{1}$, ${Z}_{2}$, and $Y$ (Fig. 12a) increase as $r$ increases. As for the parameters of the PM strategy, we see that the value of the critical age $A$ and the threshold ${Z}_{PM}$ (Fig. 12b) decrease aiming to increase PM interventions.

Fig. 12

Effect of the shelf-life variability on the optimal control parameters (variation of r). (a) Variations of the thresholds (${Z}_{1}$, ${Z}_{2}$, $Y$). (b) Variation of the critical age A and the threshold Z_PM

8 Comparative Study

We apply the simulation-based optimization approach described in Sect. 5 to compare between the optimal total cost of the proposed joint control policy PPMP and five other policies. The first policy used for comparison is the proposed production control policy without the preventive maintenance control MHPP described by Eqs. (15) to (17). The second policy considered is from the literature and is a joint control policy that combine the classical HPP for production control and the age-based preventive maintenance [4] we note HPP_PM.

The third joint policy used for comparison, it combines EPQ policy and the age-based preventive maintenance control policy we note EPQ_PM (Widyadana et al. [43]). We consider the same parameters used in previous sections.

The fourth and fifth policies consider preventive maintenance strategies that are widely used in manufacturing systems. Barlow and Hunter [44] presented details of these preventive maintenance strategies. The first, is age replacement policy (ARP) and is based on the conducting a preventive maintenance at the time of failure or after a constant period of machine operation. The second is block replacement policy (BRP) and it consists of conducting a preventive maintenance at the time of the machine failure or after fixed time intervals, regardless of the age of the machine. These preventive maintenance strategies are combined with MHPP production policy and are noted respectively MHPP_ARP and MHPP_BRP.

Figure 13 show a comparison of the optimal total cost of the policies used for comparison (PPMP, MHPP, HPP_PM, EPQ_PM, MHPP_ARP, and MHPP_BRP) while varying cost and system parameters. First thing to notice is that the optimal total cost incurred when applying the proposed joint control policy PPMP is lower than that of the other policies. And the policy that represents the highest incurred total cost is MHPP since it does not integrate PM actions. In this case, the non-operational times of the machine increase so does the CM costs and the backlog costs.

Fig. 13

Variation of the optimal total cost for PPMP, HPP_PM, EPQ_PM, MHPP, MHPP_BRP, and MHPP_ARP in function of cost and system parameters. (a) The impact of backlog cost ${\mathrm{C}}_{1}^{-}$. (b) The impact of disposal cost ${C}_{p}$. (c) The impact of CM cost. (d) The impact of PM cost. (e) The impact of Shelf-life variability

From Fig. 13a, as the backlog cost ${C}_{1}^{-}$ increases, PPMP allow the system to minimize the number of perished products since it integrates the age of inventory into production control. This phenomenon is due to the advantage of multiple hedging levels provided by PPMP to monitor different sub-stocks with different ages. Unlike the other policies that does not take into consideration the evolution of the age of a product.

From Fig. 13b, as the disposal cost ${C}_{p}$ increases, PPMP allow the system to be more protected against backlog since the demand is satisfied in a certain order by pulling from the oldest stock before pulling from the new stock. This kind of queuing policy allow the system to minimize the risk of disposal and backlog by minimizing the number of perished products. Also, when applying PPMP, the execution of the PM interventions, increases the shelf-life value thus minimizing the risk of perishability.

From Fig. 13c, we notice that the cost gap between MHPP and the other policies integrating PM interventions increase ${C}_{cm}$ increases. In fact, MHPP becomes less interesting as ${C}_{cm}$ increases because it leads to more risks of failures.

Figure 13d shows the impact of varying the preventive maintenance cost ${C}_{pm}$ on the total incurred cost of the considered policies. We notice that when ${C}_{pm}$ increases, the PM control policy become more expensive to execute. This explains the overrun of the total cost of the policy MHPP and EPQ_PM as MHPP becomes more interesting than EPQ_PM for high values of ${C}_{pm}$.

Figure 13e shows the impact of varying shelf-life variability. We notice that the cost advantage of PPMP gets higher as the variability increases. In fact, when the variability increases, the number of perished products increases and so does the costs for backlog and disposal. So, when applying PPMP, a better control is provided since it allows the system to track the quantity of each sub-stock at each age and adjust the production rate accordingly to minimize the risk of disposal and backlog. Also, the PM actions are executed in order to reduce this variability.

To sum up, the comparative study of the considered policies in terms of total incurred cost shows that the PPMP gives better results than the other policies for a wide range of system and cost configurations. This is due to its ability to avoid unnecessary interventions of PM on the one hand and avoid backlog cost since it offers multiple hedging levels to control different stock with different ages on the other hand. Moreover, the PPMP minimize the risk of perishability since it ensures a certain priority rule that ensures that products having the shortest remaining shelf-lives satisfy demand first.

9 Managerial insights and implementation

Manufacturing systems dealing with products with a limited shelf-life face major challenges in terms of finding the best control policy that take into consideration the age of a product and the degradation of the machine to minimize the total cost. By implementing the proposed joint control policy, the manager is capable of deciding simultaneously on the production rate as a function of the quantity of inventory on the hand and on when to execute PM actions in order to minimize the total cost. Since the shelf-life of the products increase as the machine degrades, the PM interventions allow on one the hand to restore the machine to “as good as new state” and, on the other hand restoring the shelf-life of the products to their best value. To implement the proposed joint control policy, the manager is required to monitor the different inventory levels and the state of the machine (operational, under repair, or under PM interventions).

Figure 14 illustrates a logic chart that serves to guide decision makers throughout the implementation for the proposed joint control policy PPMP for the basic case studied. The manager has to track the stock level, monitor the machine mode and its age. The latter is set to zero at the end of each maintenance intervention. Then, according to the PM optimal control parameters (${A}^{*}$ = 5711,${Z}_{PM}^{*}$ = 425), if the machine is operational, PM interventions are executed, and the machine’s age must be reset to zero.

Fig. 14

Implementation logic chart for PPMP

As for the production control policy, the manager should be able to regulate the production rate knowing the different values of the thresholds with ${Z}_{1}^{*}=$ 419,${Z}_{2}^{*}=$ 802 and ${Y}^{*}=$ 358. The production rate can be set to its maximum level (60 products/U.T), ${{u}_{{Z}_{1}}^{P}}^{*}$ (~ 17 products/U.T) or ${{u}_{{Z}_{2}}^{P}}^{*}$ (~ 32 products/U.T), or zero, based on the inventory level of each sub-stock. Accordingly, if the level of the second sub-stock is less than the threshold ${Y}^{*}=$ 358, then the manager has to regulate the production rate using the threshold ${Z}_{2}^{*}$ = 802. Meaning if the inventory level in the first sub-stock is lower than 802, the production rate must be set 60 products/U.T; if it is higher, then the machine must stop producing; and if it is equal to it, then the production rate is set to ${{u}_{{Z}_{2}}^{P}}^{*}$(~ 32 products/U.T). However, if the level of inventory of the second sub-stock is higher than ${Y}^{*}$ = 358, then the manager must regulate the production rate using the threshold ${Z}_{1}^{*}$ = 419. In this case, for instance, if the inventory level in the first sub-stock is higher than 419, the machine stops producing. If it is lower than 419, then the production rate is set to 60 products/U.T. Otherwise, if the inventory level is equal to 419, then the production rate must be set to ${{u}_{{Z}_{1}}^{P}}^{*}$ (~ 17 products/U.T).

Our proposed joint control policy has a wide range of applications for different types of industries looking to establish an effective and dynamic plan for their maintenance and production activities under which the shelf-lives of the products is depend on the machine’s age. By implementing our cost-effective proposed joint control policy, the manufacturers are able to minimize the total incurred cost composed of backlog, holding, disposal, and maintenance (corrective and preventive).

10 Conclusion

In this paper, we address a production-planning and maintenance control problem for unreliable manufacturing systems producing perishable products and subject to random breakdowns and repairs. Given that the objective is to minimize a total cost composed of backlog, inventory holding, disposal, and maintenance, we propose a structure of a joint production and maintenance control policy. Based on the literature, we propose an integrated production maintenance policy called perishable production maintenance policy (PPMP) that combines a production control policy of feedback nature with multiple hedging levels and, an age-based peplacement policy for maintenance control. This policy considers the effect of machine degradation on the mean value of shelf-life and on the shelf-life variability. In fact, the increase of the machine’s age results in a reduction of the mean value of the shelf-life and an increase of shelf-life variability. This phenomenon is often studied in the literature but only in qualitative way. In this paper, we propose a qualitative relationship between the shelf-life of the products and the age of the machine. In order to solve the problem, a simulation-based optimization approach was adopted. It combines simulation techniques, design of experiment, and response surface methodology.

Sensitivity analyses were conducted in order to observe the behavior of the system governed by the proposed joint control policy. It is seen that the backlog cost and the disposal cost have opposite effects on the control parameters. Also, the preventive maintenance cost and the corrective maintenance cost have opposite effects on the control parameters. When the disposal cost is high, the systems tend to execute more PM interventions to restore the shelf-life values to its highest. Results also reveal the important effect of machine degradation on the shelf-life reduction and on the decision-making process and how it affects the PM interventions. This consideration could lead to better managerial decisions to reduce the optimal total cost.

Afterwards, a comparative study is established between the proposed joint control policy and other policies from the literature. Results show that the proposed control policy PPMP gives the best results in terms of minimizing the total cost. This is due to its capacity to integrate the age of inventory as it evolves in time and to determine the production rate accordingly. The comparative study carried out demonstrates the advantage of the PPMP policy which allows executing PM actions to reduce the risk of backlog and disposal by increasing the shelf-life mean value and reducing shelf-life variability.

Future research could be explored based on this work. For example, this study can be studied in the case of multiple-type products. Moreover, a future study can incorporate random disposal costs depending on the shelf-life of the products. Also, as we established in the literature review that there is a relationship between quality loss and products perishability, which means that this study can be utilized in the configurations of quality control policies. In addition, the studied problem can be considered as a multi-objective optimization problem by minimizing the total cost and the total number of perished products, as in Assid et al. [45] who combined a quantitative criterion such as minimizing the total cost and qualitative criterion such as customer satisfaction, and in Wang et al. [46] who establishes a dual-objective optimization model for the selection of milling parameters such as power consumption and process time are minimized.