Introduction

Polypropylene, which is a commodity polymer, can be used to produce tapes that have high molecular orientation and higher mechanical properties than the standard non-oriented polypropylene. These tapes when combined with polypropylene matrix, which is non-oriented, constitute a self-reinforced polymeric composite (SRPP). The composite is produced by heating up the tapes, which causes their outer sheath to melt while the inner core maintains its orientation. During the cool-down, the molten polymer consolidates and forms the “matrix” component of the SRPP. As these composites are reheated for forming, the oriented molecules can shrink and partially lose their orientation [1]. Hence, SRPP preforms need to be constrained during forming to avoid excessive shrinkage. Cabrera et al. [2] investigated deformation modes of woven SRPP during stamp-forming. They found that behaviour of SRPP is similar to that of the other textile-based composites and the main deformation mechanism is intra-ply shear [2]. However, SRPP was also shown to undergo additional tape drawing, which is a mechanism particular to self-reinforced polymeric composites and may be beneficial when forming complex geometries. The effect of the clamping conditions on formability of SRPP composites was investigated experimentally by Selezneva et al. [3]. Three clamping options were considered: full edge, spring and corner. These conditions triggered different degrees of stretching, shearing and draping of the preforms. As the result, the formed hemispheres exhibited different wrinkling patterns.

Draping modelling is an indispensable step of a thermoformed composite part design. There are two main factors, related to the draping, which affect mechanical behaviour of the final consolidated part.

First, the “regular” change of the local composite properties because of the draping. The draping-induced reinforcement deformation, primarily shear, changes local geometry of the fibres. The basic mechanical properties of the composite, such as stiffness and strength, therefore can strongly change due to the draping. This is a topic that’s been studied a lot, especially in recent years [4,5,6,7,8,9,10,11,12]. These analyses are included in integrated composite part design software (see, for example [13,14,15]). Once the constitutive model of reinforcement deformation during draping is identified, the local fibres geometry can be modelled quite accurately with the state-of-the-art draping modelling software, and the local mechanical properties can be calculated [16, 17].

Second, defects of the draping, the most prominent of which is wrinkling, can lead to drastic deterioration of the load-carrying ability of the consolidated part and can cause part rejection. Some studies have analysed the influence of the presence of wrinkles, created during manufacturing, on the mechanical performance of the composite [18,19,20,21]. A recent review [22] demonstrates that the presence, pattern and intensity of wrinkling can be accurately modelled once the constitutive model of the reinforcement is identified. The part design can be then done “as manufactured”, accounting for the draping process induced defects.

Mechanical behaviour of textile reinforcements during draping is an important subject in composite materials science, with hundreds of papers published. Among these papers not that many are dedicated to the identification of constitutive models of thermoplastic pre-impregnated textile sheets at the processing temperature. Since the benchmark exercise [23] there was a considerable amount of research done on glass fabric reinforced polypropylene for quantification of the constitutive models (for example, [24,25,26]). The forming studies of SRPP [27,28,29,30,31,32] are focused on determining process windows for forming of SRPP in the presence of shrinkage rather than on identification of the constitutive behaviour at processing temperature.

The present work focuses on the development and validation of an FE model for thermoforming of SRPP. The modelling approach is based on the hyperelastic law developed by Charmetant et al. [33]. The constitutive model considers the main deformation modes that occur during the forming of textile composites, such as stretching in the warp and weft directions and in-plane shear. Material behaviour associated with each deformation mode is defined in terms of a physical invariant and a strain energy density function. In the study, the strain energy functions were obtained by fitting experimental data from tensile and picture-frame shear tests, which were conducted at forming temperatures. To validate the FE model, results were compared against the experimental data for the spring-clamping condition. The states or geometries of the SRPP preform at different stages of the forming process were captured by moulding shallow domes with depths ranging from 1 to 4 cm by using a hemispherical mould with a 4.5 cm radius. To the authors’ knowledge, this is the first work where the parameters of the Boisse-Charmetant formulation are identified for SRPP and are validated in comparison with experiment, hence can be used by others for virtual investigation of the SRPP forming.

In this paper, first the material and the experimental forming studies are discussed. Next, the description of the constitutive model and the development of the FE simulation are presented. Finally, results and conclusions are given.

Experimental

Material and preform consolidation

The precursor material to SRPP is a balanced 2/2 twill PP tape fabric provided by Propex Fabrics GmbH, as shown in Fig. 1a. The preform panels were prepared by stacking in an alternating manner twelve PP fabrics and eleven 20 μm thick PP films, as shown in Fig. 1b. Panels were consolidated by hot compaction at 188 °C with a hold time of 5 min at 40 bar and an average cooling rate of 35°/min. This process was optimized for SRPP with tensile properties in mind [34]. The produced panels were 22 cm by 22 cm and 2 mm thick.

Fig. 1
figure 1

(a) 2/2 twill PP woven fabric and (b) material layup used to produce preforms

Full size image

Mechanical testing

To measure the tensile and in-plane shear behaviour at forming temperatures, tests were performed on 2 mm thick pre-consolidated panels in a convection oven at 170 °C.

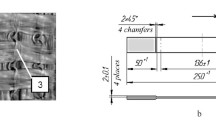
Picture frame tests, for in-plane shear properties, were performed using the picture frame setup developed at KU Leuven, and mounted on an Instron 5985 machine with a 100 kN load cell. The geometry of the picture frame fixture is shown in Fig. 2a, the picture frame is installed vertically on a tensile frame. Additional information regarding the experimental set up and the data processing associated with this test can be found in [35]. The picture frame setup was placed in a convection oven, and had to be placed at 45° to fit within the oven. Unfortunately, this prevented the use of digital image correlation. The tests were performed at a displacement rate of 20 mm/min, which corresponded to a shear angle rate of approximately 50°/min (decreasing from 54°/min at the beginning of the test to 45°/min at the maximum machine stroke, as calculated with formulae describing the kinematics of the frame in [35]). Six calibration tests with an empty frame were performed to account for friction in the setup. The average of these force-displacement diagrams was used to subtract the frictional force from the test results. After this correction, the shear angle and stress were calculated using the formulas described in [35].

Fig. 2
figure 2

(a) KU Leuven picture frame fixture: 1,2 – hinges, 3 – groove, 4 – lip, 5 – plate with screws (adapted from [23]), and (b) Peirce cantilever test fixture with clamped PP textile

Full size image

Tensile samples had a width of 20 mm and a gauge length of 80 mm, which was limited by the dimensions of the oven. Tests were carried out at 20 mm/min, which is equivalent to a nominal strain rate of 25%/min. Tests were interrupted when the samples began to pull out of the grips. Tensile tests were affected by the transverse shrinkage of the SRPP. Therefore, for future work it is recommended to test self-reinforced polymer composites using a biaxial test. This test would restrain the sample better and should minimize shrinkage. Furthermore, the induced deformation state in a biaxial test is also closer to the real deformation state during thermoforming.

As was discussed by Liang et al. [36] and Boisse et al. [22], bending stiffness is another important property to be included in the simulation, as it dictates the number and size of wrinkles. It has been shown that lower stiffness leads to finer wrinkles [36]. In contrast to what is done for continuous materials such as metals, the bending rigidity of textiles cannot be calculated directly from the tensile modulus [22]. Bending rigidity of textiles can be measured using the Peirce cantilever test [37]. It is based on the cantilever bending of a textile specimen under its own weight, as shown in in Fig. 2b. The specimen is progressively advanced until the free end makes contact with the inclined plane of the device (Fig. 2b). Assuming a linear relation between the bending moment M and the curvature χ, the specific flexural rigidity S is determined from the overhanging length l corresponding to an inclination of 41.5°:

$$ \mathrm{M}=\mathrm{G}\upchi \mathrm{S}=\frac{\mathrm{G}}{\mathrm{w}}\approx \frac{\ell^3}{8} $$

where G is the bending stiffness of the specimen, w is the weight per unit length of the specimen.

Tests on fabrics can be conducted at ambient temperatures, but composites should be tested at forming temperature to account for the matrix softening. However, SRPP composite and PP fabric would shrink at forming temperatures. Hence, PP fabric was tested at room temperature and the results were treated as the upper limit of the bending rigidity. In further refinement of the model, the viscosity of the molten polypropylene can be accounted for in addition to the bending resistance of the fabric [38].

The loading speed during the forming was 20 mm/s, hence the hemisphere was formed in 2–3 s. This gives an estimation of the maximum local shear rate of the fabric of 5–10°/s (referring to the maximum shear angle of 20°, see Fig. 11), with the minimum shear rate close to zero. The shear rate in picture frame tests was 0.7–0.9°/s, as stated in the previous section. Therefore in most of the hemisphere surface the shear rates in the forming and in the picture frame tests are of the same order of magnitude. The one decimal order of magnitude difference in the zones of maximum shear can indeed affect the results; this effect should be estimated in future work.

Thermoforming

The thermoforming tests were performed at the facilities of the SLC Lab (Leuven). A Fontijne press with integrated infrared heaters were used for forming. Two types of boundary conditions were considered: spring-support and full-edge clamping (actually the clamping was not ideal and certain blank sliding occurred). These conditions triggered different degrees of stretching, shearing and draping of the preforms. Figure 3 shows a schematic of the spring-supported and fully-clamped set up. The springs had a stiffness of 260 N/m. Preforms used for forming were 2 mm thick and 22 × 22 cm in size.

Fig. 3
figure 3

Experimental set-up with (a) spring clamping and (b) full-edge clamping

Full size image

Preforms were heated using infrared heaters. Temperature was monitored using embedded thermocouples (in the middle and near the surface) and the pyro-sensors incorporated into the heaters. Material were heated to a surface temperature of 170–175 °C. Once the set temperature was reached, it was transferred to the press using a rail system and stamped. The mould was kept at 100 °C, and the panels were demoulded once their temperature cooled down and stayed at 100 °C for 2–3 min. Throughout the study, a steel hemispherical mould with a 4.5 cm radius was used. To capture how the material behaves during forming, shallow domes were formed by partially closing the mould to 1, 2, 3 and 4 cm depths. The material was then allowed to cool down and re-solidify while preserving this intermediate geometry.

Constitutive model and parameters identification

Hyperelasticity

The hyperelastic constitutive model developed by Charmetant et al. [33] was used to model the highly non-linear mechanical properties of SRPP. The required input parameters were fitted using the experimental data. In the hyperelastic framework, the Cauchy stress tensor (σ) can be calculated from the deformation gradient tensor (F) and the strain energy potential (w):

$$ \underset{\_}{\underset{\_}{\upsigma}}=\frac{2}{\mathrm{J}}\left(\underset{\_}{\underset{\_}{\mathrm{F}}}.\frac{\updelta \mathrm{w}}{\updelta \underset{\_}{\underset{\_}{\mathrm{C}}}}.{\underset{\_}{\underset{\_}{\mathrm{F}}}}^{\mathrm{T}}\right) $$
(1)

where C is the Cauchy-Green deformation tensor and J is the Jacobian determinant of F. Material properties of the initially orthotropic material are defined along the three orthogonal directions: warp M1, weft M2 and through-the-thickness M3. Hence, strain energy density function for a hyperelastic law can be expressed [39, 40] in terms of invariants:

$$ \mathrm{w}=\mathrm{w}\left({\mathrm{I}}_1,{\mathrm{I}}_2,{\mathrm{I}}_3,{\mathrm{I}}_{41},{\mathrm{I}}_{42},{\mathrm{I}}_{43},{\mathrm{I}}_{412},{\mathrm{I}}_{423}{\mathrm{I}}_{51}{\mathrm{I}}_{52}{\mathrm{I}}_{53}\right) $$

where I1, I2 and I3 are the invariants of C:

$$ {\mathrm{I}}_1=\mathrm{Tr}\left(\underset{\_}{\underset{\_}{\mathrm{C}}}\right),\kern1.25em {\mathrm{I}}_2=\frac{1}{2}\left(\mathrm{Tr}{\left(\underset{\_}{\underset{\_}{\mathrm{C}}}\right)}^2-\mathrm{Tr}\left({\underset{\_}{\underset{\_}{\mathrm{C}}}}^2\right)\right)\kern0.5em \mathrm{and}\ {\mathrm{I}}_3=\mathrm{Det}\left(\underset{\_}{\underset{\_}{\mathrm{C}}}\right) $$

and where the mixed invariants correspond to the structural tensors:

$$ {\mathrm{I}}_{4\mathrm{i}}=\underset{\_}{{\mathrm{M}}_{\mathrm{i}}}.\underset{\_}{\underset{\_}{\mathrm{C}}}.\underset{\_}{{\mathrm{M}}_{\mathrm{i}}}\kern1.5em \left(i=1,3\right) $$
$$ {\mathrm{I}}_{4\mathrm{ij}}=\underset{\_}{{\mathrm{M}}_{\mathrm{i}}}.\underset{\_}{\underset{\_}{\mathrm{C}}}.\underset{\_}{{\mathrm{M}}_j}\kern1.25em \left(i=1,3\right) $$
$$ {\mathrm{I}}_{5\mathrm{i}}=\underset{\_}{{\mathrm{M}}_{\mathrm{i}}}.{\underset{\_}{\underset{\_}{\mathrm{C}}}}^2.\underset{\_}{{\mathrm{M}}_i}\kern1.25em \left(i=1,3\right) $$

A constitutive model for initially orthotropic materials can be derived on the basis of elementary deformation mode (e.g. in-plane elongation, shear) [33]. It can be assumed that the deformations modes are uncoupled and that the total strain energy density function can be written as the summation of n strain energy densities. Hence, the derivative of w can be expressed as:

$$ \frac{\updelta \mathrm{w}}{\updelta \underset{\_}{\underset{\_}{\mathrm{C}}}}=\sum \limits_{\mathrm{i}=1}^{\mathrm{n}}\frac{\updelta {\mathrm{w}}_{\mathrm{i}}}{\updelta {\mathrm{I}}_{\mathrm{i}}}\frac{\updelta {\mathrm{I}}_{\mathrm{i}}}{\updelta \underset{\_}{\underset{\_}{\mathrm{C}}}}\kern0.75em $$
(2)

where Ii is the strain invariant of the ith deformation mode. The expressions for the invariants for each deformation mode were derived by Charmetant et al. [33] based on physical observations. The main deformation modes influencing wrinkling of textiles are in-plane elongation, in-plane shear and transverse shear, as shown in Fig. 4. The method for obtaining the strain energy function for these modes using the experimental data will be described hereafter.

Fig. 4
figure 4

Main deformation modes of textiles during forming (adapted from [33])

Full size image

In-plane elongation

For in-plane elongation along the warp and weft fibres, Charmetant et al. [33] proposed the following expressions for the elongation invariant (Ielong) and its derivative:

$$ {\displaystyle \begin{array}{c}{\mathrm{I}}_{\mathrm{elong}}=\ln \left(\sqrt{{\mathrm{I}}_{41}}\right)=\upvarepsilon \\ {}\frac{\updelta {\mathrm{I}}_{\mathrm{elong}}}{\updelta \underset{\_}{\underset{\_}{\mathrm{C}}}}=\frac{1}{2{\mathrm{I}}_{41}}\underset{\_}{\underset{\_}{{\mathrm{M}}_1}}\end{array}} $$
(3)

In case of uniaxial loading, Ielong equals to the experimentally measured tensile strain (ε), and Eq. (1) for the Cauchy stress can be rewritten as:

$$ \underset{\_}{\underset{\_}{\upsigma}}=\frac{2}{\mathrm{J}}\left(\underset{\_}{\underset{\_}{\mathrm{F}}}.\frac{\updelta \mathrm{w}}{\updelta \underset{\_}{\underset{\_}{\mathrm{C}}}}.{\underset{\_}{\underset{\_}{\mathrm{F}}}}^{\mathrm{T}}\right)=\frac{2}{\mathrm{J}}\left(\underset{\_}{\underset{\_}{\mathrm{F}}}.\frac{\updelta {\mathrm{I}}_{\mathrm{elong}}}{\updelta \underset{\_}{\underset{\_}{\mathrm{C}}}}.{\underset{\_}{\underset{\_}{\mathrm{F}}}}^{\mathrm{T}}\right)\frac{\updelta {\mathrm{w}}_{\mathrm{elong}}}{\updelta {\mathrm{I}}_{\mathrm{elong}}} $$

The Cauchy stress component corresponding to the longitudinal tension is hence:

$$ {\upsigma}_1=\frac{1}{\sqrt{{\mathrm{I}}_{41}}}\frac{\updelta {\mathrm{w}}_{\mathrm{elong}}}{\updelta {\mathrm{I}}_{\mathrm{elong}}} $$
(4)

Experimental data is fitted by working with the curve for Ielong vs. dwelong/dIelong calculated using Eq. (3) and (4), respectively. The fitted expression for dwelong/dIelong can then be integrated to obtain the coefficients of the strain energy density (w) function. The piecewise polynomial form of the energy function that was obtained is shown in Eq. (5), and the tensile stiffness coefficient Kt0 and Kt are given in Table 1. The correlation between the experimental and fitted data is shown in Fig. 5a.

$$ {\mathrm{w}}_{\mathrm{elong}}=\left\{\begin{array}{c}\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathrm{K}}_{\mathrm{c}}{\left({\mathrm{I}}_{\mathrm{elong}}\right)}^2\\ {}\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathrm{K}}_{\mathrm{t}0}{\left({\mathrm{I}}_{\mathrm{elong}}\right)}^2\\ {}\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathrm{K}}_{\mathrm{t}}{\left({\mathrm{I}}_{\mathrm{elong}}-0.261\right)}^2+(0.261){\mathrm{K}}_{\mathrm{t}0}{\mathrm{I}}_{\mathrm{elong}}-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathrm{K}}_{\mathrm{t}0}{\left({\mathrm{I}}_{\mathrm{elong}}\right)}^2\end{array}\right.\kern1em {\displaystyle \begin{array}{c}{I}_{elong}<0\\ {}{I}_{elong}<0.261\\ {}{I}_{elong}\ge 0.261\end{array}} $$
(5)
Table 1 Selected stiffness coefficients, MPa
Full size table
Fig. 5.
figure 5

(a) experimental and fitted tensile and compressive data, and (b) non-physical wrinkling (adapted from [42]).

Full size image

No experimental data was available for the compressive behaviour (Kc) of SRPP at elevated temperature. It was previously measured that at room temperature Kc ≈ Kt [41]. However, at elevated temperature SRPP shrinks along the warp and weft axis, and hence is expected to have low compressive modulus. Charmetant et al. [33] assumed that Kc of 3D interlock textile is equal to the tensile stiffness at low strains (<1.5%), which was significantly lower than stiffness at higher strains (38 vs. 816 MPa). On the other hand, Pazmino et al. [42] warned that a large mismatch between compressive stiffness and transverse shear rigidity can cause non-physical wrinkling, as shown in Fig. 5b. To avoid this problem, some authors set Kc = 0.01Kt for non-crimp 3D textiles [42]. In the present study, two values of Kc were used in the simulation (Kc = Kt0 and Kc = 0.1Kt0), shown in Fig. 5a. As will be discussed in the results section, value that gave the best correlation with experimental results was recommended for future use.

In-plane shear

For in-plane shear, Charmetant et al. [33] proposed the following expressions for the shear invariant (Ishear) and its derivative:

$$ {\displaystyle \begin{array}{c}{\mathrm{I}}_{\mathrm{shear}}=\frac{{\mathrm{I}}_{421}}{\sqrt{{\mathrm{I}}_{41}{\mathrm{I}}_{42}}}=\sin \left(\upgamma \right)\\ {}\frac{\updelta {\mathrm{I}}_{\mathrm{shear}}}{\updelta \underset{\_}{\underset{\_}{\mathrm{C}}}}=\frac{1}{2\sqrt{{\mathrm{I}}_{41}{\mathrm{I}}_{42}}}\left(\underset{\_}{{\mathrm{M}}_1}\otimes \underset{\_}{{\mathrm{M}}_2}+\underset{\_}{{\mathrm{M}}_2}\otimes \underset{\_}{{\mathrm{M}}_1}\right)-\frac{{\mathrm{I}}_{\mathrm{shear}}}{2{\mathrm{I}}_{41}}\underset{\_}{\underset{\_}{{\mathrm{M}}_1}}-\frac{{\mathrm{I}}_{\mathrm{shear}}}{2{\mathrm{I}}_{42}}\underset{\_}{\underset{\_}{{\mathrm{M}}_2}}\end{array}} $$
(6)

where γ is the shear angle. The Cauchy stress component for in-plane shear (σ12) is thus expressed as:

$$ {\upsigma}_{12}=\frac{\updelta {\mathrm{w}}_{\mathrm{shear}}}{\updelta {\mathrm{I}}_{\mathrm{shear}}}\cos \left(\upgamma \right) $$
(7)

The experimentally measured curve is shown in Fig. 6a. This curve is atypical since there is no region of fast increase in the stress values that would correspond with the locking angle. However, from the test video it was obvious that the specimen developed wrinkles during the picture frame test, as shown in Fig. 6b. Hence, it was decided to fit the initial part of the curve, while assuming that the second half corresponds to the mixed mode shearing and wrinkling or bending behaviour. The resultant fitted curve is defined in two parts to ensure that the computed stress is negative for negative values of Ishear, as shown in Eq. (8).

$$ {\mathrm{w}}_{\mathrm{shear}}=\left\{\begin{array}{cc}-{\mathrm{K}}_{\mathrm{shear}2}.{\mathrm{I}}_{\mathrm{shear}}^3+{\mathrm{K}}_{\mathrm{shear}1}.{\mathrm{I}}_{\mathrm{shear}}^2& {I}_{shear}<0\\ {}{\mathrm{K}}_{\mathrm{shear}2}.{\mathrm{I}}_{\mathrm{shear}}^3+{\mathrm{K}}_{\mathrm{shear}2}.{\mathrm{I}}_{\mathrm{shear}}^2& {I}_{shear}>0\end{array}\right. $$
(8)
Fig. 6
figure 6

(a) Experimental and fitted in-plane shear data and (b) wrinkled picture frame specimen at the end of the test

Full size image

To check the effect of this assumption, simulations were also run using the fully fitted experimental curve, and the resultant expression for wshear is given by Eq. (9). The units for Ishear and wshear are mm/mm and MPa.

$$ {\mathrm{w}}_{\mathrm{shear}}=\left\{\begin{array}{cc}-74.{\mathrm{I}}_{\mathrm{shear}}^7-192.{\mathrm{I}}_{\mathrm{shear}}^6-193.{\mathrm{I}}_{\mathrm{shear}}^5-91.4.{\mathrm{I}}_{\mathrm{shear}}^4-18.5.{\mathrm{I}}_{\mathrm{shear}}^3+0.65.{\mathrm{I}}_{\mathrm{shear}}^2& {I}_{shear}<0\\ {}74.{\mathrm{I}}_{\mathrm{shear}}^7-192.{\mathrm{I}}_{\mathrm{shear}}^6+193.{\mathrm{I}}_{\mathrm{shear}}^5-91.4.{\mathrm{I}}_{\mathrm{shear}}^4+18.5.{\mathrm{I}}_{\mathrm{shear}}^3+0.65.{\mathrm{I}}_{\mathrm{shear}}^2& {I}_{shear}>0\end{array}\right. $$
(9)

Transverse shear

Bending stiffness is an important parameter as it dictates the shape of wrinkles [36]. However, the 3D solid elements that were used in this simulation do not have bending rigidity. Bending properties can, however, be imposed indirectly via transverse shear. The governing equations for transverse shear are defined in a similar way as for in-plane shear, hence transverse shear invariant (Itrans) and its derivative are:

$$ {\displaystyle \begin{array}{c}{\mathrm{I}}_{\mathrm{trans}}=\frac{{\mathrm{I}}_{4\upalpha 3}}{\sqrt{{\mathrm{I}}_{4\upalpha}{\mathrm{I}}_{43}}}=\sin \left({\upgamma}_{\upalpha 3}\right),\left(\upalpha =1,2\right)\\ {}\frac{\updelta {\mathrm{I}}_{\mathrm{trans}}}{\updelta \underset{\_}{\underset{\_}{\mathrm{C}}}}=\frac{1}{2\sqrt{{\mathrm{I}}_{4\upalpha}{\mathrm{I}}_{43}}}\left(\underset{\_}{{\mathrm{M}}_{\upalpha}}\otimes \underset{\_}{{\mathrm{M}}_3}+\underset{\_}{{\mathrm{M}}_3}\otimes \underset{\_}{{\mathrm{M}}_{\upalpha}}\right)-\frac{{\mathrm{I}}_{\mathrm{trans}}}{2{\mathrm{I}}_{4\upalpha}}\underset{\_}{\underset{\_}{{\mathrm{M}}_{\upalpha}}}-\frac{{\mathrm{I}}_{\mathrm{trans}}}{2{\mathrm{I}}_{43}}\underset{\_}{\underset{\_}{{\mathrm{M}}_3}},\left(\upalpha =1,2\right)\\ {}{\mathrm{w}}_{\mathrm{trans}}={\mathrm{K}}_{\mathrm{trans}}{\mathrm{I}}_{\mathrm{trans}}^2\end{array}} $$
(10)

Transverse shear behaviour at room temperature was measured indirectly by a Pierce cantilever bending test [42], as shown in Fig. 2b. An FE model was created using the same geometry and boundary conditions, and transverse shear was adjusted until the same vertical displacement was obtained. In these calculations, one element in the model thickness was used, to have an isolated influence of the transversal shear on the bending resistance. The polynomial equation that was used to represent the transverse shear behaviour is shown in Eq. (10). The same form was adopted by Pazmino et al. [42]. Based on the cantilever test conducted at room temperature, the transverse stiffness coefficient Ktrans is about 5 MPa. This value represents the upper limit of stiffness, since PP fibres will soften at high temperatures and lose their bending rigidity. The coefficient Ktrans was finally adjusted in the dome forming model to achieve the correct wrinkle geometry, as will be discussed in the results section.

Model limitations and heuristic assumptions

The use of the hyperelastic model, described above, involves a number of heuristic assumptions.:

  1. 1.

    An important assumption is that the material model parameters, identified in the tests described above and performed with a single layer of the reinforcement, can be used as parameters of 3D elements in the stack of 12 layers. This assumption is especially important for in-plane shear and bending (transverse shear).

  2. 2.

    The viscoelastic nature of the material resistance is not included in the model. The approach in [38] can be a basis for future development of a coupled visco-hyperelastic model. Certain justification for use of (hyper)elastic model is given by a recent work [43], which has compared simulations of composite forming using an elastic model on the one hand and irreversible models on the other. It has been shown that in the cases of monotonous forming the results are close in the both cases.

A rigorous verification of the validity of these assumptions and further model development will be a subject of future work.

Simulation

The finite element model was created in Abaqus 6.14. By taking advantage of the symmetry conditions, a quarter of the panel geometry was modelled. The position of the quarter panel with respect to the rigid mould as well as the imposed symmetry conditions are shown in Fig. 7. The SRPP preform was modelled using 3D explicit solid elements. Use of 3D solid elements allows full inclusion of transverse shear effects to represent bending, which is of major importance for wrinkling prediction [22]. A mesh size of 1 × 1 mm, and four elements through the thickness were used. Behaviour of SRPP was modelled using a user-defined hyperelastic material (VUMAT), which was developed by Charmetant et al. [33].

Fig. 7
figure 7

Simulation geometry and boundary conditions

Full size image

The mould was modelled as a rigid body. Two types of boundary conditions were considered. In the clamped configuration, the outer edges of the panel were fully fixed. In the case with spring clamping, boundary conditions in the model were simplified by omitting the springs. This simplification is based on the assumption that springs offer low resistance, and the preform can slide freely into the mould.

Results and discussion

The distribution of the local shear angles of the fabric for a hemispherical draping is well defined by the kinematics of the draping and is not much influenced by the details of the constitutive mechanical model. Therefore the focus in the discussion of the results will be on the wrinkling behaviour, which is strongly influenced by the details of the material behaviour and by the relation between different components of the material resistance to the deformation [22].

Simulation and test results for the (presumably) fully clamped specimen are shown in Fig. 8. The stiffness parameters used in this simulation are summarized in Table 1. Location of some of the wrinkles is indicated by the red circles. While minor wrinkles are present in both experimental and simulation results, their location is different. In the case of the experimental samples, the edges came loose from the clamps as indicated by the arrow in Fig. 8a. Hence, it can be postulated that the loss of tension in the middle of the edge permitted wrinkle formation in the highly sheared region. For future tests, the clamping fixture needs to be improved to achieve better clamping. Even if the clamping in the present experiments is not ideal, the results show sensitivity of the qualitative wrinkling characteristics to the boundary conditions.

Fig. 8
figure 8

(a) Experimental and (b) simulation results of fully clamped preforms

Full size image

Comparison between the experimental and simulation results for spring-clamping is shown in Fig. 9 and Fig. 10. The stiffness parameters used in this simulation are summarized in Table 1. Experimental results are slightly non-symmetrical because of the difficulties associated with the alignment of the panel when spring clamping was used. Both experiments and calculations (see Fig. 9a and Fig. 10a) show that there are no wrinkles at the early stages of deformation. Once the material is deformed by 2 cm (see Fig. 9b and Fig. 10b), wrinkles all around the circumference begin to appear. When 4 cm of deformation is attained (see Fig. 9c and Fig. 10c), clear folds can be observed at the four sides. Overall, good qualitative correlation between experimental and modelling results is observed.

Fig. 9
figure 9

Experimental results of the intermediate forming stages of SRPP, spring clamping: (a) 1 cm high dome, (b) 2 cm high dome and (c) 4 cm high dome

Full size image
Fig. 10
figure 10

Simulation results of the intermediate forming stages of SRPP, spring clamping: (a) 1 cm high dome, (b) 2 cm high dome and (c) 4 cm high dome

Full size image

Effect of the shear and compressive stiffness on wrinkling was also analysed to assess the significance of the assumptions. Images depicting the in-plane shear angle distribution for the two clamping conditions are shown in Fig. 11. In case of spring-clamping, in-plane shear strains were low (Ishear ≤ 0.16). In this range, the fitted curves essentially overlap, refer to Fig. 6a, and hence no difference was expected. In case of full clamping, the maximum shear angle was high (≈ 200) and in the range of the imposed locking angle. Nonetheless, no wrinkles were predicted in that region regardless of which fitted curve was used. This can be explained by the high elongation strains created by the boundary conditions. Overall, in-plane shear stiffness had minimal effect on the wrinkles observed in both clamping cases. In the future it would be interesting to measure the shear angle of the formed pieces using a photogrammetry technique to advance the present qualitative comparison to quantitative level.

Fig. 11
figure 11

In-plane shear angle in simulations with (a) spring-clamping and (b) edge clamping

Full size image

The effect of the compressive and transverse shear stiffness on the simulation results is shown in Fig. 12. Examination of the left-top image (Ktrans = 0.1 and Kc = 89 MPa) reveals presence of non-physical wrinkles that were anticipated by Pazmino et al. [42] when there is a large mismatch between these two properties. When compressive modulus is decreased (moving to the right in figure), the shape of the wrinkles becomes more realistic. However, if it is decreased too much, small wrinkles smoothen out and disappear. An alternative approach, would be to keep the same compressive modulus and to instead increase the shear modulus (moving down in the figure), while keeping in mind that Ktrans = 5 MPa is the upper limit. The optimal combination of Kc and Ktrans was chosen by comparing the simulation result in Fig. 12 to the experimental results in Fig. 9c.

Fig. 12
figure 12

Effect of compressive and transverse shear modulus on wrinkle development in spring-clamped SRPP panel. All units are in MPa. The selected combination of Kc and Ktrans is shown in bold

Full size image

Conclusions

The parameters of the Boisse-Charmetant hyperelastic material model are identified for SRPP and are validated in comparison with experiment.

The parameters of the hyperelastic law are based on the experimental data from tensile and picture frame tests at the forming temperature. Flexural or transverse shear stiffness was adjusted to capture the correct wrinkle shape. To further improve the model, this property will need to be measured experimentally. Another improvement in the model can be the inclusion of the interaction of the preform plies. Overall, the deformation of the preform during the thermoforming process was captured properly by the model. Additional improvements can be achieved by incorporating the effect of the spring-clamping into the model. It would be interesting to further extend this model to hybrid composites, which have a broader spectrum of applications.

The comparison between the simulated and experimental wrinkling pattern shows that the identified constitutive model for SRPP draping represents the behaviour of the deformed sheet adequately and can be used for analysis of the influence of the process design choices (for example, the blank holder organisation) on the quality of the final part. The results of the local reinforcement deformation can be further transferred to the stress analysis of the consolidated part and will influence the stress-strain allowances based design.