Channel coordination and profit distribution in a three-echelon supply chain considering social responsibility and product returns

Abstract

By developing markets and increasing world competition, today, companies' success is not only related to their performance but also the interaction and performance of their entire supply chain and distribution. In the supply chain strategy, operational functions, such as planning, purchasing, and financial affairs are considered all together. In the meantime, the coordination between manufacturers, distributors, and retailers is of great importance. Coordination through cooperation between distribution channels is necessary because of their potential for realizing significant profits. This study presents a mathematical model for a three-echelon supply chain. In this model, the effect of the strategy of returning goods on the amount of profit as well as on the optimal amount of wholesale-retail prices is determined. The three-echelon supply chain is represented by manufacturers, distributors, and retailers. In this study, social responsibility is considered in the model and channel coordination in this three-echelon supply chain is also considered. Hence, in addition to maximizing total profit, social responsibility is also taken into consideration. Channel coordination and optimization of the supply chain are considered in both centralized and decentralized modes. In the results, it was found that the quality of products in a consistent manner is always at a higher level than in a decentralized state. Also, it was found that if decisions are made on a coordinated basis, customers who return their goods will benefit from higher earnings than decentralized. Therefore, this model helps the firms to find out the structure, which has a better performance in terms of product quality, return policy, and social responsibility impact while reducing conflict between supply chain members. Also, through a coordinated system, firms can enhance the quality of products and return policy, which in turn improves customer satisfaction and profits.

1 Introduction

In today’s market wherein firms are competing fiercely, each firm aims to enhance its profit using different tools and methods. Applying coordination methods can be considered as one of the most effective methods in an increment of profits of supply chain members and the whole supply chain. Coordination between supply chain participants can be obtained through designing an appropriate contract between members of the supply chain such that they decide on optimal centralized decisions instead of decentralized ones. The primary objective of the coordination contract is to instigate supply chain members to make their decisions coherently. To decline channel conflict between supply chain decision-makers, different kinds of side-payment contracts have been applied by the previous scholars. Two-part tariff (Modak et al., 2016), sales rebate (Wong et al., 2009), quantity discount (Li & Liu, 2006), buy-back (Ding & Chen, 2008), and revenue-sharing (Cachon & Lariviere, 2005) are examples of payment contracts.

Corporate social responsibility (CSR) is an evolving concept, which indicates that firms are responsible to their stakeholders for the effect of its measures and decisions on society as well as the environment. Thus, as far as CSR is concerned, the firm is liable for the variety of expectations such as social, environmental, health, ethical expectations placed by society (Carroll & Buchholtz, 2014). Over time and with the emergence of the global supply chain, CSR has been becoming growingly popular so much so that it has turned into a deciding factor for making a purchase decision, so it cannot be disregarded by the organization anymore. The result of an empirical study indicates that consumers are inclined to pay a greater price for products characterized by CSR attributes (Auger et al., 2003; Trudel & Cotte, 2009), leading to the creation of shareholder value. As a result, CSR helps companies with the improvement of their competitiveness through cost-saving. Therefore, in today’s market, a lot of firms are voluntarily employing CSR to enhance their corporate image (Fombrun, 2001, 2005), control their risk (Fombrun et al., 2000; Husted, 2005), build customer royalty (Bhattacharya & Sen, 2004; Sen & Bhattacharya, 2001), to name but a few. Consequently, many prestigious companies such as Wal-Mart, Nike, Gap, and Adidas have applied a CSR strategy in their corporate through a series of codes of conduct (Amaeshi et al., 2008).

As an important aspect of product features, the quality of products significantly influences the customers' preferences and subsequently market demand. Therefore, the quality of products plays a strategic role in the supply chain competitiveness, and consequently, this factor remarkably affects the marketing strategies. Apart from the market demand, the quality of products correlates with the return quantity. In other words, the low quality of products results in consumer dissatisfaction and subsequently a lot of returns. On the other hand, when products have high quality, the consumers are satisfied with the quality of products, and consequently, the return quantity decreases. Products that have a high quality merit high sales price, because the higher price of products indicates that products are of higher quality (Kirmani & Rao, 2000; Whitfield & Duffy, 2013). Nevertheless, a high price of products results in falling market demand, in particular when market demand is highly dependent on the price of the product. On the other hand, when market demand does not depend on price, the firm tries to enhance the quality, and therefore the price of the product. Thus, there is a trade-off between the price and quality of products affecting the pricing and quality investment strategies of supply chain participants.

A centralized, decentralized model, based on the Stackelberg model, and a coordinated model are formulated to address the below questions regarding optimal solutions in different models.

• What are the optimal quality level, wholesale, selling, and buy-back prices in a CSR supply chain?

• How does the responsibility of the supply chain affect wholesale price, selling price, quality level, and buy-back price?

• How does the manufacturer make a reaction against the price-quality trade-off?

• What is the effect of the return policy on optimal quality and price solutions?

• How can a contract be designed to eliminate channel conflict between participants of the supply chain and increase their profits?

This paper aims to incorporate return policies into a socially responsible three-level supply chain by considering a channel coordination mechanism. In a manufacturer-led supply chain, contract bargaining is applied to eliminate the channel friction and share surplus profit among supply chain participants. Unlike, most previous works, which considered CSR and channel coordination issues separately, this paper considers CSR and channel coordination issues at the same time. Recently, Panda et al. (2015) explored the channel coordination issue in a socially responsible supply chain. However, they ignored the return policy and the effect of the quality of products on a demand function. Therefore, this paper develops the work of Panda et al. (2015) by considering the return policy and the quality of products. Also, although few studies in the literature have considered the effect of the return policy on a demand function, this factor is taken into consideration in this paper.

The rest of this study is outlined as follows. Section 2 reviews the previous works. In Sect. 3, model formulation is presented. In Sect. 4, we analyze the behavior of the model regarding the change of different parameters. Finally, concluding remarks are provided in Sect. 5.

2 Literature review

By reviewing the literature, it is noted that there are a lot of two-level supply chain models exploring coordination contracts for the elimination of double marginalization. However, a limited number of papers have been developed for solving channel conflict in a three-level supply chain. Elimination of channel conflict through coordination contracts is more difficult in a three-level supply chain than that in a two-level supply chain. By increasing the levels of a supply chain, designing a coordination contract gets more complex as a result of the increment of the solution space dimension. By considering a quantity discount contract, Munson and Rosenblatt (2001) explored the coordination issue in a multi-level supply chain containing a manufacturer, a retailer, and a supplier. Jaber et al. (2005) developed the previous work in terms of discount-dependent demand function and profit-sharing. Jaber and Goyal (2008) discussed order quantity contract to coordinate a multi-echelon supply chain which is consist of multiple suppliers and buyers and a single manufacturer. With consideration of the buy-back contract, Ding and Chen (2008) achieved a coordinated three-tire supply chain in which the members of the supply chain divide their profits freely. Panda (2014) coordinated a three-level supply chain including disposal cost-sharing for perishable items. They assumed that there is a coalition between the distributor and the manufacturer indicating that the disposal cost of the retailer should be divided between them. Using a quantity discount contract, Modak et al. (2014) developed a coordinated dual-channel supply chain by considering a CSR strategy. With consideration of a quality and marketing effort, Ma et al. (2013) designed a new contract for the coordination of the manufacturer and the retailer. Recently, Choi et al. (2013) used two-tariff and new revenue-sharing contracts to achieve coordination in a closed-loop supply chain (CLSC) by considering different formats for supply chain leadership. By considering different channel formats in CLSC, Taleizadeh et al. (2018a) optimized pricing, quality, effort decisions in a three-level supply chain. By considering a price and marketing-dependent demand function, Zerang et al. (2018) studied pricing decisions in a closed-loop supply chain under both centralized and decentralized decisions.

As far as an individual firm is concerned, the practice of CSR has a rich history in the context of the supply chain. However, the application of CSR in the whole supply chain has been emerging in recent years. By introducing social issues into the traditional economy, Murphy and Poist (2002) explored the responsibility approach in a supply chain characterized by CSR. Carter and Jennings (2004) did a case study research to explore the role of CSR in decisions made in a supply chain. Cruz (2008) explored the CSR issue in a dynamic supply chain where supply chain participants act based on multi-criteria decision-making. Hsueh and Chang (2008) applied CSR strategy in a three-level supply chain for coordination of the supply chain. Their results indicate that using CSR benefits the entire supply chain. Savaskan et al. (2004) extended the concept of CSR into the closed-loop supply chain. Using quantity discount, Panda et al. (2016) coordinated a two-level supply chain wherein either the retailer or the manufacturer employs a CSR strategy. Ni et al. (2010) examined the CSR issue in a two-echelon supply chain. They applied a wholesale price contract to share the CSR cost between upstream and downstream members of the supply chain. Ni and Li (2012) extended a CSR two-level supply chain by considering separate CSR cost for each supply chain member. They developed a game theory model to analyze the impact of strategic interactions between supply chain participants. Crifo et al. (2016) analyzed the French data set to investigate the impact of different CSR approaches on the economic performance of the firm. Then, regarding the quality and quantity of CSR, they compared the results. By designing a new revenue-sharing contract, Hsueh (2014) coordinated a two-echelon socially responsible supply chain. Recently, Panda et al. (2015) interestedly studied channel coordination, and CSR issues in a supply chain. They assumed the CSR cost is imposed on the manufacturer only. However, in their paper, they did not consider the return policy.

Modak et al. (2019a) considered social work donation to practice CSR in a two-level closed-loop supply chain. They investigated a centralized and three-decentralized scenarios two-part tariff contract to mitigate channel conflict between a manufacturer and a retailer. Unlike our model, they did not consider a return policy and quality considerations. Recently, Modak and Kelle (2021) applied a social work donation and a recycling policy to practice social responsibility in the CLSC. They incorporated carbon emissions tax and obtained the optimal prices, investment in recycling, the amount of donation, and replenishment. Unlike our paper, they did not consider the quality factor and coordination mechanisms to mitigate channel conflict. Also, in the same direction, Subramanian and Gunasekaran (2015), Ding et al. (2015), and Chen and Slotnick (2015) did worthwhile research studies. Azevedo et al. (2017) examined the sustainability of individual firms and their corresponding upstream firms by considering economic, social, and environmental aspects. Hosseini-Motlagh et al. (2020) investigated the coordination mechanism for acquisition price by incorporating CSR in a closed-loop supply chain. Gang et al. (2020) discussed CSR in the context of the global supply chain consisting of Chinese suppliers and multinational companies. Modak et al. (2019b) developed a three-echelon CLSC consisting of a manufacturer, several retailers, and a third party for collecting used products. They examined the relationship between CSR policy and product recycling under the manufacturer Stackelberg model and indicated that considering the CSR policy, threshold-based recycling decision is optimal. Unlike our model, they did not consider the quality level and buy-back price decisions. Also, in this paper, a discount contract is applied for mitigating channel conflict, which was not considered in their paper.

Panda et al. (2017) investigated a socially responsible two-echelon CLSC by considering the recycling policy and examined CSR through recycling practice. To resolve the channel friction in the decentralized model, they considered a revenue-sharing contract. Unlike the work of Panda et al. (2017), in this paper, we consider a three-echelon CLSC consisting of a manufacturer, a distributor, and a retailer. Also, in this paper, we incorporate the quality level of products in a demand function and investigate the impact of CSR and the return policy on the optimal quality as well as the price of the products. Also, Modak et al. (2019b) considered a return policy as a given parameter, while in this paper, we aim to optimize the rate of refund as a decision variable. Moreover, this paper develops a kind of discount contract between a manufacturer, a distributor, and a retailer to attain channel coordination, which was not investigated by Panda et al. (2017).

As an important factor in the determination of consumers' preferences, quality issues have earned incredible attention in couples of recent years. Singer et al. (2003) optimized the supplier's and retailer's quality investment in a distribution channel of disposable items. By considering three kinds of contracts, Gurnani and Erkoc (2008) extended a pricing model in a decentralized distribution channel where market demand associates with the selling effort and quality. Based on four game theory models, Hsieh and Liu (2010) optimized the best investment strategy in quality improvement with different levels of available information. Considering cooperation and non-cooperation in a dynamic supply chain, De Giovanni (2011) derived the optimal pricing, advertising, and quality investment decisions. In a just-in-time setting, Diaby et al. (2013) developed a multi-product optimization model of setup time reduction and quality improvement. Yu and Ma (2013) explored how different sequences of decision-making can affect pricing and quality improvement decisions in a two-tire supply chain wherein demand is uncertain. In recent years, Moshtagh and Taleizadeh (2017) developed a production/reproduction model in an imperfect closed-loop supply chain in which produced and reproduced items are not perceived equally, and returned items are of variable qualities. Also, Taleizadeh and Moshtagh (2019) extended a four-level CLSC by considering a quality-dependent return, imperfect production, and different qualities of produces and reproduced items. Maiti and Giri (2015) optimized pricing and quality-level decisions under five different channel power structures of three-tire CLS. Recently, Taleizadeh et al. (2017) developed a pricing model to optimize selling and buyback prices, quality level, and efforts based on different game models. By considering a price- and quality-dependent demand, Modak et al. (2018) developed a pricing model in a two-level CLSC. They examined different alternatives for collection activities and showed that collecting products using third-party logistics is disadvantageous. Based on a collection effort threshold, they determined the optimal solutions and applied two strategies to overcome channel conflict. It should be mentioned that, unlike our model, they did not consider the CSR policy and coordination mechanisms for the return policy. Zhalechian et al. (2017) considered a multi-objective hub location problem with economic, responsiveness and social issues under uncertainty. In their model, they considered an M/M/c queuing system and social responsibility measures. To solve the model, they proposed the possibilistic programming, fuzzy multiobjective programming and self-adaptive differential evolution algorithm.

In addition to the quality of products that affect the return quantity, buy-back price and return policy exert significant influence on return quantity. Most works in the literature studying product return investigated a business to business (B2C) return policies that mainly occur between a retailer and a manufacturer. They primarily studied the supply chain coordination obtained through the return contract (Cai et al., 2009; Emmons & Gilbert, 1998; Pasternack, 1985; Webster & Weng, 2000; Yao et al., 2005). Few works in the literature studied return strategies between a business and a customer. The previous researches mainly focused on the impact of return policies on consumers' reactions in a general sense. However, the buyback price of the products can directly affect the return quantity of the products. In a direct sales model, Mukhopadhyay and Setoputro (2004) examined the effect of return strategies on customers' decisions regarding return and buying. However, they disregard the impact of product quality. They further developed a multi-stage model of pricing in an online selling setting to investigate the optimal prices, quality level, and return policy (Mukhopadhyay & Setaputra, 2007). Yu and Wang (2008) optimized marketing and return policies in a direct selling framework. By considering an online-selling model, Bonifield et al. (2010) studied the correlation between return policies and quality level. Li et al. (2013) incorporated a return policy in a direct selling system to investigate the optimal price and quality level. Taleizadeh et al. (2018b) studied a green chain with both coordination and pricing strategies. Keyvanshokooh et al. (2013) considered a multi-period, multi-product, multi-echelon supply chain with forward/reverse logistics and returned products. They developed a dynamic pricing approach to find the acquisition price for the products. Fadaei et al. (2019) considered the partial and full coordination in serial N-echelon supply chains with a profit-sharing contract and uncertain demand.

On the whole, reviewing the highlighted literature review, we can notice that there is no work in the literature considering the CSR, channel coordination, bargaining, return policy, and quality factor jointly. More specifically, this paper contributes to the literature by developing the work of Panda et al. (2015) in the following ways:

• 1. They did not consider the return policy in their paper, although in today's market, the possibility of returning products by customers plays an important role in the competitiveness of a firm and can be considered as an inseparable part of a supply chain.

• 2. In this paper, the effect of the return policy is incorporated in a demand function.

• 3. Despite the undeniable effect of the quality level of product on market demand, Panda et al. (2015) ignored this very important factor. Therefore, we discuss the effect of the quality level of products by considering its effect on both market demand and return quantity functions in our research.

Also, this paper contributes to the work of Panda et al. (2017) by considering a three-level supply chain and using a discount contract to mitigate channel conflict between three supply chain members. Furthermore, unlike Panda et al. (2017), this work optimizes the quality of the products and refund rates, which was considered as a parameter in Panda et al. (2017).

3 Model formulation

This chapter deals with defining the problem, after introducing the notation used in mathematical models and using the game theory strategy to obtain optimal decision variables followed by developing mathematical models.

3.1 Notations

The symbols and signs used in this study including parameters, decision variables, and dependent variables, are presented below.

Parameters
$c$	Cost of producing the final products imposed on the producer
$\alpha$	Basic market demand for produced products
$\beta$	Basic market demand for produced products
$\delta$	Sensitivity of demand to the quality of produced goods
$\gamma$	Sensitivity of the demand to the refund of a returning good
$\phi$	Number of basic returning goods
$\varphi$	Sensitivity of the number of returning products to the refund
$\upsilon$	Sensitivity of the number of returning products to the quality of goods
$\lambda$	Cost of quality improvement
$\theta$	CSR coefficient
Decision variables
$p$	Sale price of produced goods
$\omega _{d}$	Distributor wholesale price
$\omega _{m}$	Producer wholesale price
$q$	Quality Level of produced goods
$r$	Rate of refund
$p_{C}$	Sale price of goods produced in a centralized system
$q_{C}$	Quality level of goods produced in a centralized system
$r_{C}$	Rate of returning goods refund in a centralized system
Dependent variables
$PP_{c}$	Net profit in a centralized decision-making system
$CS_{c}$	Consumers’ surplus in a centralized decision-making system
$PP_{{ds}}$	Net profit in a decentralized decision-making system
$\pi _{C}$	Total profit function in a centralized decision-making system
$\pi _{r}$	Retailer’s profit function in a decentralized decision-making system
$\pi _{d}$	Distributer’s profit function in a decentralized decision-making system
$\pi _{m}$	Producer’s profit function in a decentralized decision-making system
$\mu$	Rate of discount at the manufacturer’s wholesale price
$\bar{\mu }$	Maximum discount rate at the manufacturer’s wholesale price
$\underline{\mu }$	Minimum discounts rate at manufacturer’s wholesale prices
$\mu ^{b}$	Optimal discount rate at the manufacturer’s wholesale price under the coordinated decision mode
$\rho$	Discount rate at distributor’s wholesale price
$\bar{\rho }$	Maximum discount rate at the distributor’s wholesale price
$\underline{\rho }$	Minimum discount rate at the distributor’s wholesale price
$\rho ^{b}$	Optimal discount rate at the distributor’s wholesale price under coordinated decision-making mode

3.2 Assumptions

To model the described problem, the following assumptions were considered.

Assumption 1

The demand of customers referring to the retailer for supplying goods follows a linear function, relative to the price of the final product, the quality of the products, and the sale price of the returned goods, and it is written by:

$$D = \alpha - \beta p + \delta q + \gamma r$$

(1)

where $\alpha ,\beta ,\delta ,\gamma \ge 0$. In this equation, $\alpha$ is the basic market demand for this product, $\beta$ is the customer’s sensitivity to the price of this product, $\delta$ is the degree of sensitivity of demand to the quality of products, and $\gamma$ is the sensitivity parameter for the refund of a returned item. Assuming that the demand function must be non-negative, then we have:

$$p \in \left( {0,\left( {\alpha + \delta q + \gamma r} \right)/\beta } \right).$$

Assumption 2

Moreover, the return value (R) is a linear function dependent on the purchase price of the returned goods and product quality, which is presented by.

$$R = \phi + \varphi r - \upsilon q$$

(2)

where $\varphi ,\upsilon$. In this equation, $\phi$ is the basic return value for this product, which is independent of the amount of the returned goods refund and the product quality, $\varphi$ is the sensitivity of the number of returning products to the refund (the higher the sale price of a retrogressive product, the more customers are willing to return the purchased goods), and $\upsilon$ is the sensitivity of the number of returned goods to the quality of products. The higher the quality of the products, the fewer customers willing to return them.

Assumption 3

Deficiency is not allowed at any level.

Assumption 4

The delivery time from producer to the distributor and from the distributor to the retailer was considered zero.

Assumption 5

The demand for manufactured goods is considered fixed and constant.

3.3 Modeling

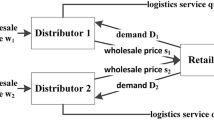
Consider a three-level supply chain consisting of a manufacturer, a distributor, and a retailer. The producer produces goods with the quality of $q$ and a cost of $c$ and sells them to a distributor at a wholesale price of $\omega _{m}$. Then, the distributor sells these products to the retailer at a wholesale price of $\omega _{d}$, and ultimately, the retailer meets customer demand by selling these products at the final price of $p$. In this model, the manufacturer promises to customers that if they are dissatisfied with the quality of the products, they can return them at any time and receive r amount of money as a refund $0 \le r \le p$. If $r = 0$, it means that the retailer does not pay any money for returning the goods from the customers, and if $r = p$, it means that customers receive the refund at the same purchased price.

In this model, the manufacturer tries to increase the quality of the product by controlling the failure rate at the production stage and reducing defective items. The greater the cost of increasing the quality of products, the higher the quality of the goods will be. Hence, similar to the studies of Hosseini-Motlagh et al. (2020) and Gang et al. (2020), in this thesis, it was assumed that the costs of increasing the quality follow the convex function of $C = \lambda q^{2}$.

As mentioned, this strategy model is called CSR. Most of the world’s leading and dominant brands and companies are struggling with extreme pressure to manage a socially responsible supply chain. A common strategy to reduce these pressures is to provide a set of behavioral codes by the core company for its business partners. As a result, other members of the supply chain are involved in the CSR strategy, while the producer is the main member of the supply chain.

Therefore, in this research, it is assumed that the producer is investing based on the CSR strategy and adjusts the CSR according to the performance of the channel. The cost of CSR is divided among the supply chain members through transitional pricing. In this thesis, the impact of CSR is modeled based on the consumer's surplus.

When a company employs CSR regardless of the competing companies, it improves its goodwill, since it largely indicates the intention to increase stakeholder satisfaction. As a result, customers are willing to pay a higher price than the base price for the products. Consequently, similar to the study of Panda et al. (2015), we consider consumer surplus in the profit function as an effect of the CSR strategy. The consumer’s surplus is the difference between the maximum price the consumer is willing to pay and the market price that the customer pays. Thus, the consumer surplus is written by:

$$\int_{{p_{{\min }} }}^{{p_{{\max }} }} {Ddp = } \int_{{\left( {\alpha + \delta q + \gamma r - D} \right)/\beta }}^{{\left( {\alpha + \delta q + \gamma r} \right)/\beta }} {\left( {\alpha + \delta q + \gamma r} \right)dp = } \frac{{D^{2} }}{{2\beta }}$$

(3)

If $\theta \in \left[ {0,1} \right]$ is a ratio of CSR related to producer social responsibility, then the producer puts $\theta D^{2} /\beta$ as a consumer’s surplus in the profit function. $\theta = 0$ means that the producer maximizes net profit, indicating that he/she maximizes the total welfare. In this research, since the producer is socially responsible, it is assumed that his/her profit function includes net profit from selling the products to the distributor and the consumer’s surplus obtained by using the CSR strategy.

3.4 Centralized decision-making system

Assume that all members of the channel are willing to cooperate and make a decision. Therefore, under this system, there will be only one marketing channel, in which a product category is produced and sold to customers at a price of $p_{C}$. Moreover, in this system, so-called the CSR strategy is used. Thus, the surplus of the consumer from the shareholders is accumulated in the channel and is calculated in the total profit function. The total profit function in the centralized system is written by:

$$\pi _{C} = \left( {p_{C} - c} \right)\left( {\alpha - \beta p_{C} + \delta q_{C} + \gamma r_{C} } \right) - \lambda q^{2} - r\left( {\phi + \varphi r_{C} - \upsilon q_{C} } \right) + \frac{\theta }{{2\beta }}\left( {\alpha - \beta p_{C} + \delta q_{C} + \gamma r_{C} } \right)^{2}$$

(4)

Proposition 1

When the following conditions are established, $\pi _{C}$ in $p_{C}$, $q_{C}$, and $r_{C}$ is concave, and there is a single optimal solution for the single decision-maker.

$$\theta < 2 - \max \left\{ {\frac{{\delta ^{2} }}{{2\beta \lambda }},\frac{{2\delta ^{2} \varphi + 2\delta \gamma \upsilon + 2\gamma ^{2} \lambda }}{{\beta \left( {4\varphi \lambda - \upsilon ^{2} } \right)}}} \right\}$$

(5)

By solving the first derivative of the $\pi _{C}$ function for $p_{C}$, $q_{C}$, and $r_{C}$, the equilibrium optimal response for this centralized system is obtained by:

$$p_{C}^{*} = \frac{{\left[ {\alpha \left( {1 - \theta } \right) + \beta c} \right]\left( {\upsilon ^{2} - 4\varphi \lambda } \right) + \phi \left( {1 - \theta } \right)\left( {\delta \upsilon + 2\gamma \lambda } \right) + 2c\left( {\delta ^{2} \varphi + \gamma ^{2} \lambda + \delta \gamma \upsilon } \right)}}{{\beta \left( {2 - \theta } \right)\left( {\upsilon ^{2} - 4\varphi \lambda } \right) + 2\delta ^{2} \varphi + 2\gamma ^{2} \lambda + 2\delta \gamma \upsilon }}$$

(6)

$$q_{C}^{*} = \frac{{\delta \left[ {\phi \gamma - 2\varphi \left( {\alpha - \beta c} \right)} \right] + \upsilon \left[ {\beta \phi \left( {2 - \theta } \right) - \gamma \left( {\alpha - \beta c} \right)} \right]}}{{\beta \left( {2 - \theta } \right)\left( {\upsilon ^{2} - 4\varphi \lambda } \right) + 2\delta ^{2} \varphi + 2\gamma ^{2} \lambda + 2\delta \gamma \upsilon }}$$

(7)

$$r_{C}^{*} = \frac{{\left( {\beta c - \alpha } \right)\left( {\delta \upsilon + 2\gamma \lambda } \right) + 2\beta \phi \lambda \left( {2 - \theta } \right) - \delta ^{2} \phi }}{{\beta \left( {2 - \theta } \right)\left( {\upsilon ^{2} - 4\varphi \lambda } \right) + 2\delta ^{2} \varphi + 2\gamma ^{2} \lambda + 2\delta \gamma \upsilon }}$$

(8)

Furthermore, by substituting the optimal values of $p_{C}$, $q_{C}$, and $r_{C}$ in $\pi _{C}$ the optimal total profit rate is obtained.

3.5 Decentralized decision making-system

In a decentralized supply chain, unlike the centralized supply chain, where a single decision-maker exists, each member of the supply chain makes optimal decisions. When members of the channel act independently and optimize their individual goals, it is essentially a non-cooperative decision-making process. Here, a decentralized system was developed that the Stackelberg game is used to solve. The Stackelberg game is a kind of strategic game, in which at least one member of the supply chain is the frontrunner (leader), who makes the decisions based on optimal decisions of the other members of the chain, and the rest of the members are identified as followers.

In this research, a Stackelberg-producer game is considered in which the distributor is the first follower of the producer and the retailer is a follower of the distributor. This game is a kind of sequential game in which the manufacturer applies his/her optimal strategy to the distributor. Accordingly, the distributor finds the optimal strategy and communicates with the retailer.

Ultimately, based on the distributor’s optimal strategy, the retailer determines its optimal strategy. The decision-making process consists of two Stackelberg games, one between the producer and the distributor and the other between the distributor and the retailer. In this study, to obtain the optimal solutions for these two games, the retrogressive inference method is used.

The profit functions of the supply chain members are expressed by:

$$\pi _{m} = \left( {\omega _{m} - c} \right)\left( {\alpha - \beta p + \delta q + \gamma r} \right) - \lambda q^{2}$$

(9)

$$\pi _{d} = \left( {\omega _{d} - \omega _{m} } \right)\left( {\alpha - \beta p + \delta q + \gamma r} \right)$$

(10)

$$\pi _{r} = \left( {p - \omega _{d} } \right)\left( {\alpha - \beta p + \delta q + \gamma r} \right) - r\left( {\phi + \varphi r - \upsilon q} \right)$$

(11)

Therefore, the total profit of the producer is written by:

$$v_{m} = \pi _{m} + \frac{\theta }{{2\beta }}\left( {\alpha - \beta p + \delta q + \gamma r} \right)^{2}$$

(12)

As mentioned, in this research, a retrogressive method is used to solve the Stackelberg model. Therefore, first, the retailer’s optimal decisions (which are followed by the second) are obtained.

• Retailer’s optimal decisions

By considering the optimal values related to the distributor and producer as a parameter, the retailer makes the optimal decisions as follows:

Proposition 2

When the condition (13) exists, $\pi _{r}$ is concave in $p$ and $r$, and there is a single optimal answer for the retailer.

$$\varphi \ge \frac{{\gamma ^{2} }}{{4\beta }}$$

(13)

By solving the first-order conditions, $\frac{{\partial \pi _{r} }}{{\partial p}} = 0$ and $\frac{{\partial \pi _{r} }}{{\partial r}} = 0$, the retailer’s optimal decisions are obtained by:

$$p^{*} = \frac{{2\alpha \varphi - \phi \gamma + \omega _{d} \left( {2\beta \varphi - \gamma ^{2} } \right) + q\left( {2\delta \varphi + \gamma \upsilon } \right)}}{{4\beta \varphi - \gamma ^{2} }}$$

(14)

$$r^{*} = \frac{{\alpha \gamma - 2\beta \phi + q\left( {\delta \gamma + 2\beta \upsilon } \right) - \beta \gamma \omega _{d} }}{{4\beta \varphi - \gamma ^{2} }}$$

(15)

• Distributor’s optimal decisions

After obtaining the retailer’s optimal decisions, substituting the optimal solutions of $p^{*}$ and $r^{*}$ in the distributor’s profit function ($\pi _{d}$) the optimal solution of the distributor is obtained.

Proposition 3

Existing condition (16), $\pi _{d}$ is concave in $\omega _{d}$, and there is a single optimal solution for the distributor.

$$\varphi \ge \frac{{\gamma ^{2} }}{{4\beta }}$$

(16)

By solving $\frac{{\partial \pi _{d} }}{{\partial \omega _{d} }} = 0$, the optimal value of $\omega _{d}$ is obtained by:

$$\omega _{d}^{*} = \frac{{2\alpha \varphi - \phi \gamma + q\left( {2\delta \varphi + \gamma \upsilon } \right) + 2\beta \varphi \omega _{m} }}{{4\beta \varphi }}$$

(17)

• Producer’s optimal decisions

After obtaining optimal feedback from retailers and distributors and placing them in the producer's profit function ($v_{m}$), we obtain the producer's optimal decisions.

Proposition 4

Once the condition (18) exists, $\pi _{m}$ is concave in $\omega _{m}$ and $q$ and there is a single optimal decision for the producer.

$$\phi < \frac{{\left( {\alpha - \beta c} \right)\left[ { - 2\delta ^{2} \varphi \theta \left( {2\delta \varphi + \gamma \upsilon } \right) + 4\beta \varphi \gamma \lambda \upsilon } \right] + 2\beta c\delta \left( {2\delta \varphi + \gamma \upsilon } \right)^{2} - 8\beta \delta \varphi ^{2} \lambda \left[ {9\beta c + \alpha \left( {7 - 2\theta } \right)} \right] + 16\delta \varphi \gamma ^{2} \lambda }}{{2\gamma ^{2} \lambda \left( {4\delta \gamma + \beta \upsilon } \right) - \delta ^{2} \gamma \theta \left( {2\delta \varphi + \gamma \upsilon } \right) - 4\beta \delta \varphi \gamma \lambda \left( {7 - 2\theta } \right)}}$$

(18)

Therefore, by solving the first-order conditions, $\frac{{\partial v_{m} }}{{\partial \omega _{m} }} = 0$ and $\frac{{\partial v_{m} }}{{\partial q}} = 0$ the producer’s optimal decisions are written as follows:

$$\omega _{m}^{*} = \frac{{8\varphi \lambda \left( {\alpha + \beta c} \right)\left( {\gamma ^{2} - 4\beta \varphi } \right) + 4\beta \phi \varphi \gamma \lambda \left( {4 - \theta } \right) - 8\beta \varphi ^{2} \lambda \left[ {4\left( {\alpha + \beta c} \right) - \alpha \theta } \right] + \beta c\left( {2\delta \varphi + \gamma \upsilon } \right)^{2} - 4\phi \gamma ^{3} \lambda }}{{\beta \left[ {16\varphi \gamma ^{2} \lambda + \left( {2\delta \varphi + \gamma \upsilon } \right)^{2} - 8\beta \varphi ^{2} \lambda \left( {8 - \theta } \right)} \right]}}$$

(19)

$$q^{*} = \frac{{\left( {2\delta \varphi + \gamma \upsilon } \right)\left[ {\phi \gamma - 2\varphi \left( {\alpha - \beta c} \right)} \right]}}{{\beta \left[ {16\varphi \gamma ^{2} \lambda + \left( {2\delta \varphi + \gamma \upsilon } \right)^{2} - 8\beta \varphi ^{2} \lambda \left( {8 - \theta } \right)} \right]}}$$

(20)

Moreover, by placing $\omega _{m}^{*}$ and $q^{*}$ in Eqs. (14), (15) and (17) the optimal values of $p^{*}$, $r^{*}$, and $\omega _{d}^{*}$ are obtained by:

$$p^{*} = \frac{{4\varphi \gamma ^{2} \lambda \left( {3\alpha + \beta c} \right) - 8\beta \varphi ^{2} \lambda \left[ {\alpha \left( {7 - \theta } \right) + \beta c} \right] + 4\beta \phi \varphi \gamma \lambda \left( {7 - \theta } \right) + \beta c\left( {2\delta \varphi + \gamma \upsilon } \right)^{2} - 6\phi \gamma ^{3} \lambda }}{{\beta \left[ {16\varphi \gamma ^{2} \lambda + \left( {2\delta \varphi + \gamma \upsilon } \right)^{2} - 8\beta \varphi ^{2} \lambda \left( {8 - \theta } \right)} \right]}}$$

(21)

$$r^{*} = \frac{{4\beta \phi \varphi \lambda \left( {8 - \theta } \right) - \left( {\alpha - \beta c} \right)\left[ {\gamma \left( {\upsilon ^{2} + 4\varphi \lambda } \right) + 2\delta \varphi \upsilon } \right] - \phi \gamma \left( {6\gamma \lambda + \delta \upsilon } \right) - 2\delta ^{2} \phi \varphi }}{{16\varphi \gamma ^{2} \lambda + \left( {2\delta \varphi + \gamma \upsilon } \right)^{2} - 8\beta \varphi ^{2} \lambda \left( {8 - \theta } \right)}}$$

(22)

$$\omega _{d}^{*} = \frac{{4\varphi \lambda \left( {3\alpha + \beta c} \right)\left( {\gamma ^{2} - 4\beta \varphi } \right) + \beta c\left( {2\delta \varphi + \gamma \upsilon } \right)^{2} + 4\beta \phi \varphi \gamma \lambda \left( {6 - \theta } \right) - 6\phi \gamma ^{3} \lambda + 8\alpha \beta \varphi ^{2} \lambda \theta }}{{\beta \left[ {16\varphi \gamma ^{2} \lambda + \left( {2\delta \varphi + \gamma \upsilon } \right)^{2} - 8\beta \varphi ^{2} \lambda \left( {8 - \theta } \right)} \right]}}$$

(23)

Furthermore, by placing the optimum values of $\omega _{m}^{*}$, $q^{*}$, $p^{*}$, $r^{*}$, and $\omega _{d}^{*}$ in Eqs. (12), (10) and (11), the optimal profit rate of producer, distributor, and retailer is obtained.

3.6 Supply chain coordination

The producer as a member of the supply chain, with the social responsibility, always wants to receive larger size orders from the retailer, since the producer will be able to act more competitively in line with CSR. On the other hand, the retailer has no reason to order at larger sizes than the decentralized decision-making mode. Therefore, the retailer will leave the optimal model in the centralized decision-making structure provided that the manufacturer provides an incentive scheme to compensate for the cost of getting out of the optimality through the distributor. Consider that as a motivational scheme, the manufacturer will offer a discount at the wholesale price to the distributor, which is the middle and the intermediary member between the producer and the retailer.

In response to this, the distributor would force the retailer to increase the order quantity, by providing a discount on the wholesale price. Members of the supply chain will participate in such schemes, and such discounts will be practical if there are two conditions:

• The retailer must order based on the optimal decision-making mode (the custom value that is desirable throughout the supply chain, not just for the retailer),

• Under any discount scheme at wholesale prices, each member of the supply chain must attain at least some of their profit in decentralized decision-making mode (by leaving their optimal decisions and participating in the discounts scheme, they will not be in a worse position in terms of profitability).

In general, in multi-level supply chains, each member establishes a one-to-one relationship only with the member directly associated and assumes that there are no other members in the chain. The producer can provide a discount on the wholesale price to the distributor, as long as the decentralized profits are guaranteed.

Similarly, retailers will accept the discount offer at wholesale prices from the distributor’s profit and will order based on centralized decision-making mode provided that the cost of leaving the optimality is compensated by outperforming by a discount at wholesale price.

In the process of discounts, the distributor plays a central role, since he/she preserves the role of mediator to maintain the flow of the incentive discounts scheme from the manufacturer to the retailer, and the flow of the order quantity from the retailer to the manufacturer. In this way, the distributor will receive more profit than the decentralized model. Therefore, when a discount plan is provided at wholesale prices to resolve the conflicts between targets in the supply chain, the distributor decides on two maters:

• The minimum discounts at wholesale prices from the manufacturer to the distributor

• The maximum discounts on wholesale prices from the distributor to the retailer.

Allowed values for these two matters depend on each other. The flow of determining the discount values can be assessed under two scenarios. In the first scenario, the decision-making process is from the manufacturer to the retailer, and in the second scenario, the decision-making flow is from the retailer to the manufacturer. In the first scenario, the producer and distributor decide on the minimum and maximum discount rate on the wholesale price of the manufacturer. Then, in this specified range, they decide on the distribution of the generated surplus. Based on the decisions made at this stage, the distributor and retailer will also achieve a certain range for discounts in distributor wholesale quantities so that the winning-winning state is guaranteed. In the second scenario, retailers first decide on discounts and profit-sharing, and then based on this, the distributor will deal with the manufacturer. These two scenarios will produce different results and responses.

Nevertheless, the first approach is to examine, from producer to retailer, since it is assumed that the producer is the leader of the supply chain. Another reason is that in the real world, any discounts from the manufacturer will flow through the supply chain to the customers, and these types of schemes will begin with manufacturers. Therefore, in general, a plan for supply chain coordination will include two coordination and two negotiation (bargaining) agreements.

In the process of coordinating the supply chain, the sequence of activities will be as follows:

Step 1 The manufacturer and distributor find discount rates on the wholesale price to achieve the winning-winning state, provided that the distributor must compensate the retailer losses for the change in order quantity.

Step 2 Within the determined discount range set in the first step, the manufacturer will bargain with the distributor for a certain share of the generated profit. The decentralized profit plus the profit share here is the producer’s optimal profit. Similarly, the profit in the decentralized mode plus the profit share in this step represents the distributor’s total profit.

Step 3 Given the created intermediary profit (additional profit reached by the distributor), the distributor and the retailer will determine the winning-winning range for a discount at the distributor’s wholesale prices.

Step 4 Distributors and retailers will determine the profits share through bargaining.

Suppose that the manufacturer suggests a discount of $\mu \omega _{m}^{*} (\mu \ge 0)$ to the distributor. The total profit of the manufacturer under this discount will be as follows:

$$\begin{aligned} v_{m}^{{wd}} & = \left( {\omega _{m}^{*} - c} \right)\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) + \frac{\theta }{{2\beta }}\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right)^{2} - \lambda q_{C}^{{*2}} \\ & \quad - \mu \omega _{m}^{*} \left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) \\ \end{aligned}$$

(24)

The manufacturer can offer a discount on the wholesale price as long as at least the decentralized profits are maintained. In other words, $v_{m}^{{wd}} \ge v_{m}^{*}$. If μ is assumed as the maximum discount rate that satisfies the mentioned inequality, $\bar{\mu }$ is computed by:

$$\bar{\mu } = \frac{{\left( {\omega _{m}^{*} - c + \frac{\theta }{{2\beta }}} \right)\left( {D_{C}^{*} - D_{D}^{*} } \right) - \lambda \left( {q_{C}^{{*2}} - q_{D}^{*} } \right)}}{{\omega _{m}^{*} D_{C}^{*} }}$$

(25)

where $D_{C}^{*} = \alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*}$ and $D_{D}^{*} = \alpha - \beta p_{D}^{*} + \delta q_{D}^{*} + \gamma r_{D}^{*}$.

Therefore, the minimum amount of retailer that the manufacturer can offer to the distributor is as follows:

$$\underline{{\omega _{m} }} = \left( {1 - \overline{\mu } } \right)\omega _{m}^{*}$$

(26)

Similarly, the distributor may accept a discount offer from the manufacturer, as long as the profit is provided and the loss is compensated in the decentralized decision-making system.

If the distributor requests the minimum discount of $\underline{\mu } \omega _{m}^{*}$. There should be $\pi _{d}^{{wd}} = \pi _{d}^{*} + \left[ {\pi _{r}^{*} - \pi _{r}^{{wd}} } \right]$, then by placing this phrase.

$$\begin{aligned} & \left( {\omega _{d}^{*} - \omega _{m}^{*} } \right)\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) + \underline{\mu } \omega _{m}^{*} \left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) \\ & \quad = \left( {\omega _{d}^{*} - \omega _{m}^{*} } \right)\left( {\alpha - \beta p_{D}^{*} + \delta q_{D}^{*} + \gamma r_{D}^{*} } \right) \\ & \quad \quad + \left[ \begin{gathered} \left( {p_{D}^{*} - \omega _{d}^{*} } \right)\left( {\alpha - \beta p_{D}^{*} + \delta q_{D}^{*} + \gamma r_{D}^{*} } \right) - r_{D}^{*} \left( {\phi + \varphi r_{D}^{*} - \upsilon q_{D}^{*} } \right) \hfill \\ - \left( {\left( {p_{C}^{*} - \omega _{d}^{*} } \right)\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) - r_{C}^{*} \left( {\phi + \varphi r_{C}^{*} - \upsilon q_{C}^{*} } \right)} \right) \hfill \\ \end{gathered} \right] \\ \end{aligned}$$

(27)

By simplifying the above expression, the value of $\underline{\mu }$ will be as follows:

$$\underline{\mu } = \frac{{\left( {\omega _{d}^{*} - \omega _{m}^{*} } \right)\left( {D_{C}^{*} - D_{D}^{*} } \right) + \left( {p_{D}^{*} - \omega _{d}^{*} } \right)D_{D}^{*} - \left( {p_{C}^{*} - \omega _{d}^{*} } \right)D_{C}^{*} - r_{D}^{*} \left( {\phi + \varphi r_{D}^{*} - \upsilon q_{D}^{*} } \right) + r_{C}^{*} \left( {\phi + \varphi r_{C}^{*} - \upsilon q_{C}^{*} } \right)}}{{\omega _{m}^{*} D_{C}^{*} }}$$

(28)

Therefore, the manufacturer can have the maximum wholesale price demand as follows:

$$\overline{{\omega _{m} }} = \left( {1 - \underline{\mu } } \right)\omega _{m}^{*}$$

(29)

According to the presented explanation, for each $\omega _{m} \in \left( {\underline{{\omega _{m} }} ,\overline{{\omega _{m} }} } \right)$, the producer’s profits are in the winning-winning mode, and after compensating for the loss of the retailer, the distributor’s profit is also obtained in the winning-winning mode. In this wholesale price range, the manufacturer and the distributor will bargain over a certain amount of the wholesale price that effectively distributes the generated surplus profit.

Here, we use the concept of Nash equilibrium to calculate the ideal amount for the wholesale price under the discounts. One of the important features of the Nash equilibrium is that the output will be in the random form since it depends on the bargaining of the members participating in equilibrium. In the Nash bargaining model, the objective function of the product model is to benefit the members of the cooperation which should be maximized. Each member’s benefit means the difference between profits from co-operation and profit in decentralized decision-making mode. Hence, we will have:

$$Max_{{\underline{\mu } \le \mu \le \overline{\mu } }} \left[ {v_{m}^{{wd}} - v_{m}^{*} } \right]\left[ {\pi _{d}^{{wd}} - \left( {\pi _{d}^{*} + \left( {\pi _{r}^{*} - \pi _{r}^{{wd}} } \right)} \right)} \right]$$

(30)

By replacing the terms we will have:

$$\begin{aligned} & Max_{{\underline{\mu } \le \mu \le \overline{\mu } }} \left[ {\left( {\omega _{m}^{*} - c} \right)\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) + \frac{\theta }{{2\beta }}\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right)^{2} - \lambda q_{C}^{{*2}} } \right. \\ & \quad - \mu \omega _{m}^{*} \left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) - v_{m}^{*} ][\left( {\omega _{d}^{*} - \omega _{m}^{*} } \right)\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) \\ & \quad \quad + \mu \omega _{m}^{*} \left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) - \left. {\left( {\pi _{d}^{*} + \left( {\pi _{r}^{*} - \left( \begin{gathered} \left( {p_{C}^{*} - \omega _{d}^{*} } \right)\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) \hfill \\ - r_{C}^{*} \left( {\phi + \varphi r_{C}^{*} - \upsilon q_{C}^{*} } \right) \hfill \\ \end{gathered} \right)} \right)} \right)} \right] \\ \end{aligned}$$

(31)

By solving the above model, the optimal value of $\mu$ is obtained as follows:

$$\mu ^{b} = \frac{\begin{gathered} 2c\beta \left( {D_{D}^{*} - D_{C}^{*} } \right) + 2D_{D}^{*} \beta p_{D}^{*} - 2\beta D_{C}^{*} \left( {p_{C}^{*} - 2\omega _{m}^{*} } \right) - 4\beta D_{D}^{*} \omega _{m}^{*} + \theta \left( {D_{C}^{{*2}} - D_{D}^{{*2}} } \right) \hfill \\ + 2\beta \lambda \left( {q_{D}^{{*2}} - q_{C}^{{*2}} } \right) + 2\beta \upsilon \left( {q_{D}^{*} r_{D}^{*} - q_{C}^{*} r_{C}^{*} } \right) + 2\beta \phi \left( {r_{C}^{*} - r_{D}^{*} } \right) + 2\beta \varphi \left( {r_{C}^{*} - r_{D}^{*} } \right)\left( {r_{C}^{*} + r_{D}^{*} } \right) \hfill \\ \end{gathered} }{{4D_{C}^{*} \omega _{m}^{*} \beta }}$$

(32)

Therefore, the rate of the wholesale price, in this case, is as follows:

$$\omega _{m}^{b} = \left( {1 - \mu ^{b} } \right)\omega _{m}^{*}$$

(33)

In this case, the distributor’s profit is as follows:

$$\pi _{d}^{{ib}} = \left( {\omega _{d}^{*} - \omega _{m}^{b} } \right)\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right)$$

(34)

Accordingly, the distributor and the retailer will disclose the discount at the distributor’s wholesale price. If $\bar{\rho }\omega _{d}^{*}$ expresses the maximum discount on the wholesale price that the distributor provides for the retailer, we will have:

$$\pi _{d}^{{ib}} - \bar{\rho }\omega _{d}^{*} \left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) = \pi _{d}^{*}$$

(35)

Then, we have:

$$\bar{\rho } = \frac{{\left( {\omega _{d}^{*} - \omega _{m}^{b} } \right)D_{C}^{*} - \left( {\omega _{d}^{*} - \omega _{m}^{*} } \right)D_{D}^{*} }}{{\omega _{d}^{*} D_{C}^{*} }}$$

(36)

Thus, the minimum wholesale price for a distributor under a discount policy is as follows:

$$\underline{{\omega _{d} }} = \left( {1 - \bar{\rho }} \right)\omega _{d}^{*}$$

(37)

If the distributor provides such a minimum discount for the retailer, the retailer’s profit will be formulated as follows:

$$\pi _{r}^{{wd}} = \left( {p_{C}^{*} - \omega _{d}^{*} } \right)\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) - r_{C}^{*} \left( {\phi + \varphi r_{C}^{*} - \upsilon q_{C}^{*} } \right) + \rho \omega _{d}^{*} \left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right)$$

(38)

Given the $\pi _{r}^{{wd}} \ge \pi _{r}^{*}$, $\underline{\rho }$ will be the minimum acceptable discount as follows:

$$\underline{\rho } = \frac{{\left( {p_{D}^{*} - \omega _{d}^{*} } \right)D_{D}^{*} - \left( {p_{C}^{*} - \omega _{d}^{*} } \right)D_{C}^{*} - r_{D}^{*} \left( {\phi + \varphi r_{D}^{*} - \upsilon q_{D}^{*} } \right) + r_{C}^{*} \left( {\phi + \varphi r_{C}^{*} - \upsilon q_{C}^{*} } \right)}}{{\omega _{d}^{*} D_{C}^{*} }}$$

(39)

Therefore, the maximum acceptable value for the wholesale price that the distributor provides to the retailer is as follows:

$$\overline{{\omega _{d} }} = \left( {1 - \underline{\rho } } \right)\omega _{d}^{*}$$

(40)

For each $\omega _{d} \in \left( {\underline{{\omega _{d} }} ,\overline{{\omega _{d} }} } \right)$, the retailer and distributor benefit under a winning-winning policy. In the range provided for the distributor’s wholesale price, the two parties will bargain to earn a share of the generated profit. As in the previous section, we also use the Nash bargaining model here. Then, the model will be as follows:

$${\text{Max}}_{{\underline{\rho } \le \rho \le \overline{\rho } }} \left[ {\pi _{d}^{{ib}} - \rho \omega _{d}^{*} \left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) - \pi _{d}^{*} } \right]\left[ {\pi _{r}^{{wd}} - \pi _{r}^{*} } \right]$$

(41)

Solving the presented Nash model, the optimal value of ρ is obtained by:

$$\rho ^{b} = \frac{{D_{D}^{*} \left( {p_{D}^{*} - 2\omega _{d}^{*} + \omega _{m}^{*} } \right) - D_{C}^{*} \left( {p_{C}^{*} - 2\omega _{d}^{*} + \omega _{m}^{b} } \right) - \upsilon q_{C}^{*} r_{C}^{*} + r_{C}^{*} \left( {\phi + r_{C}^{*} \varphi } \right) + r_{D}^{*} \left( { - \upsilon q_{D}^{*} + \phi + r_{D}^{*} \varphi } \right)}}{{2\omega _{d}^{*} D_{C}^{*} }}$$

(42)

As a result, the optimal wholesale price of the distributor to the retailer is also obtained under the discount contract as follows:

$$\rho ^{b} = \omega _{d}^{b} = \left( {1 - \rho ^{b} } \right)\omega _{d}^{*}$$

(43)

Finally, in general, the profits of the supply chain members in the discount contracts are given by:

$$\pi _{m}^{b} = \left( {\omega _{m}^{b} - c} \right)\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) - \lambda q_{C}^{{*2}}$$

(44)

$$\pi _{d}^{b} = \left( {\omega _{d}^{b} - \omega _{m}^{b} } \right)\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right)$$

(45)

$$\pi _{r}^{b} = \left( {p_{C}^{*} - \omega _{d}^{b} } \right)\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) - r_{C}^{*} \left( {\phi + \varphi r_{C}^{*} - \upsilon q_{C}^{*} } \right)$$

(46)

$$v_{m}^{b} = \left( {\omega _{m}^{b} - c} \right)\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right) + \frac{\theta }{{2\beta }}\left( {\alpha - \beta p_{C}^{*} + \delta q_{C}^{*} + \gamma r_{C}^{*} } \right)^{2} - \lambda q_{C}^{{*2}}$$

(47)

It should be considered that it means eliminating the contradiction in the goals of the supply chain.

4 Model solving and analysis

In this chapter, to illustrate the application of the proposed models in this research, the sample problems were designed and solved. In the next chapter, the sensitivity of the model to some more important and influential parameters will be analyzed.

4.1 Numerical example

This section deals with the problem design for the developed model and then the problem analysis. Numerical examples for centralized, decentralized, and coordinated systems are solved.

In a production system considering the return policy and CSR, the following parameters are considered as: $\alpha = 100$, $\beta = 10$, $\delta = 5$, $\gamma = 5$, $\phi = 10$, $\varphi = 3$, $\upsilon = 5$, $\theta = 0.5$, $c = 50$, $\lambda = 350$.

By placing the above values in the concavity conditions, it is seen that the profit functions of the producer, the distributor, the retailer, and the total profit function are concave. Therefore, using the optimal solutions presented in the preceding sections, the optimal decisions of the producer, distributor, and retailer are made in the Stackelberg-producer system as well as optimal decisions under concentrated and coordinated conditions. The optimal solutions obtained from these models are presented in Table 1.

Table 1 Optimal solutions of the models

4.2 Sensitivity analysis

In this section, for each centralized, decentralized, and coordinated model, several numerical experiments were performed separately to evaluate the sensitivity of the optimal response to changes in the values of some parameters. To evaluate the behavior of the model by changing the key parameters, the sensitivity analyses to the parameters of $\alpha$, $\beta$, $\theta$, $\phi$, $\varphi$, $\lambda$ and $\upsilon$ are presented in Tables 2, 3, 4, 5, 6 and 7. Moreover, changes in the variables of the different decision and profit functions are shown in Figs. 1, 2, 3, 4, 5 and 6. Note that the changes to the decentralized state were shown with $D$ and changes to the coordinated mode were indicated by Co.

Table 2 Sensitivity analysis of $\alpha$ in decentralized and coordinated systems

Table 3 Sensitivity analysis to the parameter $\beta$ in decentralized and coordinated systems

Table 4 Sensitivity analysis of the parameter $\theta$ in decentralized and coordinated systems

Table 5 Sensitivity analysis of the $\varphi$ parameter in decentralized and coordinated systems

Table 6 Sensitivity analysis of parameter $\lambda$ in decentralized and coordinated systems

Table 7 Sensitivity analysis of the $\upsilon$ parameter in decentralized and coordinated systems

Fig. 1

Changes in the decision and profit variables of members in terms of the parameter $\alpha$ change

Fig. 2

Changes in the decision and profit variables of the members according to the parameter $\beta$ change

Fig. 3

Changes in the decision and profit variables of the members according to the parameter $\theta$ change

Fig. 4

Changes in the decision and profit variables of members in terms of change in $\varphi$

Fig. 5

Changes in the decision and profit variables of members in terms of change in $\lambda$

Fig. 6

Changes in the decision and profit variables of the members in terms of the change in $\upsilon$ parameter

According to Table 2 and Fig. 1, when the base demand for manufactured goods (α) increases $\omega _{m}^{*}$, $\pi _{d}^{*}$, $\pi _{m}^{*}$, $r^{*}$, $q^{*}$, $\omega _{d}^{*}$, and $\pi _{r}^{*}$ also are increased. When the demand for manufactured goods increases, the optimal production policy moves toward the production of higher quality goods and higher prices. Moreover, the retailers purchase the returned goods from the customers at a higher price. The results show that by increasing α, the profit of the producer, distributor, and retailer and total supply chain is increased. The results of Table 3 and Fig. 2 show that by increasing the customer’s sensitivity to the price of products, the producer prefers to produce products with a lower price and quality. Moreover, the retailer returns the returning products at a lower price. Thus, the profit of the producer, distributor, retailer, and the total supply chain profit will be reduced.

According to Table 4 and Fig. 3, by increasing the social responsibility coefficient ($\theta$), the wholesale price of the distributor, the producer, and the sales price of the products is decreased slightly and the quality of the products is increased. Similarly, the retailer pays more money for returning the returned goods. Based on the results, with increasing social responsibility, all the decision variables change to increase the customer’s satisfaction. Furthermore, according to the consumer’s surplus function, with increasing $\theta$, the profit of the members of the supply chain increases. In a practical point of view, achieving the appropriate social responsibility level helps the firm to increase the content of customers, which in turn can generate higher demand for products and higher profits.

According to Table 5 and Fig. 4, with the increased sensitivity of the number of returning goods to the refund rate ($\varphi$), the price of the produced goods is reduced slightly. Moreover, the manufacturer reduces the quality of manufactured goods. Given the fact that the objective of the supply chain is to reduce the purchased goods returning, with the increase in the sensitivity of the number of returned items to the refund, the retailer reduces the sale price of returning goods.

As seen in Table 6 and Fig. 5, the increase in the quality cost coefficient does not have a significant effect on wholesale prices. However, it reduces the wholesale price of the producer and distributor in both centralized and decentralized decision-making systems very slightly. Moreover, with increasing $\lambda$, the discounts offered in the centralized decision-making mode increase. In other words, to reach the Nash equilibrium point, the manufacturer and retailer should give more discounts to their downstream member. This can be caused by the fact that as the quality of the product decreases by an increase in the quality cost, consequently, and consequently the demand decreases, to compensate this effect, more discount is offered at wholesale prices. This will reduce the retail price and, as a result, partially compensate for the reduced number of customers. The important thing regarding the table is that, as expected, all three members of the supply chain in a coordinated manner will be more profitable than the decentralized state, which is a prerequisite for acquiring a coordination mechanism. Furthermore, the profit of the entire supply chain in a coordinated mode (i.e., the total profit of the producer, distributor, and retailer) is exactly equal to the supply chain profit in the centralized decision-making mode. This fact means that the contradiction in goals and decisions is resolved. The implication is that the firm should try to coordinate supply chain members to make centralized decisions, while they do not lose profit.

According to Table 7 and Fig. 6, an increase in the quality impact coefficient in the quantity of the returned goods means that the quality of the goods will play a more important role in the number of the returned goods. In Table 7, it can be observed that by increasing the quality impact coefficient in the number of returned goods, the retail price will increase slightly in either decentralized or centralized mode. On the other hand, in these circumstances, the wholesale prices of goods also show a non-significant growth rate. One important point in Table 7 is that the proposed discount decreases with increasing $\upsilon$. Similar to the preceding tables, and as expected, the profit of each member of the supply chain in 4.1 coordinated manners is always higher than the decentralized mode for any amount of $\upsilon$, and it makes the provided coordinating mechanism efficient.

5 Concluding remarks

In this research, the intention is to study the mathematical model of a supply chain consisting of producer, distributor, and retailer to determine wholesale and retail prices under the policy of returning goods. The decision variable is wholesale and retail the price, quality of manufactured products, and the buy-back price of the returned goods to the customer. Therefore, the goal is to determine the optimal value of decision variables in such a way that the total profit of the system is maximized. One of the tools used in this study is the theory of games in a collaborative model. After formulating each model, the Stackelberg-producer game is used to obtain optimal answers. Then, a numerical example was presented to illustrate the presented model numerically, and finally, by analyzing the sensitivity, we examined the effect of different parameters on optimal values and total profit. In this research, the effect of parameters such as the basic demand of manufactured goods, customer sensitivity to price, social responsibility coefficient, the amount of the base of the returned goods, the sensitivity of the number of returning goods to the amount of refund, the coefficient of cost of quality and the coefficient of quality impact on the amount of returned goods reviewed.

By comparing two decentralized and coordinated systems, in the coordinated mode, the quality of the products and the price paid to customers for the returned goods (the price of the reflows) are always higher than the decentralized ones now. Thus, according to the sensitivity analysis, the application of the coordinated system is not only for the benefit of each member of the supply chain (the profit of each member in the coordinated mode is at least equal to or greater than the profit of the same member in the decentralized decision-making mode) but also for the benefit of customers. In other words, because the quality of goods and the amount of the refund are factors that affect customer satisfaction, customers are also coordinated by the stakeholders. The result of sensitivity analysis and numerical example indicates the following important managerial insights: (1) As the market base for goods increases or sensitivity of customers to price decreases, the manufacturer increases the price, quality, and refund amount increases because by increasing the demand and popularity of the product, decreasing the sensitivity of customers to the price of products, or increasing the effect of quality, the firm increases the price and the quality of products to increases its profit. (2) By increasing the social responsibility coefficient ($\theta$), decision variables change in the favor of consumers' satisfaction. In other words, the price of sales of products decreases, and the quality of products increases. Also, the retailer pays more money for the return of returning goods. Also, with the increase in social responsibility, the profit of the members of the supply chain will increase. Therefore, a higher level of social responsibility helps the firm to increase its popularity and customer satisfaction as well as profits. (3) When the value of the base of returning goods ($\phi$) or the sensitivity of the number of returning goods increases to the amount of refund ($\varphi$), the price of the products, as well as the amount of the refund, will be reduced. Supply chain members decide in a way that the number of return items will be reduced. (4) An increase in the cost-of-quality ratio results in a reduction in the wholesale price of the producer and the distributor in either centralized or decentralized decision making. Also, the discounts offered in the centralized decision-making mode increase. In other words, to reach the Nash equilibrium point, the manufacturer and retailer should give more discounts to their downstream member.

There are some limitations involved in this paper, which can be considered a future study. First, this model assumed that the supply chain has only one retailer. However, in reality, a supply chain consists of multiple retailers. Apart from the coordination mechanism investigated in this paper, other coordination mechanisms (e.g., buy-back policy) can be further discussed and compared with the introduced contracts. Further possible future study direction is to consider different game theory models in addition to manufacturer-Stackelberg investigated in this research.