1 Introduction

Transportation is one of the largest energy-consuming sectors in the world, and with increasing urbanization and the expansion of decorated lifestyles, the use of vehicles and the average mileage of each vehicle have risen recently. One of the resulting consequences is the production of waste tires that are environmentally harmful. Every year, approximately one million tons of tire material are disposed of in the world. Some conventional methods (e.g., burning, stockpiling, and landfilling), adopted for disposing and managing these hazardous wastes, are proved to have a higher amount of adverse impact on the health of human beings, environment, and ecological systems (Yadav and Tiwari 2019). Due to their high stability, waste tires are highly detrimental to the environment and distort the face of nature.

As we know, a truck tire consumes about 22 gallons of oil and the retreading process saves up to 70% of the crude oil consumption. New tires use four times more material than retreaded tires, and the amount of energy used to produce them is three times that of retreaded tires (Tanzadeh and Haghighat 2012). As a result, the disposal of end-of-life tires has become a controversial economic and environmental dilemma and there is an urgent need to improve the value of worn-out tires. Accordingly, ways of managing this issue, which can significantly enhance their value, are being sought universally.

As another significant point, the study of several closed-loop supply chains with regard to global factors can play a critical role in enhancing their performance. In today’s dynamic business environment, the competition is no more among firms, however, among supply chains to gain competitive advantages. This causes to global supply chain (khai loon 2014). In several countries, some percentages of raw materials for tires are supplied through other countries, making decision makers need a global supply chain. Customs duties (tariffs on products when they are transported between countries) and exchange rates (between currencies) are two significant global factors that they are considered here.

The prominent goal of this study is to formulate a multi-objective, multi-product, multi-period, and multi-echelon mathematical model for the tire supply chain such that the most practical factors such as uncertainty, product shortage, the percentage of the raw materials received from the foreign supplier, customs duty, and exchange rates are considered simultaneously. This model is applicable for tire manufacturing companies and products with cycles similar to those of the tire manufacturing industry.

The remainder of the current study is organized as follows. In Sect. 2, the primary relevant studies and research gaps are discussed. In Sect. 3, the details of the problem including some definitions, assumptions, and mathematical formulation are explained. In Sects. 4 and 5, the suggested method for solving the proposed multi-objective stochastic model is described. In Sect. 6, a case study is discussed and applied to test the proposed approach. Finally, the conclusions and future studies are stated in Sect. 7.

2 Literature review

Based on the topic discussed in the present study, the literature is reviewed in two streams.

2.1 Tire closed-loop supply chain

Dehghanian and Mansouri (2009) developed a three-objective mathematical model for designing a sustainable waste tire recovery network. Their goals include balancing social and environmental impacts and economic issues. Using the Eco-indicator index and the analytic hierarchy process (AHP) method, they computed the parameters of environmental and social impacts. Sasikumar et al. (2010) focused on the reverse chain of end-of-life tires and provided a formulation to maximize the profit of a multi-echelon SCND. In their study, the maximum allowed distance between the initial centralized points and the customers is determined by using the sensitivity analysis. Their model has single objective, single product and certain demand, and the retreading of the truck tire is considered as a case study. Subulan et al. (2015) designed a multi-configuration logistics network that addresses environmental issues through the Eco-indicator 99 index. They solved their multi-objective model via interactive fuzzy goal programming. In their study, demands for new tires, retreading and the rate of return of end-of-life tires are assumed as fixed parameters. Considerations such as external suppliers with global factors (customs duty and exchange rates) are not seen in their study. Hassanzadeh Amin et al. (2017) presented an optimal multi-period, multi-product, and single-objective model to maximize profits and solve the model with MILP. They used the decision tree method to assess the net present value under the conditions of uncertainty of demand and return of the product. Pedram et al. (2017) examined a case study for automobile tire and used the “Scenario Analysis” technique and GAMS (General Algebraic Modeling System) 24.0.1 software to maximize profits and manage waste (by retreading tires) to reduce pollution. Their model has single period; the distribution and retailer locations, the collection, recycling, and retreading centers are predetermined and fixed. For the first time, Sahebjamnia et al. (2018) studied a sustainable tire closed-loop SCND and formulated a multi-objective MILP formulation. For large-sized networks, they implemented hybrid metaheuristic algorithms. In their study, the single-period model is used and certain parameters are considered. Also, Fathollahi-Fard et al. (2018) proposed a three-echelon formulation for designing the location and allocation of a tire closed-loop SCND. Shi et al. (2019) introduced a new closed-loop supply chain mode which hypothesizes some barriers for such a mode exist for the whole supply chain from the remanufacturers’ management and government support. Yıldızbaşı et al. (2020) assessed the social sustainable supply chain indicators using an integrated approach of fuzzy technique for order preference by similarity to an ideal solution (TOPSIS) and fuzzy AHP. They studied the automotive industry in Turkey to assess them in terms of social sustainability.

2.2 Global supply chain with regard to waste management

Meixell and Gargeya (2005) reviewed operations management formulations in global supply chains.

They emphasized that a few formulations have modeled according to the practical issues in the design of global supply chain formulations. They classified papers based on global considerations, such as corporate income tax, exchange rates, currency, tariffs, and non-tariff trade barriers. Liu and Papageorgiou (2013) addressed the production, distribution and capacity planning of global supply chains with regard to customer service level, cost, and responsiveness simultaneously. They developed a multi-objective mixed-integer linear programming (MILP) formulation with total lost sales, total flow time, and total cost as essential objective functions. Lee et al. (2017) studied how firms make plant location and inventory level decisions to serve global markets. They investigated not only differences in transportation costs, wages, and subsidies across countries but also competition and exchange rate changes among firms. Hassanzadeh Amin and Baki (2017) designed a mathematical formulation for a closed-loop SCND by considering global factors, including customs duties and exchange rates. The formulation is a multi-objective MILP model under uncertain demand. In this model, only one strategy for waste management is considered and product shortage is not considered.

Zerang et al. (2018) studied a closed-loop global supply chain in which the manufacturer manipulates both manufacturing from raw materials and remanufacturing from the second-hand products collected by third party simultaneously. They assumed that the market demand depends on marketing efforts and selling price. Koberg and Longoni (2019) identified the critical elements of sustainable SCND in global supply chains and proposed a systematic review of SCND in global supply chains. They concluded some useful outcomes along environmental, social and economic dimensions. Rezaei and Maihami (2019) studied a closed-loop global supply chain which is structured to sell the products in a first and a secondary market. As a significant point, they applied the game theory in sustainability in a new competitive SCND structure. Cohen and Lee (2020) identified the reaction strategies of firms to changes in government policy that are relevant to global manufacturing and logistics. This includes policy changes, such as tariffs, taxes, content requirements, and investment incentives. Boronoos et al. (2020) developed a multi-objective MILP formulation for a closed-loop green global SCND problem. Their formulation minimizes the total robustness costs and total CO2 emissions in both forward and reverse directions, simultaneously. Abdolazimi et al. (2020) designed a multi-level closed-loop supply chain network under deterministic and uncertain conditions to maximize the time delivery, and minimize total costs, and environmental impacts under the uncertainty of some parameters. They studied their proposed approach in a tire production factory.

2.3 Research gap

Although many researchers have considered different aspects of the closed-loop SCND with a variety of significant practical factors such as batteries, iron and steel, and hospital waste, only a few studies have focused on developing a stochastic multi-objective closed-loop global SCND formulation with particular focus on the tire production processes. In most papers, the uncertainty of parameters such as return rates and demand has not been considered. Accordingly, to fill the research gap in the literature, the current study develops a closed-loop global SCND formulation, including demand uncertainty and product return rates. In the suggested model, critical factors such as dividing suppliers into internal and external categories, forcing manufacturers to buy a percentage of raw material from external suppliers, and considering the shortage of customer demand are included. A summary of the literature review is provided in Table 1 to determine the contribution of the current study.

Table 1 Summary of recent studies
Full size table

3 Problem description

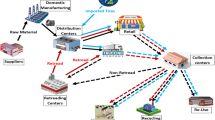
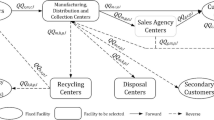
This paper, considering waste management, studies the issues of today's world and adds the necessary flexibility to the model. It specifically addresses the tire life cycle with two objectives: the first is maximizing total profits, and the second is minimizing the Eco-indicator 99. The tire life cycle in the network, as shown in Fig. 1, can be divided into the two following categories.

  1. (I)

    In the forward direction, the manufacturers produce raw materials from internal or external suppliers whereby, in the case of import of raw materials, the external suppliers bear the customs costs and exchange rates. (It should be noted that in some countries, a percentage of tire raw materials is imported.) Then, after the production, the tires are transferred to the distribution points and the retailers receive the products from the distributors according to their periodicity. Due to limitations of supplier capacity, this may not be possible for the last requests.

  2. (II)

    In the reverse direction, waste tires are transmitted by dealers and initial collection centers to centralized return sites for inspection and waste management. To attract and retain customers, the policy is that customers receive new tires with a discount rate if they return tire waste. After the inspection, according to the quality level, the used tires are transferred to retreading, recycling, cement or electricity plants, and landfill centers.

Fig. 1
figure 1

A closed-loop supply chain of tire [2]

Full size image

In order to better clarify of practical conditions of the proposed problem, in the following subsections, two significant topics (i.e., several recovery options of the end-of-life tires and the Eco-indicator 99) are explained briefly.

3.1 End-of-life tires and several recovery options

Different recovery options can be discussed as follows.

  1. (I)

    Direct reuse: Reuse is one of the most significant waste prevention strategies. Although the importance of preparation for reuse is evident, preparation centers for reuse are not common in the traditional waste SCND (Gusmerotti et al. 2019).

  2. (II)

    Retreading: Up to 80% of the cost of tire materials can be saved via the retreading process (Debo and Wassenhove 2005). The significant point is that retreaded tires and newly produced tires have approximately the same mileage. However, they can be sold with a 30–50% discount (Sasikumar et al. 2010).

  3. (III)

    Recycling: This process informs the recovery of materials from granulate tires (Panagiotidou and Tagaras 2005; Shakhsi-Niaei and Esfandarani 2019).

  4. (IV)

    Preparing for waste tire modified concrete production: The rubber tire particles can be used in concrete to replace mineral aggregates. This method is applied in some leading countries (Karabash and Cabalar 2015; Cabalar and Karabash 2015; Akbarimehr et al. 2019).

  5. (V)

    Recovery of energy: Studies emphasize that the energy of 242 million scrap tires equals 12 million barrels of oil. Accordingly, they can be used for electricity generation (Subulan et al. 2015).

  6. (VI)

    Disposal: In order to manage tire waste, landfilling is the least preferred option (Ferrao et al. 2008).

All of the above-discussed recovery options, except (I) and (IV), are considered in the proposed formulation to reflect the real-world conditions of the proposed practical case study more accurately. In this way, the most widely used recovery methods are evaluated to save production time and minimize damage to nature and the preservation of raw materials, the need for the import of raw materials from abroad will decrease and national production will increase.

3.2 The methodology of Eco-indicator 99

The methodology of Eco-indicator 99 is a life cycle assessment-based approach and damage modeling, which is applied for estimating and quantifying the environmental effects of a product or process. These predetermined guides, used by designers and production managers, apply the Eco standard indicator to measure the environmental aspects of the product. In this approach, the main damages are categorized into three divisions (Pishvaee and Razmi 2012):

  • Human health: production of carcinogenic substances.

  • Ecosystem quality: climate change, ozone layer degradation, and acidity of the earth.

  • Sources depletion: consumption of fossil fuels and minerals.

In the methodology, the environmental effects, studied in the product life cycle, include the following phases: (1) raw material attainment, (2) production, (3) transportation/distribution, (4) use, (5) end-of-life collecting, (6) end-of-life processing, (7) energy recovery, (8) remanufacturing, (9) recycling, (10) storage/warehousing, and (11) disposal (Subulan et al. 2015).

In the Eco-indicator 99 calculation, the utilization of tires by end users is ignored in the proposed mathematical model, because it does not affect on decision making.

3.3 Assumptions

According to the realistic conditions of the practical case study and the proposed problem, the main assumptions are organized as follows.

  • The lead times of transportation between the stages are ignored.

  • Shortages for dealers are allowed.

  • The sale price of new tires is cheaper if end-of-life tires are left with the tire dealer.

  • The number of tires returned from a predetermined tire dealer is a fraction of the maximum demand of that dealer.

  • All facilities have a limited capacity.

  • The locations of manufacturers and suppliers are predefined and fixed.

  • In all the stages of the closed-loop SCND, the cost parameters do not change throughout the several time periods. This is except for the cost of the initial setup for the established factories.

  • The cost of the initial setup grows seasonally, such that it becomes more expensive to establish a new factory over time.

  • Since a percentage of tire raw materials is imported, for those suppliers who are abroad, the customs duty and exchange rates are included.

  • All production, distribution, collection, recycling, and retreading centers are in a country, and only suppliers can be considered as being internal and external.

3.4 Mathematical programming model

The nomenclature, parameters, and decision variables are defined in “Appendix”. The multi-objective, multi-product, multi-period, and multi-echelon closed-loop SCND design is formulated as the following mathematical model.

Equation (1) represents the profit function obtained from the difference between income and expenses.

$$MaxZ1 = TREV - (TOP + TFC + TRMC + TPRC + TTC + TRC + TCC + TMPC + TIC + TDC + TSC)$$
(1)

Equation (2) shows the total revenue of the CLSC, which is obtained by selling end-of-life tires for energy recovery, retreaded tires, new brand tires, and recycled materials for other usages.

$$\begin{aligned} {\text{TREV}} = & \mathop \sum \limits_{p} \mathop \sum \limits_{d} \mathop \sum \limits_{r} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot \alpha_{ps} \cdot X2_{{pdrv\left( {t - 1} \right)s}} \cdot SL1_{p} \\ & + \mathop \sum \limits_{p} \mathop \sum \limits_{d} \mathop \sum \limits_{r} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot (X2_{pdrvts} - \left( {\alpha_{ps} } \right)X2_{{pdrv\left( {t - 1} \right)s}} ) \cdot SL2_{P} + \\ & \mathop \sum \limits_{a} \mathop \sum \limits_{d} \mathop \sum \limits_{r} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot X3_{adrvts} \cdot SL3_{a} + \mathop \sum \limits_{p} \mathop \sum \limits_{k} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot X5_{pkwvts} \cdot SL4_{p} + \\ & \mathop \sum \limits_{c} \mathop \sum \limits_{n} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot Qs_{cnts} \cdot SL5_{c} \\ \end{aligned}$$
(2)

Equations (3) and (4) represent the overall fixed operating and setup costs for the facilities.

$${\text{TOP}} = \mathop \sum \limits_{l} \mathop \sum \limits_{t} Oc1_{l} \cdot Y1_{lt} + \mathop \sum \limits_{d} \mathop \sum \limits_{t} Oc2_{d} \cdot Y2_{dt} + \mathop \sum \limits_{k} \mathop \sum \limits_{t} Oc3_{k} \cdot Y3_{kt} + \mathop \sum \limits_{n} \mathop \sum \limits_{t} Oc4_{n} \cdot Y4_{nt }$$
(3)
$$\begin{aligned} {\text{TFC}} = & \mathop \sum \limits_{l} \mathop \sum \limits_{t} F1_{lt} \cdot (Y1_{lt} - Y1_{lt - 1} ) + \mathop \sum \limits_{d} \mathop \sum \limits_{t} F2_{dt} \cdot (Y2_{dt} - Y2_{dt - 1} ) + \\ & \mathop \sum \limits_{k} \mathop \sum \limits_{t} F3_{kt} \cdot \left( {Y3_{kt} - Y3_{kt - 1} } \right) + \mathop \sum \limits_{n} \mathop \sum \limits_{t} F4_{nt} \cdot \left( {Y4_{nt} - Y4_{nt - 1} } \right) \\ \end{aligned}$$
(4)

Equations (5) to (13) show total production costs, total remanufacturing costs, total transport costs between different stages, total recycling costs, total collection costs, material purchasing costs, total inventory carrying costs, total disposal costs, and the cost of final product shortages against the retailers' demands, respectively.

$${\text{TRMC}} = \mathop \sum \limits_{p} \mathop \sum \limits_{l} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot {\text{RTC}}_{pl} \cdot {\text{RTR}}_{plts}$$
(5)
$${\text{TPRC}} = \mathop \sum \limits_{p} \mathop \sum \limits_{i} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot PC_{pi} \cdot Q_{pits}$$
(6)
$$\begin{aligned} {\text{TTC}} = & \mathop \sum \limits_{c} \mathop \sum \limits_{m} \mathop \sum \limits_{i} \mathop \sum \limits_{z} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot h_{z} \cdot TC2_{czv} \cdot D11_{miz} \cdot Qp_{cmivts} + \\ & \mathop \sum \limits_{p} \mathop \sum \limits_{i} \mathop \sum \limits_{d} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} .X1_{pidvts} .TC_{pv} .D1_{id} + \\ & \mathop \sum \limits_{p} \mathop \sum \limits_{d} \mathop \sum \limits_{r} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot X2_{pdrvts} \cdot TC_{pv} \cdot D2_{dr} + \\ & \mathop \sum \limits_{a} \mathop \sum \limits_{d} \mathop \sum \limits_{r} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot X3_{adrvts} \cdot C1_{av} \cdot D2_{dr} + \\ & \mathop \sum \limits_{p} \mathop \sum \limits_{k} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot X5_{pkwvts} \cdot TC_{pv} \cdot D5_{kw} + \\ & \mathop \sum \limits_{p} \mathop \sum \limits_{k} \mathop \sum \limits_{n} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot X6_{pknvts} \cdot TC_{pv} \cdot D6_{kn} + \\ & \mathop \sum \limits_{p} \mathop \sum \limits_{k} \mathop \sum \limits_{l} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot X7_{pklvts} \cdot TC_{pv} \cdot D7_{kl} + \\ & \mathop \sum \limits_{a} \mathop \sum \limits_{l} \mathop \sum \limits_{d} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot X8_{aldvts} \cdot TC1_{av} \cdot D8_{ld} + \\ & \mathop \sum \limits_{p} \mathop \sum \limits_{l} \mathop \sum \limits_{ n} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot X9_{p\ln vts} \cdot TC_{pv} \cdot D9_{\ln } + \\ & \mathop \sum \limits_{c} \mathop \sum \limits_{n} \mathop \sum \limits_{i} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot X10_{cnivts} \cdot TC3_{cv} \cdot D10_{ni} \\ \end{aligned}$$
(7)
$${\text{TRC}} = \mathop \sum \limits_{p} \mathop \sum \limits_{n} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot {\text{RC}}_{pn} \cdot {\text{REC}}_{pnts}$$
(8)
$${\text{TCC}} = \mathop \sum \limits_{p} \mathop \sum \limits_{j} \mathop \sum \limits_{k} \mathop \sum \limits_{v} \mathop \sum \limits_{t} Y5_{jkvt} \cdot RE_{pjt} \cdot (TC_{pv} + CC_{p} ) \cdot D4_{jk} + \mathop \sum \limits_{p} \mathop \sum \limits_{r} \mathop \sum \limits_{k} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot X4_{prkvts} \cdot TC_{pv} \cdot D3_{rk}$$
(9)
$${\text{TMPC}} = \mathop \sum \limits_{c} \mathop \sum \limits_{m} \mathop \sum \limits_{i} \mathop \sum \limits_{z} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot h_{z} \cdot \left( {1 + b_{cmz} } \right) \cdot {\text{PUC}}_{cmz} \cdot Qp_{cmivts}$$
(10)
$$\begin{aligned} {\text{TIC}} = & \mathop \sum \limits_{p} \mathop \sum \limits_{i} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot I1_{pits} \cdot IC1_{pi} + \mathop \sum \limits_{p} \mathop \sum \limits_{d} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot I2_{pdts} \cdot IC2_{pd} + \\ & \mathop \sum \limits_{a} \mathop \sum \limits_{d} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot I3_{adts} \cdot IC3_{ad} + \mathop \sum \limits_{p} \mathop \sum \limits_{k} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot I4_{pkts} \cdot IC4_{pk} + \\ & \mathop \sum \limits_{c} \mathop \sum \limits_{i} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot I5_{cits} \cdot IC5_{ci} \\ \end{aligned}$$
(11)
$$\begin{aligned} {\text{TDC}} = & \mathop \sum \limits_{p} \mathop \sum \limits_{k} \mathop \sum \limits_{l} \mathop \sum \limits_{n} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot \left( {X6_{pknvts} + X9_{p\ln vts} } \right) \cdot \left( {1 - \beta_{p} } \right) \cdot e \cdot INC_{p} \\ & + \mathop \sum \limits_{p} \mathop \sum \limits_{k} \mathop \sum \limits_{l} \mathop \sum \limits_{n} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot \left( {X6_{pknvts} + X9_{p\ln vts} } \right) \cdot \left( {1 - \beta_{p} } \right)\left( {1 - e} \right) \cdot LNFC_{p} + \left( {1 - e} \right) \cdot LNFC_{p} + \\ & \mathop \sum \limits_{p} \mathop \sum \limits_{r} \mathop \sum \limits_{j} \mathop \sum \limits_{k} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} \left( {p_{s} \cdot X4_{prkvts} + RE_{pjt} \cdot Y5_{jkvt} } \right) \cdot d_{p} \cdot e \cdot INC_{p} \\ & + \mathop \sum \limits_{p} \mathop \sum \limits_{r} \mathop \sum \limits_{j} \mathop \sum \limits_{k} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} \left( {p_{s} \cdot X4_{prkvts} + RE_{pjt} \cdot Y5_{jkvt} } \right) \cdot d_{p} \cdot \left( {1 - e} \right) \cdot LNFC_{P} \\ \end{aligned}$$
(12)
$${\text{TSC}} = \mathop \sum \limits_{p} \mathop \sum \limits_{r} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot UD_{prts} \cdot Cd_{prt} \mathop \sum \limits_{a} \mathop \sum \limits_{r} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot UD1_{arts} \cdot Cd1_{art}$$
(13)

Equation (14) minimizes the total Eco-indicator 99 value through the CLSC. This is obtained by multiplying the standard index amounts for each life cycle phase and their respective predefined values.

$${\text{Min}} Z2 = {\text{EIMP}} + {\text{ EIPR}} + {\text{ EITR}} + {\text{EIWH}} + {\text{EICL}} + {\text{ EIEOP}} {-}{\text{ EIER}} {-}{\text{ EIRTR}} {-}{\text{ EIREC}} + {\text{EIDS}}$$
(14)

Equations (15)–(23) represent the total environmental impact of the following phases, respectively: material purchasing, production, distribution/transport, end-of-life collection, end-of-life processing, energy recovery, tire remanufacturing, warehousing, tire recycling, and tire disposal.

$${\text{EIMP}} = \mathop \sum \limits_{c} \mathop \sum \limits_{m} \mathop \sum \limits_{i} \mathop \sum \limits_{z} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot EI1_{cz} \cdot Qp_{cmivts} + \mathop \sum \limits_{c} \mathop \sum \limits_{n} \mathop \sum \limits_{i} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot EI2_{c} \cdot X10_{cnivts}$$
(15)
$${\text{EIPR}} = \mathop \sum \limits_{p} \mathop \sum \limits_{i} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot {\text{EIP}}_{pi} \cdot Q_{pits}$$
(16)
$$\begin{aligned} {\text{EITR}} = & \mathop \sum \limits_{p} \mathop \sum \limits_{i} \mathop \sum \limits_{d} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot EIT1_{pv} \cdot X1_{pidvts} \cdot D1_{id} \\ & + \mathop \sum \limits_{p} \mathop \sum \limits_{d} \mathop \sum \limits_{r} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot EIT1_{pv} \cdot X2_{pdrvts} \cdot D2_{dr} + \mathop \sum \limits_{a} \mathop \sum \limits_{d} \mathop \sum \limits_{r} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot EIT2_{av} \cdot X3_{adrvts} \cdot D2_{dr} + \\ & \mathop \sum \limits_{p} \mathop \sum \limits_{k} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot EIT1_{pv} \cdot X5_{pkwvts} \\ & D5_{kw} + \mathop \sum \limits_{p} \mathop \sum \limits_{k} \mathop \sum \limits_{n} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot EIT1_{pv} \cdot X6_{pknvts} \cdot D6_{kn} + \mathop \sum \limits_{p} \mathop \sum \limits_{k} \mathop \sum \limits_{l} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot EIT1_{pv} \cdot X7_{pklvts} \cdot \\ & D7_{kl} + \mathop \sum \limits_{a} \mathop \sum \limits_{l} \mathop \sum \limits_{d} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} EIT2_{av} .X8_{aldvts} \cdot D8_{ld} + \mathop \sum \limits_{p} \mathop \sum \limits_{l} \mathop \sum \limits_{n} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot EIT1_{pv} \cdot X9_{p\ln vts} \cdot \\ & D9_{\ln } + \mathop \sum \limits_{c} \mathop \sum \limits_{n} \mathop \sum \limits_{i} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot EIT3_{cv} \cdot X10_{cnivts} \cdot D10_{ni} + \mathop \sum \limits_{c} \mathop \sum \limits_{m} \mathop \sum \limits_{i} \mathop \sum \limits_{z} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot EIT3_{cv} \cdot Qp_{cmivts} \cdot D11_{miz} \\ \end{aligned}$$
(17)
$${\text{EICL}} = \mathop \sum \limits_{p} \mathop \sum \limits_{r} \mathop \sum \limits_{k} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot EIC1_{pv} \cdot X4_{prkvts} \cdot D3_{rk} + \mathop \sum \limits_{p} \mathop \sum \limits_{j} \mathop \sum \limits_{k} \mathop \sum \limits_{v} \mathop \sum \limits_{t} EIC2_{pv} \cdot Y5_{jkvt} \cdot RE_{pjt} \cdot D4_{jk}$$
(18)
$${\text{EIEOP}} = \mathop \sum \limits_{p} \mathop \sum \limits_{r} \mathop \sum \limits_{k} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot {\text{EIE}}_{pk} \cdot X4_{prkvts} + \mathop \sum \limits_{p} \mathop \sum \limits_{j} \mathop \sum \limits_{k} \mathop \sum \limits_{v} \mathop \sum \limits_{t} {\text{EIE}}_{pk} \cdot {\text{RE}}_{pjt} \cdot Y5_{jkvt}$$
(19)
$${\text{EIER}} = \mathop \sum \limits_{p} \mathop \sum \limits_{k} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot {\text{EIR}}_{pw} \cdot X5_{pkwvts}$$
(20)
$${\text{EIRTR}} = \mathop \sum \limits_{p} \mathop \sum \limits_{l} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot {\text{EIRM}}_{{{\text{pl}}}} \cdot {\text{RTR}}_{{{\text{plts}}}}$$
(21)
$${\text{EIREC}} = \mathop \sum \limits_{p} \mathop \sum \limits_{n} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot {\text{EIRC}}_{{{\text{pn}}}} \cdot {\text{REC}}_{{{\text{pnts}}}}$$
(22)
$$\begin{aligned} {\text{EIDS}} = & \mathop \sum \limits_{p} \mathop \sum \limits_{k} \mathop \sum \limits_{l} \mathop \sum \limits_{n} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \cdot EII_{p} \cdot \left( {X6_{pknvts} + X9_{p\ln vts} } \right) \\ & . \left( {1 - B_{p} } \right) \cdot e + \mathop \sum \limits_{p} \mathop \sum \limits_{k} \mathop \sum \limits_{l} \mathop \sum \limits_{n} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} EIL_{p} \left( {X6_{pknvts} + X9_{p\ln vts} } \right) \cdot \left( {1 - B_{p} } \right) \cdot \left( {1 - e} \right) + \\ & \mathop \sum \limits_{p} \mathop \sum \limits_{r} \mathop \sum \limits_{j} \mathop \sum \limits_{k} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} EII_{p} \cdot \left( {p_{s} \cdot X4_{prkvts} + RE_{pjt} \cdot Y5_{jkvt} } \right) \cdot d_{p} \cdot e + \\ & \mathop \sum \limits_{p} \mathop \sum \limits_{r} \mathop \sum \limits_{j} \mathop \sum \limits_{k} \mathop \sum \limits_{v} \mathop \sum \limits_{t} \mathop \sum \limits_{s} EIL_{p} \cdot \left( {p_{s} \cdot X4_{prkvts} + RE_{pjt} \cdot Y5_{jkvt} } \right) \cdot d_{p} \cdot \left( {1 - e} \right) \\ \end{aligned}$$
(23)

s.t.

Constraints (24)–(26) guarantee that the production, remanufacturing, and recycling amounts are not more than the capacities of these facilities.

$$\mathop \sum \limits_{p} Q_{pits} \le Cap_{i} \quad \forall i,t,s$$
(24)
$$\mathop \sum \limits_{p} RTR_{plts} \le Cap1_{l} \cdot Y1_{lt} \quad \forall l,t,s$$
(25)
$$\mathop \sum \limits_{p} REC_{pnts} \le Cap2_{n} \cdot Y4_{nt} \quad \forall n,t,s$$
(26)

Constraints (27)–(31) emphasize that the storage capacity for each type of material and the new brand tires at each new tire factory, each type of retreaded and new brand tires at each distribution point, and each type of used tires at each centralized return site can be calculated in each period.

$$I1_{pits} = I1_{pits - 1} + Q_{pits} - \mathop \sum \limits_{d} \mathop \sum \limits_{v} X1_{pidvts} \quad \forall p,i,t,s$$
(27)
$$I2_{pdts} = I2_{pdts - 1} + \mathop \sum \limits_{i} \mathop \sum \limits_{v} X1_{pidvts} - \mathop \sum \limits_{r} \mathop \sum \limits_{v} X2_{pdrvts} \quad \forall p,d,t,s$$
(28)
$$I3_{adts} = I3_{adts - 1} + \mathop \sum \limits_{l} \mathop \sum \limits_{v} X8_{aldvts} - \mathop \sum \limits_{r} \mathop \sum \limits_{v} X3_{adrvts} \quad \forall a,d,t,s$$
(29)
$$\begin{aligned} I4_{pkts} = & I4_{pkts - 1} + \mathop \sum \limits_{r} \mathop \sum \limits_{v} X4_{prkvts} + \mathop \sum \limits_{j} \mathop \sum \limits_{v} RE_{pjt} \cdot Y5_{jkvt} \\ & - \mathop \sum \limits_{w} \mathop \sum \limits_{v} X5_{pkwvts} - \mathop \sum \limits_{l} \mathop \sum \limits_{v} X7_{pklvts} - \mathop \sum \limits_{n} \mathop \sum \limits_{v} X6_{pknvts} - d_{p} \left( {\mathop \sum \limits_{r} \mathop \sum \limits_{v} X4_{prkvts} + \mathop \sum \limits_{j} \mathop \sum \limits_{v} RE_{pjt} \cdot Y5_{jkvt} } \right)\quad \forall p,k,t,s \\ \end{aligned}$$
(30)
$$I5_{cits} = I5_{cits - 1} + \mathop \sum \limits_{m} \mathop \sum \limits_{v} Qp_{cmivts} + \mathop \sum \limits_{n} \mathop \sum \limits_{v} X10_{cnivts} - \mathop \sum \limits_{p} Q_{pits} \cdot h_{cp} \quad \forall c,i,t,s$$
(31)

Constraint (32) ensures that at least the external supplier supplies ƛ% of the raw material.

$$\mathop \sum \limits_{m} \mathop \sum \limits_{v} Qp_{c,m,i,v,t,s} *\mathchar'26\mkern-10mu\lambda \le \mathop \sum \limits_{mp} \mathop \sum \limits_{v} Qp_{c,mp,i,v,t,s} \quad \forall c,i,t,s$$
(32)

The storage capacity limits for new tire factories, distribution points, and centralized return sites are represented in constraints (33)–(35), respectively. The levels of inventory at each centralized return point and established distribution point cannot exceed their capacity.

$$\mathop \sum \limits_{p} Ps1_{p} \cdot I1_{{{\text{pits}}}} + \mathop \sum \limits_{c} CS_{c} \cdot I5_{{{\text{cits}}}} \le Tscap_{i} \quad \forall i,t,s$$
(33)
$$\mathop \sum \limits_{p} Ps1_{p} \cdot I2_{pdts} + \mathop \sum \limits_{a} Ps2_{a} \cdot I3_{adts} \le MIcap1_{d} \cdot Y2_{dt} \quad \forall d,t,s$$
(34)
$$\mathop \sum \limits_{p} Ps1_{p} \cdot I4_{pkts} \le MIcap2_{k} \cdot Y3_{kt} \quad \forall k,t,s$$
(35)

Constraints (36) and (37) are the amounts of the inputs to the distribution centers and the centralized return point; they are as large as the storage capacity of these centers.

$$\mathop \sum \limits_{p} \mathop \sum \limits_{i} \mathop \sum \limits_{v} X1_{pidvts} + \mathop \sum \limits_{a} \mathop \sum \limits_{l} \mathop \sum \limits_{v} X8_{aldvts} \le MIcap1_{d} \cdot Y2_{dt} \quad \forall d,t,s$$
(36)
$$\mathop \sum \limits_{p} \mathop \sum \limits_{r} \mathop \sum \limits_{v} X4_{prkvts} + \mathop \sum \limits_{p} \mathop \sum \limits_{j} \mathop \sum \limits_{v} RE_{pjt} \cdot Y5_{jkvt} \le MIcap2_{k} \cdot Y3_{kt} \quad \forall k,t,s$$
(37)

Constraints (38) and (39) show that the total amount of the sent goods and lost demands is equal to the amount of each retailer's demand.

$$\mathop \sum \limits_{d} \mathop \sum \limits_{v} X2_{pdrvts} + UD_{prts} = DE1_{prts} \quad \forall p,r,t,s$$
(38)
$$\mathop \sum \limits_{d} \mathop \sum \limits_{v} X3_{adrvts} + UD1_{arts} = DE2_{arts} \quad \forall a,r,t,s$$
(39)

Constraint (40) indicates that the percentage of products returning from the demand market is equal to the number of goods sent to the centralized return sites.

$$\mathop \sum \limits_{d} \mathop \sum \limits_{v} X2_{pdrvts} \cdot a_{ps} = \mathop \sum \limits_{k} \mathop \sum \limits_{v} X4_{prkvts} \quad \forall p,r,t,s$$
(40)

Constraints (41) and (42) indicate what percentage of the products goes to retreading centers and what percentage to the recycling factory.

$${\text{RTR}}_{plts} \cdot y1_{lt} = O_{pl} \cdot \mathop \sum \limits_{k} \mathop \sum \limits_{v} X7_{pklvts} \quad \forall p,l,t,s$$
(41)
$$\mathop \sum \limits_{n} \mathop \sum \limits_{v} X9_{p\ln vts} = \left( {1 - O_{pl} } \right) \cdot \mathop \sum \limits_{k} \mathop \sum \limits_{v} X7_{pklvts} \quad \forall p,l,t,s$$
(42)

Constraint (43) states that the number of types of p-type tires recycled in company n is equal to the percentage of tires that came from the retreading point and centralized return sites.

$${\text{REC}}_{pnts} \cdot y4_{nt} = \beta_{p} \cdot \left( {\mathop \sum \limits_{k} \mathop \sum \limits_{v} X6_{pknvts} + \mathop \sum \limits_{l} \mathop \sum \limits_{v} X9_{p\ln vts} } \right) \quad \forall p,n,t,s$$
(43)

Constraint (44) emphasizes that the total amount of recycled materials sent to manufacturers and secondary markets is as much as the recycled materials produced at recycling factory n.

$$\mathop \sum \limits_{i} \mathop \sum \limits_{v} X10_{cnivts} + Qs_{cnts} = \mathop \sum \limits_{p} REC_{pnts} \cdot h_{cp} \quad \forall c,n,t,s$$
(44)

Constraint (45) states that all of tires that are being retreaded are transferred to the distributor's point.

$$\mathop \sum \limits_{d} \mathop \sum \limits_{v} X8_{aldvts} = {\text{RTR}}_{plts} \quad \forall p = a,l,t,s$$
(45)

Constraint (46) ensures that initial collection centers are connected by only one vehicle to a centralized return point.

$$\mathop \sum \limits_{k} \mathop \sum \limits_{v} Y5_{jkvt} = 1\quad \forall j,t$$
(46)

Constraints (47)–(50) show the minimum amount of inventory in the centers that they can establish.

$$\mathop \sum \limits_{p} \mathop \sum \limits_{i} \mathop \sum \limits_{v} X1_{pidvts} + \mathop \sum \limits_{a} \mathop \sum \limits_{l} \mathop \sum \limits_{v} X8_{aldvts} \ge MT1_{d} \cdot Y2_{dt} \quad \forall d,t,s$$
(47)
$$\mathop \sum \limits_{p} \mathop \sum \limits_{r} \mathop \sum \limits_{v} X4_{prkvts} + \mathop \sum \limits_{p} \mathop \sum \limits_{j} \mathop \sum \limits_{v} RE_{pjt} \cdot Y5_{jkvt} \ge MT2_{k} \cdot Y3_{kt} \quad \forall k,t,s$$
(48)
$$\mathop \sum \limits_{a} \mathop \sum \limits_{d} \mathop \sum \limits_{v} X8_{aldvts} \ge MT3_{l} \cdot Y1_{lt} \quad \forall l,t,s$$
(49)
$$\mathop \sum \limits_{c} \mathop \sum \limits_{i} \mathop \sum \limits_{v} X10_{cnivts} + \mathop \sum \limits_{c} Qs_{cnts} \ge MT4_{n} \cdot Y4_{nt} \quad \forall n,t,s$$
(50)

Constraints (51)–(58) indicate the capacity of machines to transport materials and products among various facilities.

$$\mathop \sum \limits_{p} \mathop \sum \limits_{d} X1_{pidvts} \le VCap_{v} \cdot N1_{ivt} \quad \forall i,v,t,s$$
(51)
$$\mathop \sum \limits_{p} \mathop \sum \limits_{r} X2_{pdrvts} + \mathop \sum \limits_{a} \mathop \sum \limits_{r} X3_{adrvts} \le VCap_{v} \cdot N2_{dvt} \quad \forall d,v,t,s$$
(52)
$$\mathop \sum \limits_{p} \mathop \sum \limits_{k} X4_{prkvts} \le VCap_{v} \cdot N3_{rvt} \quad \forall r,v,t,s$$
(53)
$$\mathop \sum \limits_{p} \mathop \sum \limits_{k} Y5_{jkvt} \cdot RE_{pjt} \le VCap_{v} \cdot N4_{jvt} \quad \forall j,v,t$$
(54)
$$\mathop \sum \limits_{p} \mathop \sum \limits_{w} X5_{pkwvts} + \mathop \sum \limits_{p} \mathop \sum \limits_{n} X6_{pknvts} + \mathop \sum \limits_{p} \mathop \sum \limits_{l} X7_{pklvts} \le VCap_{v} \cdot N5_{kvt} \quad \forall k,v,t,s$$
(55)
$$\mathop \sum \limits_{a} \mathop \sum \limits_{d} X8_{aldvts} + \mathop \sum \limits_{p} \mathop \sum \limits_{n} X9_{p\ln vts} \le VCap_{v} \cdot N6_{lvt} \quad \forall l,v,t,s$$
(56)
$$\mathop \sum \limits_{c} \mathop \sum \limits_{i} X10_{cnivts} \le VCap_{v} \cdot N7_{nvt} \quad \forall n,v,t,s$$
(57)
$$\mathop \sum \limits_{c} \mathop \sum \limits_{i} Qp_{cmivts} \le VCap_{v} \cdot N8_{mvt} \quad \forall m,v,t,s$$
(58)

Constraints (59)–(62) indicate that a factory is maintained until the end of the design period.

$$Y1_{lt} \le Y1_{lt + 1} \quad \forall l,t = T - 1$$
(59)
$$Y1_{dt} \le Y2_{dt + 1} \quad \forall d,t = T - 1$$
(60)
$$Y3_{kt} \le Y3_{kt + 1} \quad \forall k,t = T - 1$$
(61)
$$Y4_{nt} \le Y4_{nt + 1} \quad \forall n,t = T - 1$$
(62)

The final constraints represent the type of decision variables.

$$Y1_{lt} ,Y2_{dt} ,Y3_{kt} ,Y4_{nt} ,Y5_{jkvt} \varepsilon \left( {0,1} \right)$$
(63)
$$X1_{pidvts} ,X2_{pdrvts} ,X3_{adrvt} ,X5_{pkwvts} ,X6_{pknvts} ,X7_{pklvts} , \ldots \ge 0$$
(64)

4 Stochastic programming

According to the practical conditions of the proposed problem, in this study, some parameters, including demand and return rate, are assumed uncertain. Here, uncertainty is in accordance with a two-stage stochastic programming and its uncertainty parameters are considered as possible scenarios. The following formulation is a common approach for two-stage stochastic programming (Brige and louveaux 2011):

$$\begin{gathered} {\text{Min}}\;z = c^{T} x + \mathop \sum \limits_{s} p^{s} b^{{s^{T} }} y^{s} \hfill \\ St. \hfill \\ Ax = d, \hfill \\ B^{s} x + D^{s} y^{s} = h^{s} ,s\varepsilon S \hfill \\ x \ge 0,\;y^{s} \ge 0 \hfill \\ \end{gathered}$$
(65)

The nature of this type of problem indicates that the decisions of the first stage (x) are made, while all the scenarios (S), the probability of their occurrence (p), and the values of the corresponding random parameters are known. However, the decisions of the second stage (ys) are taken, while one of the possible scenarios (S) has happened.

In the current study, the two-stage stochastic programming is planned such that in the first stage, it is decided for the establishment and non-establishment of facilities. Then, in the second stage, it determines the amount of production, the amount of retreading, and the amount of recycling.

5 The improved augmented ε-constraint (AUGMECON2)

The ε-constraint is one of the precise methods for solving multi-objective problems that have been very efficient and have been used in many problems, such as scheduling issues, operation sequences, and maintenance and repairs (Mavrotas 2009).

Here, the augmented ε-constraint method version 2 (AUGMECON2) is used. AUGMECON improves the typical ɛ-constraint to generate Pareto optimal solutions. In general, AUGMECON tries to address most of the weak points of the typical ɛ-constraint. In the conventional AUGMECON, the problem is formulated as the following mathematical model (Mavrotas and Florios 2013):

$$\begin{gathered} Max\left( {f_{1} \left( x \right) + eps*\left( {S_{2} /r_{2} + \ldots + S_{p} /r_{p} } \right)} \right) \hfill \\ St. \hfill \\ f_{2} \left( x \right) + S_{2} = \varepsilon_{2} , \hfill \\ . \hfill \\ . \hfill \\ f_{p} \left( x \right) + S_{p} = \varepsilon_{p} , \hfill \\ x\varepsilon S \hfill \\ \end{gathered}$$
(66)

where ɛ2; ɛ3;...; ɛp are the parameters of the RHS for the predetermined iteration drawn from the grid points of objectives 2, 3,..., p. Parameters r2, r3,..., rp are the ranges of the respective objectives. Scenarios S2, S3,..., Sp are distributed uniformly in eps ϵ [\({10}^{-6}\),\({10}^{-3}\)] and the surplus variables of the respective constraints. In the improved version of AUGMECON, named AUGMECON2, the objective is somewhat modified as follows:

$$Max(f1(x) + eps \times (S_{2} /r_{2} + 10^{( - 1)} \times \, n + 10^{ - p - 2} )) \times S_{2} /r_{2} ))$$
(67)

This modification should be done to perform a type of lexicographic optimization on the rest of the objectives if there are any optimum alternatives. For further studies, Mavrotas (2009) and Brige and Louveaux (2011) are suggested.

6 Case study

In order to represent the efficiency of the proposed MILP formulation for real-life applications, an Iranian tire industry is explained. Iran Tire is an automobile tire manufacturer in Tehran, Iran. It produces several types of tire with particular specifications such as quality and size. A percentage of their raw materials is imported. Accordingly, the supply chain consists of two suppliers (internal and external), a manufacturing company, two distribution points, two dealer centers, a temporary warehouse, a collection center, two retreading centers, two recycling centers, and a cement plant for fuel consumption. There are also two kinds of retreaded and new tires, i.e., bus and truck tires, as well as two kinds of material, i.e., steel and rubber. The planning time period is divided into two six-month periods. In this network, there are two types of transportation vehicles with several capacities, costs and environmental impacts. According to the decision maker, the costs are considered in a specific currency or monetary unit (e.g., $, €, etc.). Other parameters of the problem are given in Table 2.

Table 2 Parameters of case study and their ranges
Full size table

To consider the uncertainty of the model’s parameters, 18 (3 × 3 × 2) scenarios are defined. Thus, for new and retreaded tires, there are three modes; and two modes for the return rate of the products are considered. Data related to the demand for retreading and new tires are uncertain with an increase of 10% and a reduction of 20% from the previous data. The probability of the occurrence of each scenario is given in Table 3.

Table 3 Probability of different scenarios
Full size table

After running the model, on a personal computer with 2.8 GHz CPU and 8 GB main memory, the model was run through optimization software GAMS 24.0.1, including CPLEX 9.0, and the relationship between the first and second objectives in ten Pareto points is given in Table 4. Also, their performances are shown in Fig. 2. As can be concluded, the first and second objectives have a direct relationship, such that when the first objective is increased, the second objective increases also.

Table 4 Ten Pareto points derived from the objective functions
Full size table
Fig. 2
figure 2

Changes of the first objective to change the second objective in uncertainty conditions

Full size image

To consider the uncertainty of the model’s parameters, 18 (3 × 3 × 2) scenarios are defined. Thus, for new and retreaded tires there are three modes; two modes for the return rate of the products are considered. Data related to the demand for retreading and new tires are uncertain with an increase of 10% and a reduction of 20% from the previous data. The probability of the occurrence of each scenario is given in Table 3.

7 Sensitivity analysis

This section examines the effects of essential parameters such as the exchange rate and customs duty rates on the proposed mathematical model. Based on the decision maker's view, the importance of the objective functions may differ. The sensitivity analysis was performed based on three points (points A, B, and C), as indicated in Fig. 2. In this study, with an increase and decrease in the customs duty and exchange rates, the formulation is resolved (Figs. 3, 4). After each run, the values obtained from the first objective function are represented in Figs. 5, 6, 7 related to the exchange rate. It is clear that as the rate rises, the profit decreases. Therefore, the existence of an unsustainable economy in the country will be a risk to the global supply chain. Similarly, by analyzing sensitivity to customs duties, presented in Figs. 8, 9, 10, similar results are obtained. From a management perspective, national decisions about customs duties can affect organizational profit and decision making.

Fig. 3
figure 3

Forward logistic network for product type 1

Full size image
Fig. 4
figure 4

Reverse logistic network for product type 1

Full size image
Fig. 5
figure 5

Changes in the first objective relative to the exchange rate (point A in Fig. 2)

Full size image
Fig. 6
figure 6

Changes in the first objective relative to the exchange rate (see point B in Fig. 2)

Full size image
Fig. 7
figure 7

Changes in the first objective relative to the exchange rate of money (point C in Fig. 2)

Full size image
Fig. 8
figure 8

Changes to the first objective relative to the rate of customs duties (point A in Fig. 2)

Full size image
Fig. 9
figure 9

Changes to the primary objective relative to the rate of customs duties (point B in Fig. 2)

Full size image
Fig. 10
figure 10

Changes to the first objective relative to the rate of customs duties (point C in Fig. 2)

Full size image

8 Conclusions and future guides

In the current study, a MILP formulation has been used in order to study a closed-loop SCND with a two-objective function, i.e., maximizing profit and minimizing Eco-indicator 99 in a multi-product, multi-period, and multi-echelon formulation for tires. In this mathematical formulation, the constraints of supplying raw materials by external suppliers, shortage, and uncertainty are included. This proposed formulation was tested using a case study inspired by a tire industry in Tehran, Iran. In this research, it is observed that an optimal network with global factors can be very different, because the formulation is sensitive to customs duty and exchange rates. Both factors are related to economic, political, and other important national issues, and without considering the limitations of supplying raw materials by external suppliers, profits would increase by about 12%. On the other hand, by comparing the output of the model in the deterministic and stochastic modes, it can be concluded that not only the final profit rate in those two modes is different, but also the facilities that open and even the CPU solution time are different.

The following suggestions are given for future studies: Considering uncertainty in most of the parameters of the problem, the model is closer to reality and can be more reliable than the model output. If the size of the problem increases, GAMS 24.0.1 software cannot be solved and the solution time will increase; thus, there is an undeniable need to use metaheuristic and heuristic methods. Considering factors such as disturbances and failures in the components of the chain, as well as considering the lead time, is a significant element that can be aimed. The model can also be developed with consideration of external customers and tire imports, along with other important international factors such as income tax.