Thermal stresses in an orthotropic hollow sphere under thermal shock: a unified generalized thermoelasticity

Abstract

This paper deals with the thermoelasticity problem in an orthotropic hollow sphere. A unified governing equation is derived which includes the classical, Lord–Shulman and Green–Lindsay coupled theories of thermoelasticity. Time-dependent thermal and mechanical boundary conditions are applied to the inner and outer surfaces of the hollow sphere and the problem is solved analytically using the finite Hankel transform. The inner surface of the sphere is subjected to a thermal shock in the form of a prescribed heat flux. Subsequently, the thermal response, radial displacement, as well as radial, tangential, and circumferential stresses of the sphere are determined. The influence of different orthotropic material properties and relaxation time values is investigated and presented graphically. The obtained results demonstrate excellent agreement with the existing literature.

1 Introduction

Spherical vessels are extensively utilized across diverse engineering sectors like marine, aerospace, petrochemical, and mechanical. In addition to the mechanical loads that these structures experience, the coupling phenomenon between thermal and mechanical behaviors of materials holds significant relevance in diverse fields such as acoustics, geology, geophysics, and engineering. The thermal loads associated with these phenomena can sometimes reach magnitudes that lead to structural failure. To address this issue, generalized theories of thermoelasticity have been developed in recent decades. These theories introduce modifications to the energy equation, transforming it into a hyperbolic partial differential equation that admits finite speed for the propagation of thermal waves. Unlike classical theories, generalized thermoelasticity theories offer a more realistic approach to addressing engineering problems involving high heat fluxes, short time intervals, and low temperatures. In this regard, Lord and Shulman’s theory is one of the most well-known generalized thermoelasticity theories, which incorporates a relaxation time to modify Fourier’s law of heat conduction. Another thermoelasticity theory that admits the second sound effect is Green–Lindsay theory. Green and Lindsay introduced alterations to the stress–strain relationship and the energy equation by incorporating two relaxation times, which establish connections between stress, entropy, and the rate of temperature change. However, the governing equations of thermoelasticity are inherently complex due to the intricate coupling between elastic and thermal fields. This coupling leads to the introduction of additional constants and relaxation times in generalized thermoelasticity theories, further complicating the governing equations. As a result, analytical solutions, especially in the context of generalized theories, have not been extensively developed. Furthermore, the growing demand for materials with enhanced strength-to-weight ratios has prompted advances in the design of novel materials such as fiber-reinforced composites and manufacturing processes. The utilization of composite materials or diverse manufacturing techniques for spheres may lead to anisotropic mechanical properties. Consequently, it becomes imperative to analyze the response of structures composed of such materials to accurately predict their behavior and performance.

Tanigawa and Takeuti [1] studied a hollow sphere’s transient thermal stress problem. They obtained the distribution of the transient thermoelastic stresses using the Laplace transform. In their approach, stress and temperature distribution were determined simultaneously. Hata [2] investigated the thermal shock in a hollow sphere caused by rapid uniform heating. They employed Ray’s theory to extract closed-form relations for dynamic stresses. However, in their approach, no generality is considered for the thermal load. Misra et al. [3] discussed the generation of thermal stresses in an aeolotropic homogeneous continuum solid with a spherical cavity. They used Laplace transform to obtain temperature, stress, and displacement distributions. Wang et al. [4] using the separation of variables, presented numerical results to show the uniformly heated hollow spheres’ dynamic stress responses. They solved the problem by resolving the radial displacement into two functions. One of these functions satisfies homogeneous mechanical boundary conditions while the other fulfills inhomogeneous boundary conditions. A method to obtain the temperature distribution is not presented in their work. Kiani and Eslami [5] solved the thermally nonlinear thermoelasticity problem of an isotropic homogeneous thick sphere subjected to a heat flux. They employed the Lord–Shulman theory of thermoelasticity and solved the problem using the generalized differential quadrature method and Newmark time marching scheme. Bagri and Eslami [6] studied the dynamic response of an isotropic annular disk using Lord and Shulman’s theory of thermoelasticity. The problem is solved using the Laplace transform and Finite Element Method. They also investigated the effects of relaxation time and thermoelastic coupling coefficient. Javani et al. [7] proposed a unified formulation that includes Lord–Shulman, Green–Lindsay, and Green–Naghdi theories, to investigate the thermo-visco-elastic response of a hollow sphere under thermal shock. They solved the problem using Newmark time marching and Finite Element methods. In the context of FGM and orthotropic materials, some new studies in thermoelasticity are recently published [8,9,10,11,12,13]. Alavi et al. [14] studied the thermoelastic behavior of thick functionally graded hollow spheres under combined thermal and mechanical loads. Mechanical and thermal properties of FGM sphere are assumed to be functions of radial position. Lee [15] presented quasi-static thermoelastic for multilayered spheres. The governing equation’s general solutions are obtained in the transform domain using the Laplace transform. The solution is obtained using the matrix similarity transformation and inverse Laplace transform. Stampouloglou et al. [16] studied the axisymmetric thermoelastic problem for a radially nonhomogeneous equal thickness spherical shell. They solved the problem under a radially varying temperature field, with axisymmetric geometry and loading. Bagri and Eslami [17] proposed a unified formulation to investigate both cylinders and spheres made of an anisotropic heterogeneous material. The proposed formulation covers generalized theories of coupled thermoelasticity based on the Lord–Shulman, Green–Lindsay, and Green–Naghdi models. They solved the problem in a sphere and cylinder subjected to thermal shock using Laplace transform and numerically calculated the inversions. Sharifi [18] proposed a unified formulation to investigate the thermal shock problem in an orthotropic cylinder. The formulation is based on the Green–Lindsay and Lord–Shulman theories of thermoelasticity. They solved the problem using the finite Hankel transform.

Despite extensive investigations, to the best of the authors’ knowledge, the problem of generalized coupled thermoelasticity in the orthotropic sphere remains unaddressed in the existing literature. This research paper aims to fill this gap by providing an analytical solution for the aforementioned problem. This study presents a unified formulation for the thermoelasticity problem based on the classical, Lord–Shulman, and Green–Lindsay’s theories of thermoelasticity for an orthotropic hollow sphere. The thermal boundary conditions entail prescribing a heat flux on the inner surface and a constant temperature on the outer surface of the sphere. Meanwhile, the mechanical boundary conditions involve constant displacement for the inner boundary while traction is prescribed on the outer boundary. The problem has been assumed to be one-dimensional and the finite Hankel transform is utilized to obtain the solution for the displacement and temperature fields. As a case study, we examine an orthotropic sphere exposed to a constant heat flux on its inner surface while maintaining a zero temperature on the outer surface. The numerical outcomes of this scenario are then depicted in the form of graphical figures, illustrating the propagation and reflection of temperature and stress waves. To validate the accuracy of the obtained solution, the generalized coupled thermoelasticity problem is reduced to a special case, and a comparison is made with results obtained by other researchers, demonstrating excellent agreement. Furthermore, the effects of orthotropic material and different relaxation times on the temperature distribution, displacement, and stresses are investigated and depicted through graphical representations.

2 Formulation

To unify the classical dynamic, Lord–Shulman, and Green–Lindsay theories of thermoelasticity, it is possible to formulate the system of equations that expresses the relations between stress–strain fields, the heat conduction equation, and the equation of motion in the following manner [9, 19]:

$$ C_{ijkl} u_{k,lj} + F_{i} - \beta_{ij} \left( {T_{,i} + t_{1} \dot{T}_{,i} } \right) = \rho \ddot{u}_{i}. $$

(1a)

$$ K_{ij} T_{,ij} = \rho c\left( {\dot{T} + t_{2} \ddot{T}} \right) + \left( {1 + t_{3} \frac{\partial }{\partial t}} \right)\left( { T_{0} \beta_{ij} \dot{\varepsilon }_{ij} - \rho Q} \right). $$

(1b)

$$ \sigma_{ij} = C_{ijkl} u_{k,l} - \beta_{ij} \left( {T + t_{1} \dot{T}} \right). $$

(1c)

It can be seen that, when $t_{1} = t_{2} = t_{3} = 0$ these equations reduce to classical dynamic theory, when $t_{1} = 0$ and $t_{2} = t_{3}$, Lord–Shulman theory can be deduced; and setting $t_{3} = 0$ leads to Green–Lindsay theory of thermoelasticity.

Now, consider a hollow orthotropic sphere with the inner radius of $a$ and the outer radius of $b$ in undisturbed condition and at the reference temperature $T_{0}$. We use a spherical coordinate $\left( {r, \theta , \varphi } \right)$ with the sphere’s center as the origin. Since the sphere is subjected to spherically symmetric boundary conditions, the displacement $u = \left[ {u\left( {r, t} \right), 0, 0} \right]$ and temperature $T$ are assumed to be functions of radius ($r$) and time ($t$) only. Consequently, the problem is simplified to a one-dimensional form [10, 20]. Thus, the relations between stress and strain components are [10, 21]:

$$ \left[ {\begin{array}{*{20}c} {\sigma_{r} } \\ {\sigma_{\theta } } \\ {\sigma_{\varphi } } \\ {\tau_{\theta \varphi } } \\ {\tau_{\varphi r} } \\ {\tau_{r\theta } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{13} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & {C_{23} } & 0 & 0 & 0 \\ {C_{13} } & {C_{23} } & {C_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right]\left( {\left[ {\begin{array}{*{20}c} {\varepsilon_{r} - \alpha_{r} \Delta T} \\ {\varepsilon_{\theta } - \alpha_{\theta } \Delta T} \\ {\varepsilon_{\varphi } - \alpha_{\varphi } \Delta T} \\ {\gamma_{\theta \varphi } } \\ {\gamma_{\varphi r} } \\ {\gamma_{r\theta } } \\ \end{array} } \right]} \right). $$

(2)

where $C_{ij}$ are the elastic constants and $\alpha_{r}$, $\alpha_{\theta }$, and $\alpha_{\varphi }$ are the thermal expansion coefficients in $r$, $\theta ,\varphi$ directions, respectively. Due to symmetry, by omitting all displacement components and all derivatives in the $\theta$ and $\varphi$ directions, the equation of motion in spherical coordinates is obtained as [10, 20]:

$$ \frac{{\partial \sigma_{r} }}{\partial r} + \frac{1}{r}\left( {2\sigma_{r} - \sigma_{\theta } - \sigma_{\varphi } } \right) + \rho b_{i} = \rho \ddot{u}. $$

(3)

in which $\rho$ is the density and $b_{i}$ is the body force. The strain components can be expressed in terms of the non-vanishing displacement component as follows:

$$ \varepsilon_{r} = \frac{\partial u}{{\partial r}} ;\varepsilon_{\theta } = \varepsilon_{\varphi } = \frac{u}{r};\gamma_{\theta \varphi } = \gamma_{\varphi r} = \gamma_{r\theta } = 0. $$

(4)

Finally, in the absence of body forces and using Eqs. (1a), (1b), (1c), (2), (3), and (4), the equation of motion in terms of displacement and temperature can be expressed in the following form:

$$ C_{11} \left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{2}{r}\frac{\partial u}{{\partial r}}} \right) - \left( {C_{22} + 2C_{23} + C_{33} - C_{12} - C_{13} } \right)\frac{u}{{r^{2} }} - \beta_{11} \left( {\frac{\partial \psi }{{\partial r}} + t_{1} \frac{{\partial \dot{\psi }}}{\partial r}} \right) + \frac{1}{r}\left( {\beta_{33} + \beta_{22} - 2\beta_{11} } \right)\left( {\psi + t_{1} \dot{\psi }} \right) = \rho \frac{{\partial^{2} u}}{{\partial t^{2} }}. $$

(5)

in which a dot over the quantity is the partial derivative of it with respect to time and:

$$ \beta_{11} = C_{11} \alpha_{r} + C_{12} \alpha_{\theta } + C_{13} \alpha_{\varphi }. $$

(6a)

$$ \beta_{22} = C_{12} \alpha_{r} + C_{22} \alpha_{\theta } + C_{23} \alpha_{\varphi }. $$

(6b)

$$ \beta_{33} = C_{13} \alpha_{r} + C_{23} \alpha_{\theta } + C_{33} \alpha_{\varphi }. $$

(6c)

and

$$ \psi = T\left( {r,t} \right) - T_{0}. $$

(7)

Also, in cases with spherically symmetric thermal boundary conditions and no internal heat generation, $K_{11} = K_{22} = K_{33} = K$ and the temperature distribution becomes independent of θ and φ [22]; thus, using Eqs. (4) and Eq. (1b) the conduction equation can be expressed in the following form:

$$ K\left( {\frac{{\partial^{2} \psi }}{{\partial r^{2} }} + \frac{2}{r}\frac{\partial \psi }{{\partial r}}} \right) - T_{0} \beta_{11} \left( {\frac{{\partial \dot{u}}}{\partial r} + t_{3} \frac{{\partial \ddot{u}}}{\partial r}} \right) - T_{0} \left( {\beta_{22} + \beta_{33} } \right)\left( {\frac{{\dot{u}}}{r} + t_{3} \frac{{\ddot{u}}}{r}} \right) = \rho c\left( {\frac{\partial \psi }{{\partial t}} + t_{2} \frac{{\partial^{2} \psi }}{{\partial t^{2} }}} \right). $$

(8)

The non-vanishing stress components, namely $\sigma_{r}$, $\sigma_{\theta }$, and $\sigma_{\varphi }$, are related to the displacement components and the temperature as:

$$ \sigma_{r} = C_{11} \frac{\partial u}{{\partial r}} + (C_{12} + C_{13} )\frac{u}{r} - \beta_{11} \left( {\psi + t_{1} \dot{\psi }} \right). $$

(9a)

$$ \sigma_{\theta } = C_{12} \frac{\partial u}{{\partial r}} + \left( {C_{22} + C_{23} } \right)\frac{u}{r} - \beta_{22} \left( {\psi + t_{1} \dot{\psi }} \right). $$

(9b)

$$ \sigma_{\varphi } = C_{13} \frac{\partial u}{{\partial r}} + \left( {C_{23} + C_{33} } \right)\frac{u}{r} - \beta_{33} \left( {\psi + t_{1} \dot{\psi }} \right). $$

(9c)

In terms of mechanical boundary conditions, the inner surface of the sphere experiences a constant displacement, while traction is prescribed on the outer surface:

$$ u^{ } \left( {a,t} \right) = f_{1} \left( t \right). $$

(10a)

$$ \sigma_{r} \left( {b,t} \right) = f_{2} \left( t \right). $$

(10b)

where $f_{1} \left( t \right)$ and $f_{2} \left( t \right)$ are defined time-dependent functions. By substituting Eq. (9a) in Eq. (10b), we have

$$ C_{11} \frac{\partial u}{{\partial r}}\left| {_{r = b} } \right. + \left( {C_{12} + C_{13} } \right)\frac{{u\left( {b,t} \right)}}{b} = f_{2} \left( t \right) + \beta_{11} \left( {\psi \left( {b,t} \right) + t_{1} \dot{\psi }\left( {b,t} \right)} \right). $$

(11)

As observed, we consider the mechanical boundary conditions to be time-dependent and expressed in a general form. Concerning the initial conditions of the radial displacement field, we have

$$ u_{ } \left( {r,0} \right) = f_{3} \left( r \right). $$

(12a)

$$ \dot{u}_{ } \left( {r,0} \right) = f_{4} \left( r \right). $$

(12b)

where $f_{3} \left( r \right)$ and $f_{4} \left( r \right)$ are defined functions of the radial position. For the energy equation, temperature is prescribed on the outer surfaces of the sphere, and the inner surface is subjected to a heat flux. Thus, we assumed the boundary and initial conditions in the following form:

$$ - k\frac{\partial \psi }{{\partial r}}\left| {_{{_{r = a} }} } \right. = g_{1} \left( t \right). $$

(13a)

$$ \psi \left( {b,t} \right) = g_{2} \left( t \right). $$

(13b)

$$ \psi \left( {r,0} \right) = g_{3} \left( r \right). $$

(13c)

$$ \dot{\psi }\left( {r,0} \right) = g_{4} \left( r \right). $$

(13d)

where $g_{1} \left( t \right)$ and $g_{2} \left( t \right)$ are defined time-dependent functions and $g_{3} \left( r \right)$ and $g_{4} \left( r \right)$ are defined functions of the radial position.

3 The method of solution

For the sake of analysis, using the following dimensionless parameters, the proceeding equations may be changed into the dimensionless form [17]:

$$ \begin{gathered} \hat{r} = \frac{r}{l}\;\;\;\;\;\;\;\;\;\;\;\;\hat{t} = \frac{t\gamma }{l}\;\;\;\;\;\;\;\;\hat{q}_{i} = \frac{{q_{i} l}}{{kT_{0} }}\;\;\;\;\;\;\;\hat{\psi } = \frac{\psi }{{T_{0} }} \hfill \\ \hat{u} = \frac{{C_{11} }}{{l\beta_{11} T_{0} }}u\;\;\;\hat{\sigma }_{r} = \frac{{\sigma_{r} }}{{\beta_{11} T_{0} }}\;\;\hat{\sigma }_{\theta } = \frac{{\sigma_{\theta } }}{{\beta_{11} T_{0} }}\;\;\;\hat{\sigma }_{\varphi } = \frac{{\sigma_{\varphi } }}{{\beta_{11} T_{0} }} \hfill \\ \hat{t}_{1} = \frac{{t_{1} \gamma }}{l}\;\;\;\;\;\;\,\;\;\hat{t}_{2} = \frac{{t_{2} \gamma }}{l}\;\;\;\;\;\;\hat{t}_{3} = \frac{{t_{3} \gamma }}{l} \hfill \\ \end{gathered}. $$

(14)

where

$$ l = \frac{k}{\rho c\gamma }. $$

(15)

$$ \gamma = \sqrt {\frac{{C_{11} }}{\rho }}. $$

(16)

Dropping the hat sign for convenience, and introducing:

$$ u = r^{{ - \frac{1}{2}}} w. $$

(17a)

$$ \psi = r^{{ - \frac{1}{2}}} \theta. $$

(17b)

Equations (4) and (8) could be rewritten as:

$$ \frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{{\partial r}} - v^{2} \frac{w}{{r^{2} }} - \left( {\frac{\partial \theta }{{\partial r}} + t_{1} \frac{{\partial \dot{\theta }}}{\partial r}} \right) + \frac{1}{r}\left( {D - \frac{3}{2}} \right)\left( {\theta + t_{1} \dot{\theta }} \right) = \frac{{\partial^{2} w}}{{\partial t^{2} }}. $$

(18)

$$ \frac{{\partial^{2} \theta }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \theta }{{\partial r}} - \frac{1}{4}\frac{\theta }{{r^{2} }} - C\left( {\frac{{\partial \dot{w}}}{\partial r} + t_{3} \frac{{\partial \ddot{w}}}{\partial r}} \right) - C\left( {D - \frac{1}{2}} \right)\left( {\frac{{\dot{w}}}{r} + t_{3} \frac{{\ddot{w}}}{r}} \right) = \frac{\partial \theta }{{\partial t}} + t_{2} \frac{{\partial^{2} \theta }}{{\partial t^{2} }}. $$

(19)

in which

$$ v^{2} = \frac{{C_{22} + 2C_{23} + C_{33} - C_{12} - C_{13} }}{{C_{11} }} + \frac{1}{4}. $$

(20)

$$ D = \frac{{\beta_{33} + \beta_{22} }}{{\beta_{11} }}. $$

(21)

$$ C = { }\frac{{T_{0} \beta_{11}^{2} }}{{\rho cC_{11} }}. $$

(22)

The coefficient $D$ quantifies the impact of accounting for orthotropic material behavior, while $C$ represents the thermomechanical coupling coefficient. It’s worth noting that when material properties are equal in different directions, $D$ and $v^{2}$ equal $2$ and $2.25$, respectively, causing the equations for the orthotropic sphere to simplify to those of an isotropic material [17]. For the mechanical boundary and initial conditions, we have:

$$ w^{ } \left( {a,t} \right) = \frac{{C_{11} \sqrt a }}{{l\beta_{11} T_{0} }}f_{1} \left( t \right) = f_{1}^{*} \left( t \right). $$

(23a)

$$ \frac{\partial w}{{\partial r}}\left| {_{r = b} } \right. + h_{1} w\left( {b,t} \right) = \frac{\sqrt b }{{\beta_{11} T_{0} }}f_{2} \left( t \right) + \frac{{\sqrt b g_{2} \left( t \right)}}{{T_{0} }} = f_{2}^{*} \left( t \right). $$

(23b)

$$ w_{ } \left( {r,0} \right) = \frac{{C_{11} \sqrt r }}{{l\beta_{11} T_{0} }}f_{3} \left( r \right) = f_{3}^{*} \left( r \right). $$

(23c)

$$ \dot{w}_{ } \left( {r,0} \right) = \frac{{C_{11} l\sqrt r }}{{\gamma \beta_{11} T_{0} }}f_{4} \left( r \right) = f_{4}^{*} \left( r \right). $$

(23d)

where

$$ h_{1} = \frac{1}{b}\left( {\frac{{C_{12} + C_{13} }}{{C_{11} }} - \frac{1}{2}} \right). $$

(24)

Similarly, the thermal boundary and initial conditions take the following form:

$$ \frac{\partial \theta }{{\partial r}}\left| {_{r = a} } \right. + h_{2} \theta \left( {a,t} \right) = - \frac{l\sqrt a }{{T_{0} }}g_{1} \left( t \right) = g_{1}^{*} \left( t \right). $$

(25a)

$$ \theta \left( {b,t} \right) = \frac{\sqrt b }{{T_{0} }}g_{2} \left( t \right) = g_{2}^{*} \left( t \right). $$

(25b)

$$ \theta \left( {r,0} \right) = \frac{\sqrt r }{{T_{0} }}g_{3} \left( r \right) = g_{3}^{*} \left( r \right). $$

(25c)

$$ \dot{\theta }\left( {r,0} \right) = \frac{l\sqrt r }{{\gamma T_{0} }}g_{4} \left( r \right) = g_{4}^{*} \left( r \right). $$

(25d)

where

$$ h_{2} = - \frac{1}{2a}. $$

(26)

To solve the coupled thermoelasticity equations (Eqs. (18) and (19)), $w\left( {r,t} \right)$ and $\theta \left( {r,t} \right)$ are resolved into two components [23]:

$$ w\left( {r,t} \right) = w_{1} \left( {r,t} \right) + w_{2} \left( {r,t} \right). $$

(27)

$$ \theta \left( {r,t} \right) = \theta_{1} \left( {r,t} \right) + \theta_{2} \left( {r,t} \right). $$

(28)

Then, the boundary value problem related to the displacement equation is resolved into the following two boundary value problems. In which, boundary conditions are assigned to the first homogeneous part of the differential equation ($w_{1} \left( {r,t} \right)$ and $\theta_{1} \left( {r,t} \right)$) and initial conditions to the second inhomogeneous part ($w_{2} \left( {r,t} \right)$ and $\theta_{2} \left( {r,t} \right)$):

$$ \frac{{\partial^{2} w_{1} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial w_{1} }}{\partial r} - v^{2} \frac{{w_{1} }}{{r^{2} }} = \ddot{w}_{1}. $$

(29a)

$$ w_{1} \left( {a,t} \right) = f_{1}^{*} \left( t \right). $$

(29b)

$$ \frac{{\partial w_{1} }}{\partial r}\left| {_{r = b} } \right. + h_{1} w_{1} \left( {b,t} \right) = f_{2}^{*} \left( t \right). $$

(29c)

$$ w_{1} \left( {r,0} \right) = 0. $$

(29d)

$$ \dot{w}_{1} \left( {r,0} \right) = 0. $$

(29e)

and

$$ \frac{{\partial^{2} w_{2} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial w_{2} }}{\partial r} - v^{2} \frac{{w_{2} }}{{r^{2} }} - \frac{\partial \theta }{{\partial r}} + \frac{1}{r}\left( {D - \frac{3}{2}} \right)\left( {\theta + t_{1} \dot{\theta }} \right) = \ddot{w}_{2}. $$

(30a)

$$ w_{2} \left( {a,t} \right) = 0. $$

(30b)

$$ \frac{{\partial w_{2} }}{\partial r}\left| {_{r = b} } \right. + h_{1} w_{2} \left( {b,t} \right) = 0. $$

(30c)

$$ w_{2} \left( {r,0} \right) = f_{3}^{*} \left( r \right). $$

(30d)

$$ \dot{w}_{2} \left( {r,0} \right) = f_{4}^{*} \left( r \right). $$

(30e)

The energy equation is treated similarly:

$$ \frac{{\partial^{2} \theta_{1} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial \theta_{1} }}{\partial r} - \frac{1}{4}\frac{{\theta_{1} }}{{r^{2} }} = \dot{\theta }_{1} + t_{2} \ddot{\theta }_{1}. $$

(31a)

$$ \frac{{\partial \theta_{1} }}{\partial r}\left| {_{r = a} } \right. + h_{2} \theta_{1} \left( {a,t} \right) = g_{1}^{*} \left( t \right). $$

(31b)

$$ \theta_{1} \left( {b,t} \right) = g_{2}^{*} \left( t \right). $$

(31c)

$$ \theta_{1} \left( {r,0} \right) = 0. $$

(31d)

$$ \dot{\theta }_{1} \left( {r,0} \right) = 0. $$

(31e)

and

$$ \left\{ {\frac{{\partial^{2} \theta_{2} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial \theta_{2} }}{\partial r} - \frac{1}{{4r^{2} }}\theta_{2} } \right\} - C\left( {\frac{{\partial \dot{w}}}{\partial r} + t_{3} \frac{{\partial \ddot{w}}}{\partial r}} \right) - C\left( {D - \frac{1}{2}} \right)\left( {\frac{{\dot{w}}}{r} + t_{3} \frac{{\ddot{w}}}{r}} \right) = \dot{\theta }_{2} + t_{2} \ddot{\theta }_{2}. $$

(32a)

$$ \frac{{\partial \theta_{2} }}{\partial r}\left| {_{r = a} } \right. + h_{2} \theta_{2} \left( {a,t} \right) = 0. $$

(32b)

$$ \theta_{2} \left( {b,t} \right) = 0. $$

(32c)

$$ \theta_{2} \left( {r,0} \right) = g_{3}^{*} \left( r \right). $$

(32d)

$$ \dot{\theta }_{2} \left( {r,0} \right) = g_{4}^{*} \left( r \right). $$

(32e)

Equations (29) and (31) are Bessel-type equations and could be solved using the finite Hankel transform [24]:

$$ {\mathcal{H}}_{ } \left[ {w_{1} \left( {r,t} \right);\xi_{m} } \right] = \overline{w}_{1} \left( {\xi_{m} ,t} \right) = \mathop \smallint \limits_{a}^{b} rw_{1} \left( {r,t} \right){\mathcal{K}}_{1} \left( {r,\xi_{m} } \right){\text{d}}r. $$

(33)

$$ {\mathcal{H}}_{ } \left[ {\theta \left( {r,t} \right);\lambda_{n} } \right] = \overline{\theta }_{1} \left( {\lambda_{n} ,t} \right) = \mathop \smallint \limits_{a}^{b} r\theta_{1} \left( {r,t} \right){\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right){\text{d}}r. $$

(34)

where ${\mathcal{K}}_{1} \left( {r,\xi_{m} } \right)$ and ${\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right)$ are the kernels of the transformation. The selection of the appropriate kernel depends on both the general form of the equation and the specified boundary conditions. For the current problem, the transformation kernels are defined as follows [25]:

$$ {\mathcal{K}}_{1} \left( {r,\xi_{m} } \right) = J_{v} \left( {\xi_{m} r} \right)Y_{v} \left( {\xi_{m} a} \right) - J_{v} \left( {\xi_{m} a} \right)Y_{v} \left( {\xi_{m} r} \right). $$

(35)

$$ {\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right) = J_{0.5} \left( {\lambda_{n} r} \right)Y_{0.5} \left( {\lambda_{n} b} \right) - J_{0.5} \left( {\lambda_{n} b} \right)Y_{0.5} \left( {\lambda_{n} r} \right). $$

(36)

where $\xi_{m}$ and $\lambda_{n}$ are the positive roots of the following characteristic equations:

$$ Y_{v} \left( {\xi_{m} a} \right)\left[ {\xi_{m} J^{\prime}_{v} \left( {\xi_{m} b} \right) + h_{1} J_{v} \left( {\xi_{m} b} \right)} \right] - J_{v} \left( {\xi_{m} a} \right)\left[ {\xi_{m} Y^{\prime}_{v} \left( {\xi_{m} b} \right) + h_{1} Y_{v} \left( {\xi_{m} b} \right)} \right] = 0. $$

(37)

$$ Y_{0.5} \left( {\lambda_{n} b} \right)\left[ {\lambda_{n} J^{\prime}_{0.5} \left( {\lambda_{n} a} \right) + h_{2} J_{0.5} \left( {\lambda_{n} a} \right)} \right] - J_{0.5} \left( {\lambda_{n} b} \right)\left[ {\lambda_{n} Y^{\prime}_{0.5} \left( {\lambda_{n} a} \right) + h_{2} Y_{0.5} \left( {\lambda_{n} a} \right)} \right] = 0. $$

(38)

The inverse transformations are defined as [25]:

$$ {\mathcal{H}}^{ - 1}_{ } \left[ {\overline{w}_{1} \left( {\xi_{m} ,t} \right);r} \right] = w_{1} \left( {r,t} \right) = \mathop \sum \limits_{m = 1}^{\infty } a_{m} \overline{w}_{1} \left( {\xi_{m} ,t} \right){\mathcal{K}}_{1} \left( {r,\xi_{m} } \right). $$

(39)

$$ {\mathcal{H}}^{ - 1}_{ } \left[ {\overline{\theta }_{1} \left( {\lambda_{n} ,t} \right);r} \right] = \theta_{1} \left( {r,t} \right) = \mathop \sum \limits_{n = 1}^{\infty } b_{n} \overline{\theta }_{1} \left( {\lambda_{n} ,t} \right){\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right). $$

(40)

where

$$ a_{m} = \frac{1}{{\mathop \smallint \nolimits_{a}^{b} r\left\{ {{\mathcal{K}}_{1} \left( {r,\xi_{m} } \right)} \right\}^{2} {\text{d}}r}} = \frac{{\pi^{2} }}{2} \frac{{\xi_{m}^{2} e_{1}^{2} }}{{J_{v}^{2} \left( {\xi_{m} a} \right)\left( {h_{1}^{2} + \xi_{m}^{2} \left[ {1 - \left( {\frac{v}{{\xi_{m} b}}} \right)^{2} } \right]} \right) - e_{1}^{2} }}. $$

(41)

$$ b_{n} = \frac{1}{{\mathop \smallint \nolimits_{a}^{b} r\left\{ {{\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right)} \right\}^{2} {\text{d}}r}} = \frac{{\pi^{2} }}{2} \frac{{\lambda_{n}^{2} e_{2}^{2} }}{{e_{2}^{2} - J_{0.5}^{2} \left( {\lambda_{n} b} \right)\left( {h_{2}^{2} + \lambda_{n}^{2} \left[ {1 - \left( {\frac{0.5}{{\lambda_{n} a}}} \right)^{2} } \right]} \right)}}. $$

(42)

in which

$$ e_{1} = \xi_{m} J^{\prime}_{v} \left( {\xi_{m} b} \right) + h_{1} J_{v} \left( {\xi_{m} b} \right). $$

(43)

$$ e_{2} = \lambda_{n} J^{\prime}_{0.5} \left( {\lambda_{n} a} \right) + h_{2} J_{0.5} \left( {\lambda_{n} a} \right). $$

(44)

Applying the finite Hankel transform to Eqs. (29a) and (31a), yields:

$$ \frac{{\partial^{2} \overline{w}_{1} \left( {\xi_{m} ,t} \right)}}{{\partial t^{2} }} + \xi_{m}^{2} \overline{w}_{1} \left( {\xi_{m} ,t} \right) = \frac{2}{\pi }\left[ {\frac{{J_{v} \left( {\xi_{m} a} \right)}}{{e_{1} }}f_{2}^{*} \left( t \right) - f_{1}^{*} \left( t \right)} \right] = G\left( t \right). $$

(45)

$$ t_{2} \frac{{\partial^{2} \overline{\theta }_{1} \left( {\lambda_{n} ,t} \right)}}{{\partial t^{2} }} + \frac{{\partial \overline{\theta }_{1} \left( {\lambda_{n} ,t} \right)}}{\partial t} + \lambda_{n}^{2} \overline{\theta }_{1} \left( {\lambda_{n} ,t} \right) = \frac{2}{\pi }\left[ {g_{2}^{*} \left( t \right) - \frac{{J_{0.5} \left( {\lambda_{n} b} \right)}}{{e_{2} }}g_{1}^{*} \left( t \right)} \right] = V\left( t \right). $$

(46)

Equations (45) and (46) are a nonhomogeneous ordinary differential equation, which can be solved in the following manner:

$$ \overline{w}_{1} \left( {\xi_{m} ,t} \right) = \frac{1}{{\xi_{m} }}\mathop \smallint \limits_{0}^{t} G\left( \tau \right)\sin \left( {\xi_{m} \left( {t - \tau } \right)} \right){\text{d}}\tau. $$

(47)

$$ \overline{\theta }_{1} \left( {\lambda_{n} ,t} \right) = \frac{2}{\Delta }\left\{ {\mathop \smallint \limits_{0}^{t} V\left( \tau \right){\text{e}}^{{ - \frac{1}{{2t_{2} }}\left( {t - \tau } \right)}} {\text{sin}}\left( {\frac{\Delta }{{2t_{2} }}\left( {t - \tau } \right)} \right) {\text{d}}\tau } \right\}. $$

(48)

where $\Delta = \sqrt {4t_{2} \lambda_{n}^{2} - 1}$. Using the inversion relations (Eqs. (39) and (40)), we have:

$$ w_{1} \left( {r,t} \right) = \mathop \sum \limits_{m = 1}^{\infty } \frac{1}{{\xi_{m} }}a_{m} {\mathcal{K}}_{1} \left( {r,\xi_{m} } \right)\mathop \smallint \limits_{0}^{t} G\left( \tau \right)\sin \left( {\xi_{m} \left( {t - \tau } \right)} \right){\text{d}}\tau. $$

(49)

$$ \theta_{1} \left( {r,t} \right) = \mathop \sum \limits_{n = 1}^{\infty } b_{n} {\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right)\frac{2}{\Delta }\left\{ {\mathop \smallint \limits_{0}^{t} V\left( \tau \right){\text{e}}^{{ - \frac{1}{{2t_{2} }}\left( {t - \tau } \right)}} {\text{sin}}\left( {\frac{\Delta }{{2t_{2} }}\left( {t - \tau } \right)} \right){\text{d}}\tau } \right\}. $$

(50)

Up to now, we have successfully solved the first set of equations. To address the second set of equations, we adopt the following forms for $w_{2} \left( {r,t} \right)$ and $\theta_{2} \left( {r,t} \right)$ [23]:

$$ w_{2} \left( {r,t} \right) = \mathop \sum \limits_{m = 1}^{\infty } A\left( t \right) \cdot {\mathcal{K}}_{1} \left( {r,\xi_{m} } \right). $$

(51)

$$ \theta_{2} \left( {r,t} \right) = \mathop \sum \limits_{n = 1}^{\infty } B\left( t \right) \cdot { }{\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right). $$

(52)

in which $A\left( t \right)$ and $B\left( t \right)$ are time-dependent functions that remain undetermined and need to be derived. It’s important to emphasize that the chosen form for $w_{2} \left( {r,t} \right)$ and $\theta_{2} \left( {r,t} \right)$ satisfies the related boundary conditions (Eqs. (30b), (30c) and Eqs. (32b), (32c)). Substituting Eqs. (49), (50), (51), and (52) into Eqs. (30a) and (32a) yields:

$$ \left[ {\ddot{A} + \xi_{m}^{2} A} \right]{\mathcal{K}}_{1} \left( {r,\xi_{m} } \right) = \left[ {B + b_{n} \overline{\theta }_{1} + t_{1} \left( {\dot{B} + b_{n} \dot{\overline{\theta }}_{1} } \right)} \right]\left[ { - \frac{{\partial {\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right)}}{\partial r} + \left( {D - \frac{3}{2}} \right)\frac{{{\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right)}}{r}} \right]. $$

(53)

$$ \left[ {t_{2} \ddot{B} + \dot{B} + \lambda_{n}^{2} B} \right]{\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right) = - C\left[ {\dot{A} + a_{m} \dot{\overline{w}}_{1} + t_{3} \left( {\ddot{A} + a_{m} \ddot{\overline{w}}_{1} } \right)} \right]\left[ {\frac{{\partial {\mathcal{K}}_{1} \left( {r,\xi_{m} } \right)}}{\partial r} + \left( {D - \frac{1}{2}} \right)\frac{{{\mathcal{K}}_{1} \left( {r,\xi_{m} } \right)}}{r}} \right]. $$

(54)

By leveraging the orthogonal property of the Bessel functions, we arrive at the following equation [24]:

$$ \mathop \smallint \limits_{a}^{b} r{\mathcal{K}}_{1} \left( {r,\xi_{m} } \right){\mathcal{K}}_{1} \left( {r,\xi_{p} } \right){\text{d}}r = S_{m} \delta_{mp}. $$

(55)

$$ \mathop \smallint \limits_{a}^{b} r{\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right){\mathcal{K}}_{2} \left( {r,\lambda_{p} } \right){\text{d}}r = Q_{n} \delta_{np}. $$

(56)

where $\delta$ is the Kronecker delta and

$$ S_{m} = \frac{{\pi^{2} }}{2}\frac{{\xi_{m}^{2} e_{1}^{2} }}{{J_{v}^{2} \left( {\xi_{m} a} \right)\left( {h_{1}^{2} + \xi_{m}^{2} \left[ {1 - \left( {\frac{v}{{\xi_{m} b}}} \right)^{2} } \right]} \right) - e_{1}^{2} }}. $$

(57)

$$ Q_{n} = \frac{{\pi^{2} }}{2}\frac{{\lambda_{n}^{2} e_{2}^{2} }}{{e_{2}^{2} - J_{0.5}^{2} \left( {\lambda_{n} b} \right)\left( {h_{2}^{2} + \lambda_{n}^{2} \left[ {1 - \left( {\frac{0.5}{{\lambda_{n} a}}} \right)^{2} } \right]} \right)}}. $$

(58)

Multiplying Eq. (53) by $r{\mathcal{K}}_{1} \left( {r,\xi_{m} } \right)$, and Eq. (54) by $r{\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right)$, integrating over the interval from $a$ to $b$, and subsequently applying the orthogonality relation, we obtain:

$$ \ddot{A} + \xi_{m}^{2} A = L_{1} \left[ {B + b_{n} \overline{\theta }_{1} + t_{1} \left( {\dot{B} + b_{n} \dot{\overline{\theta }}_{1} } \right)} \right]. $$

(59)

$$ t_{2} \ddot{B} + \dot{B} + \lambda_{n}^{2} B = CL_{2} \left[ {\dot{A} + a_{m} \dot{\overline{w}}_{1} + t_{3} \left( {\ddot{A} + a_{m} \ddot{\overline{w}}_{1} } \right)} \right]. $$

(60)

in which

$$ L_{1} = \frac{1}{{S_{m} }}\mathop \smallint \limits_{a}^{b} \left[ { - \frac{{\partial {\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right)}}{\partial r} + \left( {D - \frac{3}{2}} \right)\frac{{{\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right)}}{r}} \right]r{\mathcal{K}}_{1} \left( {r,\xi_{m} } \right){\text{d}}r. $$

(61)

$$ L_{2} = \frac{ - 1}{{Q_{n} }}\mathop \smallint \limits_{a}^{b} \left[ {\frac{{\partial {\mathcal{K}}_{1} \left( {r,\xi_{m} } \right)}}{\partial r} + \left( {D - \frac{1}{2}} \right)\frac{{{\mathcal{K}}_{1} \left( {r,\xi_{m} } \right)}}{r}} \right]r{\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right){\text{d}}r. $$

(62)

The appropriate form for the initial conditions can be derived by substituting Eqs. (30d) and (30e) into (51):

$$ w_{2} \left( {r,0} \right) = A\left( 0 \right) \cdot {\mathcal{K}}_{1} \left( {r,\xi_{m} } \right) = f_{3}^{*} \left( r \right). $$

(63)

$$ \dot{w}_{2} \left( {r,0} \right) = \dot{A}\left( 0 \right) \cdot { }{\mathcal{K}}_{1} \left( {r,\xi_{m} } \right) = f_{4}^{*} \left( r \right). $$

(64)

Using the orthogonality relation, Eqs. (63) and (64) lead to:

$$ A\left( 0 \right) = \frac{1}{{S_{m} }} \mathop \smallint \limits_{a}^{b} rf_{3}^{*} \left( r \right){\mathcal{K}}_{1} \left( {r,\xi_{m} } \right) {\text{d}}r. $$

(65)

$$ \dot{A}\left( 0 \right) = \frac{1}{{S_{m} }} \mathop \smallint \limits_{{\text{a}}}^{b} rf_{4}^{*} \left( r \right){\mathcal{K}}_{1} \left( {r,\xi_{m} } \right){\text{d}}r. $$

(66)

The initial conditions for the energy equation can be obtained similarly:

$$ B\left( 0 \right) = \frac{1}{{Q_{n} }} \mathop \smallint \limits_{a}^{b} rg_{3}^{*} \left( r \right){\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right) {\text{d}}r. $$

(67)

$$ \dot{B}\left( 0 \right) = \frac{1}{{Q_{n} }} \mathop \smallint \limits_{{\text{a}}}^{b} rg_{4}^{*} \left( r \right){\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right) {\text{d}}r. $$

(68)

It’s evident that Eqs. (59) and (60) are coupled and can be uncoupled through some mathematical manipulations [13]. Differentiating Eqs. (59) and (60) with respect to time results in:

$$ \dddot A + \xi_{m}^{2} \dot{A} = L_{1} \left[ {b_{n} \dot{\overline{\theta }}_{1} + \dot{B} + t_{1} \left( {\ddot{B} + b_{n} \ddot{\overline{\theta }}_{1} } \right)} \right]. $$

(69)

(70)

(71)

(72)

Now substituting $\ddot{B}$ from Eq. (60) in Eq. (71) leads to:

$$ A^{\left( 4 \right)} + \xi_{m}^{2} \ddot{A} = L_{1} \left[ {b_{n} \ddot{\overline{\theta }}_{1} + \frac{{CL_{2} }}{{t_{2} }}\left( {\dot{A} + a_{m} \dot{\overline{w}}_{1} + t_{3} \left( {\ddot{A} + a_{m} \ddot{\overline{w}}_{1} } \right)} \right) - \frac{1}{{t_{2} }}\dot{B} - \frac{1}{{t_{2} }}\lambda_{n}^{2} B} \right]. $$

(73)

Now by substituting $B$ from Eq. (59) and $\dot{B}$ from Eq. (69) into Eq. (73) we have:

(74)

It can be observed that Eq. (74) is independent of $B$. Now similarly, substituting $A^{\left( 4 \right)}$ from Eq. (71) into Eq. (72) yields:

(75)

Then substituting $\dddot A$ from Eq. (69) into Eq. (75) yields:

(76)

And now by substituting $\dot{A} + t_{3} \ddot{A}$ from Eq. (60) into Eq. (76), we have:

(77)

Equations (74) and (77) represent the decoupled ordinary differential equation forms of equations (59) and (60). By substituting Eqs. (45) and (46) into these equations, we simplify them as follows:

(78)

(79)

Solving Eqs. (78) and (79) gives $A\left( t \right)$ and $B\left( t \right)$ and as a result $w_{2} \left( {r,t} \right)$ and $\theta_{2} \left( {r,t} \right)$. The solutions of these equations are dependent on the initial conditions; therefore, $A\left( t \right)$ and $B\left( t \right)$ are presented in the case study section. Now, both parts of $w\left( {r,t} \right)$ and $\theta \left( {r,t} \right)$ are obtained and using Eq. (17a), (17b), closed-form relations for $u\left( {r,t} \right)$ and $\psi \left( {r,t} \right)$ are as follows:

$$ u\left( {r,t} \right) = \frac{1}{\sqrt r }\left( {\mathop \sum \limits_{m = 1}^{\infty } a_{m} \overline{w}_{1} \left( {\xi_{m} ,t} \right){\mathcal{K}}_{1} \left( {r,\xi_{m} } \right) + \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } A\left( t \right) \cdot { }{\mathcal{K}}_{1} \left( {r,\xi_{m} } \right)} \right). $$

(80)

$$ \psi \left( {r,t} \right) = \frac{1}{\sqrt r }\left( {\mathop \sum \limits_{n = 1}^{\infty } b_{n} \overline{\theta }_{1} \left( {\lambda_{n} ,t} \right){\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right) + \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } B\left( t \right) \cdot { }{\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right)} \right). $$

(81)

The methodology employed in this study holds potential for resolving problems featuring various kinds of thermal–mechanical boundary conditions by selecting the suitable kernel of the transformation.

4 Case study

For numerical computations of the thermoelasticity problem of an orthotropic sphere under external loads, the following material properties have been considered for the calculations:

$$ \begin{gathered} a = 1 m\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;b = 2 m\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;T_{0} = 200.15 K \hfill \\ c = 262{ }{\raise0.7ex\hbox{$J$} \!\mathord{\left/ {\vphantom {J {Kg}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${Kg}$}}\;\;\;\;\;\;\;\;\;\;\;k = 0.918{\raise0.7ex\hbox{$w$} \!\mathord{\left/ {\vphantom {w {mK}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${mK}$}}\;\;\;\;\;\;\;\rho = 7.96e3{ }{\raise0.7ex\hbox{${Kg}$} \!\mathord{\left/ {\vphantom {{Kg} {m^{3} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${m^{3} }$}} \hfill \\ \alpha_{11} = 15e - 6{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 K}}\right.\kern-0pt} \!\lower0.7ex\hbox{$K$}}\;\;\;\;\;\;\alpha_{22} = 23e - 6{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 K}}\right.\kern-0pt} \!\lower0.7ex\hbox{$K$}}\;\;\;\;\;\;\alpha_{33} = 15e - 6{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 K}}\right.\kern-0pt} \!\lower0.7ex\hbox{$K$}} \hfill \\ C_{11} = 17.44e9 {\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {m^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${m^{2} }$}}\;\;C_{22} = 17.27e9 {\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {m^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${m^{2} }$}}\;\;C_{33} = 19.16e9{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {m^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${m^{2} }$}} \hfill \\ C_{12} = 6.17e9{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {m^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${m^{2} }$}}\;\;\;C_{13} = 5.97e9{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {m^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${m^{2} }$}}\;\;\;\;C_{23} = 4.96e9{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {m^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${m^{2} }$}} \hfill \\ \end{gathered}. $$

(82)

For thermal boundary conditions, a thermal shock in the form of heat flux is prescribed on the inner surface of the sphere and the mechanical boundary conditions include a constrained inner surface, and the outer surface is considered to be traction-free:

$$ u\left( {a,t} \right) = 0. $$

(83a)

$$ \sigma_{r} \left( {b,t} \right) + \tau_{r} \left( {b,t} \right) = 0. $$

(83b)

$$ - \frac{\partial \psi }{{\partial r}}\left| {_{r = a} } \right. = q_{in}. $$

(84a)

$$ \psi_{ } \left( {b,t} \right) = 0. $$

(84b)

The mechanical and thermal initial conditions are:

$$ u\left( {r,0} \right) = 0. $$

(85a)

$$ \dot{u}\left( {r,0} \right) = 0. $$

(85b)

$$ \psi_{ } \left( {r,0} \right) = 0. $$

(86a)

$$ \dot{\psi }\left( {r,0} \right) = 0. $$

(86b)

Therefore, we have:

$$ A\left( 0 \right) = 0. $$

(87a)

$$ \dot{A}\left( 0 \right) = 0. $$

(87b)

$$ B_{ } \left( 0 \right) = 0. $$

(88a)

$$ \dot{B}\left( 0 \right) = 0. $$

(88b)

using Eqs. (25a), (25b), (25c), (25d) and (46) leads to:

$$ g_{1}^{*} \left( t \right) = q_{in}. $$

(89a)

$$ g_{2}^{*} \left( t \right) = 0. $$

(89b)

$$ V\left( t \right) = \frac{2\sqrt a }{\pi }\frac{{J_{0.5} \left( {\lambda_{n} b} \right)}}{{J_{0.5} \left( {\lambda_{n} a} \right)}}q_{in}. $$

(89c)

Therefore:

$$ \overline{\theta }_{1} \left( {\lambda_{n} ,t} \right) = \frac{4}{\Delta }\frac{{\sqrt a J_{0.5} \left( {\lambda_{n} b} \right)}}{{\pi J_{0.5} \left( {\lambda_{n} a} \right)}}\mathop \smallint \limits_{0}^{t} q_{in} \left( \tau \right){\text{e}}^{{ - \frac{1}{{2t_{2} }}\left( {t - \tau } \right)}} {\text{sin}}\left( {\frac{\Delta }{{2t_{2} }}\left( {t - \tau } \right)} \right) {\text{d}}\tau. $$

(90)

Also, Considering Eqs. (23a), (23b), (23c), (23d) and (45) leads to:

$$ f_{1}^{*} \left( t \right) = 0. $$

(91a)

$$ f_{2}^{*} \left( t \right) = 0. $$

(91b)

$$ G\left( t \right) = 0. $$

(91c)

And, as a result:

$$ \overline{w}_{1} \left( {\xi_{m} ,t} \right) = 0. $$

(92)

Then, substituting Eqs. (90) and (92) into Eqs. (49) and (50) gives:

$$ w_{1} \left( {r,t} \right) = 0. $$

(93)

$$\begin{aligned} \theta_{1} \left( {r,t} \right) &= \mathop \sum \limits_{n = 1}^{\infty } b_{n} \frac{4}{\Delta }\frac{{\sqrt a J_{0.5} \left( {\lambda_{n} b} \right)q_{in} }}{{\pi J_{0.5} \left( {\lambda_{n} a} \right)}}\frac{2}{{\Delta \left( {\Delta^{2} + 1} \right)}} \\ & \quad \left( {\Delta t_{2} - t_{2} {\text{exp}}\left( {\frac{ - t}{{2t_{2} }}} \right)\left[ {\sin \left( {\frac{\Delta t}{{2t_{2} }}} \right) + \Delta {\text{cos}}\left( {\frac{\Delta t}{{2t_{2} }}} \right)} \right]} \right){\mathcal{K}}_{2} \left( {r,\lambda_{n} } \right). \end{aligned}$$

(94)

This way Eqs. (78) and (79) yield:

$$ t_{2} \frac{{{\text{d}}^{4} A}}{{{\text{d}}t^{4} }} + \left[ {1 - CL_{1} L_{2} t_{1} t_{3} } \right]\frac{{{\text{d}}^{3} A}}{{{\text{d}}t^{3} }} + \left[ {t_{2} \xi_{m}^{2} + \lambda_{n}^{2} - CL_{1} L_{2} (t_{1} + t_{3} )} \right]\frac{{{\text{d}}^{2} A}}{{{\text{d}}t^{2} }} + \left[ {\xi_{m}^{2} - CL_{1} L_{2} } \right]\frac{{{\text{d}}A}}{{{\text{d}}t^{ } }} + \xi_{m}^{2} \lambda_{n}^{2} A = L_{1} \left[ {b_{n} \frac{2\sqrt a }{\pi }\frac{{J_{0.5} \left( {\lambda_{n} a} \right)}}{{J_{0.5} \left( {\lambda_{n} b} \right)}}q_{in} } \right]. $$

(95)

$$\begin{aligned}&t_2 \frac{d^4B}{dt^4}+\left[1-CL_1L_2t_1t_3\right] \frac{d^3B}{dt^3}+\left[t_2\xi_m^2+\lambda_n^2-CL_1L_2(t_1+t_3)\right] \frac{d^2B}{dt^2}\\ &\quad+\left[\xi_m^2-CL_1L_2\right]\frac{dB}{dt}+\xi_m^2\lambda_n^2B\\ &\quad=CL_2\left[b_nL_1\left(\left(t_1\ddot{\bar{\theta}}_1+\dot{\bar{\theta}}_1\right)+t_3 \left(t_1\mathop{\bar{\theta}_1}\limits^{...}+\ddot{\bar{\theta}}_1\right)\right)\right]. \end{aligned}$$

(96)

Now, we can calculate $\dot{\overline{\theta }}_{1}$, $\ddot{\overline{\theta }}_{1}$ and by differentiating Eq. (94), and solving Eq. (95) results in:

$$ A\left( t \right) = \frac{{2L_{1} b_{n} \sqrt a q_{in} J_{0.5} \left( {\lambda_{n} b} \right)}}{{\pi \lambda_{n}^{2} \xi_{m}^{2} J_{0.5} \left( {\lambda_{n} a} \right)}} + \mathop \sum \limits_{i = 1}^{4} c_{i} e^{{\alpha_{i} t}}. $$

(97)

And using Eqs. (59), (60), (69), and (70), the relation between $A\left( t \right)$ and $B\left( t \right)$ can be deduced in the following form:

$$ B\left( t \right) = Q_{1} \frac{{{\text{d}}^{3} A}}{{{\text{d}}t^{3} }} + Q_{2} \frac{{{\text{d}}^{2} A}}{{{\text{d}}t^{2} }} + Q_{3} \frac{{{\text{d}}A}}{{{\text{d}}t^{ } }} + Q_{4} A - \frac{{(t_{2} - t_{1} )}}{{\left( {t_{1}^{2} \lambda_{n}^{2} + t_{2} - t_{1} } \right)}}b_{n} \overline{\theta }_{1}. $$

(98)

where

$$ Q_{1} = - \frac{{t_{1} t_{2} }}{{L_{1} \left( {t_{1}^{2} \lambda_{n}^{2} + t_{2} - t_{1} } \right)}}. $$

(99a)

$$ Q_{2} = - \frac{{t_{1} - t_{2} - t_{1}^{2} t_{3} CL_{1} L_{2} }}{{L_{1} \left( {t_{1}^{2} \lambda_{n}^{2} + t_{2} - t_{1} } \right)}}. $$

(99b)

$$ Q_{3} = - \frac{{t_{1} t_{2} \xi_{m}^{2} - t_{1}^{2} CL_{1} L_{2} }}{{L_{1} \left( {t_{1}^{2} \lambda_{n}^{2} + t_{2} - t_{1} } \right)}}. $$

(99c)

$$ Q_{4} = - \frac{{ - (t_{2} - t_{1} )\xi_{m}^{2} }}{{L_{1} \left( {t_{1}^{2} \lambda_{n}^{2} + t_{2} - t_{1} } \right)}}. $$

(99d)

Substituting Eq. (97) into (98) leads to:

$$ B\left( t \right) = \frac{{2b_{n} \sqrt a q_{in} J_{0.5} \left( {\lambda_{n} b} \right)}}{{\pi \lambda_{n}^{2} J_{0.5} \left( {\lambda_{n} a} \right)}} - \frac{{(t_{2} - t_{1} )}}{{\left( {t_{1}^{2} \lambda_{n}^{2} + t_{2} - t_{1} } \right)}}b_{n} \overline{\theta }_{1} + \mathop \sum \limits_{i = 1}^{4} \left( {Q_{1} \alpha_{i}^{3} + Q_{2} \alpha_{i}^{2} + Q_{3} \alpha_{i} + Q_{4} } \right)c_{i} {\text{e}}^{{\alpha_{i} t}}. $$

(100)

in which, $\alpha_{i}$’s are the roots of the following equation:

$$ t_{2} x^{4} + \left( {1 - CL_{1} L_{2} t_{1} t_{3} } \right)x^{3} + \left( {t_{2} \xi_{m}^{2} + \lambda_{n}^{2} - CL_{1} L_{2} (t_{1} + t_{3} } \right))x^{2} + \left( {\xi_{m}^{2} - CL_{1} L_{2} } \right)x + \xi_{m}^{2} \lambda_{n}^{2} = 0. $$

(101)

and $c_{i}$’s can be obtained using Eqs. (87a), (87b) and (88a), (88b);

$$ \left( {\begin{array}{*{20}c} {c_{1} } \\ {c_{2} } \\ {c_{3} } \\ {c_{4} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 1 & 1 & 1 & 1 \\ {\alpha_{1} } & {\alpha_{2} } & {\alpha_{3} } & {\alpha_{4} } \\ {S_{1} } & {S_{2} } & {S_{3} } & {S_{4} } \\ {\alpha_{1} S_{1} } & {\alpha_{2} S_{2} } & {\alpha_{3} S_{3} } & {\alpha_{4} S_{4} } \\ \end{array} } \right)^{ - 1} \left( {\begin{array}{*{20}c} {R_{1} } \\ 0 \\ {R_{2} } \\ 0 \\ \end{array} } \right). $$

(102)

where

$$ S_{1} = Q_{1} \alpha_{1}^{3} + Q_{2} \alpha_{1}^{2} + Q_{3} \alpha_{1} + Q_{4}. $$

(103a)

$$ S_{2} = Q_{1} \alpha_{2}^{3} + Q_{2} \alpha_{2}^{2} + Q_{3} \alpha_{2} + Q_{4}. $$

(103b)

$$ S_{3} = Q_{1} \alpha_{3}^{3} + Q_{2} \alpha_{3}^{2} + Q_{3} \alpha_{3} + Q_{4}. $$

(103c)

$$ S_{4} = Q_{1} \alpha_{4}^{3} + Q_{2} \alpha_{4}^{2} + Q_{3} \alpha_{4} + Q_{4}. $$

(103d)

and

$$ R_{1} = - \frac{{2L_{1} b_{n} \sqrt a q_{in} J_{0.5} \left( {\lambda_{n} b} \right)}}{{\pi \lambda_{n}^{2} \xi_{m}^{2} J_{0.5} \left( {\lambda_{n} a} \right)}}. $$

(104a)

$$ R_{2} = - \frac{{(t_{2} - t_{1} )}}{{\left( {t_{1}^{2} \lambda_{n}^{2} + t_{2} - t_{1} } \right)}}\frac{{2b_{n} \sqrt a q_{in} J_{0.5} \left( {\lambda_{n} b} \right)}}{{\pi \lambda_{n}^{2} J_{0.5} \left( {\lambda_{n} a} \right)}}. $$

(104b)

To validate the obtained solution for the thermoelasticity problem in an orthotropic sphere, we examine the thermoelasticity problem of an isotropic sphere experiencing a sudden and uniform temperature increase $\theta_{0}$ across the entire sphere. While an orthotropic sphere exhibits varying mechanical and thermal properties along three orthogonal axes, when these properties are equivalent in all directions, the orthotropic sphere effectively simplifies into an isotropic sphere. In essence, the isotropic sphere serves as a particular case of the more general orthotropic sphere, characterized by uniform material properties in all directions. Figures 1 and 2 exhibit the history of radial and tangential stresses, respectively. It is observed that when the orthotropic sphere possesses identical properties in different directions and the relaxation times are disregarded, the obtained results align with those presented by Hata [2] for the isotropic sphere. In Hata’s work, nondimensional time and nondimensional stress components are defined as follows:

$$ \hat{t} = \frac{{V_{e} t}}{a}. $$

(105)

$$ \hat{\sigma }_{r} = \frac{{\left( {1 - 2v} \right)\sigma_{r} }}{{E\alpha T_{0} }}. $$

(106)

$$ \hat{\sigma }_{\theta } = \frac{{\left( {1 - 2v} \right)\sigma_{\theta } }}{{E\alpha T_{0} }}. $$

(107)

Fig. 1

Comparison of radial stress with Hata [2] in the case of b/a = 5

Fig. 2

Comparison of tangential stress with Hata [2] in the case of b/a = 5

To explore the thermoelastic responses of the orthotropic sphere to a thermal shock, we’ve conducted a comparative analysis involving three theories: classical theory, Lord–Shulman, and Green–Lindsay. Figure 3 illustrates the history of nondimensional temperature at the mid-radius of the orthotropic sphere for all aforementioned theories. It’s evident that in the Lord–Shulman and Green–Lindsay theories, an abrupt change occurs in temperature at the initial moments due to their incorporation of a finite speed for the thermal wave. Moreover, the coefficient of the second derivate of the variable with respect to the time in the wave equation indicates the speed of the propagated wave. Hence, because both Lord–Shulman and Green–Lindsay models assume the same value for relaxation times, the histories of nondimensional temperature are coincident for both theories.

Fig. 3

History of nondimensional temperature at mid-radius for different theories

Figure 4 depicts the history of nondimensional displacement at mid-radius of the orthotropic sphere for all of the theories. Remarkably, the Green–Lindsay theory foresees higher peak values in the displacement field compared to the other theories. It’s important to highlight that, despite the thermal responses of Lord–Shulman and Green–Lindsay theories being coincident, their displacement responses differ. This discrepancy arises from the fact that Green–Lindsay theory introduces an additional relaxation time into the equation of motion, whereas Lord–Shulman’s equation of motion lacks any relaxation time.

Fig. 4

History of nondimensional displacement at mid-radius for different theories

Figures 5, 6 and 7 display the history of nondimensional radial, tangential, and circumferential stresses at the mid-radius of the sphere for various theories, respectively. It can be seen, in classical theory, stress starts to decrease right from the outset due to the assumption of an infinite velocity for the temperature wave. Conversely, in generalized theories, the temperature wave takes longer to propagate to radial positions, causing a delayed reduction in stress. Additionally, an abrupt jump occurs in the initial moments in the Green-Lindsay theory when the wavefront reaches a radial position. This is a consequence of the presence of a temperature gradient in the stress components (Eq. 9a), (9b), (9c). While these jumps completely disappear after $t = 4$, because the temperature gradient diminishes across the sphere with the rise in medium’s temperature. It can be inferred from the results shown in Figs. 6 and 7, while some differences are detected, there are only minor differences for the tangential and circumferential stress histories.

Fig. 5

History of nondimensional radial stress at mid-radius for different theories

Fig. 6

History of nondimensional tangential stress at mid-radius for different theories

Fig. 7

History of nondimensional circumferential stress at mid-radius for different theories

Figure 8 exhibits the impact of relaxation time on the history of nondimensional temperature at mid-radius of the sphere according to Green–Lindsay theory. The results demonstrate that with an increase in relaxation time, the peak temperature value escalates; however, it happens at later points in times. The velocity of propagated temperature wave can be determined utilizing the following equation:

$$ V_{t} = \sqrt {\frac{1}{{t_{2} }}} = \sqrt {\frac{1}{0.85}} = 1.085. $$

(108)

Fig. 8

History of nondimensional temperature at mid-radius for Green–Lindsay theory and different values of relaxation time

The analysis demonstrates that an increase in relaxation time leads to a lower velocity for the temperature wave and a decrease in the gradient of temperature with respect to time. This results in the temperature wave taking more time to reach its peak position.

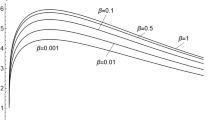
Figures 9, 10 and 11 show the effect of the different values of relaxation time on the nondimensional displacement, radial stress, and tangential stress components at mid-radius of the sphere based on Green–Lindsay theory. As depicted in Fig. 9, with higher relaxation times, the peak value of nondimensional displacement increases and occurs at a later point in time. This phenomenon arises from the heightened energy absorption associated with an increase in relaxation time, leading to larger temperature and displacement peaks.

Fig. 9

History of nondimensional radial displacement at mid-radius of the sphere for Green–Lindsay theory for different values of relaxation time

Fig. 10

History of nondimensional radial stress at mid-radius of the sphere for Green–Lindsay theory for different values of relaxation time

Fig. 11

History of nondimensional tangential stress at mid-radius of the sphere for Green–Lindsay theory for different values of relaxation time

Figures 10 and 11 clearly illustrate that because the thermal load is applied to the inner boundary of the sphere, the initial stress peak is compressive and the first peak of stress is negative, resulting from the temperature rise. As observed in Fig. 10, as the relaxation time increases from 0.85 to 1.73 (resulting in a decrease in the velocity of the thermal wave from 1.085 to 0.76), the amplitude of the abrupt jump escalates. Conversely, for the $t_{2} = 3.94$, the abrupt jump completely vanishes. It’s important to note that with $t_{2} = 3.94$, the velocity of the thermal wave is 0.504. At this point, when the thermal wave reaches r = 1.5, the elastic wave has already reached the outer surface, colliding and initiating reflection with a reversed sign. Also, as is mentioned earlier, an increase in relaxation time leads to a decrease in the gradient of temperature with respect to time and it can result in a reduction or complete elimination of the abrupt jump at the initial moments.

As depicted in Fig. 11, similar to the history of nondimensional radial stress, initially the thermoelastic wave is in compressive mode as it starts to propagate from the displacement-type inner boundary. However, it transitions into a tensile mode when it returns from the traction-free outer boundary. Subsequent stress peaks are similarly either added negatively or positively, due to the reflections from the boundaries.

Figures 12, 13 and 14 depict the history of nondimensional radial displacement, radial stress, and tangential stress at different radial positions of the sphere for Green–Lindsay theory for $t_{1} = t_{2} = 0.85$. In the prescribed thermal boundary conditions, the spherical dilatation wave propagates outward from the inner boundary. The influence of the mechanical boundary conditions on the propagation and the reflection of the stress wave can be seen in Figs. 13 and 14. The thermoelastic wave begins in a compressive mode as it initiates propagation from the inner boundary. However, upon returning from the outer boundary, it shifts into a tensile mode. This behavior arises from the application of traction-free boundary conditions on the outer surface of the orthotropic sphere, whereas the displacement-type inner boundary reflects the wave in the same mode it encounters. Additionally, these figures clearly demonstrate the abrupt jump in the stress component histories at the initial moments of the applied thermal shock.

Fig. 12

History of nondimensional radial displacement at different radial positions for Green–Lindsay theory

Fig. 13

History of nondimensional radial stress at different radial positions for Green–Lindsay theory

Fig. 14

History of nondimensional tangential stress at different radial positions for Green–Lindsay theory

Figure 15 shows the distribution of temperature across the thickness of the orthotropic sphere for Green–Lindsay theory. It is evident that each point’s temperature gradually rises over time until reaches the steady-state condition. Unlike the parabolic form observed in classical theory, generalized theories adopt a hyperbolic energy equation, which causes the formation of the temperature wave.

Fig. 15

Through-thickness variation of nondimensional temperature for Green–Lindsay theory at different times

The wavefront of the temperature wave is depicted in Fig. 15 for ${\text{Time}} = 0.25$, ${\text{Time}} = 0.5,$ and ${\text{Time}} = 0.75$. Specifically, the temperature wave corresponding to ${\text{r}} = 1$ and ${\text{Time}} = 0.25$ originates at about $0.2$ and diminishes to zero at about ${\text{r}} = 1.28$. Additionally, it is evident that at ${\text{Time}} = 1$, the temperature wave approximately reaches the outer boundary, aligning with the temperature wave propagation dimensionless velocity of $1.085$ derived from Eq. (108).

Figures 16, 17 and 18 show the through-thickness variation of the nondimensional radial displacement, radial stress, and tangential stress at different times for Green–Lindsay theory for $t_{1} = t_{2} = 0.85$. As depicted in Fig. 16, the fixed inner boundary condition causes the sphere to expand outward. The effect of the boundary conditions on the propagation of elastic waves is also evident in Figs. 17 and 18. These figures reveal that the radial and tangential stresses are compressive at intervals smaller than ${\text{Time}} = 0.92$ and become tensile after this point. Indeed, this change indicates the onset of wave reflection, signifying that the elastic wave is now propagating back into the medium but in the opposite direction. The abrupt jumps in the stress waves can also be seen in these figures. As Fig. 8 demonstrates, during the initial moments of the thermal shock application, the gradient of the temperature with respect to the time is high. This leads to the higher amplitude in the abrupt jump in elastic waves, as is seen in Figs. 17 and 18. As time progresses and the system approaches the steady state in temperature distribution, the amplitude of the abrupt jump gradually decreases.

Fig. 16

Through-thickness variation of nondimensional radial displacement for Green–Lindsay theory at different times

Fig. 17

Through-thickness variation of nondimensional radial stress for Green–Lindsay theory at different times

Fig. 18

Through-thickness variation of nondimensional tangential stress for Green–Lindsay theory at different times

Figures 19, 20 and 21 illustrate the history of nondimensional radial displacement, radial stress, and tangential stress at different radial positions of the sphere for Lord–Shulman theory at $t_{2} = t_{3} = 0.85$. Similar to Green–Lindsay theory, the spherical dilatation wave propagates outward from the inner boundary and traction-free boundary conditions on the outer surface change the mode of the thermoelastic wave, while the displacement-type inner boundary reflects the wave in the same mode that it encounters.

Fig. 19

History of nondimensional radial displacement at different radial positions for Lord–Shulman theory

Fig. 20

History of nondimensional radial stress at different radial positions for Lord–Shulman theory

Fig. 21

History of nondimensional tangential stress at different radial positions for Lord–Shulman theory

Figures 22, 23 and 24 depict the through-thickness variation of the nondimensional radial displacement, radial stress, and tangential stress at different times for Lord–Shulman theory at $t_{2} = t_{3} = 0.85$. The onset of wave reflection can also be seen in these figures. In Fig. 22, ${\text{Time}} = 0.25$, ${\text{Time}} = 0.5,$ and ${\text{Time}} = 0.75$ show the displacement wave propagation, while ${\text{Time}} = 1$, ${\text{Time}} = 1.25,$ and ${\text{Time}} = 1.5$ indicate the wave reflection from the outer radius of the sphere.

Fig. 22

Through-thickness variation of nondimensional radial displacement for Lord–Shulman theory at different times

Fig. 23

Through-thickness variation of nondimensional radial stress for Lord–Shulman theory at different times

Fig. 24

Through-thickness variation of nondimensional tangential stress for Lord–Shulman theory at different times

Also, Figs. 23 and 24 illustrate the presence of stress wavefronts at various time instances. Notably, at ${\text{Time}} = 0.25$, the stress wavefront is located at $1.2$ and progressively advances through the medium as time passes. During the initial stages of the thermal shock application the gradient of the elastic wavefront with respect to time is larger and gradually diminishes over time, while the magnitude of the wavefront increases with the progression of time.

Figures 25, 26 and 27 show how the nondimensional displacement, radial stress, and tangential stress components are affected when orthotropic material is taken into account based on the Green–Lindsay theory. For the material that is used in this section ${\text{ D}} = 2.14$, and for isotropic materials, ${\text{D}} = 2$. The effect of the orthotropicity is shown by plotting two extreme cases of ${\text{D}}$. It is observed that an increase in the orthotropic coefficient leads to higher magnitudes of radial and tangential stresses. Incorporating this parameter during the design stage can be advantageous in controlling stress levels by selecting materials with specific mechanical properties.

Fig. 25

Effect of orthotropicity on the history of nondimensional radial displacement for Green–Lindsay theory

Fig. 26

Effect of orthotropicity on the history of nondimensional radial stress for Green–Lindsay theory

Fig. 27

Effect of orthotropicity on the history of nondimensional tangential stress for Green–Lindsay theory

5 Conclusion

This study deals with the generalized coupled thermoelasticity problem in an orthotropic sphere. A unified formulation based on the classical, Lord–Shulman, and Green–Lindsay theories of thermoelasticity is presented for the orthotropic sphere. The problem is one-dimensional and solved analytically using finite Hankel transform. The inner boundary is constrained, while the outer boundary is traction-free. For the thermal boundary conditions, the inner boundary experiences a thermal shock in the form of heat flux, while the outer boundary is subjected to a constant temperature.

Closed-form relations are presented for the displacement and temperature distributions due to using an analytical method to solve the problem. Distributions of temperature, displacement, radial, and hoop stresses at several times and along the radius of the sphere are obtained and shown in the figures for both Lord–Shulman and the Green–Lindsay theories. Also, a comparison between all the theories is conducted and has been presented in graphically. From these graphs, it is possible to calculate the speed of propagation of the elastic and thermal waves.

In addition, the effects of different relaxation times and material properties on the stress waves and temperature are shown in the figures for the Green–Lindsay theory. Observations from the figures indicate that as the relaxation time increases, the peak values of the graphs for temperature, displacement, and stresses also increase, but these peaks occur at later time points. This behavior is due to the fact that with a longer relaxation time, a thermal wave exhibits greater inertia, causing thermal disturbances to propagate at lower speeds, which in turn results in greater energy absorption within the structure. Furthermore, it is seen in the figures that increases in the orthotropic coefficient lead to higher magnitude in the displacement, as well as radial and hoop stresses.

To validate the obtained results of this solution, the generalized coupled thermoelasticity problem is reduced to a special case, and the outcomes are compared with the findings of Hata [2] which shows excellent agreement. The method employed in this research applies to a wide range of problems in thermoelasticity. The results presented in this study have practical applications for researchers in material science, as well as designers of new materials in various domains, including mechanical engineering, acoustics, geophysics, and optics.