1 Introduction

The simplest approach to describe fracture propagation in continuous bodies is linear elastic fracture mechanics in conjunction with Griffith’s laws; the former theory provides a characterization of the crack opening displacement (COD) and state of stress asymptotically close to the tip, whilst Griffith’s criteria are used to determine the critical energetic threshold for the crack evolution. Within this framework asymptotic solutions of the classical fracture problems (opening, shearing and tearing modes) are essentially based on the concept of stress intensity factor K, i.e., the amplitude of the most singular term in the asymptotic expansion for stress. Higher order singularities are usually eliminated by adopting suitable physical requirements as the energy integrability. The so-called small scale yielding assumption, say the existence of a region within which the stress field is reasonably approximated by the K-terms only, has been elucidated in [26], where the proper condition to hold true for having such dominance of K fields has been established. However linear elastic fracture mechanics fails to describe stresses and displacements in the very neighbourhood of the crack tip, providing, there, infinite tensile stresses and a COD given as a square root function of the distance from the tip.

For both metallic alloys and rocks, experimental evidences at the micro-scale revealed that crack expansion is anticipated by strain localisation, micro-cracking and void nucleation, see the review paper [7] and references therein. Within this process zone, a decrease of the above mentioned tensile stresses can be detected as a consequence of energy dissipative mechanisms and elastic interactions of the main crack front with micro-defects, see [24]. More recently analogous phenomena have been demonstrated to take place at the nano-scale for ceramics and glasses, see, e.g., [8] and [12]. These local behaviours are typically associated with a departure from the predictions of the linear elastic model, and are responsible for the size scaling of the material properties.

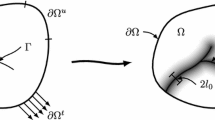
It is worth to notice that the CODs measured in [12] for an alumino-silicate glass (see Fig. 4 therein) and in [37] for an amorphous glassy polymer (see Figs. 22 and 23 therein) look very similar to those derived by Barenblatt [4] after supposing the existence of a cohesive zone near the crack tip. Hence the crack can conveniently be divided into an outer region, r≥d I , where the crack lips are truly traction-free, and an inner region, r≤d II , where the crack lips do exchange cohesive forces, see Fig. 1. Here r is the radial distance from the tip.

Fig. 1
figure 1

Qualitative profile of the crack opening shape as found in [4] (under the hypothesis of a cohesive zone r<d II ) and experimentally observed in [12, 37]

Full size image

Whilst the forces of internal cohesion were initially introduced to avoid the stress singularity in the vicinity of the crack tip, they could also serve as a phenomenological macroscopical description of cleavage mechanisms occurring at the micro or nano scales. Recently, inverse techniques have been developed in order to elucidate the relation between CODs, measured with micro-scale precision, and the cohesive tractions, see [37] and [39].

The refined description of the fracture process zone, in terms of its geometry, material properties and time-evolution, currently represents a theoretical and experimental challenge: to this aim several different approaches can be retrieved from the literature. In particular, one can distinguish between atomistic theories, studying the fracture of a single crystal, e.g., [3], and continuum theories, where either the hypothesis of linear elasticity is relaxed, e.g., [9], or phenomenological damage variables are introduced, e.g., [32]. For the latter theories, the variational approach to fracture, proposed in [11], provide a mathematically well-grounded framework, as well as a clear justification of possible numerical solution strategies, see [10]. It is not the purpose of this paper to summarize and review the cited results. Conversely, in order to model the region surrounding the crack tip, where strain localizes and the material cleaves, we focus on nonlocal elasticity and, in particular, on its simplest form known as strain-gradient elasticity. As we will soon discuss, nonlocal elastic forces can provide the same CODs as those obtained assuming cohesive forces, despite being associated to thermodynamically reversible processes. Whilst we are aware that in many circumstances nonlocal elastic forces do not play a dominant role, we are also confident that fracture processes could see the interplay of plastic, damage and strain-gradient effects to produce the correct material behaviour.

Already [17], and more recently [35], extended the linear elastic fracture model to nonlocal interactions to describe the roughness of the crack front and its trapping against forward advance, due to the presence of material heterogeneities at the micro-scale. They considered a dependence of the stress intensity factor on the entire crack geometry via a convolution with a long-ranged kernel. Linear strain gradient elasticity renounces to such a level of generality by assuming the stored elastic energy as a quadratic form of the strain and strain-gradient only. Despite this simple assumption, the occurrence of a process zone and a rough estimate of its characteristic length can be achieved. An important result in this direction has been recently provided in [22] and [20]: by solving plane-strain crack problems in dipolar elasticity they have proved that also a linear, purely elastic, continuum can model the presence of a cohesive-like zone. In particular, adopting the simplified isotropic constitutive dependence of the elastic energy on strain gradient proposed among others by [18], they obtained a COD which asymptotically exhibits a r 3/2 variation as in Fig. 1, giving raise to cohesive effects and material strengthening. Using hyper-singular integral equations, they estimated the limit of the process zone, d II in Fig. 1, to range from 0.45 to \(0.77 \sqrt{c}\) depending on the actual Poisson ratio; here \(\sqrt{c}\) is the only characteristic length of the considered constitutive relation. Similarly, extending previous results in [41] and using couple-stress elasticity, [34] analysed the effects of the characteristic lengths in bending and torsion (ℓ b ,ℓ t ) on mode III problems for semi-infinite cracks. Within the same framework, [21] analyzed the case of a finite-length crack. Both reported a similar transition from the asymptotic r 3/2 terms to the far field r 1/2 terms in a region from d II =0.5ℓ t to d I =5ℓ b . In all these cases the so-called total stress, summing the contribution of the stress and the divergence of hyperstress, see (6), remains singular for r→0 and in particular diverges as r −3/2. However this singularity, much stronger than the classical square root, does not violate boundedness of the energy release rate, see for more details [36].

In the present paper, for both plane-strain and antiplane crack opening, we limit ourselves to the analysis of asymptotic fields, but extend the previous results to consider the most general elastic constitutive relation for an isotropic strain-gradient material. This leads to consider five additional constitutive parameters: four of them represent material characteristic lengths, whilst the last one is a coupling parameter, see Sect. 3. Such general form for the strain-gradient Hooke law was already introduced in [30]; the necessary conditions on the constitutive parameters for a positive definite energy functional can be found in [15, 31] or, more recently, in [13].

By using four characteristic lengths for the material micro-structure we are able to obtain a more refined description of stress fields approaching the crack tip; the explicit closed-form dependence of both the stress intensity factors and the energy release rates on these characteristic lengths is derived and discussed. Since based on the linear part of the material response, these results should be of relevant interest also to develop more complex, possibly non-linear, material relationships as those adopted in strain-gradient plasticity, see for instance [16].

The paper is organized as follows. In Sect. 2 a brief recall of the gradient elasticity equations for an hyperelastic solid is provided. Within this framework, in Sect. 3, the characteristic internal lengths of an isotropic material are listed and compared to other well-known quantities of more standard use. Section 4 concerns with the statement of the strain gradient constitutive laws and the corresponding governing equations in the case of antiplane and inplane elasticity through which the tearing, opening and shearing fracture modes can be described. In Sect. 5 the asymptotic solutions of these equations are explicitly reported. Finally in Sect. 6, for all the cases studied, after deriving closed-form expressions for the J-integrals, we discuss which are the optimal micro-structures, in terms of ratios among the material characteristic lengths, in order to affect the energy release rates and, consequently, the micro-structural strengthening effect. The closed form expressions reported in Sects. 5, 6 and in Appendices A–B have been obtained and checked using the software Mathematica for algebraic computations.

2 Governing Equations for Strain-Gradient Elasticity

Here we briefly recall the governing equations for hyperelastic strain-gradient solids; we limit this resumé to the case of small deformations, since the subsequent analysis fits within this assumption. For further details and the account of finite deformations, the interested reader is referred to [19] and [30], or, for more recent contributions, to [13] or [33].

2.1 Kinematics and Balance Laws

We denote \(\mathcal{D}\subset \mathbb{R}^{3}\) the reference configuration of the body, u i the components of the displacement field with respect to a fixed orthonormal frame and E ij :=(u i,j +u j,i )/2 the components of the infinitesimal strain field. Moreover D ijk :=E ij,k =(u i,jk +u j,ik )/2 denote the components of the third-order tensor field measuring the gradient of the infinitesimal strain. Let us remark that one can always decompose the infinitesimal strain gradient field in the sum of two mutually orthogonal contributions, see [19]:

$$ D_{i j k} = \widetilde{D}_{i j k} + \widehat{D}_{i j k}, $$
(1)

where

$$ \widetilde{D}_{i j k} := \dfrac{1}{3} ( E_{i j, k}+E_{j k, i}+E_{k i, j} ),\qquad \widehat{D}_{i j k} := \dfrac{1}{3} ( \varepsilon_{j k l} d_{l i} +\varepsilon_{i k l} d_{l j} ),\quad d_{l i} := \varepsilon_{l j k} E_{i j, k}. $$
(2)

Hence \(\widetilde{D}\) is characterized by 10 independent components being a third-order tensor which is symmetric under permutations of all its indices. Instead \(\widehat{D}\) is characterized by 8 independent components being determined univocally by the second-order deviatoric tensor d. The condition for d to be deviatoric is easily proven, since \(d = \operatorname{grad} \operatorname{curl}u\) and, therefore, \(\operatorname{tr} d= \operatorname{div} \operatorname{curl}u =0\).

An elasticity theory is referred to as “strain-gradient”, or sometimes as “second-gradient”, if, not only the strain, but also the gradient of the strain contribute to the stored elastic energy; the most general form for the stored energy functional can therefore be written, see [30], as

$$ \psi= \hat{\psi}(E_{i j}, D_{i j k})= \overline{ \psi}(E_{i j}, \widetilde{D}_{i j k},d_{i j}). $$
(3)

“Couple-stress” theories refer to a particular case of (3) where the stored energy is postulated not to depend on the completely-symmetric part of the strain gradient, but on E and d only, see for instance [38].

The total energy is hence postulated as the sum of the total stored elastic energy and the potential energy of external forces \(\mathcal{L}=\mathcal{E}+\mathcal{Q}\) with

$$ \mathcal{E}:=\int _{\mathcal{D}} \psi,\qquad-\mathcal{Q}:=\int _{\mathcal{D}} b_{i} u_{i}+\int _{\partial\mathcal{D}} (t_{i} u_{i}+\tau_{i} u_{i,j}n_{j} )+ \int _{{\partial\partial \mathcal{D}}} f_{i} u_{i}, $$
(4)

where \(\partial\mathcal{D}\) is the boundary of \(\mathcal{D}\) and \(\partial\partial\mathcal{D}\) its edges, if any. We have used standard names for the body forces b, the tractions t, the double-forces τ and the edge forces f. The stationarity of \(\mathcal{L}\) implies the principle of virtual working,

$$ \int_{{\mathcal{D}}} ( S_{i j} \delta E_{i j} + P_{i j k} \delta D_{i j k } )=\int _{\mathcal{D}} b_{i} \delta u_{i}+\int _{\partial\mathcal{D}} (t_{i} \delta u_{i}+\tau_{i} \delta u_{i,j}n_{j} )+\int _{{\partial\partial\mathcal{D}}} f_{i} \delta u_{i}, $$
(5)

to hold true, for every admissible virtual displacement field δu. In (5) the quantities

$$ S_{i j } := \frac{\partial\psi}{\partial E_{i j }},\qquad P_{i j k } := \frac{\partial\psi}{\partial D_{i j k }}, $$
(6)

are respectively the stress and hyperstress fields. Since P shares the same symmetry properties of D, also the hyperstress can be decomposed according to (1) into a completely symmetric part \(\widetilde{P}\) and a deviatoric second order tensor p; the strain gradient contribution to (5) can therefore be split as:

$$ P_{i j k} \delta D_{i j k} = \widetilde{P}_{i j k} \delta\widetilde {D}_{i j k} +\widehat{P}_{i j k} \delta \widehat{D}_{i j k} = \widetilde{P}_{i j k} \delta \widetilde{D}_{i j k} +\dfrac{2}{3} p_{i j} \delta d_{i j}. $$
(7)

We remark that in strain-gradient theories the boundary \(\partial \mathcal{D}\) and its edges \(\partial\partial\mathcal{D}\) can be respectively decomposed in the non-intersecting union of four and two different regions, respectively:

$$ \partial\mathcal{D}=\partial\mathcal{D}_n^n \cup\partial \mathcal {D}_n^e \cup\partial\mathcal{D}_e^n \cup\partial\mathcal {D}_e^e;\qquad\partial\partial \mathcal{D}=\partial\partial\mathcal {D}^n \cup\partial\partial \mathcal{D}^e. $$
(8)

The pedices e and n here indicate “essential” and “natural” boundary condition. Accordingly we will call \(\partial\mathcal{D}_{n}^{\star}:=\partial \mathcal{D}_{n}^{n} \cup\partial\mathcal{D}_{n}^{e}\) the region where tractions are applied, \(\partial\mathcal{D}^{n}_{\star}:=\partial \mathcal{D}_{n}^{n} \cup\partial\mathcal{D}_{e}^{n}\) the region where contact double-forces are applied, \(\partial\mathcal{D}_{e}^{\star}:=\partial \mathcal{D}_{e}^{n} \cup\partial\mathcal{D}_{e}^{e}\) the region where the displacement is prescribed and \(\partial\mathcal{D}^{e}_{\star }:=\partial\mathcal{D}_{n}^{e} \cup\partial\mathcal{D}_{e}^{e}\) the region where the normal derivative of the displacement is prescribed; for more details see [13].

By standard localization arguments of the principle of virtual working (5) the local balance laws for strain-gradient elasticity follow:

(9)

which must be used together with the essential boundary conditions

$$ u_{h}=\overline{u}_{h}\quad \mathrm{on}\ \partial \mathcal{D}^{\star }_{e},\qquad u_{h,i} n_{i}= \overline{w}_{h}\quad \mathrm{on}\ \partial \mathcal{D}^e_{\star}, \qquad u_{h}=\overline{u}_{h}\quad \mathrm{on}\ \partial \partial\mathcal{D}^e. $$
(10)

In (9) \(\hat{X}_{B}\) for B=1,2 indicate local coordinates for every part of the boundary \(\partial\mathcal{D}\); accordingly the tensor field of components \(Q_{B i}:= \partial\hat{X}_{B}/\partial X_{i}\) project three-dimensional vectors onto the boundary, while the surface-gradient is indicated as the derivation with respect to the \(\hat{X}_{B}\) coordinates. Finally ν B are the components in the surface coordinate system of the Darboux tangent-normal vector. We remark that Eq. (9)4 can not be deduced if the hyperstress P is singular in the edge; a more detailed discussion of this item is reported in Sect. 5.4.

For linearly elastic isotropic solids, the most general constitutive relations for stress and hyperstress read as S ij =C ijhk E hk and P ijk =G ijklpq E lp,q where C is the standard fourth-order elasticity tensor determined by the two Lamé constants λ and μ, and G is a sixth-order constitutive tensor univocally determined by five second-gradient elastic moduli, see [30]:

(11)

Apparently the stored elastic energy is a quadratic form of the strain and strain-gradient fields; the explicit conditions required to guarantee its positive definiteness were recently stated in [13] and read as follows:

(12)

where the elastic parameters γ i (i=1,…,5) are given in terms of the constitutive parameters in (11) by the following definitions

(13)

3 Characteristic Lengths for Linear Elastic Isotropic Materials

Based on the conditions (12) for a positive definite energy, we introduce an equivalent set of strain-gradient moduli, namely four characteristic lengths and a coupling parameter. We discuss the relevant deformations weighted by each of them and their relationships to other strain-gradient moduli used in the literature, as the characteristic lengths in bending and torsion of couple-stress theories, see [34]. For the sake of conciseness we do not state the general constitutive relation (11) for linearly elastic strain gradient solids in terms of these characteristic lengths, but we limit ourselves to exhibit its reduced form in the case of antiplane and plane strains, see Sect. 4.

Conditions (12) require four of the strain-gradient moduli to be positive. Since the physical dimensions of γ i /μ for i=1,…,5 are length squared, we introduce four independent lengths as characteristics of the material:

(14)

Only the modulus γ 3 could be positive, negative or vanishing and, indeed, it represents a coupling parameter between the completely symmetric part \(\widetilde{P}\) of the hyper-stress and the deviatoric part of the strain gradient d, see [13].

The characteristic lengths (14) describe different independent micro-structural material properties. Typical strain-gradient fields which are weighted by each one of them are shown in Fig. 2. Therein it is clearly seen that ℓ t and ℓ b allow to penalize respectively torsional and bending deformations of the material elements, while ℓ s and ℓ e measure the energetic cost of differential-shearing and differential-elongation respectively. It is possible to observe that, even for isotropic materials, the uniform-bending, the differential-elongation and the differential-bending deformations are constitutively coupled by the elastic modulus γ 3; this last can hence be seen as a kind of second-order Poisson ratio.

Fig. 2
figure 2

Examples of deformations of a material square element weighted the four characteristic lengths: ℓ t , ℓ b , ℓ s and ℓ e

Full size image

For the energy to be positive definite, conditions (12) dictate not only the characteristic lengths to be positive, but mutual relationships among them. For instance, maximizing the ratio \(\ell_{t}^{2}/\ell_{s}^{2}\) given in (14) over all the possible γ i satisfying (12), we obtain 0≤ℓ t ≤2 ℓ s .

The definitions (14) do include well-know assumptions for the strain energy density found in the literature. For instance, the case of couple-stress elasticity, [38] and [34], is recovered letting γ 1=γ 2=γ 3=0, therefore, obtaining

$$ \ell_{e}^2= 0,\qquad\ell_b^2 = \dfrac{\gamma_4 + 6 \gamma_5}{\mu},\qquad\ell_{s}^2 = \dfrac{\ell_b^2}{16}, \qquad\ell_t^2 = \dfrac{3 \gamma_5}{2 \mu}. $$
(15)

Hence in couple stress theories only two characteristic lengths are independent, the so-called bending and torsion characteristic lengths, respectively ℓ b and ℓ t . Note that ℓ s the weight of differential-shear is determined by ℓ b , whilst both the weight ℓ e of differential-elongation and the coupling γ 3 are assumed vanishing.

The constitutive assumption proposed by [18] and discussed by [29] is also frequently used, see for instance [22]; it is expressed through only one strain-gradient constitutive modulus c as follows

$$ \hat{\psi}_{L\!M}(E_{i j}, D_{i j h}) := \dfrac{\lambda}{2} E_{ii} E_{jj} + \mu E_{i j} E_{i j} +\dfrac{c \lambda}{2}\, D_{i i m} D_{j j m} + c \mu D_{i j m} D_{i j m}. $$
(16)

This case can be recovered from the general form (14), letting γ 1=c(λ+2μ), γ 2=4cμ, γ 3=−4cλ/3, γ 4=8c(2λ+3μ)/9 and γ 5=4cμ/9. For the characteristic lengths one obtains:

$$ \ell_{e}^2 = c \, (2+\lambda/\mu ),\qquad \ell_b^2 = \dfrac {16\, c}{9} (3+\lambda/\mu ),\qquad \ell_s^2=c,\qquad\ell_t^2 = 2c. $$
(17)

Hence none of them vanishes, but all are determined as functions of only one characteristic length, \(\sqrt{c}\), and the Poisson ratio ν, since λ/μ=2ν/(1−2ν). From now on we will refer to the assumptions (17) as Simplified Mindlin (SM) materials. Finally note that the differential-elongation and the differential-shear characteristic lengths are equivalent, via the Poisson modulus, to the characteristic lengths \(\hat{\ell}_{1}\) and \(\hat {\ell}_{2}\) introduced in [30], as

$$ \ell_e^2 = 2 \dfrac{1-\nu}{1-2 \nu} \hat{ \ell}_1^2,\qquad\ell_s^2 = \hat{ \ell}_2^2. $$
(18)

4 Governing Equations for Antiplane & Plane Strain Fracture Modes

In order to study the three classical fracture modes, say the tearing, opening and shearing modes, we explicit derive the reduced form of the constitutive relationships under antiplane and plane-strain assumptions. The corresponding Navier equations, i.e., the balance equations in terms of displacement fields, are also deduced, see (22) and (27). In the following subsections their asymptotic solutions are deduced.

4.1 The Case of Antiplane Strain: Constitutive Laws and Navier Equation

Antiplane strain displacement field is of the form:

$$ u_1= 0,\qquad u_2=0,\qquad u_3= w(x_1,\,x_2), $$
(19)

with respect to a suitable fixed frame in the reference configuration; it is suitable for describing the tearing fracture mode, or mode III. Apparently, given (19), the only non-vanishing strain components are E 13=E 31=w ,1/2 and E 23=E 32=w ,2/2; consequently the only non-vanishing components of the associated strain-gradient are:

(20)

Using the constitutive relations (11), (13) and (14), the corresponding non-vanishing components of the hyperstress fields are:

(21)

For more details on the derivation of such form of the constitutive relation we refer to [13].

Replacing these last into Eqs. (9) and using the strain gradients (20), the usefulness of the definitions (14) becomes apparent as one obtains the following form of the Navier balance law:

$$ w_{, \alpha\alpha} - \ell_{s}^2\, w_{, \alpha\alpha\beta\beta}=0, $$
(22)

with α,β=1,2 and ℓ s defined as in (14). The strain gradient correction of the antiplane Navier equation is then proportional to a double-laplacian of the displacement w. Remark that couple-stress theory prescribes exactly the same form for the Navier equation of antiplane problems; in that case, however, the coefficient of the double-laplacian depends only on the strain-gradient constants γ 4 and γ 5, whilst in (22) ℓ s does depend on all of them.

4.2 The Case of Plane Strain: Constitutive Laws and Navier Equation

Similarly, in order to study inplane opening and shearing fracture modes, we examine the reduced form of strain-gradient relationships assuming plane-strain deformations. The plane-strain assumption is enforced assuming the three-dimensional displacement field in the form:

$$ u_1= u_1(x_1,\,x_2),\qquad u_2= u_2(x_1,\,x_2),\qquad u_3=0, $$
(23)

with respect to a suitable fixed frame in the reference configuration. Apparently, given (23), E i3=E 3i =0 for i=1,2,3; moreover the only non-vanishing components of the associated strain-gradient are

(24)

Hence, using the constitutive relations (11), (13) and (14), the corresponding non-vanishing components of the hyperstress field are

(25)
(26)

for α=1, β=2 and for α=2, β=1. Also in this case we refer to [13] for more details on the derivation of (25).

Again the Navier form of the balance law demonstrates the advantage of the definitions (14): replacing (25) and (26) into Eqs. (9) and using definition (24), one obtains

$$ \mu\, u_{\alpha, \beta\beta} +(\lambda+\mu) u_{\beta, \beta\alpha} - \mu \bigl[ \ell_{e}^2 u_{\alpha, \beta\beta\gamma\gamma} + \bigl( \ell_{e}^2-\ell_{s}^2 \bigr) \epsilon_{\alpha\beta\delta} \epsilon_{\beta\zeta\eta} u_{\zeta, \eta\delta\gamma\gamma} \bigr]=0, $$
(27)

with ℓ e and ℓ s as in (14). While the first two addends in (27) account for the standard Navier operator of plane elasticity, the last two represent the contribution of strain gradient terms. For later use, the plane-strain Navier equation (27) can be written in absolute notation as:

$$ \varDelta u + \dfrac{\lambda+\mu}{\mu}\, \nabla(\operatorname{div} u)- \varDelta \bigl[ \ell_{e}^2 \varDelta u +\bigl(\ell_{e}^2- \ell_{s}^2\bigr) \operatorname{curl}\operatorname{curl}u \bigr]=0. $$
(28)

5 Asymptotic Solutions for Antiplane and Inplane Opening Modes

Within the discussed framework of strain-gradient elasticity we examine the problem of stress/strain localization around a crack for all the three opening modes of standard fracture mechanics. In particular, we study the behaviour of the strain-gradient solutions asymptotically close to the tip of a rectilinear crack. Hence, referring to Fig. 1, we focus our attention within the region r<d II , where the strain-gradient energy contributions, due to strain/stress localization, are dominant with respect to standard strain energy. We provide upper bound estimates for the limit radius d II as function of the material characteristic lengths.

5.1 Domain Definition, Boundary Conditions and Asymptotic Forms of Navier Equations

We examine the domain \(\mathcal{D}:=\{ (r, \theta): r>0, -\pi< \theta< \pi\}\) centered around the crack tip o, refer to Fig. 3. The boundary \(\partial\mathcal{D}\) is composed by the two opposite lips \(\mathcal{L}^{\pm}\), whilst the boundary of the boundary \(\partial\partial\mathcal{D}\) is composed by the point o. In all these sets the applied external actions, introduced in (9) are assumed to vanish, i.e.,

$$ t(r, \theta=\pm\pi)=0,\qquad \tau(r, \theta=\pm\pi)=0, \qquad f_o=0. $$
(29)
Fig. 3
figure 3

Polar coordinates centered in the tip of the crack. The lips \(\mathcal{L}^{\pm}\) are supposed free as both traction and contact double-forces do vanish on them. Also the edge point o is suppose free of forces

Full size image

Equations (22) and (27) represent the correct differential problems to be solved respectively for the antiplane and in-plane cases. To derive their asymptotic forms we introduce dimensionless coordinates \(\hat{X}_{\alpha}=X_{\alpha}/d_{I\!\! I}\) so that the two equations are respectively rescaled to:

(30)

where g ,α now means derivation of the quantity g with respect to the \(\hat{X}_{\alpha}\) coordinate and η a positive small scale parameter; in particular η:=d II /ℓ s (resp. η:=d II /ℓ e ) for the antiplane (in-plane) case.

The leading terms of the asymptotic expansions of w and u valid for small η,

$$ w=w^{(0)}+\eta w^{(1)}+\cdots,\qquad u_{\alpha}=u_{\alpha}^{(0)}+ \eta u_{\alpha}^{(1)}+\cdots, $$
(31)

are governed by Eqs. (30) with η→0. We limit our attention to the leading terms w (0) and u (0) only; hence we are led to consider only the highest order derivatives in (30) and, therefore, to neglect the contribution of standard elastic terms. Dropping the (0) apices, the reduced forms of Navier’s equations, which are considered in what follows, are finally written:

$$ \varDelta \varDelta w=0,\qquad \varDelta \varDelta u + \biggl(1- \frac{\ell_{s}^2}{\ell_{e}^2} \biggr) \varDelta ( \operatorname{curl}\operatorname{curl}u ) =0, $$
(32)

for the antiplane and in-plane cases, respectively. Similarly, in the limit η→0, one can easily check that the first gradient contributions to tractions t, double-forces τ and edge forces f in the boundary conditions (29), fade away with respect to strain-gradient terms; thus, also the boundary conditions will depend on the intrinsic characteristic lengths only.

5.2 Asymptotic Solution for Antiplane Mode

In the spirit of the Williams expansion [40], the asymptotic solution of the antiplane problem is found assuming the form w(r,θ)=r α W(θ) for the transverse displacement, with α≥1 to assure integrability of the energy. The displacement is assumed anti-symmetric with respect to the θ=0 axis, i.e., W(−θ)=−W(θ). Accordingly the bulk balance equation (32)1 reduces to:

$$ W''''+2 \bigl(\alpha(\alpha-2) +2\bigr) W''+ \alpha^2 (\alpha-2)^2 W=0, $$
(33)

together with the boundary conditions (29)1,2:

(34)

The expressions of t ± and τ ± in (34) can be derived from (9)2,3 once using polar coordinates and the assumed form of w(r,θ).

Facing a system of linear differential equations, we assume the solution in the form \(W(\theta) = \overline{W} \exp(i \kappa \theta )\) and, accordingly, obtain a standard eigenvalue problem. First substituting into the bulk balance equation (33), the relationship between the angular wavelength κ and the exponent α is derived. It turns out to be independent from material constants and reads

$$ (\kappa-\alpha) (\kappa-\alpha+2) (\kappa+\alpha-2) (\kappa+ \alpha)=0. $$
(35)

Then, evaluating the boundary conditions (34) with the assumed form of W(θ), we obtain a homogeneous linear system. Non-trivial solutions are found only if the determinant of the associated 4×4 matrix vanishes. After cumbersome simplification of the determinant, we obtain

$$ 64 \ell_t^4 \bigl( \ell_t^2-8 \ell_{s}^2 \bigr)^2 \alpha^2 (\alpha-2)^2 ( \alpha-1)^4 \sin^2(2 \pi \alpha) = 0, $$
(36)

which dictates the admissible values for the exponent α. We recall that \(0<\ell_{t}^{2} < 4 \ell_{s}^{2}\); thus, Eq. (36) could be solved solely in terms of α. Apart from the root α=1, the first root of (36) strictly greater than 1 is α=3/2. Using the required anti-symmetry of W, the associated eigenvectors are determined and the general solution in terms of displacement is written in the form

$$ w(r,\theta)= \varGamma r \sin\theta+ C_{I\!\!I\!\!I} r^{3/2} \biggl(\dfrac{3 \sin\theta/2}{16 (\ell_{s}/\ell_t)^2-3}-\sin \dfrac{3 \theta}{2} \biggr), $$
(37)

for Γ and C III two arbitrary constants. Remark that the first addend in (37) corresponds to α=1: it physically represents a field of uniform shear and does not contribute to the strain-gradient energy density. The solution (37) is in perfect agreement with the solution obtained in [34], but it is obtained in a setting more general than couple stress elasticity, as ℓ s and ℓ t are the ones defined in (14).

We recall that (37) is valid only asymptotically close to the tip, i.e., within r<d II for d II /ℓ s →0. To estimate an upper bound for the value d II , in which this solution still has a reasonable validity, we seek for the radius d at which the strain-gradient energy density associated to (37) equals the strain energy density associated to the classical far-field solution \(w_{f}(r,\,\theta) \propto K_{I\!\!I\!\!I} \sqrt{r} \sin\theta/2\). Details of such calculation are reported in Appendix A; the results, however, are shown in Fig. 4 where d/ℓ s is plotted against the ratio ℓ t /ℓ s ; recall that ℓ t =0 and ℓ t =2ℓ s are the boundaries of the domain of positive definiteness. For r<d the strain-gradient contributions in the elastic energy are certainly greater than the standard strain terms; this fact justifies the radius d as an upper bound for d II : we see that, for a wide class of materials (namely those with ℓ t ≳ℓ s ), a ball of radius 0.5ℓ s is a fair approximation for the validity region of the asymptotic solution. The obtained estimate is actually consistent with the one provided in [34] and deduced from the complete solution, matching the asymptotic and far fields via the Wiener-Hopf technique.

Fig. 4
figure 4

Estimate of the process zone radius d/ℓ s is given in terms of the characteristic internal length ℓ t for the antiplane problem

Full size image

5.3 Asymptotic Solution for Inplane Modes

The asymptotic solution for the inplane problem is found assuming the form

$$ u_r(r,\theta)= r^\alpha U_r( \theta),\qquad u_\theta(r,\theta) = r^\alpha U_\theta(\theta),\quad\alpha\ge1, $$
(38)

for the radial u r and tangential u θ components of the displacement field. Again the request on α assures the elastic energy to be integrable. Inserting (38) in the bulk balance equations (32)2 we obtain

(39)

together with the boundary conditions (29)1

(40)

meaning the radial and tangential components of the tractions on the lips, and the boundary conditions (29)2

(41)

meaning the radial and tangential components of the double forces on the lips. The previous expressions of tractions (40) and double forces (41) can be derived from (9)2,3 once using polar coordinates and the assumed form of the inplane displacement.

As (39)–(41) constitute a homogeneous system of linear ordinary differential equations, the solution is sought in the form \(\{U_{r}(\theta), U_{\theta}(\theta)\}^{\top}= \{ \overline{U},\overline{V} \}^{\top}\exp(i \kappa \theta)\). First substituting into the bulk balance equations (39) we obtain the relationship between the angular wavelength and the exponent α: notably, as in the antiplane mode, also this relationship turns out to be independent from material constants and reads

$$ (\kappa-\alpha-1) (\kappa-\alpha+1)^2 (\kappa-\alpha+3) (\kappa + \alpha-3) (\kappa+\alpha-1)^2 (\kappa+\alpha+1)=0. $$
(42)

Hence, evaluating the boundary conditions (40)–(41) with the assumed form of U r (θ) and U θ (θ), we obtain an homogeneous linear system. Non-trivial solutions are found only if the determinant of the associated 8×8 matrix vanishes; after heavy symbolic calculations this condition reduces to:

$$ \frac{\alpha^4 (\alpha-1)^8 (\alpha-2)^4 \sin^4(2 \pi \alpha )}{ ((\alpha-3) (\ell_{s}/\ell_{e})^2-\alpha-1 )^2}=0. $$
(43)

Equation (43) dictates the admissible values for the exponent α. Again, apart from the evident root α=1 the smallest root, strictly greater than 1, is α=3/2. Let us remark that the condition (43) holds for any strain-gradient material, independently from the choice of the constitutive constants. The eigenvectors associated to α=1 and α=3/2 are consequently determined and the general solution can be written as the sum of two contributions; a displacement field which is skew-symmetric with respect to θ=0 axis:

(44)

and a displacement field which is symmetric with respect to θ=0 axis:

(45)

Here Γ 1,…,Γ 3 and C 1,…,C 4 are arbitrary constants. The constitutive constant k 1,…,k 8 are shown in Appendix B as function of the material characteristic lengths; if, for these k i constants, the values specialized for SM materials are used, the solutions (44) and (45) reduce to the cases examined in [2] and [22]. Here we have used the apices II and I as the displacement fields (44) and (45) represent the heirs of inplane shearing and inplane opening modes respectively. Again remark that the terms in (44) and (45) scaling as r do not contribute to the strain-gradient energy density.

Similarly to the antiplane case, we recall that (44) and (45) are valid only asymptotically close to the tip, i.e., for r<d II . To estimate such an upper bound d II , we seek for the radius d at which the strain-gradient energy density associated to (44) and (45) equals the strain energy density associated to the classical far-field solutions. The results, relative to the inplane opening mode (45), are shown in Fig. 5: d/ℓ e is plotted against the ratios ℓ s /ℓ e and ℓ b /ℓ e for a vanishing γ 3. For r<d the strain-gradient contributions in the elastic energy are certainly greater than the standard strain terms; this fact justifies d as an upper bound for d II . From Fig. 5 we see that, for a wide class of materials (namely those with ℓ b ≳ℓ e and ℓ s ≳0.6ℓ e ), a ball of radius 0.5ℓ e is a fair approximation for the validity region of the asymptotic solution; this estimate loosely depends on the material Poisson ratio. The obtained estimate is actually consistent with the one deduced from the full-field solution derived in [22] for the case of SM materials.

Fig. 5
figure 5

Estimate of the process zone radius d/ℓ e in terms of the characteristic internal length ℓ s and ℓ b for the in-plane opening problem: predictions for C 4=0 (a), and C 2=0 (b). Solid and dashed curves stand respectively for ν=0.2 and ν=0.4

Full size image

5.4 Edge Force Condition in the Crack Tip

As the hyper-stress field are singular in the same point where the edge o is located, the localization of the balance law (9)4, expressing the edge force in terms of the hyperstress P, can not be deduced for the crack tip.

However a balance condition for forces acting on the tip can still be derived by using a suitable test field in the principle of virtual working (5). To this aim one can consider a test field δu having support on a ball \(\mathcal{B}_{\varepsilon}\) of radius ε centered in the crack tip o and then taking the limit for a vanishing radius. The set \(\mathcal{B}_{\varepsilon}\) has three edges: the two edges on the lips \(P_{\varepsilon}^{\pm}:= (-\varepsilon, 0^{\pm})\) and the tip o; the resulting balance of forces reads then

$$ \lim_{\varepsilon\rightarrow0} \biggl( f_i\bigl(P_\varepsilon^+\bigr) + f_i\bigl(P_\varepsilon^-\bigr) +\int _{\partial\mathcal{B}_{\varepsilon}} t_i \biggr) = f_i^o,\quad i=1,2,3, $$
(46)

where f o is the external applied force on the tip.

For all the displacement fields (37), (44) and (45) the argument of the limit in (46) is identically zero, independently from all the constants C and Γ. This means that these solutions satisfy also the condition (29)3 for a tip free of forces, which were not used to deduce them. A simple calculation shows that if a non-vanishing force f o is considered on the crack tip, one must necessarily account, in the asymptotic solutions, for additional, more regular, terms scaling as r 2.

6 Discussion of Results

The results obtained in terms of displacement fields, for the antiplane and inplane crack opening problems, are here discussed with a three-fold aim. First an equivalence between strain-gradient effects and cohesive forces (à la Barenblatt) is introduced in terms of COD profiles. Then the rates of elastic energy release associated to crack propagation are computed in order to examine, from an energetic point of view, how strengthening effects of strain-gradient materials depend on the actual values of their characteristic lengths. In this respect, the five considered strain-gradient moduli endow the material with a micro-structural description much more refined than in couple-stress or SM theories. Finally we emphasize some special features of the deformation fields which are characteristic of strain-gradient elasticity and that could, therefore, be used for a direct measurement of the material moduli.

6.1 Cohesive-Like Effects

In his celebrated paper [4] Barenblatt proposed to introduce a suitable field of tractions between the crack lips in order to eliminate the stress singularity. These contact forces, supposed non-vanishing only in a vicinity of the crack tip, were intended to model the “molecular forces of cohesion” within the process zone. It is well known that such a field of cohesive force induces a COD profile which asymptotically scales as r 3/2.

We here compare the classical solutions due to Barenblatt, with those obtained for strain-gradient materials in (37) and (45).Footnote 1 Equating the leading terms in the crack opening displacements (CODs) leads to establish an equivalence between the strain-gradient characteristic lengths and a given distribution of elastic cohesive forces between the lips.

To the aim, we focus first on the inplane opening mode and suppose acting on the crack lips two opposite far-field forces, ±Pe 2 at distance R from the tip, and a system of opposite tractions t ±(r)=±g 2(r)e 2 in the tip vicinity, refer to Fig. 6. Therefore, using Muskhelishvili’s method, one find that the leading part of the asymptotic solution for the Barenblatt COD is

$$ v_B(r)= \dfrac{4 (1-\nu^2)}{\pi Y} \biggl[ \biggl( \dfrac{P}{\sqrt{R}} + \int _{0}^{\infty} \dfrac{g_2(s) }{\sqrt{s}}\,ds \biggr) \sqrt{r} + \biggl(\dfrac{P}{R^{3/2}}+\int _{0}^{\infty} \dfrac{g_2(s) }{3 s^{3/2}}\,ds \biggr) r^{3/2} + \cdots \biggr], $$
(47)

where Y is the material Young modulus. As suggested in [4] the distribution of contact actions g 2 is chosen to let vanish the coefficient of \(\sqrt{r}\), responsible for the stress divergence as r→0. Hence, choosing \(\int g_{2}(s)/ \sqrt{s}\,ds=-P/\sqrt{R}\), one obtains

$$ v_B(r)= \dfrac{4 (1-\nu^2)}{\pi Y} \biggl(-\dfrac{1}{R} \int _{0}^{\infty} \dfrac{g_2(s) }{\sqrt{s}}\,ds + \int _{0}^{\infty} \dfrac{g_2(s) }{3s^{3/2}}\,ds \biggr) r^{3/2} + \cdots{.} $$
(48)

Finally as the forces P are applied far away from the tip, one lets R→∞ to get

$$ v_B(r)= \dfrac{4 (1-\nu^2)}{3 \pi Y} \biggl( \int _{0}^{\infty} \dfrac{g_2(s)}{s^{3/2}}\,ds \biggr) r^{3/2} + \cdots $$
(49)

which is the leading term of the crack opening displacement for a cohesive material within standard elasticity. The corresponding COD in strain-gradient elasticity, is easily obtained from (45) as

$$ v_{SG}(r) = \lim_{\theta\rightarrow\pi} u_\theta^{\mathrm{I}} = \bigl( C_4 (2 - k_7 + k_8)-5 C_2 k_6 \bigr) r^{3/2}+\cdots, $$
(50)

corresponding to the amplitudes C 2 and C 4, determined by the far field conditions, and to the constants k 6, k 7, k 8 reported in Appendix B. Therefore strain-gradient elasticity can provide the same asymptotic COD of Barenblatt cohesive model as long as v B ≡v SG , implying

$$ \dfrac{4 (1-\nu^2)}{3\pi} \biggl(\int _{0}^{\infty} \dfrac{g_2(s) }{s^{3/2}}\,ds \biggr) = T_2(\ell_{e}, \ell_{s}, \ell_b, \gamma_3) C_2 + T_4(\ell_{e}, \ell_{s}, \ell_b, \gamma_3) C_4, $$
(51)

for T 2 and T 4 given by

$$ T_2:=\dfrac{512 Y \ell_e^2}{15 \ell_b^2-40 \gamma_3-16 \ell_e^2-240 \ell_s^2}, $$
(52)

and

$$ T_4:=\dfrac{1024 Y \ell_e^2 (5 \ell_s^2 (-21 \ell_b^2+8 \gamma_3-32 \ell_e^2 )+\ell_e^2 (9 \ell_b^2+24 \gamma_3+16 \ell_e^2 )+1680 \ell_s^4 )}{3 (5 \ell_e^2+3 \ell_s^2 ) (9 \ell_b^2+24 \gamma_3+16 (\ell_e^2-9 \ell_s^2 ) ) (15 \ell_b^2-40 \gamma_3-16 (\ell_e^2+15 \ell_s^2 ) )}. $$
(53)

The quantities T 2 and T 4, having physical dimensions of a pressure, can be though as equivalent cohesive force distributions provided by the material micro-structure.

Fig. 6
figure 6

Far-field force P and cohesive tractions g 2 for the inplane opening mode. The radius d I labels the zone outside of which the cohesive effects becomes vanishing

Full size image

For the SM materials, using (17), one easily see that Eqs. (52) and (53) reduce to T 2=16Y(1−ν)/(3−8ν) and T 4=160Y(1−ν)/(39−48ν) respectively; hence, within the region r<d II where (51) holds, also SM materials do provide cohesive effects, see also [22]. Instead, any strain-gradient material with a vanishing differential-elongation characteristic length does not show cohesive effects as clearly ℓ e →0 implies T 2→0 and T 4→0.

The general expressions (52) and (53) are plotted in Fig. 7 against the ratios ℓ s /ℓ e and ℓ b /ℓ e assuming γ 3=0. One observes a monotonic increase of both the equivalent cohesive forces as the upper boundary of the region:

$$ 9 \ell_b^2+24 \gamma_3+16 \ell_e^2\leq144 \ell_s^2, $$
(54)

for the admissible constitutive lengths, is approached. The inequality (54) translates the condition (12)2, i.e. γ 2>0, for a positive definite elastic energy in terms of characteristic lengths. While T 4 diverges approaching this limit, see the denominator in (53), T 2 diverges on a set outside the admissible region, namely on the dashed line in Fig. 7a.

Fig. 7
figure 7

Intensity of equivalent cohesive forces \(|T_{2}|/(Y \ell_{e}^{2})\) (a) and \(|T_{4}|/(Y \ell_{e}^{2})\) (b) as functions of the ratios ℓ s /ℓ e and ℓ b /ℓ e for γ 3=0. The black points correspond to SM materials

Full size image

Using similar arguments, one obtains relations analogous to (51) for all the examined modes; in particular, for the tearing mode (37), one finds:

$$ \dfrac{2 }{3\pi} \biggl(\int _{0}^{\infty} \dfrac{g_3(s) }{s^{3/2}}\, ds \biggr) = T_{I\!\!I\!\!I}(\ell_s, \ell_t) C_{I\!\!I\!\!I},\quad T_{I\!\!I\!\!I}:= \dfrac{32 \mu \ell_s^2}{3 \ell_t^2-16 \ell_s^2}, $$
(55)

for T III an equivalent distribution of elastic forces which relate the strain-gradient characteristic lengths ℓ s and ℓ t to the cohesive forces g 3 acting in the out-of-plane direction. The coefficient T III is plotted in Fig. 9 as a solid curve: it turns out to be a monotonic increasing function of the ratio ℓ t /ℓ s . Then the maximum cohesive effects in antiplane problems are attained at the limit value ℓ t =2ℓ s of the admissible region, while the cohesion effect would vanish if ℓ s →0. In the same figure SM materials are represented by the grid line at \(\ell_{t}/\ell_{s}=\sqrt{2}\), cf. (17).

We remark that the cohesive effects demonstrated in both (51) and (55) are valid sufficiently close to the crack tip, namely in the range of validity of the asymptotic solutions, say r≲0.5ℓ e and r≲0.5ℓ s respectively.

6.2 Energy-Release Rates

A characterization of the strain-gradient strengthening can also be given in terms of energy. Recently, in [36], the authors provided the general form of the elastic energy release rate in finite strain-gradient elasticity. Therein special emphasis was paid to the contribution of edge forces to the actual value of the associated J-integral; indeed, this last must be suitably extended to cope with the edge points of the path, say Γ, of its definition. In particular, the extended form of J-integral provided in [36] depends on the closure \(\overline{\varGamma}\) and reads as

$$ J(\overline{\varGamma}):=\int _{\varGamma} (\psi n_1 - t_l u_{l,1} -\tau_l u_{l,1 q} n_q ) - ( f_l u_{l,1} ) |_{P^+}+ ( f_l u_{l,1} ) |_{P^-}, $$
(56)

where Γ is a suitable path circumventing the crack tip and \(P^{\pm}:= \varGamma\cap\mathcal{L}^{\pm}\) its edge points on the crack lips. Here, as usual, n 1 denotes the component of the normal to Γ towards the direction of crack propagation (supposedly e 1), ψ the elastic energy density, u the displacement, t, τ and f the tractions, double-forces and edge forces as given in (9).

Substituting the solution (45) in the J-integral expression (56), we obtain the energy release rate associated to the inplane opening mode as:

$$ J_{I}=J_{22}(\ell_e,\ell_s, \ell_b,\gamma_3) C_2^2+ J_{44}(\ell_e,\ell_s,\ell_b, \gamma_3) C_4^2+ 2 J_{24}( \ell_e,\ell_s,\ell_b,\gamma_3) C_2 C_4, $$
(57)

where the functions of the characteristic lengths J 22, J 44 and J 24 are reported in Appendix B. It can be easily checked that when ℓ e →0 then J I →0, whilst for SM materials (17) the functions J 22, J 44 and J 24 do not vanish; they result indeed proportional, via suitable functions of the Poisson ratio, to the unique SM characteristic length \(\sqrt{c}\), refer to (70). We remark that, as discussed in [36], the contribution of edge forces implies an energetic coupling between inplane sliding and opening modes as the J-integral turns out to be not, as in standard elasticity, a quadratic diagonal form of the amplitude factors. However, since the non-diagonal terms would appear only in mixed mode crack problems, here we have limited the discussion to the purely symmetric loading cases, for which the amplitudes of the sliding modes, C 1 and C 3 in (44), are vanishing and, therefore, J I is a quadratic form of C 2 and C 4 only.

Similarly, substituting the solution (37) in (56), the energy release rate for the tearing mode is computed to be:

$$ J_{I\!\!I\!\!I} = 72 \pi \mu \ell_s^2 C_{I\!\!I\!\!I}^2 \dfrac{ \ell_t^2 (8 \ell_{s}^2-\ell_t^2 )}{ (16 \ell_{s}^2-3\ell_t^2 )^2}. $$
(58)

Here, contrary to inplane cases, the edge forces contributions in (56) identically vanish.

In Fig. 8 the coefficients for the energy release rates (57) are plotted as functions of the micro-structural parameters ℓ s /ℓ e and ℓ b /ℓ e ; we have chosen γ 3=0, but qualitatively similar plots can be given for γ 3≠0. In both figures, the SM materials are represented by a black points. For these materials, indeed, the ratios ℓ b /ℓ e and ℓ s /ℓ e depend of the Poisson ratio only; however, to have γ 3=0, we obtain ℓ b /ℓ e ≃1.5 and ℓ s /ℓ e ≃0.7.

When comparing Figs. 7 and 8, we observe the same qualitative dependences of cohesive force intensities and energy release rates on the characteristic length ratios. In particular, from Figs. 8, we again deduce that materials with ℓ s /ℓ e and ℓ b /ℓ e approaching the upper boundary (54) are associated to the highest energy release rates. Conversely, the energy release rates become vanishing as soon as ℓ b →0 and ℓ s →0.8ℓ e or for ℓ e →0. Similarly in Fig. 9 the energy release rate J III is plotted as a dashed curve against the ratio ℓ t /ℓ s ; again in general agreement with the cohesive effect the maximum is reached at the boundary of the admissible region when ℓ t →2ℓ s .

Fig. 8
figure 8

Coefficients for the energy release rate J I in (57): (a) \(J_{22}/(\mu\ell_{e}^{2})\), (b) \(J_{44}/(\mu\ell_{e}^{2})\) and (c) \(J_{24}/(\mu\ell_{e}^{2})\) as functions of the ratios ℓ s /ℓ e and ℓ b /ℓ e for γ 3=0

Full size image
Fig. 9
figure 9

Intensity of cohesive forces |T III |/μ (solid curve) and energy release rate \(J_{I\!\!I\!\!I}/(72 \pi\mu\ell_{s}^{2} C_{I\!\!I\!\!I}^{2})\) (dashed curve) for the tearing mode as functions of the micro-structural parameter ℓ t /ℓ s

Full size image

As soon as the material lengths approach the boundaries of the admissible regions in Figs. 8 and 9, the energy is characterized by a vanishing cost of at least one strain-gradient deformation. It seems then that having a reduced stiffness, along suitable strain-gradient deformations, leads to increase the material energetic release. Starting from the actual material microstructure, say geometric patterns or textures at the microscale, these results could be extended to indicate the optimal values of micro-structural parameters to provide sensible strengthening effects within a given crack opening mode.

6.3 Observable Quantities

Equations (57) and (58) reveal that, when the characteristic lengths associated to differential extension, ℓ e , and differential shear, ℓ s , tend to zero, the strain-gradient contributions to the energy release rates tend to vanish. These results are consistent with the d II -estimates provided in Sect. 5: as the amplitudes of the process zones are estimated to be of the same magnitude order of ℓ e and ℓ s , their vanishing enforces these zones to collapse around the crack tip. Conversely, observations of the displacement fields at the micro/nano scales, in both tearing and opening modes, can hopefully provide a direct measurement for the amplitudes of the regions where the CODs reveal a cusp-like behaviour. In this section we discuss peculiar observable features of the strain-gradient asymptotic solution which could allow for a coarse, but direct, estimation of the characteristic lengths. We point out that modern techniques, such as the digital correlation of images acquired by atomic force microscopes, allow for very high resolutions, up to micro or even nano-scales, as well as for the elimination of rugosity effects, see for instance [23].

Inspection of the polar representation of the asymptotic displacement fields, for both antiplane (37) and plane-strain conditions (44) and (45), shows a non-monotone multi-harmonic dependence on the azimuthal coordinate θ. In particular, for inplane opening tests, the strain-gradient solution (45) predicts the deformations shown in Fig. 10, for Γ 1=Γ 2=0, whilst the one associated to the shearing mode are displayed in Fig. 11, for Γ 3=0. There we have respectively plotted the deformations \(u_{I}/\sqrt{J_{I}}\) and \(u_{I\!\!I}/\sqrt{J_{I\!\!I}}\) associated to the sequence of values ℓ b /ℓ e and ℓ s /ℓ e depicted in Fig. 7; these ratios are used as independent of the C constants.

Fig. 10
figure 10

Deformed shapes of a circular disk with radius r≪ℓ e surrounding the crack tip for inplane opening mode: (a) C 4=0, (b) C 2=0. These plots are at fixed toughness as correspond to the fields \(u_{I}/\sqrt{J_{I}}\), for ℓ s /ℓ e =0.8 and ℓ b /ℓ e varied along the path depicted in Fig. 7

Full size image
Fig. 11
figure 11

Deformed shapes of a circular disk with radius r≪ℓ e surrounding the crack tip for shear opening mode: (a) C 3=0, (b) C 1=0. These plots are at fixed toughness as correspond to the fields \(u_{I\!\!I}/\sqrt{J_{I\!\!I}}\), for ℓ s /ℓ e =0.8 and ℓ b /ℓ e varied along the path depicted in Fig. 7

Full size image

On the other hand, in tearing tests, the strain-gradient solution (37) predicts the presence of a uniform shear field, scaling as r and whose amplitude is determined by the constant Γ, and of a strain-gradient component associated with non-uniform strains. This last contribution scales as r 3/2, it is controlled by the amplitude C III and it is characterized by a circular sector around the crack tip where the transverse displacement changes sign. Notice that the angle α i in Fig. 12a, which determine the width of the sector where the transverse displacement changes sign, depends only on the ratio ℓ t /ℓ s , as from (37) one easily obtains:

$$ \alpha_i=2 \cos^{-1} \biggl( \dfrac{2}{\sqrt{16-3 (\ell_t/\ell_{s})^2}} \biggr). $$
(59)

This function is shown in Fig. 12b for ℓ t /ℓ s in [0,2]: progressive increase of ℓ t /ℓ s yields stronger cohesive effects (Fig. 9) and forces the inversion angle to vanish monotonically. Accurate measurements of the inversion angle α i , within the process zone of materials under tearing conditions, could then serve to directly estimate the ratio between the torsion and differential-shear characteristic lengths. Certainly, the uniform-shear component must be filtered out, but this account to a simple Fourier analysis over the measured field w(r,θ) as a function of θ, see Eq. (37) or Fig. 12a.

Fig. 12
figure 12

(a) Polar plot of the antiplane displacement for ℓ t =ℓ s : uniform-shear component (dashed), strain-gradient component (gray) and whole field (thick black); (b) the inversion angle α i as a function of the ratio ℓ t /ℓ s in [0,2]

Full size image

Aiming to estimate the strain-gradient moduli, the inspection of the deformations fields near the tip seems to be a promising experimental approach in comparison with the studies reported in [27] or [28]. These latter were based on simple tension, bending or torsion tests where the contributions of strain-gradient were not dominant; as a matter of fact, the strain-gradient moduli were estimated after filtering out, from the measured values of bending or torsional stiffness, the contribution of homogeneous deformations, refer for instance to [1]. Instead, the direct experimental inspection of some strain-gradient effects and relies on local measurements in zones where non-homogenous deformations are dominant. This behavior is in close analogy with nanoindentation tests, where the effects of material length scales on hardness can be accurately predicted, see, e.g., [5] and [25]. Certainly, more attention must be paid to select both suitable candidate materials and experimental set-ups to reach the necessary resolution even for modest strain levels.

7 Further Developments

The results presented in Sect. 6 provide several hints on the fracturing process of strain-gradient materials. In particular, emphasis has been posed on the dependence of CODs and energy release rates on the material characteristic lengths; the aim was both to establish the effects of specific internal micro-structures on the material toughness properties and to enlighten possible constitutive identification procedures which are based on microscale measurements.

Accordingly future developments will be devoted to design an experimental setup able to record full-field displacement measures of structured samples under inplane opening and tearing tests. In order to get measurements accurate at the micro/nano scales, refined airbrush painted speckle patterns, see, e.g., [37], or digital correlation of atomic force microscope images, see, e.g., [23], are currently available methods.

Development efforts will be also pursued to establish a micro-macro constitutive identification for structured materials, as metallic alloys or textured composites; in particular, one should focus on the characterization of proper boundary value problems which guarantee a “generalized” Hill lemma to hold true within the framework of strain-gradient elasticity. As strain gradient effects become more important when the associated characteristic lengths are comparable with the specimen size, the envisaged constitutive identification should not assume the heterogeneity dilution inside the Representative Volume Element, see, e.g., [14]; as proved in [6] the dilution hypothesis leads indeed to a negligible influence of the heterogeneities, as the resulting Cosserat moduli depend on the square of the inclusions volume fraction.