1 Introduction

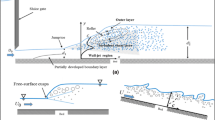
The hydraulic jump is a sudden transition from supercritical to subcritical flow, with an abrupt discontinuity in the air–water interface (Fig. 1). There are important engineering applications of the hydraulic jump phenomenon. For example, it is used to dissipate energy in turbulent flow over dams, weirs, and spillways for prevention of channel scour downstream from the structures, to recover downstream head in irrigation networks, and to aerate water for city water supplies. As stated in Chanson [1], knowledge about turbulent hydraulic jumps is insufficient. This is in spite of great efforts made by earlier researchers. Most of the existing prediction methods have considered the phenomenon as a single-phase water flow, unable to realistically allow for the effects of commonly observed air entrainment and bubble motions in hydraulic jumps. The purpose of this paper is to achieve improved predictions of hydraulic jump as a bubbly two-phase turbulent flow.

Fig. 1
figure 1

Hydraulic jump downstream of a sluice gate, created by a downstream tailgate. Point A is the origin of the Cartesian coordinate system (x 1, x 2)

Full size image

A hydraulic jump will form when supercritical flow transitions to subcritical flow. According to the classical theory of hydraulic jumps, in a horizontal or slightly inclined channel, the approach flow Froude number, Fr1, the initial depth, d 1, and a downstream sequent depth, d 2, satisfy the equation

$$\frac{{d_{2} }}{{d_{1} }} = \frac{1}{2}\left( {\sqrt {1 + 8{\text{Fr}}_{1}^{2} } - 1} \right)$$
(1)

Classic analyses produced some useful results such as the classifications of the types of jump, the characterisation of water surface profiles, estimates of the height and length of jump, and the loss of energy in the jump [2]. Castro-Orgaz and Hager [3] gave more detailed discussions about classic hydraulic jumps. The classical theory has assumed hydrostatic pressure distribution, without consideration of a possible air content in the flow. To what extent should hydrostatic pressure calculations be corrected because air bubbles are present in the water?

Rajaratnam [4] as well as Murzyn and Chanson [5] reported hydraulic jump experimental data, showing strong turbulence, highly non-uniform velocity profiles across the depth. Importantly, the non-uniformity implies that hydraulic jump modelling should avoid using the logarithmic law as the boundary condition at the channel bottom. Unfortunately, this is often not the case in the literature. In addition, Valiani [6] and Chanson [7] observed non-zero momentum flux in the roller and a significant amount of air entrainment in hydraulic jumps. There are rapid fluctuations of the free surface associated with rollers and air volume fraction. Can we achieve improved predictions through taking these factors into account? Producing a large number of flow field snapshots for given hydraulic conditions, and further obtaining statistical mean and fluctuations is a key strategy.

Computer modelling is an efficient approach to revealing detailed structures of hydraulic jumps. Murzyn and Chanson [8] mentioned the presence of the secondary phase as the main challenge in the treatment of hydraulic jumps. This phase is airflow above the free surface and air mass entrained across it. Previously, numerical techniques of different levels of complexity were used to simulate hydraulic jumps. Gharangik and Chaudhry [9] used Boussinesq equations for one‐dimensional unsteady, rapidly varied flows. Castro-Orgaz et al. [10], Khan and Steffler [11], and Zhou and Stansby [12] used depth-averaged formulations. In Khan and Steffler [11], the depth-averaged model was based on the St. Venant momentum equation, along with an algebraic scheme for turbulence closure. The equation was modified to allow for velocity distribution effects. Recently, Castro-Orgaz et al. [10] used depth-averaged equations, together with the k-ε turbulence closure. On the one hand, the depth-averaged modelling approach may be inadequate, because of significantly non-uniform distributions of pressure, velocity and turbulence across the depth in hydraulic jumps, as seen in Rajaratnam [4] and Murzyn and Chanson [5]. On the other hand, the secondary phase is important, but it is absent from the above-mentioned Eulerian computer models. López et al. [13] and De Padova et al. [14] simulated hydraulic jumps using Lagrangian Smoothed Particle Hydrodynamics models, which also excluded the secondary phase. López et al. [13] faced difficulties in handling cases where Fr1 > 5, but suggested that using the k-ε model improved the results. For turbulence closure, De Padova et al. [14] used the concept of mixing length, which is difficult to accurately specify for complex flows like hydraulic jumps.

Recently, a limited number of researchers, including Bayon et al. [15], Bayon-Barrachina and López-Jiménez [16], and Witt et al. [17], reported computations of hydraulic jumps using two-phase flow techniques. None of these models include all important aspects of the open-channel hydraulic jump problem. Additionally, the bottom wall has been treated with a logarithmic wall function, with the wall distance in the range of 30 < y + < 300. This does not explicitly resolve the viscous sub-layer, and hence there are uncertainties about predictions of turbulent shear and bottom shear stress in the jump. As Chanson and Brattberg [18] pointed out, air–water flow properties in the shear region of a hydraulic jump are poorly understood. There is a need for further studies.

The main objectives of the present research are to investigate air entrainment behaviour, air bubble distributions, turbulence characteristics, and distributed bottom shear stress in hydraulic jumps as two-phase flow. In the following, the modelling methodologies will be described in Sect. 2. Next, computational results will be presented, along with discussions in Sect. 3. Lastly, conclusions will be drawn in Sect. 4.

2 Methodologies

2.1 Reynolds-averaged momentum and continuity equations

The two-phase flow of an air–water mixture is considered incompressible. Let ρ 1 and ρ 2 denote the densities of air (gas phase) and water (liquid phase), and μ 1 and μ 2 denote their dynamic viscosities, respectively. The volume-averaged density, ρ, and viscosity, μ, of the fluid mixture are

$$\rho = \alpha_{2} \rho_{2} + (1 - \alpha_{2} )\rho_{1} ;\quad \mu = \alpha_{2} \mu_{2} + (1 - \alpha_{2} )\mu_{1}$$
(2)

where α 2 is the volume fraction of water. The volume fraction of air is given by α 1 = 1 − α 2.

Using the Cartesian coordinate system (Fig. 1), the motion of the fluid mixture is governed by the Reynolds-averaged Navier–Stokes equations

$$\frac{{\partial u_{i} }}{\partial t} + u_{j} \frac{{\partial u_{i} }}{{\partial x_{j} }} = - \frac{1}{\rho }\frac{\partial p}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left( {\nu \frac{{\partial u_{i} }}{{\partial x_{j} }}} \right) + \frac{{\partial \tau_{ij} }}{{\partial x_{j} }} + g_{i} + F_{{_{i} }}$$
(3)

where u i is the Reynolds averaged velocity component of the fluid mixture in the x i -direction; t is the time; p is the Reynolds-averaged pressure; ν is the kinematic viscosity of the fluid mixture; τ ij is the specific Reynolds stress tensor; g i is the acceleration of gravity in the x i -direction; F i is the surface tension resulting in a body force in the x i -direction.

The phase volume fractions are tracked using the volume of fluid (VOF) method, discussed in Hirt and Nichols [19]. The interfacial boundary is tracked by a piecewise linear interpolation capturing scheme. The VOF equation for the volume fraction of the liquid phase is given by

$$\frac{{\partial \alpha_{2} }}{\partial t} + \frac{{\partial \left( {\alpha_{2} u_{j} } \right)}}{{\partial x_{j} }} = 0$$
(4)

This equation has assumed a system comprising immiscible fluid phases (or zero mass transfer between the phases) and without mass sources.

The volume force F i (Eq. 3) allows for the effects of surface tension at the air–water interface on mixture motion, when air and water are present in a cell. F i is formulated based on a continuum method. Details about this method have been described in Brackbill et al. [20].

2.2 Turbulence closure scheme

Components of τ ij (Eq. 3) are unknown, resulting from the nonlinear interaction of unresolved velocity fluctuations. Their effects on the Reynolds-averaged flow field are parameterised on the basis of the Boussinesq approximation: \(\tau_{ij} = 2\nu_{t} S_{ij} - \frac{2}{3}k\delta_{ij}\). Here, ν t is the kinematic eddy viscosity; S ij is the mean strain-rate tensor, given by S ij  = (∂u i /∂x j +∂u j /∂x i )/2; k is the specific turbulence kinetic energy; and δ ij is the Kronecker delta, being equal to one for i = j, and zero for i ≠ j. The eddy viscosity is expressed as

$$\nu_{t} = C_{\mu } \frac{{k^{2} }}{\varepsilon }$$
(5)

where ε is the rate of dissipation of turbulence kinetic energy; and C μ is a model constant.

The turbulence quantities are obtained from the standard k–ε model. For a two-phase mixture of air and water, the model equations can be written as

$$\frac{\partial k}{\partial t} + u_{j} \frac{\partial k}{{\partial x_{j} }} = 2\nu_{t} S_{ij} S_{ij} - \varepsilon + \frac{\partial }{{\partial x_{j} }}\left[ {(\nu + \nu_{t} /\sigma_{k} )\frac{\partial k}{{\partial x_{j} }}} \right]$$
(6)
$$\frac{\partial \varepsilon }{\partial t} + u_{j} \frac{\partial \varepsilon }{{\partial x_{j} }} = C_{1\varepsilon } \frac{\varepsilon }{k}2\nu_{t} S_{ij} S_{ij} - C_{2\varepsilon } \frac{{\varepsilon^{2} }}{k} + \frac{\partial }{{\partial x_{j} }}\left[ {(\nu + \nu_{t} /\sigma_{\varepsilon } )\frac{\partial \varepsilon }{{\partial x_{j} }}} \right]$$
(7)

where σ k , σ ε , C 1ε , C 2ε , and C μ are model constants, equal to 1.00, 1.30, 1.44, 1.92., and 0.09, respectively. For more details about the k–ε model, refer to Wilcox [21].

2.3 Boundary condition

The model channel (Fig. 1) is bounded by four types of boundaries: inlet (HA), outlet (HG, FE, EC, and BC), vertical wall (GJ, FJ, and DB), and horizontal wall (AB). At these boundaries, the imposed conditions are as follows: At the inlet, the pressure distribution is hydrostatic; the free surface elevation (Fig. 1, y o) and the longitudinal velocity component (Fig. 1, u o) are prescribed. At the outlet, the pressure is set to the atmospheric pressure.

At the vertical smooth wall, the logarithmic law of the wall is applied

$$\frac{{u_{2} }}{{u_{\tau } }} = \frac{1}{\kappa }\ln \left( {\frac{{x_{1} }}{{\nu /u_{\tau } }}} \right) + 5$$
(8)

where u τ is the friction velocity; κ is the von Karman constant (equal to 0.41); and ν is the kinematic viscosity (equal to μ/ρ) of the fluid mixture. Importantly, we ensure the mesh resolutions for the regions adjacent to the wall to be fine enough to resolve the logarithmic layer. The first computing node off the adjacent wall is placed at the wall distance (\(y^{ + } = \frac{{x_{1} }}{{\nu /u_{\tau } }}\)) ranging from 35 and 350. This justifies the use of the logarithmic law of the wall [22], because the viscous effect of the vertical wall has negligible influence on the hydrodynamics in the model channel.

At the horizontal smooth wall, the flow velocity obeys the no-slip condition. We ensure that the wall distance of the first node off the wall is \(y^{ + } = \frac{{x_{2} }}{{\nu /u_{\tau } }} < 1\) or the Reynolds number based on u τ is less than unity. Thus, it is valid to apply the zero velocity condition at the wall. The viscous force is appropriately accounted for in the first layer of the computing nodes off the wall, and the viscous sub-layer is resolved, through mesh refinement. At y + < 1, the linear relationship holds

$$\frac{{u_{1} }}{{u_{\tau } }} = \frac{{x_{2} }}{{\nu /u_{\tau } }}$$
(9)

For more details, refer to White [22].

2.4 Initial condition

The flow field (Fig. 1) was initialised in three different ways. The idea is to examine the independence of flow predictions on the initial conditions used. The three conditions at time t = 0 are illustrated, respectively, in panels (a–c) of Fig. 2.

Fig. 2
figure 2

Initial water surface profiles used in model runs

Full size image

In panel (a) of Fig. 2, in the reservoir upstream of the sluice gate (Fig. 1), the water surface is horizontal, with α 2 = 1 (or 100% water) for x 2 ≤ y o, and α 2 = 0 (or 100% air) for x 2 > y o. Downstream of the gate, the water surface is a straight, sloping line through the top of the gate opening (Fig. 1, point J) and the point above the crest (Fig. 1, point D) of the weir, at a vertical distance (measured from point D) equal to the depth of critical flow. The water volume fraction is α 2 = 1 below the water surface, and α 2 = 0 above. As shown in Chow [2], the critical depth is calculated as \(y_{c} = \sqrt[3]{{q^{2} /g}}\), where q is the per unit width discharge, and g is the gravity. The height of the weir is adjusted such that the water surface elevation over the weir provides the expected sequent depth (Eq. 1). At time t = 0, the flow in the entire model channel is at a state of rest (or u 1 = u 2 = 0). The use of the above-mentioned initial condition greatly reduces computing time needed to reach a state of quasi-equilibrium.

In panel (b) of Fig. 2, the initial condition is generated by superimposing a small-amplitude square wave to the water surface shown in panel (a) of the figure. This wave has an amplitude of 0.28 cm, and a wavelength of 10 cm. The wave extends from x 1 = 93.01–102.99 cm, measured from point A (Fig. 1).

In panel (c) of Fig. 2, the initial condition is generated by superimposing several small-amplitude square waves to the water surface shown in panel (a) of Fig. 2. The waves have the same amplitude and wavelength as in panel (b) of Fig. 2. The waves extend from x 1 = 63.05–132.95 cm, measured from point A (Fig. 1).

If the predicted flows at equilibrium for individual simulations using different initial conditions are virtually the same, we interpret that the initial conditions used have no significant influences on model predictions.

2.5 Numerical techniques

We seek numerical solutions to the governing partial differential equations (Eqs. 3, 4, 6 and 7) using the finite volume methods. Details of the methods can be found in Chung [23]. The model domain (Fig. 1) is discretised into a large number of non-overlapping control volumes. The governing equations are integrated over each control volume, surrounding by two neighbouring grid points. The idea is to obtain a system of discrete, algebraic conservation equations for the discretised control volumes (or cells) and control surfaces. For the pressure field, a pressure equation is obtained by manipulating equations [4, 5]. The solution process uses a pressure-based solver. For more details, refer to Chung [23].

Discrete values of scalar quantities are stored at the cell centre. Therefore, the evaluation of a scalar quantity, φ, at a downstream cell centre requires the value of φ at the upstream cell centre and at the interface between the cells. Using the Taylor series expansion linear reconstruction approach of Barth and Jespersen [24], the interface value φ f is interpolated from the cell-centred values using the second-order upwind scheme as \(\phi_{f} = \phi + \nabla \phi \cdot \vec{r}\), where \(\vec{r}\) is the displacement vector from the upstream cell centroid to face centroid. The spatial gradients for the face value as well as secondary diffusion terms and velocity derivatives are evaluated using the least square cell-based method, given in Chung [23]. A geometric coefficient matrix is obtained by formulating the change in cell values between the neighbouring cells. The cell gradient is determined by solving the minimisation problem for the system of coefficient matrix, using the least squared approximation and Gram-Schmidt decomposition process.

The pressure field as well as mass flux are not known a priori. They are obtained as part of the solution. Using a co-locate scheme, pressure and velocity are stored at the cell centre. Following Rhie and Chow [25], the face velocities are evaluated by momentum-weighted averaging, which prevents unrealistic checker-boarding of the pressure field. The face value of the pressure is interpolated using the pressure staggering option (PRESTO!) scheme, which is similar to the staggered-grid scheme in Patankar [26]. Note that a discrete continuity balance for a staggered control volume is satisfied.

The temporal development of the flow is obtained by integrating the unsteady model equations (Eqs. 3, 4, 6 and 7) over time. Let n denote the current time step, and Δt denote the time step interval. At new time step n + 1, the dependent variable in question is evaluated using the first-order explicit time-marching scheme: φ n+1 = φ n + f(φ n)Δt, where f(φ) represents collectively the spatial integration of every term in the model equations. The value of φ at the current time step is used to evaluate the function f. For numerical stability, the maximum allowable time step interval is constrained by the Courant number. In this paper, we used Δt = 5.0 × 10−4 s, set the convergence residual criterion to 10−5, and carried out a maximum of 120 iterations at each time step.

3 Validation of mean parameters

3.1 Independence of flow predictions on initial conditions and mesh configurations

The key geometric features of the computational model channel (Fig. 1) match those of the laboratory channel described in Kucukali and Chanson [27] for hydraulic jump experiments, one of which has approach flow Froude number equal to 5.8, as determined from the depth-averaged velocity and initial depth of the approach flow. Details about the experiment and results have been reported in Kucukali and Chanson [27]. Measurements of air volume distribution from the experiment will be used for data comparison. In Fig. 1, the model channel has a horizontal bed, a head tank of 0.1 m long, and a sluice gate with a 0.025 m opening to force supercritical flow. The gate is followed by a horizontal channel of 1.75 m long. Further downstream, a 0.061-m high tailgate controls the downstream water depth and maintains subcritical flow condition. The domain is discretised into structured quadrilateral computational mesh, with resolutions of Δx 1 = Δx 2 = 2.5 mm. The resolutions adjacent to the solid walls are refined to resolve the boundary layer, as explained in Sect. 2.3. A summary of the simulation conditions, control parameters and their values are given in Table 1.

Table 1 A summary of simulation conditions, control parameters and their values
Full size table

Three model runs (Runs 1, 2 and 3) were carried out using the different initial conditions of water level (Fig. 2a–c). Each of the runs commenced from a state of rest at model time t = 0, and produced developing water surface profile and flow velocity field. After 36 s of model time, the development of the water surface showed stable hydraulic jumps. The runs continued for a model time period of T = 90 s (Table 1), each taking about 165 h of computing time on 36 processors. In Fig. 3, the predicted velocity vectors for Run 1 (Fig. 2a) are plotted for cells where the water volume fraction α 2 ≥ 0.86 at time t = 90 s. In the figure, x′ = (x 1 − x 0)/d 1, measuring longitudinal distances from the toe of the hydraulic jump, normalised by its initial depth d 1. Along the length of the channel, the top region above the vectors is mostly occupied by air. It is possible to connect cells to form a curve above which the air volume fraction is α 1 ≥ 0.86. This curve is considered to represent the water surface η at the particular model time. An examination of the predictions for Runs 1, 2 and 3 (Fig. 2) at other model times (not shown) reveals temporal fluctuations in the flow field around a state of certain equilibrium. This is realistic, given the turbulent nature of hydraulic jump.

Fig. 3
figure 3

Vertical cross section showing velocity vectors at model time t = 90 s for cells where the water volume fraction α 2 ≥ 0.14. Vectors for cells where α 2 < 0.14 have been skipped

Full size image

The predicted air volume fraction α 1 varies in space or is a function of (x 1, x 2). At a given x 1 location, the depth-averaged air volume fraction \(\hat{\alpha }_{1} (t,x_{1} )\) between the water surface and the channel bed can be obtained by evaluating the integral

$$\hat{\alpha }_{1} (t,x_{1} ) = \frac{1}{\eta }\int_{0}^{\eta } {\alpha_{1} (t,x_{1} ,x_{2} )dx_{2} }$$
(10)

\(\hat{\alpha }_{1} (t,x_{1} )\) contains temporal fluctuations because of the turbulent nature of the jump. We obtained large sets of \(\hat{\alpha }_{1}\) data from the model output for time t n  = 36, 36 + ∆t, 36 + 2∆t,…, 90 s where ∆t = 0.0005 s, which correspond to a sampling rate of 2 kHz, and a sample size of N = 108,000. We determined the average and maximum values of the data sets’ corresponding entities: \(\hat{\alpha }_{1} (t_{i} ,x_{1} )\), i = 1, 2, 3,…, N, and compared the results in Fig. 4 between Runs 1, 2, and 3. The comparison demonstrates that the different initialisations (Fig. 2a–c) have produced consistent results. This means that the independence of equilibrium model results on initial conditions used was achieved. Time averaged results presented henceforward mean averages of the N corresponding entities of data sets in question, unless otherwise stated.

Fig. 4
figure 4

Comparison of distributed air volume fraction α 1 between runs R1, R2 and R3. The α 1 values are double averaged values

Full size image

In addition to the demonstrated independence of model results on initialisations, further sensitivity analyses show acceptable comparisons (Table 2) of model predictions, using different mesh configurations and the k-ω model, details of which can be found in Wilcox [21]. These comparisons confirm the suitability of using 2.5-mm mesh resolutions. Murzyn et al. [28] observed bubbles with a diameter smaller than 2.5 mm in the turbulent shear region of hydraulic jumps with 2.0 ≤ Fr1 ≤ 4.8. It is understood that the 2.5-mm mesh is not adequate to represent the smallest bubbles in the flow, and is not intended to capture bubble breakup or the transport of small bubbles.

Table 2 Sensitivity analysis in terms of the length (L r ) of the roller, the height of the jump (h j  = d 2 − d 1), along with the thickness (b j ) of the jet flow region, the peak velocity (v p ) of the jet, the local maximum (α1max) of air volume fraction below the free surface, and the bottom shear stress (τ b ) at three selected x 1 locations
Full size table

In terms of the bottom shear stress (Table 2), the k-ω model produced lower values than the k–ε model. The choice of the k–ε model in this paper is supported by Shekari et al.’s [29] recent assessment of various turbulence closure models for simulations of submerged hydraulic jump, which concludes that the k–ε model gives acceptable predictions of the longitudinal velocity.

The results shown in Fig. 4 indicate that the pressure distribution in the hydraulic jump is non-hydrostatic due to the presence of a significant percentage of air volume. In the analysis of hydraulic jumps, hydrostatic calculations of pressure forces will give overestimations.

3.2 The flow field

In Fig. 5a, the time-averaged position of the fluctuating water surface is plotted, along with vertical profiles of time-averaged velocity component u 1 at 13 selected longitudinal locations. A jet of water is seen to enter the jump bottom at x′ = 0. There is a decrease in flow velocity and an increase in flow depth in the direction of flow. As shown in Fig. 3, a series of small rollers develop on the surface of the jump, whereas the downstream water surface is relatively smooth. Below the rollers, there are pockets of entrained air of relatively high concentration. Air entrained through hydraulic jumps can cause safety problems for some hydraulic systems. Examples include an excessive air pressure drop in a penstock during the course of intake-gate closure [30].

Fig. 5
figure 5

Vertical cross sections showing: a the water surface and vertical profiles (solid curves) of the longitudinal velocity component u 1 at 13 selected locations along the roller length of the hydraulic jump; b the delineation of distinct regions of the velocity field. The dashed line in a connects points of zero u 1 values. The longitudinal distance measures from the toe of the jump

Full size image

From the velocity field (Fig. 5a), three distinct flow regions (Fig. 5b) can be identified: (1) a jet flow region, (2) an advective shear layer, and (3) a recirculation region. For practical purposes, the thickness of the jet flow region may be considered to be equal to d 1. In this region, the incoming jet persists beyond the toe of the jump and maintains its transverse flow thickness. This flow region is characterised by a dominating longitudinal velocity component and velocity magnitude that is an order of magnitude greater than the rest of the flow regions. The peak velocity, observed at the impingement, decays in magnitude exponentially along the channel length. The turbulent advective shear layer is located between the jet region and the recirculation region, which is characterised by a large longitudinal velocity gradient, strong mixing and transfer of kinetic energy. The velocity profiles indicate that the upper boundary of the turbulent shear layer grows linearly downstream of the impingement. The recirculation region exists in the upper portion of the jump, above the stagnation line, featuring large-scale vortex generation and negative x 1-component velocity. In Fig. 5a, b, the approach flow is partially developed, the approach flow Froude number is Fr1 = 5.9, and the initial depth of the jump is d 1 = 0.0171 m.

On the basis of experimental data, Hager et al. [31] expressed the length of the roller, L r , (Fig. 5b) as a hyperbolic function of the approach flow Froude number Fr1 based on the vertically-averaged velocity

$$\frac{{L_{r} }}{{d_{1} }} = - 12 + 160\tanh \left( {\frac{{{\text{Fr}}_{1} }}{20}} \right)$$
(11)

Recently, Wang and Chanson [32] made laboratory observations of hydraulic jumps in the range of 1.5 < Fr1 < 8.5, and related L r to Fr1 as

$$\frac{{L_{r} }}{{d_{1} }} = 6\left( {Fr_{1} - 1} \right)$$
(12)

For the simulation condition of this paper, the expression of Hager et al. [31] gives L r /d 1 = 33.88 and the expression of Wang and Chanson [32] gives L r /d 1 = 35.4; the corresponding lengths of the roller are L r  = 0.579 m and L r  = 0.606 m, respectively. The numerical prediction from this paper gives L r /d 1 = 33, which is in close agreement with the experimental results of 33.88 and 35.4.

The u 1 velocity profiles (Fig. 5a) within the roller length of the hydraulic jump suggest that the flow is rotational throughout the jump. The S-shaped velocity profiles in the jump result from the shear stress arising from the interaction: (1) between the channel bottom and the jet flow, and (2) between the jet flow and the recirculation flow. Here, the typical boundary layer equations for a flat plate are not applicable due to the absence of irrotational outer flow. This implies that the longitudinal pressure gradient dp/dx 1 cannot be computed by inviscid equations such as Bernoulli or the Euler equation. Consequently, there is no discernible monotonic boundary layer that demarcates the viscous and inviscid flow regions. Nevertheless, the line (Fig. 5a, the arrows and dotted curve) connecting the vertical locations of local peak longitudinal velocity may give some ideas about the behaviour of flow adjacent to the bottom boundary. The boundary layer thickness may be estimated as the distance from the solid surface at which the viscous flow velocity is equal to 99% of the local peak velocity (Fig. 5a, the arrows).

The resulting bottom boundary layer (Fig. 6, the dashed curve) initiates just after the gate opening, close to the vena contracta, grows linearly in the supercritical flow region, and plateaus at the jump toe. Within the roller length (Fig. 5b), the boundary layer exhibits minor vertical fluctuations, which suggests transverse advective transport (in the x 2 direction) and diffusion of x 1-momentum in the zone. Additionally, the constant boundary layer thickness in the jump may suggest that the local Reynolds number, based on the longitudinal coordinate, x 1, and local peak velocity, u 1max (Fig. 5a, the arrows), stay relatively constant.

Fig. 6
figure 6

Development of the bottom boundary layer. Its thickness extends from the channel bottom to the dashed curve where the longitudinal velocity component u 1 is equal to 99% of the local maximum of u 1. The thickness grows along the length of the channel from underneath the sluice

Full size image

For the near-wall region of hydraulic jumps, let b denote the half width of the wall jet, based on the height from the channel-bed where u 1max/2 occurs. By fitting experimental data of mean horizontal water velocity for the near-wall region, Lin et al. [33] constructed a similarity function of the form: u 1/u 1max = 2.3(x 2/b)0.42[1– erf(0.866x 22 /b)]. Predicted velocity profiles (Fig. 5a) from the present study are in close agreement with Lin et al.’s [33] similarity solution, as shown in Table 3.

Table 3 Coefficient of determination R2 between the predictions of mean horizontal water velocity from the present study and the similarity solution of Lin et al. [33] for the near-wall region of hydraulic jumps, and between the predictions and the laboratory measurements of Hager [34]
Full size table

Hager [34] made laboratory measurements of mean horizontal water velocity from nine longitudinal locations [(x 1 − x o)/L r  = 0.2, 0.3,…, 1.0] in classic hydraulic jumps at two different values for the Froude number (Fr1 = 5.5 and 6.85). For each of these locations, Hager [34] reported normalised velocity U = (u 1 − u 1s )/(u 1max − u 1s ) at a number of normalised vertical distances above the point where u 1 = u 1max. Here, u 1s is the maximum backward velocity. From the model predictions of the present study, for each of the longitudinal locations, values of U are obtained at the same vertical distances as the measurements; the correlation between the predicted and measured U profiles is analysed. The results of the coefficient of determination, R2, for the nine locations are presented in Table 3. The coefficient is shown to be within an acceptable range of values.

3.3 Air entrainment

A snapshot (Fig. 7) of the air volume fraction α 1 contours indicates that air entrainment initiates at the flow impingement at the toe of the jump. Air bubbles break into smaller bubbles at the entrance of the turbulent shear layer (Fig. 5b). The bubbles are then advected downstream through the shear layer and form larger bubbles in the region of lesser shear possibly through collision and coalescence. We caution that the 2.5-mm mesh resolution used is inadequate to resolve the smallest bubbles as reported in Murzyn et al. [28] and simulate bubble breakup. Simulations with the smallest bubbles and the breakup process included are expected to improve bubble-size predictions. Sufficiently large air packets are driven to the free surface further downstream by buoyancy and advection. Those bubbles that do not escape through the free surface are partially advected in the swirling motions of surface rollers and reintroduced to the upstream shear layer. These predicted behaviour of air bubbles matches the experimental observations made by Chanson [35].

Fig. 7
figure 7

Vertical cross sections showing snapshots of distributed air bubbles below the free water surface at model time of t = 36 s

Full size image

The model predicts that the bulk of air bubbles (Fig. 7) are present in the turbulent shear layer (Fig. 5b). Note that this prediction is independent of the initial conditions used, as demonstrated by the comparison in Fig. 4.

In Fig. 8, model predictions of air volume fraction α 1 distributions (the thick solid curves) are compared with available measurements (the open circle makers), made by Kucukali and Chanson [27] with dual conductivity probes. The measurements of air content show that the local α 1 maxima decrease in the longitudinal direction, while the upper boundary of the turbulent shear region tilts slightly upward, as shown by the local α 1 minima (Fig. 8, the upper dashed dotted curve). Errors in the predictions of the local α 1 maxima range from 0.01 to 9.4%. The predicted α 1 values are slightly lower than the measured α 1 values for regions below the local α 1 maxima. The predicted thickness of the shear layer and the predicted linear growth of its upper boundary are in close agreement with the measurements.

Fig. 8
figure 8

Predicted α 1 profiles (the solid curves) at seven locations along the length of the jump, in comparison to α 1 measurements (the open circle and cross markers)

Full size image

Chanson [36] suggested that the α 1 distribution in the turbulent advective shear layer follows a Gaussian distribution of the form

$$\alpha_{1} = \alpha_{1\hbox{max} } \exp \left[ { - 2\frac{{(x_{2} /d_{1} - x_{2\hbox{max} } /d_{1} )^{2} }}{{\Delta x_{2}^{2} }}} \right]$$
(13)

where α 1max is the local α 1 maximum value occurring at the location of x 2 = x 2max , Δx 2 is the dimensionless 50% bandwidth where α 1 = 0.5α 1max . The predicted α 1 values (the solid curves) within the shear layer appear to agree reasonably well with values of α 1 calculated using Eq. (13). Note that at any given x 1 location, the non-hydrostatic bottom pressure, p b , in the hydraulic jump can be determined as \(p_{b} = \int_{0}^{\eta } {\rho g\left( {1 - \alpha_{1} } \right)dx_{2} }\). Due to the presence (α 1 ≠ 0) of air bubbles, calculations using the hydrostatic approximation (ignoring the air bubbles) will produce errors. Sample calculations of the bottom pressure show errors as large as 16.2, 15.4, 16.8, and 16.2% at x′ = 5, 10, 15, and 20, respectively.

From experimental data, Hager [37] derived an equation for the free water surface of hydraulic jump

$$\frac{{x_{2} - d_{1} }}{{d_{2} - d_{1} }} = \tanh \left( {1.5\frac{{x_{1} - x_{0} }}{{L_{r} }}} \right)$$
(14)

With the model results of d 1 = 0.0171 m, L r  = 0.565 m, d 2 = 0.139 m, x 0 = 0.4 m, Eq. (14) produces the long-dashed curve shown in Fig. 8. This curve is plotted below the predicted water surface (as interpreted in this paper). The reason is that the predicted water surface is actually the dividing boundary line between the upper region with α 1 ≥ 0.86 and the lower region below the threshold α 1 value of 0.86. We used a volume fraction of 0.86 purely to avoid isolated droplets of air–water mixture to appear above the free surface interface in the contour plot (Fig. 7). The curve given by Eq. (14) is plotted through points for which the model predictions give α 1 < 0.5, except near the toe of the jump. From the model predictions we extracted data of the free surface (x 2 coordinates) using a volume fraction of 0.5 at eight x 1 locations between x′ = 4.2 and 35, and compared the predicted x 2 values with the x 2 values calculated from Eq. (14). The relative errors at the locations range from 1.6 to 13.6%. The average of the errors is 4.4%. This confirms the quality of the predictions.

3.4 Turbulence

The model predicts the Reynolds averaged flow velocity components u 1 and u 2 (Eq. 3), along with the specific turbulence kinetic energy k (Eq. 6). This permits the determination of turbulence intensity, defined as \(i = \left( {\frac{2}{3}k} \right)^{1/2} \left( {u_{1}^{2} + u_{2}^{2} } \right)^{ - 1/2}\). Let i max denote the maximum value of i, and k max denote the maximum value of k in the flow. Contours of time averaged k/k max and i/i max are shown in Fig. 9a, b, respectively. The turbulence intensity is high in a region within 3d 1 from the toe of the jump in the turbulent shear layer. It decreases in magnitude further downstream. Its maximum value occurs at the onset of the turbulent shear region, just downstream of the toe. A momentum exchange between the fluctuating velocity components in the shear layer suppresses the velocity differential. Turbulence penetrates into the bottom flow adjacent to the channel bed at x′ = 10. The maximum turbulence intensity is i max  = 0.685.

Fig. 9
figure 9

Contours of time-averaged turbulence quantities: a normalised specific turbulence kinetic energy k/k max; b normalised turbulence intensity i/i max

Full size image

The turbulence kinetic energy is strong at the toe of the jump due to a large mean strain rate at the point of impingement. It is advected downstream through the turbulent shear layer by the mean flow. In the transverse direction, k is conveyed by turbulent transport, which results from the interaction of fluctuating velocity components. Velocity fluctuations arise due to velocity gradient. The turbulence kinetic energy penetrates into the region adjacent to the bottom wall located between x′ = 10 and 22.5. Most of k is transported up to the recirculation region, where it is ultimately dissipated via the energy cascade mechanism. At x′ > 40, k becomes insignificant at a small distance beyond the roller length. The maximum value of k is k max  = 0.830 m2/s3.

3.5 Bottom shear stress

The bottom shear stress, τ b , is related to the friction velocity (Eq. 9) as \(\tau_{b} = \rho u_{\tau }^{2}\). From the model output, large sets of τ b data: τ b (t i , x 1), i = 1, 2, 3,…, N, were obtained. The sample size N is the same as \(\hat{\alpha }_{1}\) (Eq. 9). For a given x 1 location, the time-averaged value of τ b (t i , x 1), i = 1, 2, 3,…, N, was determined. The distribution of the time-averaged τ b along the length of the channel was plotted a solid curve in Fig. 10. This curve shows variations in the time-averaged τ b along the channel. A peak value of τ p  = 39.9 Pa occurs just downstream of the sluice gate (Fig. 1), where the exiting supercritical flow is at its maximum velocity. Downstream from the peak value location, the time-averaged τ b decreases. It decreases by approximately 34% just before the toe of the hydraulic jump, and further decreases steadily in the longitudinal direction beyond the toe until the end of the roller length (Fig. 5b). Beyond the roller length, it asymptotically approaches zero.

Fig. 10
figure 10

Distribution of the bottom shear stress, τ b , along the model channel, normalised by its maximum value τ p ; and distribution of the transient bottom shear stress σ τ , normalised by τ p

Full size image

At a given x 1 location, the root-mean-square deviation σ τ of τ b (t i , x 1), i = 1, 2, 3,…, N, normalised by τ p , was calculated. Its distribution along the length of the channel is shown as a dashed curve in Fig. 10. σ τ represents transient fluctuations in the bottom shear stress. The spatial distribution shows a peak value at the first quarter of the roller length and has a slightly positive skew.

The prediction of the bottom shear stress, τ b , appears to be logical; the peak value is seen in the region of maximum velocity just after the gate opening and decreases thereafter. Downstream of the jump toe, τ b decreases gradually and tends to approach zero asymptotically. The decrease is presumably due to an increase in flow depth and hence a decrease in flow strength. Interestingly the curve of decreasing τ b (Fig. 10) in the longitudinal direction is not smooth; rather the rate of change of the curve, ∂ 2 τ b /∂x 21 , oscillates, giving a smoothed-out, stepped appearance. The alternating signs of ∂ 2 τ b /∂x 21 suggest the existence of additional mechanisms through which the shear force on the wall is intensified/suppressed. The above-discussed predictions of longitudinal variations in τ b are consistent with the Preston tube measurements of τ b by Imai and Nakagawa [38]. Their measurements, made from experiments of steady hydraulic jumps [2] at the approach flow Froude number of Fr1 = 6.5, show an asymptotically decreasing τ b in the longitudinal direction.

Imai and Nakagawa [38] and Chanson [39] obtained measurements of τ b from experiments of undular jumps [2] at lower Froude numbers (Fr1 = 1.6 and 1.48, respectively). They both reported a more rapidly decreasing τ b beyond the jump toe in undular jumps than in steady jumps.

One possible explanation of the rate of change of the τ b curve (Fig. 10) is the variation in effective viscosity near the solid boundary due to turbulence. The effective viscosity used to compute the wall shear stress is the combination of the physical fluid property, μ, and the virtual turbulent property, μ t . Since the turbulent viscosity is modelled as a function of the specific turbulence kinetic energy, k, and the specific turbulence energy dissipation rate, ε (Eq. 8), turbulent activities near the wall, as identified in the k contours at \(10 < x^{\prime} < 22.5\) (Fig. 9a), would have an impact on the bottom shear stress. Note that k enters the calculations of eddy viscosity (Eq. 5), which in turn is input to the calculations of the specific Reynolds stress τ ij . This stress is a force term in Eq. (3) for the calculations of the velocity component u 1. The velocity component enters the calculations of the friction velocity (Eq. 9).

Another possible explanation is the effect of pressure gradient in the flow near the solid boundary. In the case of an adverse pressure gradient, fluid elements close to the boundary experience a retarding force due to viscous wall stress and the pressure gradient. In response to the adverse momentum influx, the flow is decelerated, thereby reducing the velocity gradient ∂u 1/∂x 2 at the boundary (x 2 = 0). The consequent shear force is less than the resulting shear force in the absence of pressure gradient. Conversely, a negative pressure gradient works with the flow to magnify the advective component of acceleration, effectively increasing the velocity gradient at the boundary. The interaction of turbulence, dynamic pressure, and the inertial terms may further explain the existence of the variance of τ b in the first half of the roller length.

The transient bottom shear stress can be interpreted as an indicator for the region of temporal variability. Physically, this represents regions of pulsing τ b . The region where i penetrates the bottom flow, \(10 < x^{\prime} < 22.5\) (Fig. 9b), is within the region where bulk of transient τ b is seen, \(0 < x^{\prime} < 35\) (Fig. 10). This agrees with the fact that k physically represents the root-mean-squared value of the fluctuating velocity components. The dominant presence of temporally variable velocity components near the bottom may cause τ b to fluctuate in time. This has significant implication with respect to channel scour, erosion, or fluvial morphodynamics. Fatigue is the weakening of materials caused by repeated, cyclical stress loading. In a man-made channel, the nominal stress of such loading may, over a long time period, undermine the bed material with stresses much less than the strength of the materials. In a natural stream, fluctuating bottom shear stresses may interact with a movable bed to affect local sediment transport, leading to erosion, formation of ripples, dunes, and undesirable downstream alluviation. The transient bottom shear stress may shed light on certain aspects of long term structural integrity and fluvial morphodynamics not-so-obvious in the design of hydraulic structures.

It appears that the curve of normalised transient bottom shear stress (Fig. 10, the thin solid curve) can be represented by a right-skewed Gumbel distribution of the form

$$\sigma_{\tau } = \frac{1}{\beta }\exp [x^{{{\prime \prime }}} /\beta + \exp ( - x^{{{\prime \prime }}} /\beta )]$$
(15)

where \(\beta = \frac{{\sqrt {3/2} }}{\pi }\Delta x_{1}\); \(x^{{{\prime \prime }}} = (x_{1} - x_{p} )/d_{1}\); x p is the location of the peak transient bottom shear stress; Δx 1 is the dimensionless 50% bandwidth where σ τ is equal to 50% of its peak value. The aforementioned CFD approach to calculation of bottom shear stress would be particularly useful given the difficulties of directly measuring the bottom shear stress. The difficulties are due to instrument limitations as well as experimental constraints.

4 Discussions

The verification of the two-phase flow method discussed in this paper has been performed to ensure the relevance of CFD predictions to the hydraulic jump phenomenon. Key predictions have been shown to agree reasonably well with independent experimental results. These includes the roller length reported in Hager et al. [31], bubble behaviour in Chanson [35], air volume fraction (equivalently air concentration) distributions in Kucukali and Chanson [27], and the free surface profile in Hager [37]. Lin et al. [33] obtained non-intrusive measurements of flow velocity at Froude numbers up to Fr1 = 5.35. It would be interesting to obtain more measurements of flow velocity and turbulence for data comparison in future investigations.

This paper has been limited to the condition of a single Froude number, future investigations should explore the differences between jumps of different Froude numbers. In addition, the paper is limited to two-dimensional representation of the phenomenon, simulating a case where the width to approach depth ratio is sufficiently large. In addition, Witt et al. [17] found that two-dimensional simulations of a hydraulic jump (Fr1 = 4.82) produced quantity of entrained air that compared within 10% of experimental values of Murzyn et al. [28]. Witt et al. [17] reported that the three-dimensional simulation of the same jump provided additional information on bubble dynamics (bubble size distribution, bubble transport) and flow physics (behaviour of vertical structures) albeit the improvements came at a cost of two orders of magnitude increase in computing time. The increased computational time of three-dimensional simulations was deemed unjustifiable for the purpose of this paper. Moreover, simulating the jump of interest (Fr1 = 5.9) in three-dimensions would have required finer mesh and therefore much longer computing time than the three-dimensional jump simulated by Witt et al. [17] (Fr1 = 4.82).

5 Conclusion

This paper reports computer model predictions of the hydraulic jump as bubbly two-phase flow. The predictions produce the flow velocity field of an air–water mixture, the air–water interface, and air volume fraction below the interface, along with turbulence quantities. The bubbly two-phase flow method uses the Reynolds-averaged Navier–Stokes equations to describe fluid mixture motions, the volume of fluid method to track the interface, and the k-ε model to obtain turbulence closure. The following conclusions have been reached:

  • The model predictions capture the essence of the internal flow structures, air entrainment, turbulence properties, and bottom shear stress. The key to success in predicting the jet flow structure immediately above the bottom lies in properly resolving the viscous sub-layer and hence eliminating uncertainties in the bottom boundary condition (Eq. 9).

  • A turbulent advective shear layer is shown to form between the bottom jet flow and the upper recirculation flow. The prediction of the length of recirculation region (Figs. 5b, 10) agrees reasonably well with the experimental results of Hager et al. [31].

  • The majority of entrained air bubbles are advected downstream through the shear layer, either being degassed or being re-entrained towards the end of the roller length (Fig. 7). The quality of the predicted linear growth of the layer and air volume fraction within the layer is validated by Kucukali and Chanson’s [27] experimental data. Air bubbles in the water below the free surface lead to non-hydrostatic pressure distribution. Under the hydraulic condition considered in this paper, hydrostatic pressure calculations are expected to give an overestimation of the actual pressure by up to 20%, even for the downstream half of the roller length (Fig. 4).

  • There are high levels of turbulence at the impingement (Fig. 9a). The bulk of the turbulence kinetic energy is advected to the recirculation region via the shear layer, where it is ultimately dissipated. A small portion of the turbulence kinetic energy penetrates down into the jet region.

  • The predicted distribution of bottom shear stress shows a peak value just after the gate opening and a decaying trend along the length of a hydraulic jump toward downstream (Fig. 10), which is realistic. For the first time, this paper reveals a significant transient bottom shear stress associated with temporal fluctuations of the jump (Eq. 15). This has important implications to bottom erosion.

  • The hydraulic jump phenomenon is complicated. This paper shines light on aspects of air entrainment, turbulent shear stress, and interaction between flow structures and the bottom shear stress in the jump. The prediction method discussed in this paper is useful for modelling hydraulic jumps and advancing the understanding of air–water flow properties.

The novelty of resolving the viscous sublayer in two-phase hydraulic jump flow at the laboratory scale has greatly enhanced the accuracy in computations of the bottom shear stress. The Gumbel distribution for describing the transient bottom shear stress represents a new contribution to the body of knowledge about two-phase hydraulic jumps.