1 Introduction

Hydraulic jump is a free-surface phenomenon caused by the transition of supercritical flow to subcritical open-channel flow. Hydraulic jumps are characterized by strong turbulence and air entrainment. They are often used as energy dissipaters below hydraulic structures. Several researchers have experimentally investigated the flow and turbulence characteristics of hydraulic jumps [14, 31, 34, 36, 37, 53]. The entrainment of air is an influential environmental consideration in the operation of hydropower projects and the sustenance of aquatic ecosystems. The entrained air also modifies the flow characteristics, leading to flow bulking and change in buoyancy. The properties of air–water flow in open channels have received considerable attention in the seminal works of Rao and Kobus [35], Wood [52] and others. While field measurements are the best method to quantify the air entrainment, they are not often financially viable and may not represent the most commonly encountered scenarios [51].

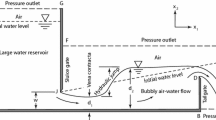
The two-phase air–water flow properties associated with hydraulic jumps have been studied extensively through physical modelling [7, 8, 30, 47, 54]. These experimental studies have acknowledged that the two-phase flow in a hydraulic jump is bubbly as depicted in Fig. 1a, with the wall-jet like supercritical flow retarded by the adverse pressure gradient and forming a recirculation zone near the free surface, referred to as the roller (Fig. 1a). The reverse flow of the roller impacts the upstream wall-jet at the jump toe, initiating a turbulent shear layer starting at the toe and expanding in the vertical direction further downstream (Fig. 1a). Two typical types of air-entrainment processes have been reported in open-channel flows [4]. Local or singular aeration occurs when a singularity or discontinuity is created in the free surface at the location where the jet-like flow impinges the surrounding waters, as shown schematically in Fig. 1b. This singularity is referred to as a free-surface cusp [10]. Air gets trapped in the free-surface cusp and is entrained into the flow. On the other hand, interfacial aeration occurs at the air–water interface (Fig. 1c). Air is entrained into the flow when the turbulent kinetic energy generated in the flow is large enough to overcome the surface tension and gravity effects. It must be noted here that the two mechanisms are not necessarily mutually exclusive.

Fig. 1
figure 1

Schematic of a the classical hydraulic jump (CHJ), b local or singular aeration in open-channel flows, c interfacial aeration in open-channel flows

Full size image

Experimental studies have used several measuring techniques to measure the air concentration C in highly aerated hydraulic jumps, including conductivity phase-detection probes [7, 44, 48], visual and imaging techniques [16, 21, 28] and optical fibre probes [30]. As noted by Boyer et al. [1], all these techniques have their inherent limitations. As the Froude number \(F_{1} = U_{1} /\sqrt {gd_{1} }\) increases, where \(U_{1}\) and \(d_{1}\) are the velocity and flow depth at the jump toe and g is the acceleration due to gravity, both the air entrainment and flow dynamics are enhanced. Experimental researchers have used acoustic displacement meters to locate the free surface at different streamwise locations. The accuracy of these instruments reduces with increasing Froude number as the free-surface deformations and splashing become stronger [29]. However, several inferences about the air concentration distribution in CHJ have been revealed by these measurements which will be discussed in later sections.

Recent advances in computer hardware and multiphase flow models have rendered numerical modelling as a feasible alternative to examine the internal structure of turbulence in hydraulic jumps [12, 26]. A comprehensive review of hydraulic jumps literature was provided by Valero et al. [45] and Viti et al. [46], highlighting the most significant numerical simulations and their main achievements. Early numerical studies on hydraulic jumps were carried out by Chippada et al. [9] and Qingchao and Drewes [33]. These two-dimensional (2D) simulations were interested to capture the free-surface fluctuations of the jump but over-looked the air-entrainment characteristics. Ma et al. [23] also carried out a 2D simulation of hydraulic jump and presented the profiles of the flow characteristics. The first quantitative validation of air concentration profiles of hydraulic jumps was presented by Ma et al. [24] using a sub-grid air-entrainment model. Subsequently, Witt et al. [51] presented the validation of air concentration along with the bubble dynamics and described the physics associated with air entrainment using the Volume of Fluid (VOF) model for free-surface tracking in conjunction with a Reynolds-Averaged Navier–Stokes (RANS) model. However, RANS models do not reproduce the strong fluctuations near the free surface, resulting in erroneous results in the roller region [24]. The Froude numbers for the three-dimensional (3D) simulations presented by Ma et al. [24] and Witt et al. [51] were 1.8 and 4.8, respectively. Recently, Jesudhas et al. [20] used a hybrid RANS-LES approach termed as Improved Delayed Detached Eddy Simulation (IDDES) to predict the velocity and turbulence characteristics of a high Froude number (F1 = 8.5) hydraulic jump. The free-surface was captured using the VOF model with High-Resolution Interface-capturing (HRIC) technique. While the study showcased the capabilities of the numerical model to capture the flow and turbulence characteristics in a high Froude number classical hydraulic jump (CHJ), a more rigorous analysis of the two-phase flow properties predicted by the model for multiple Froude numbers was needed. Likewise, a validated computational model to predict the two-phase flow properties in canonical multiphase flow field such as the hydraulic jumps can serve as a base case and aid in the evaluation of the characteristics of other types of flow fields where two-phase flow measurements are difficult. Furthermore, most experiments provide measurements at a point or on a plane, whereas the complete three-dimensional (3D) flow field is available from the CFD simulation. This would enable us to evaluate the coherent structures in the flow and their dynamics that is responsible for free-surface fluctuations and aeration in hydraulic jumps.

With the above motivations, two classical hydraulic jumps with two flow conditions (Table 1) were simulated using 3D, unsteady IDDES in conjunction with VOF multiphase model. Henceforth, test TR1 represents \({\text{F}}_{ 1}\) = 7.5, Re = 6.8 × 104 and TR2 represents \({\text{F}}_{ 1}\) = 7.5, Re = 1.4 × 105 flow cases. The two-phase flow properties predicted by the simulation are exhaustively compared with the experimental results of Wang [47]. The free-surface characteristics, jump-toe oscillations and pressure fluctuations are also analyzed. Since the complete 3D flow field is available from the simulations, the air–water flow dynamics in classical hydraulic jumps is examined by evaluating the vorticity magnitudes and coherent structures in the flow. The present paper also evaluates the advantages and shortcomings of the numerical model with pertinent discussions.

Table 1 Flow conditions of the classical hydraulic jumps presented in this study
Full size table

2 Numerical modelling

Modelling turbulence in hydraulic jumps is not trivial due to the presence of different turbulence mechanisms and its associated scales. Traditionally researchers have used Reynolds-Averaged Navier–Stokes (RANS) approaches to model turbulence in hydraulic jumps [23, 51]. However, the RANS models are inherently isotropic and do not reproduce turbulence accurately in flows with strong anisotropic structures. Large eddy simulations are another option, however it has been estimated that LES is 10–100 times costlier than RANS computations since it requires a finer grid and also calculates the mean quantities by time-averaging the unsteady quantities over a long sampling time [11]. In order to reduce the computational costs and also to adequately capture the unsteady features of the flow, an endeavor has been made by researchers to combine the RANS and LES modeling approaches. The objective is to perform LES only where it is needed and use RANS in regions where it is reliable and efficient. Though several hybrid RANS-LES approaches are available in literature, one of the most prominent and widely used representatives is the detached eddy simulation (DES), first described by Spalart [43]. It was termed ‘detached eddy’ simulation because it was meant to resolve the detached eddies far from the boundaries using LES and employ RANS models in the near-wall regions. It is ideally suited for a flow field like the hydraulic jump where the predominant mechanism for turbulence generation is the shear layer and not the wall. For the present study an improved formulation of the DES model termed as IDDES is employed. This version avoids the “log-law mismatch” error by defining a new sub-grid length scale that not only depends on the grid size but also on the wall normal distance [41]. In the near-wall region, SST k–ω RANS model is used as it performs better in adverse pressure gradient flows [25]. More details on the IDDES model and its formulation are presented in Jesudhas [18] and not repeated here for brevity.

For modelling the free-surface, the VOF model [42] is used. In the present Eulerian approach, the air–water multiphase flow is solved using a single set of momentum equations, shared by both the phases (air and water). In other words, air and water are mathematically treated as a single inter-penetrating continua; the fluid domain itself consists of a ‘mixture’ of the phases. An indicator function α also termed as volume fraction can be defined at each computational cell, which takes the value between 1 for the cell completely filled with the continuous fluid i.e., liquid and 0 for the cell completely filled with the dispersed fluid i.e., gas. Therefore at any given time instant, (1 − α) represents the instantaneous air concentration (void fraction) at that location, thereby capturing the transport of air within the flow [20, 51]. The single equation VOF modelling approach is predominantly used for modelling ‘dilute’ bubbly flows [2]; it is employed in the present study to evaluate its performance in simulating aerated flows like the hydraulic jump. Moreover, the VOF approach is less computationally intense than the more exhaustive two-equation model (separate momentum equations for air and water) and therefore based on its performance it could be used as a viable alternative to physical modelling for practical applications. A brief discussion of the equations used in the flow solver is presented.

The single set of continuity and the momentum equations shared by both the phases can be written in the integral form as:

$$\frac{\partial }{{\partial {\text{t}}}}\int_{\text{V}} {\uprho{\text{dV}} + \oint_{\text{A}} {(\uprho{\mathbf{u}})\cdot{\mathbf{n}}{\text{dA}} = 0} }$$
(1)
$$\frac{\partial }{{\partial {\text{t}}}}\int_{\text{V}} {\uprho{\mathbf{u}}{\text{dV}} + \oint_{\text{A}} {\uprho{\mathbf{u}} \otimes {\mathbf{u}} \cdot {\mathbf{n}}{\text{dA}} = - \oint_{\text{A}} {{\text{p}}{\mathbf{I}} \cdot {\mathbf{n}}{\text{dA}} + \oint_{\text{A}} {{\mathbf{T}}\cdot{\mathbf{n}}{\text{dA}} + \oint_{\text{V}} {{\mathbf{F}}{\text{dV}}} } } } }$$
(2)

where n is the unit normal vector to the surface element dA, ρ is the fluid mixture density, u is the instantaneous velocity vector of the fluid mixture, p is the instantaneous pressure of the fluid mixture, I is the identity matrix, and T is the viscous stress tensor which for a turbulent flow is the sum of laminar and turbulent stress tensors Tl and Tt, respectively. The body force term F can be any relevant force that is expected to influence the flow.

The physical properties of the fluid mixture (ρ and \(\upmu\)) at any given location, can be calculated from the volume fraction α, as weighted contributions from the two phases

$$\uprho =\uprho_{\text{w}}\upalpha +\uprho_{\text{a}} (1 -\upalpha)$$
(3)
$$\upmu =\upmu_{\text{w}}\upalpha +\upmu_{\text{a}} (1 -\upalpha)$$
(4)

where \(\uprho_{\text{w}}\) and \(\upmu_{\text{w}}\) are the density and viscosity of water and \(\uprho_{\text{a}}\) and \(\upmu_{\text{a}}\) are the density and viscosity of air respectively. Since the mass and momentum transport equations (Eqs. 1 and 2) are solved for a fluid mixture rather than individual phases, the transport of air is not explicitly modelled in the VOF approach. However, an additional transport equation for the volume fraction α, described by the following conservation equation is solved at each time-step, this can be written as:

$$\frac{\partial }{{\partial {\text{t}}}}\int_{\text{V}} {\upalpha{\text{dV}} + \int_{\text{S}} {\upalpha{\mathbf{u}} \cdot {\mathbf{n}}{\text{dA}} = 0} }$$
(5)

The discretization of the transient term in Eq. (5) is fairly straightforward, however for the convective term \(\int_{\text{S}}^{{}} {\upalpha{\mathbf{u}} \cdot {\mathbf{n}}{\text{dA}}}\), the standard discretization schemes are known not to approximate the large spatial variations of the phase volume fraction. This can cause smearing of the air–water interface [38]. Hence, to achieve necessary compression of the interface, an artificial compression term is introduced into the volume fraction Eq. (5). The equation is re-written as:

$$\frac{\partial }{{\partial {\text{t}}}}\int_{\text{V}} {\upalpha{\text{dV}} + \int_{\text{S}} {\upalpha{\mathbf{u}} \cdot {\mathbf{n}}{\text{dA}} + \int_{\text{S}} {{\mathbf{v}}_{{{\text{c}}_{\text{i}} }}\upalpha(1 -\upalpha) \cdot {\mathbf{n}}{\text{dA}} = 0} } }$$
(6)

here \({\mathbf{v}}_{{{\text{c}}_{\text{i}} }}\) is an artificial compressive velocity that is applied normally at the interface between the phases to reduce numerical diffusion. Here \({\mathbf{v}}_{{{\text{c}}_{\text{i}} }}\) is defined as

$${\mathbf{v}}_{{{\text{c}}_{\text{i}} }} = {\text{C}}_{\upalpha} \left| {\mathbf{u}} \right|\frac{{\nabla\upalpha}}{{\left| {\nabla\upalpha} \right|}}$$
(7)

\({\text{C}}_{\upalpha}\) is termed as the sharpening factor. It must be noted that the hydraulic jumps considered in this study has a partially developed inflow condition, which meant little air pre-entrainment occurs at the supercritical flow free surface [44]. Therefore, the present hydraulic jump inflow conditions can be primarily characterized with the Froude and Reynolds numbers [5, 47], due to the overwhelming relevance of the turbulent and gravitational effects. However, earlier studies have shown that size of entrained air pockets in highly turbulent flows is proportional to surface tension [15]. Hence, previous numerical studies have included surface tension to accurately capture the rate of air entrainment within the flow [51] [19]and [20]. Based on these studies, a constant surface tension coefficient \(\upsigma = 0.074\;{\text{N/m}}\) was used at the air–water interface. When the surface tension coefficient is constant, tangential component of surface tension force becomes zero. The vector normal to the interface is calculated using the volume fraction

$${\mathbf{n}} = \nabla\upalpha$$
(8)

The curvature of the interface K can be expressed in terms of the divergence of the unit normal vector n, as:

$$\text{K} = - \nabla \cdot \frac{{\nabla_{\upalpha} }}{{\left| {\nabla_{\upalpha} } \right|}}$$
(9)

Therefore, the expression for the normal component of the surface tension force \(f_{{\upsigma,n}}\) i.e., Eq. (9) can be re-written as:

$${\text{f}}_{{\upsigma,n}} = -\upsigma\nabla \cdot \left( {\frac{{\nabla_{\upalpha} }}{{\left| {\nabla_{\upalpha} } \right|}}} \right)$$
(10)

Since the tangential component of the surface tension force is zero in our present study, only the normal component of surface tension force is included in Eq. (2). Further details on the VOF model and the High-Resolution Interface-Capturing Technique is available in Jesudhas [18]. It must also be noted that the interaction between the phases or mass transfer is not considered in the present study. Also, no other mass flux terms are included for the dispersed phase (air) in the present formulation.

The details of the simulation domain for TR1, along with the boundary conditions are shown in Fig. 2a. No-slip boundary conditions are applied at the side walls. The initial conditions of volume fraction within the domain was set using user-defined field functions as shown in Fig. 2a to save computational time. Structured hexahedral mesh with near-wall prism layers are used in the simulations. The mesh consists of 8.1 and 10 million cells for TR1 and TR2, respectively. A portion of the computation mesh used in the study is shown in Fig. 2b. Fine prism layer mesh with a stretching factor of 1.5 was used within 2 mm near the bed (RANS region) to resolve the influence of the wall. This yielded a \({\text{y}}^{ + }\) value between 1 and 5 within the wall jet region, this is consistent with guidance range presented by Witt et al. [51]. The grid sizes in the LES region were determined based on the well-known integral-scale criteria [32, 40]. The IDDES blending function depicting the RANS and LES regions (Fig. 2c) was monitored at several time steps to confirm this. It must also be noted that the choice of the grid resolution was not only based on the flow parameters but also based on the two-phase flow characteristics [51] such as the free-surface profile. More details on the grid resolution is presented in Jesudhas [18] and Jesudhas et al. [20] and hence not repeated here. It can be observed from Fig. 2c, that LES is performed near the free surface, indicating that the grid resolution is sufficiently small at these locations to capture the time-dependent free-surface fluctuations and breakup. This simulates interfacial aeration automatically, thus not necessitating any additional air entrainment models at the interface.

Fig. 2
figure 2

a Schematic of the simulation domain for TR1, b portion of the mesh for TR1, c typical instantaneous contour of IDDES Blending function showing the LES and URANS regions

Full size image

The equations were solved using STAR-CCM+v11.06 a finite-volume solver with a timestep of \(1 {\text{ms}}\). The solution was considered to have converged when the residuals of continuity and momentum fell below \(10^{ - 6}\). Several other parameters such as velocity at different streamwise locations, convective Courant number, etc., were also monitored to ensure that a dynamic steady state was achieved before calculating the mean quantities. The simulation was initially run for 30 s beyond which the two-phase flow characteristics were averaged for 10 s.

3 Experimental conditions

The numerical simulation results were compared with the physical modelling data collected at the University of Queensland [47]. Classical hydraulic jumps were modelled during the experiments in a horizontal rectangular channel. The observation section of the channel had a 3.2 m long smooth bed and 0.4 m high glass sidewalls. Water was discharged into the channel from an upstream head tank through a full-width rounded sluice gate. The rounded edge of the gate ensured no contraction of the discharging flow. The flow rate was measured with a Venturi meter in the water supply pipeline that fed into the head tank. The longitudinal position of the hydraulic jump and the downstream water level were controlled using a full-width sharp-crested weir at the downstream end of the channel.

A variety of instrumentation was used for the measurements of the dynamic and two-phase flow properties. These included acoustic displacement meters recording instantaneous water surface positions at 50 Hz, conductivity phase-detection probes recording instantaneous air concentration at 20,000 Hz, and total pressure probe recording instantaneous total pressure at 2000 Hz. The time-averaged water surface position, air concentration and total pressure were averaged respectively over a period of 180 s, 45 s and 180 s, respectively. The phase-detection probe and total pressure probe were intrusive probes of which the vertical positions were controlled with a rail-mounted trolley and monitored using a digital scale. Further details of experimental setup can be found in Wang [47].

4 Results and discussion

4.1 Mean quantities

As mentioned earlier, one of the main objectives of the present study was to comprehensively compare the different quantities predicted by the numerical simulations with the experimental results. This would enable researchers to quantitively evaluate the accuracy of the IDDES model coupled with VOF and HRIC for the simulation of hydraulic jumps at high Froude numbers.

Figure 3a shows the comparison of the non-dimensional mean streamwise velocity \(U /U_{1}\) profiles predicted by the simulation with the experimental results of Wang [47] at different streamwise locations in the central plane for test TR1. The velocity profiles of the CHJ resembles that of a typical wall jet in the near bed region, with zero velocity at the bed, increasing to a local maximum value \(U_{max}\) and then decreasing to negative values in the roller region. The region between the wall-jet region and the roller is the shear layer which begins at the jump toe and expands in the vertical direction. It can be seen that the profiles predicted by the simulation follow this trend. It must be noted that [47] used both a Pitot tube and a conductivity phase-detection probe to measure the velocity. The Pitot tube was employed in the wall-jet region while the conductivity probe was used in the aerated roller region. It can be seen that the velocity profiles predicted by the simulation agree well with the experimental results in the wall-jet region at x* = 8.4, 12.5 and 18.8. Here, x* is defined as \((x - x_{1} ) /d_{1} ,\) where \(x_{1}\) is the distance of the jump toe from the gate and d1 is the inflow water depth immediately upstream of the jump. The discrepancy at x* = 4.2 is mostly attributed to the experimental uncertainty associated with the determination of mean jump toe position to which the measurement results are fairly sensitive in the near-toe region. The discrepancies between the experimental and numerical results arise in the aerated roller region. The conductivity probe measures the interfacial velocity between air and water, while the simulations treat the fluid as a mixture. Hence the differences between the velocities are higher in the regions of large air concentrations. The higher instrumentation uncertainty associated with the statistical correlation analysis in the gravity-driven recirculation region should not be ignored as well.

Fig. 3
figure 3

Comparison of a mean streamwise velocity profiles, b, c decay of local maximum streamwise velocity at given cross-sections

Full size image

Figure 3b, c show the decay of maximum velocity in the streamwise direction in the central plane of the hydraulic jump. Figure 3b uses the conventional length scale \(d_{1}\) to normalize the streamwise distance [34]. It can be seen that the present results follow the exponential decay reported by other researchers for the same Froude number. The difference in decay between TR1 and TR2 suggests the influence of Reynolds number on the energy dissipation processes. Wang [47] used the roller length \(L_{r}\) to normalize the streamwise distance causing the experimental data to be clustered as shown in Fig. 3c. Here, \(L_{r}\) is defined as the longitudinal distance measured from the jump toe, over which the mean depth increases monotonically from \(d_{1}\) to \(d_{2} .\) It can be seen from Fig. 3a–c that the velocity predicted by both TR1 and TR2 simulations are in agreement with the experimental data in the wall-jet region.

Figure 4a presents the comparison of normalised mean total pressure \(p /(0.5\rho_{\text{w}} U_{1}^{2} )\), where p is the total pressure and \(\rho_{w}\) the density of water, with the experimental results of Wang [47] at different streamwise locations in the central plane of test TR1. The profiles of normalized total pressure agree well with the experimental results. As expected, the peak of total pressure occurs within the high-speed wall-jet region, before decreasing to zero at the air–water interface (free surface). Wang [47] reported that the vertical location of the maximum mean total pressure \(p_{max}\) is between \(0.5 < y /d_{1} < 0.9\), and the simulations predict a similar value. Figure 4b shows the decay of maximum total pressure \(p_{max}\) along the streamwise direction in the central plane. The results of both TR1 and TR2 agree well with the experimental results by clustering into a narrow band. Figure 4c shows the normalized vertical location of \(U_{max}\) and \(p_{max}\) along the streamwise direction in the central plane. The vertical locations of \(U_{max}\) and \(p_{max}\) are close as reported by Wang [47]. The simulation and experimental results agree well with each other for both TR1 and TR2. In the legend of the figure, YPmax and YUmax refer to the vertical location of maximum pressure and velocity, respectively.

Fig. 4
figure 4

Comparison of a mean total pressure profiles, b variation of maximum total pressure in the streamwise direction, c variation of the location of maximum velocity and maximum total pressure in the streamwise direction

Full size image

Figure 5a shows the comparison of mean air concentration profiles with the experimental results at different streamwise locations for TR1. The value of C increases from zero near the bed and reaches a local maximum value \(C_{max}\) in the shear layer. It decreases towards the outer edge of the shear layer, followed by a rapid increase and reaching unity in the air region. As noted earlier, the VOF model treats the air–water as an interpenetrating continua (mixture) and solves a single momentum equation for it. While this has significant computational cost benefits, it can also induce numerical (artificial) diffusion near the interface. The careful design of the mesh and the inclusion of sharpening factor can reduce this but does not eliminate it. Hence the dip of the air concentration profile after Cmax near the free surface is not as abrupt in the numerical results in Fig. 5a. The region from the bed to the vertical location \(y_{0}\) where the air concentration once again starts to increase rapidly, is called as the air–water shear layer [29]. Murzyn and Chanson [29] measured the location of the free surface using an acoustic displacement meter and concluded that the location of the free surface is close to the location of \(y_{0}\). The region above this position (\(y_{0}\)) is called the upper free-surface region characterized by sprays, splashes and air–water projections. It is also dominated by interfacial aeration at the free surface. As a result, the uncertainties in the concentration measurement in both the experiments and the numerical simulations increase significantly in this region. It must be noted that the air–water shear layer is the most practically relevant region for determining design parameters such as \(C_{max}\). It can be seen from Fig. 5a, the numerical simulations over predict the air concentration in the hydraulic jump. This is similar to the results of Witt et al. [51] where the artificial diffusion results in the over prediction of air concentration for a lower Froude number of 4.58. This can be reduced by the inclusion of sharpening factor (\(C_{\alpha }\) in Eq. 7). Jesudhas [18] studied the influence of sharpening factor on the flow properties of a classical hydraulic jump of high Froude number (F > 8.5) and compared them with experimental results. It was found that while the increase in sharpening factor improves the prediction of air concentration in the flow, it also resulted in non-physical free-surface profiles due to the inclusion of artificial compressive force at the interface. Hence a lower value of sharpening factor was recommended along with careful mesh design. Based on this, a very low value of \(C_{\alpha }\) = 0.2 was used in the present study. The numerical model was able to reproduce the overall trend of the air concentration profiles in the air–water shear layer and the upper free surface layer. Figure 5b shows the decay of the maximum air concentration \(C_{max}\) in the streamwise direction for TR1 and TR2. As previously inferred from Fig. 5a, the simulations over predict the \(C_{max}\) values. The trend in the decay of \(C_{max}\) is similar to the experimental results until \((x - x_{1} ) /d_{1} < 0.4\) beyond which there is a disparity caused by the artificial diffusion. However, the decay of the local mean air concentration at different streamwise location agrees well with the experimental results as observed in Fig. 5c. From Fig. 5 it is apparent the VOF model has the capabilities to predict the trend of air concentration distribution in hydraulic jumps of high Froude numbers, whereas the value can be over-predicted. While the use of the sharpening factor improves the prediction, the optimal value of sharpening factor value is somewhat contentious and might change with the Froude number. More importantly, as mentioned in the numerical modelling section, the VOF model uses a single mass and momentum transport equation to solve for an equivalent air–water fluid mixture i.e., the explicit transport of air is not captured. While this may not significantly affect the flow properties (velocity and pressure) due to the large density difference between the phases, it would potentially affect the prediction of air concentration. Further research of these hydraulic jumps using the two-equation (transport equations for air and water) Eulerian model is needed to address this issue.

Fig. 5
figure 5

a Comparison of air concentration profiles, b variation of maximum air concentration, c variation of the mean air concentration in the streamwise direction

Full size image

Figure 6a shows the comparison of mean free surface profiles between the experiments and simulations. It must be noted that there is a slight difference between the experimental and numerical results in the roller region, largely due to the subjective definition of jump toe position. The comparison suggests that simulated jump is overall allocated about 3d1 downstream of the physical model. Such a difference is also responsible of the overestimate of air concentration and velocities by the numerical model (Figs. 3, 5). In addition, the experiments used displacement meters to measure the height of free surface, and the sprays, splashes and air–water projections in the upper free surface region may cause the slight discrepancy in the free surface profiles. Figure 6b shows the sequent depths predicted by the simulation with other experimental data. It can be seen that the present simulation agrees well with the Belanger’s equation. Wang [47] used the roller length \(L_{\text{r}}\) to collapse the mean free surface into a thin band as shown in Fig. 6c. The results of the present simulations follow the expected trend. It is apparent that the mean free surface predicted by the present simulations agrees well with the expected trend in experimental data.

Fig. 6
figure 6

a Comparison of mean free surface profiles, b variation of conjugate depth ratio with Froude number, c variation of mean free surface profile within the roller region

Full size image

Figure 7a, b show the 3D mean free surface predicted by the simulation for TR1 and TR2, respectively. The normalized mean streamwise velocity contours are also superimposed on the 3D mean free surface. The jump toe location can be defined as the region were the free surface increases abruptly (dashed circle in Fig. 7a, b). Several researchers have reported on the three-dimensional features in the jump toe region [47, 54]. It can be observed from Fig. 7a, b that the present simulations predict this three-dimensionality well. The free surface velocity contours show the maximum negative velocity in the central region of the roller. This is caused by the “climb of the wall jet” near the side walls. The free surface undulations are also visible in the mean free surface as marked in Fig. 7a, b. The visual observations during the experimental study showed intense free surface fluctuations close to the jump toe (\(0 < (x - x_{1} ) /d_{1} < 20\)). The flow physics responsible for these fluctuations will be discussed in later section.

Fig. 7
figure 7

a, b Three-dimensional mean free-surface predicted by the simulation for the two Reynolds numbers

Full size image

Figure 8a shows the distribution of turbulent kinetic energy, \(TKE = 0.5(\overline{{(u^{\prime } )^{2} }} + \overline{{(v^{\prime } )^{2} }} + \overline{{(w^{\prime } )^{2} }} )\), in the central plane for test TR1. Here \(u^{{\prime }} , v^{{\prime }}\), and \(w^{{\prime }}\) are the turbulent fluctuations in the x, y and z directions, respectively. Also plotted are the mean velocity vectors depicting the roller region (RR) and the wall-jet (WJ) like flow below. As mentioned earlier, the shear layer between the roller and the wall jet flow begins at the toe and expands in the vertical direction. As expected, the shear layer corresponds to the location of maximum turbulent kinetic energy. It can be seen from Fig. 8a that the turbulence generated by the interaction between the roller and wall jet dominates the CHJ flow field and the contribution from the bed is negligible. The streamwise and vertical flux of turbulent kinetic energy, \(F_{u} = 0.5(\overline{{(u^{{\prime }} )^{3} }} + \overline{{(u^{{\prime }} )(v^{{\prime }} )^{2} }} + \overline{{(u^{{\prime }} )(w^{{\prime }} )^{2} }} )\) and \(F_{v} = 0.5(\overline{{(v^{{\prime }} )^{3} }} + \overline{{(u^{{\prime }} )^{2} (v^{{\prime }} )}} + \overline{{(v^{{\prime }} )(w^{{\prime }} )^{2} }} )\) are presented in Fig. 8b, c, respectively. The positive sign of the streamwise and vertical fluxes of turbulent kinetic energy above the shear layer indicates that the fluxes are in the downstream direction and towards the free surface. Also, the negative sign of the streamwise and vertical fluxes of turbulent kinetic energy below the shear layer indicates that the flux is in the upstream direction and towards the bed in this region. Arrows are added in Fig. 8b, c to show the direction of the flux of turbulent kinetic energy. As discussed earlier, the criteria for interfacial aeration is that the surface tension of the free surface must be overcome by the turbulence generated below the free surface [4]. Hence, it is imperative to analyse the flow structures responsible for the transport of turbulent kinetic energy towards the free surface.

Fig. 8
figure 8

Contours in the central plane of TR1; a turbulent kinetic energy, b streamwise flux of turbulent kinetic energy, c vertical flux of turbulent kinetic energy (arrows in Figs. a and b denote the direction of flux of turbulent kinetic energy)

Full size image

4.2 Coherent structures

Figure 9a, b show an instantaneous snapshot of the 3D free surface for tests TR1 and TR2, respectively, colored with the vorticity magnitude. These figures show intense deformations of the free surface starting at the jump toe. The free surface is devoid of any deformations upstream of the jump toe, and the intensity of the free-surface deformations reduce as one moves further downstream. This is consistent with experimental results which show that the maxima of free-surface fluctuations occur within the first 30% of the jump roller [3]. The high values of vorticity magnitude are concentrated near the jump toe, giving rise to the larger free-surface deformations in that region. Downstream of the roller, the vortical structures are dissipated and the free surface deformations vanish gradually. The regions of high vorticity magnitude on the free surface are caused by the interaction of the sub-surface vortices with the free surface. The interacting vortices deform the free surface. Sarpkaya [39] studied this interaction and described at least five different types of free-surface deformations that can be caused by the sub-surface vortices. The intensity of this deformation is not only dependent on the vorticity magnitude, but also on the type and orientation of the vortical structure. Hence, the high-vorticity patches do not always coincide with the locations of the maximum deformation.

Fig. 9
figure 9

Instantaneous free surface colored with vorticity magnitude; a TR1, b TR2

Full size image

The \(\lambda_{2}\) criteria Jeong and Hussain [17] can be applied to deduce the vortical structures causing the free-surface deformations. Figure 10 shows the iso-surface of \(\uplambda_{2} = - 1750\) colored with the vorticity magnitude. The shear layer of the CHJ is composed of a large number of small vortex worm-like structures. These structures are generated in the shear layer, and as they are transported towards the free surface by the upward flow in the recirculation region, they continuously interact with each other causing them to stretch and further break down into even smaller scales. The translucent instantaneous free surface of CHJ is also shown in Fig. 10. The interactions between the vortex worms and the free surface are also indicated by the dashed circles with the label A. One of these interactions is magnified in the inset in Fig. 10. These vortex worms are responsible for the flux of turbulent kinetic energy towards the free surface.

Fig. 10
figure 10

\(\lambda_{2}\) iso-surface showing the instantaneous vortical structures and their interaction with the free surface in TR1

Full size image

4.3 Mechanism of air entrainment

The jump toe of a CHJ oscillates horizontally about a mean position [13, 22, 27, 48]. The horizontal oscillations of the jump toe were obtained from the record of the instantaneous pressure monitored at different x-locations at a fixed vertical elevation corresponding to the supercritical depth at the jump toe (y = \(d_{1}\)). The dominant frequency of the jump toe motion f was calculated based on the fast Fourier transform (FFT) of the pressure data. Figure 11a shows the comparison of the Strouhal numbers (\({\text{St = }}f d_{1} /U_{1}\)) predicted by the simulation with available experimental results. The simulated frequencies of the jump toe oscillations are in reasonable agreement with the experimental results and follow the trend reported by other researches. To further understand the turbulent mechanisms within the flow, the period (T) of the horizontal oscillations of the jump-toe was split into 6 equal time steps. The instantaneous free surface and the evolution of the z-vorticity at different time instants are shown in Fig. 11 for test TR1. At time \(t = T /6,\) the toe of the hydraulic jump can be visually observed at \((x - x_{1} ) /d_{1} = - 4\) and moves to a maximum distance of \((x - x_{1} ) /d_{1} = 3\) at \(t = 4T /6\). Most of the vorticity is generated near the toe, and the structures are advected towards the free surface. As they reach the free surface, the turbulent kinetic energy carried by these vortices is dissipated in the processes of deformation and breaking up of the free surface. The synergy between the vortical structures (vortex worms) and the free-surface deformations can be observed at several time instances (marked with dashed circles). It is also seen that pockets of air enter the flow at the jump toe and are advected within the shear layer.

Fig. 11
figure 11

a Comparison of Strouhal numbers of horizontal jump-toe oscillations with available experimental results, b movement of the jump toe of TR1 superimposed with contours of z-vorticity (dashed circles denote the interaction of the vortical structures with the free surface)

Full size image

To understand this localized air-entrainment process, the instantaneous plots of the CHJ free surface with the instantaneous velocity vectors at two different time steps for test TR1 are plotted in Fig. 12a, b. It must be noted here that the velocity vectors are plotted only within the water region i.e., C > 0.5. The time steps were chosen to depict the regularly occurring phenomenon. Pockets of air enter the CHJ flow field at the location of the jump toe as indicated in Fig. 12a. This local aeration is caused by the impingement of the high-velocity jet flow into the roller. The large pockets of entrained air are advected downstream by horizontal vortices (marked by the blue arrows) in the shear layer. Similar flow patterns have been observed in experimental studies [6, 54]. These horizontal vortices are also responsible for the oscillations of the jump toe. In the shear layer, the larger air pockets are broken down into smaller pockets during advection. There is a steady supply of air due to the local aeration at the jump toe, causing the local maximum air concentration \(C_{max}\) to occur within the shear layer. The vortex worms generated in the shear layer also interact with the free surface. If the turbulent kinetic energy carried by these vortex worms is sufficient to overcome the surface tension, interfacial aeration would take place. Both local aeration and interfacial aeration mechanisms can be observed in a CHJ as evidenced in Fig. 12b. The singular air entrainment mechanism at the jump toe provides a fairly constant relative air flux to the water discharge, which is almost independent of the Froude number, the interfacial air–water mixing is highly determined by the level of free-surface fluctuations [49]. For a high Froude number hydraulic jump, the air flux in the upper roller region can be as high as that in the shear layer. However, it must be emphasised that Wang and Chanson [49] took account of the upper free-surface region (C > 0.5) in computing the air fluxes; it is uncertain how much of the air flux in this region truly mixes with the flow.

Fig. 12
figure 12

Aeration mechanisms in TR1 (blue curved arrows in b represent the horizontal vortices that advect the air pockets entrained at the jump toe)

Full size image

5 Conclusions

This study presents the results of unsteady, three-dimensional, computational simulations of a high Froude number classical hydraulic jump. The free surface was captured using Volume of Fluid multiphase model with High-Resolution Interface-capturing technique. The simulation captured the velocity, pressure and free surface location and dynamics of the hydraulic jumps with reasonable accuracy. The air concentration profiles predicted by the simulation followed the trend reported by experimental studies. However, the values of air concentration were over predicted by the simulations. One of the short-comings of the VOF model is that it adopts a “semi-two-phase flow” approach i.e., treating air and water as a mixture. This contributes to the discrepancies in the predicted air concentration. The predictions could be further improved by adopting an optimized sharpening factor. However, the value of sharpening factor is problem dependent and needs further investigation. The free-surface fluctuations and the jump-toe oscillations were also accurately captured by the present simulations. The coherent structures that are responsible for air entrainment were also captured by the simulations. The vortex worms generated in the shear layer of the jumps are transported towards the free surface due to the recirculating motion of the roller. These vortex worms cause the flux of turbulent kinetic energy towards the free surface, leading to its deformation and break up. Local aeration at the jump toe was caused by the impact of the wall jet flow on the jump roller. The air pockets entrained at the jump toe are advected downstream due to the horizontal convection of the vortices in the shear layer. To summarize, within the air–water shear layer, the local aeration was found to be the dominant mechanism of aeration and, near free surface, interfacial aeration becomes more dominant. The availability of the three-dimensional velocity field from the simulations aids in a better prediction of the flow mechanisms that cause air entrainment. The present paper highlights the pros and cons of using Improved Delayed Detached Eddy Simulations in conjunction with Volume of Fluid (VOF) multiphase model for predicting the free surface and air-entrainment characteristics of hydraulic jumps at high Froude numbers that are of practical interest in hydraulic engineering.