Groundwater Management in a Food Security Context

Abstract

This article analyzes the sustainability of market-based instruments such as tradable permits for the management of a renewable aquifer used for irrigated agriculture. In our dynamic hydro-economic model, a water agency aims at satisfying a food security constraint within a tradable permit scheme in the presence of myopic heterogeneous agents. We identify analytically the viability kernel that defines the states of the resource yielding inter-temporal feasible paths able to satisfy the set of constraints over time and the associated set of viable quota policies. We then illustrate the theoretical results of the paper with numerical simulations based on the Western La Mancha aquifer.

1 Introduction

With 20% of over-exploited aquifers in the world (WWAP 2015), groundwater resources are under extreme pressure (Wada et al. 2010). With drinking water, water demand for agriculture remains the main pressure on aquifers, and this pressure is increasing as the population continues to grow. Indeed, it has been estimated that agriculture will need to produce 60% more food in 2050 than it does today (FAO 2014), and will thus require more and more water for irrigation and crop production. To face this potential water crisis, water managers are mobilized to ensure a sustainable management of renewable aquifers by limiting the volume of water available for irrigation with respect to the level of recharge. Such a limitation impacts directly the agricultural production and can be dramatic for population in developing countries. Maintaining a sufficient level of agricultural activity may also be justified by social and economic motives like employment in rural areas or relative competitiveness of local farmers with respect to agricultural markets. The issue of sustainable management of renewable aquifers is thus strongly connected to the objective of food security.

The question of sustainable aquifer management has been investigated in the literature. Notably, the use of market-based instruments such as transferable permits has been proposed as a promising way to replenish an aquifer (Provencher 1993), or to efficiently manage groundwater for irrigated agriculture (Latinopoulos and Sartzetakis 2015). Groundwater markets consist in a cap and trade system for water rights. A water agency is assumed to set a cap on the available volume of water and assign individual quotas on an annual basis to farmers who can trade them on the market. The nature of the water rights differs significantly according to the countries which have implemented water markets such as Chile, the USA and Australia. Differences may concern the extent of aquifer regulation at a national or local level, the existence, or the lack thereof, of a system of prior appropriation by senior rights holders as in the USA, the rules of quota allocation in perpetuity or for a given period of time and joint or separate management of groundwater and surface water markets (see Montginoul et al. (2016) and Wheeler et al. (2016) for recent surveys on groundwater trading experiences). On the contrary, some European countries like France do not allow farmers to trade their individual irrigation quotas (Figureau et al. 2014; de Frutos Cachorro et al. 2016).

A common feature of groundwater markets is the transferability of water rights. Transferability ensures that water is used by farmers with maximum efficiency. As farmers differ in their productivity, economic efficiency implies that an efficient farmer will produce more than a less efficient farmer with the same volume of water. As a consequence, efficiency implies that the total water extraction provides the maximum amount of food production. The crucial role of transferability has also been pointed out by Knapp et al. (2003). They showed that transfers between agriculture and urban sectors, between regions and/or within a region, result in efficient aquifer management. Finally, the successful implementation of transferable quotas in fisheries (Branch 2008; Chu 2009; Pereau et al. 2012) argues in favor of the use of transferable permits in aquifers since similarities between groundwater and biological renewable resources have been highlighted (Roumasset and Wada 2012).

This paper aims at addressing the management of water as a renewable and limited resource using transferable quotas in a dynamic hydro-economic model based on the seminal Gisser and Sanchez (1980) in the context of food security. The state-of-the-art of this literature, including management issues and game theoretical models, can be found in Rubio and Casino (2001), Koundouri (2004), Booker et al. (2012), Madani and Dinar (2013), Tomini (2014) and de Frutos et al. (2014). Regulation has been justified by Esteban and Albiac (2011, 2012) and Esteban and Dinar (2016) when the decline in the water table creates negative externalities on surrounding ecosystems. In that case regulation is needed when agents, at an individual level, have no incentive to take into account the impacts of their resource use on ecosystems. Regulation can be achieved by implementing a water management system based on transferable permits among farmers as in Latinopoulos and Sartzetakis (2015). This paper contributes to the existing literature by introducing a food security constraint in the design of the water agency policy. The Gisser-Sanchez model is extended with a water agency which has to implement intertemporal management of groundwater by setting limits on total extraction at each period to achieve food production objectives. In particular, the paper determines the conditions under which the water agency is constrained in the setting of the water cap and how the water agency deals with economic efficiency, agricultural production and the sustainability of the resource.

Analysis of our hydro-economic model relies on the weak invariance (Aubin 1990) or viable control method (Clarke et al. 1995). This approach focuses on identifying inter-temporal feasible paths within a set of desirable objectives or constraints (Béné et al. 2001). This framework has already been applied to renewable resource management and especially to the regulation of fisheries (Martinet et al. 2007; Doyen and Pereau 2012), but its application to groundwater management is original. By introducing food production objectives, the viability method shows how water authorities can achieve sustainability objectives for both the resource and the farmers. This method provides a new explanation for the “Gisser-Sanchez Effect” in the context of groundwater markets by showing which intertemporal quota policies can be implemented by a water agency.

The paper is structured as follows: Sect. 2 is devoted to the description of our dynamic hydro-economic model and Sect. 3 introduces the objectives of the water agency. Section 3 characterizes the feasible resource states and the viable water policies under several constraints. An application based on the Western La Mancha aquifer illustrates the main results in Sect. 5. The last section concludes.

2 The Hydro-Economic Model

2.1 The Resource Dynamics

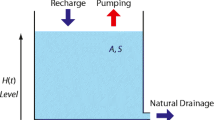
An aquifer is described by its state variable (ie the water table) $H(t)\in [0;S_L]$ at time t where $S_L$ stands for the height of the ground surface. The aquifer is empty at $H(t)=0$ and full at $H(t)=S_L$. The water table increases with constant recharge $R>0$ and is reduced by the extraction Q(t) dedicated to irrigated agriculture. The total volume of extracted water Q(t) corresponds to the quota set by a water agency. We assume that a proportion $\mu$ of the water used for irrigation comes back to the aquifer where $0<\mu <1$ stands for the non-absorption coefficient.

Based on Gisser and Sanchez (1980), the dynamics of the resource is

$$\begin{aligned} H(t+1)= & {} H(t)+\frac{R}{AS}-\frac{(1-\mu )}{AS}Q(t), \\ H(0)= & {} H_{0}, \nonumber \end{aligned}$$

(1)

where A stands for the area of the aquifer and S the storage coefficient.

Equation (1) can be rewritten as

$$\begin{aligned} H(t+1)=H(t)+\frac{1-\mu }{AS}\left( Q_{R}-Q(t)\right) , \end{aligned}$$

(2)

where $Q_{R}=\frac{R}{1-\mu }$ stands for the level of extraction which maintains a constant water table ($H(t+1)=H(t)$). This equilibrium constraint takes the form of a horizontal line in the state-control (H, Q) space. Above the line given by $Q_R$, extraction exceeds the net recharge ($Q(t)> Q_{R}$) and the water table diminishes. An extraction lower than the threshold extraction $Q_R$ induces an increase in the water table.

2.2 The Water Permit Market

We assume a set of n heterogeneous farmers using water extracted from the aquifer, denoted by $w_{i}$, as the only input to irrigate their crops. The total crop income is given by the product of the crop yield $y_{i}$ and the constant price of the agricultural product $p_{y}$. The crop-water production function $y_{i}(w_{i})$ increases at a decreasing rate with $y_{i}^{\prime }(w_{i})>0$ and $y_{i}^{\prime \prime }(w_{i})<0$. This modeling of the agricultural sector is consistent with the literature (Latinopoulos and Sartzetakis 2015; de Frutos Cachorro et al. 2016). With respect to Latinopoulos and Sartzetakis (2015), we consider one crop and one group of farmers instead of two crops and two associated groups of identical farmers who can trade their irrigation quotas. However, the analytical structure is the same. A valuable extension can be found in de Frutos Cachorro et al. (2016), who assume that each farmer can choose the share of land that will be used for different crops.¹

The pumping cost function c(H) is assumed to be decreasing and convex with respect to the water table with $c^{\prime }(H)<0$ and $c^{\prime \prime }(H)>0$. The externality occurs through the extraction cost, which increases when the water table becomes lower. Moreover, the unit extraction cost is assumed to be the same for farmers at each point of the aquifer.

The individual profit of farmer i (before the implementation of a quota market) can be written as follows:

$$\begin{aligned} \pi _{i}(H(t),w_{i}(t))=p_{y}y_{i}(w_{i}(t))-c(H(t))w_{i}(t). \end{aligned}$$

(3)

We further assume that a water agency allocates transferable water quotas $q_{i}(t)$ to the n farmers at the beginning of each period t. Each farmer can buy or sell quota units on the market at a unit price m(t) to have the right to extract and use water. It is assumed that water permits are not transferable over time, implying that banking or borrowing of water permits is not possible. The total water quota demand depends on the optimal individual quota demands denoted by $D_{i}^{*}(H(t),m(t))$ which are the outcome of the maximisation of individual profits given by:

$$\begin{aligned} \max _{w_{i},q_{i}}\pi _{i}(H(t),w_{i}(t)) - m(t)q_{i}(t) \nonumber \\ \text{ subject } \text{ to } w_{i}(t) \le q_{i}(t). \end{aligned}$$

(4)

When the quota constraint does not bind, the optimal water consumption is derived from $\partial \pi _{i}(H(t),w_{i}(t))/ \partial w_{i}(t)=0$ and the individual demand for water quotas is nil $D_{i}^{*}(H(t),m(t))=0$. Otherwise when $\partial \pi _{i}(H(t),w_{i}(t))/ \partial w_{i}(t)=\lambda _i>0$ with $\lambda _i$ the Lagrange multiplier associated to the quota constraint, it can be shown that the quota constraint binds and optimality condition is given by²:

$$\begin{aligned} y_{i}^{\prime }(q_{i}(t))=\frac{m(t)+c(H(t))}{p_{y}}. \end{aligned}$$

(5)

Taking the total differential of Eq. (5) shows that the individual quota demand function increases with the water table ($\partial D_{i}^{*}/\partial H=\frac{c^{\prime }(H)}{ p_{y}y_{i}^{\prime \prime }}>0$) and decreases with the quota price ($\partial D_{i}^{*}/\partial m=\frac{1}{p_{y}y_{i}^{\prime \prime }}<0$) since $y_{i}^{\prime \prime }<0$ and $c^{\prime }(H)<0$. Let be $Q^{s}=Q(t)$ the total amount of quotas allocated by the water agency to the farmers where $Q^{s}$ stands for the quota supply. The aggregated demand for quotas at a given price m(t) is denoted by $D^{*}(H(t),m(t))=\sum _{i}D_{i}^{*}(H(t),m(t))$. The equilibrium quota price is determined by the clearing-market condition on the water market implying equality between quota supply and demand: $Q(t)=D^{*}(H(t),m(t))$. It can be shown that the equilibrium quota price $m^{*}(t)=m^{*}(H(t),Q(t))$ is an increasing function of the water table ($\partial m^{*}/\partial H=-c^{\prime }(H)>0$) and a decreasing function of the quota supply ($\partial m^{*}/\partial Q=-\frac{p_{y}}{\beta }<0$) with $\beta =-\sum _{i}\frac{1}{y_{i}^{\prime \prime }}>0$. An increase in the water quota supply with unchanged demand implies a decrease in the quota price. When the water table is high, pumping costs are low. This increases water extraction and thus the demand for permits, pushing the water price up.

In the sequel of the paper, we consider the following specifications for the crop-water production function and the cost function. The crop-water production function is assumed to be quadratic (Burness and Brill 2001; Latinopoulos and Sartzetakis 2015) as follows:

$$\begin{aligned} y_{i}(w_{i}(t))=a_i w_{i}(t)-\frac{b_{i}}{2}w_{i}^{2}(t), \end{aligned}$$

(6)

where $a_{i}>0$ and $b_{i}>0$ are technical parameters. Marginal productivity is positive and decreasing. Individual production reaches its maximum for $\overline{w_{i}}=a_i/b_{i}$ yielding $\overline{y_{i}} =a_i^{2}/2b_{i}$. This implies that individual water extraction is bounded as follows: $w_{i}\in [0,\overline{w_{i}}]$. We deduce that the maximum amount of water consumption is $\overline{W} =\sum _{i=1}^{n}\overline{w_{i}}$ and the maximum amount of production is therefore $\overline{Y}=\sum _{i=1}^{n}\overline{y_{i}}$.

The unitary cost c(H(t)) is given by

$$\begin{aligned} c(H(t))= & {} c_{1}(S_L-H(t)), \nonumber \\= & {} c_{0}-c_{1}H(t), \end{aligned}$$

(7)

where $c_{0}=c_1 S_L$ stands for a fixed cost and $c_{1}$ is the marginal pumping cost. When the water table is at its maximum elevation, the unit cost is nil (Rubio and Casino 2001).

Based on these specifications, the individual quota water demand given by Eq. (5) is

$$\begin{aligned} q_{i}^{*}(t)= \frac{a_i}{b_{i}}-\frac{c_{0}}{p_{y}b_{i}}-\frac{m(t) }{p_{y}b_{i}} +\frac{c_{1}}{p_{y}b_{i}}H(t). \end{aligned}$$

(8)

Summing the individual demands yields the aggregate water demand for quotas³

$$\begin{aligned} Q^{*}(t)=\overline{W}-\beta \frac{c_{0}}{p_{y}}-\beta \frac{m(t)}{p_{y}}+\beta \frac{c_{1}}{p_{y}}H(t), \end{aligned}$$

(9)

with

$$\begin{aligned} \overline{W}=\sum _{i=1}^{n}\overline{w_{i}};\beta =\sum _{i=1}^{n}\frac{1}{b_{i}}. \end{aligned}$$

(10)

We deduce the equilibrium water price $m^{*}(t)$

$$\begin{aligned} m^{*}(t)=\frac{p_{y}}{\beta } (\overline{W}-Q(t)) -c_{0}+c_{1}H(t). \end{aligned}$$

(11)

3 The Water Agency Constraints

We consider a management strategy of the water agency in a food security context such that the total production generated by the n farmers has to meet a minimum production level set by the public authorities. Since water is a limiting resource for farmers, the objective of the water agency can be in conflict with the agricultural production objectives. This section shows how the water market and the food security objective can be rewritten in terms of constraints.

3.1 The Water Permit Price Constraint

Assuming that the water market is active due to a positive demand for quotas yields a positive price for the water permit $m^{*}(t)$:

$$\begin{aligned} 0\le m^{*}(t). \end{aligned}$$

(12)

This positivity condition on $m^{*}(t)$ yields a state-control constraint

$$\begin{aligned} Q(t)\le \overline{W}-\frac{\beta c_{0}}{p_{y}} +\frac{c_{1}\beta }{p_{y}} H(t). \end{aligned}$$

(13)

By denoting the above function by $Q_M$, it implies

$$\begin{aligned} Q(t)\le Q_M(H(t)). \end{aligned}$$

(14)

The tradable water permit constraint entails a superior limit for the total water extraction Q(t). This superior bound $Q_M$ is an increasing function of the state variable H(t) in the state-control (H, Q) space. This bound depends on the economic parameters of farmers. Below the bound $Q_M$, pumping costs are low, which raises water demand and ensures a positive quota price. In the opposite case, the quota price is nil and there is no demand for quotas.

3.2 The Food Security Constraint

To deal with productive goals, the aggregate production of the agricultural sector has to satisfy a production target

$$\begin{aligned} Y_{\lim }\le Y^{*}(t), \end{aligned}$$

(15)

with the aggregate production $Y^{*}(t)=\sum _{i=1}^{n}y_{i}^{*}(t)$. This production target implies a corresponding amount of water quotas needed for irrigation. Since water is the only input used by farmers, it is possible to associate to each amount of extracted water a particular amount of production. By substituting $m^{*}$ given by Eq. (11) within $q_{i}^{*}$ in Eq. (8), we obtain

$$\begin{aligned} q_{i}^{*}(t)=\frac{1}{b_{i}}\left( a_i-\left( \frac{\overline{W} -Q(t)}{ \beta }\right) \right) , \end{aligned}$$

(16)

and thus the optimal individual production becomes

$$\begin{aligned} y_{i}^{*}(t)=\frac{1}{2b_{i}}\left( a_i^{2}-\left( \frac{\overline{W} -Q(t)}{\beta }\right) ^{2}\right) . \end{aligned}$$

(17)

Summing the individual productions $y_{i}^{*}(t)$ in Eq.  (17) yields the aggregate production

$$\begin{aligned} Y^{*}(t)=\overline{Y}-\frac{1}{2\beta }\left( \overline{W} -Q(t)\right) ^{2}, \end{aligned}$$

(18)

with $\overline{Y}=\sum _{i=1}^{n}\overline{y_{i}}$.

The aggregate production constraint $Y_{\lim }\le Y^{*}(t)$ implies thus

$$\begin{aligned} Y_{\lim } \le \overline{Y}-\frac{1}{2\beta }\left( \overline{W} -Q(t)\right) ^{2}, \end{aligned}$$

(19)

which in turn entails the following bound on the water supply Q(t)

$$\begin{aligned} Q_{FS}\le Q(t), \end{aligned}$$

(20)

where $Q_{FS}$ is constant and independent of the state variable

$$\begin{aligned} Q_{FS}=\overline{W}-\sqrt{2\beta \left( \overline{Y}-Y_{\lim }\right) }. \end{aligned}$$

(21)

Not surprisingly, the existence of $Q_{FS}$ imposes that production objective $Y_{\lim }$ cannot exceed its maximum value $\overline{Y}$. Moreover, the positivity of the food security constraint (ie $Q_{FS}\ge 0$) yields a minimum value: $Y_{\lim }\ge Y^{\min }$ with $Y^{\min }=\overline{Y}-\left( \overline{W}^{2}/2\beta \right)$.

4 Viability Analysis

Taking into account the described hydro-economic model, this section shows how the two constraints defined in the previous section imply conditions on the water extraction and the water resource. We then consider how the water agency can implement a quota policy which satisfies all the constraints in a dynamic context. We characterize the sustainability of the system based on the concept of viability kernel consisting in the set of initial water table levels for which there exists at least one quota regime that satisfies our constraints indefinitely.

4.1 The Resource Constraint

The existence of the water permit price constraint $Q(t)\le Q_{M}(H(t))$ and of the food security constraint $Q_{FS}\le Q(t)$ limits the level of the water table. Combining Eqs. (14) and (20) gives

$$\begin{aligned} Q_{FS} \le Q \le Q_{M}. \end{aligned}$$

(22)

This yields a critical threshold on the water table

$$\begin{aligned} H_{\lim }\le H(t), \end{aligned}$$

(23)

where $H_{\lim }$ is such that

$$\begin{aligned} H_{\lim }(Y_{\lim }) = S_L -\frac{p_{y}}{c_{1}\beta }\sqrt{2\beta \left( \overline{Y}-Y_{\lim }\right) }, \end{aligned}$$

with $S_L=c_0/c_1$. Substituting the value of $Y^{\min }$ that ensures that the food security constraint is binding ($Q_{FS} \ge 0$) implies a condition on the amount of resource threshold. It gives

$$\begin{aligned} H^{\min } = \frac{1}{c_1} \left( c_0 -\frac{p_{y} \overline{W}}{\beta }\right) . \end{aligned}$$

The value of $H^{\min }$ is positive under the condition

$$\begin{aligned} c_0 > \frac{p_{y} \overline{W}}{\beta }. \end{aligned}$$

(24)

Equation (24) states that the marginal extraction cost of the last unit of water ($c_0$) is higher than the maximum value of marginal product (Rubio and Casino 2001).⁴ A violation of Condition (24) means that the food security constraint associated with the minimum extraction is not a binding constraint for the resource.

4.2 The Maximum Food Security Objective

Simultaneously satisfying the food security constraint ($Q_{FS}\le Q(t)$) and the equilibrium constraint ($Q(t)\le Q_{R}$) implies

$$\begin{aligned} Q_{FS}\le Q_{R}. \end{aligned}$$

(25)

This condition implies that if the food security constraint is too demanding, extraction required for the corresponding production is greater than the equilibrium recharge of the aquifer. In this case, the water table diminishes and it is not possible to define any sustainable water extraction. The maximum value of production $Y^{\max }$ able to ensure a sustainable aquifer management is computed with the limiting case, where the equilibrium water extraction $Q_R$ and the food security constraint $Q_{FS}$ overlap ($Q_{FS}=Q_{R}$). We deduce therefore:

$$\begin{aligned} Y^{\max }= \overline{Y}-\frac{(\overline{W}-Q_{R})^{2}}{2\beta }. \end{aligned}$$

(26)

We can note that $Y^{\max }$ is below the maximum amount of production $\overline{Y}$ obtained for a nil extraction cost. We can associate with this value $Y^{\max }$ an upper bound on the water table:

$$\begin{aligned} H^{\max } = \frac{1}{c_1} \left( c_0 -\frac{p_{y} ( \overline{W}-Q_R)}{\beta }\right) . \end{aligned}$$

To summarize, it turns out that $H_{\lim }$ lies in the interval $[H^{\min },H^{\max }]$ according the value of $Y_{\lim }$ from the interval $[Y^{\min },Y^{\max }]$.

4.3 Viability Kernel

The dynamics of the aquifer given by Eq. (1) are taken into account in combination with

• 1. the water permit price constraint with Eq. (14): $Q(t)\le Q_{M}(H(t))$,

• 2. the food security constraint with Eq. (20): $Q_{FS} \le Q(t)$,

• 3. the resource constraint with Eq. (23): $H(t) \ge H_{\lim }$.

In an infinite horizon context, the viability kernel can be formally defined as the set of initial situations $H_{0}$ such that there exists water extraction Q(t) and resources H(t), which satisfy the previous constraints, for all time $t=0,1,...\infty$. It can be written as

$$\begin{aligned} Viab=\left\{ H_0 | \exists Q(.) \text{ satisfying } \text{(14)-(20)-(23) } \forall t=0,1,.., \infty \right\} . \end{aligned}$$

We obtain the following proposition:⁵

Proposition 1

Assuming that $Y^{\min } \le Y_{\lim } \le Y^{\max }$, we obtain

• If $Q_{FS} > Q_{R}$ then viability cannot be achieved $Viab=\emptyset$. In that case, for every initial water table state $H_0$, every trajectory violates the constraints at least for a period of time.

• If $Q_{FS}\le Q_{R}$ the viability kernel is $Viab=\left[ H_{\lim },S_L \right]$ where $S_L$ stands for the maximum height of the aquifer. In that case, if and only if $H_0 \ge H_{\lim }$, there exists a water quota strategy complying with the constraints over time.

Proposition (1) shows that the viability of the quota management depends on the initial amount of available water in the aquifer as compared to the minimum resource threshold $H_{\lim }$ deduced from the amount of water extraction $Q_{FS}$ needed to satisfy the food security constraint given by $Y_{\lim }$. Two non-viable cases can occur. The first situation emerges when the initial level of the water table $H_0$ is lower than the tipping point of the resource state $H_{\lim }$. The second case occurs when the food production objective is too demanding. In this case, water extraction $Q_{FS}$ exceeds the equilibrium water extraction $Q_{R}$ which maintains the water table constant.

Fig. 1

Viable cases ($Q_{FS}^{\prime } \le Q_R$) and non-viable cases ($Q_{FS}^{\prime \prime } > Q_R$). For $Q_{FS}^{\prime }$, the viability kernel is given by the area located above the $Q_{FS}^{\prime }$ line and below the $Q_M$ line

Figure 1 shows the viability kernel in the state-control (H, W) space. It represents two horizontal straight lines $Q_{R}$ and $Q_{FS}$ and an increasing linear function $Q_M$. As explained above, $Q_{R}$ is the equilibrium extraction level corresponding to the aquifer recharge, $Q_{FS}$ the food security constraint and $Q_M$ the water permit constraint. The intercept of $Q_M$ with the Y-axis depends on the values of the parameters given by Condition (24). The intersection of the two constraints $Q_M$ and $Q_{R}$ gives the critical value for the water table $H_{\mathsf {\lim }}$. The viability domain corresponds to the area which lies above the food security constraint $Q_{FS}$ and below the water permit constraint $Q_M$. In this area, the viability domain allows increasing or decreasing water dynamics depending on whether the system is above or below the equilibrium water extraction $Q_{R}$.

Figure 1 considers different values for the food constraint. For a food target $Q_{FS}^{\prime \prime }$ higher than $Q_{R}$, the recharge of the aquifer cannot compensate the extraction. The water table will constantly decline as shown by the arrows pointing left. Starting from a high level of water table, water will become scarce at first. But the quota price will constantly decrease with the depletion of the water stock until water is no longer scarce. At a low water table level below $H_{\lim }^{\prime \prime }$ resulting in high pumping costs, the water quota market is no longer economically relevant. The viability kernel is empty. The threshold stock $H_{\lim }^{\prime \prime }$ required to satisfy the food target $Q_{FS}^{\prime \prime }$ is too high with respect to the equilibrium water extraction. On the contrary, for a food target $Q_{FS}^{\prime }$ lower than $Q_{R}$, the water table will constantly rise. Starting from an initial stock located below the threshold $H_{\lim }^{\prime }$ is not a viable case due to high pumping costs. When the water table goes beyond $H_{\lim }^{\prime }$, the water table can rise or fall depending on whether the viable quota implemented by the water agency is above or below the equilibrium water extraction $Q_{R}$. The quota price will remain positive in this area due to the existence of a positive water demand. For $Q_{FS}^{\prime }$ the viability kernel is thus given by the area located above the $Q_{FS}^{\prime }$ line and below the $Q_M$ line. If, by allowing high water extractions, the water table reaches its critical value $H_{\lim }^{\prime }$, then the water agency will be constrained by the water quota associated with $Q_{FS}^{\prime }$. The limit case $Q_{FS}=Q_{R}$ corresponds to the maximum amount of agricultural production $Y_{\lim }=Y^{\max }$.

The next section derives for the conditions on the water quotas which ensure that the water table remains above its critical value $H_{\lim }$ and belongs to the viability kernel.

4.4 The Gisser-Sanchez Effect Revisited

The viable controls have to maintain the water table of the aquifer within the viability kernel using the dynamic programming structure depicted in Doyen and Lara (2010). In other words, the viable water quotas Q(t) set by the water agency have to comply with the additional intertemporal condition $H_{\lim }\le H(t+1)$. We assume that at each period farmers buy the amount of quotas they need to maximise their annual rent for the equilibrium quota price. The viable water quotas are derived from Proposition (1). Using Eq. (1), we obtain

$$\begin{aligned} Q(t)\le Q_{R}+\frac{AS}{(1-\mu )}\left( H(t)-H_{\lim }\right) . \end{aligned}$$

(27)

Denoting by $Q_D$ the above function, the dynamic context of the resource threshold yields

$$\begin{aligned} Q(t)\le Q_D(H(t)). \end{aligned}$$

(28)

This dynamic constraint leads to a superior bound for the water extraction given by $Q_D(H(t))$. This superior limit is an affine and increasing function of the state variable H(t).

The comparison between the slopes of $Q_D$ and $Q_M$ shows⁶ that the dynamic viability constraint $Q_D$ is binding and reduces the viability domain under the following condition:

$$\begin{aligned} \frac{c_1(1-\mu )(p_y/\beta )}{AS} > 1. \end{aligned}$$

(29)

Condition (29) refers to the much-debated “Gisser-Sanchez Effect” which states that optimal groundwater regulation by a regulator offers few benefits compared to the open access situation. The difference between no control and optimal control by a central regulator is nil when the left-hand side of Eq.  (29) is sufficiently small (see equation (30) in the Gisser-Sanchez model). This occurs when the product of the aquifer’s area and the storage coefficient is large and the slope of the water demand is small ($k=p_y/\beta$) (Koundouri 2004). Within the context of groundwater markets, a small value means that the water agency is not temporally constrained in setting viable quotas. However, when Condition (29) is binding, the “Gisser-Sanchez Effect” no longer holds and regulation matters. In our viability framework, this shows that the water agency is dynamically constrained in its water quota setting at each period. Numerical illustrations of a real case study confirm that such restrictions on the quota supply can exist.

We are then able to specify the viable quotas $Q_{Viab}$ associated with the viable water tables.

Proposition 2

Considering that $Q_{FS}\le Q_{R}$, the viable quotas associated with $Viab= \left[ H_{\lim },S_L \right]$ are

$$\begin{aligned} Q_{Viab}=\left[ Q_{FS},min(Q_M,Q_D) \right] . \end{aligned}$$

Several quota policies may exist, implying different strategies and trade-offs between the resource and the economic constraints. Low amounts of quota benefit the resource and can even increase it when $Q_{FS}<Q_{Viab}<Q_{R}$. On the contrary, high quotas closed to the minimum between $Q_M$ and $Q_D$ promote more water extraction and decrease the water table.

Figure 2 displays the viable quota policies when the viability kernel is not empty and when Condition (29) holds in the state-control (H, W) space. The dynamic constraint $Q_D$ is represented by an increasing linear function with a negative intercept with the Y-axis for $H_{\lim } > \frac{(1-\mu )Q_R}{AS}$. This configuration also satisfies Condition (24). This dynamic constraint $Q_D$ on the quota setting shows that the viable quota domain is reduced. In other words, there is less leeway to manage the aquifer, as shown in Fig.  (2). When Condition (29) is satisfied, $Q_D$ becomes active and the viable quota domain lies within the area between $Q_D$ and $Q_{FS}$. The reduced viable quota domain is the area between $Q_M$ and $Q_D$. When Condition (29) is not active, the domain of viable quota policies coincides with the viability kernel. Based on numerical examples, the next section will show how both configurations are possible.

Fig. 2

Viable water quotas when the quota dynamic constraint is active under the condition $\frac{c_1(1-\mu )(p_y/\beta )}{AS} > 1$ and when $Q_{FS}=Q_R$

5 Numerical Illustration

The model is numerically tested on the Western La Mancha aquifer located in Spain. This aquifer has been studied in several papers by Esteban and Albiac (2011, 2012) and recently by Esteban and Dinar (2016). It supplies around 90% of the irrigation water used in that region. These papers are also based on the Gisser-Sanchez model. We consider the following values (from Esteban and Dinar 2016):

Parameters	Description	Units	Value
$\mu$	Return flow rate	Unitless	0.2
R	Natural recharge	$\mathrm{Mm^{3}}$	360
AS	Aquifer area times storativity	$\mathrm{Mm^{3}/m}$	126
$c_{0}$	Pumping costs intercept	€$\mathrm{/Mm^{3}}$	320, 000
$c_{1}$	Pumping costs slope	€$\mathrm{/Mm^{3}m}$	500
$H_{0}$	Initial water table	m	640

The Gisser-Sanchez model specifies an aggregate linear water demand $W=g-kp_{w}$ where g and k stand for the water demand intercept and slope with $g,k>0$ (€$\mathrm{/Mm^{3}}$) and $p_{w}$ the water price (in €$\mathrm{/Mm^{3}}$). We need to link the coefficients of the aggregate irrigation water demand to the parameters of the water input production function for farmers. By identification with our model, and in particular Eq.  (9) with $m(t)=0$, the intercept of the demand-for-water function is $g=\overline{W}$ and the slope of the demand-for-water function is $k=\beta /p_{y}$ with $\overline{W}$ and $\beta$ given by Eq.  (10).

Esteban and Dinar (2016) estimated different irrigation water demand functions. We select two water demands denoted by WD1 and WD2 (and corresponding to B1 and B3 in Esteban and Dinar 2016) which illustrate the two configurations of our theoretical model with $n=100$ farmers and $p_{y}=1.5$.

Parameters	Description	WD1 Value	WD2 Value
g	Water demand intercept	4400.73	726.71
k	Water demand slope	0.097	0.7272
a	Production coefficient	30,245.57	666.21
b	Squared production coefficient	687.28	91.67

Heterogeneity between the farmers is introduced through the values of $b_{i}$ as a uniform random variable over the interval $[b*(1-\delta ),b*(1+\delta )]$ with a dispersion rate $\delta =10\%$.

Based on the parameters concerning the first water demand function (WD1), it turns out that Condition (29) is not satisfied, meaning that the dynamic viability constraint $Q_D$ is not binding. At each period, the water agency can implement a quota policy that belongs to the viable quota domain (above the $Q_{FS}$ line and below the $Q_{M}$ line). Figure 3 displays the time path of the water table H(t), the water quotas Q(t) and the quota price m(t). We assume that the water agency sets the food security target $Q_{FS}=419.64$ $\mathrm{Mm^{3}}$ to achieve the production target $Y_{\lim }=1205$ tons. Since $Q_{FS} \le Q_R$, the viability kernel is not empty and implies a critical value for the water table equal to $H_{\lim }=551.90$ m. Figure 3(a, c, e) shows that the aquifer tends toward its threshold value $H_{\lim }$ only after 50 years but always remains above it. During that period the amount of water extracted remains higher than the equilibrium recharge $Q_{R}$. Some viable quotas start at 2, 400 $\mathrm{Mm^{3}}$ and decrease slowly to $Q_{FS}$. The path of the quota price follows the same pattern, starting at a high price when the water table is high (about 24000 €), decreasing afterwards, but remaining positive (about 200 €). The fall in the water table raises the pumping cost of the farmers, which decreases the water demand and the quota price.

To show the impact of the dynamic viability constraint $Q_D$ on the quota setting, we consider a decrease in the coefficient b from 687.28 to 210.28. Such a change implies a more elastic water demand with new coefficients $g=14383.11$ and $k=0.317$. To achieve the same production target $Y_{\lim }$, the corresponding security constraint is given by $Q_{FS}=418.52$ $\mathrm{Mm^{3}}$, implying a threshold for the water table equal to $H_{\lim }=557.85$ m. For theses values, Condition (29) is now satisfied, meaning that the viable quota domain is reduced. Some water quotas implemented by the water agency decrease to 7, 000 $\mathrm{Mm^{3}}$ in the first years as shown in Fig. 3(b, d, f). H(t) and Q(t) converge towards their threshold values significantly earlier compared to the previous case, but remain above them.

The analysis of the second water demand function (WD2) shows that Condition (29) is satisfied, implying a binding dynamic viability constraint $Q_D$. When $Q_{FS}=441.93$ $\mathrm{Mm^{3}}$ is lower than $Q_{R}$, the threshold value $H_{\lim }$ is equal to 639.22  m and is closed to its initial value $H_{0}$. This reduces the set of viable quotas the water agency can implement. Figure 4 displays the associated viable trajectory for the water table H(t), the quotas Q(t) and the quota price m(t). In the first years, water extractions are limited to lower values $Q=510$ $\mathrm{Mm^{3}}$ and converge fastly to their threshold values in few periods. The water table remains above its threshold value, maintaining a positive quota price.

Fig. 3

Water Demand 1: Trajectories of the water table H(t), the quotas Q(t) and the quota price m(t). a Water table H(t). b Water table H(t). c Quotas Q(t). d Quotas Q(t). e Price quota m(t). f Price quota m(t)

Fig. 4

Water Demand 2: Trajectories of the water table H(t), the quotas Q(t) and the quota price m(t). a Water table H(t). b Quotas Q(t). c Price quota m(t)

6 Conclusion

This paper examines the problem of groundwater management in irrigated agriculture. A water agency is assumed to allocate a total amount of water to farmers using tradable permits. Our contribution to the existing literature (see Latinopoulos and Sartzetakis 2015) is to emphasize how the water agency deals with the constraint of food security defined as an objective of a minimum amount of agricultural production for the whole agricultural sector. In a dynamic hydro-economic model, we determine the feasibility conditions under which the water agency ensures the joint sustainability of the resource and the agricultural activity. The paper uses the viability approach to deal with constraints in a dynamic setting.

Our results show that the food security constraint leads to a threshold being imposed on the water resource. When the food security constraint is too demanding with respect to the net recharge, or when the initial level of the water table is below the threshold value, the over-exploitation of the aquifer leads to its depletion. In the other cases, the water agency can achieve sustainability objectives which simultaneously account for water conservation, economic efficiency and maintenance of agricultural activity. However the paper also shows how the food security constraint impacts the design of water policies in a tradable quota market and revisits the well-known Gisser-Sanchez Effect (Koundouri 2004; Tomini 2014). The analytical condition behind this effect is the same which determines whether or not the water agency is dynamically constrained in the setting of the quota supply. Based on numerical examples related to the Western La Mancha aquifer (Esteban and Albiac 2011; Esteban and Dinar 2016), our results show that the set of viable quotas can be strongly reduced.

Future extensions could be considered. A first one consists in introducing an individual constraint on farmers with guaranteed payoffs. By dealing with an aggregate food security objective together with individual constraints for heterogenous farmers, the water agency will address equity and acceptability issues when setting the quota supply and the initial allocation of the water permits (Ballestero et al. 2002). A second extension relies on the introduction of a stochastic rate of the natural recharge. de Frutos et al. (2014) showed that such an uncertainty can create incentives for the water agency to allow more extraction in the long run than in the short run. It suggests the use of robust viability theory to address dynamical control problems under constraints with uncertainty (Doyen and Lara 2010; Regnier and Lara 2015).

Appendix

1.1 Optimality Conditions

The Lagrangian corresponding to the problem (4) with $w_{i} \ge 0$ and $q_{i} \ge 0$ is

$$\begin{aligned} L=\pi _{i}\left( H,w_{i}\right) -mq_{i}+\lambda _{i}\left( q_{i}-w_{i}\right) \end{aligned}$$

The Kuhn-Tucker conditions are

$$\begin{aligned} L_{w_{i}}^{\prime }= & {} \frac{\partial \pi _{i}\left( H,w_{i}\right) }{ \partial w_{i}}-\lambda _{i} \le 0; ({=}0 \text{ if } w_{i}>0),\\ L_{q_{i}}^{\prime }= & {} -m+\lambda _{i} \le 0; ({=}0 \text{ if } q_{i}>0),\\ \lambda _{i}\ge & {} 0\text {, }\lambda _{i}\left( q_{i}-w_{i}\right) =0. \end{aligned}$$

If $\lambda _{i}=0$, the constraint does not bind then $w_{i}^{*}$ is solution of $\partial \pi _{i}\left( H,w_{i}\right) /\partial w_{i}=0$ and $q_{i}=0$. Otherwise $\lambda _{i}>0$ implies a positive quota price $m>0$. It shows that the constraint binds $q_{i}=w_{i}$ and $\frac{\partial \pi _{i}\left( H,q_{i}\right) }{\partial q_{i}}=m$ which gives Eq.  (5).

1.2 Proof of the Viability Kernel

Proof

Consider the dynamics

$$\begin{aligned} H(t+1)=H(t)+\frac{1-\mu }{AS}\left( Q_{R}-Q(t)\right) , \end{aligned}$$

with $Q_{R}=\frac{R}{1-\mu }$.

We first show that $Q_{FS}\le Q_{R}$ implies $Viab=\left[ H_{\lim }, S_L \right]$.

Assume that $H_0 \ge H_{\lim }$, choose $Q(t)=Q_{FS}$ then

$$\begin{aligned} H(t)+\frac{1-\mu }{AS}\left( Q_{R}-Q(t)\right) =H(t)+\frac{1-\mu }{AS}\left( Q_{R}-Q_{FS}\right) \ge H{(t)} \ge H_{\lim }. \end{aligned}$$

Hence $\left[ H_{\lim }, S_L \right]$ is viable and $Viab=\left[ H_{\lim }, S_L \right]$.

Now if $Q_{FS}>Q_R$, we show by forward induction that $\forall H_0 \ge H_{\lim }$

$$\begin{aligned} H(1)= & {} H(0)- \left( \frac{1-\mu }{AS}\right) \left( Q_{FS}-Q_{R})\right) , \\ H(2)= & {} H(0)-2 \left( \frac{1-\mu }{AS}\right) \left( Q_{FS}-Q_{R})\right) , \\ H(t)= & {} H(0)-t \left( \frac{1-\mu }{AS}\right) \left( Q_{FS}-Q_{R})\right) . \end{aligned}$$

Hence $\exists t^{*}$ such that $H(t^{*})< H_{\lim }$, it implies that $Viab=\emptyset$.

1.3 Dynamic Constraint $Q_D$

The constraint on the state variable $H_{\lim } \le H(t+1)$ implies

$$\begin{aligned} H_{\lim }\le & {} H(t)+\frac{R}{AS}-\frac{(1-\mu )}{AS}Q(t), \\\Longleftrightarrow & {} Q(t)\le Q_{R}-\frac{AS}{(1-\mu )}H_{\lim } +\frac{AS}{ (1-\mu )}H(t). \end{aligned}$$

By denoting $Q_D= Q_{R}-\frac{AS}{(1-\mu )}H_{\lim } +\frac{AS}{(1-\mu )}H(t)$, it gives $Q(t)\le Q_D(H(t))$. We look at the conditions depending on the sign of $Q_M-Q_D$ under which this dynamic constraint is binding and reduces the viability kernel. By definition, $Q_D(H_{\lim })=Q_R$ and since Q is bounded by $Q_R$, it implies that for $H=H_{\lim }$

$$\begin{aligned} Q_M(H_{\lim })< Q_D(H_{\lim }). \end{aligned}$$

It yields

$$\begin{aligned} \overline{W}-Q_R<\frac{\beta }{p_{y}}(c_{0}- c_{1}H_{\lim }). \end{aligned}$$

The expression of $Q_M-Q_D$ is given by

$$\begin{aligned} Q_M-Q_D=\overline{W}-Q_R-\frac{\beta c_{0}}{p_{y}} +\frac{c_{1}\beta }{p_{y}} H-\frac{AS}{1-\mu }(H-H_{\lim }). \end{aligned}$$

Using the two previous expressions gives

$$\begin{aligned} Q_M-Q_D< & {} \frac{\beta }{p_{y}}(c_{0}- c_{1}H_{\lim }) -\frac{\beta c_{0}}{ p_{y}} +\frac{c_{1}\beta }{p_{y}}H-\frac{AS}{1-\mu }(H-H_{\lim }), \nonumber \\ Q_M-Q_D< & {} \frac{c_{1}\beta }{p_{y}}(H-H_{\lim })-\frac{AS}{1-\mu }(H-H_{\lim }). \end{aligned}$$

When $H>H_{\lim }$ the condition ensuring $Q_M-Q_D>0$ is

$$\begin{aligned} \frac{c_1(1-\mu )(p_y/\beta )}{AS} > 1, \end{aligned}$$

and corresponds to Eq.  (29) in the text.