Introduction

Groundwater models are widely used in hydro-economics as they present an efficient approach to investigate the effects of contrasting management policies on groundwater (Harou et al. 2009; Akter et al. 2014). Hydro-economic models can be used to optimize pumping rates so as to maximize the overall benefits of competing agents (Babel et al. 2005; Momblanch et al. 2016) or identify the trade-off between the benefits of groundwater extraction (e.g. irrigation) and the associated damages (e.g. streamflow depletion; Pulido-Velázquez et al. 2006). When an aquifer containing fossil water (“fossil aquifer”) is considered, transient approaches provide the optimum trajectory of pumping rate to develop the stock of the aquifer until the resource is exhausted (Gisser and Sanchez 1980a). When an aquifer containing a renewable groundwater resource (“renewable aquifer”) is considered, the trajectory of the pumping rate tends to move toward a stabilized value that may theoretically be sustained in the long term. Groundwater models used in hydro-economics can be classified in two types: (1) lumped (so-called “bathtub”) models where the aquifer is described with a uniform water level and (2) spatially distributed models, based on the resolution of the diffusivity equation where groundwater level may vary in space and time. While distributed models are necessarily more faithful with the reality and therefore more appropriate for case studies (Gorelick 1983; Pulido-Velázquez et al. 2006), the former bathtub models have proved to be relevant for conceptual and generic discussions on groundwater management strategies (Katic and Grafton 2012).

Bathtub models have become one of the main reference models used by water economists; in particular, these models have been the basis for the controversial conclusions of Gisser and Sanchez (1980b) which have been long debated in the economic literature (Koundouri 2004). The structure of bathtub models is radically simple: a single-cell aquifer with groundwater recharge as input, and pumping and natural drainage as outputs (Fig. 1). The net groundwater withdrawal rate is (1 − μ)W, where μ is the return flow coefficient and W the pumping rate. The aquifer is described with a single variable: the water height (H), which can be translated to water volume (G), given the surface area (A), and storage coefficient (S) of the aquifer. Under a series of hypotheses, Gisser and Sanchez (1980b) conclude that the difference between an optimal groundwater management by cooperating agents and the open access situation with myopic maximizing agents is so small that public intervention cannot be justified. The study has become famous mainly due to this disturbing result. Since then, several papers have questioned this result. Brill and Burness (1994), Koundouri (2004) and Tomini (2014) identified some limitations on the model’s assumptions concerning the linearity of the water demand or the cost functions and the value of some key parameters such as the discount factor.

Fig. 1
figure 1

The one-cell (so-called “bathtub”) aquifer model. The aquifer is recharged by R (groundwater recharge) and drained by Wn. A is the aquifer area and S the aquifer storage coefficient

Full size image

Gisser and Sanchez (1980b) mention the occurrence of natural aquifer discharge in their conceptual model (Wn in Fig. 1); however, and quite unexpectedly, this term is ignored in their water balance equation (Dumont 2015). Should net withdrawals exceed recharge over the long run [(1 − μ)W > R], the aquifer will necessarily dry out. Conversely, the aquifer will necessarily overflow if net withdrawals remain below recharge [(1 − μ)W < R]. For the system to become stable over the long run (steady state), net withdrawals should necessarily equal the groundwater recharge, which explains why natural discharge has often been ignored, or at least assumed to be subtracted as a constant term from the natural recharge in part of the water economic literature. Furthermore, the lack of consideration of natural drainage has promoted the persistent “water budget myth” that net withdrawals can equal groundwater recharge in the long run without causing harmful damages (Bredehoeft 2002; Devlin and Sophocleous 2004).

In contrast to Gisser and Sanchez (1980b), the same authors do consider natural drainage in the water balance equation in other contemporary studies (Gisser and Sanchez 1980a; Gisser 1983). In these latter studies, which show that the steady-state regime for the water table is determined by a critic boundary value for which the natural discharge is nil, Wn is expressed with a conductance model depending on the water table. A literature review highlights that the declinations of the Gisser-Sanchez model most often do not consider natural drainage in the water budget (Table 1). This hypothesis can be justified when recharge (and natural drainage) are both negligible, as is the case for fossil groundwater resources (Gisser 1983). However, this hypothesis is questionable when both recharge and natural drainage are present, as is the case for unconfined aquifers, which benefit from recharge and interact with surface water bodies and ecosystems.

Table 1 Consideration of drainage in the water budget (WB) and ecosystem damages in the welfare function (WF). Articles sorted by chronological order
Full size table

Natural aquifer drainage may flow directly into the ocean in coastal areas, in which case it may be considered as a regrettable loss of freshwater; however, natural aquifer drainage also constitutes the base flow to streams, contributes to replenish lakes, and supports phreatophytes and wetlands. All these outputs support ecosystems and contribute to the so-called environmental flows. Initially introduced for rivers, environmental flows refer to the quantity of water that is necessary to maintain valued features of ecosystems (Sophocleous 2007; Tharme 2003); additionally, this definition has been extended to groundwater-dependent ecosystems that rely, directly or indirectly, on the occurrence of groundwater (Eamus et al. 2006; Murray et al. 2003). For aquifers in interaction with surface-water bodies, groundwater extraction entails a decrease in natural drainage, called capture (Lohman 1972; Konikow and Leake 2014). When natural drainage from an aquifer of economic interest supports groundwater-dependent ecosystems, groundwater development may therefore threaten environmental flows (Qureshi et al. 2012)—for instance, pumping may have negative impacts on streamflow requirements for fish and other aquatic species, the health of riparian and wetland ecosystems and other environmental needs (Zhou 2009).

With the looming interest for the protection of environmental flows, a series of recent studies introduced environmental damages resulting from groundwater extraction into hydro-economic models (Esteban and Albiac 2011, 2012; Skurray and Pannell 2012; Esteban and Dinar 2013). These studies introduced environmental damages as the difference between groundwater withdrawal and recharge (Esteban and Albiac 2011, 2012) or through ecosystem health functions based on the groundwater level (Esteban and Dinar 2013, 2016). Esteban and Dinar (2016) discuss the impact of various nonlinear cost functions, which may present threshold effects. The results of these studies highlight the importance of considering environmental costs on the optimum trajectory of groundwater extraction and further challenge the conclusions of Gisser and Sanchez (1980b).

While environmental flows have been introduced in the welfare function of several hydro-economic studies, they remain disregarded in the water budget (Table 1). The aim of this paper is to investigate the importance and advantages of considering explicitly natural drainage in the water budget of hydro-economic models. The hydro-economic model consists of a dynamic stock-flux framework where the volume of water in the aquifer stands for the state variable and the volume of extracted water for users the control variable. The objective is to optimize the trajectory of the control variable so as to maximize a welfare function over time (Bellman 1957; Sorger 2015). The methodological approach for the resolution of the optimal trajectory stands in the tradition of discrete-time models for the management of groundwater resources proposed by Burt (1964, 1967) and several authors after as Provencher and Burt (1993), Knapp and Olson (1995) or Krishnamurthy (2017) in a deterministic and stochastic framework.

The paper is organized as follows—the hydro-economic model is developed taking into account environmental flows both in the water budget and in the welfare function; the resolution of the optimum pumping trajectory is presented; how the introduction of environmental flows in the water budget of the aquifer and in the welfare function of the social planner impacts the optimal trajectory for pumping is investigated ( the numerical illustration is based on the Western La Mancha aquifer in southwest Spain).

Methods

Aquifer dynamics

Following Gisser and Mercado (1972) and Gisser and Sanchez (1980a, b), the water budget of the unconfined aquifer sketched in Fig. 1 is given by:

$$ AS\left[H\left(t+1\right)-H(t)\right]=R-\left(1-\mu \right)W(t)-{W}_n(t) $$
(1)

where A stands for the surface area of the aquifer,S is the storage coefficient, H(t) the height of the water table above the base of the aquifer at time t, R the exogenous and constant natural recharge, W(t) groundwater extraction at time t, μ the return flow coefficient with 0 < μ < 1 and Wn(t) the natural discharge at time t. In this study, it will be considered that aquifer drainage supports groundwater-dependent ecosystems and therefore contributes to environmental flows.

Following Gisser and Sanchez (1980a), the aquifer natural discharge, Wn(t), can be modeled as a function of the groundwater level, H(t), with a linear conductance model, which is a common approach for the description of stream–aquifer flow (Cousquer et al. 2017; Ebel et al. 2009; Morel-Seytoux 2009):

$$ {W}_n(t)=c\left[H(t)-{H}_{\mathrm{min}}\right] $$
(2)

where c is a conductance parameter and Hmin the water level which gives a nil aquifer drainage [Wn(t) = 0 for H = Hmin]. In the pristine initial conditions before pumping starts, [H(t = 0) = Hmax], natural discharge should equal the natural recharge: Wn(t) = R. Under these conditions, the conductance parameter c can be expressed as follows: c = R/(Hmax − Hmin) > 0. Instead of using Eq. (2), Gisser and Sanchez (1980a) assumed an equivalent relation of the form:

$$ {W}_n(t)=-\alpha +\gamma H(t) $$
(3)

where α stands for the slope and γ for the intercept (ordinate at origin) of the natural discharge linear function. Their expressions can be derived from Eq. (2) and the expression of the conductance parameter:

$$ \alpha =\frac{R{H}_{\mathrm{min}}}{H_{\mathrm{max}}-{H}_{\mathrm{min}}}>0;\gamma =\frac{R}{H_{\mathrm{max}}-{H}_{\mathrm{min}}}>0 $$

The critical boundary value Hmin implying Wn(t) = 0 can then be expressed as follows: Hmin = α/γ.

The volume of water defined by G(t) = AS × H(t) can be introduced in Eq. (1) where Wn(t) can be substituted by its expression in Eq. (3), which yields:

$$ G\left(t+1\right)=\kappa G(t)+R+\alpha -\left(1-\mu \right)W(t) $$
(4)

with \( 0<\kappa =1-\frac{\gamma }{AS}<1 \). See Burt (1967) and de Frutos Cachorro et al. (2014) for similar notations. Note that ensuring a positive natural discharge implies G(t) ≥ Gmin = AS × Hmin.

The values of pumping and aquifer stock at the steady state (with notation ss), Wss and Gss, respectively, can be obtained from Eq. (4), which yields:

$$ {W}_{\mathrm{ss}}=\frac{R+\alpha }{1-\mu }-\frac{1-\kappa }{1-\mu }{G}_{\mathrm{ss}} $$
(5)

It should be noted that the stabilized value of net pumping rate should not exceed groundwater recharge, which reads: \( 0\le {W}_{\mathrm{ss}}\le \frac{R}{1-\mu } \).

The economic model

The objective of a social planner is given by the following welfare function defined as the sum of private benefits of agents minus the environmental damage D(G):

$$ V\left(W(t),G(t)\right)= aW(t)-\frac{b}{2}W{(t)}^2-\left({c}_0-{c}_1G(t)\right)W(t)-D\left(G(t)\right) $$
(6)

As in Gisser and Sanchez (1980b), the linear irrigation demand from farmers is given by W(t) = g − kp(t) with p the price of water, and g > 0 and k > 0 stand for the intercept and the slope of the water demand function, respectively. The farmer’s total income is measured by the first two terms of Eq. (6) with a = g/k and b = 1/k. The third term of Eq. (6) refers to the linear cost function. C[G(t)] = c0 − c1G(t) where c0 > 0 and c1 > 0 respectively stand for the intercept and the slope of the pumping cost function. When G(t) = Gmax = c0/c1, the pumping cost is nil. The final term measures the cost of ecosystem damages specified as follows:

$$ D\left(H(t)\right)=\varphi \left(R-{W}_n(t)\right)+\theta \left({H}_{\mathrm{max}}-H(t)\right) $$
(7)

The first term of Eq. (7) consists of the cost of the aquifer depletion measured by the capture variable defined as the difference between the natural recharge and the natural discharge. This is of interest for damage to ecosystems associated with consumptive uses (river base flow, transpiration by phreatophytes). It differs from Esteban and Albiac (2011, 2012) who considered the difference between extraction, (1 − μ)W(t), and the natural recharge R. Coefficient φ > 0 measures the cost of damages to ecosystem for each cubic meter of depletion. The second term refers to another kind of damage cost related to the difference between the maximum (initial) and the current water levels (Esteban and Dinar 2013). It is mostly relevant for nonconsumptive uses of groundwater (for example, to avoid subsidence). This specification is more in line with the ecosystem benefit function of Esteban and Dinar (2016). Coefficient θ > 0 is also a measure of the cost of damages to the ecosystem for each meter of depletion (or height of water level drop).

The substitution of Wn by its expression from Eq. (3) and using G(t) as the new state variable gives an expression of ecosystem damages, D, as a simple function of G:

$$ D\left[G(t)\right]={d}_0-{d}_1G(t) $$
(8)

with \( {d}_0=\varphi \left(R+\alpha \right)+\frac{\theta }{AS}{G}^{\mathrm{max}}>0 \) and \( {d}_1=\varphi \left(1-\kappa \right)+\frac{\theta }{AS}>0 \). Coefficients d0 and d1 respectively stand for the intercept and the slope of the damage function.

Resolution

The resolution of the model consists of deriving the state and control trajectories which satisfied the dynamics and the objective of the social planner together with the steady-state values of these variables. It is assumed that the social planner aims at maximizing social welfare given by the discounted present value of the farmer’s income and environmental damages. Substituting Eq. (7) into Eq. (6) gives:

$$ SW\left(W(t),G(t)\right)= aW(t)-\frac{b}{2}W{(t)}^2-\left({c}_0-{c}_1G(t)\right)W(t)-{d}_0+{d}_1G(t) $$
(9)

The program of the social planner becomes:

$$ \underset{W(.)}{\max }{\sum}_{t=0}^{\infty }{\beta}^t SW\left[W(t),G(t)\right] $$
(10)

where β stands for the discount factor with 0 < β < 1. The discount factor, which is a sensitive parameter in any optimum-trajectory economic approach (Brill and Burness 1994), favors the present, since it gives a smaller value to profit or utility made in the future. Equation (10) stands under the dynamic constraint described by Eq. (4) and the initial value of the volume of water G(t = 0) = Gmax.

The resolution is adapted from Burt (1967) and consists of rewriting the problem Eq. (10) ) in such a way that only terms in the state variable G will appear. The water extraction terms in Eq. (10) are replaced by their expression in Eq. (4) as a function of G at different periods. Taking the derivative with respect to G at time t yields the following finite second-order difference equation:

$$ G\left(t+1\right)=2\left(1+\frac{1-\beta }{2\beta }+\epsilon \right)G(t)-\frac{1}{\beta }G\left(t-1\right)+\frac{\left(1-\kappa \beta \right)\left(a-{c}_0-\frac{b\left(R+\alpha \right)}{1-\mu}\right)-{c}_1\beta \left(R+\alpha \right)-\left(1-\mu \right){d}_1}{\beta \left(\frac{b\kappa}{1-\mu }-{c}_1\right)} $$
(11)

with \( \epsilon =\frac{b\left(1-\kappa \right)\left(1-\kappa \beta \right)+{c}_1\left(1-\mu \right)\left(1+\beta -2\kappa \beta \right)}{2\beta \left( b\kappa -{c}_1\left(1-\mu \right)\right)}>0 \) under the condition \( \frac{b\kappa}{1-\mu }>{c}_{1.} \)

The general solution is the sum of the particular solution and the solution of the homogenous equation:

$$ G(t)=\overline{G}+{A}_1{\lambda}_1^t+{A}_2{\lambda}_2^t $$
(12)

with \( \overline{G} \) the particular solution:

$$ \overline{G}=\frac{c_1\beta \left(R+\alpha \right)+\left(1-\mu \right){d}_1-\left(1-\kappa \beta \right)\left(a-{c}_0-\frac{b\left(R+\alpha \right)}{1-\mu}\right)}{\frac{b\left(1-\kappa \right)}{1-\mu}\left(1-\kappa \beta \right)+{c}_1\left(1+\beta -2\kappa \beta \right)} $$
(13)

while λ1 and λ2 are the roots of the homogeneous equation such that λ1 is the stable root (0 < λ1 < 1) and λ2 the unstable one (λ2 > 1):

$$ {\lambda}_1=\left(1+\frac{1-\beta }{2\beta }+\epsilon \right)-\sqrt{{\left(\frac{1-\beta }{2\beta }+\epsilon \right)}^2+2\epsilon } $$
(14)

It can be shown that A2 = 0 and \( {A}_1={G}_0-\overline{G} \), leading to the expression of the optimum trajectory for the aquifer stock:

$$ G(t)=\overline{G}+\left({G}_0-\overline{G}\right){\lambda}_1^t $$
(15)

and the associated decision rule, the pumping rate:

$$ W(t)=\frac{R+\alpha -\left(1-\kappa \right)\overline{G}}{1-\mu }+\frac{\kappa -{\lambda}_1}{1-\mu}\left({G}_0-\overline{G}\right){\lambda}_1^t $$
(16)

It can be shown that λ1 decreases with ϵ since \( \frac{\partial {\lambda}_1}{\partial \epsilon }<0 \). A higher value of λ1 also implies a slower adjustment of the volume of water G(t) to its steady-state equilibrium value \( \overline{G} \).

To highlight the consequences of considering environmental flows in the water budget and as damage in the welfare function, the different values of stabilized pumping rate and volume of water are derived from Eq. (13). Table 2 shows that only the configuration which leads to a nonzero drainage corresponds to the configuration where environmental flows are considered both in the water budget and in the welfare function.

Table 2 Comparison of optimum steady-state values of aquifer stock (G), aquifer drainage (Wn) and pumping rate (W), depending on the consideration of drainage in the water budget (with Wn) and environmental damages in the welfare function [with D(G)]. When Wn is not considered (first row), its value is zero
Full size table

Results

An empirical illustration of the hydro-economic model—Eqs. (15) and (16)—is provided based on the Western La Mancha aquifer, which lies in southwest Spain. This aquifer is subject to relatively intense pumping, mainly for irrigation purposes, which threatens groundwater-dependent ecosystems, in particular wetlands. For a thorough description of the context, the reader may refer to Martínez-Santos et al. (2008), Esteban and Albiac (2012) and references herein. Parameter values used in the current study (Table 3) originate from the investigations of Esteban and Albiac (2011, 2012) together with Esteban and Dinar (2016). The simulation program can be found in the electronic supplementary material (ESM).

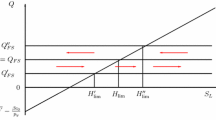
Table 3 Aquifer and cost parameters from Esteban and Albiac (2011, 2012). Pumping, recharge, and drainage rates are expressed as volume per year. Parameters of the drainage function are obtained from Eq. (2) with data provided by Martínez-Santos et al. (2008) and Esteban and Albiac (2012)
Full size table

The water extraction paths and associated volumes are displayed in Fig. 2. The numerical values of the associated steady states are provided in Table 4. In all simulations, the initial state corresponds to a full aquifer G(t = 0) = Gmax with no water extraction W = 0 and a maximum drainage Wn = R. As in Gisser and Sanchez (1980b), trajectory 1 disregards both aquifer drainage in the water budget and damages on environmental flows in the welfare function. With this approach, the volume reaches a steady-state value at 80,241 Mm3. When environmental flows are considered in the welfare function (trajectory 2), as in Esteban and Albiac (2011, 2012), the volume reaches a higher steady state (82,321 Mm3), but the extraction rate tends to the same value than trajectory 1 (450 Mm3).

Fig. 2
figure 2

Comparison of trajectories to steady state for groundwater extraction (Wn) and stock of the aquifer (G) with and without consideration of drainage in the water budget (WB) and ecosystem damages in the welfare function (WF)

Full size image
Table 4 Comparison of optimum steady-state values of aquifer stock (G) aquifer drainage (Wn) and pumping rate (W) for the Western La Mancha aquifer case study. All the variables are in Mm3. Numbers 1–4 in italic refer to trajectories in Fig. 2
Full size table

When natural drainage is included in the water budget but environmental flows remain disregarded in the welfare function (trajectory 3), the water volume G reaches a lower steady-state value at 75,708 Mm3, which is below the critical level Gmin= 75,900 Mm3. As in Gisser and Sanchez (1980a, see Fig. 3 in their paper), it is considered that when the water volume reaches the critical boundary values (Gmin), pumping should be adjusted to avoid drainage to become negative and maintain the stock at Gmin. Trajectory 4 corresponds to the optimum extraction path when considering both aquifer drainage in the water budget and ecosystem damages in the welfare function. As expected, the corresponding extraction rate tends to 296 Mm3, which is the most limiting configuration for groundwater development.

Trajectories 2 and 4 both consider ecosystem damages in their welfare functions, but differ on the consideration of natural drainage, which is not considered in trajectory 2, but is considered for trajectory 4. The stock remains higher for the former (82,321 Mm3) than for the latter (78,696 Mm3; Fig. 2). This may seem paradoxical as the abstraction rate is higher for the former (450 Mm3/year) than for the latter (296 Mm3/year). This is due to the fact that for trajectory 4, the bathtub model is “pierced” to account for aquifer drainage, while the former disregards the existence of this natural outflow. This also explains that the stabilized stock for trajectory 1 (80,241 Mm3) is higher than for trajectory 4 (78,696 Mm3), though the latter consider the cost of ecosystem damages.

It should be noted that for trajectories that do not consider aquifer drainage in the water budget (trajectories 1 and 2), the abstraction rate will necessarily tend to [R/(1 − μ)] whatever the parameters chosen to account for ecosystem damages. This is also the case for trajectory 3, which does not account for ecosystem damages (for these three configurations, aquifer drainage will necessarily tend to zero). The only trajectory that leads to an optimum stabilized value of net withdrawal rate below groundwater recharge and therefore, a nonzero value for aquifer drainage, is trajectory 4. For this trajectory, extraction values may be higher than the natural recharge during the first years, but remains below afterwards and stabilizes at 296 Mm3/year, allowing natural drainage to remain at 122 Mm3/year.

The comparison of the different steady-state values of the state and control variables (Table 4), highlights that the approach presented by Esteban and Albiac (2011, 2012) and Esteban and Dinar (2016) may lead to overestimates of the volume of water which can be allocated to users. Due to the lack of consideration of natural drainage in trajectories 1 and 2, both are subject to the water-myth-budget criticism; hence, only trajectories 3 and 4 are consistent with the aquifer water balance. Results show that the consideration of environmental flows as an environmental damage for the society yields an increase in the steady-state volume of water of 3.68% (2,796 Mm3; Table 4); however, this comes at the expense of an important decrease in the volume of extracted water for irrigation of 34% (154 Mm3).

Discussion and conclusion

This paper analyzed the importance of aquifer drainage for the definition of optimum groundwater management in the presence of ecosystem damages, which is of interest for water managers, so as to determine trajectories for the water resource and water extraction, maximizing the welfare of the society regarding both human and environmental needs. Several recent studies consider the cost of ecosystem damages in their welfare functions (Esteban and Albiac 2011, 2012; Esteban and Dinar 2016); however, following Gisser and Sanchez (1980b), they do not consider aquifer drainage in the aquifer water budget but focus on recharge. This can be considered as an illustration of the “water budget myth” described by Devlin and Sophocleous (2004).

To address these limitations, the present study proposes an explicit introduction of natural drainage in the water budget equation and considers its dependence on the water level through a linear relationship with a conductance model. The drainage function is adjusted with two parameters (slope and intercept) that should be carefully evaluated or calibrated together with the other model parameters. Particular attention should be paid to model parameter values when model results are used to define legal frameworks.

The introduction of aquifer drainage is not only justified for conceptual reasons, it also leads to markedly different optimum trajectories as highlighted by the comparative analysis conducted in the present study. Models that do not consider aquifer drainage in their water budget necessarily converge to a value of optimum net abstraction rate corresponding to groundwater recharge. Whatever the value of cost parameters, the net abstraction rate will necessarily converge to this value, which is regrettable, as in many cases, this stabilized value, that should be maintained in the long term, is of high interest for the water managers. In particular, this study shows that the omission of natural discharge may lead a water manager to allocate excessive pumping quotas.

As an alternative to the explicit introduction of aquifer drainage in the aquifer water budget, it may appear as attractive to consider a constant value for natural drainage that would be subtracted from the actual groundwater recharge to constitute an exploitable recharge. This could make sense so long as an appropriate value of exploitable recharge is used; however, this approach presents two limitations. First, as already mentioned, the net abstraction rate always tends to the exploitable recharge rate when natural drainage is not considered in the water budget, which means that in such a case, only the trajectory is optimized (dynamics of stock allocation), not the equilibrium value of the pumping rate. Second, the natural drainage is known to vary with the water level, which cannot be accounted when a constant value of natural drainage is chosen.

It is of interest to deal with simple and parsimonious models, but bathtub hydro-economic models are necessarily a crude conceptualization of reality. One of the main limitations is the lack of consideration of space. Any change in the water level is assumed to be instantaneous over the domain of interest. In the real world, pressure diffuses gradually from pumping wells so that the impacts of pumping may be contrasted in space and delayed in time, which should be mentioned when discussing results with water managers. Another limitation of the presented approach is the description of environmental damages with simple linear damage functions. Esteban and Dinar (2016) propose more complex ecosystem health functions which are closer to realistic conditions; however, more complex functions are necessarily more parameterized, which becomes an issue when parameter values are poorly constrained. From an economic perspective, this approach could be extended by considering other water demands from public water systems (Hansen 2012) and by inserting viability constraints over a food security constraint for the agricultural sector and/or a lower bound for environmental flows (Pereau et al. 2017). Stylized hydro-economical models are proven to be didactic and useful tools for generic discussions on groundwater management. When dealing with renewable aquifers, for which recharge is not negligible and damages to environmental flows deserve to be considered, these models should explicitly consider natural drainage in the aquifer water budget.