Using Tradable Water Permits in Irrigated Agriculture

Abstract

The present paper examines, both theoretically and empirically, the environmental and economic benefits of introducing a policy to optimally manage groundwater used in irrigated agriculture and the efficiency potential of allowing trading of water permits. We confirm the results appearing separately in the literature on optimal resource management and tradable permits, that both tradable water permits and non-tradable quotas provide the basic mechanism for sustainable water use and yield substantial economic benefits and that allowing trading of water permits improves efficiency. In order to derive the above results we develop a discrete time model to realistically describe farmer’s myopic behavior, while using a continuous time model to describe optimal management. We also incorporate into the analysis the economic effect of sea water intrusion in the aquifer and we estimate the cost of water overexploitation under myopic behavior. The empirical part of the paper is based on simulations using data from an agricultural region in Northern Greece. The main contribution of the paper is the introduction of heterogeneity in crops’ production and market characteristics. We show that the more diverse are the crops, in technology and market prices, and the stricter is the water constraint, the higher are the benefits from using a tradable water permit system.

1 Introduction

The rapidly increasing scarcity of fresh water resources stresses the need to allocate water resources efficiently, especially in irrigated agriculture which accounts for a large share of total water use. Existing mechanisms providing water for irrigation free of charge or at heavily subsidized rates are failing to manage the increasing demand and degraded (polluted and depleted) supply. Therefore, the introduction of systems to efficiently manage irrigation water is urgently needed. Although various water allocation schemes have already been used in irrigated agriculture, a number of which involve some sort of water pricing, none applies optimal water pricing. Despite numerous constraints associated with the application of optimal water pricing,¹ the expected efficiency gains from allocating water to the most productive user in the short-run and providing incentives for technology improvements in the long-run justify further research in the area.² Direct pricing and the use of tradable water permits are the main methods of allocating water, although a number of variants have been applied in practice.³

Tradable water permits are commonly considered as one of the most efficient market-based instruments for groundwater allocation. Water permit markets could yield the right price and lead to the efficient allocation with limited costs for overall planning and management. Assuming the existence of well-defined water rights, the institutions for distributing them and the appropriate monitoring infrastructure, a water permit market would ensure that water goes to the higher value use. Water permits are also consistent with the EU guidelines for water policy that promote the use of economic instruments providing water use efficiency and financial incentives. ⁴

The relevant literature has been developed along two separate lines. The main part of the literature examines the problem of optimal allocation of groundwater over time.⁵ The other stream of the literature, evaluates various water market approaches, based mainly on price instruments, to improve both water quality and quantity management.⁶ However, to the best of our knowledge there are no studies attempting to combine the above two approaches. The present paper attempts to do so both theoretically, developing two distinct modelling approaches to describe myopic farmers’ behavior and optimal management, and empirically, through simulations using actual data from an agricultural region in Northern Greece.

The results of the paper first confirm that in the absence of any water management system, individual farmers, acting myopically, deplete the available water resources very fast. Both tradable water permit and non-tradable water quota systems, if well-designed, provide the basic mechanism for sustainable water use, avoiding costs such as those associated with sea water intrusion, yielding thus, substantial economic benefits. A tradable water permit system always minimizes the cost of achieving the minimum water table target set to prevent salinization. The economic improvement over a non-tradable water quota system is positively related to the degree of differentiation in crops’ production and market characteristics. The more diverse are the crops sharing the same aquifer, the higher are the benefits from using a tradable water permit system. Furthermore, the efficiency improvement is positively related to the strictness of the water policy target.

The above results are well established separately in the literature on open access resources and tradable permits. The contribution of the current paper, apart from bringing these two parts of the literature together, lies first in the development of a realistic framework to describe farmers’ myopic behavior. We use a discrete time model that best describes myopic behavior since in this framework farmers ignore the dynamics of the aquifer, that is, the future impact of their actions on groundwater levels. On the other hand we model social planner’s choice in the standard way, using a continuous time model. Second, by explicitly modelling the effect of sea water intrusion into the aquifer on crops’ production function, we are able to estimate the cost of water overexploitation under myopic behavior. Third, and probably most important, we introduce heterogeneity by assuming two types of crop associated with different production functions and market prices. Although, under the simplifying assumptions made, our data yield a relatively small advantage of trading water permits, the sensitivity analysis shows that the efficiency gains of trading could be substantial when crops exhibit high degree of heterogeneity. This is because trading of permits allows scarce water resources to be used in irrigating the most efficient crop. Considering that in reality, at least in the Mediterranean region, many different crops producing heterogeneous quality products (for example conventional versus organic) share the same aquifer, the degree of heterogeneity is quite high and thus, the benefits from introducing a tradable water permit system are expected to be substantial.

Although most of the literature focuses on the use of water charges, there is some work highlighting the reasoning and the importance of using tradable water permit systems. For example, Ballestero et al. (2002) suggest that tradable permits may significantly improve water use efficiency, while they can also help to confront water scarcity and groundwater depletion. Hadjigeorgalis (2009) suggests that the use of water permits in smallholder agriculture, a typical situation in most agricultural areas around the world, is likely to reduce the risk on farmers’ income. Tradable permits are often considered as the most appropriate water policy measure to cope with problems such as the continuous decline of groundwater levels and/or the heavy discount on future benefits (Griffin 2006). Furthermore, as shown in the three cases presented in Marino and Kemper (1999), water markets can improve efficiency by providing flexibility in periods of water shortages. Lastly, the proper use of water permits may also enable water planners to better approximate the optimal water allocation, recovering thus in the long-run the potential gains from groundwater management (Provencher 1993).

2 The Model

We assume two groups of farmers, each cultivating an area of equal size to produce a homogenous product. We further assume that all pumped water is used in agricultural activities and particularly to irrigate the two high water demanding crops.

All farmers pump water from a single-cell unconfined aquifer, illustrated in Fig. 1, where the groundwater resource is determined by a single variable such as the volume of water remaining in the aquifer or the height of the aquifer (water table). Throughout this type of aquifer—which is often called “bathtub”— the water table and its fluctuation are both considered as uniform (Brozovic et al. 2006). ⁷ For simplicity we do not take into account the drawdown within the well, because it is considered to have a constant and small effect on the pumping level during each irrigation period. Within this framework, the pumping level $z_{w}$ in a well is defined by the following equation, $z_{w}=S_{L}-H_{t}$, where $S_{L}$ is the height of the ground surface level and $H_{t}$ is the height of water table at time $t$.

Fig. 1

Water level changes associated with groundwater pumping

On the production side, in order to focus on the water use problem, we assume that yield is a function of the amount of groundwater, $q$, with all other variables held constant (Burness and Brill 2001). Thus, we model the relationship between crop yield and water use as a simple crop-water production function which takes the following quadratic form,⁸ $^{,}$ ⁹

$$\begin{aligned} f\left( q_{r,t}\right) =a_{r}q_{r,t}-b_{r}q_{r,t}^{2}+g_{r}, \end{aligned}$$

(1)

where $q_{r,t}$ is the per hectare annual volume of water applied $(m^{3}/ha)$ for each type of crop $(r=1,2)$. $a>0$, $b>0$ and $g>0$ are the fitting coefficients specific to each type of crop, which depend on climate conditions, soil properties, agronomic management practices in the reference area and irrigation methods. These coefficients are assumed to be constant over time as long as soil salinity is below a threshold level, which is crop specific (depending on the salt tolerance of each crop). Beyond this threshold level the fitting coefficients may change to some extend due to the salinity effect on crop-productivity. Specifically, when the water table falls below a critical level ($H_{min}$), sea water intrusion is occurring (water salinization), decreasing the productivity of groundwater. Thus, we divide the time horizon into two periods: (a) before salinization ($H_{{ t}}>H_{min}$) and (b) after salinization ($H_{{t}}<H_{min}$) that differ with respect to the fitting coefficients in (1).

We assume that the marginal cost, $MC_{t}$, which equals the average cost, $AC_{t}$, of pumping water at time $t$, depends only on the pumping level, $z_{w}$. Since we do not consider drawdown within the well, the pumping level is the same as the water level of the aquifer, which implies zero marginal cost of the drawdown. For simplicity, we assume a linear average and marginal cost function independent of water quality (in our case the salinity level),¹⁰

$$\begin{aligned} AC_{t}=MC_{t}=c_{0}\left( S_{L}-H_{t}\right) , \end{aligned}$$

(2)

where $c_{0}$ is the marginal cost per $m^{3}$ of water pumped, per $m$ of lift.

Since we assume a uniform water table and a negligible drawdown within the wells, marginal cost of pumping water is the same for both groups of farmers. Therefore, water withdrawal differs between the two groups only due to differences in their crop-water production function and market prices. Thus, the annual net benefit per hectare, $NB$, for each group of farmers is,

$$\begin{aligned} NB_{r,t}=p_{r}f\left( q_{r,t}\right) -MC_{t}q_{r,t}-Cnw_{r}, \end{aligned}$$

(3)

where $p_{r}$ is the market price of each group’s crop and $Cnw_{r}$ is the cost of all other inputs, assumed constant and independent of the total water use.

We model the effect of farming on the water table following Gisser and Sanchez (1980) assuming that the rate of change in the height of the water table, $\dot{H}$, is a function of the total volume of water used in irrigated agriculture (total water pumped), as well as of certain hydrological conditions in the reference area, described by the following differential equation,

$$\begin{aligned} \dot{H}=\frac{1-\alpha }{AS}\left[ \frac{N}{1-\alpha }-Q_{t}\right] ,\;H(0)=H_{0},\;H(T)\geqslant H_{c}, \end{aligned}$$

(4)

where $N$ is the constant natural recharge of the aquifer, $\alpha$ is the constant return flow coefficient ($0<\alpha <1$), $Q_{t}$ is the total volume of water pumped and used at time $t$, $A$ is the uniform at all depths, surface area of the groundwater reservoir, $S$ is the storativity coefficient, $H_{c}$ is the height of the bottom of the aquifer and $H_{0}$ is the initial height of the water table.

3 The Benchmark Model of Myopic Farmers’ Behavior

The basic principles of groundwater aquifer exploitation in a typical common pool model have been discussed thoroughly in the literature.¹¹ One of the main results is that in the absence of institutional rules (such as water pricing, water quotas, etc.) individual farmers’ decisions concerning water pumping ignore the consequences of their actions to other water users and to the future status of the regional groundwater stock (Knapp et al. 2003). Therefore, individual farmers act myopically, pumping water at rates that maximize their annual income, ignoring the dynamics of the aquifer, that is, the future impact of their action on groundwater levels, and consequently on other farmers’ as well as their own future revenues, and taking the actions of the other farmers as given. Future revenues are affected by increasing pumping costs and possible changes in the crop-water production function due to salinization.

Alternatively, strategic behavior has been used to describe farmers’ behavior. In this contexts both noncooperative open-loop and feedback Nash equilibria have been considered in the literature (see for example Laukkanen and Koundouri (2006) and Roseta-Palma and Brasao (2004)). Laukkanen and Koundouri (2006) find substantial benefits from optimal water management even when farmers consider the effect of their actions on the groundwater stock, while Roseta-Palma and Brasao (2004) show that strategic considerations may take farmers even further away from the optimum compared to the myopic solution. Given that for our numerical estimations we use a region with many, small farmers sharing a relatively large aquifer, we choose to model their behavior as completely myopic. If the number of farmers is small, they could take into account the external effects of their actions and in the extreme, a monopolistic farmer could be completely farsighted.

Therefore, we assume farmers do not take into account changes in the pumping level $z_{w}$ and thus, they assess their marginal pumping costs at the beginning of each irrigation period, taking into account only the previous period’s water abstractions. Similarly, they ignore the possible effects of salinization on their production function. This type of behavior is best described using a discrete time approach.

In addition, we assume that farmers face high investment costs and significant agricultural market constraints that affect their ability to switch to other type of crops. That is, crop changes are not considered as an economically viable solution and farmers can only adjust their water application levels.

For simplicity, it is also assumed that the two groups of farmers irrigate a total land area of equal size, $M$ hectares each. Furthermore, the allocation of land among farmers within each group is not considered. Therefore, total annual water use is $Q_{t}=M\sum _{r=1}^{2}q_{r,t}$. Substituting this into Eq. (4), and expressing it as a discrete-time equation, yields,

$$\begin{aligned} H_{t+1}-H_{t}=\frac{1}{AS\left( 1-\alpha \right) }\left[ \frac{N}{\left( 1-\alpha \right) }-M\sum _{r=1}^{2}q_{r,t}\right] . \end{aligned}$$

(5)

Farmers act myopically, choosing annual water withdrawal so as to maximize their annual net benefit (given in (3)), without taking into account their decision’s long-term effects on the water table. Thus, each individual farmer in group $r$, chooses $q_{r,t}$ according to, $MNB_{r,t}=0\Rightarrow p_{r}f^{\prime }\left( q_{r,t}\right) =MC_{t}$. Substituting $f^{\prime }(q_{r,t})$ and $MC_{t}$ from Eqs. (1) and (2) respectively yields,

$$\begin{aligned} q_{r,t}=\frac{a_{r}}{2b_{r}}-\frac{1}{2b_{r}p_{r}}c_{0}\left( S_{L}-H_{t}\right) . \end{aligned}$$

(6)

Aggregation yields the annual total water use,

$$\begin{aligned} Q_{t}=M\left[ \Psi -\Omega c_{0}\left( S_{L}-H_{t}\right) \right] , \end{aligned}$$

(7)

where $\Psi =\sum _{r=1}^{2}\frac{a_{r}}{2b_{r}}$ and $\Omega =$ $\sum _{r=1}^{2}\frac{1}{2b_{r}p_{r}}$.

As shown in “Appendix 1”, simple substitutions allow us to formulate a first-order difference equation for the total groundwater use $Q_{t+\Delta \tau }=f(Q_{t})$, which is solved for the time path of the aggregate groundwater use,

$$\begin{aligned} Q_{t}^{m}=\widehat{Q}+\widetilde{Q}\varphi ^{t}. \end{aligned}$$

(8)

Combining Eqs. (8) and (7) and solving for $H_{t}$, yields the time-path of the water table level,

$$\begin{aligned} H_{t}^{m}=H_{0}-\frac{\widetilde{Q}}{Mc_{0}\Omega }+\frac{\widetilde{Q} \varphi ^{t}}{Mc_{0}\Omega }. \end{aligned}$$

(9)

where the superscript $m$ denotes equilibrium values in the case that farmers act myopically. Furthermore, we denote by $\widehat{Q}$ the groundwater use that would keep the height of the water table constant $\left( from (4), \widehat{Q}=Q_{\mid \dot{H}=0}=\frac{N}{1-\alpha }\right)$, and by $\widetilde{Q}$ the water abstraction above $\widehat{Q}$ at the initial period $\left( \widetilde{Q}=Q_{0}-\widehat{Q}\right)$, where $Q_{0}=M\left[ \Psi -\Omega c_{0}\left( S_{L}-H_{0}\right) \right]$. Finally, we define $\varphi =1-\left( 1-\alpha \right) \frac{c_{0}\Omega }{AS}M$ which is assumed positive, that is, $c_{0}\Omega <\frac{AS}{\left( 1-\alpha \right) M}$, and is less than one since $\alpha <1$. Given this assumption, the time paths of both $Q$ and $H$ are nonoscillatory and they are convergent.

Under myopic behavior, the time paths of the aggregate groundwater use and the water table depend on the initial water balance in the aquifer (water demand at the initial period $Q_{0}$ and hydrological parameters $S_{{L }}$, $N$, $\alpha$, $A$ and $S$), the marginal costs of pumping water ($c_{0}$), the crops’ market price ($p_{r}$) and diminishing marginal returns of pumping (included in $\Omega$). Aggregate groundwater use is equal to its level that would keep the height of the water table constant $\widehat{Q}$, plus the net water abstraction at the initial period $\widetilde{Q}$ multiplied by a continuously decreasing fraction, given the convergence condition. It is clear that $Q_{0}^{m}=Q_{0}$. The level of the water table equals its initial level $H_{0}$ minus the net water abstraction at the initial period $\widetilde{Q}$ multiplied by a continuously increasing fraction $\frac{1-\varphi ^{t}}{Mc_{0}\Omega }$. Again, it is clear that $H_{0}^{m}=H_{0}$.

4 Social Planner’s Policy Options

Contrary to the myopic farmer’s behavior, the social planner behaves in a farsighted manner, taking into account the intertemporal repercussions of water use. That is, his objective is to choose a groundwater resource allocation that maximizes the aggregate long-term net benefit maintaining a minimum stock of groundwater, $H_{min}$, at the end of the planning period, which is specified so as to take into account the sustainability of the resource and the risk of salinization. We assume that the social planner has full information regarding the hydrological and the agro-economic conditions along the reference area.¹² The model used in this section is based on previous studies examining the optimal intertemporal groundwater allocation.¹³

The social planner needs to determine the optimal aggregate yearly quota and then allocate the volume of water per hectare to farmers in each of the two groups ($r=1,2$). In order to achieve this objective, the social planner may implement either a tradable water permit or a non-transferable quota system. In what follows we examine and compare these two systems.

4.1 Tradable Water Permits System

Under a tradable water permits system, each farmer receives, at each time period, a number of water permits, $\overline{q}_{r,t}$, $r=1,2$, free of charge. After receiving her water entitlement, the farmer decides whether to buy or sell water permits and how many to trade, based on her annual water needs. Water entitlements are not transferable through time, that is, no banking or borrowing of water permits is allowed.¹⁴ Thus, the total water volume used by all irrigators during a typical year $t$ is, $\overline{Q}_{t}=M\sum _{r=1}^{2}\overline{q}_{r,t}=M \sum _{r=1}^{2}q_{r,t}$. Assuming a perfectly competitive market for water permits¹⁵ and zero transaction costs,¹⁶ efficiency requires that at the equilibrium the two groups of farmers’ marginal net benefits are equalized, that is, $MNB_{1,t}=MNB_{2,t}$. Since we assume a frictionless market, the initial allocation of permits does not affect the system’s efficiency.

The aggregate water constraint $\overline{Q}_{t}$ and the efficiency condition define a system of two equations which is solved for the water volume used by each group of farmers at $t$, as a function of the aggregate water quota,

$$\begin{aligned} q_{i,t}=s_{i}\frac{\overline{Q}_{t}}{M}+\theta _{i}, \end{aligned}$$

(10)

where, $i,j=1,2$, $s_{i}=\frac{p_{j}b_{j}}{p_{i}b_{i}+p_{j}b_{j}}$ is a weight ($s_{1}+s_{2}=1$) and $\theta _{i}=\frac{a_{i}p_{i}-a_{j}p_{j}}{ 2\left( p_{i}b_{i}+p_{j}b_{j}\right) }$ is a parameter with zero sum across groups ($\theta _{1}+\theta _{2}=0$), both of which depend on the two groups’ market and technology characteristics. The group of farmers with the most efficient crop-water production technology will use a higher share of the predetermined amount of groundwater at $t$, regardless of the initial allocation of permits. If both groups had the same technology and faced the same market price, they would share $\overline{Q}_{t}$ equally.

The social planner determines the optimal path of aggregate water use over the planning period, taking into account the optimal choice of farmers at each time period (given in Eq. 10). It does so by maximizing the sum of the flow of individual farmers’ net benefits¹⁷ subject to the transition equation given in Eq. (4). A fixed time horizon is used instead of the infinite horizon, since this concept better fits the planning process of a regulating agency (Xepapadeas 1996). Furthermore, the social planner has to guarantee that at $T$, a minimum level of the water table $H_{min}$ is preserved. Therefore, the social planner solves,

$$\begin{aligned}&\underset{\overline{Q}_{t}}{\max }\int \limits _{0}^{T}e^{-\delta t}M \sum \limits _{r=1}^{2}NB_{r,t}dt \\&\text {subject to,} \nonumber \\ \dot{H}&=\frac{1}{AS}\left[ N-\left( 1-\alpha \right) \overline{Q}_{t} \right] ,\;H(0)=H_{0},\;H(T)=H_{min}, \nonumber \end{aligned}$$

(11)

where $\delta$ denotes the discount rate.¹⁸ Note that, since $\sum \nolimits _{r=1}^{2}NB_{r,t}=\sum \nolimits _{r=1}^{2}\big [ p_{r}f\left( q_{r,t}\right)$ $-c_{0}(S_{L}-H_{t})q_{r,t}\big ]$, and using (10), we can express the policy maker’s objective as a function of $\overline{Q}_{t}$, that is, $\sum \nolimits _{r=1}^{2}NB_{r,t}\left( \overline{Q}_{t}\right)$.

The solution of the above optimal control problem, provided in “Appendix 2”, yields the optimal paths for the aggregate annual allowable use of groundwater resources and the water table’s level,

$$\begin{aligned} \overline{Q}_{t}^{p}&= \widehat{Q}-\frac{AS}{1-\alpha }\left( \rho _{1}^{p}X_{1}^{p}e^{\rho _{1}^{p}t}+\rho _{2}^{p}X_{2}^{p}e^{\rho _{2}^{p}t}\right) , \end{aligned}$$

(12)

$$\begin{aligned} H_{t}^{p}&= H_{0}-\frac{\widetilde{Q}}{Mc_{0}\Omega }+\frac{N}{\delta AS} +X_{1}^{p}e^{\rho _{1}^{p}t}+X_{2}^{p}e^{\rho _{2}^{p}t}, \end{aligned}$$

(13)

where the superscript $p$ denotes the equilibrium under the tradeable water permits system, $\widehat{Q}$ and $\widetilde{Q}$ have been defined above, $X_{i}^{p}=\frac{H_{0}e^{\rho _{j}^{p}T}-H_{min}-\left( e^{\rho _{j}^{p}T}-1\right) \left( H_{0}-\frac{\widetilde{Q}}{Mc_{0}\Omega }+\frac{N }{\delta AS}\right) }{e^{\rho _{j}^{p}T}-e^{\rho _{i}^{p}T}}$, $i,j=1,2$ and $\rho _{1,2}^{p}=\frac{\delta }{2}\pm \sqrt{\frac{\delta ^{2}}{4}+\frac{ \left( 1-\alpha \right) \delta M\Omega c_{0}}{AS}}$. The annual volume of water used by each farmer under a tradable water permit system can be derived by substituting $\overline{Q}_{t}^{p}$ from Eq. (12) into (10).

Under a tradable permit system the time paths of water table level (13) and aggregate annual allowable use of groundwater resources (30) depend on the hydrological parameters, the initial ($H_{0}$) and the minimum allowable ($H_{min}$) water table level, the discount rate ($\delta$), production and cost parameters and final markets’ prices.

4.2 Non-tradable Quota System

Under a non-tradeable water quota management system, annual water quotas are granted, as in the tradeable water permits system, free of charge to farmers in each time period. However, contrary to the previous system, farmers are not allowed to trade their water quotas. We assume that water quotas are allocated based on the historical use of irrigation water. Specifically, the maximum volume of water per hectare that each farmer in group $r$ is permitted to use during the year $t$ is,

$$\begin{aligned} \overline{q}_{r,t}=v_{t}q_{r,0} \end{aligned}$$

(14)

where, $q_{r,0}$ is the initial individual pumping water volume, given in Eq. (6), and $v_{t}$ is the rate of reduction in water use over time (as compared to the initial volumes). This rate is assumed to be the same for both groups of farmers. Assuming that all farmers use up their quota in each time period, the water volume used by each group of farmers at $t$ is, $q_{r,t}=\overline{q}_{r,t}=v_{t}q_{r,0}$, instead of Eq. (10) used in the case of tradeable water permits. The total water volume used by all irrigators during a typical year $t$ is $Q_{t}=M\sum _{r=1}^{2}q_{r,t}=\overline{Q}_{t}=M\sum _{r=1}^{2}v_{t}q_{r,0}$.

The policy maker solves again the optimal control problem defined in (11). As shown in “Appendix 3” the solution of this problem yields the following optimal paths for the aggregate annual allowable use of groundwater resources and the water table level,

$$\begin{aligned} \overline{Q}_{t}^{q}&= \widehat{Q}-\frac{AS}{\left( 1-\alpha \right) }\left( \rho _{1}^{q}X_{1}^{q}e^{\rho _{1}^{q}t}+\rho _{2}^{q}X_{2}^{q}e^{\rho _{2}^{q}t}\right) , \end{aligned}$$

(15)

$$\begin{aligned} H_{t}^{q}&= H_{0}-\Theta +\frac{N}{\delta AS}+X_{1}^{q}e^{\rho _{1}^{q}t}+X_{2}^{q}e^{\rho _{2}^{q}t}, \end{aligned}$$

(16)

where, the superscript $q$ denotes the equilibrium under the non-tradeable water quota system, $X_{i}^{q}=\frac{H_{0}e^{\rho _{j}^{q}T}-H_{min}-\left( e^{\rho _{j}^{q}T}-1\right) \left( \Theta ^{q}+\frac{N}{\delta AS}\right) }{ e^{\rho _{j}^{q}T}-e^{\rho _{i}^{q}T}}$, $i,j=1,2$, $\rho _{1,2}^{q}=\frac{ \delta }{2}\pm \sqrt{\frac{\delta ^{2}}{4}+\frac{\delta M\Omega ^{q}c_{0}\left( 1-\alpha \right) }{AS}}$, $\Theta =\frac{\Psi ^{q}}{c_{0}} -\left( S_{L}-H_{0}\right) -\frac{N}{Mc_{0}\Omega ^{q}\left( 1-\alpha \right) }$, $\Omega ^{q}=\frac{\left( q_{1,0}+q_{2,0}\right) ^{2}}{2\left( p_{1}b_{1}q_{1,0}^{2}+p_{2}b_{2}q_{2,0}^{2}\right) }$ and $\Psi ^{q}=\frac{ p_{1}a_{1}q_{1,0}+p_{2}a_{2}q_{2,0}}{q_{1,0}+q_{2,0}}$. Under a non-tradeable water quota system the annual volume of water used by each farmer is derived by substituting $\overline{Q}_{t}^{q}$ from (15), into Eq. (14), noting that $v_{t}=\frac{ \overline{Q}_{t}}{MQ_{0}}$.

The time paths of water table level and aggregate annual allowable use of groundwater under non-tradable quota system differ from a tradable permit system in the following: (a) the diminishing marginal returns of pumping ($\Omega$) have been replaced by a ratio ($\Omega ^{q}$) that estimates the average (per m$^{3}$) income effect of the quadratic term of production functions at the initial pumping volumes ($q_{i,0}$) and (b) the optimal levels of water application per crop ($\Psi$) have been replaced by a ratio that estimates the average (per m$^{3}$) income effect of the linear term of production functions at the initial pumping volumes ($q_{i,0}$).

5 Empirical Application

Although we have derived analytical solutions for the myopic farmers’ behavior and the two farsighted policy options, comparison among the three equilibria is not possible given the complexity of the solutions. For this reason we resort to simulations in order to compare the three equilibria. ¹⁹

5.1 Study Area and Data

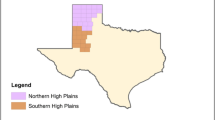
The data used in this Section have been collected from the Moudania agricultural region in Northern Greece, in which groundwater is the main source of irrigation water. The basic criteria for selecting this particular region are the following: (a) agriculture is one of the main activities in the area, (b) groundwater is intensively used for irrigation, (c) there is a deficit in the water balance of the river basin and (d) there are many, small farmers sharing a relatively large aquifer, supporting thus our assumption of myopic behavior. It should be also noted that the water used for local agricultural activities derives solely from pumping numerous wells (more than 800 wells in the study area), the majority of which are located in the southern part of the basin as shown in the last part of Fig. 2, implying that the majority of farmers will be affected by sea water intrusion.

Fig. 2

Map of the study area

Current agricultural practices in the region are extremely dependent on water resources, leading to a severe over-pumping of the aquifer. According to a local water management plan, the annual demand for water outweighs the annual supply by $5.5$ million m$^{3}$/year, causing a steady decline in the aquifer’s water level equal to 0.6 m/year (Latinopoulos 2003). Table 1 summarizes the main hydrological data for the study area.

Table 1 Hydrological data in the study area

Almost 50 % of the irrigated area is cultivated with olive trees. In the remaining area, the prevailing crops are: orchard trees (30 % of the total area), vegetables, cotton and corn. In order to feed the data into our theoretical model, we assume that there are only two crops, olive and orchard trees, each of which occupies half of the total irrigated area ($M=$ 1,300 ha).²⁰

Given the high percentage of permanent crops, that is, crops that are actually associated with high investment costs, the restructuring of the area’s cropping plans seems to be an economically inefficient solution. ²¹ For this reason, the potential increase of the marginal pumping cost of water is not going to alter the crop-mix of the area. Therefore, the water demand functions for both groups of farmers are equivalent to the crop-water production functions given in Eq. (1).

The coefficients $a_{r}$, $b_{r}$ and $g_{r}$ of these functions are estimated according to the local climate, soil and crop characteristics, as well as, to water application efficiency and irrigation scheduling. They are in fact the result of a regression analysis (linear OLS regression) on crop responses to the corresponding sequential reductions of water application. Crop responses on different water use levels are estimated using CROPWAT, a computer software provided by FAO (Smith 1992).²²

The effect of irrigation water salinity ($EC_{{w}}$) to crop production functions is calculated following Maas (1984). That is, we measure, at $t=0$ ($H_{{0}}=60$m), the actual mean value of $EC_{{w}}=1.7$ dS/m across the study area and predict a 50 % increase in its value if the average water table height falls below 50 m ($H_{{min}}=50$ m). We have chosen the critical level $H_{{min}}$, taking into account the existing wells’ depth and the hydrological data in the study area (Latinopoulos 2003). Below this level we expect significant intrusion of seawater into the aquifer that could affect productivity. Due to the high uncertainty of these prediction we use a 30 % uncertainty level. Furthermore, since olive trees are also considered as moderately tolerant crops (Maas 1984), increased salinization does not affect the production function of crop 1. Therefore, only the production function of crop 2 (orchards) will change if the height of the water table falls below $50m$, as shown in Table 2 that presents the two crops’ production functions and all other relevant agro-economic data.

Table 2 Agro-economic data in the study area

Substituting these data in Eq. (3) gives the net benefit functions for both groups of farmers. It is worth mentioning that olive trees is a less water demanding crop, with a relatively higher market price thus, yielding higher net benefits per hectare of cultivated land.

5.2 Results of the Optimization Model

A time horizon (planning period) of 40 years ($t\in [0,T],$ $T=40$) is chosen and used in both cases examined: the myopic farmer’s behavior and the social planner’s choice of management system.

5.2.1 Myopic Farmer’s Behavior

As already mentioned, the myopic farmer’s behavior model is based on the hypothesis that each farmer maximizes her net benefit given the pumping decisions of other farmers. Substituting the data from Tables 1 and 2, employing $f(q_{2,t})_{\mid (H_{t}>H_{\mathrm{min}})}$, into (8), the resulting time path for the aggregate water use, is,

• (a) $Q_{t}^{m}=11,620,647+5,922,472(0.9989)^{t}, t=1,...,16$ At $t=16$ the height of the water table falls below $50m$ and thus, thereafter we use $f(q_{2,t})_{\mid (H_{t}<H_{\mathrm{min}})}$ and aggregate water use is,

• (b) $Q_{t}^{m}=11,620,647+5,553,128(0.9987)^{\left( t-16\right) }, t=17,...,40$

Likewise, from Eq. (9), the time path for the water table’s height is,

• (a) $H_{t}^{m}=-513.81+573.81(0.9989)^{t}, t=1,...,16$

• (b) $H_{t}^{m}=-414.23+464.01(0.9987)^{\left( t-16\right) }, t=17,...,40$

Since the value of the base of the exponential term $\varphi =1-\left( 1-\alpha \right) \frac{c_{0}\Omega }{AS}M$ in both (8) and (9) is very close to unity, both with and without salinization, the time paths of $Q$ and $H$ are converging very slow. That is, there is only a very small decline in the long term use of groundwater resources, indicating the limited effect of water pumping costs to current and future decisions of farmers. The effect of salinization after $t=17$ has only a small effect on $Q_{t}$. The annual reduction of water withdrawals in the next twenty to forty years is estimated to be equal to 2.2 and 3.0 % of the current usage, respectively. Hence, given the current deficit water balance, a substantial drawdown of the water table (i.e. a decline of water stock) is expected. The average annual drop of the water table level is equal to 0.58m (the range of this measure varies from 0.55 to 0.61m/year), resulting in a total drawdown of 23.1m, at the end of the planning period ($t=40$).

5.2.2 Tradable Water Permit System

In order to implement the social planner’s model in the study area, we need to determine the appropriate discount rate and to set the environmental target of the water policy, that is, the terminal value of the water table level. A generally accepted social discount rate for this kind of problems usually varies from 2 to 4 % (Pearce and Ulph 1995), Spackman (2006) and thus, we choose a discount rate equal to $3\,\%$. Concerning the terminal value of the water table, a value equal to $50\, m$ was chosen ($H_{T}=H_{\min }=50$) to safeguard the minimum impact of the drawdown to the coastal areas, that is, to minimize seawater intrusion into coastal wells as discussed above. Substituting these values and the hydrologic and socioeconomic data of Tables 1 and 2, into Eqs. (13) and (12 ) yields the time-paths for the water table height and aggregate water use in the case of tradable water permits,

$$\begin{aligned} H_{t}^{p}&= -474.14+529.57e^{-0.00102t}+4.56e^{0.03102t},\;t=1,...,40,\\ \overline{Q}_{t}^{p}&= 11,620,647+5,285,723e^{-0.00102t}-1,382,069e^{0.03102t}, \;t=1,...,40. \end{aligned}$$

5.2.3 Non-Tradable Quota System

In a similar way, using Eqs. (16) and (15 ) yields the time-paths for the water table height and aggregate water use in the case of non-tradable water quotas,

$$\begin{aligned} H_{t}^{q}&= -500.56+555.94e^{-0.00098t}+4.63e^{0.03098t},\;t=1,...,40,\\ \overline{Q}_{t}^{q}&= 11,620,647+5,312,043e^{-0.00098t}-1,398,829e^{0.03098t}, \;t=1,...,40. \end{aligned}$$

Direct observation of the results under the two water management systems reveals that there are very small differences, which is due to the similarity of both $X$’s and $\rho$’s values. This is not surprising given the small differences between the two crops’ production functions and the use of the same terminal value of the water table level $H_{min}$ under both policies.

5.2.4 Comparison of the Three Models

Figure 3 illustrates aggregate water use in both models confirming the expectation that farmers’ myopic decisions lead to overexploitation of groundwater resources.²³ Myopic farmers use water extensively, with the difference in the water pumped relative to optimal management estimated at $2.02$ millions $m^{3}$ (a 13 % increase in water use) at $t=1$, reaching $5.38$ millions $m^{3}$ (a 43 % higher consumption), at $t=40$. This divergence is due to the fact that myopic farmers do not consider the scarcity value of groundwater resources and the salinization effect, while the social planner’s water management policy, is taking into consideration the constraint on the water table level $H_{min}$. Under myopic behavior, at $t=17$ there is a sudden drop in water use due to the effect of salinization, which results in reduced productivity. As noted above, we use a $30\,\%$ uncertainty level regarding the increase in the value of $EC_{{w}}$ after the water table level drops below $H_{min}$. However, varying the value of $EC_{{w}}$ between an increase of $20\,\%$ to 80 % after $t=17$, does not have any significant effects on $Q_{t}^{m}$ and can hardly be observed in Fig. 3.

Fig. 3

Time path of aggregate water use under myopic farmers’ behavior and the social planner’s management policy

While myopic farmers’ water use does not vary significantly over time, with the exception of the jump at $t=17$, it decreases significantly under both water management policies. This is because the scarcity rent embodied in the permit price increases over time. This results in the widening of the difference in the water use over time.

Figure 4 illustrates the height of the water table’s time path. The myopic farmer’s model results in an almost linear negatively slopped function, leading to a water table height equal to 36.9 m at $t=40$, far below $H_{min}$. On the other hand, social planner’s time-path for the stock availability is an exponential function leading, through a smooth transition path, to the pre-selected water table level $H_{min}=50$.

Fig. 4

Water table height’s time path under farmer’s myopic behaviour and the social planner’s optimum

Figure 5 illustrates the aggregate net benefits results under the three models. The application of the social planer’s restrictions in water withdrawal over time results in significant decreases in farmers’ income relative to the myopic behavior for the time period before salinization affects production of crop 2. However, when the water table falls below the critical value of $H_{{min}}=50\,\hbox {m}$, at $t=17$, myopically acting farmers experience significant losses due to the salinity effect. For the time period $t=\left\{ 1,\ldots ,16\right\}$, the total annual cost of the tradable permit approach (forgone net benefits relative to the myopic farmer’s model) ranges from €81,000 ($t=1$), up to €129,000 ($t=16$). However, after salinization, $t>16$, the foregone net benefits of myopic farmers relative to the case that water is managed range from €143,000 ($t=40$) up to €$510,000$ ($t=17$). Thus, the total economic benefits from implementing a tradable permit system are equal to €$10,459,490$ which is equivalent to the $8.4\,\%$ of the aggregate annual net benefits in the myopic farmer’s model.

Fig. 5

Aggregate net benefits’ time path in all three models

These results correspond to the prediction that the value of $EC_{w}$ increases by 50 % over its initial value for $t>16$. As shown in Fig. 5, the tradable water permit system yields higher aggregate benefits for the whole range of $30\,\%$ uncertainty level we consider. In particular the total economic benefits of tradable water permit system are €$3,852,888$ (or 3.1 % of the myopic aggregate annual net benefits) if the increase of $EC_{w}$ is 20 % and €$15,702,824$ (or 12.7 %) if the increase is 80 %.

Figure 5 illustrates also the economic efficiency of tradable emission permits. Aggregate benefits are higher in each and every period when trade of water permits is allowed. Furthermore, the net benefits’ spread between the two water management policies increases over time. However, the additional benefits derived are small (0.4 % of the aggregate net benefits).²⁴ This result is not surprising, considering the similarity of the two groups of farmers’ marginal benefits, in the area examined.

The benefits’ spread between the two policies increases as the two groups of farmers become more diverse or when a stricter water constraint is imposed. To illustrate these predictions, we perform sensitivity analysis with respect to the most valued crop’s price, production technology and the terminal time period. We also simulate the model under various scenaria of simultaneously varying these model’s parameters. The sensitivity analysis’ results presented in Table 3 illustrate that the implementation of a tradable water permit policy could substantially increase aggregate net benefits (the difference ranges from $1.06\,\%$ up to $28.42\,\%$) in cases of diverse, in terms of production and market characteristics, crops.

Table 3 Sensitivity analysis of benefits’ spread (expressed in percentages) with respect to model’s parameters

Figure 6 illustrates the difference between total net benefits resulting from allowing trade of water permits in three of the above nine scenarios. The larger difference in aggregate benefits is derived under Scenario 8 that involves a spread in prices and the crop water production functions as well as a stricter constraint.

Fig. 6

Graphical representation of aggregate net benefits under three characteristic scenarios

It should be noted that in the main part of the paper we made the assumption of just two homogeneous crops in order to simplify the analysis. However, as noted in the description of the area, the two permanent crops are not the only ones cultivated in the Region of Moudania, covering 80 % of the irrigated area. Furthermore, we do not take into consideration heterogeneity within the two groups, steaming for example from conventional versus organic products. In reality the degree of differentiation, both in production and market characteristics, is much larger than the simple two-crop differentiation with similar water-crop production functions presented in the main part of the paper. However, the assumptions of the model allowed us to present quite simple analytical results of a fairly complicated problem and to explicitly discuss the dependence of trading’s’ net benefits on the level of differentiation.

We extent the sensitivity analysis to time horizon $T$ and discount rate $\delta$, following Mori and Perrings (2012). Table 4 presents the effect of varying $T$ and $\delta$ on the additional net benefits from implementing a tradable permit. It is clear that the economic results are not very sensitive to the initial assumptions of discount rate and time horizon.

Table 4 Sensitivity analysis of benefits’ spread (expressed in percentages) with respect to the interest rate and time horizon

Given that we have assumed a perfectly competitive market for water permits, the time path for the price of water permits, $P_{t}^{w}$, is given by $P_{t}^{w}=MNB_{1,t}=MNB_{2,t}$. We can calculate the price of water permits by calculating the marginal net benefits, using the optimum individual water use ($q_{r,t}$). Thus, the time path for the market price of water permits is,

$$\begin{aligned} P_{t}^{w}=0.0156+0.007e^{-0.00102t}+0.055e^{0.03102t}. \end{aligned}$$

Figure 7 illustrates the time path of the tradable water permits price which increases in a slightly exponential way through time. The price at the first period is equal to $0.079$ €$/\hbox {m}^{3}$, while at the final period ($t=40$) is equal to $0.210$ €$/\hbox {m}^{3}$. Given that the market is perfectly competitive, this price increase is due to the increasing over time scarcity rent of the resource.

Fig. 7

Water permits price’s time path

6 Conclusions

The paper examines the problem of groundwater allocation over time in irrigated agriculture using innovative models and emphasizing on the heterogeneity of the crop production functions and prices. First, we examine farmers’ myopic behavior concerning water abstractions within a discrete time model, capturing the time lag in farmers’ decision making. Second, using an optimal control approach, we consider two types of management systems to optimally allocate the water resource over time and across different farmers’ groups: a non-tradable water quota system and a tradable water permit system.

In the absence of any water management system, farmers’ act myopically depleting groundwater resources very fast, especially when pumping costs are insignificant as is the case in many agricultural areas. The speed of depletion depends on the current water balance of the aquifer, as well as, on its initial stock (water table) level. Implementing any of the two management systems yields a smooth adjustment to a water table level that avoids sea water intrusion in the water basin. Both water management systems achieve the water target, avoiding considerable economic costs that would result from overexploitation of the resource under myopic behavior. However, a tradable water permit system minimizes these costs. The difference between the two management systems is larger the most diverse are the agro-economic characteristics among farmers’ groups and the stricter is the policy target. Since, in most cases, a water basin supports many different crops, the benefits from implementing a tradable water permit system could be substantial. The results of the paper support the urgent call for implementing optimal water management in irrigated agriculture and provide a clear policy recommendation favoring the use of tradable water permit systems, especially in water basins in which diverse crops are cultivated.

A number of extensions could be considered, including the explicit modelling of different quality products within the same type of crop (organic versus conventional), allowing for banking of water permits and stochasticity. Although in the present paper we have assumed that the recharge rate remains constant over time, in reality there is considerable stochasticity, which will influence welfare results. One expects that water permits could provide additional benefits in this case because they internalize the relevant buffer value. Allowing for stochasticity, changes of prices and interest rates over time are some of the extensions of the present paper we are currently consider.

Appendices

Appendix 1: Time Path Under Myopic Behavior

Using the time-adjusted Eq. (6), we derive water use for time period $t+1$, $q_{r,t+1}$, by substituting the corresponding height of the water table, $H_{t+1}$, from Eq. (5). Then we derive the change in water use between the two successive time periods,

$$\begin{aligned} q_{r,t+1}-q_{r,t}=\frac{c_{0}}{2ASb_{r}p_{r}}\left[ N-\left( 1-\alpha \right) M\sum _{r=1}^{2}q_{r,t}\right] . \end{aligned}$$

(17)

Similarly we obtain the change in aggregate water use over the two periods,

$$\begin{aligned} Q_{t+1}-Q_{t}=\frac{c_{0}\Omega }{AS}\left[ N-\left( 1-\alpha \right) M\sum _{r=1}^{2}q_{r,t}\right] . \end{aligned}$$

(18)

The above two equations express the time path for individual and aggregate groundwater use in irrigated agriculture as discrete-time functions.

Utilizing the initial condition $H(0)=H_{0}$, Eq. (6) and (7) yields the initial individual and total pumping water volumes, $q_{r,0}$ and $Q_{0}$. The initial conditions allow us to formulate a first-order difference equation for the total groundwater use $Q_{t+\Delta \tau }=f(Q_{t})$.

In order to solve a first order difference equation for the total groundwater use it is necessary to find a formula that satisfies $Q_{t+\Delta \tau }=f(Q_{t})$.

Equation (9) can be used as the base for formulating the first order difference equation, which can be written as,

$$\begin{aligned} Q_{t+1}+1=\Delta Q_{t}+K\ , \end{aligned}$$

(19)

where by (18), $\Delta =1-\left( 1-a\right) \frac{c_{0}\Omega }{AS}M$ and $K=\frac{c_{0}\Omega }{AS}N$.

The first step in solving Eq. (19) is to find a particular solution, denoted as $Q_{s}$, which is actually any solution to the above first order difference equation. A constant over time variable is applied in Eq. (19) (Pemberton and Rau 2001), yielding the following particular solution,

$$\begin{aligned} Q_{s}=\frac{N}{1-\alpha }. \end{aligned}$$

The associated homogenous equation of (19) is $Z_{t+1}=\Delta Z_{t}$ ; hence the complementary solution is $\Phi \Delta ^{t}$, where $\Phi$ is an arbitrary constant. Therefore, the general solution to the difference equation is,

$$\begin{aligned} Q_{t}=\frac{N}{1-\alpha }+\Phi \Delta ^{t}. \end{aligned}$$

(20)

The value of the constant $\Phi$ is derived using the boundary condition $Q_{0}$ and thus, the final solution concerning the time path of the aggregate groundwater use is,

$$\begin{aligned} Q_{t}=\frac{N}{1-\alpha }+\left( Q_{0}-\frac{N}{1-\alpha }\right) \left[ 1-\left( 1-\alpha \right) \frac{c_{0}\Omega }{AS}M\right] ^{t}. \end{aligned}$$

(21)

Appendix 2: Time Path Under Tradable Water Permits

The current value Hamiltonian for the optimal control problem presented in (11) is:

$$\begin{aligned} \mathcal {H}=M\sum \limits _{r=1}^{2}NB_{r,t}\left( \overline{Q}_{t}\right) + \frac{\mu }{AS}\left[ N-\left( 1-\alpha \right) \overline{Q}_{t}\right] \end{aligned}$$

(22)

where $\mu$ is the costate variable reflecting the shadow value of groundwater (i.e. the change in the marginal use cost of groundwater as the height of the water table changes over time). This parameter differentiates the social from the private optimal solution. Given the current value Hamiltonian and assuming an interior solution, the necessary conditions for optimization (optimality condition and adjoint equation respectively) are,

$$\begin{aligned} \frac{\partial \mathcal {H}}{\partial \overline{Q}_{t}}&= 0, \end{aligned}$$

(23)

$$\begin{aligned} \dot{\mu }&= \delta \mu -\frac{\partial \mathcal {H}}{\partial H_{t}}=\delta \mu -c_{0}\overline{Q}_{t}. \end{aligned}$$

(24)

Condition (23) requires that the total marginal net benefits from water use are equal to the shadow value of the actual volume of water pumped from the aquifer. This condition is solved for $\mu$ as function of $\overline{Q}_{t}$ and $H_{t}$.²⁵ Solving the state equation for $\overline{ Q}_{t}$ as a function of $\dot{H}$ and substituting, yields the shadow value of groundwater,

$$\begin{aligned} \mu =\frac{AS}{\left( 1-\alpha \right) }\left[ \frac{\Psi }{\Omega }-\frac{ N-AS\dot{H}}{M\Omega \left( 1-\alpha \right) }-c_{0}\left( S_{L}-H_{t}\right) \right] . \end{aligned}$$

(25)

Differentiating Eq. (25) with respect to time and equating to the right hand side of (24) yields, $\frac{AS}{\left( 1-\alpha \right) }\left[ \frac{AS\ddot{H}_{t}}{M\Omega \left( 1-\alpha \right) }+c_{0} \dot{H}_{t}\right] =\delta \mu -c_{0}\overline{Q}_{t}$. Substituting $\mu$ from (25) and $\overline{Q}_{t}\$from the state equation, and rearranging terms gives the following second order differential equation,

$$\begin{aligned} \ddot{H}_{t}-\delta \dot{H}_{t}-\frac{M\Omega \left( 1-\alpha \right) \delta c_{0}}{AS}H_{t}+\frac{M\Omega \left( 1-\alpha \right) }{AS}\delta c_{0}\left( \Theta +\frac{N}{\delta AS}\right) =0. \end{aligned}$$

(26)

The general solution of the above differential equation can be estimated by reducing it to a first order equation after factorization,

$$\begin{aligned} H_{t}^{p}=H_{0}-\frac{\widetilde{Q}}{Mc_{0}\Omega }+\frac{N}{\delta AS} +X_{1}e^{\rho _{1}t}+X_{2}e^{\rho _{2}t}, \end{aligned}$$

(27)

where, $X_{1}$ and $X_{2}$ are arbitrary constants, while $\rho _{1}$, $\rho _{2}$ are the roots of the polynomial function, after the factorization of differential operators, defined as,

$$\begin{aligned} \rho _{1,2}^{p}=\frac{\delta }{2}\pm \sqrt{\frac{\delta ^{2}}{4}+\frac{ M\Omega \left( 1-\alpha \right) \delta c_{0}}{AS}} \end{aligned}$$

(28)

where the superscript $p$ denotes the equilibrium under the tradeable water permits system. Applying the boundary conditions $H(0)=H_{0}$ and $H(T)=H_{min}$ to (13), yields $X_{i}$, $i,j=1,2$,

$$\begin{aligned} X_{i}^{p}=\frac{H_{0}e^{\rho _{j}^{p}T}-H_{min}-\left( e^{\rho _{j}^{p}T}-1\right) \left( \Theta +\frac{N}{\delta AS}\right) }{e^{\rho _{j}^{p}T}-e^{\rho _{i}^{p}T}} \end{aligned}$$

(29)

Then, the aggregate annual allowable use of groundwater resources is,

$$\begin{aligned} \overline{Q}_{t}^{p}=\widehat{Q}-\frac{AS}{\left( 1-\alpha \right) }\left( \rho _{1}^{p}X_{1}^{p}e^{\rho _{1}^{p}t}+\rho _{2}^{p}X_{2}^{p}e^{\rho _{2}^{p}t}\right) . \end{aligned}$$

(30)

Appendix 3: Time Path Under Non-Tradable Water Quotas

The policy maker solves again the optimal control problem defined in (11). The necessary conditions for the Hamiltonian’s maximization (22) are given by Eqs. (23) and (24). Noting that, $v_{t}=\frac{\overline{Q}_{t}}{MQ_{0}}$, and using (14), we have $\frac{\partial q_{r,t}}{\partial \overline{Q}_{t}}=\frac{ q_{i0}}{MQ_{0}}$. Solving the optimality condition $\frac{\partial \mathcal {H }}{\partial \overline{Q}_{t}}=0$, yields the shadow value of groundwater $\mu$ under the quota management system. Following the same steps as in the previous Section, we derive the first order equation,

$$\begin{aligned} H_{t}^{q}=H_{0}-\Theta +\frac{N}{\delta AS}+X_{1}e^{\rho _{1}t}+X_{2}e^{\rho _{2}t}, \end{aligned}$$

(31)

where, $\Theta =\frac{N\Omega ^{q}}{M\left( 1-\alpha \right) c_{0}}+S_{L}+- \frac{\Psi ^{q}}{c_{0}}$, $\Omega ^{q}=2\frac{ p_{1}b_{1}q_{1,0}^{2}+p_{2}b_{2}q_{2,0}^{2}}{\left( q_{1,0}+q_{2,0}\right) ^{2}}$ and $\Psi ^{q}=\frac{p_{1}a_{1}q_{1,0}+p_{2}a_{2}q_{2,0}}{ q_{1,0}+q_{2,0}}$. The roots of this function are,

$$\begin{aligned} \rho _{1,2}^{q}=\frac{\delta }{2}\pm \sqrt{\frac{\delta ^{2}}{4}+\frac{ M\left( 1-\alpha \right) \delta c_{0}}{AS\Omega ^{q}}}, \end{aligned}$$

(32)

where the superscript $q$ denotes the equilibrium under the non-tradeable water quota system. Applying the same as before boundary conditions $H(0)=H_{0}$ and $H(T)=H_{min}$ to (31), yields $X_{i}^{q}$, $i,j=1,2$,

$$\begin{aligned} X_{i}^{q}=\frac{H_{0}e^{\rho _{j}^{q}T}-H_{min}-\left( e^{\rho _{j}^{q}T}-1\right) \left( \Theta ^{q}+\frac{N}{\delta AS}\right) }{e^{\rho _{j}^{q}T}-e^{\rho _{i}^{q}T}} \end{aligned}$$

(33)

Then, the aggregate annual allowable use of groundwater resources is,

$$\begin{aligned} \overline{Q}_{t}^{q}=\widehat{Q}-\frac{AS}{\left( 1-\alpha \right) } \left( \rho _{1}^{q}X_{1}^{q}e^{\rho _{1}^{q}t}+\rho _{2}^{q}X_{2}^{q}e^{\rho _{2}^{q}t}\right) . \end{aligned}$$

(34)