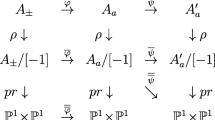Improved elliptic curve hashing and point representation

Abstract

For a large class of functions $f:\mathbb {F}_q\rightarrow E(\mathbb {F}_q)$ to the group of points of an elliptic curve $E/\mathbb {F}_q$ (typically obtained from certain algebraic correspondences between E and $\mathbb {P}^1$), Farashahi et al. (Math Comput 82(281):491–512, 2013) established that the map $(u,v)\mapsto f(u)+f(v)$ is regular, in the sense that for a uniformly random choice of $(u,v)\in \mathbb {F}_q^2$, the elliptic curve point $f(u)+f(v)$ is close to uniformly distributed in $E(\mathbb {F}_q)$. This result has several applications in cryptography, mainly to the construction of elliptic curve-valued hash functions and to the “Elligator Squared” technique by Tibouchi (in: Christin and Safavi-Naini (eds) Financial cryptography. LNCS, vol 8437, pp 139–156. Springer, Heidelberg, 2014) for representating uniform points on elliptic curves as close to uniform bitstrings. In this paper, we improve upon Farashahi et al.’s character sum estimates in two ways: we show that regularity can also be obtained for a function of the form $(u,v)\mapsto f(u)+g(v)$ where g has a much smaller domain than $\mathbb {F}_q$, and we prove that the functions f considered by Farashahi et al. also satisfy requisite bounds when restricted to large intervals inside $\mathbb {F}_q$. These improved estimates can be used to obtain more efficient hash function constructions, as well as much shorter “Elligator Squared” bitstring representations.

1 Introduction

1.1 Mapping to elliptic curves

Many elliptic curve cryptosystems involve representing a base field element $u\in \mathbb {F}_q$ as a rational point $f(u)\in E(\mathbb {F}_q)$ of the elliptic curve $E/\mathbb {F}_q$ where the computations are carried out. Moreover, it is often desirable for the corresponding “encoding function” $f:\mathbb {F}_q\rightarrow E(\mathbb {F}_q)$ to be efficiently computable in constant time (i.e. independently of the value of u) rather than in an iterative, probabilistic manner.

A number of methods [2, 4, 8, 10, 13, 15, 18, 20, 27, 29, 32] have been proposed to construct such functions f, starting with the technique used in Boneh and Franklin’s identity-base encryption scheme [3], which only applies to a specific family of supersingular curves, and especially with Shallue and van de Woestijne’s paper [28], whose construction applies to essentially all isomorphism classes of elliptic curves, but as observed by Tibouchi [31], they all admit a geometric description along the following lines.

For some of them (notably Icart’s function [18] and its variants as studied by Kammerer et al. and Couveignes and Kammerer [8, 20]), there exists a diagram:

(1)

where $h:C\rightarrow E$ is a covering of E over $\mathbb {F}_q$, and $\pi :C\rightarrow \mathbb {P}^1$ induces a bijection on points (it is an exceptional cover of $\mathbb {P}^1$ in the terminology of Fried [16]). The map $f:\mathbb {F}_q\subset \mathbb {P}^1(\mathbb {F}_q)\rightarrow E(\mathbb {F}_q)$ can then be defined on points as $h\circ \pi ^{-1}$. Recently, Couveignes and Lercier [9] proposed a more systematic study of a subset of such constructions, which they call “parametrizations”, where the morphism $\pi$ is required to be multiradical.

The other constructions (including Skałba’s [29], Shallue and van de Woestijne’s [28] and their variants) arise from several coverings:

(2)

where the $\pi _i$’s are no longer bijections on points, but simply satisfy that $\pi _1\big (C_1(\mathbb {F}_q)\big )\cup \cdots \cup \pi _\ell \big (C_\ell (\mathbb {F}_q)\big ) = \mathbb {P}^1(\mathbb {F}_q)$. The map $f:\mathbb {F}_q\subset \mathbb {P}^1(\mathbb {F}_q)\rightarrow E(\mathbb {F}_q)$ can then be defined on points as $f(u) = h_i\big (\pi _i^{-1}(u)\big )$ for the first index i such that $u\in \pi _i\big (C_i(\mathbb {F}_q)\big )$. For all existing constructions of this type, the function fields of the coverings $\pi _i$ are linearly disjoint quadratic extensions of $\mathbb {F}_q(u)$, so that membership in the images $\pi _i\big (C_i(\mathbb {F}_q)\big )$ (and their various Boolean combinations) can be determined efficiently by evaluating quadratic characters.

Constructions of the same form have also been considered for obtaining maps $f:\mathbb {F}_q\rightarrow X(\mathbb {F}_q)$ to points on curves $X/\mathbb {F}_q$ of higher genus (especially hyperelliptic curves of genus 2, since they are the most cryptographically significant).

1.2 Hashing to elliptic curves

The first application of the above constructions to cryptography was hashing to curve points. It is common, especially in pairing-based cryptography, that a certain value (a message, an identity, etc.) has to be hashed to an element of the group of points of an elliptic curve (or to the Jacobian of a curve of higher genus), in such a way that the hash function can be reasonably modeled as a random oracle.

One approach that has been considered is to take a function $f:\mathbb {F}_q\rightarrow E(\mathbb {F}_q)$ as above, a hash function $\mathfrak {h}:\{0,1\}^*\rightarrow \mathbb {F}_q$, and combine the two together by hashing a message m as $\mathfrak {H}(m) = f\big (\mathfrak {h}(m)\big )$. This is actually sufficient for certain cryptographic schemes, in the sense that they can be proved secure in the random oracle model for $\mathfrak {h}$, but this is not the case in general. Indeed, $\mathfrak {H}$ is typically easy to distinguish from a random oracle to $E(\mathbb {F}_q)$, because the image of f consists of only a fraction of all points on the curve and image membership can be tested for efficiently: as a result, one can distinguish between $\mathfrak {H}$ and an actual random oracle to $E(\mathbb {F}_q)$ by asking for the hashes of a few messages, and checking whether none of them falls outside $f(\mathbb {F}_q)$.

Formal conditions under which a hash function construction can securely replace a random oracle in essentially any cryptographic protocol are given by Maurer et al.’s indifferentiability framework [23], and Brier et al. [4] have applied them to the elliptic curve setting, establishing that a hash function construction $\mathfrak {H}(m) = F\big (\mathfrak {h}(m)\big )$ is indifferentiable from a random oracle in $E(\mathbb {F}_q)$ when $F : \mathbb {F}_q\rightarrow E(\mathbb {F}_q)$ is an admissible encoding in the following sense.

A function $F : \mathbb {F}_q\rightarrow E(\mathbb {F}_q)$ is called $\alpha$-admissible if F is: (1) efficiently computable; (2) efficiently samplable (one can compute a close to uniform preimage of any point efficiently); and (3) $\alpha$-regular (for s uniformly distributed in $\mathbb {F}_q$, the statistical distance of the distribution of F(s) and the uniform distribution on $E(\mathbb {F}_q)$ is less than $\alpha$: see Definition 3). They call such a function F simply admissible when $\alpha$ is a negligible function of q (namely, $\alpha =o\big ((\log q)^{-k}\big )$ for any positive k), and prove the admissibility of:

$$\begin{aligned} F_1:\mathbb {F}_q\times \mathbb {Z}/N\mathbb {Z}\rightarrow & {} E(\mathbb {F}_q) \nonumber \\ (u,v)\mapsto & {} f(u) + vG \end{aligned}$$

(3)

for any curve such that $E(\mathbb {F}_q)$ is a cyclic group of order N generated by G and f is a function $f:\mathbb {F}_q\rightarrow E(\mathbb {F}_q)$ verifying mild conditions (all maps from the previous paragraph qualify, in particular). Due to the scalar multiplication, that construction is rather slow, however. They also prove the admissibility of the following much more efficient construction:

$$\begin{aligned} F_2:\mathbb {F}_q\times \mathbb {F}_q\rightarrow & {} E(\mathbb {F}_q) \nonumber \\ (u,v)\mapsto & {} f(u) + f(v) \end{aligned}$$

(4)

but only when f is Icart’s function, and the proof involves rather painful geometric arguments.

A much simpler approach was later proposed by Farashahi et al. [12], who prove that the function $F_2$ of (4) is regular whenever f satisfies certain bounds expressed in terms of character sums on $E(\mathbb {F}_q)$, and they show how such bounds can be obtained for any map f of the form (1) or (2) as a consequence of a theorem of Weil (essentially, the Riemann hypothesis for function fields). This yields a relatively efficient hash function construction to elliptic curves from any function f of one of those forms, and also generalizes to hash function constructions to Jacobians of curves of higher genus.

1.3 Representing elliptic curve points as uniform bitstrings

For certain applications related to anonymity and privacy, elliptic curve cryptography presents a weakness: points on a given elliptic curve, when represented in a usual way (even in compressed form) are easy to distinguish from random bit strings. For example, the usual compressed bit string representation of an elliptic curve point is essentially the x-coordinate of the point, and only about half of all possible x-coordinates correspond to valid points (the other half being x-coordinates of points of the quadratic twist). This makes it relatively easy for an attacker to distinguish ECC traffic (the transcripts of multiple ECDH key exchanges, say) from random traffic, and then proceed to intercept, block or otherwise tamper with such traffic.

An efficient approach to solve this problem was proposed by Bernstein et al. [2]. Their idea is to leverage an efficiently computable, efficiently invertible algebraic function $\iota$ that maps the integer interval $S=\{0,\dots ,(p-1)/2\}$ injectively to $E(\mathbb {F}_p)$. Since $\iota$ is injective, a uniformly random point P in $\iota (S)\subset E(\mathbb {F}_p)$ has a uniformly random preimage $\iota ^{-1}(P)$ in S, so that P can be represented as the binary expansion of the integer $\iota ^{-1}(P)$ if it exists. If p is close to a power of 2, a uniform point in $\iota (S)$ will have a close to uniform bit string representation. This approach is simple and efficient, but limited to special elliptic curves such as Edwards and Montgomery curves [2, 17] for which $\iota$ exists.

A variant of that approach, “Elligator Squared”, was recently suggested by Tibouchi [30], eliminating most of the limitations of Bernstein et al.’s method. The idea is to represent $P\in E(\mathbb {F}_q)$ by a randomly sampled preimage under an admissible encoding $F_2$ of the form (4). By Farashahi et al.’s results, such encodings can be obtained for all known point encodings, and in particular for all elliptic curves. Moreover, the representation of a uniformly random point is close to uniformly distributed in $(\mathbb {F}_q)^2$ by the regularity of $F_2$. Since $F_2$ is essentially surjective, no rejection sampling is necessary contrary to Bernstein et al.’s method, yielding record performance [1]. Its main drawback, however, is that points are represented as elements of $(\mathbb {F}_q)^2$ (or rather, as bitstring representations thereof), which take up at least twice as much space as Bernstein et al.’s representations.

1.4 Our contributions

In this paper, we revisit Farashahi et al.’s character sum estimates with the goal of improving the efficiency of hash function constructions and Tibouchi’s “Elligator Squared” method for representing points on elliptic curves as uniform bitstrings.

Our improvements are twofold. Firstly, in Sect. 2, we establish that for any function f subject to the same conditions as introduced by Farashahi et al. (and verified by constructions of the form (1), (2)), the following map is regular:

$$\begin{aligned} F_3:\mathbb {F}_q\times V\rightarrow & {} E(\mathbb {F}_q)\nonumber \\ (u,v)\mapsto & {} f(u) + g(v) \end{aligned}$$

(5)

for any map $g:V\rightarrow E(\mathbb {F}_q)$ from a set of cardinality $\#V= \Omega (q^\varepsilon )$ and with small collision probability (for example, an injective map, or one with preimages of cardinality bounded by some small integer). This implies that the following variants of (3), (4) are also regular:

$$\begin{aligned} \begin{aligned} F_1':\mathbb {F}_q\times [0,q^\varepsilon )&\rightarrow E(\mathbb {F}_q)&F_2':\mathbb {F}_q\times V_\varepsilon&\rightarrow E(\mathbb {F}_q) \\ (u,v)&\mapsto f(u) + vG \qquad&(u,v)&\mapsto f(u) + f(v) \end{aligned} \end{aligned}$$

(6)

where $G\in E(\mathbb {F}_q)$ is any point of order $\ge q^\varepsilon$ and $V_\varepsilon \subset \mathbb {F}_q$ is any subset of cardinality $\Omega (q^\varepsilon )$. This result is technically very simple, but has valuable consequences. It is especially interesting for point representation, as it provides a way to obtain Elligator Squared-like representations of length $(1+\varepsilon )\log _2 q$ instead of $2\log _2 q$ (by sampling preimages under $F_2'$ instead of $F_2$), which makes the Elligator Squared construction almost as space efficient as Bernstein et al.’s. For hash function constructions, it says that indifferentiable hashing can be obtained from shorter random oracles, and also settles the long-standing open question of whether admissibility can be obtained for all elliptic curves at a cost of less than two base field exponentiations: indeed, for $\varepsilon$ small enough, the scalar multiplication in $F_1'$ becomes cheaper than a base field exponentiation!

Secondly, in Sect. 3, we show that the techniques introduced by Farashahi et al. to prove that functions f of the form (1) or (2) satisfy character sum bounds of the form

$$\begin{aligned} \bigg | \sum _{u\in \mathbb {F}_q} \chi \big (f(u)\big ) \bigg | = O(\sqrt{q}) \end{aligned}$$

for all nontrivial characters $\chi$ of $E(\mathbb {F}_q)$ can be extended to obtain similar bounds (only a logarithmic factor worse) on arbitrary intervals ¹ within $\mathbb {F}_q$. More precisely, for all nontrivial characters of $E(\mathbb {F}_q)$ and all intervals $I\subset \mathbb {F}_q$, we obtain a bound of the form

$$\begin{aligned} \bigg | \sum _{u\in I} \chi \big (f(u)\big ) \bigg | = O(\sqrt{q}\log p) \end{aligned}$$

where p is the characteristic of $\mathbb {F}_q$. As a consequence, we get admissibility for variants of the maps $F_1'$, $F_2'$ of (6) in which the variable u is taken from any large interval (of length q / O(1)) within $\mathbb {F}_q$. This is of practical relevance for hashing or point representation on elliptic curves defined over prime fields $\mathbb {F}_p$ when p is not pseudo-Mersenne (such as most pairing-friendly elliptic curves, and many other standardized curves). Indeed, when hashing to a 256-bit curve of that type, for example, one traditionally needs to obtain a hash value in $\mathbb {F}_p$, which typically involves reducing a digest of at least 384 bits modulo p, since usual hash functions return bitstrings. A similar problem arises when representing an Elligator Squared value $(u,v)\in (\mathbb {F}_p)^2$ (or $\mathbb {F}_p\times V_\varepsilon$ when using $F'_2$) as a bitstring: to get uniform bitstrings, elements of $\mathbb {F}_p$ have to be greatly enlarged. Our result solves this problem completely by allowing u to be chosen from an interval of length a power of 2 (say $[0,2^{255})$ in the 256-bit case), making it possible to use the output of a standard hash function directly, and to directly obtain representation as bitstrings instead of base field elements.

Both of these improvements admit direct generalizations to the higher genus setting, in which one uses a function $f:\mathbb {F}_q\rightarrow X(\mathbb {F}_q)$ to hash to the group $J(\mathbb {F}_q)$ where J is the Jacobian of X, or to represent uniform divisor classes in $J(\mathbb {F}_q)$ as close to uniform bitstrings.

2 Stronger regularity bounds for encodings

In this section, we show how we can improve upon the regularity bounds from [12] for encodings to elliptic curves. We first formulate and prove a simple generalization of [12, Th. 3] in Sect. 2.2, and then discuss applications to elliptic curves in Sect. 2.3. The results extend naturally to higher genus algebraic curves, as shown in Appendix 2.4. We refer to Sect. 2.1 for standard definitions regarding probability distributions on finite sets and regularity, and to [19, 22] for background materials on characters of abelian groups and finite fields.

2.1 Statistical distance and regularity: some definitions

For $\mathscr {D}_S$ (or just $\mathscr {D}$ if the context is clear) a probability distribution on a finite set S, we write $\Pr [s\leftarrow \mathscr {D}_S]$ for the probability assigned to the singleton $\{s\}\subset S$ by $\mathscr {D}_S$. The uniform distribution on S is denoted by $\mathscr {U}_S$ (or just $\mathscr {U}$ if the context is clear).

In this paper, we will usually consider families of distributions $\mathscr {D}_{S_q}$ defined on sets $S_q$ associated with finite fields $\mathbb {F}_q$, and evaluate statistical quantities $\alpha _q$ related to these distributions. Such a quantity $\alpha _q$ will be called $negligible$ when $\alpha _q = o\big ((\log q)^{-k}\big )$ for all positive k.

Definition 1

(Statistical distance) Let $\mathscr {D}$ and $\mathscr {D}'$ be two probability distributions on a finite set S. The statistical distance between them is defined as the $L^1$-norm:²

$$\begin{aligned} \Delta _1(\mathscr {D},\mathscr {D}')= & {} \sum _{s\in S} \big | \Pr [s\leftarrow \mathscr {D}] - \Pr [s\leftarrow \mathscr {D}']\big |. \end{aligned}$$

We simply denote by $\Delta _1(\mathscr {D})$ the statistical distance between $\mathscr {D}$ and $\mathscr {U}$:

$$\begin{aligned} \Delta _1(\mathscr {D})= & {} \sum _{s\in S} \Big | \Pr [s\leftarrow \mathscr {D}] - \frac{1}{\#S}\Big |, \end{aligned}$$

and say that $\mathscr {D}$ is $\varepsilon$-statistically close to uniform when $\Delta _1(\mathscr {D})\le \varepsilon$. When $\Delta _1(\mathscr {D})$ is negligible, we simply say than $\mathscr {D}$ is statistically close to uniform.³ The squared Euclidean imbalance $\Delta ^2_2(\mathscr {D})$ of $\mathscr {D}$ is the square of the $L^2$-norm between $\mathscr {D}$ and $\mathscr {U}$:

$$\begin{aligned} \Delta ^2_2(\mathscr {D})=\sum _{s \in S} \Big | \Pr [s\leftarrow \mathscr {D}]-\frac{1}{\#S}\Big |^2. \end{aligned}$$

Definition 2

(Pushforward) Let S, T be two finite sets and F any mapping from S to T. For any probability distribution $\mathscr {D}_S$ on S, we can define the pushforward $F_*\mathscr {D}_S$ of $\mathscr {D}_S$ by F as the probability distribution on T such that sampling from $F_*\mathscr {D}_S$ is equivalent to sampling a value $s\leftarrow \mathscr {D}_S$ and returning F(s). In other words:

$$\begin{aligned} \Pr \big [t\leftarrow F_*\mathscr {D}_S\big ] = \Pr \big [s\leftarrow \mathscr {D}_S;\ t=F(s)\big ] = sum_{s\in F^{-1}(t)} \Pr [s\leftarrow \mathscr {D}_S]. \end{aligned}$$

Definition 3

(Regularity) Let S, T be two finite sets and F any mapping from S to T. We say that F is $\alpha$-regular when $F_*\mathscr {U}_S$ is $\alpha$-close to the uniform distribution. We may omit $\alpha$ if it is negligible.

Definition 4

(Collision probability) The collision probability $\rho$ of a map $F:S\rightarrow T$ is:

$$\begin{aligned} \rho = \Pr \big [ (s,s')\leftarrow \mathscr {U}_{S^2};\ F(s)=F(s') \big ] = \frac{1}{\#S^2}\cdot \#\{ (s,s')\in S^2\ |\ F(s)=F(s') \}. \end{aligned}$$

2.2 A general regularity bound

Let A be any finite abelian group (denoted additively), and $f_i:U_i\rightarrow A$, $g:V\rightarrow A$ arbitrary functions from finite sets $U_i,V$ to A for some s and $1\le i \le s$. We consider the following mapping:

$$\begin{aligned} F:U_1 \times \cdots \times U_s \times V\rightarrow & {} A \\ (u_1,\dots ,u_s,v)\mapsto & {} f_1(u_1) + \cdots + f_s(u_s) + g(v). \end{aligned}$$

We can obtain bounds on the regularity of F from bounds on the character sums $S_{f_i}(\chi )$ defined by $S_{f_i}(\chi ) = \sum _{u\in U_i} \chi \big (f_i(u)\big )$ for nontrivial characters $\chi$ of A on the one hand, and on the collision probability of g on the other hand. Indeed, the following theorem is a simple generalization of [12, Th. 3].

Lemma 1

Assume that for all nontrivial characters $\chi$ of A, the inequality $|S_{f_i}(\chi )|\le S_i$ holds, and denote by $\rho$ the collision probability of g. Then, the mapping F defined above is $\alpha$-regular with $\alpha = (\prod _{i=1}^s S_i)/\#U^s\sqrt{\rho \#A}$.

Proof

For any $a\in A$, denote by N(a) the number of elements $(u_1,\dots ,u_s,v)$ of $T=U_1 \times \cdots \times U_s \times V$ such that $F(u_1,\dots ,u_s,v) = a$. It follows from usual orthogonality relations of characters that:

$$\begin{aligned} N(a)= & {} \sum _{(u_1,\dots ,u_s,v)\in \prod _{i=1}^s U_i \times V} \frac{1}{\#A} \sum _{\chi } \chi \big (F(u_1,\dots ,u_s,v) - a\big ) \\= & {} \frac{1}{\#A} \sum _{\chi } S_{f_1}(\chi ) \cdots S_{f_s}(\chi ) S_g(\chi ) \chi (-a) \end{aligned}$$

where sums on $\chi$ extend over all characters of the abelian group A. The contribution of the trivial character $\chi _0$ is clearly $\#T/\#A$. Therefore, we have:

$$\begin{aligned} \frac{N(a)}{\#T} - \frac{1}{\#A}= & {} \frac{1}{\#A\#T} \sum _{\chi \ne \chi _0} S_{f_1}(\chi ) \cdots S_{f_s}(\chi ) S_g(\chi ) \chi (-a). \end{aligned}$$

In particular, the squared euclidean imbalance of the distribution induced by F on A, which is given by:

$$\begin{aligned} \Delta _2^2\big (F_*\mathscr {U}_T\big )= & {} \sum _{a\in A} \left| \frac{N(a)}{\#T} - \frac{1}{\#A} \right| ^2, \end{aligned}$$

can be expressed as follows:

$$\begin{aligned} \Delta _2^2\big (F_*\mathscr {U}_T\big )= & {} \sum _{a\in A} \frac{1}{\#A^2\#T^2} \sum _{\chi ,\chi '\ne \chi _0} \left( \prod _{i=1}^s S_{f_i}(\chi ) \right) S_g(\chi ) \chi (-a) \cdot \overline{ \left( \prod _{i=1}^s S_{f_i}(\chi ) \right) S_g(\chi ') \chi '(-a)} \\= & {} \frac{1}{\#A^2\#T^2} \sum _{\chi ,\chi '\ne \chi _0} \left( \prod _{i=1}^s {|S_{f_i}(\chi )|^{2}}\right) | S_g(\chi )|^2 \sum _{a\in A} (\chi \overline{\chi '})(-a), \end{aligned}$$

and by orthogonality again, the sum over $a\in A$ in the last list vanishes unless $\chi = \chi '$, in which case it evaluates to $\#A$. Hence:

$$\begin{aligned} \Delta _2^2\big (F_*\mathscr {U}_T\big )= & {} \frac{1}{\#A\#T^2} \sum _{\chi \ne \chi _0} \left( \prod _{i=1}^s {|S_{f_i}(\chi )|^{2}}\right) |S_g(\chi )|^2 \le \frac{ (S_1 \cdots S_s)^2 }{\#A\#U^{2s}\#V^2} \sum _{\chi } |S_g(\chi )|^2. \end{aligned}$$

Moreover, we have:

$$\begin{aligned} \sum _\chi |S_g(\chi )|^2 = \sum _{(v,v')\in V^2} \sum _\chi \chi \big (g(v)-g(v')\big ) = \#V^2\cdot \rho \cdot \#A \end{aligned}$$

since the character sum vanishes unless there is a collision between g(v) and $g(v')$, in which case it evaluates to $\#A$. As a result:

$$\begin{aligned} \Delta _2^2\big (F_*\mathscr {U}_T\big ) \le \frac{(S_1\cdots S_s)^2}{\#U^{2s}} \cdot \rho \end{aligned}$$

and the Cauchy–Schwarz relation between the squared euclidean imbalance and the statistical distance to uniform gives:

$$\begin{aligned} \Delta _1\big (F_*\mathscr {U}_T\big ) \le \sqrt{\Delta _2^2\big ((F_*\mathscr {U}_T\big )} \sqrt{\#A} \le \frac{S_1\cdots S_s}{\#U^{s}} \sqrt{\rho \#A} \end{aligned}$$

as required. $\square$

Corollary 1

Assume that for all nontrivial characters $\chi$ of A, the inequality $|S_f(\chi )|\le S$ holds for all i, and that g has preimage size bounded by some constant d (i.e. $\#g^{-1}(\{a\})\le d$ for all $a\in A$). Suppose also that all the sets $U_i$ are equal: $U_1=\cdots =U_s=U$. Then, the mapping F defined above is $\alpha$-regular with

$$\begin{aligned} \alpha= & {} (S/\#U)^s\sqrt{d\#A/\#V}. \end{aligned}$$

Proof

Indeed, the collision probability of g is then bounded as:

$$\begin{aligned} \rho = \frac{1}{\#V^2}\cdot \#\{(v,v')\in V^2\ |\ g(v)=g(v')\} = \frac{1}{\#V^2} \sum _{v\in V} \#g^{-1}\big ( \{g(v)\} \big ) \le \frac{d}{\#V}. \end{aligned}$$

Hence, the result follows from Lemma 1. $\square$

2.3 Application to elliptic curve encodings

Consider now an encoding $f:\mathbb {F}_q\rightarrow E(\mathbb {F}_q)$ to the group of points of an elliptic curve over $\mathbb {F}_q$, and recall the following definition proposed by Farashahi et al. [12].

Definition 5

The encoding f is said to be B-well-distributed for some positive constant B if for all nontrivial characters $\chi$ of $E(\mathbb {F}_q)$, the character sum $S_f(\chi ) = \sum _{u\in \mathbb {F}_q} \chi \big (f(u)\big )$ is bounded as $\big |S_f(\chi )\big |\le B\sqrt{q}$.

Farashahi et al. have shown how to prove that known encoding functions to elliptic curves (of the form (1) or (2), say) are indeed B-well-distributed for some small B depending on the encoding construction but not on q.

Then, fix $g:V\rightarrow E(\mathbb {F}_q)$ any function from a set V of cardinality $\#V\ge q^\varepsilon$ and with preimage size bounded by d. Assuming that f is B-well-distributed, Corollary 1 applied to f and g with $s=1$ shows that the map $F_3:\mathbb {F}_q\times V\rightarrow E(\mathbb {F}_q)$ from 5, given by $F_3(u,v) = f(u) + g(v)$, is $\alpha$-regular for:

$$\begin{aligned} \alpha = \frac{B\sqrt{q}}{q}\sqrt{\frac{d\cdot (q+2\sqrt{q}+1)}{\#V}} \le \frac{B\sqrt{d}}{q^{\varepsilon /2}}\cdot (1+q^{-1/2}), \end{aligned}$$

which is negligible (it is smaller than the inverse of any polynomial function of $\log q$ for large enough q) for constant B and d. As a result, the maps $F'_1, F'_2$ defined in (6) are indeed regular. If we assume furthermore that f is efficiently invertible and has preimage size bounded by d (which usually follows trivially for a suitable d from the fact that it is algebraic), then $F_3$ (and hence $F'_1,F'_2$) are also efficiently and uniformly samplable using Algorithm 1, and thus admissible in the terminology of [4]. This implies in particular that:

• if $\mathfrak {h}_1:\{0,1\}^*\rightarrow \mathbb {F}_q, \mathfrak {h}_2:\{0,1\}^*\rightarrow [0,q^\varepsilon )$ are hash functions modeled as independent random oracles, then $m\mapsto f\big (\mathfrak {h}_1(m)\big ) + \mathfrak {h}_2(m)G$ is indifferentiable from a random oracle to $E(\mathbb {F}_q)$ for any element $G\in E(\mathbb {F}_q)$ of order greater than or equal to $q^\varepsilon$. This provides indifferentiable hashing to $E(\mathbb {F}_q)$ from as few as $(1+\varepsilon )\log _2 q$ random oracle bits (and for $\varepsilon$ small enough, it gives indifferentiable hashing for a smaller computational cost than 2 base fields exponentiations);

• similarly, if $\mathfrak {h}_1:\{0,1\}^*\rightarrow \mathbb {F}_q, \mathfrak {h}_2:\{0,1\}^*\rightarrow V_\varepsilon$ are hash functions modeled as independent random oracles with $V_\varepsilon \subset \mathbb {F}_q$ a subset of cardinality greater than or equal to $q^\varepsilon$, then $m\mapsto f\big (\mathfrak {h}_1(m)\big ) + f\big (\mathfrak {h}_2(m)\big )$ is indifferentiable from a random oracle to $E(\mathbb {F}_q)$;

• in the spirit of [30], if $P\in E(\mathbb {F}_q)$ is a uniformly random point, then a uniformly random preimage of P under $F'_1$ (resp. $F'_2$) is statistically close to uniform in $\mathbb {F}_q\times [0,q^\varepsilon )$ (resp. $\mathbb {F}_q\times V_\varepsilon$), and can be efficiently sampled using Algorithm 1, which provides a close-to-uniform point representation technique from a set of cardinality as small as $q^{1+\varepsilon }$.

As mentioned in the introduction, we can also extend those results to the restriction of f to a large enough interval of $\mathbb {F}_q$. Indeed, let us introduce the following definition (where, as mentioned earlier, an interval of $\mathbb {F}_q$ is any subset of the form $H+x[m,\dots ,m+k]$ where H is a subgroup of $\mathbb {F}_q$, $x\in \mathbb {F}_q$ and m, k are non negative integers).

Definition 6

The encoding f is said to be B-strongly well-distributed for some positive constant B if for all nontrivial characters $\chi$ of $E(\mathbb {F}_q)$ and all intervals $I\subset \mathbb {F}_q$, the restricted character sum $S_f(\chi ;I) = \sum _{u\in I} \chi \big (f(u)\big )$ is bounded as $\big |S_f(\chi ;I)\big |\le B\sqrt{q}\cdot \log p$, where p is the characteristic of $\mathbb {F}_q$.

We will show in Sect. 3 that the same techniques as used by Farashahi et al. to show that encodings are well-distributed can be adapted to prove that they are also strongly well-distributed.

Now, consider a B-strongly well-distributed f to $E(\mathbb {F}_q)$ and a mapping $g:V\rightarrow E(\mathbb {F}_q)$ with preimage size bounded by d from a set of cardinality $\#V\ge q^\varepsilon$, and fix an interval $I\subset \mathbb {F}_q$ of cardinality $\#I\ge q/c$ for some constant c. Corollary 1 applied to $f|_I$ and g with $s=1$ shows that the map $F_{3,I}:I\times V \rightarrow E(\mathbb {F}_q)$ given by $F_{3,I}(u,v) = f(u) + g(v)$ is $\alpha$-regular for:

$$\begin{aligned} \alpha = \frac{B\sqrt{q}\cdot \log p}{q/c}\sqrt{\frac{d\cdot (q+2\sqrt{q}+1)}{\#V}} \le \frac{cB\sqrt{d}\cdot \log p}{q^{\varepsilon /2}}\cdot (1+q^{-1/2}), \end{aligned}$$

which is again negligible for constant B, c, d. This is especially interesting in the case when $q=p$ is prime. Then, for some $\varepsilon >0$, let $k_1 = \lfloor \log _2 p\rfloor$ and $k_2 = \lceil (1+\varepsilon )\log _2 p\rceil -k_1$, and identify bitstrings in $\{0,1\}^k$ with integers in $[0,2^k)$. We can then introduce:

$$\begin{aligned} \begin{aligned} F_{1,I}':\{0,1\}^{k_1}\times \{0,1\}^{k_2}&\rightarrow E(\mathbb {F}_p)&F_{2,I}':\{0,1\}^{k_1}\times \{0,1\}^{k_2}&\rightarrow E(\mathbb {F}_p)\nonumber \\ (u,v)&\mapsto f(u) + vG \qquad&(u,v)&\mapsto f(u) + f(v). \end{aligned} \end{aligned}$$

The previous bound says that $F_{1,I}'$ is $\big (2+o(1)\big )B p^{-\varepsilon /2}\log p$-regular, and $F_{2,I}'$ is $\big (2+o(1)\big )B \sqrt{d}\cdot p^{-\varepsilon /2}\log p$-regular. If f has bounded preimage size, they are thus both admissible encodings (using the variant of Algorithm 1 where only preimages in $f^{-1}(Q)\cap I$ are considered in Steps 5, 8 for preimage sampling) from bitstrings of length $k_1+k_2\sim (1+\varepsilon )\log _2p$ to $E(\mathbb {F}_p)$. As a result, we get:

• efficient indifferentiable hash functions to $E(\mathbb {F}_p)$ from random oracles to the set $\{0,1\}^{k_1+k_2}$ of bitstrings of length $k_1+k_2\sim (1+\varepsilon )\log _2p$;

• efficient representation of uniform points in $E(\mathbb {F}_p)$ as close to uniform bitstrings of length $k_1+k_2\sim (1+\varepsilon )\log _2p$.

This is a major improvement over the approach described in [4, 30] for hashing and point representation, which requires strings of length $\sim (5/2)\log _2p$ when p is not close to a power of 2 (not a pseudo-Mersenne prime, say).

2.4 Extension of Sect. 2.3 to higher genus curves

In this section, we briefly discuss how the results of Sect. 2.3 extend to the case of encodings to algebraic curves of arbitrary genus.

Consider a mapping $f:\mathbb {F}_q\rightarrow X(\mathbb {F}_q)$ to the rational points of a curve $X/\mathbb {F}_q$ of genus $g_X$, and let J denote the Jacobian of X. Assume that X has an $\mathbb {F}_q$-rational point O, so that we can fix an embedding $X\hookrightarrow J$ (sending a point P to the degree 0 divisor $(P)-(O)$). In that situation, Farashahi et al. [12] define what it means for f to be a well-distributed encoding.

Definition 7

The encoding f is said to be B-well-distributed for some positive constant B if for all nontrivial characters $\chi$ of $J(\mathbb {F}_q)$, the character sum $S_f(\chi ) = \sum _{u\in \mathbb {F}_q} \chi \big (f(u)\big )$ (where f(u) is identified with its image in $J(\mathbb {F}_q)$ under the embedding $X\hookrightarrow J$) is bounded as $\big |S_f(\chi )\big |\le B\sqrt{q}$.

Similarly, we introduce the definition of strong well-distributed encodings f to $X(\mathbb {F}_q)$.

Definition 8

The encoding f is said to be B-strongly well-distributed for some positive constant B if for all nontrivial characters $\chi$ of $J(\mathbb {F}_q)$ and all intervals $I\subset \mathbb {F}_q$, the restricted character sum $S_f(\chi ;I) = \sum _{u\in I} \chi \big (f(u)\big )$ is bounded as $\big |S_f(\chi ;I)\big |\le B\sqrt{q}\cdot \log p$, where p is the characteristic of $\mathbb {F}_q$.

Then the results of Sect. 2.3 generalize in a straightforward way. Indeed, suppose that f is B-well-distributed and fix $g:V\rightarrow X(\mathbb {F}_q)$ any function from a set V of cardinality $\#V\le q^\varepsilon$ and with preimage size bounded by d. Assuming that f is B-well-distributed, Corollary 1 applied to f and g with $s=g_X$ shows that the map:

$$\begin{aligned} F:\mathbb {F}_q^{g_X}\times V\rightarrow & {} J(\mathbb {F}_q) \\ (u_1,\dots ,u_{g_X},v)\mapsto & {} f(u_1) + \cdots + f(u_{g_X}) + g(v) \end{aligned}$$

is $\alpha$-regular for:

$$\begin{aligned} \alpha = \left( \frac{B\sqrt{q}}{q}\right) ^{g_X}\sqrt{\frac{d\cdot (q+2g_X\sqrt{q}+1)^{g_X}}{\#V}} \le \frac{B^{g_X}\sqrt{d}}{q^{\varepsilon /2}}\cdot (1+g_Xq^{-1/2})^{g_X}, \end{aligned}$$

which is negligible (it is smaller than any polynomial function of $\log q$ for large enough q) for constant B, d and $g_X$. As a result, the following generalizations of the maps from (6):

$$\begin{aligned} F_1'':\mathbb {F}_q^{g_X}\times [0,q^\varepsilon )\rightarrow & {} J(\mathbb {F}_q) \\ (u_1,\dots ,u_{g_X},v)\mapsto & {} f(u_1) + \cdots + f(u_{g_X}) + vG \\ F_2'': \mathbb {F}_q^{g_X}\times V_\varepsilon\rightarrow & {} J(\mathbb {F}_q) \\ (u_1,\dots ,u_{g_X},v)\mapsto & {} f(u_1) + \cdots + f(u_{g_X}) + f(v) \end{aligned}$$

are again regular. If we assume that f is efficiently invertible and has preimage size bounded by d, we obtain admissibility, and get:

• efficient indifferentiable hash functions to the group $J(\mathbb {F}_q)$ from a random oracle to the set $\mathbb {F}_q^{g_X}\times [0,q^\varepsilon )$ (or $\mathbb {F}_q^{g_X}\times V_\varepsilon$) of cardinality as low as $q^{g_X+\varepsilon }$, which is essentially optimal, since $\#J(\mathbb {F}_q) = q^{g_X+o(1)}$;

• efficient representation of uniform group elements in $J(\mathbb {F}_q)$ as close to uniform elements of those same sets.

Similarly, if f is B-strongly well-distributed and $g:V\rightarrow E(\mathbb {F}_q)$ is as above, then for any interval $I\subset \mathbb {F}_q$ of cardinality $\#I\ge q/c$ for some constant c. Corollary 1 applied to $f|_I$ and g with $s=g_X$ shows the map:

$$\begin{aligned} F_I:I^{g_X}\times V\rightarrow & {} J(\mathbb {F}_q) \\ (u_1,\dots ,u_{g_X},v)\mapsto & {} f(u_1) + \cdots + f(u_{g_X}) + g(v) \end{aligned}$$

is $\alpha$-regular for:

$$\begin{aligned} \alpha = \left( \frac{B\sqrt{q}\cdot \log p}{q/c}\right) ^{g_X}\sqrt{\frac{d\cdot (q+2g_X\sqrt{q}+1)^{g_X}}{\#V}} \le \frac{\big (cB\log p\big )^{g_X}\sqrt{d}}{q^{\varepsilon /2}}\cdot (1+g_Xq^{-1/2})^{g_X}, \end{aligned}$$

which is again negligible for constant $B,c,d,g_X$. In the case when $q=p$ is prime, define as in Sect. 2.3 two integers $k_1,k_2$ as $k_1 = \lfloor \log _2 p\rfloor$ and $k_2 = \lceil (g_X+\varepsilon )\log _2 p\rceil -g_X\cdot k_1$, and identify bitstrings in $\{0,1\}^k$ with integers in $[0,2^k)$. We can then introduce:

$$\begin{aligned} F_{1,I}'':\{0,1\}^{g_X\cdot k_1}\times \{0,1\}^{k_2}\rightarrow & {} J(\mathbb {F}_p)\\ (u_1,\dots ,u_{g_X},v)\mapsto & {} f(u_1) + \dots + f(u_{g_X}) + vG \nonumber \\ F_{2,I}'':\{0,1\}^{g_X\cdot k_1}\times \{0,1\}^{k_2}\rightarrow & {} J(\mathbb {F}_p)\\ (u_1,\dots ,u_{g_X},v)\mapsto & {} f(u_1) + \dots + f(u_{g_X}) + f(v). \end{aligned}$$

The previous bound ensures that $F_{1,I}'', F_{2,I}''$ are both $\widetilde{O}(p^{-\varepsilon /2})$-regular. If f has bounded preimage size, they are thus both admissible encodings from bitstrings of length $g_X\cdot k_1+k_2\sim (g_X+\varepsilon )\log _2p$ to $J(\mathbb {F}_p)$. As a result, we get:

• efficient indifferentiable hash functions to $J(\mathbb {F}_p)$ from random oracles to the set $\{0,1\}^{g_X\cdot k_1+k_2}$ of bitstrings of length $g_X\cdot k_1+k_2\sim (g_X+\varepsilon )\log _2p$;

• efficient representation of uniform group elements in $J(\mathbb {F}_p)$ as close to uniform bitstrings of length $g_X\cdot k_1+k_2\sim (g_X+\varepsilon )\log _2p$.

3 Character sums on intervals of curves

Throughout this paper, a “curve” means a smooth, projective, geometrically integral curve over a finite field (the field $\mathbb {F}_q$ unless otherwise specified).

Let $h:X\rightarrow Y$ be a branched covering (i.e. a finite separable morphism) of curves over $\mathbb {F}_q$, and $\xi ,\pi :X\rightarrow \mathbb {P}^1$ be rational functions. We also assume that Y has an $\mathbb {F}_q$ rational point, and fix the embedding $Y\hookrightarrow J$ of Y into its Jacobian variety J defined by that rational point. The goal of this section is to obtain bounds on character sums:

$$\begin{aligned} S_{h,\xi ,\pi }(\chi ,\omega ;I) = \sum _{\begin{array}{c} P\in X(\mathbb {F}_q)\\ \pi (P)\in I, \xi (P)\ne \infty \end{array}} \chi \big (h(P)\big )\omega \big (\xi (P)\big ), \end{aligned}$$

(7)

where $\chi$ is a nontrivial character of $J(\mathbb {F}_q)$, $\omega$ is a multiplicative character of $\mathbb {F}_q$, and $I\subset \mathbb {F}_q$ is any interval. Under mild conditions on $h,\xi ,\pi$, we will obtain a bound of the form:

$$\begin{aligned} \big | S_{h,\xi ,\pi }(\chi ,\omega ;I) \big | = O(q^{1/2}\log p) \end{aligned}$$

(8)

where p is the characteristic of $\mathbb {F}_q$. This extends the results of Farashahi et al. [12, §4] giving similar bounds (without the $\log p$ factor) in the case when $I=\mathbb {F}_q$, and makes it possible to prove that encoding functions $\mathbb {F}_q\rightarrow Y(\mathbb {F}_q)$ constructed as in (1) or (2) are strongly well-distributed in the sense of Definition 6 (or Definition 8 in the higher genus case).

The idea is to express $S_{h,\xi ,\pi }(\chi ,\omega ;I)$ in terms of the sums:

$$\begin{aligned} \widetilde{S}_{h,\xi ,\pi }(\chi ,\omega ,\psi ) = \sum _{\begin{array}{c} P\in X(\mathbb {F}_q)\\ \pi (P), \xi (P)\ne \infty \end{array}} \chi \big (h(P)\big )\omega \big (\xi (P)\big )\psi \big (\pi (P)\big ) \end{aligned}$$

(9)

for all additive characters $\psi$ of $\mathbb {F}_q$. The sums $\widetilde{S}_{h,\xi ,\pi }(\chi ,\omega ,\psi )$ are Artin character sums along X and can therefore be bounded using a theorem by Weil (the Riemann–Hypothesis for curves). Standard exponential sum estimates then yield an explicit bound of the form (8).

We first recall some background on Artin character sums in Sect. 3.1, then state our precise version of (8) and prove it in Sect. 3.2, and finally give a quick rundown in Sect. 3.3 of how it can be applied just like [12, Th.7] to prove that encodings to algebraic curves are strongly well-distributed.

3.1 Background on Artin characters

Consider an abelian covering $\widetilde{Y}\rightarrow Y$ of curves over $\mathbb {F}_q$ with Galois group G (i.e. a finite morphism such that $\mathbb {F}_q(\widetilde{Y})/\mathbb {F}_q(Y)$ is abelian with Galois group G). Any character of G determines, via the Artin map, a corresponding character on the group of $\mathbb {F}_q$-divisors on Y prime to the ramification locus S of $\widetilde{Y}\rightarrow Y$, which extends to a multiplicative map $\chi :{{\mathrm{Div}}}_{\mathbb {F}_q}(Y)\rightarrow \mathbb {C}$ vanishing on divisors not prime to S. Let us call such a map $\chi$ an Artin character of Y. One associates to $\chi$ a distinguished effective divisor $\mathfrak {f}(\chi )$ of support S called the conductor (in particular, if $\widetilde{Y}\rightarrow Y$ is unramified, $\mathfrak {f}(\chi )=0$; the character itself is then said to be unramified).

We mainly consider the following three types of Artin characters (we only give their values on $\mathbb {F}_q$-rational points, since this suffices for our purposes):

• 1. Artin characters arising from Artin–Schreier coverings: the function field of $\widetilde{Y}$ is then $\mathbb {F}_q(\widetilde{Y}) = \mathbb {F}_q(Y)[t]/(t^p-t-\pi )$ for some rational function $\pi$ of Y not of the form $u^p-u$ in ${\bar{\mathbb {F}}}_q(Y)$. The Galois group is $\mathbb {Z}/p\mathbb {Z}$, and the Artin symbol $\sigma _y$ at an unramified point $y\in Y(\mathbb {F}_q)$ is trivial if and only if $\pi (y)$ is of the form $x^p-x$ for some $x\in \mathbb {F}_q$, i.e. ${{\mathrm{Tr}}}_{\mathbb {F}_q/\mathbb {F}_p}\big (\pi (y)\big ) = 0$. As a result, Artin characters arising from this covering are of the form $y\mapsto \exp \big (\frac{2ic\varvec{\pi }}{p}{{\mathrm{Tr}}}_{\mathbb {F}_q/\mathbb {F}_p}\big (\pi (y)\big )$ on rational points for some $c\in \mathbb {Z}/p\mathbb {Z}$. More generally, by considering constant multiples of $\pi$, we obtain that $\psi (\pi )$ determines an Artin character of Y for any additive character $\psi$ of $\mathbb {F}_q$ and any rational function $\pi$ as above.

• 2. Artin characters arising from Kummer coverings: the function field of $\widetilde{Y}$ is then $\mathbb {F}_q(\widetilde{Y}) = \mathbb {F}_q(Y)[t]/(t^n-\xi )$ for some $n>1$ dividing $q-1$ and some rational function $\xi$ which is not an n-th power in ${\bar{\mathbb {F}}}_q(Y)$. The Galois group is $(\mathbb {Z}/n\mathbb {Z})^\times$, and the Artin symbol $\sigma _y$ at an unramified point $y\in Y(\mathbb {F}_q)$ is trivial if and only if $\xi (y)$ is an n-th power. As a result, Artin characters arising from this covering are of the form $y\mapsto \omega \big (\xi (y)\big )$ for some multiplicative character $\omega$ of $\mathbb {F}_q$ of order dividing n. And conversely, $\omega (\xi )$ gives rise to an Artin character of Y for any multiplicative character $\omega$ of $\mathbb {F}_q$ and any rational function $\xi$ which is not a perfect power in ${\bar{\mathbb {F}}}_q(Y)$.

• 3. Artin characters attached to characters of the Jacobian. Assume that Y has an $\mathbb {F}_q$-rational point, providing an embedding $Y\hookrightarrow J$ of Y into its Jacobian J. Denote by F the Frobenius endomorphism of J. Then $1-F$ is an unramified abelian covering of J of group $J(\mathbb {F}_q)$, and pulling it back along $Y\hookrightarrow J$ yields an unramified abelian covering $\widetilde{Y}\rightarrow Y$ of group $J(\mathbb {F}_q)$. As a result, any character $\chi$ of $J(\mathbb {F}_q)$ gives rise to an unramified Artin character of Y, with the obvious action on rational points and divisors: the image of $y\in Y(\mathbb {F}_q)$ is simply $\chi (y)$ under the identification of $Y(\mathbb {F}_q)$ as a subset of $J(\mathbb {F}_q)$ using $Y\hookrightarrow J$.

The product $\chi _1\chi _2$ of two Artin characters $\chi _1,\chi _2$ is an Artin character, and if $\chi _1$, $\chi _2$ have disjoint ramification loci (which is in particular the case when one of them is unramified), the conductor of the product is given as $\mathfrak {f}(\chi _1\chi _2) = \mathfrak {f}(\chi _1) + \mathfrak {f}(\chi _2)$. Furthermore, one can pull back Artin characters along morphisms: if $\chi$ is an Artin character on Y and $h:X\rightarrow Y$ any non constant morphism of curves, one can define an Artin character $h^*\chi$ on X by pulling back the Galois covering. It is given on divisors by $h^*\chi (D) = \chi (h_*D)$, and is unramified if $\chi$ is unramified.

The main tool for estimating sums of Artin character is the following theorem by Weil, obtained as a consequence of the Riemann hypothesis for curves (see, for example, [21, §2] or [26, Chap. 9]), which gives a bound on sums of the form $S_Y(\chi ) = \sum _{P\in Y(\mathbb {F}_q)} \chi (P)$ where $\chi$ is a nontrivial Artin character on Y.

Lemma 2

If $\chi$ is a nontrivial Artin character on the curve Y is of genus $g_Y$, the following bound holds: $| S_Y(\chi ) | \le (2g_Y-2+\deg \mathfrak {f}(\chi ))\sqrt{q}$.

3.2 A bound for $S_{h,\xi ,\pi }(\chi ,\omega ;I)$

Let $\mathbb {F}_q$ be a finite field of characteristic p. Now consider the situation described at the beginning of this section: we have a branched covering $h:X\rightarrow Y$, rational functions $\xi ,\pi :X\rightarrow \mathbb {P}^1$ (which are not constant, say), a nontrivial character $\chi$ of $J(\mathbb {F}_q)$ where J is the Jacobian of Y, an additive character $\psi$ of $\mathbb {F}_q$ and a multiplicative character $\omega$ of $\mathbb {F}_q$. We want to estimate the sum $\widetilde{S}_{h,\xi ,\pi }(\chi ,\omega ,\psi )$ defined by (9).

Suppose for simplicity that $\xi$ is not a perfect power in ${\bar{\mathbb {F}}}_q(X)$ and $\pi$ is not of the form $u^p-u$ in ${\bar{\mathbb {F}}}_q(X)$. Then, we have Artin characters $\omega (\xi )$ and $\psi (\pi )$ on X. We denote their product by $\lambda$. This character has been studied in detail by Perel’muter [25] and more recently by Castro and Moreno [5]. In particular, they show [5, Th. 13]:

Lemma 3

Suppose that $\omega$ and $\psi$ are not both trivial characters. Then $\lambda = \omega (\xi ) \psi (\pi )$ is a ramified Artin character, and its conductor satisfies $\deg \mathfrak {f}(\lambda ) \le \deg (\pi )_\infty +l+s-r-a$ (with equality when $\omega$ and $\psi$ are both nontrivial), where $(\pi )_\infty$ is the divisor of poles of $\pi$ (counted positively), and l the number of poles of $\pi$, s the number of points in the support of $(\xi )$, r the number of points common to the supports of $(\pi )_\infty$ and $(\xi )$, and a the number of points in the union of the supports of $(\pi )_\infty$ and $(\xi )$ where $\lambda$ is unramified.

Furthermore, $\chi$ also defines an unramified Artin character on Y which can be pulled back to an unramified Artin character $h^*\chi$ of X. Let $\widetilde{\chi }= \lambda \cdot h^*\chi$. Then by definition, for any point $P\in X(\mathbb {F}_q)$ such that $\pi (P),\xi (P)\ne \infty$, we have: $\widetilde{\chi }(P) = \chi \big (h(P)\big )\omega \big (\xi (P)\big )\psi \big (\pi (P)\big )$. As a result, the sum $\widetilde{S}_{h,\xi ,\pi }(\chi ,\omega ,\psi )$ is almost the same as $S_X(\widetilde{\chi })$: they differ at most by the number of points $P\in X(\mathbb {F}_q)$ which are poles of $\pi$ or $\xi$ but where $\lambda$ is nonzero (hence unramified), and there are at most a such points, using the notations of Lemma 3. The following extension of [12, Th.7] follows.

Theorem 1

Let $h:X\rightarrow Y$ be a branched covering of curves, $\xi ,\pi :X\rightarrow \mathbb {P}^1$ non constant rational functions, $\chi$ a nontrivial character of $J(\mathbb {F}_q)$ where J is the Jacobian of Y, $\psi$ an arbitrary additive character of $\mathbb {F}_q$ and $\omega$ an arbitrary multiplicative character $\omega$ of $\mathbb {F}_q$. Assume that h does not factor through a nontrivial unramified covering of Y, and that $\xi$ is not a perfect power in ${\bar{\mathbb {F}}}_q(X)$ and $\pi$ not of the form $u^p-u$ in ${\bar{\mathbb {F}}}_q(X)$. Then, we have:

$$\begin{aligned} \big | \widetilde{S}_{h,\xi ,\pi }(\chi ,\omega ,\psi ) \big | \le \big (2g_X-2 + 2\deg \xi + 2\deg \pi \big ) q^{1/2}. \end{aligned}$$

Proof

The case when $\omega$ and $\psi$ are both trivial follows directly from [12, Th. 7] (for reference: $h^*\chi$ must be nontrivial, since h would factor through the unramified covering defined by the kernel of $\chi$; thus $\big |S_X(h^*\chi )\big | \le (2g_X-2)q^{1/2}$ by Lemma 2, and clearly $\big | \widetilde{S}_{h,\xi ,\pi }(\chi ,\omega ,\psi ) \big | \le \big |S_X(h^*\chi )\big | + \deg \xi + \deg \pi$).

Thus, we can assume that at least one of $\omega$ or $\psi$ is nontrivial, and thus $\lambda = \omega (\xi )\psi (\pi )$ is ramified, with $\deg \mathfrak {f}(\lambda )\le \deg (\pi )_\infty +l+s-r-a$ with the notations of Lemma 3. Moreover, $\widetilde{\chi }= \lambda \cdot h^*\chi$ has the same conductor and is in particular nontrivial. By the previous observation, we have:

$$\begin{aligned} \big | \widetilde{S}_{h,\xi ,\pi }(\chi ,\omega ,\psi ) \big |\le & {} \big | S_X(\widetilde{\chi }) \big | + a \\\le & {} \big (2g_X - 2 + \deg (\pi )_\infty +l+s-r-a\big )q^{1/2} + a \text { (by Lemma 2) } \\\le & {} \big (2g_X - 2 + \deg (\pi )_\infty +l+s\big )q^{1/2}. \end{aligned}$$

Moreover, $\deg (\pi )_\infty = \deg \pi ^*(\infty ) = \deg \pi \cdot 1$, and similarly $l\le \deg \pi$, $s\le \deg \xi ^*\big ((0)+(\infty )\big )=2\deg \xi$. Hence $| \widetilde{S}_{h,\xi ,\pi }(\chi ,\omega ,\psi ) | \le (2g_X-2 + 2\deg \xi + 2\deg \pi ) q^{1/2}$ as required. $\square$

Remark 1

It is easy to verify that the result still holds even when the condition on $\xi$ and $\pi$ isn’t verified, as those cases essentially reduce to the case of trivial characters. Similarly, the theorem remains true when $\xi$ or $\pi$ is constant, with the convention that the degree is then zero.

Let $I\subset \mathbb {F}_q$ an arbitrary interval of $\mathbb {F}_q$. We can obtain an estimate of $S_{h,\xi ,\pi }(\chi ,\omega ;I)$ using the following bound, which is easily established following the proof of Kohel and Shparlinski’s [21, Lemma 3] together with the more precise version of Vinogradov’s inequality due to Cochrane [6]. The lower order constant 3/2 can be improved slightly for large p [7, 24], but will suffice for our purposes.

Lemma 4

Denote by $\Psi$ the group of additive characters of $\mathbb {F}_q$. We have:

$$\begin{aligned} \sum _{\psi \in \Psi } \bigg | \sum _{\beta \in I} \psi (\beta ) \bigg | \le q\left( \frac{4}{\varvec{\pi }^2}\log p + \frac{3}{2}\right) \end{aligned}$$

where p is the characteristic of $\mathbb {F}_q$, and $\varvec{\pi }=3.14\dots$ is the circle constant (in boldface to avoid confusion).

Theorem 2

Let $h:X\rightarrow Y$ be a branched covering of curves, $\xi ,\pi :X\rightarrow \mathbb {P}^1$ non constant rational functions, $\chi$ a nontrivial character of $J(\mathbb {F}_q)$ where J is the Jacobian of Y, $\omega$ an arbitrary multiplicative character of $\mathbb {F}_q$. Assume that h does not factor through a nontrivial unramified covering of Y. Then, we have:

$$\begin{aligned} \big | S_{h,\xi ,\pi }(\chi ,\omega ;I) \big | \le \big (2g_X-2 + 2\deg \xi + 2\deg \pi \big ) q^{1/2} \Big (\frac{4}{\varvec{\pi }^2}\log p+\frac{3}{2}\Big ). \end{aligned}$$

Proof

To see this, write, using the orthogonality property of additive characters:

$$\begin{aligned} S_{h,\xi ,\pi }(\chi ,\omega ;I)&= \sum _{\beta \in I} \sum _{\begin{array}{c} P\in X(\mathbb {F}_q)\\ \pi (P)=\beta , \xi (P)\ne \infty \end{array}} \chi \big (h(P)\big )\omega \big (\xi (P)\big ) \\&= \sum _{\beta \in I} \sum _{\begin{array}{c} P\in X(\mathbb {F}_q)\\ \pi (P)\ne \infty , \xi (P)\ne \infty \end{array}} \chi \big (h(P)\big )\omega \big (\xi (P)\big ) \cdot \frac{1}{q} \sum _{\psi \in \Psi } \psi \big (\pi (P) - \beta \big ) \\&= \sum _{\psi \in \Psi } \widetilde{S}_{h,\xi ,\pi }(\chi ,\omega ,\psi )\cdot \frac{1}{q} \sum _{\beta \in I} \psi (-\beta ). \end{aligned}$$

The result then readily follows from Lemma 4 and Theorem 1. $\square$

3.3 Application to encodings

Let us now succinctly discuss how Theorem 2 enables us to prove that encodings are strongly well-distributed in exactly the same way as Farashahi et al. [12] use their result to establish that they are well-distributed.

Take Icart’s function [18] as an example: it is defined for any elliptic curve $E:y^2 = x^3+ax+b$ ($a\ne 0$) over a field $\mathbb {F}_q$ such that $q\equiv 2\pmod 3$, and admits a simple geometric description of the form (1). Indeed, as discussed in [11, 12, 14], if we define $h:C\rightarrow E$ to be the branched covering of curves such that $\mathbb {F}_q(C) = \mathbb {F}_q(E)[u]/(u^4 - 6xu^2 + 6yu - 3a)$ (where x, y are the rational functions on E defined in the Weierstrass equation), then the rational function u on C is a morphism $\pi :C\rightarrow \mathbb {P}^1$ that induces a bijection $C(\mathbb {F}_q)\overset{\sim }{\longrightarrow }\mathbb {P}^1(\mathbb {F}_q)$ on rational points. Icart’s function $f:\mathbb {F}_q\rightarrow E(\mathbb {F}_q)$ can then be defined as $h\circ \pi ^{-1}$ on $\mathbb {F}_q\subset \mathbb {P}^1(\mathbb {F}_q)$. Therefore, we have, for any interval $I\subset \mathbb {F}_q$ and any nontrivial character $\chi$ of $E(\mathbb {F}_q)$:

$$\begin{aligned} S_f(\chi ;I) = \sum _{u\in I} \chi \big (f(u)\big ) = \sum _{\begin{array}{c} P\in C(\mathbb {F}_q) \\ \pi (P)\in I \end{array}} \chi \big (h(P)\big ) = S_{h,1,\pi }(\chi ,\omega _0;I) \end{aligned}$$

for $\omega _0$ the trivial multiplicative character of $\mathbb {F}_q$.

Moreover, those papers have computed that C is of genus $g_C=7$, and it is easy to see (by eliminating y between $y^2-x^3-ax-b$ and $u^4-6xu^2+6yu-3a$, say) the rational function $\pi$ is of degree $\deg \pi = 3$. As a result, we obtain $|S_f(\chi ;I)| \le (2\cdot 7-2+2\cdot 3)q^{1/2}\big (\frac{4}{\varvec{\pi }^2}\log p+\frac{3}{2}) = \big (72/\varvec{\pi }^2+o(1)\big )q^{1/2}\log p$. In other words:

Theorem 3

Icart’s function f is $\big (72/\varvec{\pi }^2+o(1)\big )$-strongly well-distributed.

In particular, the results of Sect. 2.3 apply to Icart’s function. Similarly, the same approach as in [12] shows that all other known types of encodings, such as the Kammerer–Lercier–Renault encoding to genus 2 hyperelliptic curves [20], the Shallue–van de Woestijne encoding [28], and the Ulas encoding [32] of the form (2) are also strongly well-distributed.