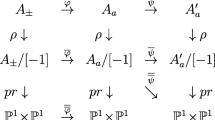SwiftEC: Shallue-van de Woestijne Indifferentiable Function to Elliptic Curves

Abstract

Hashing arbitrary values to points on an elliptic curve is a required step in many cryptographic constructions, and a number of techniques have been proposed to do so over the years. One of the first ones was due to Shallue and van de Woestijne (ANTS-VII), and it had the interesting property of applying to essentially all elliptic curves over finite fields. It did not, however, have the desirable property of being indifferentiable from a random oracle when composed with a random oracle to the base field.

Various approaches have since been considered to overcome this limitation, starting with the foundational work of Brier et al. (CRYPTO 2011). For example, if $f:\mathbb F_{q}\rightarrow E(\mathbb F_{q})$ is the Shallue–van de Woestijne (SW) map and $\mathfrak {h}_1,\mathfrak {h}_2$ are two independent random oracles to $\mathbb F_{q}$, we now know that $m\mapsto f\big (\mathfrak {h}_1(m)\big )+f\big (\mathfrak {h}_2(m)\big )$ is indifferentiable from a random oracle. Unfortunately, this approach has the drawback of being twice as expensive to compute than the straightforward, but not indifferentiable, $m\mapsto f\big (\mathfrak {h}_1(m)\big )$. Most other solutions so far have had the same issue: they are at least as costly as two base field exponentiations, whereas plain encoding maps like f cost only one exponentiation. Recently, Koshelev (DCC 2022) provided the first construction of indifferentiable hashing at the cost of one exponentiation, but only for a very specific class of curves (some of those with j-invariant 0), and using techniques that are unlikely to apply more broadly.

In this work, we revisit this long-standing open problem, and observe that the SW map actually fits in a one-parameter family $(f_u)_{u\in \mathbb F_{q}}$ of encodings, such that for independent random oracles $\mathfrak {h}_1, \mathfrak {h}_2$ to $\mathbb F_{q}$, $F:m\mapsto f_{\mathfrak {h}_2(m)}\big (\mathfrak {h}_1(m)\big )$ is indifferentiable. Moreover, on a very large class of curves (essentially those that are either of odd order or of order divisible by 4), the one-parameter family admits a rational parametrization, which lets us compute F at almost the same cost as small f, and finally achieve indifferentiable hashing to most curves with a single exponentiation. Our new approach also yields an improved variant of the Elligator Squared technique of Tibouchi (FC 2014) that represents points of arbitrary elliptic curves as close-to-uniform random strings.

1 Introduction

Indifferentiable Hashing to Elliptic Curves. Numerous cryptographic primitives and protocols constructed over elliptic curve groups involve hashing to an elliptic curve: they assume the existence of a public function $\mathfrak {H}$ mapping arbitrary bit strings to elliptic curve points/group elements. Moreover, the function $\mathfrak {H}$ is supposed to behave “like a random oracle”. Such a functionality is required for example for many password-authenticated key exchange protocols, identity-based encryption schemes, short signature schemes, verifiable random functions, oblivious PRFs and more. It is therefore important to understand how it can be efficiently instantiated in practice, and moreover with constant-time implementations, since the data that is hashed to the curve is often sensitive and can thus be compromised by timing side-channel attacks. This problem is in fact currently the subject of an IETF standardization effort within the Crypto Forum Research Group [FHSS+22].

It became an active research topic about a decade ago, particularly after the work of Brier et al. [BCI+10], which applied Maurer et al.’s indifferentiability framework [MRH04] to properly formalize what it meant for $\mathfrak {H}$ to “behave like a random oracle”, and proposed several constructions satisfying the required properties. The design paradigm that emerged at the time as the main approach to hashing to elliptic curve groups combines so-called encoding functions to the elliptic curve, which are algebraic (or piecewise algebraic) maps from the base field to the group of points on the curve, with random oracles to the base field and other sets that are “easy to hash to”, as well as simple arithmetic operations on the curve.

More precisely, consider for instance¹ the problem of hashing to the subgroup $\mathbb {G}$ of cofactor h in $E(\mathbb F_{q})$, where E is an elliptic curve defined over the finite field $\mathbb F_{q}$ and such that $E(\mathbb F_{q})$ is cyclic of order n with generator P. Then Brier et al. [BCI+10] showed that the following construction:

$$\begin{aligned} \mathfrak {H}_{\text {slow}}(m) = [h] \cdot \Big ( f\big (\mathfrak {h}_1(m)\big ) + [\mathfrak {h}_2(m)] P \Big ) \end{aligned}$$

(1)

is indifferentiable from a random oracle when $\mathfrak {h}_1$ and $\mathfrak {h}_2$ are modeled as independent random oracles to $\mathbb F_{q}$ and $\mathbb {Z}/n\mathbb {Z}$ respectively (which are easy to realize, heuristically, using bitstring-valued hash functions) and $f:\mathbb F_{q}\rightarrow E(\mathbb F_{q})$ is a mapping (the encoding function) satisfying mild conditions. This means that whenever² a cryptographic scheme or protocol is proved secure in the random oracle model with respect to a $\mathbb {G}$-valued random oracle $\mathfrak {H}$, that random oracle can be instantiated securely with the construction $\mathfrak {H}_{\text {slow}}$.

As we have mentioned, the construction above requires a suitable encoding function $f:\mathbb F_{q}\rightarrow E(\mathbb F_{q})$. A number of candidates were known at the time for various classes of elliptic curves, such as those of Shallue and van de Woestijne [SvdW06], Ulas [Ula07] or Icart [Ica09], and many more have been proposed since [KLR10, FT10, Far11, FT12, FJT13, BHKL13, WB19]. All of them can be computed in constant time at the cost of one full size exponentiation in $\mathbb F_{q}$ (typically a square root or cube root computation), which dominates the complexity, plus a few other less costly operations in the field, like multiplications, inversions and Jacobi symbol computations.

In contrast, the second term of $\mathfrak {H}_{\text {slow}}$ is a full-size scalar multiplication over the curve, which typically exceeds the computationally cost of a field exponentiation by a factor of 10 or more depending on base field size and curve arithmetic. This makes $\mathfrak {H}_{\text {slow}}$ a fairly inefficient construction.

To alleviate this issue, Brier et al. also proved that the following construction is also indifferentiable from a random oracle:

$$\begin{aligned} \mathfrak {H}_{\text {square}}(m) = [h] \cdot \Big ( f\big (\mathfrak {h}_1(m)\big ) + f\big (\mathfrak {h}_2(m)\big ) \Big ) \end{aligned}$$

(2)

when $\mathfrak {h}_1$ and $\mathfrak {h}_2$ are modeled as independent random oracles to $\mathbb F_{q}$, and when f is specifically Icart’s function. The result was later extended by Farashahi et al. [FFS+13], who showed that basically all of the known encoding functions f could also be plugged into that construction. This provides indifferentiable hashing to arbitrary elliptic curves at the cost of essentially two base fields exponentiations.

On the other hand, in certain primitives and protocols proved secure with respect to a $\mathbb {G}$-valued random oracle $\mathfrak {H}$, one can show that $\mathfrak {H}$ can be securely instantiated using the following simpler construction:

$$\begin{aligned} \mathfrak {H}_{\text {non-unif}}(m) = [h] \cdot f\big (\mathfrak {h}(m)\big ) \end{aligned}$$

(3)

where $\mathfrak {h}$ is modeled as a random oracle to $\mathbb F_{q}$. This construction is not nearly as well-behaved as (2). In fact, f usually only reaches a fraction of the points on $E(\mathbb F_{q})$, and induces a non-uniform distribution over its image, so that $\mathfrak {H}_{\text {non-unif}}$ can typically be efficiently distinguished from a random oracle, and in particular it is not indifferentiable in the sense discussed so far. Nevertheless, certain primitives and protocols do not require the full strength of indifferentiability, and $\mathfrak {H}_{\text {non-unif}}$ is sometimes sufficient to let their security proofs go through.

A rough idea of why this happens is that, in a random oracle proof of security, the simulator generally wants to program the random oracle by setting the hash of some message m to a value Q, but that point Q itself can usually be anything depending on some randomness. So assuming that $h=1$, the simulator might typically want to set $\mathfrak {H}(m)$ to $Q = [r]\cdot P$ for some random r, say. Now if $\mathfrak {H}$ is defined in the protocol using a construction like (3), the simulator would pick a random r and set $\mathfrak {h}(m)$ to one of the preimages $u\in f^{-1}(P)$ if $P\in f(\mathbb F_{q})$. If however P is not in the image of f, the simulator would pick another random r and try again.

Therefore, construction (3), while less general and well-behaved than (2), is sometimes good enough for security at half the computational cost. This is a substantial difference in terms of efficiency that practitioners may be sensitive to, so much so that both of these constructions are in fact proposed in the current IETF draft [FHSS+22]. Construction (3), however, comes with the caveats that applications using it “SHOULD carefully analyze the security implications of nonuniformity”, and that “cryptographic protocols whose security analysis relies on a random oracle that outputs points with a uniform distribution MUST NOT” use it. This results in the somewhat unfortunate situation that implementers have to choose between two approaches for implementing hashing to elliptic curves: one which is secure in all cases but slower, and one which is faster but requires a careful analysis to ascertain that it does not fully compromise the security of the scheme.

The Quest for Fast Indifferentiable Hashing. Ideally, one would prefer to have the best of both worlds: indifferentiable hashing at the cost of a single exponentiation in the base field instead of two. Obtaining this for general elliptic curves is a long-standing open problem.

In special cases, solutions exist: this is particularly the case for supersingular curves of j-invariant 0 and 1728, for which it has long been known [BF01, FT10] that an “almost bijective” encoding function f exists; it is then easy to check that plugging that f into construction (3) does achieve indifferentiability. Unfortunately, those types of supersingular curves, which were popular to reach the 80-bit security level in pairing applications in the early 2000s, are no longer used today due to exceedingly large parameters at higher security levels. Moreover, there are strong reasons to believe that almost bijective encodings cannot exist for general elliptic curves [Tib14b].

Progress towards addressing the general open problem was made by Tibouchi and Kim [TK17], who extended the statistical results of Farashahi et al., and established in particular that, asymptotically, it was possible to achieve indifferentiable hashing at a cost of less than two exponentiations by tweaking construction (1) with a random oracle $\mathfrak {h}_2$ mapping to a short interval. That result is mostly of theoretical significance, however, since it requires very large base fields to provide meaningful error bounds.

Recently, Koshelev [Kos22] made a practically significant advance, by showing that indifferentiable hashing at the cost of a single exponentiation was possible for certain ordinary curves of j-invariant 0 over suitable base fields. This is still a negligible fraction of all elliptic curves, but it is practically relevant since it includes pairing-friendly curves like some of the BLS curves [BLS03] used today. Koshelev’s approach is also the first one considered in the last decade or so that substantially departs from the framework of constructions (1)–(3) above. While those earlier techniques reduce the problem of indifferentiable hashing to the encoding function $f:\mathbb F_{q}\rightarrow E(\mathbb F_{q})$, which is defined over a one-dimensional domain, Koshelev bases his construction on a map $F:\mathbb F_{q}^2\rightarrow E(\mathbb F_{q})$ with a two-dimensional range. Looking back at Brier et al.’s original proof for the indifferentiability of construction (2) using Icart’s encoding function, this is fairly natural (since that proof was constructed around a two-dimensional argument), but it is an important shift in perspective.

In this paper, we use a similar idea (albeit very different techniques) to settle the open problem for a large class of elliptic curves: for essentially all curves over fields $\mathbb F_{q}$ with $q\equiv 1\pmod 3$ with either odd order or order divisible by 4 (this includes almost all elliptic curves in current use), we are able to construct a new indifferentiable hashing, which we call SwiftEC, at the cost of a single exponentiation in the base field.

Representing Points as Uniform Random Strings. A very different question, but which has been tackled using similar techniques, was introduced in Bernstein et al.’s Elligator paper [BHKL13]: how can one represent a uniform point on $E(\mathbb F_{q})$ in a public way as a close to uniform random bit string? The stated goal was to achieve a form of steganography for censorship circumvention. Indeed, network traffic containing points on a certain elliptic curve (e.g. public keys for encryption or signature) represented in usual ways (either as full coordinates (x, y), in compressed form $(x,{{\,\textrm{sgn}\,}}y)$ or in x-only form) can be easily distinguished from random, which may lead to automated traffic interruption or targeted surveillance.

As a countermeasure, Bernstein et al. suggested to use an encoding function $f:\mathbb F_{q}\rightarrow E(\mathbb F_{q})$ with the property that it maps an interval $I\subset \mathbb F_{q}$ of length $\approx q/2$ injectively into $E(\mathbb F_{q})$. Then, any point in f(I) can be represented by its unique preimage under f in I. In particular, if q is close to a power of two, this readily gives a simple representation of random elements in $f(I)\subset E(\mathbb F_{q})$ as uniform random bit strings (and when q is far from a power of two, it suffices to represent elements of I as uniform random bit strings, which can be easily done by expanding the representation and introducing randomness).

This approach has two drawbacks. First, suitable encodings f that are injective over a large interval are hard to construct, and only known for limited families of elliptic curves [Far11, FJT13, BHKL13], all of order divisible by 3 or 4 (and hence not including curves of prime order, for example). Second, one needs to address the issue of points falling outside f(I). Since the goal is to represent random points on $E(\mathbb F_{q})$ as bit strings, the assumption is that in the cryptographic protocol under consideration, the point to represent is obtained by some sort of random process, and it is possible to use rejection sampling until reaching f(I). Since the image size covers roughly half of all points on the curve, this will require about two iterations on average, often an acceptable cost. However, if the process generating the point is expensive, rejecting may be less than ideal.

Tibouchi’s Elligator Squared paper [Tib14a] addressed these shortcomings by, in essence, applied construction (2) above “in reverse”. One of the key properties that makes construction (2) an indifferentiable hash function is the fact that, for an encoding function $f:\mathbb F_{q}\rightarrow E(\mathbb F_{q})$, the following map:

$$\begin{aligned} \begin{aligned} f^{\otimes 2}:\mathbb F_{q}^2&\rightarrow E(\mathbb F_{q}) \\ (u,v)&\mapsto f(u) + f(v) \end{aligned} \end{aligned}$$

(4)

induces a close-to-uniform distribution on its image. In particular, a uniformly random preimage of a uniformly random point in $E(\mathbb F_{q})$ is close to uniform in $\mathbb F_{q}^2$. This provides a simple solution to the point representation problem that works for general elliptic curves and can represent all points, avoiding the need for rejection sampling inside the protocol to reach a particular subset of the curve. However, representation size is about twice as large as Elligator (a drawback partially addressed in subsequent work [TK17]) and the representation function, computing uniformly random preimages under $f^{\otimes 2}$, is also somewhat more complicated and costly than that of Elligator.

Basically, to compute a random preimage of $P\in E(\mathbb F_{q})$, one picks a uniform $v\in \mathbb F_{q}$ and computes u as a preimage of $P-f(v)$. However, rejection sampling is necessary to ensure the uniformity of the distribution, which requires multiple iterations, each of them evaluating the function f (at a cost of a field exponentiation each).

In this paper, as a by-product of our new SwiftEC construction, we also obtain ElligatorSwift, a much faster variant of Elligator Squared over all the curves over which SwiftEC is defined. The idea is that fully computing the underlying encoding in the forward direction becomes unnecessary, saving many field exponentiations in the process.

Contributions and Technical Overview. The starting point of our work is to revisit the first construction of an encoding function to general elliptic curves, originally due to Shallue and van de Woestijne [SvdW06]. We observe that construction actually had a number of interesting properties that have not been considered so far, and that we manage to build upon with suitable additional analysis. To describe them, we need to first recall a few facts about the Shallue–van de Woestijne encoding itself.

Given an elliptic curve $E:y^2 = g(x) =x^3+ax+b$ over a finite field $\mathbb F_{q}$ of characteristic $\ge 5$, Shallue and van de Woestijne construct a certain algebraic surface S in the affine space over $\mathbb F_{q}$ together with three rational functions $x_1,x_2,x_3$ such that the product $g(x_1)g(x_2)g(x_3)$ is a square. This means in particular that, when evaluated at any point P of $S(\mathbb F_{q})$ (outside of the locus of poles), at least one of $x_1(P)$, $x_2(P)$ or $x_3(P)$ must be the x-coordinate of a point in $E(\mathbb F_{q})$. Indeed, the product $g\big (x_1(P)\big )g\big (x_2(P)\big )g\big (x_3(P)\big )$ is a square in $\mathbb F_{q}$, and since the product of three nonsquares in $\mathbb F_{q}$ is a nonsquare, at least one of the factors must be square, yielding the x-coordinate of a point in $E(\mathbb F_{q})$. Based on that, we can define an encoding function from $S(\mathbb F_{q})$ to $E(\mathbb F_{q})$ simply by mapping a point P to one of the points of x-coordinate $x_i(P)$ that works (selecting the index i and the sign of the y-coordinate in a predetermined way).

The second step of the construction is to note that the specific surface S under consideration can in fact be seen as a one-parameter family of conics over $\mathbb F_{q}$. Based on that, Shallue and van de Woestijne fix the value of the parameter, obtain a single non-degenerate conic over $\mathbb F_{q}$, and use the fact that such a conic always admits a rational parametrization to obtain a map $\mathbb F_{q}\rightarrow S(\mathbb F_{q})$ to the chosen conic. Composing with the previous map finally gives an encoding $\mathbb F_{q}\rightarrow E(\mathbb F_{q})$ as desired, which can be used in constructions (1)–(3) above for hashing, and in the Elligator Squared framework: this is what is usually known as the Shallue–van de Woestijne encoding.

Our contributions rely on two novel observations regarding that original construction:

• first, for a large class of elliptic curves E which we characterize in detail, the surface S regarded as a family of conics actually admits a global, two-parameter parametrization over $\mathbb F_{q}$. This means that one can effectively construct a rational map $\mathbb F_{q}^2 \rightarrow S(\mathbb F_{q})$ that is essentially a bijection. This result is obtained using techniques due to van Hoeij and Cremona [vHC06] classifying conics over function fields;

• second, unlike each of the maps defined by individual conics, the map from $S(\mathbb F_{q})$ as a whole to the set $X_{E,\mathbb F_{q}}$ of elements of $\mathbb F_{q}$ which are x-coordinates on $E(\mathbb F_{q})$ is admissible: it satisfies the sufficient conditions of Brier et al. [BCI+10] to construct indifferentiable hashing. The most important of those conditions is regularity: the image of a uniform point in $S(\mathbb F_{q})$ is close to uniform in $X_{E,\mathbb F_{q}}$. We are able to establish that property by giving a precise description of the preimage of an $x\in X_{E,\mathbb F_{q}}$: it consists of the union of one algebraic curve drawn on S (the set of points P such that $x_1(P)=x$, say) and two halves of two other curves (the subset of the curves given by $x_2(P)=x$ and $x_3(P)=x$ respectively, with the condition that $g(x_1(P))$ is a nonsquare). By counting points on those curves and curve subsets, we are able to establish the required statistical properties, and deduce that $S(\mathbb F_{q})\rightarrow X_{E,\mathbb F_{q}}$ is admissible.

Combining those two observations, we obtain, for a large, explicit class of elliptic curves E (including almost all curves in practical use), an admissible encoding $\mathbb F_{q}^2\rightarrow X_{E,\mathbb F_{q}}$. Adding a sign bit to choose the y-coordinate on E yields an admissible encoding $F:\mathbb F_{q}^2\times \{0,1\}\rightarrow E(\mathbb F_{q})$ as well, which can be computed at the cost of a single exponentiation in $\mathbb F_{q}$ (namely, the square root computation needed to derive the y-coordinate). This has the two consequences mentioned above, over the elliptic curves E of interest:

• given a hash function $\mathfrak {h}$ modeled as a random oracle with values in $\mathbb F_{q}^2\times \{0,1\}$ (which is easy to heuristically instantiate), the map $m\mapsto F\big (\mathfrak {h}(m)\big )$ is indifferentiable from a random oracle, and can be computed at the cost of a single exponentiation. This is the SwiftEC construction;

• given a uniform point on the curve, we can efficiently sample a uniform preimage of it under F, and this becomes a close-to-uniformly distributed element of $\mathbb F_{q}^2\times \{0,1\}$. Since such an element is easy to represent as a uniform bit string, we thus obtain an Elligator Square-like representation technique which is much faster than Elligator Square itself, as it requires far fewer field exponentiations on average. This is the ElligatorSwift construction.

In addition, we also get indifferentiable hashing to the set $X_{E,\mathbb F_{q}}$ without any field exponentiation at all. This even faster construction, XSwiftEC, is particularly interesting in context where x-only arithmetic is feasible, such as for example BLS signatures [BLS01].

2 Preliminaries

2.1 Quadratic Residuosity

Throughout this paper, $\mathbb F_{q}$ denotes the finite field with q elements. We only consider finite fields of characteristic $\ne 2,3$. The quadratic character $\chi _2:\mathbb F_{q}\rightarrow \{-1,0,1\}$ is the map that sends 0 to 0, nonzero squares to 1 and nonzero nonsquares to $-1$. It is well-defined, multiplicative, and extends the unique nontrivial multicative group morphism $\mathbb F_{q}^\times \rightarrow \{-1,1\}$. A related map is ${{\,\textrm{IsSquare}\,}}$, which sends all squares to 1 and nonsquares to 0.

When q is prime, the quadratic character coincides with the Legendre symbol, and can be computed efficiently by repeated applications of quadratic reciprocity. This can be implemented in fast constant time [Por20, Ham21, AG21], similar to the constant-time binary GCD technique of Bernstein–Yang for field inversion [BY19]. Similarly, the quadratic character over extension fields can be computed fast by descending to the prime field, and ${{\,\textrm{IsSquare}\,}}$ can be trivially computed from $\chi _2$.

We also fix an efficiently computable map ${{\,\textrm{sgn}\,}}:\mathbb F_{q}\rightarrow \{-1,0,1\}$ called the “sign”, with the property that ${{\,\textrm{sgn}\,}}0 = 0$, ${{\,\textrm{sgn}\,}}x\ne 0$ for $x\ne 0$, and ${{\,\textrm{sgn}\,}}(-x)=-{{\,\textrm{sgn}\,}}x$. The choice is arbitrary, but for example over prime fields, it is customary to use the sign of an integer representative in the interval $(-q/2,q/2)$ (over extension fields, one might choose the sign of the first nonzero coefficient in some basis over the prime field).

An element $x\in \mathbb F_{q}$ which is a square has exactly two square roots (except 0 which has just one), exactly one of which is of nonnegative sign. We denote it by $\sqrt{x}$; it typically requires a single base field exponentiation to compute (although slightly faster approaches may exist over extension fields).

2.2 Elliptic Curves and Isogenies

An elliptic curve is a smooth projective curve of genus 1 endowed with a distinguished rational point. Such curves admit the definition of a point addition law, which gives the curve a structure as group variety, with the distinguished point playing the role of the group identity. Over $\mathbb F_{q}$, any elliptic curve can be written up to isomorphism in the short Weierstrass form:

$$\begin{aligned} E:y^2 = x^3+ax+b, \end{aligned}$$

for some $a,b\in \mathbb F_{q}$ such that the discriminant $\varDelta _E := -16(4a^3+27b^2)$ is nonzero. On such a curve, group inverses are defined by $-(x,y) = (x, -y)$ and the points of order 2 are those with $y=0$. When $\varDelta _E$ is a square there are either zero or three points of order 2. Otherwise, there is exactly one.

We denote by $E(\mathbb F_{q})$ the group of $\mathbb F_{q}$-rational points of E. The cardinality of this group is always $\#E(\mathbb F_{q})=q-t+1$ for some t bounded by $|t|\le 2\sqrt{q}$. We say that the curve is supersingular if t is a multiple of the field characteristic, and otherwise the curve is ordinary. We focus on the case of ordinary elliptic curves, where finding adequate and efficient encodings has long been a greater challenge.

An isogeny is any non-constant rational map between elliptic curves that is also a group homomorphism. Up to an isomorphism, a separable isogeny is uniquely determined by its kernel and its degree as a rational map is equal to the size of the kernel. Any isogeny $\phi :E\rightarrow E'$ has a dual isogeny $\hat{\phi }:E'\rightarrow E$ such that the composition $\hat{\phi }\circ \phi$ equals the multiplication-by-d map, where $d=\deg (\phi )$. Two curves over a finite field are isogenous if and only if they have exactly the same number of points.

2.3 Point Counting and Character Sums

A generalization of the result above on the number of rational points of an elliptic curve is that any (absolutely irreducible) smooth curve of bounded genus over $\mathbb F_{q}$ has a number of points over $\mathbb F_{q}$ close to q. More precisely, the following celebrated result holds:

Lemma 1 (Hasse–Weil bound)

For any smooth projective absolutely irreducible curve $X/\mathbb F_{q}$ of genus g, we have:

$$\begin{aligned} \big | \#X(\mathbb F_{q}) - (q+1) \big | \le 2g\sqrt{q}. \end{aligned}$$

For curves of bounded degree, the number of points at infinity is also bounded, and we thus get a bound of the form $\#X^{\text {aff}}(\mathbb F_{q}) = q + c\sqrt{q} + O(1)$ ($|c|\le 2g$) on the number of affine points on X.

A related result concerns character sums on such curves. Let $\chi$ be a multiplicative character of $\mathbb F_{q}$ (a group homomorphism $\mathbb F_{q}^\times \rightarrow \mathbb {C}^\times$ extended by 0 at 0), and $f\in \mathbb F_{q}(X)$ a rational function on the curve X. We consider the following character sum:

$$ W(X,\chi ,f) = \sum _{\begin{array}{c} P\in X(\mathbb F_{q}) \\ f(P)\ne \infty \end{array}} \chi \big (f(P)\big ). $$

Using the Bombieri–Weil methodology, Perret [Per91] proves the following bound. See also [CM00, TK17].

Lemma 2 (Perret)

Let X be a smooth projective absolutely irreducible curve of genus g over $\mathbb F_{q}$, $\chi$ a nontrivial multiplicative character of order $m | q-1$, and $f\in \mathbb F_{q}(X)$ a rational function which is not a perfect m-th power in $\bar{\mathbb {F}}_q(X)$. The character sum $W(X,\chi ,f)$ can be bounded as:

$$\begin{aligned} \big | W(X,\chi ,f) \big | \le (2g-2 + 2\deg f)\sqrt{q}. \end{aligned}$$

2.4 Quadratic Residuosity over Function Fields

Many results of classical arithmetic over $\mathbb {Q}$ and number fields have analogues over function fields. This is in particular the case for quadratic reciprocity. We recall some of the relevant results below. An exhaustive treatment is provided in Rosen’s textbook [Ros02, pp. 23-31].

For a fixed monic irreducible polynomial $f\in \mathbb F_{q}[t]$, we define the quadratic residue symbol $\left( \frac{g}{f}\right) _2$ for any $g\in \mathbb F_{q}[t]$ as the image of g under the quadratic character of the finite field $\mathbb F_{q}[t]/(f)$. In other words:

$$ \left( \frac{g}{f}\right) _2 = {\left\{ \begin{array}{ll} 0 &{} \text {if}\, f\, \text {divides}\, g; \\ 1 &{} \text {if}\, g\,\text {is coprime to}\, f\, \text {and a square modulo}\, f; \\ -1 &{} \text {if}\,g\, \text {is coprime to}\, f\, \text {and a nonsquare modulo}\, f. \end{array}\right. } $$

We then extend this symbol to not necessarily irreducible f’s by multiplicativity, similarly to how the Jacobi symbol extends the Legendre symbol. If $f = \alpha f_1^{e_1}\cdots f_n^{e_n}$ with $\alpha \in \mathbb F_{q}^\times$ and the $f_i$ irreducible, we let:

$$ \left( \frac{g}{f}\right) _2 = \prod _{i=1}^{n} \left( \frac{g}{f_i}\right) _2. $$

Note that the symbol does not depend on the leading coefficient ${{\,\textrm{lc}\,}}(f)=\alpha$ of f.

Lemma 3

The quadratic residue symbol has the following properties.

• If $g_1\equiv g_2\pmod f$, $\left( \frac{g_1}{f}\right) _2 = \left( \frac{g_2}{f}\right) _2$.

• $\left( \frac{g_1g_1}{f}\right) _2 = \left( \frac{g_1}{f}\right) _2\left( \frac{g_2}{f}\right) _2$.

• $\left( \frac{g}{f_1f_2}\right) _2 = \left( \frac{g}{f_1}\right) _2\left( \frac{g}{f_2}\right) _2$.

• $\left( \frac{g}{f}\right) _2\ne 0$ if and only if f and g are coprime.

• If g is a nonzero square modulo f, then $\left( \frac{g}{f}\right) _2=1$ (but the converse does not need to hold).

Furthermore, it satisfies the following law of quadratic reciprocity. For $f,g\in \mathbb F_{q}[t]$ coprime and nonzero, it holds that:

$$ \left( \frac{g}{f}\right) _2 \left( \frac{f}{g}\right) _2 = (-1)^{\frac{q-1}{2}\deg f \deg g} {{\,\textrm{lc}\,}}(f)^{\frac{q-1}{2}\deg g} {{\,\textrm{lc}\,}}(g)^{\frac{q-1}{2}\deg f}. $$

2.5 Statistical Notions

For $\mathscr {D}$ a probability distribution on a finite set S, we write $\Pr [s\leftarrow \mathscr {D}]$ for the probability assigned to the singleton $\{s\}\subset S$ by $\mathscr {D}$. The uniform distribution on S is denoted by $\mathscr {U}_S$ (or just $\mathscr {U}$ if the context is clear).

Definition 1 (Statistical distance)

Let $\mathscr {D}$ and $\mathscr {D}'$ be two probability distributions on a finite set S. The statistical distance between them is defined as the $\ell _1$ norm:

$$ \varDelta _1(\mathscr {D},\mathscr {D}')=\frac{1}{2} \sum _{s\in S} \big | \Pr [s\leftarrow \mathscr {D}] - \Pr [s\leftarrow \mathscr {D}']\big |. $$

We simply denote by $\varDelta _1(\mathscr {D})$ the statistical distance between $\mathscr {D}$ and $\mathscr {U}_S$:

$$\begin{aligned} \varDelta _1(\mathscr {D})=\frac{1}{2} \sum _{s\in S} \Big | \Pr [s\leftarrow \mathscr {D}] - \frac{1}{\#S}\Big |, \end{aligned}$$

and say that $\mathscr {D}$ is $\varepsilon$-statistically close to uniform when $\varDelta _1(\mathscr {D})\le \varepsilon$. When $\varDelta _1(\mathscr {D})$ is negligible, we simply say than $\mathscr {D}$ is statistically close to uniform.

Definition 2 (Pushforward)

Let S, T be two finite sets and F any mapping from S to T. For any probability distribution $\mathscr {D}_S$ on S, we can define the pushforward $F_*\mathscr {D}_S$ of $\mathscr {D}_S$ by F as the probability distribution on T such that sampling from $F_*\mathscr {D}_S$ is equivalent to sampling a value $s\leftarrow \mathscr {D}_S$ and returning F(s). In other words:

$$ \Pr \big [t\leftarrow F_*\mathscr {D}_S\big ] = \Pr \big [s\leftarrow \mathscr {D}_S;\ t=F(s)\big ] = \mu _S\big (F^{-1}(t)\big ) = \sum _{s\in F^{-1}(t)} \Pr [s\leftarrow \mathscr {D}_S], $$

where $\mu _S$ is the probability measure defined by $\mathscr {D}_S$.

Definition 3 (Regularity)

Let S, T be two finite sets and F any mapping from S to T. We say that F is $\varepsilon$-regular when $F_*\mathscr {U}_S$ is $\varepsilon$-close to the uniform distribution. We may omit $\varepsilon$ if it is negligible.

2.6 Admissible Encodings

In their work on the construction of indifferentiable hashing to elliptic curves, Brier et al. [BCI+10] define the notion of an admissible map $F:S\rightarrow R$ between two sets. The definition, which generalizes an early notion introduced by Boneh and Franklin [BF01], is as follows.

Definition 4 (Admissible encoding)

A function $F:S \rightarrow R$ between finite sets is an $\varepsilon$-admissible encoding if it satisfies the following properties:

• Computable: F is computable in deterministic polynomial time.

• Regular: F is $\varepsilon$-regular (in the sense of the previous section).

• Samplable: there is an efficient randomized algorithm $\mathscr {I}:R\rightarrow S\sqcup \{\bot \}$ such that for any $r \in R$, $\mathscr {I}(r)$ induces a distribution that is $\varepsilon$-statistically close to the uniform distribution in $F^{-1}(r)$.

F is an admissible encoding if it is $\varepsilon$-admissible for some negligible $\varepsilon$.

That notion satisfies the suitable properties such that, given an S-valued random oracle $\mathfrak {h}$, the composition $F\circ \mathfrak {h}$ is indifferentiable from a R-valued random oracle.

Moreover a similar results holds for arbitrary compositions of admissible functions (even though admissibility need not be preserved under composition). Namely, if $F_i:S_i\rightarrow S_{i-1}$ are admissible encodings for $i=1,\dots ,n$, then it also holds that, given an $S_n$-valued random oracle $\mathfrak {h}$, the composition $F_1\circ \cdots \circ F_n\circ \mathfrak {h}$ is indifferentiable from a $S_0$-valued random oracle (even though it does not always hold that $F_1\circ \cdots \circ F_n$ is admissible).

3 The SW Encoding Family

In their seminal ANTS–VII paper [SvdW06], Shallue and van de Woestijne constructed the first encoding function to arbitrary elliptic curves. In this section, we give a description of that construction (restricted for simplicity to base fields of characteristic $\ge 5$) that is slightly different but essentially equivalent to the original one, and then we state new properties of that construction.

In the entire section, we fix an elliptic curve $E:y^2 = x^3 + ax + b$ over the finite field $\mathbb F_{q}$ (q prime power not divisible by 2 or 3), and denote by $X_{E,\mathbb F_{q}}$ the subset of $\mathbb F_{q}$ consisting of x-coordinates of points in $E(\mathbb F_{q})$; in other words:

$$\begin{aligned} X_{E,\mathbb F_{q}} = \big \{ x\in \mathbb F_{q}\ ;\ \exists y,\ (x,y) \in E(\mathbb F_{q}) \big \}. \end{aligned}$$

3.1 Construction of the Shallue–van de Woestijne Encoding

Let g and h be the polynomials over $\mathbb F_{q}$ defined by:

$$\begin{aligned} g(u) = u^3 + au + b \quad \text {and}\quad h(u) = 3u^2 + 4a. \end{aligned}$$

The starting point of the Shallue–van de Woestijne construction is the construction of a rational map $\psi :S\rightarrow V$ from the following quasi-affine surface in the (x, y, u) affine space:

$$\begin{aligned} S:x^2 + h(u) y^2 = -g(u),\quad y\ne 0 \end{aligned}$$

(5)

to the following threefold in the $(x_1,x_2,x_3,z)$ affine 4-dimensional space:

$$\begin{aligned} V:z^2 = g(x_1) g(x_2) g(x_3). \end{aligned}$$

The rational map $\psi$ is given by the following explicit equations and clearly defined everywhere on S:

$$\begin{aligned} \begin{aligned} x_1&= \frac{x}{2y} - \frac{u}{2}&x_2&= -\frac{x}{2y} - \frac{u}{2} \\ x_3&= u + 4y^2&z&= \frac{g(u+y^2)}{y}\cdot R\Big (u, \frac{x}{2y} - \frac{u}{2}\Big ) \end{aligned} \end{aligned}$$

(6)

where $R(u,v) = u^2+uv+v^2 + a$. When referring to a point P on S, we will denote by $x_1(P)$, $x_2(P)$, $x_3(P)$ and z(P) the corresponding coordinates of $\psi (P)$ in V. In particular, this defines $x_1$, $x_2$, $x_3$ and z as rational functions on the surface.

A remarkable property of the threefold V is that for any point $(x_1,x_2,x_3,z)\in V(\mathbb F_{q})$, at least one of the three values $x_1,x_2,x_3$ must be in $X_{E,\mathbb F_{q}}$. Indeed, $g(x_1) g(x_2) g(x_3)$ is a square in $\mathbb F_{q}$, so by multiplicativity of the quadratic character, they cannot be all nonsquares (and in fact, there must be exactly one or three squares among them, except possibly when $z=0$).

As a result, one can therefore map points on $S(\mathbb F_{q})$ to $X_{E,\mathbb F_{q}}$ by first mapping to $V(\mathbb F_{q})$ with $\psi$, and then selecting one of the coordinates $x_1,x_2,x_3$ in a prescribed order. For example, in this paper we will consider the following map:

$$\begin{aligned} F_0:S(\mathbb F_{q})&\rightarrow X_{E,\mathbb F_{q}} \nonumber \\ P&\mapsto {\left\{ \begin{array}{ll} x_3(P) &{} \text {if}\, g\big (x_3(P)\big )\, \text {is a square;} \\ x_2(P) &{} \text {if}\, g\big (x_3(P)\big )\, \text {is not a square but}\, g\big (x_2(P)\big )\, \text {is;} \\ x_1(P) &{} \text {if neither}\, g\big (x_3(P)\big )\, \text {nor}\, g\big (x_2(P)\big )\, \text {are squares.} \end{array}\right. } \end{aligned}$$

(7)

Note that $F_0(P)$ is very efficient to compute from the coordinates (x, y, u) of P using the formulas of (6) and a few quadratic character computations. In particular, it requires no field exponentiation.

Of course, once we have an element $\bar{x}\in X_{E,\mathbb F_{q}}$, it is easy to deduce a point in $E(\mathbb F_{q})$: simply compute a square root of $g(\bar{x})$ to get the y-coordinate up to sign. Since we prefer to select the sign separately, we define the following extended map to $E(\mathbb F_{q})$ which takes an additional input bit b:

$$\begin{aligned} \begin{aligned} F_0^+:S(\mathbb F_{q})\times \{0,1\}&\rightarrow E(\mathbb F_{q}) \\ (P,b)&\mapsto \Big ( F_0(P),\ (-1)^b \sqrt{g\big (F_0(P)\big )} \Big ). \end{aligned} \end{aligned}$$

(8)

The construction offers a way to map to $E(\mathbb F_{q})$ provided that one can construct rational points on the surface S itself, which may not be a priori obvious. Fortunately, as seen from Eq. (5), each of the curves $S_{u_0}$ on S obtained by fixing u to some $u_0\in \mathbb F_{q}$ are simply conics over $\mathbb F_{q}$, with equations:

$$\begin{aligned} x^2 + h(u_0) y^2 = -g(u_0),\quad y\ne 0. \end{aligned}$$

Now, a conic over $\mathbb F_{q}$ always admits a rational parametrization. Therefore, we can construct a map $\mathbb F_{q}\rightarrow S_{u_0}(\mathbb F_{q})$ that can then be composed with $F_0^+$ to obtain an encoding function $F_{0,u_0}:\mathbb F_{q}\rightarrow X_{E,\mathbb F_{q}}$ (and similarly to $E(\mathbb F_{q})$). This is basically the approach taken in the original paper of Shallue and van de Woestijne [SvdW06].

Note that obtaining the parametrization of the conic $S_{u_0}$ for a fixed $u_0$ requires an a priori costly precomputation (it requires finding a point on the conic, typically by trial-and-error: this costs a square root, and a number of quadratic character computations that is hard to bound uniformly). Therefore, while it may be tempting to try and define a two-parameter map $\mathbb F_{q}^2\rightarrow X_{E,\mathbb F_{q}}$ by $(t,u)\mapsto F_{0,u}(t)$, this is not usually workable for hashing purposes, since a new parametrization would have to be computed for any new input u.

Nevertheless, we show in the remainder of this section that the maps $F_0$ and $F_0^+$ on the surface $S(\mathbb F_{q})$ as a whole have nice statistical properties, and it would therefore be beneficial to overcome the difficulty of efficiently parametrizing it. That problem will then be addressed, at least for a large class of elliptic curves E, in Sect. 4 below.

3.2 Geometry of the SW Family

For a fixed element $\bar{x}\in X_{E,\mathbb F_{q}}$, we now want to describe the set of points in $S(\mathbb F_{q})$ that map to $\bar{x}$ under the encoding $F_0$ of (7). By the previous description of the encoding, this is the union of three disjoint sets:

$$ F_0^{-1}(\bar{x}) = C_{\bar{x}}^{(3)}(\mathbb F_{q}) \sqcup C_{\bar{x}}^{(2)}(\mathbb F_{q})^+ \sqcup C_{\bar{x}}^{(1)}(\mathbb F_{q})^+, $$

where $C_{\bar{x}}^{(i)}$ are algebraic curves on S defined by the condition that $x_i = \bar{x}$ ($i\in \{1,2,3\}$) and $C_{\bar{x}}^{(i)}(\mathbb F_{q})^+$ is the subset of $C_{\bar{x}}^{(i)}(\mathbb F_{q})$ under the condition that $g\big (x_j(P)\big )$ is not a square for $j\ne i$. Note that since there are always exactly only 1 or 3 squares, it suffices to define

$$\begin{aligned} C_{\bar{x}}^{(1)}(\mathbb F_{q})^+ := \{ P\in C_{\bar{x}}^{(1)}(\mathbb F_{q});~x_2(P)~\text {not a square}\} \end{aligned}$$

$$\begin{aligned} C_{\bar{x}}^{(2)}(\mathbb F_{q})^+ := \{ P\in C_{\bar{x}}^{(2)}(\mathbb F_{q});~x_1(P)~\text {not a square}\} \end{aligned}$$

We would like to count the number of points in each of these sets. The first step is to understand the geometry of the curves $C_{\bar{x}}^{(i)}$. It is easy to see that, for a generic $\bar{x}$, they are hyperelliptic curves of genus 2.

Consider for example $C_{\bar{x}}^{(3)}$. It is given by the equations (cf. (6)):

$$\begin{aligned} u+4y^2 = \bar{x} \quad \text {and}\quad x^2 + h(u)y^2 = -g(u). \end{aligned}$$

Eliminating $u=\bar{x}-4y^2$ between those two equations, we see that $C_{\bar{x}}^{(3)}$ is isomorphic to the curve in the (y, x) affine plane given by the equation:

$$\begin{aligned} x^2 = -g(\bar{x} - 4y^2) - h(\bar{x}-4y^2)y^2. \end{aligned}$$

The right-hand side is a polynomial of degree 6 in y, namely:

$$\begin{aligned} 16y^6 - 24\bar{x}y^4 + 9\bar{x}^2y^2 - g(\bar{x}), \end{aligned}$$

whose discriminant is a polynomial of degree exactly 11 in $\bar{x}$ (or exactly 9 if $a=0$). We thus get that $C_{\bar{x}}^{(3)}$ is a hyperelliptic curve of genus 2, except for at most 11 points $\bar{x}$. Other than for those exceptional points, we have:

$$ \#C_{\bar{x}}^{(3)}(\mathbb F_{q}) = q + c_3\sqrt{q} + O(1), \quad \text {for some}\, c_3\, \mathrm{{such\,that}}\, |c_3|\le 4. $$

by the Hasse–Weil bound. Note that the O(1) term comes from the fact that we consider the affine situation rather than the projective one, and we could easily provide an explicit bound for it, but this is typically not of interest for cryptographic applications.

By a similar analysis, we find that both $C_{\bar{x}}^{(1)}$ and $C_{\bar{x}}^{(2)}$ are isomorphic to the curve in the (u, v) affine plane (where $v=y\big [ (u+2\bar{x})^2 + h(u) \big ]$) of equation:

$$\begin{aligned} v^2 = -g(u) \cdot \big [ (u+2\bar{x})^2 + h(u) \big ]. \end{aligned}$$

The right-hand side is a polynomial of degree 5 in u, namely:

$$ -4\big (u^5 + \bar{x} u^4 + (\bar{x}^2 + 2a)u^3 + (a\bar{x} + b)u^2 + (a\bar{x}^2 + b\bar{x} + a^2)u + b(\bar{x}^2 + a)\big ), $$

and its discriminant is always of degree 14 in $\bar{x}$ (the degree 14 coefficient is $2^{16}\cdot 3\cdot (4a^3+27b^2)\ne 0$). Thus, $C_{\bar{x}}^{(1)}$ and $C_{\bar{x}}^{(2)}$ are hyperelliptic curves of genus 2, except for at most 14 points $\bar{x}$. Other than for those exceptional points, we therefore have:

$$ \#C_{\bar{x}}^{(1)}(\mathbb F_{q}) = q + c_1\sqrt{q} + O(1) \quad \text {for some}\, c_1\, \text {such that}\, |c_1|\le 4 $$

$$ \#C_{\bar{x}}^{(2)}(\mathbb F_{q}) = q + c_2\sqrt{q} + O(1) \quad \text {for some}\,c_2\, \text {such that}\,|c_2|\le 4 $$

by the Hasse–Weil bound.

It remains to evaluate the cardinality of the subsets $C_{\bar{x}}^{(i)}(\mathbb F_{q})^+\subset C_{\bar{x}}^{(i)}(\mathbb F_{q})$ for $i\in \{1,2\}$. One can do so in various ways, but the simplest is probably to relate them to character sums. Consider for example the following character sum on $C_{\bar{x}}^{(1)}$:

$$ W_1 := W\big (C_{\bar{x}}^{(1)},\chi _2,g\circ x_2\big ) = \sum _{P\in C_{\bar{x}}^{(1)}(\mathbb F_{q})} \chi _2\Big (g\big (x_2(P)\big )\Big ), $$

where $\chi _2$ is the quadratic multiplicative character of $\mathbb F_{q}$. The term $\chi _2\Big (g\big (x_2(P)\big )\Big )$ is equal to $-1$ if $g\big (x_2(P)\big )$ is not a square in $\mathbb F_{q}$, which is exactly when $P\in C_{\bar{x}}^{(1)}(\mathbb F_{q})^+$. Moreover, it is otherwise equal to 1 (for points outside $C_{\bar{x}}^{(1)}(\mathbb F_{q})^+$ such that $x_2(P)\ne 0$) or 0 (for points outside $C_{\bar{x}}^{(1)}(\mathbb F_{q})^+$ such that $x_2(P)=0$). As a result, we have:

$$\begin{aligned} W_1&= (-1)\cdot \#C_{\bar{x}}^{(1)}(\mathbb F_{q})^+ + 1\cdot (\#C_{\bar{x}}^{(1)}(\mathbb F_{q}) - \#C_{\bar{x}}^{(1)}(\mathbb F_{q})^+ - N_0) + 0\cdot N_0 \\&= \#C_{\bar{x}}^{(1)}(\mathbb F_{q}) - 2\cdot \#C_{\bar{x}}^{(1)}(\mathbb F_{q})^+ - N_0, \end{aligned}$$

where $N_0 = O(1)$ is the number of points in $C_{\bar{x}}^{(1)}(\mathbb F_{q})$ such that $x_2(P)=0$. This gives:

$$ \#C_{\bar{x}}^{(1)}(\mathbb F_{q})^+ = \frac{1}{2} \#C_{\bar{x}}^{(1)}(\mathbb F_{q}) - \frac{W_1}{2} + O(1) = \frac{q}{2} + \frac{c_1}{2}\sqrt{q} - \frac{W_1}{2} + O(1), $$

where the O(1) term accounts both for $N_0$ and for the fact that we consider an affine situation instead of a projective one.

Then, by the character sum estimate of Lemma 2, we have:

$$ |W_1| \le \big (4-2 + 2\deg (g\circ x_2)\big )\sqrt{q} + O(1) = (2+2\cdot 3\cdot 2)\sqrt{q} + O(1) = 14\sqrt{q}+O(1) $$

since $x_2 = -u-\bar{x}$ on $C_{\bar{x}}^{(1)}$ is a rational function of degree 2. It then follows that:

$$ \#C_{\bar{x}}^{(1)}(\mathbb F_{q})^+ = \frac{q}{2} + c_1^+\sqrt{q} + O(1) \quad \text {for some}\, c_1^+\, \text {such that}\, |c_1^+|\le \frac{4+14}{2} = 9. $$

Obviously, the exact same argument applies to $C_{\bar{x}}^{(2)}$, yielding:

$$ \#C_{\bar{x}}^{(2)}(\mathbb F_{q})^+ = \frac{q}{2} + c_2^+\sqrt{q} + O(1) \quad \text {for some}\, c_2^+\, \text {such that}\, |c_2^+|\le 9. $$

Combining all the previous estimates, we finally obtain the following result.

Theorem 1

For all $\bar{x}\in X_{E,\mathbb F_{q}}$ except at most 39 of them, the number of preimages of $\bar{x}$ under the $F_0$ map of Eq. (7) is close to 2q, and the difference is bounded as:

$$\begin{aligned} \big | \#F_0^{-1}(\bar{x}) - 2q \big | \le 22\sqrt{q} + O(1). \end{aligned}$$

Proof

Indeed, except for the at most $11+14+14 = 39$ exceptional points mentioned above, we have:

$$ \#F_0^{-1}(\bar{x}) = \Big (1+\frac{1}{2}+\frac{1}{2}\Big )q + \big (c_1^+ + c_2^+ + c_3\big )\sqrt{q} + O(1) $$

and since $\big |c_1^+ + c_2^+ + c_3|\le 4+9+9 = 22$, the result follows.

3.3 The SW Family Is Admissible

Using Theorem 1, we are now in a position to prove that the encoding function $F_0$ is admissible in the sense of Sect. 2.6. The main step in doing so is to prove that it is regular.

Lemma 4

The map $F_0:S(\mathbb F_{q})\rightarrow X_{E,\mathbb F_{q}}$ of Eq.  (7) is $\varepsilon$-regular for $\varepsilon =\big (6+o(1)\big )q^{-1/2}$.

Proof

Let $\varDelta = \varDelta _1\big ((F_0)_*\mathscr {U}_{S(\mathbb F_{q})}\big )$ be the statistical distance between the distribution induced by $F_0$ on $X_{E,\mathbb F_{q}}$ and the uniform distribution. By definition, we have:

$$ \varDelta = \frac{1}{2} \sum _{\bar{x}\in X_{E,\mathbb F_{q}}} \bigg | \frac{\#F^{-1}(\bar{x})}{\#S(\mathbb F_{q})} - \frac{1}{\#X_{E,\mathbb F_{q}}} \bigg |. $$

Now for each element $\bar{x}\in X_{E,\mathbb F_{q}}$, there are exactly two points of $E(\mathbb F_{q})$ with x-coordinate equal to $\bar{x}$, except if $g(\bar{x})=0$, in which case there is exactly one (and this happens for at most three values of $\bar{x}$). Taking the point at infinity into account, we therefore get:

$$ \#X_{E,\mathbb F_{q}} = \frac{1}{2} \#E(\mathbb F_{q}) + O(1) = \frac{q}{2} + c_E\sqrt{q} + O(1) \quad \text {for some}\,c_E\, \text {with}\,|c_E|\le 1 $$

by yet another application of the Hasse–Weil bound. Up to sign, the constant $c_E$ is half the normalized Frobenius trace of E.

Moreover, $S(\mathbb F_{q})$ is the disjoint union of the various affine conics $\big \{ x^2+h(u_0)y^2 = -g(u_0),\ u=u_0 \big \}$ for all $u_0\in \mathbb F_{q}$. Those conics are nondegenerate whenever $g(u_0)h(u_0)\ne 0$, in which case they have $q+O(1)$ points. In remaining exceptional cases, they have at most 2q points. As a result, we get:

$$ \#S(\mathbb F_{q}) = \big (q-O(1)\big )\cdot \big (q+O(1)\big ) + O(1)\cdot O(q) = q^2 + O(q). $$

As for the number of preimages of F, we know by Theorem 1 that for each $\bar{x}\in X_{E,\mathbb F_{q}}\setminus X_{\text {bad}}$, where $X_{\text {bad}}$ is a set of 39 points, there exists $c_{0,\bar{x}}\in [-22,22]$ such that:

$$\begin{aligned} \#F^{-1}(\bar{x}) = 2q + c_{0,\bar{x}}\sqrt{q} + O(1) \quad \quad \forall \bar{x}\in X_{E,\mathbb F_{q}}\setminus X_{\text {bad}} \end{aligned}$$

For $\bar{x}\in X_{\text {bad}}$, we can still obtain a less strict but simpler bound: note that for any fixed $u = u_0\in \mathbb F_{q}$ the equations $\bar{x} = x_1(x, y, u_0)$, $\bar{x} = x_2(x, y, u_0)$ and $\bar{x} = x_3(x, y, u_0)$ have at most 2, 2, and 4 solutions in S, respectively (these solutions are given explicitly in Sect. 6). Hence, any point can have at most 8 preimages for any fixed $u_0$ and at most 8q preimages in all.

We can now bound $\varDelta$ as follows:

$$\begin{aligned} 2\varDelta&= \sum _{\bar{x}\in X_{E,\mathbb F_{q}}\setminus X_{\text {bad}}} \bigg | \frac{\#F^{-1}(\bar{x})}{\#S(\mathbb F_{q})} - \frac{1}{\#X_{E,\mathbb F_{q}}} \bigg | + \sum _{\bar{x}\in X_{\text {bad}}} \bigg | \frac{\#F^{-1}(\bar{x})}{\#S(\mathbb F_{q})} - \frac{1}{\#X_{E,\mathbb F_{q}}} \bigg | \\&= \sum _{\bar{x}\in X_{E,\mathbb F_{q}}\setminus X_{\text {bad}}} \bigg | \frac{2q + c_{0,\bar{x}}\sqrt{q} + O(1)}{q^2 + O(q)} - \frac{1}{q/2 + c_E\sqrt{q} + O(1)} \bigg | {}\\ {}&\qquad \qquad + \sum _{\bar{x}\in X_{\text {bad}}} \bigg | \frac{c_{\text {bad},\bar{x}}q}{q^2+O(q)} - \frac{1}{q/2 + c_E\sqrt{q} + O(1)} \bigg | \\&= \sum _{\bar{x}\in X_{E,\mathbb F_{q}}\setminus X_{\text {bad}}} \frac{1}{q} \bigg | \big (2+c_{0,\bar{x}}q^{-1/2}+O(q^{-1})\big ) - \big (2-c_E q^{-1/2}+O(q^{-1})\big ) \bigg | {} \\ {}&\qquad \qquad + \sum _{\bar{x}\in X_{\text {bad}}} \frac{1}{q} \bigg | \big (c_{\text {bad},\bar{x}} + O(q^{-3})\big ) - \big (2-c_E q^{-1/2}+O(q^{-1})\big ) \bigg | \\&= \sum _{\bar{x}\in X_{E,\mathbb F_{q}}\setminus X_{\text {bad}}} \frac{1}{q} \bigg | \big (c_{0,\bar{x}}+c_E\big ) q^{-1/2}+O(q^{-1}) \bigg | + \sum _{\bar{x}\in X_{\text {bad}}} \frac{1}{q} \bigg | c_{\text {bad},\bar{x}} - 2 + O(q^{-1/2}) \bigg | \end{aligned}$$

where each of the constants $c_{0,\bar{x}}$ is in $[-22,22]$ and each of the constants $c_{\text {bad},\bar{x}}$ is in [0, 8]. In particular, $|c_{0,\bar{x}}+c_E| \le 23$ and $|c_{\text {bad},\bar{x}}-2| \le 6$ for all $\bar{x}$, and we have:

$$\begin{aligned} 2\varDelta&\le \frac{\#\big (X_{E,\mathbb F_{q}}\setminus X_{\text {bad}}\big )}{q}\cdot \big (23q^{-1/2} + O(q^{-1})\big ) + \frac{\#X_{\text {bad}}}{q} \cdot \big (6 + O(q^{-1/2})\big ) \\&= \frac{\frac{1}{2} q + O(\sqrt{q})}{q}\cdot \big (23+o(1)\big )q^{-1/2} + \frac{39}{q}\cdot \big (6+o(1)\big ) \\&= \Big (\frac{23}{2} + o(1)\Big ) q^{-1/2} \le 2\cdot \big (6 + o(1)\big ) q^{-1/2} \end{aligned}$$

as required.

As an easy consequence, we obtain the following theorem.

Theorem 2

The map $F_0:S(\mathbb F_{q})\rightarrow X_{E,\mathbb F_{q}}$ of Eq. (7) is $\varepsilon$-admissible for $\varepsilon =\big (6+o(1)\big )q^{-1/2}$. In particular, if $\mathfrak {h}$ is a random oracle with values in $S(\mathbb F_{q})$, $F_0\circ \mathfrak {h}$ is indifferentiable from an $X_{E,\mathbb F_{q}}$ random oracle.

Moreover, the same results hold for $F_0^+:S(\mathbb F_{q})\times \{0,1\}\rightarrow E(\mathbb F_{q})$.

Proof

By definition, we need to prove that $F_0$ is efficiently computatable, $\varepsilon$-regular and $\varepsilon$-samplable. Computability is obvious. Regularity is the result of Lemma 4. And 0-samplability is obtained using the preimage sampling algorithm discussed in Sect. 6 below. To fix ideas, we sketch its construction.

Fix $\bar{x}\in X_{E,\mathbb F_{q}}$. As previously mentioned, for any fixed $u_0\in \mathbb F_{q}$, there are at most 8 preimages $(x,y,u)\in F^{-1}(\bar{x})$ such that $u=u_0$ (at most two coming from each of $x_1$ and $x_2$ and four coming from $x_3$). We can efficiently compute all those preimages and in particular count them. Therefore, the following simple rejection sampling algorithm has an output distribution uniform in $F^{-1}(\bar{x})$: pick $u_0$ uniformly at random, compute the list $L_{u_0}$ of preimages with $u=u_0$, restart with probability $1-\#L_{u_0}/8$ and otherwise return a random element of $L_{u_0}$.

Finally, the extension to $F_0^+$ is straightforward.

4 Parametrizing the SW Conic

4.1 Parametrizability Conditions

In the previous section, we have seen how the Shallue–van de Woestijne construction could be leveraged to construct admissible encodings $F_0:S(\mathbb F_{q})\rightarrow X_{E,\mathbb F_{q}}$ and $F_0^+:S(\mathbb F_{q})\times \{0,1\}\rightarrow E(\mathbb F_{q})$. However, we have also seen that mapping to $\mathbb F_{q}$-points on the surface S efficiently (without base field exponentiations) is a priori not straightforward, since the most naive approach involves finding points on new conics for all inputs.

Fortunately, the surface S has a fairly simple description: it can be seen as a one-parameter family of conics (the conics $S_u$; this is also called a relative conic over the u-line, or a fibration in conics, etc.). In any case, finding a global, two-parameter parametrization of S is thus a function field analogue of the classical problem, studied by Legendre, of finding rational points on conic over $\mathbb {Q}$.

In their paper [vHC06], van Hoeij and Cremona show that Legendre’s original approach can be directly adapted to the function field case. They provide necessary and sufficient conditions for the existence of solutions, as well as an effective algorithm to compute the parametrization if it exists.

A special case of their main result in as follows.

Lemma 5 (van Hoeij–Cremona)

Let r, s be polynomials in $\mathbb F_{q}[u]$ that are coprime, squarefree, and such that at least one of them is of odd degree. Then, the following projective conic over $\mathbb F_{q}(t)$:

$$\begin{aligned} X^2 + rY^2 + sZ^2 = 0 \end{aligned}$$

admits rational points over $\mathbb F_{q}(u)$ (i.e., a global rational parametrization) if and only if the following two conditions hold:

• 1. $-r$ is a square in $\mathbb F_{q}[u]/(s)$

• 2. $-s$ is a square in $\mathbb F_{q}[u]/(r).$

Moreover, if this is the case, there is an efficient algorithm to compute those points.

Proof

This is a special case of [vHC06, Th. 1]. More precisely, the assumptions ensure that the conic is in reduced form and in “case 1”, in the terminology of van Hoeij and Cremona, and the squareness conditions are equivalent to the existence of a “solubility certificate”.

The proof presented by van Hoeij and Cremona is constructive in that it yields an explicit algorithm for finding the rational parametrization. Our case of interest, corresponding to the surface S, is $r = h(u) = 3u^2+4a$ and $s = g(u) = u^3+au+b$ (except when $a=0$, in which case a slight adjustment is necessary to meet the assumptions of the theorem). In that case, if a parametrization exists, it can be put in the form where $Z=1$, and X, Y are polynomials of degree 2 and 1 in u respectively, as will be shown below. These polynomials depend only on the parameters a, b of the target elliptic curve, so the polynomial coefficients can be precomputed while their evaluation at a given u is done at runtime.

4.2 Curves with a Parametrizable SW Conic

Due to the conditions in Lemma 5, the SwiftEC encoding is not applicable to every ordinary elliptic curve. We present a different characterization of these conditions from the point of view of the target curve’s geometric properties.

Theorem 3

The surface S, as a one-parameter family of conics, admits a global two-parameter parametrization if and only if the following three conditions are satisfied.

• 1. The size of the field satisfies $q \equiv 1 \mod 3$ (i.e., $-3$ is a square in $\mathbb F_{q}$).

• 2. The discriminant $\varDelta _E = -16(4a^3+27b^2)$ is a square in $\mathbb F_{q}$ (i.e. E has either zero or three points of order 2).

• 3. At least one of the constants $\nu _{\pm } = \frac{1}{2}(-b \pm \sqrt{-3\varDelta _E}/36)$ is a square in $\mathbb F_{q}$.

Proof

As a first observation, note that if we let $r=h(u)$ and $s=g(u)$, then r and s are indeed coprime (their resultant is $4a^3+27b^2 = -\varDelta _E/16\ne 0$) and s is of odd degree and squarefree. Moreover, r is squarefree if and only if $a\ne 0$. For now, we assume that $a\ne 0$, so that Lemma 5 applies directly. We will treat the special case of $a=0$ at the end.

Let us first assume that $-h$ is a square in $\mathbb F_{q}[u]/(g)$ and $-g$ is a square in $\mathbb F_{q}[u]/(h).$ Note that h and g are coprime since their resultant is $4a^3+27b^2 = -\varDelta _E/16\ne 0$, so the law of quadratic reciprocity over function fields gives

$$\begin{aligned} \nonumber \left( \frac{-h}{g}\right) _2 \left( \frac{g}{-h}\right) _2&= (-1)^{\frac{q-1}{2}\deg g \deg h}\chi _{2}(1)^{\deg h} \chi _{2}(-3)^{\deg g}\nonumber \\ 1\cdot \left( \frac{g}{-h}\right) _2&= 1 \cdot 1 \cdot \chi _{2}(-3), \end{aligned}$$

(9)

where $\left( \frac{\cdot }{f}\right) _2$ and $\chi _{2}(\cdot )$ denote quadratic residue symbols over $\mathbb F_{q}[u]/(f)$ and $\mathbb F_{q}$, respectively.

On the other hand, we have

$$1 = \left( \frac{-g}{h}\right) _2= \left( \frac{-1}{h}\right) _2 \left( \frac{-g}{h}\right) _2 = \chi _{2}(-1)^2\left( \frac{g}{-h}\right) _2 = \left( \frac{g}{-h}\right) _2,$$

so (9) reduces to $\chi _{2}(-3) = 1$, which shows the necessity of condition 1.

Next, since $-g$ is a square in $\mathbb F_{q}[u]/(h)$, there exists $\alpha ,\beta \in \mathbb F_{q}$ such that:

$$\begin{aligned} -g&\equiv (\alpha u + \beta )^2 \pmod h \\ -u^3 - au - b&\equiv \alpha ^2 u^2 + 2\alpha \beta u + \beta ^2 \pmod {3u^2+4a} \\ \frac{4a}{3}u - au - b&\equiv -\frac{4a}{3}\alpha ^2 + 2\alpha \beta u + \beta ^2 \pmod {3u^2+4a} \\ \frac{a}{3}u - b&= 2\alpha \beta u + \big (-\frac{4a}{3}\alpha ^2 + \beta ^2\big ). \end{aligned}$$

It follows that the constants $\alpha ,\beta$ satisfy

$$\begin{aligned} \frac{a}{3}&= 2\alpha \beta \end{aligned}$$

(10)

$$\begin{aligned} b&= \frac{4a}{3}\alpha ^2-\beta ^2. \end{aligned}$$

(11)

Recalling that $a\ne 0$, it follows from (10) that $\alpha ,\beta \ne 0$ and we can substitute $\beta = a/(6\alpha )$ into (11) to obtain

$$\begin{aligned} 48 a \alpha ^4 - 36 b \alpha ^2 - a^2 = 0, \end{aligned}$$

(12)

which is a quadratic equation on $\alpha ^2$ whose discriminant is $36^2b^2 + 192a^3 = -3\varDelta _E$. Since $-3$ is a square, it follows that $\varDelta _E$ must also be a square for $\alpha ^2$ to exist, showing the necessity of condition 2. The solution to (12) is then given by

$$\begin{aligned} \alpha ^2 = \frac{36b \pm \sqrt{-3\varDelta _E}}{96a} = \frac{-3}{4a}\nu _{\pm }. \end{aligned}$$

(13)

If a is a square this means that at least one of $\nu _{\pm }$ must be a square for $\alpha$ to exist. On the other hand, if a is not a square then the same condition always holds since the product $\nu _+\nu _- = -a^3/27$ is a non-square.

The proof of the converse is similar: if conditions 2 and 3 are met then there exists $\alpha ,\beta \in \mathbb F_{q}$ that are solutions to (10) and (11), which shows that $-g$ has a square root mod h, and then condition 1 together with (9) shows that $-h$ is a square mod g.

Finally, consider the special case $a=0$. In that case, since $h(u)=3u^2$, we can apply the change of variables $Y' = uY$ to reduce to the case of the conic:

$$\begin{aligned} X^2 + 3Y^2 + gZ^2 = 0, \end{aligned}$$

i.e., $r=3$ and $s=g$. It is then clear that r and s are coprime, squarefree, and one of them is of odd degree. Moreover, the condition that $-s$ is a square modulo r is vacuous, and the condition that $-r$ is a square modulo s simply says that $-3$ is a square in $\mathbb F_{q}[u]/(g)$; since that etale algebra admits either $\mathbb F_{q}$ or $\mathbb {F}_{q^3}$ as a factor, this is equivalent to $-3$ being a square in $\mathbb F_{q}$, namely $q\equiv 1 \pmod 3$ as required. This shows that in this case, condition 1 is necessary and sufficient. The result still holds, however, because conditions 2 and 3 become vacuous: the discriminant $\varDelta _E = -16(27b^2) = -3\cdot 12^2 b^2$ is always a square, and one of $\nu _{\pm }$ is always zero.

Out of the three conditions in Theorem 3, condition 1 is the most restrictive discarding half of the prime fields. Condition 3 only fails about 1/4 of the time, whereas condition 2 fails half of the time. However, conditions 2 and 3 are not isogeny-invariant and so they may be circumvented under certain conditions by finding a small-degree isogeny and mapping to the isogenous curve instead, as discussed in the next section.

Notable curves that satisfy the conditions for SwiftEC include the NIST P-256 curve, the curve secp256k1 used in Bitcoin [SEC10] and the pairing-friendly curve BLS12-381 [Bow17] as well as all BN curves [BN06] and BLS curves [BLS03] over any field with $q \equiv 1\mod 3$. On the other hand, curves such as the Ed448-Goldilocks curve [Ham15] and the NIST P-384 curve are incompatible due to the field cardinality alone.

4.3 Reaching More Curves with Isogenies

While Theorem 3 discards the possibility of applying SwiftEC directly to curves with a non-square discriminant, here we present a small modification that can work around this condition, at least some of the time. The condition that the discriminant be a square is invariant under isomorphisms, but not under isogenies. Hence, we may hope that there is an isogenous curve that satisfies the condition and compose the SwiftEC encoding to this curve with the isogeny to obtain a map to the original curve. Curves with a non-square discriminant always contain exactly one point of order 2, so one may be tempted to exploit the small 2-isogeny that is available. The following result shows that this intuition is correct, and indicates exactly when this is possible.

Theorem 4

Let $E/\mathbb F_{q}$ be an elliptic curve with non-square discriminant. There exists a curve $E'$ with square discriminant isogenous to E over $\mathbb F_{q}$ if and only if $E(\mathbb F_{q})$ has a point of order 4. In this case, the isogeny can always be taken to be of degree 2.

Proof

First suppose we have a point $P_4\in E(\mathbb F_{q})$ of order 4, and let $P_2 = 2P_4$ be the unique point of order 2 in $E(\mathbb F_{q})$. If $\phi :E\rightarrow E'$ is the isogeny with kernel $<P_2>$, then $\phi (P_4)$ is a point of order 2 in $E'$. There must also exist a point $P_2'\in E'(\mathbb F_{q})$ of order 2 generating the dual isogeny $\hat{\phi }$, and we cannot have $\phi (P_4) = P'_2$ because $\hat{\phi }(P_2') =0$ but $\hat{\phi }(\phi (P_4)) = 2P_4 \ne 0$. This means we have two distinct points of order 2 in $E'$, and their addition yields a third point of order 2, so $E'$ must have a square discriminant as desired.

Conversely, if E has no point of order 4 then the group order is divisible by 2 exactly once, so any isogenous curve will also have exactly one point of order 2 and hence have a non-square discriminant.

Note that the application of the 2-isogeny is a 2-to-1 map that would make the distribution easily distinguishable from uniform. However, in essentially all cases of interest, one needs to sample points only in a specific subgroup orthogonal to the 2-torsion subgroup. For instance, consider Curve25519 [Ber06] which is non-compatible with our construction because it does not have a square discriminant. The curve is given by

$$\begin{aligned} E_{25519}:y^2 = x^3 + 486662x^2 + x \end{aligned}$$

over the prime field of size $p = 2^{255}-19$. The group order for this curve is $\#E_{25519} = 8\ell$ where $\ell$ is a large prime, and points in the $\ell$-torsion subgroup are used in the ECDH scheme. We can use SwiftEC to map onto the 2-isogenous curve

$$\begin{aligned} E':y^2 = x^3 - 102314837774592x + 398341948567736549376 \end{aligned}$$

which does satisfy all conditions of Theorem 3. By composing with the 2-isogeny generated by $P'_2 = (-11679888,0)$ and the multiplication-by-4 map, we are able to hash into the $\ell -$torsion subgroup of Curve25519 at the cost of only an additional 20 field multiplications, 7 squarings and 11 additions. This is to our knowledge the only currently known way of hashing deterministically and indistinguishably into this subgroup using a single square root.

Likewise, condition 3 may also be circumvented with isogenies and in this case we are not limited to degree 2 only. For instance, the curve secp521r1 also known as NIST P-521 already has a square discriminant but fails condition 3. However, it is 5-isogenous to the curve

$$\begin{aligned}&E'': y^2 = x^3 + ax+b,\\&a=0x149a4e89bde4ad2e72c830ce3df36200e03c1abb6403f3a50cc56be41b0bd98f6a2bb16b7...\\&~~~~~~~...5027c89a68174a7c458a0333ff283225259b57414a2e04a0681ca279a0\\&b=0x49d903da04fb382a8daec077738d7f3f5a2ca21e053847fb43c4740c39eaf3d2727a9898...\\&~~~~~~~...d710bdcfa306450d7102a03bf9164294ee1a849928687cc8b343a3ed24 \end{aligned}$$

which satisfies all the conditions for SwiftEC, so we can map onto secp521r1 by using our construction on $E''$ and then composing with a 5-isogeny at negligible overhead. Since the group order is coprime to 5, the isogeny is already a bijection.

In this way, one can always expect to find some isogeny of arbitrary degree that will work, so condition 3 can in principle always be circumvented, although an isogeny of small degree is more desirable for efficiency reasons. On the other hand, Theorem 4 shows that condition 2 fails irremediably if and only if the group order is divisible by 2 exactly once, so overall we heuristically expect SwiftEC to be adaptable to a fraction 3/4 of all elliptic curves over fields with $q\equiv 1\mod 3$.

5 The SwiftEC Encoding

5.1 Efficient Computation

As a proof of principle, we have prepared a Sage implementation of SwiftEC that allows adding new compatible curves in a simple way. This implementation makes explicit the number of field operations needed and uses a constant number of them, but is non-constant time to the degree that the built-in field operations are. Our implementation is freely available at https://github.com/Jchavezsaab/SwiftEC.

For curves with $a \ne 0$, the implementation makes use of the polynomials $X_0(u), Y_0(u)$ that evaluate a point in $S_u$ as discussed in Sect. 4. Since these polynomials only depend on the curve coefficients a, b, they are precomputed and stored in the form of five field elements, with explicit formulas provided in the extended version of this work [CRT22]. On input u, t, the initial point $(X_0(u),Y_0(u))\in S_u$ is evaluated and then a second point $(X,Y)\in S_u$ is obtained from the parametrization

$$\begin{aligned} X(u,t)&= \frac{g(u)+h(u)(Y_0(u)-tX_0(u))^2}{X_0(u)(1+t^2h(u))}, \\ \nonumber Y(u,t)&= Y_0(u) + t(X - X_0(u)). \end{aligned}$$

(14)

In the case where $a=0$, we have simply $g(u) = u^3 + b$ and $h(u) = 3u^2$. In this case the van Hoeij-Cremona algorithm described in Sect. 4 always yields the point at infinity $(X_0:Y_0:Z_0) = (\sqrt{-3}:1:0)$, so the formulas for the parametrization have to be adjusted. We can skip the computation of $X_0(u),Y_0(u)$ altogether and apply the following formulas directly:

$$\begin{aligned} X(u,t)&= \frac{u^3+b-t^2}{2t}, \\ \nonumber Y(u,t)&= \frac{X(u,t)+t}{u\sqrt{-3}}. \end{aligned}$$

(15)

Finally, we apply the map $\psi$ from (6) to get a point $(x_1,x_2,x_3,z)\in V(\mathbb F_{q})$. It is not actually necessary to compute the z-coordinate of this point, and the $x_i$ coordinates are computed projectively so that what we actually obtain is a projective triplet $(x_1:x_2:x_3:\lambda )$. Note that this introduces a small bias towards the point at infinity: if any of the $x_i$ are infinite then we have to set $\lambda =0$ and all three points will be interpreted as being infinite. However, we neglect this since the bias is negligible and dealing with this case explicitly would produce a non-constant-time implementation.

We must then find which of the $x_i$ is the x-coordinate of a point in $E(\mathbb F_{q})$, choosing one arbitrarily but deterministically if all three are. This can be implemented in constant time as shown in Algorithm 1 which prioritizes $x_3$.

Finally, we use a single inverse to compute the affine x-coordinate and a square root computation (the only one throughout the whole program) to recover the y-coordinate. Note that there is a free choice for the sign of y in the end, which we integrate as an additional input bit.

5.2 XSwiftEC: x-Only Computation Without Exponentiation

Note that the only inverse and square root needed for SwiftEC are at the very end when the affine x, y coordinates are computed. However, there are many applications where obtaining an output in x-only projective coordinates is acceptable, and these operations can be omitted. The resulting XSwiftEC algorithm requires no inversions, square roots or exponentiations of any kind, but only two Jacobi symbol computations that are considerably cheaper and other elementary field operations.

This is particularly useful for the cases when SwiftEC is composed with a 2-isogeny as described in Sect. 4.3: even if an affine x, y output is desired, we are better off using XSwiftEC and recovering the affine coordinates after applying the projective x-only 2-isogeny formulas.

Although the output $(x:\lambda )$ that is obtained is indistinguishable from uniform as a projective pair, the individual values of x and $\lambda$ are not and may leak information about the input. This can be easily circumvented by multiplying both coordinates by a random field element, or it may be ignored to avoid relying on randomness in applications where this leakage is not a concern.

5.3 Implementation Results

We summarize in Table 1 the cost in operations for each version of SwiftEC. The most noteworthy feature is the requirement of only one square root computation (and none when the y coordinate is not required), which is an improvement on previous admissible encodings to ordinary elliptic curves. Moreover, the square-root and the inversion can be performed simultaneously for further savings as described by Hamburg [Ham12].

The results shown are for the $a\ne 0$ implementation. The implementations for $a=0$ always save exactly 7 additions and 6 multiplications due to the simpler formulas in (15).

Table 1. Cost in operations of our implementations of SwiftEC for field additions, squarings, multiplications, Jacobi symbol computations, inversions, and square roots.

6 SwiftEC For Point Representation: ElligatorSwift

In this section we describe an algorithm to efficiently compute a uniformly random preimage of any point under SwiftEC. The existence of this algorithm is required for the encoding to be admissible, which is crucial for using SwiftEC as part of a cryptographically secure hash function as described in Sect. 2. Moreover, it is important in practice because it allows us to encode points in an elliptic curve as uniform bitstrings, as is done in Elligator [BHKL13] and Elligator Squared [Tib14a].

Compared to Elligator Squared, our ElligatorSwift construction has the advantage that it does not need to compute any encodings in the forward direction. Indeed, all we need is to sample a random $u\in \mathbb F_{q}$ and then find an inverse $F^{-1}_{0,u}(P)$ of the SW encoding.

We first focus on inverting the map $\Psi$ and note that under a change of variables $v = x/2y - u/2$ and $w = 2y$, the image in (6) becomes

$$\begin{aligned} x_1&= v,\quad \quad x_2 = -u -v,\quad \quad x_3 = u + w^2, \end{aligned}$$

while the equation for the conic becomes

$$\begin{aligned} w^2 (u^2 + uv + v^2 + a) = -(u^3+au+b). \end{aligned}$$

(16)

This yields up to four possible preimages for a given point $(x,y)\in E(F)$, namely:

• 1. $v = x$ and $w^2$ derived from (16), if x was drawn from $x_1$

• 2. $v = -u-x$ and $w^2$ derived from (16), if x was drawn from $x_2$

• 3,4. $w^2 = x - u$ and v derived from (16), if x was drawn from $x_3$,

where the last case actually contains two preimages since (16) is a quadratic equation for v with solutions

$$v = \frac{-u}{2}\pm \frac{\sqrt{-w^2(4u^3+4au+4b+3w^2u^2+4aw^2)}}{2w^2}.$$

Moreover, all cases have a duplicity from choosing the sign of $w = \sqrt{w^2}$, so there are up to 8 preimages in total per elliptic curve x coordinate. Note that flipping the sign of w produces a new point in S that maps to the same x coordinate, so in cases where we need to distinguish between the choice of sign for the elliptic curve y coordinate this can be encoded into w by always choosing ${{\,\textrm{sgn}\,}}(w) = {{\,\textrm{sgn}\,}}(y)$. This choice gives up to 4 preimages for each pair of coordinates (x, y), and allows the decoder to recover the correct choice of ${{\,\textrm{sgn}\,}}(y)$ when computing SwiftEC in the forward direction.

Of course, some of the square roots needed may not exist and so different values of u will yield a different number of preimages of a given point (including possibly none). On top of this, if the preimage comes from cases 1 or 2 but results in values where all three $x_i$ yield points in $E(\mathbb F_{q})$, then the preimage will be invalid even if the square root is well-defined since Algorithm 1 in the forward encoding would have prioritized $x_3$ over the intended one. Care must therefore be taken to check for the existence of the various square roots and restart the procedure when appropriate, as shown in Algorithm 2. This makes the algorithm run in non-constant time but ensures that the preimage is uniformly sampled.

What remains is just to switch back to x, y coordinates and invert the parametrization (14) to recover the parameter t.

Remark: For implementations with $a=0$ we must take into account the different parametrization formulas in (15). In this case, lines 29 and 30 of Algorithm 2 can be replaced by simply $t\leftarrow Yu\sqrt{-3}-X$, where the constant $\sqrt{-3}$ is part of the precomputed parameters.

We assume that the square root function returns Null for non-squares. It is easy to see that the output of Algorithm 2 is uniformly distributed since each u is attempted with a random choice of one of the 4 cases, so the probability of each u being successful is proportional to how many preimages exist under it.

The main cost of Algorithm 2 is an average of 1.5 square root computations per iteration. Since most points have roughly 2q preimages as per Theorem 1, we can expect each choice of u to contain on average 2 valid preimages out of the 8 possible ones, and so the expected number of iterations is 4. Notice however that a failed iteration can be aborted before computing any square roots by first computing the corresponding Jacobi symbols, which can be done much more efficiently with constant-time efficient implementations such as [Por20, Ham21, AG21] (by a factor of around $10\times$ for most commonly-used primes). The cost of ElligatorSwift is therefore always exactly 1 or 2 square root computations, and 6 Jacobi symbol computations on average. This is a considerable improvement over Elligator Squared, with an average cost of 6.5 square roots.

As for curves where we need to compose SwiftEC with an isogeny, we can obtain a corresponding variant of ElligatorSwift by composing with the dual isogeny, but this has the side effect of introducing a multiplication by the isogeny degree in the round trip. This can be circumvented by adding a point division before applying ElligatorSwift, which is important for demonstrating that the encoding with the isogeny trick is still admissible. However, the resulting ElligatorSwift construction would be unappealing in terms of efficiency.

7 Conclusion

In this paper we presented SwiftEC, which is the first admissible and constant-time encoding using a single square root that is applicable to a large class of ordinary elliptic curves. This construction can lead to considerable performance speedup compared to previously known methods. For instance, an efficient implementation of SwiftEC and ElligatorSwift for secp256k1 benchmarked suggest computational savings of more than $50\%$ when compared to their Elligator Squared counterparts [Wui22]. On the other hand, in applications such as hashing into BLS curves where we ultimately aim to map to points belonging to the elliptic curve subgroups $\mathbb {G}_1$ and $\mathbb {G}_2$, the dominant cost might not be the square-root computation associated to SwiftEC’s savings, but rather the clearing of a per-curve fixed cofactor (typically, this cofactor is relatively small for $\mathbb {G}_1$ but much larger for $\mathbb {G}_2$).

While some curves remain incompatible with SwiftEC, our construction applies to roughly 3/4 of all curves over fields with $q \equiv 1 \mod 3$. The inverse encoding also results in an Elligator-like encoding that is significantly more efficient than previous constructions, using more than four times less square roots on average than Elligator Squared, while retaining the same data transmission size of two field elements.

It is still an open problem to determine if there are any workarounds that could extend this encoding to more of the non-compatible curves, or even to find a single-square root admissible encoding that could be applied to all ordinary elliptic curves.