Nonexistence of generalized bent functions from $\mathbb {Z}_{2}^{n}$ to $\mathbb {Z}_{m}$

Abstract

In this paper, several nonexistence results on generalized bent functions $f:\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}_{m}$ are presented by using the knowledge on cyclotomic number fields and their imaginary quadratic subfields.

1 Introduction

Let m and n be positive integers, $m\ge 2$, $\mathbb {Z}_{m}=\mathbb {Z}/m\mathbb {Z}=\{0, 1,\ldots , m-1\}$. A mapping $f:\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}_{2}$ is called a Boolean function with n variables. The Fourier transform of the function f is given by $W_{f}:\mathbb {Z}_{2}^{n} \rightarrow \mathbb {R}$ with

$$\begin{aligned} W_{f}(y)=\sum _{x\in \mathbb {Z}_{2}^{n}}(-1)^{f(x)+x\cdot y}, \end{aligned}$$

where $x\cdot y=\sum _{i=1}^{n}x_{i}y_{i}\in \mathbb {Z}_{2}$ and $\mathbb {R}$ is the field of real numbers. A Boolean function f is called a bent function if $\big |W_f(y)\big |=2^{\frac{n}{2}}$ holds for every $y\in \mathbb {Z}_{2}^{n}$. Bent functions from $\mathbb {Z}_{2}^{n}$ to $\mathbb {Z}_{2}$ are introduced and studied by Rothaus [7] in 1976. Kumar et al. [3] generalized the notation in 1985 by considering the functions from $\mathbb {Z}_{m}^{n}$ to $\mathbb {Z}_{m}$, and in 2009 [8], Schmidt studied another generalized bent function from $\mathbb {Z}_{2}^{n}$ to $\mathbb {Z}_{m}$, especially $m= 2^{h}$. In this paper we will deal with functions $f:\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}_{m}$. For $m=2$, this is the usual Boolean function. Let $\zeta _{m}=e^{\frac{2\pi \sqrt{-1}}{m}}\in \mathbb {C}$, the Fourier transform of f is given by $W_{f}:\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}[\zeta _{m}]\subseteq \mathbb {C}$ with

$$\begin{aligned} W_{f}(y)=\sum _{x\in \mathbb {Z}_{2}^{n}}(-1)^{x\cdot y}\zeta _{m}^{f(x)}\ \ \ \ \left( y\in \mathbb {Z}_{2}^{n} \right) . \end{aligned}$$

(1)

The inverse Fourier transform is

$$\begin{aligned} \zeta _{m}^{f(x)}=\frac{1}{2^{n}}\sum _{y\in \mathbb {Z}_{2}^{n}}(-1)^{x\cdot y}W_{f}(y)\ \ \ \ \left( x\in \mathbb {Z}_{2}^{n} \right) , \end{aligned}$$

(2)

and from (1) we get

$$\begin{aligned} \sum _{y\in \mathbb {Z}_{2}^{n}}|W_f(y)|^{2}&=\sum _{y\in \mathbb {Z}_{2}^{n}}\sum _{x,x'\in \mathbb {Z}_{2}^{n}}(-1)^{(x+x')\cdot y}\zeta _{m}^{f(x)-f(x')}\\&=\sum _{x,x'\in \mathbb {Z}_{2}^{n}}\zeta _{m}^{f(x)-f(x')}\sum _{y\in \mathbb {Z}_{2}^{n}}(-1)^{(x+x')\cdot y}\\&=2^{n}\sum _{x\in \mathbb {Z}_{2}^{n}}1=2^{2n}. \end{aligned}$$

Therefore, the maximum value $M=max\{\big |W_{f}(y)\big |:y\in \mathbb {Z}_{2}^{n}\}$ has lower bound $2^{\frac{n}{2}}$ and $M=2^{\frac{n}{2}}$ if and only if $\big |W_{f}(y)\big |=2^{\frac{n}{2}}$ for all $y\in \mathbb {Z}_{2}^{n}$.

Definition 1

A function $f:\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}_{m}$ is called (m, n)-generalized bent function if $\big |W_{f}(y)\big |=2^{\frac{n}{2}}$ for all $y\in \mathbb {Z}_{2}^{n}$, (m, n)-GBF in short.

For $m=2$, this is the (Boolean) bent function in [7]. It is well-known that there exist bent functions $f:\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}_{2}$ if and only if n is even. For even numbers n, many constructions on bent functions with n variables have been found. One of the simplest examples is Rothaus’s bent function $f(x)=x_{1}x_{2}+x_{3}x_{4}+\cdots +x_{2t-1}x_{2t}$, where $n=2t$. For $m=4$ and $m=8$, several constructions and existence results on GBFs have been found in [5, 8–13]. Generalized bent functions have been widely investigated since they are applied in many fields such as communication theory, cryptography and closely related to coding theory and combinatorial design theory.

The main aim of this paper is to present several nonexistence results on (m, n)-GBFs. Firstly we collect existence results in Sect. 2 by using previous facts given in [10, 11] and some simple observations. Then we show nonexistence results in the last three sections. In Sect. 3 we prove that there is no $\{p^{l}, n\}$-type GBF for any $n\ge 1$ and any odd prime power $p^{l}$ by using a result in [4]. In Sect. 4 and Sect. 5 we use the basic knowledge on cyclotomic number field $K=\mathbb {Q}(\zeta _{m})$ to get some nonexistence results. The point is that, for (m, n)-GBFs f, the values of $W_{f}(y)$ belong to the ring $\mathbb {Z}[\zeta _{m}]$. We introduce some basic facts at the beginning of Sect. 4. Then we get further nonexistence results on GBF in Sect. 4 for semiprimitive case and in Sect. 5 for other cases by field-descent method. We end with conclusions in Sect. 6.

2 Existence results

Firstly, we collect previous existence results on (m, n)-GBF $f:\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}_{m}$ where $n\ge 1$, $m\ge 2$.

Lemma 1

(1)([7]) There exists a (2, n)-GBF if and only if n is even.

(2)([10]) If both m and n are even numbers, then there exists an (m, n)-GBF.

(3)([12]) If there exists a $(2,n+1)$-GBF, then there exists a (4, n)-GBF.

Remark 1

(A) For the proof of (2), let $m=2l$, $n=2t$, $\sigma$ be an arbitrary permutation on $\mathbb {Z}_{2}^{t}$ and $g:\mathbb {Z}_{2}^{t} \rightarrow \mathbb {Z}_{m}$ be an arbitrary function. Consider the following function $f=f(x,y):\mathbb {Z}_{2}^{t}\oplus \mathbb {Z}_{2}^{t}=\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}_{m},$

$$\begin{aligned} f(x,y)=g(y)+lx\cdot \sigma (y)\ \ \ \ (x,y\in \mathbb {Z}_{2}^{t}). \end{aligned}$$

It is easy to see that f is a GBF.

(B) The conclusion (3) has been proved in [12] as a consequence of some more general results. Here we give a direct simple proof.

Suppose that $f=f(x,x'):\mathbb {Z}_{2}^{n}\oplus \mathbb {Z}_{2}=\mathbb {Z}_{2}^{n+1}\longrightarrow \mathbb {Z}_{2} (x\in \mathbb {Z}_{2}^{n},x'\in \mathbb {Z}_{2})$ is a Boolean bent function. Then for $y\in \mathbb {Z}_{2}^{n}$ and $y'\in \mathbb {Z}_{2}$,

$$\begin{aligned} \pm 2^{\frac{n+1}{2}}= & {} W_f(y,y')=\sum _{x\in \mathbb {Z}_{2}^{n}, x'\in \mathbb {Z}_{2}}(-1)^{f(x,x')+x\cdot y+x'y'}\nonumber \\= & {} \sum _{x\in \mathbb {Z}_{2}^{n}}\left( (-1)^{f(x,0)+x\cdot y}+(-1)^{f(x,1)+x\cdot y+y'}\right) . \end{aligned}$$

(3)

For $a, b\in \mathbb {Z}_{2}=\{0,1\}$ and $y\in \mathbb {Z}_{2}^{n}$, let

then by (3) we get

$$\begin{aligned} \pm 2^{\frac{n+1}{2}}=&\left( N_{y}(0,0)+N_{y}(0,1)-N_{y}(1,0)-N_{y}(1,1)\right) \\&+(-1)^{y'}\left( N_{y}(0,0)+N_{y}(1,0)-N_{y}(0,1)-N_{y}(1,1)\right) . \end{aligned}$$

Taking $y'=0$ and 1 we get

$$\begin{aligned} 2\left( N_{y}(0,0)-N_{y}(1,1)\right) =2\left( N_{y}(0,1)-N_{y}(1,0)\right) =\pm 2^{\frac{n+1}{2}}. \end{aligned}$$

(4)

Now we define $F:\mathbb {Z}_{2}^{n} \longrightarrow \mathbb {Z}_{4}=\{0, 1, 2, 3\}$,

$$\begin{aligned} F(x)=\left\{ \begin{array}{l@{\quad }l} 0,&{}\hbox {if}~f(x,0)=f(x,1)=0\\ 1,&{}\hbox {if}~f(x,0)=0, f(x,1)=1\\ 2,&{}\hbox {if}~f(x,0)=f(x,1)=1\\ 3,&{}\hbox {if}~f(x,0)=1, f(x,1)=0. \end{array}\right. \end{aligned}$$

Then for each $y\in \mathbb {Z}_{2}^{n}$,

$$\begin{aligned} W_F(y)&=\sum _{x\in \mathbb {Z}_{2}^{n}}(-1)^{x\cdot y}\zeta _{4}^{F(x)}\ \ \ \ (\zeta _{4}=\sqrt{-1})\\&=N_{y}(0,0)+\zeta _{4}N_{y}(0,1)-N_{y}(1,1)-\zeta _{4}N_{y}(1,0)\\&=\left( N_{y}(0,0)-N_{y}(1,1)\right) +\zeta _{4}\left( N_{y}(0,1)-N_{y}(1,0)\right) . \end{aligned}$$

By (4), we get

$$\begin{aligned} |W_{F}(y)|^{2}&=\left( N_{y}(0,0)-N_{y}(1,1)\right) ^{2}+\left( N_{y}(0,1)-N_{y}(1,0)\right) ^{2}\\&=2^{n-1}+2^{n-1}=2^n. \end{aligned}$$

Therefore, F is a GBF.

(C) For even $n\ge 2$, there exist (4, n)-GBFs by Lemma 1(2). For odd $n\ge 1$, there exist Boolean bent functions $f:\mathbb {Z}_{2}^{n+1}\longrightarrow \mathbb {Z}_{2}$ by Lemma 1(1). Thus there exist (4, n)-GBFs by Lemma 1(3). Therefore, we have (4, n)-GBFs for any positive integer n.

Next we show the following simple observation.

Lemma 2

• (1) If there exist (m, n)-GBFs and $(m,n')$-GBFs, then there exist $(m,n+n')$-GBFs.

• (2) If there exists an (m, n)-GBF, then for any positive integer l there exists an (lm, n)-GBF. In other words, if there is no (m, n)-GBF, then there is no $(m',n)$-GBF for any factor $m'\ge 2$ of m.

Proof

(1) Let $f:\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}_{m}$ and $f':\mathbb {Z}_{2}^{n'} \rightarrow \mathbb {Z}_{m}$ be GBFs. It is easy to see that

$$\begin{aligned} F:\mathbb {Z}_{2}^{n+n'}\rightarrow \mathbb {Z}_{m},~~ F(x,x')=f(x)+f'(x')\qquad \left( x\in \mathbb {Z}_{2}^{n}, x'\in \mathbb {Z}_{2}^{n'}\right) \end{aligned}$$

is a GBF.

(2) Given a GBF $f:\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}_{m}$, consider the following well-defined function

$$\begin{aligned} F:\mathbb {Z}_{2}^{n}\rightarrow \mathbb {Z}_{lm}, ~~F(x)=lf(x)\qquad (x\in \mathbb {Z}_{2}^{n}). \end{aligned}$$

For each $y\in \mathbb {Z}_{2}^{n}$,

$$\begin{aligned} W_F(y)=\sum _{x\in \mathbb {Z}_{2}^{n}}(-1)^{x\cdot y}\zeta _{lm}^{F(x)} =\sum _{x\in \mathbb {Z}_{2}^{n}}(-1)^{x\cdot y}\zeta _{m}^{f(x)}=W_f(y). \end{aligned}$$

Therefore, F is a GBF if f is a GBF. $\square$

From Lemma 1(1), Remark 1(C) and Lemma 2 we know that if both m and n are even or $4\mid m$, then there exists a (m, n)-GBF. The remaining cases are

Case (I)      $2\not \mid m$, or

Case (II)      $2 \not \mid n$ and $m \equiv 2\pmod 4$.

No GBF has been constructed in the above cases by our knowledge so far. In the following three sections we will show several nonexistence results for these cases.

3 Nonexistence results (I)

In this section we present a nonexistence result on GBF as a corollary to the following lemma, which is a retelling of the main theorem in [4] given by Lam and Leung.

Lemma 3

[4] Let $m=p_{1}^{a_{1}}\cdots p_{s}^{a_{s}}$, where $p_{1},\ldots ,p_{s}$ are distinct prime numbers and $a_{i}\ge 1$ $(1\le i\le s)$. Let $S=\{\zeta _{m}^{i}:0\le i\le m-1\}$. Then for any integer $n\ge 1$, the equation $x_{1}+\cdots +x_{n}=0$ has a solution $x_{j}\in S$ $(1\le j\le n)$ if and only if $n=n_{1}p_{1}+\cdots +n_{s}p_{s}$ has a non-negative integer solution $(n_{1},\ldots ,n_{s})$.

Corollary 1

Let $m=p_{1}^{a_{1}}\cdots p_{s}^{a_{s}}$, where $p_{1},\ldots ,p_{s}$ are distinct odd prime numbers and $a_{i}\ge 1$ $(1\le i\le s)$. If

$$\begin{aligned} 2^{n}=n_{1}p_{1}+\cdots +n_{s}p_{s} \end{aligned}$$

has no non-negative integer solutions $(n_{1},\ldots ,n_{s})$, then there is no (m, n)-GBF.

Proof

Suppose that $f:\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}_{m}$ is a GBF. Then $\big |W_{f}(y)\big |^{2}=2^{n}$ for any $y\in \mathbb {Z}_{2}^{n}$. By inverse Fourier transform (2), for $0\ne a \in \mathbb {Z}_{2}^{n}$, we have

$$\begin{aligned} \sum _{x\in \mathbb {Z}_{2}^{n}}\zeta _{m}^{f(x+a)-f(x)}&=\frac{1}{2^{2n}}\sum _{x\in \mathbb {Z}_{2}^{n}}\sum _{y\in \mathbb {Z}_{2}^{n}}W_{f}(y)(-1)^{(x+a)\cdot y}\sum _{z\in \mathbb {Z}_{2}^{n}}\overline{W_{f}(z)}(-1)^{x\cdot z}\\&=\frac{1}{2^{2n}}\sum _{y,z\in \mathbb {Z}_{2}^{n}}W_{f}(y)\overline{W_{f}(z)}(-1)^{a\cdot y}\sum _{x\in \mathbb {Z}_{2}^{n}}(-1)^{x\cdot (y+z)}\\&=\frac{1}{2^{n}}\sum _{y\in \mathbb {Z}_{2}^{n}}W_{f}(y)\overline{W_{f}(y)}(-1)^{a\cdot y}=\frac{1}{2^{n}}\sum _{y\in \mathbb {Z}_{2}^{n}}\big |W_{f}(y)\big |^{2}(-1)^{a\cdot y}\\&=\sum _{y\in \mathbb {Z}_{2}^{n}}(-1)^{a\cdot y}=0. \end{aligned}$$

The left-hand side is a sum of $2^{n}$ elements and each element is a power of $\zeta _{m}$. By Lemma 3, the equation $2^{n}=n_{1}p_{1}+\cdots +n_{s}p_{s}$ has a non-negative integer solution $(n_{1},\ldots ,n_{s})$. This completes the proof of Corollary 1. $\square$

Corollary 2

There is no (m, n)-GBF provided one of the following conditions on m and n is satisfied.

• (1) m is an odd prime power and n is an arbitrary positive integer;

• (2) $m=p_{1}^{a_{1}}\cdots p_{s}^{a_{s}}$, $3\le p_{1}<p_{2}<\cdots < p_{s}$ and $2^{n}<p_{1}+p_{2}$;

• (3) $m=p_{1}^{a_{1}}p_{2}^{a_{2}}$, $p_{1}\ne p_{2}$, $a_{1}$, $a_{2}\ge 1$, $2^{n}=p_{1}p_{2}-m_{1}p_{1}-m_{2}p_{2}$ for some positive integers $m_{1}$ and $m_{2}$.

Proof

This is a direct consequence of Corollary 1.

For (1), $2^{n}=px$ has no solution $x\in \mathbb {Z}$ since p is an odd prime;

For (2), if $2^{n}=n_{1}p_{1}+\cdots +n_{s}p_{s}$ $(n_{i}\ge 0)$, then $n_{i}\ge 1$ for at least two i. Therefore, $2^{n}\ge p_{1}+p_{2}$;

For (3), if $p_{1}p_{2}-m_{1}p_{1}-m_{2}p_{2}=2^{n}=n_{1}p_{1}+n_{2}p_{2}$, then $p_{1}p_{2}-p_{1}-p_{2}=p_{1}(n_{1}+m_{1}-1)+p_{2}(n_{2}+m_{2}-1)$ which contradicts to the well-known fact that $p_{1}p_{2}-p_{1}-p_{2}$ is the largest integer N such that $N=p_{1}x_{1}+p_{2}x_{2}$ has no non-negative integer solution $(x_{1},x_{2})$. Therefore, $2^{n}=n_{1}p_{1}+n_{2}p_{2}$ has no non-negative integer solution $(n_{1},n_{2})$. $\square$

Example 1

By Corollary 2 it can be computed that there is no $(7^{a_{1}}13^{a_{2}},n)$-GBF for all $a_{1},a_{2}\ge 1$ and $1\le n\le 6$.

4 Nonexistence results (II): semiprimitive case

In this and next sections we will consider the cases $2 \not \mid n$ and $2\not \mid m$ or $m \equiv 2\pmod 4$. Firstly, we introduce some basic facts on cyclotomic number field $\mathbb {Q}(\zeta _{m})$ where $\mathbb {Q}$ is the field of rational numbers. We refer to books [2] and [14] for details. If $m \equiv 2\pmod 4$, i.e., $m=2t$ and $2\not \mid t$, we have $\mathbb {Q}(\zeta _{m})=\mathbb {Q}(\zeta _{t})$ since $\zeta _{t}=\zeta _{m}^{2}$ and $-\zeta _{m}=\zeta _{m}^{\frac{m}{2}+1}=\zeta _{2t}^{t+1}=\zeta _{t}^{\frac{t+1}{2}}$. Therefore, we can only consider $\mathbb {Q}(\zeta _{m})$ for odd m.

FACT(1). For the cyclotomic field $K=\mathbb {Q}(\zeta _{m})$ where $m\ge 3$ and $m\not \equiv 2\pmod 4$, $K/\mathbb {Q}$ is a Galois extension with degree $[K:\mathbb {Q}]=\varphi (m)$, where $\varphi (m)$ is the Euler (totient) function. The Galois group of $K/\mathbb {Q}$ is

$$\begin{aligned} Gal(K/\mathbb {Q})=\left\{ \sigma _{a}:a\in \mathbb {Z}_{m}^{*}\right\} , \end{aligned}$$

where $\mathbb {Z}_{m}^{*}=\{1\le a \le m-1: (a,m)=1\}$ is the multiplicative group of units in the ring $\mathbb {Z}_{m}$, $|\mathbb {Z}_{m}^{*}|=\varphi (m),$ and the automorphism $\sigma _{a}$ of K is defined by $\sigma _{a}(\zeta _{m})=\zeta _{m}^{a}$. We have $\sigma _{a}\sigma _{b}=\sigma _{ab}$ for $a,b\in \mathbb {Z}_{m}^{*}$. Therefore, we have the following isomorphism of groups

$$\begin{aligned} \mathbb {Z}_{m}^{*}\cong Gal(K/\mathbb {Q}), \qquad a\mapsto \sigma _{a}. \end{aligned}$$

FACT(2). Let L be any (algebraic) number field which means $L/\mathbb {Q}$ is a finite extension. An element $\alpha \in L$ is called an (algebraic) integer in L if there exists a monic polynomial $f(x)\in \mathbb {Z}[x]$ such that $f(\alpha )=0$. The set of all integers in L is a (commutative) ring, called the ring of integers in L and denoted by $\mathscr {O}_{L}$. For $K=\mathbb {Q}(\zeta _{m})$ we have

$$\begin{aligned} \mathscr {O}_{K}=\mathbb {Z}[\zeta _{m}]=\mathbb {Z}\oplus \zeta _{m}\mathbb {Z}\oplus \cdots \oplus \zeta _{m}^{\varphi (m)-1}\mathbb {Z}. \end{aligned}$$

Namely, each integer $\alpha \in \mathscr {O}_{K}$ can be uniquely expressed as

$$\begin{aligned} \alpha =a_0+a_1\zeta _{m}+\cdots +a_{\varphi (m)-1}\zeta _{m}^{\varphi (m)-1}\quad (a_{i} \in \mathbb {Z}). \end{aligned}$$

We denote the group of units in $\mathscr {O}_{L}$ by $U_{L}$, and the group of roots of unity in $\mathscr {O}_{L}$ by $W_{L}$. Then $W_{L}\subseteq U_{L}$, and for $K=\mathbb {Q}(\zeta _{m}) (2\not \mid m)$, $W_{K}=\langle \zeta _{2m}\rangle = \{\zeta _{2m}^{i}: 0\le i\le 2m-1\}$ and for $\alpha \in \mathscr {O}_{K}$, we have $\alpha \in W_{K}$ if and only if $|\sigma (\alpha )|=1$ for each $\sigma \in Gal(K/\mathbb {Q})$.

FACT(3). Let L be a number field. Any nonzero ideal A of $\mathscr {O}_{L}$ can be uniquely (up to the order) expressed as

$$\begin{aligned} A=P_{1}^{a_{1}}\cdots P_{s}^{a_{s}}, \end{aligned}$$

where $P_{1}$, $\ldots$, $P_{s}$ are distinct (nonzero) prime ideals of $\mathscr {O}_{L}$ and $a_{i}\ge 1$ $(1\le i \le s)$. In other words, the set S(L) of all nonzero ideals of $\mathscr {O}_{L}$ is a free multiplicative commutative semigroup with a basis B(L), the set of all nonzero prime ideals of $\mathscr {O}_{L}$. Such semigroup S(L) can be extended to the commutative group I(L), called the group of fractional ideals of L. Each element of I(L), called a fractional ideal, has the form $AB^{-1}$ where A, B are ideals of $\mathscr {O}_{L}$. For each $\alpha \in L^{*}=L{\setminus } \{0\}$, $\alpha \mathscr {O}_{L}$ is a fractional ideal, called a principal fractional ideal. And we have $(\alpha \mathscr {O}_{L})(\beta \mathscr {O}_{L})=\alpha \beta \mathscr {O}_{L}$ and $(\alpha \mathscr {O}_{L})^{-1}=\alpha ^{-1}\mathscr {O}_{L}$. Therefore, the set P(L) of all principal fractional ideals is a subgroup of I(L).

FACT(4). The group $C(L)=\frac{I(L)}{P(L)}$ is finite and called the (ideal) class group of L. |C(L)| is called the class number of L, denoted by h(L). An element [A] of C(L) is called the ideal class of a fractional ideal A. Therefore, $[A]^{h(L)}=1$ for any ideal class [A] in C(L).

FACT(5). Let $K=\mathbb {Q}(\zeta _{m})$ where $2\not \mid m\ge 3$, and $G=Gal(K/\mathbb {Q})=\{\sigma _{a}:a\in \mathbb {Z}_{m}^{*}\}$. Let $H=\langle \sigma _{2} \rangle$ be the cyclic subgroup of G generated by $\sigma _{2}$ and M be the subfield of K corresponding to H by Galois Theory. Namely, for $\alpha \in K$, we have $\alpha \in M$ if and only if $\sigma _{2}(\alpha )=\alpha$. H and M are called the decomposition group and decomposition field of 2 in K, respectively. We have

$$\begin{aligned}{}[K:M]=|H|=:r, ~[M:\mathbb {Q}]=[G:H]=\frac{\varphi (m)}{r}=:g, \end{aligned}$$

where $[K:M]=dim_{M}K,$ the dimension of K as a vector space over M, $[G:H]=\big |G/H\big |$. And $r=ord_{2}(m)$, the order of 2 in $\mathbb {Z}_{m}^{*}$. That is, r is the least positive integer such that $2^{r} \equiv 1\pmod {m}$.

$2\mathscr {O}_{M}$ is an ideal of $\mathscr {O}_{M}$ and

$$\begin{aligned} 2\mathscr {O}_{M}=\mathfrak {p}_{1}\mathfrak {p}_{2}\cdots \mathfrak {p}_{g}, \end{aligned}$$

where $\mathfrak {p}_{i}$ are distinct prime ideals of $\mathscr {O}_{M}$. For each $1\le i \le g$, $\mathfrak {p}_{i}\mathscr {O}_{K}=P_{i}$ is a prime ideal of $\mathscr {O}_{K}$. Therefore, we have the decomposition of 2 in $\mathscr {O}_{K}$ as

$$\begin{aligned} 2\mathscr {O}_{K}=P_{1}P_{2}\cdots P_{g}, \end{aligned}$$

where $P_{1},\ldots , P_{g}$ are distinct prime ideals of $\mathscr {O}_{K}$. From $\mathfrak {p}_{i}\subseteq \mathscr {O}_{M}$ we know that $\sigma _{2}(P_{i})=\sigma _{2}(\mathfrak {p}_{i}\mathscr {O}_{K})=\sigma _{2}(\mathfrak {p}_{i})\mathscr {O}_{K}=\mathfrak {p}_{i}\mathscr {O}_{K}=P_{i} \quad (1\le i \le g)$.

FACT(6). (decomposition law in imaginary quadratic fields) Let $d=p_{1}\cdots p_{s}$ where $p_{1}, \ldots , p_{s}$ are distinct odd prime numbers, $s\ge 1$, $K=\mathbb {Q}(\sqrt{-d})$. Then

(I). $\mathscr {O}_{K}=\{A+B\sqrt{-d}: A,~ B\in \mathbb {Z}\}$, if $d \equiv 1\pmod 4$;

$\mathscr {O}_{K}=\{\frac{1}{2}(A+B\sqrt{-d}): A, ~B\in \mathbb {Z}, ~A\equiv B\pmod 2\}$, if $d \equiv 3\pmod 4$;

(II).

$$\begin{aligned} 2\mathscr {O}_{K}=\left\{ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} P^{2}, &{}if~ d \equiv 1\pmod 4\\ P\bar{P}, P\ne \bar{P}, &{}if~ d \equiv 7\pmod 8\\ P,&{}if~ d \equiv 3\pmod 8; \end{array}\right. \end{aligned}$$

(III). For any odd prime number p,

$$\begin{aligned} p\mathscr {O}_{K}=\left\{ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} P^{2}, &{}if~ p|d\\ P\bar{P}, P\ne \bar{P}, &{}if~ p\not \mid d \hbox { and } \left( \frac{-d}{p}\right) =1\\ P,&{}if~ p\not \mid d \hbox { and } \left( \frac{-d}{p}\right) =-1, \end{array}\right. \end{aligned}$$

where P denotes a prime ideal of $\mathscr {O}_{K}$, $\bar{P}=\{\bar{\alpha }:\alpha \in P\}$ and $\left( \frac{-d}{p}\right)$ is the Legendre symbol.

After above preparations, we can prove the following result.

Theorem 1

Let m and n be odd positive integers. Assume that the following semiprimitive condition is satisfied.

There exists a positive integer l such that

$$\begin{aligned} 2^{l}\equiv -1\pmod m. \end{aligned}$$

(5)

Then there is no (m, n)-GBF and (2m, n)-GBF for any odd integer $n\ge 1$.

Proof

For any odd integer $n\ge 1$, if there is no (2m, n)-GBF, then by Lemma 2(2) there is no (m, n)-GBF. So we only need to show that there is no (2m, n)-GBF.

Suppose that there exists a GBF $f:\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}_{2m}$, then $\alpha =W_f(0)=\sum _{x\in \mathbb {Z}_{2}^{n}}\zeta _{2m}^{f(x)}\in \mathscr {O}_K$ where $K=\mathbb {Q}(\zeta _{2m})=\mathbb {Q}(\zeta _{m}), \mathscr {O}_K=\mathbb {Z}[\zeta _{m}]$ by FACT(2). And $\alpha \bar{\alpha }=\big |W_f(0)\big |^{2}=2^{n}$ since f is a GBF. Let l be the least positive integer satisfying (5). Then $r=ord_{2}(m)=2l$ and, by FACT(5), we have

$$\begin{aligned} 2\mathscr {O}_{K}=P_{1}\cdots P_{g}, ~g=\frac{\varphi (m)}{r}, \end{aligned}$$

where $P_{i}$ are distinct prime ideals of $\mathscr {O}_{K}$, and

$$\begin{aligned} 2^{n}\mathscr {O}_{K}=(P_{1}\cdots P_{g})^{n}. \end{aligned}$$

(6)

On the other hand, from $\alpha \mid \alpha \bar{\alpha }=2^{n}$, where $\bar{\alpha }$ is the complex conjugate number of $\alpha$, we have

$$\begin{aligned} \alpha \mathscr {O}_{K}=P_{1}^{a_{1}}\cdots P_{g}^{a_{g}} \quad (a_{i}\ge 0). \end{aligned}$$

By FACT(5), we know that $\sigma _{2}(P_{i})=P_{i}$, so that $\sigma _{-1}(P_{i})=\sigma _{2^{l}}(P_{i})=P_{i} ~(1\le i\le g)$. Therefore,

$$\begin{aligned} \sigma _{-1}(\alpha )\mathscr {O}_{K}=\sigma _{-1}(P_{1})^{a_{1}}\cdots \sigma _{-1}(P_{g})^{a_{g}}=P_{1}^{a_{1}}\cdots P_{g}^{a_{g}}=\alpha \mathscr {O}_{K}. \end{aligned}$$

But $\alpha =\sum _{i=0}^{\varphi (m)-1}a_{i}\zeta _{m}^{i} ~(a_{i}\in \mathbb {Z})$ by FACT(2), so we get

$$\begin{aligned} \sigma _{-1}(\alpha )=\sum _{i=0}^{\varphi (m)-1}a_{i}(\zeta _{m}^{-1})^{i}=\bar{\alpha }. \end{aligned}$$

Therefore,

$$\begin{aligned} \alpha \bar{\alpha }\mathscr {O}_{K}=(\alpha \mathscr {O}_{K})(\sigma _{-1}(\alpha )\mathscr {O}_{K})=P_{1}^{2a_{1}}\cdots P_{g}^{2a_{g}}. \end{aligned}$$

(7)

From uniqueness of the decompositions (6) and (7) of $\alpha \bar{\alpha }=2^{n}$, we have $2a_{1}=n$ which contradicts to $2\not \mid n$. Therefore, there is no (2m, n)-GBF for any odd integer $n\ge 1$. This completes the proof of Theorem 1. $\square$

At the beginning of the paper [1], the author presented an explicit description on odd integers $m\ge 3$ satisfying the semiprimitive condition (5) (for $m=1$, this condition is true automatically). For each nonzero integer d, let $d=2^{t}d'$ where $t\ge 0$ and $2\not \mid d'$. We denote t by $V_{2}(d)$. For easy displaying, we let $d_{i}:=ord_{2}(p_{i})$ in the following.

Lemma 4

[1] Let $m=p_{1}^{a_{1}}\cdots p_{s}^{a_{s}} ~(s\ge 1)$ where $p_{i}$ are distinct odd prime numbers. Then there exists $l\ge 1$ such that $2^{l}\equiv -1\pmod m$ if and only if $V_{2}(d_{i})\ge 1$ is independent of i.

Now we determine $V_{2}(d_{i})$. If $p_{i}\equiv 7\pmod 8$, then $2^{\frac{p_{i}-1}{2}}\equiv \left( \frac{2}{p_{i}}\right) =1 \pmod {p_{i}}$. Since $2\not \mid \frac{p_{i}-1}{2}$ and $d_{i}\mid \frac{p_{i}-1}{2}$, we know that $V_{2}(d_{i})=0$. If $p_{i}\equiv 3\pmod 8$, then $2^{\frac{p_{i}-1}{2}}\equiv \left( \frac{2}{p_{i}}\right) =-1 \pmod {p_{i}}$. Therefore, $d_{i}=2a$, where $a\mid \frac{p_{i}-1}{2}$. Since $\frac{p_{i}-1}{2}$ is odd, a is odd and $V_{2}(d_{i})=V_{2}(2)=1.$ If $p_{i}\equiv 5\pmod 8$, then $2^{\frac{p_{i}-1}{2}}\equiv \left( \frac{2}{p_{i}}\right) =-1 \pmod {p_{i}}$ and $\frac{p_{i}-1}{2}=2b$, $2\not \mid b$. Thus $d_{i}=4b'$, $b'\mid b$, so that $V_{2}(d_{i})=V_{2}(4)=2$. At last, for $p_{i}\equiv 1\pmod 8$, Table 1 below shows that $V_{2}(d_{i})$ can be different integers.

Table 1 The values of $V_{2}(d_{i})$ for prime numbers $p_{i}\equiv 1\pmod 8$

For odd $m=p_{1}^{a_{1}}\cdots p_{s}^{a_{s}}$, by Theorem 1 and Lemma 4 we know that if $V_{2}(d_{i})\ge 1$ is independent of i, then there is no (m, n)-GBF and (2m, n)-GBF for any odd integer $n\ge 1$. Therefore, we get the following result.

Corollary 3

Let $m=p_{1}^{a_{1}}\cdots p_{s}^{a_{s}}$ where $p_{i}$ are distinct odd prime numbers and $a_{i}\ge 1$. Then there is no (m, n)-GBF and (2m, n)-GBF for all odd integers $n\ge 1$ provided one of the following conditions is satisfied.

(I): For each $1\le i \le s$, $p_{i}\equiv 3\pmod 8$, or $p_{i}\equiv 1\pmod 8$ with $V_{2}(d_{i})=1$;

(II): For each $1\le i \le s$, $p_{i}\equiv 5\pmod 8$, or $p_{i}\equiv 1\pmod 8$ with $V_{2}(d_{i})=2$;

(III): For each $1\le i \le s$, $p_{i}\equiv 1\pmod 8$ and $V_{2}(d_{i})\ge 3$ is independent of i.

Remark 2

At the end of this section we explain the meaning of the semiprimitive condition (5). Let $K=\mathbb {Q}(\zeta _{m})$, $2\not \mid m$, and M be the decomposition field of 2 in K. The decomposition group of 2 is the subgroup $\langle \sigma _{2} \rangle$ of $G=Gal(K/\mathbb {Q})=\{\sigma _{a}:a\in \mathbb {Z}_{m}^{*}\}$. Then there exists $l\ge 1$ such that $2^{l}\equiv -1\pmod m$ $\Leftrightarrow$ $\sigma _{-1}(=\sigma _{2}^{l})\in \langle \sigma _{2} \rangle \Leftrightarrow$ for each $\alpha \in M,$ $\bar{\alpha }(=\sigma _{-1}(\alpha ))=\alpha \Leftrightarrow M\subseteq \mathbb {R}$.

Namely, the semiprimitive condition (5) is equivalent to M is a real number field. In the next section, we will show several new nonexistence results on GBF for the field M is not real.

5 Nonexistence results (III): field-descent

In this section we use the field-descent method given in [1] to show some nonexistence results on (m, n)-GBFs for odd integers $n\ge 1$. The method is based on the following result.

Lemma 5

[1] Let $K=\mathbb {Q}(\zeta _{m})$ and M be the decomposition field of 2 in K. If there exists $\alpha \in \mathscr {O}_{K}$ such that $\alpha \bar{\alpha }=2^{n}$, then there is $\beta \in {\mathscr {O}}_{K}$ such that $\beta ^{2}\in {\mathscr {O}}_{M}$ and $\beta \bar{\beta }=2^{n}$. Moreover, if [K : M] is odd, then $\beta \in {\mathscr {O}}_{M}$.

From Corollary 3 we know that for an odd prime number p, there is no $(2p^{l},n)$-GBF for any $l\ge 1$ and odd numbers $n\ge 1$ if $p\equiv 3,5\pmod 8$, or $p\equiv 1\pmod 8$ and $V_{2}(ord_{2}(p))\ge 1$. For the remaining (non-semiprimitive) case $p\equiv 7\pmod 8$, we have the following result.

Theorem 2

Let $m=p^{l}$, where $l\ge 1$ and $p\equiv 7\pmod 8$ be a prime number. Let $s=\frac{g}{2}$, where g is defined as before and $\lambda$ be the least positive odd integer such that $x^{2}+py^{2}=2^{\lambda +2}$ has a solution $(x,y),~ x, ~y\in \mathbb {Z}$. Then there is no $(2p^{l},n)$-GBF for any odd integer $1\le n<\frac{\lambda }{s}$.

Proof

Suppose there exists a $(2p^{l},n)$-GBF f, then $\alpha =W_{f}(0)\in \mathscr {O}_K ~(K=\mathbb {Q}(\zeta _{p^{l}}))$ and $\alpha \bar{\alpha }=2^n$. By Lemma 5, there exists $\beta \in {\mathscr {O}}_{K}$ such that $\beta ^{2}\in {\mathscr {O}}_{M}$ and $\beta \bar{\beta }=2^n$, where M is the decomposition field of 2 in K. Since $\left( \frac{2}{p}\right) =1$, $[K:M]=r$ is odd. Therefore, $\beta \in {\mathscr {O}}_{M}$ and $[M:\mathbb {Q}]=g=2s$, where s is odd since $\varphi (p^{l})=(p-1)p^{l-1}\equiv 2\pmod 4$. The Galois group $G=Gal(K/\mathbb {Q})$ is isomorphic to the cyclic group $\mathbb {Z}_{p^{l}}^{*}$. By Galois theory, there exists an unique quadratic field T, $\mathbb {Q}\subset T\subseteq M$, $[T:\mathbb {Q}]=2$ and $[M:T]=s$. It is well known that T is the imaginary quadratic field $\mathbb {Q}(\sqrt{-p})$ $\big ($one of the ways for proving this fact is by the quadratic Gauss sum $\sum _{i=1}^{p-1}\big (\frac{i}{p}\big )\zeta _{p}^{i}=\sqrt{-p}$, so that $\sqrt{-p}\in \mathbb {Q}(\zeta _{p})\subseteq \mathbb {Q}(\zeta _{m})=K$ and $T=\mathbb {Q}(\sqrt{-p})\big )$.

Let $N_{M/T}:M\longrightarrow T$ be the norm mapping and $\gamma =N_{M/T}(\beta )\in \mathscr {O}_{T}$, then $\gamma \bar{\gamma }=N_{M/T}(\beta )N_{M/T}(\bar{\beta })=N_{M/T}(\beta \bar{\beta })=N_{M/T}(2^{n})=2^{ns}$ where ns is odd. By FACT(6) in Sect. 4, $\gamma \in {\mathscr {O}}_{T}$ can be expressed as $\gamma =\frac{1}{2}(A+B\sqrt{-p})$ where A, $B\in \mathbb {Z}$, $A \equiv B\pmod 2$. Therefore, $2^{ns}=\gamma \bar{\gamma }=\frac{1}{4}(A^{2}+pB^{2})$. By the definition of $\lambda$ and $2\not \mid ns$ we get $ns\ge \lambda$. Therefore, there is no $(2p^{l},n)$-GBF if $2\not \mid n$ and $n<\frac{\lambda }{s}$. This completes the proof of Theorem 2. $\square$

Remark 3

(A). Let p be an odd prime number. For any $l\ge 1$, we denote $r_{l}=ord_{2}(p^{l})$ and $g_{l}=\frac{\varphi (p^{l})}{r_{l}}$. It is easy to see that if $2^{p-1}\not \equiv 1\pmod {p^{2}}$, then $r_{l}=p^{l-1}r_{1}$, so that $g_{l}=\frac{\varphi (p^{l})}{r_{l}}=\frac{\varphi (p)p^{l-1}}{r_{1}p^{l-1}}=g_{1}$ for all $l\ge 2$. It is known that $2^{p-1}\not \equiv 1\pmod {p^{2}}$ for all odd prime numbers $p<6\cdot 10^{9}$ except $p=1093$ and 3511. Thus it is enough to compute $g_{1}$ for such p.

(B). The definition of $\lambda$ is elementary. Now we prove the existence of $\lambda$ and explain its meaning from an algebraic number theory point of view. Since $\lambda$ is the least odd integer such that $x^{2}+py^{2}=2^{\lambda +2}$ has a solution $(x, y)=(A, B)\in \mathbb {Z}^{2}$, we know that both A and B are odd, so that $\delta =\frac{1}{2}(A+B\sqrt{-p})\in \mathscr {O}_{T}$ and $\delta \bar{\delta }=2^{\lambda }$. From $p\equiv 7\pmod 8$ we know that $2\mathscr {O}_{T}=P\bar{P}$ where P and $\bar{P}=\sigma _{-1}(P)$ are distinct prime ideals of $\mathscr {O}_{T}$ (FACT(6) in Sect. 4). Let [P] be the ideal class of P in the class group C(T). We have $1=[2 \mathscr {O}_{T}]=[P][\bar{P}]$, so that $[\bar{P}]=[P]^{-1}$. From $\delta \bar{\delta }\mathscr {O}_{T}=2^{\lambda }\mathscr {O}_{T}=P^{\lambda }\bar{P}^{\lambda }$ and the minimum property of $\lambda$ we get $\delta \mathscr {O}_{T}=P^{\lambda }$ or $\bar{P}^{\lambda }$ and $\lambda$ is the order of [P] in C(T). Therefore, $\lambda |h(T)$ (the class number of T). By Gauss’s genus theory, h(T) is odd for $T=\mathbb {Q}(\sqrt{-p})$ and $p\equiv 7\pmod 8$. On the other hand, we have $2^{\lambda +2}=A^{2}+pB^{2}>p$ which implies that $\lambda >\frac{\log p}{\log 2}-2$. In particular, we have $\lambda \ge 3$ if $p\equiv 7\pmod 8$ and $p\ge 23$. And $\lambda =h(T)$ if h(T) is a prime number.

Example 2

There are 11 primes satisfying $p\equiv 7\pmod 8$ within 200. Table 2 presents the values of s,  h(T) and $\lambda$ for $T=\mathbb {Q}(\sqrt{-p})$.

For $p=47, 79$ and 103, we have $s=1$ and $\lambda =5$. By Theorem 2, there is no $(2\cdot p^{l},1)$-GBF and $(2\cdot p^{l},3)$-GBF for all $l\ge 1$. For $p=199$, we have $s=1$ and $\lambda =9$. There is no $(2\cdot 199^{l},n)$-GBF for $n=1,3,5,7$ and all $l\ge 1$. Similarly, there is no $(2\cdot 191^{l},n)$-GBF for $n=1,3,5,7,9,11$ and all $l\ge 1$.

Table 2 The values of s and $\lambda$ for prime numbers $p\equiv 7\pmod 8$

The following two corollaries are direct consequences of Theorem 2 and Remark 3.

Corollary 4

Suppose that $p\equiv 7\pmod 8$ is a prime number, $2^{p-1}\not \equiv 1\pmod {p^{2}}$, and $ord_{2}(p)=\frac{p-1}{2}$. Then there is no $(2p^{l},n)$-GBF for all $l\ge 1$ and $2\not \mid n<\lambda$ where $\lambda$ is defined in Theorem 2.

Corollary 5

Suppose that $p\equiv 7\pmod 8$ is a prime number, $p\ge 23$, $2^{p-1}\not \equiv 1\pmod {p^2}$ and the ideal class number h(T) of $T=\mathbb {Q}(\sqrt{-p})$ is a prime number. Then there is no $(2p^{l},n)$-GBF for all $l\ge 1$ and $2\not \mid n<\frac{h(T)}{s}$ where $s=\frac{g_{1}}{2}$.

From now on we assume $m=p_{1}^{a_{1}}p_{2}^{a_{2}}$ where $p_{1},$ $p_{2}$ are distinct odd prime numbers, $a_{1},$ $a_{2}\ge 1$. Let $r'=ord_{2}(p_{1}^{a_{1}}),$ $r''=ord_{2}(p_{2}^{a_{2}})$, then $r=ord_{2}(m)=lcm\{r',r''\}$. Let $M_{1},$ $M_{2}$ and M be the decomposition fields of 2 in $K_{1}=\mathbb {Q}(\zeta _{p_{1}^{a_{1}}}),$ $K_{2}=\mathbb {Q}(\zeta _{p_{2}^{a_{2}}})$ and $K=\mathbb {Q}(\zeta _{m})=K_{1}K_{2}$, respectively. Then $g_{1}=[M_{1}:\mathbb {Q}]=\frac{\varphi (p_{1}^{a_{1}})}{r'}$, $g_{2}=[M_{2}:\mathbb {Q}]=\frac{\varphi (p_{2}^{a_{2}})}{r''}$ and $g=[M:\mathbb {Q}]=\frac{\varphi (m)}{r}=\frac{\varphi (p_{1}^{a_{1}})\varphi (p_{2}^{a_{2}})}{lcm\{r',r''\}} =\frac{\varphi (p_{1}^{a_{1}})}{r'}\frac{\varphi (p_{2}^{a_{2}})}{r''}\cdot gcd\{r',r''\}=g_{1}g_{2}\cdot gcd\{r',r''\}.$

Theorem 3

Suppose $p_{1}\equiv 7\pmod 8$, $p_{2}\equiv 3,5\pmod 8$ and $m=p_{1}^{a_{1}}p_{2}^{a_{2}}$ $~(a_{1}, a_{2}\ge 1)$. Then $g=2s$ and s is odd, where g is defined as above. Let $\lambda _{1}\ge 1$ be the least odd integer such that $x^{2}+p_{1}y^{2}=2^{\lambda _{1}+2}$ has a solution (x, y), x, $y \in \mathbb {Z}$. Let $\lambda _{2}\ge 1$ be the least odd integer such that $x^{2}+p_{1}y^{2}=2^{\lambda _{2}+2}p_{2}$ has a solution (x, y), x, $y \in \mathbb {Z}$. (If there is no solution $(x,y)\in \mathbb {Z}^{2}$ of $x^{2}+p_{1}y^{2}=2^{\lambda _{2}+2}p_{2}$ for any odd $\lambda _{2}\ge 1$, we assume that $\lambda _{2}=+\infty$). Let $\lambda =min\{\lambda _{1},\lambda _{2}\}$. Then there is no (m, n)-GBF and (2m, n)-GBF provided one of the following conditions is satisfied.

(I). $2\not \mid n<\frac{\lambda _{1}}{s}$ and $\left( \frac{-p_{1}}{p_{2}}\right) =-1$;

(II). $2\not \mid n<\frac{\lambda }{s}$ and $\left( \frac{-p_{1}}{p_{2}}\right) =1$.

Proof

Firstly, we consider the case $p_{1}\equiv 7\pmod 8$ and $p_{2}\equiv 3\pmod 8$. We know that

$$\begin{aligned}&r' \text{ is } \text{ odd } \text{ and } r'\mid \frac{1}{2}\varphi \left( p_{1}^{a_{1}}\right) =\frac{p_{1}-1}{2}p_{1}^{a_{1}-1},\\&r''=2b, ~b \text{ is } \text{ odd } \text{ and } b\mid \frac{1}{2}\varphi \left( p_{2}^{a_{2}}\right) =\frac{p_{2}-1}{2}p_{2}^{a_{2}-1}. \end{aligned}$$

Therefore, $g_{1}=\frac{\varphi (p_{1}^{a_{1}})}{r'}\equiv 2\pmod 4$, $g_{2}=\frac{\varphi (p_{2}^{a_{2}})}{r''}$ is odd, and $g=g_{1}g_{2}\cdot gcd\{r',r''\}=2s,$ $2\not \mid s$. The imaginary quadratic field $T=\mathbb {Q}(\sqrt{-p_{1}})$ is a subfield of $K_{1}$. Since $M\cap K_{i}=M_{i}~ (i=1,2)$ and $[M_{1}:\mathbb {Q}]=g_{1}$ is even, $[M_{2}:\mathbb {Q}]=g_{2}$ is odd, we know that $T\subseteq M_{1}\subseteq M,$ $\sqrt{-p_{2}}\not \in M.$ Therefore, $L=M(\sqrt{-p_{2}})$ is a quadratic extension of M in K. Moreover, since Gal(K / M) is the cyclic group generated by $\sigma _{2}$ and $[K:M]=\frac{\varphi (m)}{g}$ is even, we know that L is the unique quadratic extension of M in K.

Suppose that there exists a (2m, n)-GBF, $2\not \mid n\ge 1$. Then we have $\alpha \in \mathscr {O}_{K}$ such that $\alpha \bar{\alpha }=2^{n}$. By Lemma 5, there is a $\beta \in \mathscr {O}_{L}$ such that $\beta ^{2}\in \mathscr {O}_{M}$ and $\beta \bar{\beta }=2^{n}$. Since $\{1,\sqrt{-p_{2}}\}$ is a basis for extension L / M,  we have $\beta =A+B\sqrt{-p_{2}},$ A,  $B\in M$. By $\beta ^{2}=A^{2}-p_{2}B^{2}+2AB\sqrt{-p_{2}}\in \mathscr {O}_{M}$ and $\sqrt{-p_{2}}\not \in M$ we get $AB=0$. Therefore, $\beta =A\in \mathscr {O}_{L}\cap M=\mathscr {O}_{M}$ or $\beta =B\sqrt{-p_{2}}\in \mathscr {O}_{L}$.

If $\beta =A\in \mathscr {O}_{M},$ then $\gamma =N_{M/T}(\beta )\in \mathscr {O}_{T}$ where $N_{M/T}(\beta )=\varPi _{\sigma \in Gal(M/T)}\sigma (\beta )$ is the norm mapping from M to T (and also from $\mathscr {O}_{M}$ to $\mathscr {O}_{T}$). We have $\gamma \bar{\gamma }=N_{M/T}(\beta \bar{\beta })=N_{M/T}(2^{n})=2^{ns}$ where $s=\frac{g}{2}=[M:T]$. By FACT(6) in Sect. 4, $\gamma =\frac{1}{2}(x+y\sqrt{-p_{1}})$ where x,  $y\in \mathbb {Z}$. Then $x^{2}+p_{1}y^{2}=4\gamma \bar{\gamma }=2^{ns+2}$. From $2\not \mid ns$ and the definition of $\lambda _{1}$ we get $ns\ge \lambda _{1}$.

If $\beta =B\sqrt{-p_{2}}\in \mathscr {O}_{L}$ and $B\in M$, consider the element $\gamma =\prod _{\sigma \in Gal(L/T)/Gal(L/M)}\sigma (\beta )$ $=\prod _{\sigma \in Gal(M/T)}\sigma (B)\cdot \prod _{\sigma \in Gal(L/T)/Gal(L/M)}\sigma (\sqrt{-p_{2}})=N_{M/T}(B)\cdot (\pm \sqrt{-p_{2}})^{s}$ where $N_{M/T}(B)\in T$. Let $\delta =N_{M/T}(B)p_{2}^{\frac{s+1}{2}}\in T\cap \mathscr {O}_{L}=\mathscr {O}_{T}$. Then $\delta =\frac{1}{2}(x+y\sqrt{-p_{1}})$, x,  $y \in \mathbb {Z}$ and $x^{2}+p_{1}y^{2}=4\delta \bar{\delta }=4N_{M/T}(B\bar{B})p_{2}^{s+1}=4\gamma \bar{\gamma }p_{2}=2^{ns+2}p_{2}.$ Therefore, $p_{2}\not \mid xy$ and $x^{2}\equiv -p_{1}y^{2}\pmod {p_{2}}$. So $\left( \frac{-p_{1}}{p_{2}}\right) =1$. This means that if $\left( \frac{-p_{1}}{p_{2}}\right) =-1$ then $\beta =B\sqrt{-p_{2}}$ is impossible. If $\left( \frac{-p_{1}}{p_{2}}\right) =1$, from $x^{2}+p_{1}y^{2}=2^{ns+2}p_{2}$ and the definition of $\lambda _{2}$ we get $ns\ge \lambda _{2}$.

In summary, if there is a (2m, n)-GBF with odd n, then $n\ge \frac{\lambda _{1}}{s}$ when $\left( \frac{-p_{1}}{p_{2}}\right) =-1$ and $n\ge min\{\frac{\lambda _{1}}{s},\frac{\lambda _{2}}{s}\}=\frac{\lambda }{s}$ when $\left( \frac{-p_{1}}{p_{2}}\right) =1$. This completes the proof of Theorem 3 for the case $p_{1}\equiv 7\pmod 8$ and $p_{2}\equiv 3\pmod 8$.

Now we consider the case $p_{1}\equiv 7\pmod 8$ and $p_{2}\equiv 5\pmod 8$. In this case,

$$\begin{aligned}&r' \text{ is } \text{ odd } \text{ and } r'\mid \frac{1}{2}\varphi \left( p_{1}^{a_{1}}\right) ,\\&r''=4b, ~b \text{ is } \text{ odd } \text{ and } b\mid \frac{1}{4}\varphi \left( p_{2}^{a_{2}}\right) . \end{aligned}$$

Therefore, $g_{1}=\frac{\varphi (p_{1}^{a_{1}})}{r'}\equiv 2\pmod 4$, $g_{2}=\frac{\varphi (p_{2}^{a_{2}})}{r''}$ is odd, and $g=g_{1}g_{2}\cdot gcd\{r',r''\}=2s$, $2\not \mid s$. Then we have the same field extension diagram as the one in the case $(p_{1},p_{2})\equiv (7,3)\pmod 8$ except $L=M(\sqrt{p_{2}})$ for $p_{2}\equiv 5\pmod 8$. The conclusion can be derived by the similar argument. This completes the proof of Theorem 3. $\square$

Remark 4

We have seen the existence of $\lambda _{1}$ in Remark (B) of Theorem 2. Namely, $2\mathscr {O}_{T}=P\bar{P}$ and $\lambda _{1}$ is the order of the ideal class [P] in the class group C(T). In particular, $\lambda _{1}\mid h(T)=|C(T)|$. By Gauss’s genus theory, h(T) is odd, and so is $\lambda _{1}$.

Now we give a method to determine the value of $\lambda _{2}$ in the case $p_{1}\equiv 7\pmod 8$, $p_{2}\equiv 3,5\pmod 8$ and $\left( \frac{-p_{1}}{p_{2}}\right) =1$. By definition, $\lambda _{2}=+\infty$ if the equation $x^{2}+p_{1}y^{2}=2^{l+2}p_{2}$ has no solution $(x,y)\in \mathbb {Z}^{2}$ for any odd integer $l\ge 1$. Otherwise $\lambda _{2}$ is the least odd integer such that $x^{2}+p_{1}y^{2}=2^{\lambda _{2}+2}p_{2}$ has a solution $(x,y)\in \mathbb {Z}^{2}$. We claim that if $\lambda _{2}\ne +\infty ,$ then $\lambda _{2}\le \lambda _{1}$. So that $\lambda =min\{\lambda _{1},\lambda _{2}\}=\lambda _{2}$.

Suppose that $\lambda _{2}\ne +\infty ,$ then $x^{2}+p_{1}y^{2}=2^{\lambda _{2}+2}p_{2}$ has a solution $(x,y)=(A,B)\in \mathbb {Z}^{2}$. From the minimal property of $\lambda _{2}$ we know that $2\not \mid AB$, and so $\pi =\frac{1}{2}(A+B\sqrt{-p_{1}})\in \mathscr {O}_{T}$. Therefore,

$$\begin{aligned} (\pi \mathscr {O}_{T})(\overline{\pi }\mathscr {O}_{T})=(2^{\lambda _{2}}p_{2})\mathscr {O}_{T}= (P\bar{P})^{\lambda _{2}}Q\bar{Q}. \end{aligned}$$

The last equation is because of $2\mathscr {O}_{T}=P\bar{P}$ and $p_{2}\mathscr {O}_{T}=Q\bar{Q}$.

Again, from the minimal property of $\lambda _{2}$ we get

$$\begin{aligned} \pi \mathscr {O}_{T}=(P')^{\lambda _{2}}Q', ~P'\in \{P, \bar{P}\}, ~Q'\in \{Q,\bar{Q}\}. \end{aligned}$$

Therefore, $[P']^{\lambda _{2}}[Q']=1$. Namely, $[Q']$ belongs to the cyclic group of order $\lambda _{1}$ generated by [P]. On the other hand, suppose that $[P']^{l}[Q']=1$ for some l, $0\le l<\lambda _{1}-1$. If l is odd, then $\lambda _{2}=l\le \lambda _{1}-1$. If l is even, then $[\bar{P}']^{\lambda _{1}-l}[\bar{Q}']=([P']^{l}[Q'])^{-1}=1$ so that $\lambda _{2}=\lambda _{1}-l\le \lambda _{1}$.

In summary, if the equation $x^{2}+p_{1}y^{2}=2^{l+2}p_{2}$ has no solution $(x,y)\in \mathbb {Z}^{2}$ for $l=0,1,\ldots , \lambda _{1}-1$, then $\lambda _{2}=+\infty$ and $\lambda =\lambda _{1}$. Otherwise, there exists an unique odd l such that $1\le l \le \lambda _{1}$ and $x^{2}+p_{1}y^{2}=2^{l+2}p_{2}$ has a solution $(x,y)\in \mathbb {Z}^{2}$. Then $\lambda _{2}=l\le \lambda _{1}$ and $\lambda =min\{\lambda _{1},\lambda _{2}\}=\lambda _{2}$.

Example 3

Consider $m=p_{1}^{a_{1}}p_{2}^{a_{2}}$ where $p_{1}=199\equiv 7\pmod 8$. By Table 2 we know that $g_{1}=2$, $r'=\frac{\varphi (p_{1}^{a_{1}})}{g_{1}}=99\cdot 199^{a_{1}-1}$ and $\lambda _{1}=9$.

(1). For $p_{2}=59\equiv 3\pmod 8,$ $r''=2b,$ $b=29\cdot 59^{a_{2}-1},$ $g_{2}=1$. Thus $g=g_{1}g_{2}\cdot gcd\{r',r''\}=2$ and $s=\frac{g}{2}=1$. Since $\left( \frac{-p_{1}}{p_{2}}\right) =\left( \frac{-199}{59}\right) =-1$. By Theorem 3 we get that there is no $(199^{a_{1}}\cdot 59^{a_{2}}, n)$-GBF and $(2\cdot 199^{a_{1}}\cdot 59^{a_{2}}, n)$-GBF for $a_{1},$ $a_{2}\ge 1$ and $n=1, 3, 5, 7$.

(2). For $p_{2}=101\equiv 5\pmod 8,$ $r''=4b,$ $b=25\cdot 101^{a_{2}-1},$ $g_{2}=1$. Thus $g=g_{1}g_{2}\cdot gcd\{r',r''\}=2$ and $s=\frac{g}{2}=1$. Since $\left( \frac{-p_{1}}{p_{2}}\right) =\left( \frac{-199}{101}\right) =-1,$ by Theorem 3 we get that there is no $(199^{a_{1}}\cdot 101^{a_{2}}, n)$-GBF and $(2\cdot 199^{a_{1}}\cdot 101^{a_{2}}, n)$-GBF for $a_{1},a_{2}\ge 1$ and $n=1,3,5,7$.

(3). For $p_{2}=5,$ $r''=4b,$ $b=5^{a_{2}-1},$ $g_{2}=1$. Thus $g=g_{1}g_{2}\cdot gcd\{r',r''\}=2$ and $s=\frac{g}{2}=1$. From $11^{2}+199\cdot 1^{2}=320=2^{6}\cdot 5$ we get $\lambda _{2}=9-4=5$ (in fact, $21^{2}+199\cdot 1^{2}=2^{7}\cdot 5$) and $\lambda =\lambda _{2}=5$. Since $\left( \frac{-p_{1}}{p_{2}}\right) =\left( \frac{-199}{5}\right) =1,$ by Theorem 3 we get that there is no $(199^{a_{1}}\cdot 5^{a_{2}}, n)$-GBF and $(2\cdot 199^{a_{1}}\cdot 5^{a_{2}}, n)$-GBF for $a_{1},$ $a_{2}\ge 1$ and $n=1,3$.

Theorem 4

Suppose that $p_{1}\equiv 3\pmod 8$, $p_{2}\equiv 5\pmod 8$ and $m=p_{1}^{a_{1}}p_{2}^{a_{2}}$ $(a_{1}, ~a_{2}\ge 1)$. Then $g=2s$ and s is odd. Let $\lambda \ge 1$ be the least odd integer such that $p_{1}x^{2}+p_{2}y^{2}=2^{\lambda +2}$ has a solution (x, y),  x,  $y \in \mathbb {Z}$. Then there is no (m, n)-GBF and (2m, n)-GBF provided n is odd and one of the following conditions is satisfied.

(I). $\left( \frac{p_{2}}{p_{1}}\right) =1$; or

(II). $\left( \frac{p_{2}}{p_{1}}\right) =-1$ and $n<\frac{\lambda }{s}$.

Proof

We have

$$\begin{aligned} r'= & {} 2a, ~2\not \mid a, ~g_{1}=\frac{\varphi \left( p_{1}^{a_{1}}\right) }{r'} \text{ is } \text{ odd },\\ r''= & {} 4b, ~2\not \mid b, ~g_{2}=\frac{\varphi \left( p_{2}^{a_{2}}\right) }{r''} \text{ is } \text{ odd }. \end{aligned}$$

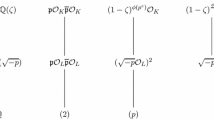
Therefore, $g=g_{1}g_{2}\cdot gcd\{r',r''\}=2g_{1}g_{2}\cdot gcd\{a,b\}=2s,$ $2\not \mid s$. From $2\not \mid g_{1}g_{2}$ we know that neither $\mathbb {Q}(\sqrt{-p_{1}})$ nor $\mathbb {Q}(\sqrt{p_{2}})$ are subfields of M. Therefore, $\sigma _{2}(\sqrt{-p_{1}})=-\sqrt{p_{1}}$ and $\sigma _{2}(\sqrt{p_{2}})=-\sqrt{p_{2}}$, so that $\sigma _{2}(\sqrt{-p_{1}p_{2}})=\sqrt{-p_{1}p_{2}}$ which means $T=\mathbb {Q}(\sqrt{-p_{1}p_{2}})$ is the quadratic subfield of M and the quadratic extension of M is $L=M(\sqrt{p_{2}}) ~(=M(\sqrt{-p_{1}}))$. Thus we have the field extension diagram as following.

Suppose that there exists a (2m, n)-GBF and $2\not \mid n\ge 1$. Then we have $\alpha \in \mathscr {O}_L$ such that $\alpha ^{2}\in \mathscr {O}_M$ and $\alpha \bar{\alpha }=2^{n}$. From $\alpha =A+B\sqrt{p_{2}}~ (A,$ $B\in M)$ and $\alpha ^{2}=A^{2}+p_{2}B^{2}+2AB\sqrt{p_{2}}\in \mathscr {O}_M$ we know that $AB=0$. Therefore, $\alpha =A\in M\cap \mathscr {O}_L=\mathscr {O}_M$ or $\alpha =B\sqrt{p_{2}}.$ If $\alpha =A\in \mathscr {O}_M$, then $\beta =N_{M/T}(\alpha )\in \mathscr {O}_T$ and $\beta \bar{\beta }=N_{M/T}(\alpha \bar{\alpha })=N_{M/T}(2^{n})=2^{ns}$. By $\beta =\frac{1}{2}(x+y\sqrt{-p_{1}p_{2}}),$ x,  $y\in \mathbb {Z},$ we have $x^{2}+p_{1}p_{2}y^{2}=2^{ns+2}$. So that $x^{2}\equiv 2^{ns+2}\pmod {p_{1}}$ and then $\left( \frac{2}{p_{1}}\right) =1$ since $2\not \mid ns$. But $\left( \frac{2}{p_{1}}\right) =-1$ since $p_{1}\equiv 3\pmod 8$. We get a contradiction. Therefore, $\alpha =B\sqrt{p_{2}}\in \mathscr {O}_L,$ $B\in M$. Let

$$\begin{aligned} \gamma =\prod _{\sigma \in Gal(L/T)/Gal(L/M)}\sigma (\alpha )=N_{M/T}(B)(\pm \sqrt{p_{2}}^{s})\in \mathscr {O}_L, \end{aligned}$$

where $N_{M/T}(B) \in T$. Then $\delta =N_{M/T}(B)p_{2}^{\frac{s+1}{2}}=\gamma \sqrt{p_{2}}\in \mathscr {O}_L\cap T=\mathscr {O}_T$ and

$$\begin{aligned} \delta \bar{\delta }=N_{M/T}(B\bar{B})p_{2}^{s+1}=\gamma \bar{\gamma }p_{2} =\left( \prod _{\sigma }(\alpha \bar{\alpha })\right) p_{2}=2^{ns}p_{2}. \end{aligned}$$

By $\delta =\frac{1}{2}(x+y\sqrt{-p_{1}p_{2}})$, x,  $y\in \mathbb {Z}$ we get $x^{2}+p_{1}p_{2}y^{2}=2^{ns+2}p_{2}$, which implies $x^{2}\equiv 2^{ns+2}p_{2}\pmod {p_{1}}$. Thus $1=\left( \frac{2p_{2}}{p_{1}}\right) =-\left( \frac{p_{2}}{p_{1}}\right)$, and $p_{2}|x$. So that $p_{2}(\frac{x}{p_{2}})^{2}+p_{1}y^{2}=2^{ns+2}$. By the definition of $\lambda$ we get $ns\ge \lambda$.

In summary, there is no (m, n)-GBF and (2m, n)-GBF if $2\not \mid n$ and $\left( \frac{p_{2}}{p_{1}}\right) =1$, or $2\not \mid n<\frac{\lambda }{s}$ and $\left( \frac{p_{2}}{p_{1}}\right) =-1$. This completes the proof of Theorem 4. $\square$

Remark 5

We explain the existence of $\lambda$ in the case $p_{1}\equiv 3\pmod 8$, $p_{2}\equiv 5\pmod 8$ and $\left( \frac{p_{2}}{p_{1}}\right) =-1$. By definition, $\lambda$ is the least odd integer such that $x^{2}+p_{1}p_{2}y^{2}=2^{\lambda +2}p_{2}$ has a solution $(x,y)\in \mathbb {Z}^{2}$. By FACT(6) in Sect. 4, we have the decomposition in $T=\mathbb {Q}(\sqrt{-p_{1}p_{2}})$, $p_{2}\mathscr {O}_T=Q^{2}$ and $2\mathscr {O}_T=P\bar{P}$ since $-p_{1}p_{2}\equiv 1\pmod 8$. We know that $Q=(p_{2},$ $\sqrt{-p_{1}p_{2}})$ is not a principal (prime) ideal in $\mathscr {O}_T$ and $[Q]^{2}=[(p_{2}\mathscr {O}_T)]=1$. Thus the order of [Q] is two. We also know that $h(T)=2k,$ $2\not \mid k$ ([6], Propositions 3 and 4). Let d be the order of [P], then $x^{2}+p_{1}p_{2}y^{2}=2^{d+2}$ has a solution $(x,y)\in \mathbb {Z}^{2}$. Thus $x^{2}\equiv 2^{d+2}\pmod {p_{1}}$, so that $1=\left( \frac{2}{p_{1}}\right) ^{d+2}=(-1)^{d+2}$, which implies that $2\mid d$ and $d=2e$. Since $d\mid h(T)=2k$ we get $e\mid k$. Therefore, e is odd. Thus both $[P^{e}]$ and [Q] are elements of order two. Since the size of the class group C(T) is $h(T)\equiv 2\pmod 4$ and then it has unique element of order two, we get $[P^{e}]=[Q]$. Therefore, $[P^{e}Q]=1$. Namely, $P^{e}Q$ is a principal ideal $\alpha \mathscr {O}_T$, where $\alpha =\frac{1}{2}(x+y\sqrt{-p_{1}p_{2}}),$ $(\alpha \bar{\alpha })\mathscr {O}_T=(P\bar{P})^{e}Q\bar{Q}=(2^{e}p_{2})\mathscr {O}_T$. Therefore, $x^{2}+p_{1}p_{2}y^{2}=2^{e+2}p_{2},$ $2\not \mid e$. From the minimal property of $\lambda$ we get that $\lambda$ is just e, the half of the order of [P].

Example 4

Let $m=p_{1}^{a_{1}}p_{2}^{a_{2}}$ $(a_{1},$ $a_{2}\ge 1)$ where $p_{1}=19\equiv 3\pmod 8$, $p_{2}=29 \equiv 5\pmod 8$, then $\left( \frac{p_{2}}{p_{1}}\right) =\left( \frac{29}{19}\right) =-1$, $r'=18\cdot 19^{a_{1}-1},$ $g_{1}=1$, $r''=28\cdot 29^{a_{2}-1},$ $g_{2}=1$ and so $g=g_{1}g_{2}\cdot gcd\{r',r''\}=2, s=\frac{g}{2}=1$. The equation $19x^{2}+29y^{2}=2^{l+2}$ has no solution $(x,y)\in \mathbb {Z}^{2}$ for $l=1,3,5,7,9$ and 11, but $2^{13+2}=32768=19\cdot 21^{2}+29\cdot 29^{2}$. We get $\lambda =13$ and , by Theorem 4, there is no $(19^{a_{1}}29^{a_{2}},n)$-GBF and $(2\cdot 19^{a_{1}}29^{a_{2}},n)$-GBF and for any $a_{1},$ $a_{2}\ge 1$ and $n=1,3,5,7,9,11$.

6 Conclusion

In this paper we deal with the existence problem of generalized bent function $f:\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}_{m}$ , called a (m, n)-GBF. In Sect. 2 we proved that there is a (m, n)-GBF if $2\mid gcd\{m,n\}$ or $4\mid m$. For the remaining cases we presented a series of nonexistence results in Sects. 3–5 including the following results.

There is no (m, n)-GBF for any odd integer $n\ge 1$ if one of the following conditions on m is satisfied (p,  $p_{1}, \ldots , p_{s}$ denote odd prime numbers, a,  $a_{1}, \ldots , a_{s}\ge 1$).

(A). $m=p^{a}$ (Corollary 2);

(B). $m=2p^{a}$, $p\equiv 3, 5\pmod 8$, or $p\equiv 1\pmod 8$ and $ord_{2}(p)$ is even (Corollary 3);

(C). $m=2p_{1}^{a_{1}}p_{2}^{a_{2}}$, $p_{1}\equiv 3 \pmod 8$, $p_{2}\equiv 5\pmod 8$ and $\left( \frac{p_{2}}{p_{1}}\right) =1$ (Theorem 4);

(D). $m=2p_{1}^{a_{1}}p_{2}^{a_{2}}\cdots p_{s}^{a_{s}}$, $p_{1},\ldots , p_{s}$ are distinct and $p_{1}\equiv p_{2} \equiv \ldots \equiv p_{s} \equiv 3\pmod 8$, or $p_{1}\equiv p_{2}\equiv \ldots \equiv p_{s} \equiv 5\pmod 8$ (Corollary 2);

In Sect. 4, the decomposition field M of 2 in $K=\mathbb {Q}(\zeta _{m})$ is real. For all cases in Sect. 5, $[M,\mathbb {Q}]=2s, 2\not \mid s$ and M contains an imaginary quadratic subfield T. The nonexistence results are derived by using field-descent method from K to M (Lemma 5), then from M to T by norm mapping, and by using some knowledge on the decomposition law of prime numbers in $\mathscr {O}_T$ and the structure of the class group of T. Next step we may consider the case that $[M,\mathbb {Q}]=4s,$ $2\not \mid s$ and M contains an imaginary quadratic subfield T. In this case we would use specific knowledge on integral basis of $\mathscr {O}_T$, the decomposition law in $\mathscr {O}_T$ and the structure of the class group of T. The derived conditions on nonexistence of GBF would be more complicated if the Galois group $G(T/\mathbb {Q})$ is cyclic.