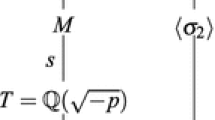Nonexistence of two classes of generalized bent functions

Abstract

We obtain some new nonexistence results of generalized bent functions from ${\mathbb {Z}}^n_q$ to ${\mathbb {Z}}_q$ (called type [n, q]) in the case that there exist cyclotomic integers in ${\mathbb {Z}}[\zeta _{q}]$ with absolute value $q^{\frac{n}{2}}$. This result generalizes two previous nonexistence results $[n,q]=[1,2\times 7]$ of Pei (Lect Notes Pure Appl Math 141:165–172, 1993) and $[3,2\times 23^e]$ of Jiang and Deng (Des Codes Cryptogr 75:375–385, 2015). We also remark that by using a same method one can get similar nonexistence results of GBFs from ${\mathbb {Z}}^n_2$ to ${\mathbb {Z}}_m$.

1 Introduction

Bent functions were first introduced by Rothaus [16] in 1976, which are functions from ${\mathbb {Z}}_2^n$ to ${\mathbb {Z}}_2$ with some property, where ${\mathbb {Z}}_m={\mathbb {Z}}/m{\mathbb {Z}}$ for a positive integer m. Dillon [1] showed that bent functions are the characteristic functions of elementary Hadamard difference sets. Bent functions have many applications to coding theory, cryptography and sequence designs [13]. In coding theory, bent functions have the maximum distance to the first order binary Reed–Muller code. In a cryptosystem, functions with large nonlinearity values are usually employed to resist linear crypto-analysis and correlation-attack, and bent functions are just the ones with maximum nonlinearity.

Bent functions have many generalizations. Kumar et al. [9] considered bent functions from ${\mathbb {Z}}_q^n$ to ${\mathbb {Z}}_q$ in 1985, where $q\ge 2$ and $n\ge 1$ are integers. Later, bent functions were generalized to arbitrary finite abelian groups [11, 17], even to arbitrary finite groups [15, 20].

A natural question is when bent functions do exist. Rothaus [16] proved that bent functions from ${\mathbb {Z}}_2^n$ to ${\mathbb {Z}}_2$ exist if and only if n is even. However, this problem is far from being solved for other types of generalized bent functions. For generalized bent functions (GBF for short) from ${\mathbb {Z}}_q^n$ to ${\mathbb {Z}}_q$ defined in [9], Kumar et al. constructed them except the case that n is odd and $q\equiv 2\pmod 4$. There are many nonexistence results for GBF defined in [9], for example, see [2,3,4, 7, 8, 14] and the references in [8]. Especially, Feng and co-authors built connections between the nonexistence of GBF and class numbers of imaginary quadratic fields in [2,3,4]. In fact, they proved stronger results that there are no algebraic integers with prescribed absolute values in some cyclotomic field. However, GBFs’ existence request that there are algebraic integers with prescribed absolute values in some cyclotomic field and some specific conditions (so-called bent conditions) are also satisfied. In [8], Jiang and Deng showed that there are no GBFs from ${\mathbb {Z}}_q^n$ to ${\mathbb {Z}}_q$ with $n=3$ and $q=2\cdot 23^e$ for $e\ge 1$. Notice that there are algebraic integers with prescribed absolute values $(2\cdot 23^e)^{\frac{3}{2}}$ in the cyclotomic field $\mathbb {Q}(\zeta _{23^e})$, but Jiang and Deng showed that the bent conditions are not satisfied.

Motivated by the results in [7, 8], we obtain further nonexistence results for GBFs from ${\mathbb {Z}}_q^n$ to ${\mathbb {Z}}_q$.

This paper is organized as follows. In Sect. 2, we list some previous work and state our main result. In Sect. 3, we list some facts of algebraic number theory which we need. We prove the main result in Sect. 4. In Sect. 5, we apply our method to GBFs from ${\mathbb {Z}}_2^n$ to ${\mathbb {Z}}_m$ and obtain similar results. Finally, a short conclusion is given.

2 Previous work and our main result

Let $q\ge 2$ be an integer, ${\mathbb {Z}}_q={\mathbb {Z}}/{q{\mathbb {Z}}}$ and $\zeta _q= exp \left( \frac{2\pi i}{q}\right)$. A function f from ${\mathbb {Z}}^n_q$ to ${\mathbb {Z}}_q$ is called a generalized bent function (GBF) of type [n, q] if $F(\lambda )\overline{F(\lambda )}=q^n$ for every $\lambda \in {\mathbb {Z}}^n_q$ where

$$\begin{aligned} F (\lambda )=\sum _{x\in {\mathbb {Z}}^n_q}\zeta ^{f(x)}_q\cdot \zeta ^{-x\cdot \lambda }_q \end{aligned}$$

is the Fourier transform of the function $\zeta ^{f(x)}_q$, $x\cdot \lambda$ is the standard dot product, and $\overline{F(\lambda )}$ is the complex conjugate of $F(\lambda )$.

Note that if there is no element in ${\mathbb {Z}}[\zeta _q]$ with absolute value $q^{\frac{n}{2}}$, then there is no GBF of type [n, q]. Feng [2] and Feng and Liu [3, 4] get nonexistence results by showing that there are no cyclotomic integers with prescribed absolute values. For a survey of their results, see [8]. In this paper, we will focus on the nonexistence of GBFs of type $[n,q=2\times p^e]$ where $p\equiv 7 \pmod 8$ is a prime. Feng [2] proved the following result:

• (1) Let $p\equiv 7 \pmod 8$ be a prime, f the order of 2 modulo $p^e$, and m the smallest odd positive integer such that $x^2+py^2=2^{m+2}$ has ${\mathbb {Z}}$-solutions. Then there is no GBF of type $[n<\frac{m}{s}, 2 p^e]$, where n is odd and $s=\frac{p^e-p^{e-1}}{2f}.$

  However, in this paper we focus on the nonexistence of GBFs in the case that there exist cyclotomic integers with prescribed absolute value. Restricting to the case $q=2p^e$ ($p\equiv 7 \bmod 8$), there are three known results:

• (2) Pei [14] proved that there is no GBF of type $[n=1,q=2\times 7]$. Notice that the absolute value of $\left( \frac{1+\sqrt{-7}}{2}\right) \sqrt{-7}\in {\mathbb {Z}}[\zeta _7]$ is $14^{\frac{1}{2}}$.

• (3) Ikeda [7] proved that there is no GBF of type $[n=1,q=2\times p^e]$, where $p\equiv 7\pmod 8$ is a prime. This result includes Pei’s result.

• (4) Jiang and Deng [8] proved that there is no GBF of type $[n=3,q=2\times 23^e]$ for each $e\ge 1$. Notice that the absolute value of $\left( \frac{3+\sqrt{-23}}{2}\right) \big (\sqrt{-23}\big )^e\in {\mathbb {Z}}[\zeta _{23^e}]$ is $(2\times 23^e)^\frac{3}{2}$.

In this article we extend (2) and (4) to a general situation by extending the methods developed in [7, 8].

We need a definition to state our result. Let $p\equiv 7\pmod 8$ be a prime number. Then 2 splits in $\mathbb {Q}(\sqrt{-p})$. Let $\mathfrak {p}$ be a prime ideal of $\mathbb {Q}(\sqrt{-p})$ above 2. We define $t_p$ to be the minimal positive integer such that $\mathfrak {p}^{t_p}$ is principal. By Gauss’s genus theory, $t_p$ is odd. For more about $t_p$, see Remark 2. In this article, our main result is the following:

Theorem 1

If $p\equiv 7 \pmod 8$ is a prime and the order of 2 modulo p is $\frac{p-1}{2}$, then there do not exist GBFs of type $[n=t_p,q=2p]$. If p further satisfies $2^{p-1}\not \equiv 1 \pmod {p^2}$, then there do not exist GBFs of type $[n=t_p,q=2p^e]$ for any $e\ge 1$.

Remark 1

The condition $2^{p-1}\not \equiv 1\pmod {p^2}$ is to ensure the order of 2 modulo $p^e$ to be $\frac{\phi (p^e)}{2}$, where $\phi$ is Euler function, see Lemma 1. For $p<6.7\times 10^{15}$, $p=3511$ is the only prime such that $p \equiv 7\pmod 8$ and $2^{p-1}\equiv 1\pmod {p^2}$, see [5].

Remark 2

Some basic facts about the number $t_p$

Of course, $t_p$ is the order of $\mathfrak {p}$ in the class group of $\mathbb {Q}(\sqrt{-p})$. The definition of $t_p$ does not depend on the choice of $\mathfrak {p}$. Another prime ideal above 2 is the inverse of $\mathfrak {p}$ in the class group, so they have the same order. By Gauss’s genus theory or class field theory [19, Theorem 10.4(b)], the class number of $\mathbb {Q}(\sqrt{-p})$ is odd. Hence $t_p$ is also odd. In [2, Remark 2] , Feng gave an estimate that $t_p>\frac{\log {p}}{\log 2}-2$. In particular, $t_p\ge 3$, if $p\ge 23$. Feng also showed that $t_p$ is the smallest odd positive integer such that $x^2 + py^2 = 2^{t_p +2}$ have solutions with $(x,y)\in {\mathbb {Z}}^2$.

We give a small table of the primes less than 200 which satisfy all conditions in Theorem 1. From the table below, it can be seen that our result includes the results of Pei and Jiang–Deng.

p	7	23	47	71	79	103	167	191	199
$t_p$	1	3	5	7	5	5	11	13	9

By the estimate in Remark 2 we know that $t_p=1$ if and only if $p=7$. So our result is different from Ikeda’s.

Now we explain the condition $n=t_p$ briefly. Fix a prime p satisfying all conditions in Theorem 1. Let $q=2p^e$ and n be a positive odd integer.

If $n<t_p$, Feng [2] actually shows that there does not exist an element in ${\mathbb {Z}}[\zeta _{q}]$ with absolute value $q^{n/2}$, so there is no GBF of type $[n,q=2p^e]$.

If $n\ge t_p$, there exist cyclotomic integers in ${\mathbb {Z}}[\zeta _{q}]$ with absolute value $q^{n/2}$, see Lemma 3. Our result shows that there is no GBF in the case $n=t_p$. Therefore, Feng’s result and our result have shown that there is no GBF of type $[n\le t_p,q=2p^e]$ for odd n. However, there are no nonexistence results of GBFs in the case $n>t_p$.

3 Basic facts from algebraic number theory

The methods of proving nonexistence results of GBFs almost all involve algebraic number theory, mainly the basic arithmetic (ideals, units, class groups) of cyclotomic fields and their subfields. The reader can consult [12, Chapter 2, 3] or [19, Chapter 2]. In this section, we list some facts and prove some results which we will need in the proof of our main theorem.

Let $m\not \equiv 2 \pmod 4$ be an integer and $F=\mathbb {Q}(\zeta _m)$ the cyclotomic field, where $\zeta _m= exp \big (\frac{2\pi i}{m}\big )$. Let $\mathcal {O}_F$ be the ring of integers in F. Then for any prime number p, we know that

$$\begin{aligned} p\mathcal {O}_F=(\mathfrak {P}_1 \mathfrak {P}_2 \cdots \mathfrak {P}_g)^e \end{aligned}$$

where $\mathfrak {P}_1, \mathfrak {P}_2, \cdots , \mathfrak {P}_g$ are distinct prime ideals of $\mathcal {O}_F$. If $e>1$, we say that p ramifies in F. For each i, $\mathcal {O}_F/\mathfrak {P}_i$ is called the residue field of $\mathfrak {P}_i$, it is a finite field containing $\mathbb {F}_p$. The degree of this extension $[\mathcal {O}_F/\mathfrak {P}_i:\mathbb {F}_p]$ is called the residue class degree of $\mathfrak {P}_i/p$. Let $\phi$ be the Euler function. Then we have the following cyclotomic decomposition laws. For proofs, see [19, Chapter 2].

Fact 1

Suppose $p\not \mid m$ and let f be the smallest positive integer such that $p^f\equiv 1 \pmod m$. Then p splits into $g=\phi (m)/f$ distinct primes in F, each of which has residue class degree f.

Fact 2

We have that p ramifies in F if and only if p|m. If $m=p^e$ is a prime power, then $p\mathcal {O}_F=(1-\zeta _m)^{\phi (m)}.$

We also need the following two facts about $\mathbb {Q}(\sqrt{-p})$. For proofs, see [12, Chapter 3].

Fact 3

Let $p\equiv 3\pmod 4$ be a prime. Then $\mathbb {Q}(\sqrt{-p}) \subset \mathbb {Q}(\zeta _p)$.

Fact 4

Let $p\equiv 7\pmod 8$ be a prime. Then 2 splits in $\mathbb {Q}(\sqrt{-p})$, say $(2)=\mathfrak {p}\overline{\mathfrak {p}}$ where $\mathfrak {p}=\left( 2,\frac{1+\sqrt{-p}}{2}\right)$ and $\overline{\mathfrak {p}}=\left( 2,\frac{1-\sqrt{-p}}{2}\right)$ are prime ideals of $\mathbb {Q}(\sqrt{-p})$.

Lemma 1

Let p be an odd prime. If the order of 2 modulo p is $\frac{p-1}{2}$ and $2^{p-1}\not \equiv 1\pmod {p^2}$. Then the order of 2 modulo $p^e$ is $\frac{\phi (p^e)}{2}$ for each $e\ge 1$.

Proof

Let $f_e$ be the order of 2 modulo $p^e$. Hence $2^ {f_e} \equiv 1 \pmod p$ and $\frac{p-1}{2} | f_e$. So it remains to prove that $2^{\frac{p-1}{2}}$ has order $p^{e-1}$. Write $2^{\frac{p-1}{2}}=1+kp$ for some $k\in {\mathbb {Z}}$. We claim that $p\not \mid k$. Otherwise we have $2^{p-1}=1+2kp+k^2p^2 \equiv 1 \pmod {p^2}$. Since $p\not \mid k$, the order of $1+kp$ modulo $p^e$ is $p^{e-1}$ by direct computation. Therefore, $f_e=\frac{p-1}{2}p^{e-1}=\frac{\phi (p^e)}{2}$. $\square$

In the remaining of this section, we give the basic setting which will be used in Sect. 4.

Let $e\ge 1$ be an integer. Let $p\equiv 7 \pmod 8$ be a prime such that the order of 2 modulo p is $\frac{p-1}{2}$ and $2^{p-1}\not \equiv 1 \pmod {p^2}$. Let $\zeta =\zeta _{p^e}= exp (\frac{2\pi i}{p^e})\in \mathbb {C}$, $L=\mathbb {Q}(\sqrt{-p})$ and $K=\mathbb {Q}(\zeta )$. Then $L\subset K$ by Fact 3. Let $\mathcal {O}_L,\mathcal {O}_K$ be the rings of integers of L and K respectively. By Fact 1 and Fact 2, we have the following prime ideal factorization.

$$\begin{aligned} p\mathcal {O}_K= & {} (1-\zeta )^{\phi (p^e)}\mathcal {O}_K, \\ p\mathcal {O}_L= & {} (\sqrt{-p}\mathcal {O}_L)^2 \end{aligned}$$

and

$$\begin{aligned} \sqrt{-p}\mathcal {O}_K= & {} ((1-\zeta )\mathcal {O}_K)^\frac{\phi (p^e)}{2}.\\ 2\mathcal {O}_L= & {} \mathfrak {p}\mathcal {O}_L \overline{\mathfrak {p}}\mathcal {O}_L \end{aligned}$$

where $\mathfrak {p}=\left( 2,\frac{1+\sqrt{-p}}{2}\right)$ and $\overline{\mathfrak {p}}=\left( 2,\frac{1-\sqrt{-p}}{2}\right)$ are prime ideals of L.

By Fact 1 and the above lemma, we know that the residue degree of 2 in $K/\mathbb {Q}$ is $\frac{\phi (p^e)}{2}$, so there are only two prime ideals above 2 in K. Hence $2\mathcal {O}_K=\mathfrak {p}\mathcal {O}_K \overline{\mathfrak {p}} \mathcal {O}_K$ where $\mathfrak {p}\mathcal {O}_K$ and $\overline{\mathfrak {p}} \mathcal {O}_K$ are prime ideals of K.

We illustrate the above decompositions by the following diagram.

Now we list a fact about the action of the Galois group on ideals. Let $\sigma _2 \in {{\text {Gal}}}(K/\mathbb {Q})$ be the automorphism such that $\sigma _2(\zeta )=\zeta ^2$. Since ${{\text {Gal}}}(K/\mathbb {Q})\cong ({\mathbb {Z}}/{p^e{\mathbb {Z}}})^{\times }$, the order of 2 modulo $p^e$ is $\frac{\phi (p^e)}{2}$ which implies that the order of $\sigma _2$ in ${{\text {Gal}}}(K/\mathbb {Q})$ is $\frac{\phi (p^e)}{2}$. Since ${{\text {Gal}}}(K/\mathbb {Q})\cong ({\mathbb {Z}}/{p^e{\mathbb {Z}}})^{\times }$ is cyclic and the degree of K / L is $\frac{\phi (p^e)}{2}$, ${{\text {Gal}}}(K/L)$ is generated by $\sigma _2$. In particular, $\sigma _2$ fixes $\mathfrak {p}\mathcal {O}_K=\left( 2,\frac{1+\sqrt{-p}}{2}\right) \mathcal {O}_K$ and $\overline{\mathfrak {p}}\mathcal {O}_K=\left( 2,\frac{1-\sqrt{-p}}{2}\right) \mathcal {O}_K$.

The following lemma will reduce the equation $\alpha \bar{\alpha }=2^n$, $\alpha \in \mathcal {O}_K$ to $\alpha \bar{\alpha }=2^n$, $\alpha \in \mathcal {O}_L$, where n is a positive integer. It is a slight refined version of [2, Lemma 2.2].

Lemma 2

If $\alpha \overline{\alpha }=2^n$ for some $\alpha \in \mathcal {O}_K$ , then there exists a unique $i\in \{0,1,\ldots ,p^e-1\}$ such that $\alpha \zeta ^{-i} \in \mathcal {O}_L$.

Proof

By the above argument, we know that $\sigma _2$ fix $\mathfrak {p}\mathcal {O}_K$ and $\overline{\mathfrak {p}}\mathcal {O}_K$. Since the prime ideal factors of $\alpha$ are $\mathfrak {p}\mathcal {O}_K$ and $\overline{\mathfrak {p}}\mathcal {O}_K$, we have an equality of ideals of $\mathcal {O}_K$:

$$\begin{aligned} (\sigma _2 (\alpha ))=(\alpha ). \end{aligned}$$

Then there is a unit u of $\mathcal {O}_K$ such that $\sigma _2(\alpha )=u\alpha$. Since is abelian, we have

$$\begin{aligned} 2^n=\sigma _2(2^n)=\sigma _2(\alpha \overline{\alpha })=\sigma _2(\alpha )\sigma _2(\overline{\alpha })=\sigma _2(\alpha )\overline{\sigma _2(\alpha )}=u\alpha \overline{u}\overline{\alpha }=2^n u\overline{u}. \end{aligned}$$

Then $u\bar{u}=1$. By the fact that is abelian again, we have $\sigma (u) \overline{\sigma (u)}=1$ for every ). By a well-known fact [19, Lemma 1.6], u is a root of unity. Hence there is a unique $i\in \{0,1,\ldots ,p^e-1\}$ such that $u=\pm \zeta ^i$. Let $\beta =\alpha \zeta ^{-i}$. Then

$$\begin{aligned} \sigma _2 (\beta )=\alpha (\pm \zeta ^{-i}), \end{aligned}$$

so $\sigma _2(\beta ^2)=\beta ^2$. Since L is the fixed field of $\sigma _2$, this implies $\beta ^2\in \mathcal {O}_L$. But $[K:L]=\frac{p-1}{2}$ is odd, so $\beta =\alpha \zeta ^{-i}\in \mathcal {O}_L$. $\square$

Remark 3

The equation $2^t=x \overline{x}$ for $x \in \mathcal {O}_L$ has explicit solutions, where $t=t_p$ is the order of $\mathfrak {p}$ in the class group of L. Let $\gamma \in \mathcal {O}_L$ such that $\mathfrak {p}^t=(\gamma )$. Note that $\pm \gamma$ and $\pm \bar{\gamma }$ have absolute value $2^{\frac{t}{2}}$. On the other hand, if $x \in \mathcal {O}_L$ has absolute value $2^{\frac{t}{2}}$, then we have

$$\begin{aligned} (x)(\overline{x})=(2^t)=\mathfrak {p}^t\overline{\mathfrak {p}}^t \end{aligned}$$

as ideals of $\mathcal {O}_L$. Then $(x)=\mathfrak {p}^a \overline{\mathfrak {p}}^{t-a}$ for some $a\in \{0,1,\ldots ,t\}$. Note that if $0<a<t$, $\mathfrak {p}^a \overline{\mathfrak {p}}^{t-a}$ is not principal by definition of t. Since (x) is principal, we have that (x) must be $\mathfrak {p}^t$ or $\overline{\mathfrak {p}}^t$. Because the units of $\mathcal {O}_L$ are $\pm 1$, we have $x=\pm \gamma$ or $\pm \bar{\gamma }$. Therefore, the elements in $\mathcal {O}_L$ with absolute value $2^{\frac{t}{2}}$ are $\pm \gamma$ and $\pm \bar{\gamma }$.

4 Proof of Theorem 1

In this section, we give the proof of Theorem 1.

Now assume that f is a GBF from ${\mathbb {Z}}^t _q$ to ${\mathbb {Z}}_q$, where $t=t_p,q=2p^e$. Then $F(\lambda )\in \mathcal {O}_K$ has absolute value $q^{\frac{t}{2}}$. We will finally get a contradiction.

Lemma 3

$F(\lambda )$ must be one of the following elements

$$\begin{aligned} (\sqrt{-p})^{et}\cdot \gamma \cdot (\pm \zeta ^i) \end{aligned}$$

or

$$\begin{aligned} (\sqrt{-p})^{et}\cdot \overline{\gamma } \cdot (\pm \zeta ^i), \end{aligned}$$

where $i\in \{0,1,\ldots ,p^e-1\}$. In particular, $F(\lambda )\notin (2)\mathcal {O}_K$.

Proof

It is easily seen that every element above has absolute value $q^{\frac{t}{2}}$.

By the prime ideal factorizations we have

$$\begin{aligned} (F(\lambda )\overline{F(\lambda )})=(q^t)=(2^tp^{et})\mathcal {O}_K=(\mathfrak {p}\mathcal {O}_K)^t{(\overline{\mathfrak {p}}\mathcal {O}_K)}^t(1-\zeta )^{\phi (p^e)et}. \end{aligned}$$

Note that $\overline{(1-\zeta )}=(1-\zeta )$, we know that the exact power of $(1-\zeta )$ in $(F(\lambda ))$ must be $\frac{\phi (p^e)et}{2}$, so $(1-\zeta )^{\frac{\phi (p^e)et}{2}}=(\sqrt{-p})^{et} |(F(\lambda ))$ as ideals of $\mathcal {O}_K$. Hence $\alpha : =\frac{F(\lambda )}{\sqrt{-p}^{et}} \in \mathcal {O}_K$ and $\alpha \overline{\alpha }=2^t$. Then by Lemma 2, we know that there is a unique $i\in \{0,1,\ldots ,p^e-1\}$ such that $\beta :=\alpha {\zeta ^{-i}} \in \mathcal {O}_L$. So $\beta \overline{\beta }=2^t$.

By Remark 3, we have that $\beta =\pm \gamma$ or $\pm \overline{\gamma }$. Hence

$$\begin{aligned} F(\lambda )=(\sqrt{-p})^{et}\cdot \alpha =(\sqrt{-p})^{et}\cdot \beta \zeta ^{i}=(\sqrt{-p})^{et}\cdot \gamma \cdot (\pm \zeta ^i) \end{aligned}$$

or

$$\begin{aligned} (\sqrt{-p})^{et}\cdot \overline{\gamma } \cdot (\pm \zeta ^i) \end{aligned}$$

for some $i\in \{0,1,\ldots ,p^e-1\}$. $\square$

Lemma 4

If $v\in {\mathbb {Z}}^t _q$ is an element of order 2, then for every $\lambda \in {\mathbb {Z}}^t _q$,

$$\begin{aligned} F(\lambda )=\pm F(\lambda +v). \end{aligned}$$

Proof

As v is of order 2, for $x\in {\mathbb {Z}}^t_q$, we have $\zeta ^{x\cdot v}_q=\pm 1$. So

$$\begin{aligned} F(\lambda )+F(\lambda +v)=\sum _{x\in {\mathbb {Z}}^t_q}{\zeta _q ^{f(x)-x\cdot \lambda }(1+\zeta _q ^{-x\cdot v})}\in (2)=\mathfrak {p}\mathcal {O}_K\cap \overline{\mathfrak {p}}\mathcal {O}_K, \end{aligned}$$

or said differently,

$$\begin{aligned} (2) | (F(\lambda )+F(\lambda +v)) \end{aligned}$$

as ideals of $\mathcal {O}_K$.

Then $F(\lambda )\in \mathfrak {p}\mathcal {O}_K \iff F(\lambda +v)\in \mathfrak {p}\mathcal {O}_K$. By the above Lemma, we have $F(\lambda +v)=F(\lambda )\cdot (\pm \zeta ^i)$ for some $i \in \{0,1,\ldots ,p^e-1\}$. Then

$$\begin{aligned} F(\lambda )+F(\lambda +v)=F(\lambda )(1\pm \zeta ^i). \end{aligned}$$

Note that if $i\ne 0$, (2) and $(1\pm \zeta ^i)$ are coprime ideals. So $(2)|(F(\lambda ))$. This contradicts to Lemma 3. Therefore, $i=0$. $\square$

The above proof is essentially the same as in [7, Lemma 3] and [8, Lemma 8].

Let G be the Sylow-2 subgroup of ${\mathbb {Z}}^t_q$. Then $G\cong \mathbb {F}^t_2$. For every $v\in G\setminus \{0\}$, define

$$\begin{aligned} N_{v}:=\{\lambda \in {\mathbb {Z}}^t_q| F(\lambda )=F(\lambda +v)\} \end{aligned}$$

and

$$\begin{aligned} M_{v}:=\{\lambda \in {\mathbb {Z}}^t_q| F(\lambda )=-F(\lambda +v)\}. \end{aligned}$$

By Lemma 4, ${\mathbb {Z}}^t_q=N_{v}\sqcup M_{v}$ (the symbol $\sqcup$ means disjoint union) and $|N_{v}|+|M_{v}|=q^t.$

Lemma 5

We have $|N_{v}|=|M_{v}|=\frac{q^t}{2}$ for each $v\in G\setminus \{0\}$.

Proof

We need the following well-know orthogonality relations,

$$\begin{aligned} \sum _{x \in {\mathbb {Z}}^t_q}{\zeta _q}^{x\cdot \alpha }= \left\{ \begin{array}{lr} 0 &{} \text {if } \alpha \ne 0,\\ q^t &{} \text {if } \alpha =0. \end{array}\right. \end{aligned}$$

Then for each $v\in G \setminus \{0\}$, we have

$$\begin{aligned} \sum _{\lambda }{F(\lambda )\overline{F(\lambda +v)}}= & {} \sum _{\lambda }\left( \sum _{x}{\zeta _q}^ {f(x)}\cdot {\zeta _q}^{-x\cdot \lambda }\right) \left( \sum _{y}{\zeta _q}^{-f(y)}\cdot {\zeta _q}^{y\cdot (\lambda +v)}\right) \\= & {} \sum _{x}\sum _{y}{\zeta _q}^{f(x)-f(y)}\cdot {\zeta _q}^{y\cdot v}\sum _{\lambda }{\zeta _q}^{-\lambda (x-y)}\\= & {} q^t \sum _{x}\sum _{y=x}{\zeta _q}^{f(x)-f(y)}\cdot {\zeta _q}^{y\cdot v}=q^t\sum _{x}{\zeta _q}^{x\cdot v}=0. \end{aligned}$$

By the definition of GBF, we have that $F(\lambda )\overline{F(\lambda )}=q^t$ for each $\lambda$. So for each $v\in G\setminus \{0\}$,

$$\begin{aligned} 0=\sum _{\lambda \in N_{v}}{F(\lambda )\overline{F(\lambda +v)}}+\sum _{\lambda \in M_{v}}{F(\lambda )\overline{F(\lambda +v)}}=q^t(|N_v|-|M_v|). \end{aligned}$$

Hence, $|N_v|=|M_v|$. Also we know that $|N_{v}|+|M_{v}|=q^t$. Therefore, $|N_{v}|=|M_{v}|=\frac{q^t}{2}$. $\square$

If $t=1$, then there is only one $2-$order element v in ${\mathbb {Z}}_q$. Note that if $\lambda \in N_v$, then $\lambda +v\in N_v$. Hence 2 divides $|N_v|$. But $|N_v|=\frac{q}{2}=p^e$ is odd. This is a contradiction. So there do not exist GBFs from ${\mathbb {Z}}_q$ to ${\mathbb {Z}}_q$.

As we have pointed out in Sect. 2, this result and the above proof are due to Ikeda [7].

In the remaining part of the proof, we assume $t\ge 3$ so that $|G|=2^t \ge 8$. Consider the following $2^{2^t -1}$ subsets of ${\mathbb {Z}}^t_q$:

$$\begin{aligned} \bigcap _{v\in G\setminus \{0\}}X_v \end{aligned}$$

where $X_v=N_{v} \text { or }M_{v}$. By Lemma 4, we have the following proposition.

Proposition 1

${\mathbb {Z}}^t_q$ is a disjoint union of these $2^{2^t -1}$ subsets.

The following lemmas will tell us that among the $2^{2^t -1}$ sets there are $2^t$ nonempty sets at most.

Lemma 6

If $u,v,w\in G\setminus \{0\}$satisfy $u+v+w=0$, then we have

$$\begin{aligned} N_u\cap N_v\cap M_w=N_u\cap M_v\cap N_w=M_u\cap N_v\cap N_w=M_u\cap M_v\cap M_w=\emptyset . \end{aligned}$$

Proof

We only need the fact $F(\lambda )\notin 2\mathcal {O}_K$, so the proof below is essentially the same as the case $p=23$ in [8, Lemma 11].

The condition implies that u, v, w are pairwise different. Note that

$$\begin{aligned}&\lambda \in N_u\cap N_v\cap M_w\\&\iff \lambda +u \in N_u\cap M_v\cap N_w\\&\iff \lambda +v \in M_u\cap N_v\cap N_w\\&\iff \lambda +w \in M_u\cap M_v\cap M_w. \end{aligned}$$

So it is enough to prove $M_u\cap M_v\cap M_w=\emptyset$. By considering the surjective group homomorphism

$$\begin{aligned}&(\,\cdot u): {\mathbb {Z}}^t_q \longrightarrow \left\{ 0,\frac{q}{2}\right\} \subset {\mathbb {Z}}_q\\&y\mapsto y\cdot u, \end{aligned}$$

we know that there are half elements of ${\mathbb {Z}}^t_q$ satisfy $y\cdot u=0$ and half elements of ${\mathbb {Z}}^t_q$ satisfy $y\cdot u\ne 0$. Note that $\zeta _q ^{y\cdot u}=1$ if $y\cdot u=0$ and $\zeta _q ^{y\cdot u}=-1$ if $y\cdot u\not =0$.

Now take an element $\lambda \in M_u\cap M_v\cap M_w$. For simplicity, let $\sum _{y}=\sum _{y}{\zeta _q ^{f(y)-\lambda \cdot y}}$. Then

$$\begin{aligned} F(\lambda )= & {} \sum _{y\in {\mathbb {Z}}^t_q}=\sum _{y\cdot u=0}+\sum _{y\cdot u\ne 0}\\= & {} -F(\lambda +u)=-\sum _{y\cdot u=0}+\sum _{y\cdot u\ne 0}. \end{aligned}$$

So we get

$$\begin{aligned} 0=\sum _{y\cdot u=0}=\sum _{y\cdot u=0, y\cdot v=0 }+\sum _{y\cdot u=0,y\cdot v\ne 0}. \end{aligned}$$

Similarly, we have

$$\begin{aligned} 0=\sum _{y\cdot v=0}=\sum _{y\cdot u=0, y\cdot v=0 }+\sum _{y\cdot u\not =0,y\cdot v=0}. \end{aligned}$$

From $F(\lambda )=-F(\lambda +w)$, we have

$$\begin{aligned} 0=\sum _{y\cdot w=0}, \end{aligned}$$

and

$$\begin{aligned} F(\lambda )=\sum _{y\cdot w\not =0}=\sum _{y\cdot (u+v)\ne 0}=\sum _{y\cdot u=0,y\cdot v\ne 0}+\sum _{y\cdot u\not =0,y\cdot v=0}=-2\sum _{y\cdot u=0,y\cdot v=0}\in 2\mathcal {O}_K. \end{aligned}$$

This contradicts to Lemma  3. So $M_u\cap M_v\cap M_w=\emptyset$. $\square$

Lemma 7

Let $\bigcap _{a\in G\setminus \{0\}}X_a$ be a subset of ${\mathbb {Z}}^t_q$ where $X_a=N_{a}$ or $M_{a}$. If $\{a\in G|X_a=N_{a}\}\cup \{0\}$ is not a subgroup of G with index 1 or 2, then $\bigcap _{a\in G\setminus \{0\}}X_a=\emptyset$.

Proof

If $A:=\{a\in G|X_a=N_{a}\}\cup \{0\}$ is not a subgroup, then there are two different elements $u,v\in A\setminus \{0\}$ such that $u+v\notin A$. Hence $X_u=N_u$, $X_v=N_v$ and $X_{u+v}=M_{u+v}$. Then by the above Lemma, we have

$$\begin{aligned} \bigcap _{a\in G\setminus \{0\}}X_a \subset N_u\cap N_v\cap M_{u+v}= \emptyset . \end{aligned}$$

Recall $G\cong \mathbb {F}^t_2$. If the index of A in G is larger than 2, then $\text {dim}_{\mathbb {F}_2}A\le t-2$ as a subspace of G. Then there is a subspace B such that $A\cap B=\{0\}$ and $\text {dim}_{\mathbb {F}_2}B\ge 2$. Take two different elements $u,v\in B\setminus \{0\}$. Then $u+v\in B\setminus \{0\}$. So u, v and $u+v$ are not in A. Hence $X_u=M_u, X_v=M_v$ and $X_{u+v}=M_{u+v}$. Then by the above Lemma, we have

$$\begin{aligned} \bigcap _{a\in G\setminus \{0\}}X_a \subset M_u\cap M_v\cap M_{u+v}= \emptyset . \end{aligned}$$

$\square$

Let $\Gamma$ be the set of subgroups of G with index 2. Since $G\cong \mathbb {F}^t_2$, so $|\Gamma |=2^t-1$ by basic linear algebra.

In virtue of Lemma 7, we define

$$\begin{aligned} N_G:=\bigcap _{v\in G\setminus \{0\}} {N_{v}} \end{aligned}$$

and

$$\begin{aligned} N_{H}:=\left( \bigcap _{v\in H\setminus \{0\}} N_{v} \right) \bigcap \left( \bigcap _{u\notin H} M_u\right) , \end{aligned}$$

for each $H\in \Gamma$.

Proposition 2

We have the decomposition

$$\begin{aligned} {\mathbb {Z}}^t_q=\left( \bigsqcup _{H\in \Gamma } N_H\right) \bigsqcup N_G. \end{aligned}$$

For each $v \in G\setminus \{0\}$,

$$\begin{aligned} N_{v}=\bigsqcup _{\Gamma \ni H\ni v} N_H\bigsqcup N_G. \end{aligned}$$

Proof

By Proposition 1, we have that ${\mathbb {Z}}^t_q$ is a disjoint union of $2^{2^t -1}$ subsets, where each subset is of the form $\bigcap _{v\in G\setminus \{0\}}X_v$ with $X_v=N_{v}$ or $M_{v}$. By Lemma 7, the only possible nonempty sets are $N_G$ and $N_H$ where $H\in \Gamma$. So ${\mathbb {Z}}^t_q=\big (\bigsqcup _{H\in \Gamma } N_{H}\big )\bigsqcup N_G.$

Since $N_{v}=N_{v}\cap {\mathbb {Z}}^t_q$, the second statement follows by the first statement. $\square$

We are now in a position to give a proof of Theorem 1.

Proof of Theorem 1

By Proposition 2, we have the following equation

$$\begin{aligned} q^t=\sum _{H\in \Gamma } |N_{H}| +|N_G|. \end{aligned}$$

(1)

For each $v\in G\setminus \{0\}$, by Lemma 5 we have

$$\begin{aligned} |N_{v}|=\frac{q^t}{2}=\sum _{\Gamma \ni H\ni v} |N_H|+|N_G| . \end{aligned}$$

Sum the latter $2^{t}-1$ equations, we have

$$\begin{aligned} (2^t-1) \frac{q^t}{2}= & {} \sum _{v\in G\setminus \{0\}}\sum _{\Gamma \ni H\ni v}{|N_H|}+(2^t-1)|N_G|\\= & {} \sum _{H\in \Gamma }\left( \sum _{v\in H \setminus \{0\}}{1}\right) {|N_H|}+(2^t-1)|N_G|=(2^{t-1}-1)\sum _{H\in \Gamma }{|N_H|}+(2^t-1)|N_G|. \end{aligned}$$

Hence

$$\begin{aligned} (2^t-1)\frac{q^t}{2}=(2^{t-1}-1)\sum _{H\in \Gamma }{|N_H|}+(2^t-1)|N_G|. \end{aligned}$$

(2)

Combining (1) and (2), we get

$$\begin{aligned} (2^t-1) \frac{q^t}{2}=(2^{t-1}-1)(q^t-|N_G|)+(2^t-1)|N_G|. \end{aligned}$$

Then

$$\begin{aligned} |N_G|=p^{te}. \end{aligned}$$

In particular, $N_G$ is not empty. However, if $\lambda \in N_G$, then we have $\lambda +v\in N_G$ for all $v\in G$, so $2^t$ divides $|N_G|=p^{te}$. This contradiction shows that there do not exist GBFs of type $[t=t_p,q=2p^e]$ for any $e\ge 1$, and this completes the proof of Theorem 1.

$\square$

5 Nonexistence of GBFs from ${\mathbb {Z}}^n_2$ to ${\mathbb {Z}}_m$

A function f from ${\mathbb {Z}}^n_2$ to ${\mathbb {Z}}_m$ is called a GBF if the equality

$$\begin{aligned} |F(\lambda )|:=\left| \sum _{x\in {\mathbb {Z}}^n_2}\zeta ^{f(x)}_m\ (-1)^{x\cdot \lambda }\right| =2^{\frac{n}{2}} \end{aligned}$$

holds for every $\lambda \in {\mathbb {Z}}^n_2$, where $x\cdot \lambda$ is the standard dot product.

There are many constructions of this type GBF, see [18]. For nonexistence results, a good reference is [10], where Liu–Feng–Feng proved many nonexistence results for GBFs of this type by showing that there are no cyclotomic integers with prescribed absolute values.

We get a nonexistence result in the case that there are cyclotomic integers with prescribed absolute values.

If $p\equiv 7 \pmod 8$ is a prime. Let $\mathfrak {p}$ be a prime ideal of $\mathbb {Q}(\sqrt{-p})$ above 2. We define $t_p$ to be the minimal positive integer such that $\mathfrak {p}^{t_p}$ is principal.

Theorem 2

If $p\equiv 7 \pmod 8$ is a prime and the order of 2 modulo p is $\frac{p-1}{2}$, then there do not exist GBFs from ${\mathbb {Z}}^{t_p} _2$ to ${\mathbb {Z}}_{2p}$. If p further satisfies $2^{p-1}\not \equiv 1 \pmod {p^2}$, then there do not exist GBFs from ${\mathbb {Z}}^{t_p} _2$ to ${\mathbb {Z}}_{2p^e}$ for any $e\ge 1$.

The proof of Theorem 2 is as same as the one of Theorem 1. So we only give a sketch:

Proof

Assume that f is a GBF from ${\mathbb {Z}}^{t_p}_2$ to ${\mathbb {Z}}_{2p^e}$. Then $F(\lambda )\overline{F(\lambda )}=2^{t_p}$.

Firstly, by tracing the arguments in Sect. 3 and Lemma 3, one can prove that $F(\lambda )$ must be one of the following elements

$$\begin{aligned} \gamma \cdot (\pm {\zeta ^i_{p^e}}) \end{aligned}$$

or

$$\begin{aligned} \overline{\gamma } \cdot (\pm {\zeta ^i_{p^e}}), \end{aligned}$$

where $\gamma \in \mathbb {Q}(\sqrt{-p})$ is a generator of $\mathfrak {p}^{t_p}$ and $i\in \{0,1,\cdots ,p^e-1\}$.

Secondly, for any $v\in {\mathbb {Z}}^t _2 \setminus \{0\}$, define $N_{v}:=\{\lambda \in {\mathbb {Z}}^{t_p}_2| F(\lambda )=F(\lambda +v)\},$ $M_{v}:=\{\lambda \in {\mathbb {Z}}^{t_p}_2| F(\lambda )=-F(\lambda +v)\}$ and $N_{all}:=\bigcap _{v\in {\mathbb {Z}}^{t_p} _2 \setminus \{0\}} {N_{v}}$. One can use the above form of $F(\lambda )$ and same arguments in Sect. s4 to formulate and prove analogues of Lemmas 4, 5, 6, 7, and Propositions 1, 2.

Finally, by a similar computation as in the proof of Theorem 1, on one hand one can prove that $|N_{all}|=1$, on the other hand $2^{t_p}$ divides $|N_{all}|$. This contradiction shows that there do not exist GBFs from ${\mathbb {Z}}^{t_p} _2$ to ${\mathbb {Z}}_{2p^e}$. $\square$

6 Conclusion and future work

In this article we give some new nonexistence results of GBFs under the condition that there exist cyclotomic integers with prescribed absolute values. The nonexistence problem is far from solved. Our future work goes toward the case when the order of 2 modulo p is less than $\frac{p-1}{2}$.