1 Introduction

Graph search problems are about the search for a graph which satisfies a given set of constraints, or to determine that no such graph exists. Often graph search problems are about the search for the set of all graphs, modulo graph isomorphism, that satisfy the given constraints. Graph search problems are typically invariant under graph isomorphism. Namely, if G is a solution, then any graph obtained by permuting the vertices of G is also a solution. When seeking solutions, the size of the search space is significantly reduced if symmetries are eliminated. The search space can be explored more efficiently when avoiding paths that lead to symmetric solutions and avoiding also those that lead to symmetric non-solutions.

One common approach to eliminate symmetries is to introduce symmetry breaking constraints [11, 29, 33, 34] which rule out isomorphic solutions thus reducing the size of the search space while preserving the set of solutions. Ideally, a symmetry breaking constraint is satisfied by a single member of each equivalence class of solutions, thus drastically restricting the search space. However, computing such symmetry breaking constraints is, most likely, intractable in general [11]. In practice, symmetry breaking constraints typically rule out some, but not all of the symmetries in the search and, as noted in the survey by Walsh [35], often a few simple constraints rule out most of the symmetries.

Shlyakhter [33] notes that the core difficulty is to identify a symmetry-breaking predicate which is both effective (rules out a large portion of the search space) and compact (so that checking the additional constraints does not slow down the search). In [10], Codish et al. introduce a symmetry breaking constraint for graph search problems. Their constraint is compact, with size polynomial in the number of graph vertices, and shown to be effective but it does not eliminate all of the symmetries in the search.

There is a large body of research that concerns identifying symmetries in a given graph. In this setting, finding symmetries is about detecting graph automorphisms. A typical application is in the context of SAT solving as described for example in [2, 4, 16–18]. In this paper the setting is different as the graph is not given but rather is the subject of the search problem.

In this paper we adopt the following terminology. Symmetry breaking constraints that break all of the symmetries, or more precisely, that are satisfied by exactly one solution in each symmetry class, are called complete. Symmetry breaking constraints which are sound i.e, satisfied by at least one solution in each symmetry class, but not complete are called partial. If a symmetry breaking constraint is satisfied exactly by the canonical representatives of the symmetry classes, it is called canonizing. Note that canonizing symmetry breaking constraints are also complete.

Computing all solutions to a graph search problem with partial symmetry breaking constraints is a two step process. First one generates the set S of solutions to the constraints, and then one applies a graph isomorphism tool, such as nauty [22] to reduce S modulo isomorphism. Often, the number of solutions in the first step is very large and then this method may fail to generate the initial set of solutions.

This paper presents a methodology to compute small sets of static canonizing symmetry breaking constraints for “small” graph search problems. Consider for example the search for a graph with n = 10 vertices. The search space consists of 245 graphs, whereas, there are only 12 005 168 such graphs modulo isomorphism (see sequence A000088 of the OEIS [28]). In theory, to break all symmetries one could construct a symmetry breaking constraint that considers all 10! = 3,628,800 permutations of the vertices. We will show how to construct a compact canonizing symmetry breaking constraint for graph search problems on 10 vertices using only 7853 permutations.

Our approach can be applied, in the terminology of [3], both in an “instance independent” fashion and “instance dependent”. When “instance independent”, it generates canonizing symmetry breaking constraints for any graph search problem and in this setting it applies to break all symmetries in graph search problems on up to 10 vertices. When “instance dependent”, it generates canonizing symmetry breaking constraints which apply to break symmetries in larger graphs which are solutions of a given graph search problem. These symmetry breaking constraints are typically smaller and easier to compute than the corresponding “instance independent” constraints. We illustrate the application of complete symmetry breaking constraints, both instance independent and instance dependent, to extend two known sequences from the OEIS related to graph enumeration.

We also observe that the derived symmetry constraints are “solver independent”. They can be applied in conjunction with any constraint solver to restrict the search to canonical solutions of a given search problem.

The rest of this paper is structured as follows. Section 2 provides a motivating example. Section 3 presents preliminary definitions and notation. Section 4 describes how we compute complete and canonizing symmetry breaking constraints. First, in Section 4.2, for instance independent graph search problems. Then, in Section 4.5, for a given graph search problem. Section 5 demonstrates a generalization of our approach to matrix search problems and illustrates its impact when solving the Equi-distant Frequency Permutation Array problem (EFPA). Section 7 concludes.

2 A motivating example

A classic example of a graph search problem relates to the search for Ramsey graphs [30]. The graph R(s, t; n) is a simple graph with n vertices, no clique of size s, and no independent set of size t. Figure 1 illustrates a R(3, 3; 5) graph. The graph contains no 3-clique and no 3-independent set. A Ramsey (s, t)-graph is a R(s, t; n) graph for some n. The set of all R(s, t;n) graphs, modulo graph isomorphism, is denoted \(\mathcal {R}(s,t;n)\). Ramsey Theory tells us that there are only a finite number of Ramsey (s, t)-graphs for each s and t, but finding all such graphs, or even determining the largest n for which they exist, is a famously difficult problem. It is unknown, for example, if there exists a R(5, 5; 43) graph and the set \(\mathcal {R}(4,5;24)\) has yet to be been fully determined, although 350,904 non-isomorphic graphs are known to belong to \(\mathcal {R}(4,5;24)\).

Fig. 1
figure 1

A R(3,3;5) Ramsey graph: edges denoted by solid lines and non-edges by dashed

Full size image

Solving the graph search problem to find all R(3,4;8) graphs without any symmetry breaking constraint results in a set of 17,640 graphs. Applying nauty [22] to these solutions identifies precisely 3 solutions modulo graph isomorphism. Introducing a partial symmetry breaking constraint as described in [9] in the search to enumerate all R(3,4;8) graphs computes only 11 graphs in a fraction of the time required to compute the full set of solutions. These too can then be reduced applying nauty to obtain the 3 solutions. Application of a complete symmetry breaking constraint as proposed in this paper results in the exact set of 3 non-isomorphic solutions.

3 Preliminaries

Throughout this paper we consider finite and simple graphs (undirected with no self loops). The set of simple graphs on n nodes is denoted \(\mathcal {G}_{n}\). We assume that the vertex set of a graph, G = (V, E), is V = {1, … , n} and represent G by its n × n adjacency matrix A defined by

$$A_{i,j}= \left\{\begin{array}{llllll}1 & \text{if } (i,j) \in E\\ 0 & \text{otherwise} \end{array}\right. $$

An n-vertices graph search problem is a predicate φ on an n × n matrix A of Boolean variables A i, j ; and a solution to a graph search problem φ is a satisfying assignment (to the variables in A) of the conjunction φ(A)∧a d j n(A) where a d j n(A) states that A is an n × n adjacency matrix:

$$ adj^{n}(A) = \underbrace{\bigwedge_{1\leq i\leq n} (\neg A_{i,i})}_{(a)}~~\wedge \underbrace{\bigwedge_{1\leq i<j\leq n} (A_{i,j}\leftrightarrow A_{j,i})}_{(b)} $$
(1)

In Constraint (1), the left part (a) states that there are no self loops and the right part (b) states that the edges are undirected. The set of solutions of a graph search problem is denoted s o l(φ) and when we wish to make the variables explicit we write s o l(φ(A)). The set s o l(φ) is typically viewed as a set of graphs. Note that \(sol(\mathit {true}) = \mathcal {G}_{n}\). The following presents two examples of graph search problems which we will refer to in rest of the paper.

Example 1

The Ramsey graph R(s, t;n) is a simple graph with n vertices, no clique of size s, and no independent set of size t. The set of all R(s, t;n) graphs, modulo graph isomorphism, is denoted \(\mathcal {R}(s,t;n)\). The search for a Ramsey graph is a graph search problem where we take the following φ R(s, t;n) as the predicate φ. Here we denote by ℘ s [n] (respectively ℘ t [n]) the set of subsets of size s (respectively t) of \(\left \{ \begin {array}{l}1,\ldots ,n\end {array} \right \}\). The left conjunct (a) states that there is no clique of size s in the graph, and the right conjunct (b) that there is no independent set of size t.

$$ \varphi_{(s,t;n)}(A) = \underbrace{\bigwedge_{I\in \wp_{s}[n]} \bigvee \left\{~\neg A_{i,j} \left| \begin{array}{l}i,j \in I, \\i<j\end{array} \right. \right\}}_{(a)} ~~\land \underbrace{\bigwedge_{I\in \wp_{t}[n]} \bigvee \left\{~A_{i,j} \left| \begin{array}{l}i,j \in I, \\i<j\end{array} \right. \right\} }_{(b)} $$
(2)

Example 2

A graph is claw-free if it does not contain the complete bipartite graph K 1,3 (sometimes called a “claw”) as a subgraph. The claw free graph search problem is formalized by taking the following φ c f(n) as the predicate φ. Each clause in the conjunction expresses for i, j, k, ℓ that there is no subgraph K 1,3 between {i} and {j, k, ℓ}.

$$ \varphi_{\mathit{cf}(n)}(A) = \bigwedge \left\{~ \begin{array}{l} \neg A_{i,j} \lor \neg A_{i,k} \lor \neg A_{i,\ell} \\ \lor A_{j,k} \lor A_{k,\ell} \lor \lor A_{j,\ell} \end{array} \left| \begin{array}{l}1\leq i\leq n,~ i\neq j,~i\neq k,\\ i\neq\ell,~1\leq j<k<\ell\leq n\end{array} \right. \right\} $$
(3)

The set of permutations π: {1, … , n} → {1, … , n} is denoted S n . For \(G = (V,E) \in \mathcal {G}_{n}\) and π ∈ S n , we define π(G) = {V,{(π(u), π(v))|(u, v) ∈ E)}. Permutations act on adjacency matrices in the natural way: If A is the adjacency matrix of a graph G, then π(A) is the adjacency matrix of π(G) obtained by simultaneously permuting with π the rows and columns of A. We adopt the tuple notation [π(1), … , π(n)] for a permutation π: {1, … , n} → {1, … , n}.

Two graphs \(G_{1},G_{2}\in \mathcal {G}_{n}\) are isomorphic, denoted G 1 ≈ G 2, if there exists a permutation π ∈ S n such that G 1 = π(G 2). Sometimes we write G 1 ≈ π G 2 to emphasize that π is the permutation such that G 1 = π(G 2). For sets of graphs H 1, H 2, we say that H 1 ≈ H 2 if for every G 1 ∈ H 1 (likewise in H 2) there exists G 2 ∈ H 2 (likewise in H 1) such that G 1 ≈ G 2.

We consider an ordering on graphs, defined viewing their adjacency matrices as strings. Because adjacency matrices are symmetric with zeroes on the diagonal, it suffices to focus on the upper triangle parts of the matrices [8].

Definition 1 (ordering graphs)

Let \(G_{1},G_{2} \in \mathcal {G}_{n}\) and let s 1, s 2 be the strings obtained by concatenating the rows of the upper triangular parts of their corresponding adjacency matrices A 1, A 2 respectively. Then, G 1 ≼ G 2 if and only if s 1 ≼ l e x s 2. We also write A 1 ≼ A 2.

One way to define the canonical representation of a graph is to take the smallest graph in the ≼ order in each equivalence class of isomorphic graphs [31]. In this paper we follow this definition for canonicity.

Definition 2 (canonicity)

Let \(G\in \mathcal {G}_{n}\) be a graph, π⊆S n , and denote the predicate \(\min _{\Pi }(G) = \bigwedge \left \{~G \preceq \pi (G) \left | \begin {array}{l}\pi \in \Pi \end {array} \right . \right \}\). We say that G is canonical if \(\min _{S_{n}}(G)\). We say that π is canonizing if \(\forall _{G\in \mathcal {G}_{n}}.\min _{\Pi }(G)\leftrightarrow \min _{S_{n}}(G)\).

Observe that in Definitions 1 and 2, the order is defined on given graphs. Often, we consider the same relation, but between adjacency matrices that contain propositional variables (representing unknown graphs, as in the case for graph search problems). Then, the expressions A 1 ≼ A 2 and minπ(A) are viewed as a Boolean constraints on the variables in the corresponding matrices.

Example 3

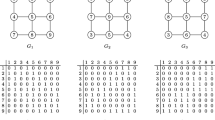
It turns out that \(\Pi = \left \{ \begin {array}{l}[2,1,3,4], [1,3,2,4], [1,2,4,3]\end {array} \right \}\) is canonizing for \(\mathcal {G}_{4}\). Namely, with only three permutations we express the information present in all 4!=24 elements of S 4. So for instance, the graph G depicted in Fig. 2a is canonical because it is smaller than its three permutations with respect to π detailed as Fig. 2b, c, and d. We come back to elaborate on why π is canonizing in Example 4.

Fig. 2
figure 2

A graph and its isomorphic representations according to: π 1 = [2,1,3,4], π 2 = [1,3,2,4], and π 3 = [1,2,4,3]

Full size image

Definition 3 (symmetry break)

Let φ(A) be a n-vertices graph search problem and σ(A) a propositional formula on the variables in A. We say that σ is a symmetry break for φ if s o l(φ(A)) ≈ s o l(φ(A)∧σ(A)). If the graphs of s o l(φ(A)∧σ(A)) are mutually non-isomorphic then we say that σ is complete. Otherwise we say that σ is partial. If the graphs of s o l(φ(A)∧σ(A)) are canonical then we say that σ is canonizing.

Lemma 1

Let π be a canonizing set of permutations for graphs of size n. Then minπ is a canonizing symmetry break for any graph search problem on n vertices.

Proof

Let A be a solution to a graph search problem on n vertices and let π be a canonizing set for graphs with n vertices. In order to prove that m i n π is a canonizing symmetry break it is sufficient to show that only the canonical member in i s o(A) = {π(A)|∀π ∈ S n } satisfies m i n π. π is a canonizing set thus by definition \(\forall G\in \mathcal {G}_{n} : min_{\Pi }(G) \leftrightarrow min_{S_{n}}(G)\). Since only the canonical graph in i s o(A) satisfies \(min_{S_{n}}\) it follows that it is the only one which satisfies m i n π. □

Corollary 1

\(\min _{S_{n}}(A)\) is a canonizing symmetry break for any graph search problem on n vertices.

Example 4

Consider the canonizing set π from Example 3 and the following 4 × 4 adjacency matrix A:

$$ A= \left[ \begin{array}{lllllllll} 0 & a & b & c \\ a & 0 & d & e \\ b & d & 0 & f \\ c & e & f & 0 \end{array}\right] \quad\quad\Pi= \left\{ \begin{array}{l} ~[2,1,3,4],\\ ~ [1,3,2,4],\\ ~ [1,2,4,3]\end{array} \right\}$$

Then, by Definition 2 and Lemma 1,

$$\min\nolimits_{\Pi}(A) = (\mathit{a b c d e f} \preceq_{lex} \mathit{a d e b c f})~\wedge~ (\mathit{a b c d e f} \preceq_{lex} \mathit{b a c d f e})~\wedge~ (\mathit{a b c d e f} \preceq_{lex} \mathit{a c b d e f}) $$

and this simplifies using properties of lexicographic orderings to:

$$\min\nolimits_{\Pi}(A) = (b c \preceq_{lex} d e) ~\wedge~ (a e \preceq_{lex} \mathit{b f}) ~\wedge~ (b d \preceq_{lex} c e) $$

To verify that π is indeed canonizing one should consider each of the permutations in π ∈ S 4∖π and prove that minπ(A) ⇒ A ≼ π(A) where A is the variable matrix detailed above. For example, when π = [2, 1, 4, 3], A ≼ π(A) means a b c d e f ≼ l e x a e d c b f which simplifies to b c ≼ l e x e d and we need to show that (b c ≼ l e x d e) ∧ (a e ≼ l e x b f) ∧ (b d ≼ l e x c e) ⇒ b c ≼ l e x e d. This is not difficult to check.

Clearly, for any set of permutations π⊂S n the predicate minπ is a partial symmetry break for graph search problems. In [9], Codish et al. introduce the following symmetry break for graph search problems where A i denotes the i th row of the adjacency matrix A and ≼ {i, j} denotes the lexicographic comparison on strings after removing their i th and j th elements.

Definition 4 (lexicographic symmetry break, 9)

Let A be an n × n adjacency matrix. Then,

$$\textsf{sb}^{*}_{\ell}(A) = \bigwedge_{1\leq i<j\leq n} A[i]\preceq_{\{i,j\}} A[j]$$

It is not difficult to observe that \(\textsf {sb}^{*}_{\ell }\) is equivalent to the predicate minπ where v a rπ is the set of permutations that swap a single pair (i, j) with 1 ≤ i < j ≤ n.

The experimental setting

In this paper all computations are performed using the Glucose 4.0 SAT solver [5]. Encodings to CNF are obtained using the finite-domain constraint compiler BEE [26]. BEE facilitates applications to find a single (first) solution, or to find all solutions for a constraint, modulo a specified set of variables. When solving for all solutions, BEE iterates with the SAT solver, adding so called blocking clauses each time another solution is found. This technique, originally due to McMillan [25], is simplistic but suffices for our purposes. All computations were performed on a cluster with a total of 228 Intel E8400 cores clocked at 2 GHz each, able to run a total of 456 parallel threads. Each of the cores in the cluster has computational power comparable to a core on a standard desktop computer. Each SAT instance is run on a single thread.

4 Canonizing symmetry breaks

The observation made in Example 3: that a canonizing set for graphs with n vertices can be much smaller than n!, motivates us to seek “small” canonizing sets that might be applied to introduce canonizing symmetry breaking constraints for graph search problems. First, we describe the application of this approach to compute relatively small instance independent canonizing sets, which induce general purpose symmetry breaks that can be used for any graph search problem. We compute these sets for graphs with n ≤ 10 vertices. We illustrate their application when breaking all symmetries in the search for Ramsey and claw-free graphs.

Second, we apply our methods to compute instance dependent canonizing sets which are computed for a given graph search problem. Namely, these sets promise that only non-isomorphic solutions will be generated when enumerating all solutions for the given graph search problem that satisfy its corresponding canonizing symmetry breaks. However, these sets are not necessarily canonizing for other graph search problem. We show that such canonizing sets can be computed for larger graphs (compare to instance independent canonizing sets) and their usage is illustrated to enumerate all non-isomorphic highly irregular graphs up to 20 vertices.

4.1 Computing canonizing sets

To compute a canonizing set of permutations for graph search problem φ on n vertices we start with some initial set of permutations π (for simplicity, assume that π = ∅). Then, incrementally apply the step specified in lines 2–3 of Algorithm 1, as long as the stated condition holds.

figure a

Lemma 2

Algorithm 1 terminates and returns a canonizing set π for the graph search problem φ.

Proof

Each step in the algorithm adds a permutation (at Line 3) and the number of permutations is bound. When the algorithm terminates with π then for G ∈ s o l(φ), if minπ(G) holds then there is no π ∈ S n such that π(G)≺G. So, G ≼ π(G) for all π ∈ S n and therefore \(\min _{S_{n}}(G)\) holds. □

Drawing on the discussion in [6, 11, 20] we do not expect to find a polynomial time algorithm to compute a canonical (or any other complete) symmetry breaking constraint for graph search problems based on Definition 2. Thus it is also unlikely to find an efficient implementation of Algorithm 1. Our implementation of Algorithm 1 is based on a SAT encoding. We repeatedly apply a SAT solver to find a counter example permutation which shows that π is not a canonizing set yet and add it to π, until an UNSAT result is obtained. In the implementation of the algorithm, care is taken to use a single invocation of the SAT solver so that the iterated calls to the solver are incremental. The constraint model used is depicted as Fig. 3 where A, B denote n × n matrices of propositional variables and π denotes a length n vector of integer variables. Constraint 4 specifies that the parameter π is a permutation on \(\left \{ \begin {array}{l}1,\ldots ,n\end {array} \right \}\). Each element of the vector is a value 1 ≤ π i ≤ n and the elements are all different. Constraint 5 specifies that the parameters A, B represent isomorphic graphs via the parameter π. Constraint 6 specifies the condition of the while loop (line 2) of Algorithm 1: A is restricted to be a solution to the given graph search problem φ, A and B are constrained B = π(A) to be isomorphic adjacency matrices (see Constraint (1)) via the permutation π. The constraint minπ(A) is imposed and also A≻B. If \({\mathit {al{g_{1}^{n}}}}(\Pi ,\varphi )\) is satisfiable, then the permutation π is determined by the satisfying assignment and added to π as specified in (line 3) of Algorithm 1.

Fig. 3
figure 3

Constraints for Algorithm 1 where A and B are n × n Boolean matrices and π = 〈π 1, … , π n 〉 is a vector of integer variables (with domain {1, … , n})

Full size image

We say that a canonizing set π of permutations is redundant if for some π ∈ π the set π∖{π} is also canonizing. Algorithm 1 may compute a redundant set. For example, if a permutation added at some point becomes redundant in view of permutations added later. Algorithm 2 iterates on the elements of a canonizing set to remove redundant permutations.

figure b

Lemma 3

If π is a canonizing set for the graph search problem φ, then so is Reduce(π,φ) computed by Algorithm 2.

Proof

Let π i be the set obtained after considering the i th permutation in Line 2 of Algorithm 2. The initial set π0 is the input to the algorithm. We prove that \(\min _{\Pi _{i}} \leftrightarrow \min _{\Pi _{i+1}}\) and conclude that minπ ↔ minR e d u c e(π). If no permutation was removed in step i then π i+1 = π i and trivially \(\min _{\Pi _{i}} \leftrightarrow \min _{\Pi _{i+1}}\). Otherwise π i+1 = π i ∖{π} for a permutation π which satisfies ∀G ∈ s o l(φ): \(\min _{\Pi _{i+1}}(G)\) ⇒ G ≼ π(G). Thus π is implied by the permutations in π i and can be removed. Therefore \(\min _{\Pi _{i+1}}(G) \leftrightarrow \min _{\Pi _{i}}(G)\). □

Our implementation of Algorithm 2 is based on a SAT encoding. The key is in the encoding for the test in Line 3. Here, for the given π and π ∈ π, we encode the constraint

$$ {alg_{2}}^{n}(\Pi,\varphi) = \underbrace{adj^{n}(A)}_{(a)} ~\land~ \underbrace{\varphi(A) ~\land~ min_{\Pi \setminus \{ \pi \}}(A) ~\land~ \pi(A) \succ A}_{(b)} $$
(7)

where the left part (a) specifies that A is the n × n adjacency matrix of some graph (see Constraint (1)), and the right part (b) is the negation of the condition in Line 3. If this constraint is unsatisfiable then π is redundant and removed from π.

4.2 Instance independent symmetry breaks

Observe that if φ = t r u e then \(sol(\varphi ) = \mathcal {G}_{n}\). Applying Algorithm 1 to compute Compute-Canonizing-Set(π, t r u e) generates canonizing symmetry breaks which apply for any graph search problem on n vertices (i.e instance independent). This is true for any set of permutations π but for simplicity assume π = ∅.

Table 1 describes the computation of irredundant instance independent canonizing permutation sets for n ≤ 10 by application of Algorithms 1 and 2. The corresponding permutation sets can be obtained from http://www.cs.bgu.ac.il/~mcodish/Papers/Tools/canonizingSets. The first 3 columns indicate the number of graph vertices, n, the number of permutations on n, and the number of non-isomorphic graphs on n vertices as specified by sequence A000088 of the OEIS [28]. The forth and fifth columns indicate the size of the canonical set of permutations computed using Algorithm 1 and the time to perform this computation. Columns six and seven are the size of the reduced canonical set of permutations after application of Algorithm 2 and the corresponding computation time. Column seven is set in boldface. These numbers present the relatively small size of the computed canonizing sets in comparison to the value of n!. Using the symmetry breaks derived from these sets we have generated the sets of all non-isomorphic graphs with up to 10 vertices and verified that their numbers correspond to those in column three. These are computed by solving the conjunction of Constraint (1) with the corresponding symmetry breaking predicate minπ the computation of which is described in Table 1.

Table 1 Computing irredundant canonizing sets of permutations for n ≤ 10
Full size table

The numbers in Table 1 also indicate the limitation of complete symmetry breaks which apply to all graphs. We do not expect to succeed to compute a canonizing set of permutations for n = 11 and even if we did succeed, we expect that the number of constraints that would then need be added in applications would be too large to be effective.

4.3 Computing Ramsey graphs with canonizing symmetry breaks

Recall Example 1 where we introduce the graph search problem for Ramsey graphs. Table 2 describes the computation of all R(4, 4; n) graphs for n ≤ 10 using a SAT solver. The table compares two configurations: one using the partial symmetry breaking predicate \(\textsf {sb}^{*}_{\ell }\) defined in [9] and the other using a canonizing symmetry break minπ where π is the canonizing set of permutations, the computation of which is described in Table 1. For each configuration we detail the size of the SAT encoding (clauses and variables), the time in seconds (except where indicated in hours) to find all solutions using a SAT solver, and the number of solutions found. Observe that the encodings using the canonizing symmetry breaks are much larger. However the sat solving time is much smaller. For n = 10 the configuration with \(\textsf {sb}^{*}_{\ell }\) requires more than 33 hours where as the configuration using minπ completes in under 7 hours. Finally note that the computation with minπ computes the precise number of solutions modulo graph isomorphism as detailed for example in [24]. These are the numbers in the rightmost column set in boldface. The solutions computed using \(\textsf {sb}^{*}_{\ell }\) contain many isomorphic solutions which need to be subsequently removed using nauty or a similar tool. One might argue that the real cost in applying the complete symmetry breaks should include their computation. To this end we note that these are general symmetry breaking predicates applicable to any graph search problem, and they are precomputed once.

Table 2 Computing \(| \mathcal {R}(4,4;n) |\) with canonizing symmetry breaking and \(\textsf {sb}^{*}_{\ell }\)
Full size table

4.4 Computing claw-free graphs with canonizing symmetry breaks

Recall Example 2 where we introduce the graph search problem for claw-free graphs. The number of claw-free graphs for n ≤ 9 vertices is detailed as sequence A086991 on the OEIS [28]. Table 3 describes the search for claw free graphs as a graph search problem. Then we use a SAT solver to compute the set of all claw free graphs on n vertices. We illustrate that using canonizing symmetry breaks, and the results detailed in Table 1, we can compute the set of all claw free graphs modulo graph isomorphism for n ≤ 10 thus computing a new value for sequence A086991. We comment that after this value for n = 10 was added to the OEIS, Falk Hüffner added further values for 10 < n ≤ 15. The column descriptions are the same as those for Table 2. For each configuration we detail the size of the SAT encoding (clauses and variables), the time in seconds to find all solutions using a SAT solver, and the number of solutions found. For this example the computation with a complete symmetry break is more costly, but it does return the precise set of canonical graphs. The sequence in the right column are set in boldface. For n ≤ 9, these are the numbers of claw-free graphs as detailed in sequence A086991 of the OEIS [28]. It is no coincidence that the number of variables indicated in the columns of Tables 2 and 3 are almost identical. These pertain to the variables in the adjacency graph and those introduced to express the instance independent symmetry breaks.

Table 3 Computing claw-free graphs with canonizing symmetry breaking and \(\textsf {sb}^{*}_{\ell }\)
Full size table

4.5 Instance dependent canonizing symmetry breaks

A canonizing set for a specific graph search problem φ is typically much smaller than a general canonizing set as the constraints in φ restrict the solution structure and hence also the symmetries within the solution space. We call such a set instance dependent. In practice we can often compute instance dependent canonizing sets for larger graphs with n > 10 vertices. For a given graph search problem φ, let us denote by π φ the canonizing set of permutations obtained from Compute-Canonizing-Set(∅, φ) of Algorithm 1. Solutions of φ obtained with the induced symmetry break predicate \(\min _{\Pi _{\varphi }}\) are guaranteed to be pairwise non-isomorphic.

In this section we demonstrate the application of instance dependent canonizing sets. Here we consider a search problem for which we seek a graph that has a particular given degree sequence.

A degree sequence is a monotonic non-increasing sequence of the vertex degrees of a graph. Degree sequences are a natural way to break a graph search problem into independent cases (one for each possible degree sequence). Thus the search for a solution or all solutions can be done in parallel.

Since a degree sequence induces a partition on the vertex set, in order to compute an instance dependent canonizing symmetry break with respect to a degree sequence, a constraint stating that B has the same degree sequence as A needs to be added to (6 ′). The following specifies that an adjacency matrix complies to a given degree sequence. Here each conjunct is a cardinality constraint on a row of A.

$$\begin{array}{@{}rcl@{}} \varphi^{\langle d_{1},\ldots,d_{n} \rangle}_{degSeq}(A) &=& \bigwedge_{1\leq i\leq n} \left( \sum\limits_{j=1}^{n} A_{i,j} = d_{i}\right) \end{array} $$
(8)

4.6 Computing highly irregular graphs per degree sequence

A connected graph is called highly irregular if each of its vertices is adjacent only to vertices with distinct degrees [1]. The number of highly irregular graphs with n ≤ 15 vertices is detailed as sequence A217246 in the OEIS [28]. By application of instance dependent canonizing symmetry breaks we extend this sequence with 5 new values. The following constraint specifies that the graph represented by adjacency matrix A with degree sequence 〈d 1, … , d n 〉 is highly irregular.

$$ \varphi_{hi}^{\langle d_{1},\ldots,d_{n} \rangle}(A) = \bigwedge_{1\leq i,j<k\leq n ~s.t~ d_{j} = d_{k}} (\neg A_{i,j} \vee \neg A_{i,k} ) \wedge \varphi^{\langle d_{1},\ldots,d_{n} \rangle}_{degSeq}(A) \wedge \varphi_{con}^{n}(A) $$
(9)

Here, the formula \(\varphi _{con}^{n}(A)\) specifies that the graph represented by adjacency matrix A is connected. The following constraint introduces propositional variables \(p^{k}_{i,j}\) to express that vertices i and j are connected by a path that consists of intermediate vertices from the set {1, … , k}.

$$\begin{array}{@{}rcl@{}} \varphi_{con}^{n}(A) &=& \bigwedge\limits_{1\leq i,j\leq n} \left( p_{i,j}^{0} \leftrightarrow A_{i,j}\right) ~\land~ \bigwedge\limits_{1\leq i,j,k\leq n} p_{i,j}^{k} \leftrightarrow \left( p_{i,j}^{k-1} \vee \left( p_{i,k}^{k-1} \land p_{k,j}^{k-1}\right)\right) ~\wedge \\ & & ~\land~ \bigwedge\limits_{1\leq i,j\leq n} \left( p_{i,j}^{n}\right) \end{array} $$
(10)

Our strategy is to compute all highly irregular graphs with n vertices in three steps: (1) We compute the set of degree sequences for all highly irregular graphs with n vertices; (2) For each degree sequence we compute an instance dependent canonizing symmetry break; (3) We apply per degree sequence, the instance dependent canonizing symmetry break to compute the corresponding set of graphs with the corresponding degree sequence.

To perform the first step we apply a result from [21] which states that any degree sequence of a highly irregular graph is of the form \(\langle m^{n_{m}},\ldots ,i^{n_{i}},\ldots ,1^{n_{1}} \rangle \) where:

  1. 1.

    n i ≥ n m for 1 ≤ i ≤ m; and

  2. 2.

    \({\sum }_{i=1}^{m} (n_{i}*i)\) and n m are positive even numbers.

It is straightforward to enumerate all degree sequences for graphs with up to 20 vertices that satisfy this property. We then apply a SAT solver to determine which of these sequences is the degree sequence of some highly irregular graph. Step (2) is performed using a SAT solver, per degree sequence, by application of the above described adaptation of Algorithm 1 to compute an irredundant instance dependent canonizing set with respect to \(\varphi _{hi}^{\langle d_{1},\ldots ,d_{n} \rangle }(A)\). In step (3) we enumerate all non-isomorphic highly irregular graphs per degree sequence with respect to the corresponding canonizing symmetry breaking constraints. We compute the graphs with a simple backtrack based (exhaustive search) program written in Java in which the variables of the adjacency matrix are assigned one by one until a solution is found.

Table 4 presents our results. The columns are divided into three pairs corresponding to the three steps described above: the first pair – computing degree sequences, the second pair – computing (instance dependent) canonizing permutation sets, and the third pair – computing solutions (using the derived canonizing symmetry breaks). Each pair presents the computation size and information on the solutions. For the first pair, the number of degree sequences. For the second pair, the average number of permutations in the canonizing permutation sets. In the third pair, the number of connected highly irregular graphs with n vertices (set in boldface). The values for n ≤ 15 vertices correspond to those detailed as sequence A217246 in the OEIS [28]. The values for n > 15 are new.

Table 4 Computing highly irregular graphs per degree sequence (time in seconds unless otherwise indicated)
Full size table

When computing solutions, as detailed in the rightmost pair of columns of Table 4, computation is performed in parallel, using a separate thread of the cluster for each degree sequence found in the first step. So for example, when n = 20, there are 151 parallel threads running with a total time of 7190.23 hours. This implies an average of about 47 hours. Note that we succeed to compute canonizing symmetry breaks for more than 20 nodes. We have not included the results in Table 4 as the subsequent graph enumeration problems involve a humongous number of graphs.

5 A generalization to matrix models

Graph search problems, as considered in this paper, are a special case of matrix search problems expressed in terms of a matrix of finite domain decision variables [13, 14, 35, 36]. Often, in such problems, both rows and columns can be permuted, possibly by different permutations, while preserving solutions. Matrix search problems with this property are called “fully-interchangeable” [36]. A graph search problem can be seen as a fully-interchangeable matrix search problem where the variables are Boolean, the matrix is symmetric and has f a l s e values on its diagonal, and symmetries involve permuting rows and columns, but only by the same permutation for both.

Similar to Definition 1, it is common to define a lex-order on matrix models. For matrices M 1 and M 2 (of the same dimension) with s 1 and s 2 the strings obtained by concatenating their rows, M 1 ≼ M 2 if and only if s 1 ≼ l e x s 2. Similar to Definition 2, the LexLeader method [11] can be applied to a fully-interchangeable matrix search problem to guarantee canonical solutions which are minimal in the lex ordering of matrices. For an n × m matrix search problem this involves potentially considering all n! × m! pairs of permutations (per n rows and per m columns). This is not practical as it means introducing n! × m! lex constraints on strings of size n × m.

To this end, the DoubleLex constraint was introduced in [13] to lexicographically order (linearly) both rows and columns. The DoubleLex constraint can be viewed as derived by a subset of the constraints imposed in the LexLeader method [35]. For a matrix with n rows and m columns this boils down to a total of only (n − 1) + (m − 1) permutations. The DoubleLex constraint has been shown to be very effective at eliminating much of the symmetry in a range of fully-interchangeable matrix search problem. Still, it does not break all of the symmetries broken by LexLeader.

To demonstrate the application of our methods to matrix models, we compare the DoubleLex symmetry break with canonical symmetry breaking for the application to EFPA (Equi-distant Frequency Permutation Array). An instance of the EFPA problem takes the form (q, λ, d, v). The goal is to find a set of v words of length q λ such that each word contains λ copies of the symbols 1 to q, and each pair of words is Hamming distance d apart. The problem is naturally expressed as a v × q λ (fully-interchangeable) matrix search problem.

Table 1 in the survey by Walsh [35] illustrates the power of the DoubleLex symmetry break. The table details the number of solutions found with DoubleLex constraint for several instances of the EFPA problem in contrast to the total number of non-symmetric solutions. It demonstrates that DoubleLex leaves very few redundant solutions.

We have adapted Algorithms 1 and 2 so that they apply to search for pairs of permutations which induce constraints to break all symmetries in fully-interchangeable matrix search problems. With these constraints we obtain only the canonical solutions. We have applied such constraints to the instances of the EFPA problem considered in [35]. For matrix search problems we initialize Algorithm 1 taking π to include the permutation pairs corresponding to the DoubleLex symmetry break.

Table 5 summarizes our results obtained, as all results in this paper, using the finite-domain constraint compiler BEE [26] with the underlying Glucose 4.0 SAT solver [5]. On the left side the table details statistics for solutions with DoubleLex: the number of permutation pairs introduced by DoubleLex, the solving time (in seconds) and the number of solutions found. The right side of the table details the same for the canonizing symmetry breaks. Here, the detailed number of permutation pairs are those for the canonizing symmetry breaks, as discovered using the versions of Algorithms 1 and 2 adapted for use with matrix models. Here we also make explicit the number of additional permutations Δ, in addition to those introduced by DoubleLex, required to provide a canonizing symmetry break. In several rows of the table, corresponding to instances where DoubleLex is in fact complete, this value is negative. In these cases no permutations were added by Algorithm 1 and several were removed by Algorithm 2 when deriving the corresponding canonizing symmetry break. It is interesting to note that, often times, for canonical symmetry breaks, only a few permutations need be added on top of these already introduced by DoubleLex. In [19], the authors provide a first experimental study on how much symmetry is left after applying the DoubleLex constraint. Table 5 (in the column labeled Δ) illustrates the cost of breaking the symmetries left after applying the DoubleLex constraint. The numbers in the rightmost columns (set in boldface) correspond to the number of distinct non-symmetric solutions. The corresponding sets of permutation pairs for the instances in Table 5 can be obtained from http://www.cs.bgu.ac.il/~mcodish/Papers/Tools/canonizingSets.

Table 5 Number of solutions for EFPA with DoubleLex and canonizing symmetry breaks
Full size table

We note that the numbers presented in the right side of Table 5 do not represent a win in time when compared to the results presented in [35]. However, it is of interest to observe that the DoubleLex symmetry break can be expressed in terms of a set of permutations which can then be considered as a starting point to derive a complete symmetry break.

To this end, we also note that other canonical orderings for matrix models have been considered as alternatives to the row-wise LexLeader order. For example, the Snake ordering [15] and the Gray ordering [27]. Based on these orderings, partial symmetry breaks such as SnakeLex were introduced and shown to be better choices for some types of problems compared to DoubleLex. We comment that it is not difficult to adapt Algorithms 1 and 2 to derive canonizing sets of permutations with respect to these alternative orderings. We leave this as a topic for future work.

6 Related work

Isomorphism free generation of combinatorial objects and particularly graphs, is a well studied topic [7, 12, 23, 31, 32]. Methods that generate the canonical representatives of each equivalence class are sometimes classified as “orderly” generation methods. This is a dynamic approach. Typically graphs are constructed by adding edges in iteration until a solution is found and backtracking when failing. In each such iteration the graph is checked to determine whether it can still be further extended: (a) to a solution of the graph search problem, and (b) to a canonical graph. Both of these tests consider only the fixed part of the partial graph. These techniques do not restrict the set of permutations to be canonical but rather consider all permutations relevant to the partially instantiated structure. Still, initially, there are very few permutations that need to be considered for (b) as the partial graph is still small. However, as the partial graph becomes more instantiated this test becomes harder and consumes more time. This approach is also the one applied in [36] for matrix search problems. In contrast our method is static. We aim to compute, before applying search, a small set of permutations that apply to break the symmetries in solutions. Our approach does not rely on which parts of the graph have already been determined during search.

7 Conclusion

We have illustrated the applicability of canonizing symmetry breaking constraints for small graph and matrix search problems. Although any row/column permutation is potentially a symmetry, we compute compact canonizing symmetry breaks, much smaller than those which consider all permutations. Our strategy is two phase. First, symmetry breaking constraints are computed. Second, these constraints are added to the model and then any solver can be applied to find (all) solutions which satisfy the model.

For graph search problems, we have presented methods that generate both instance independent and instance dependent symmetry breaking constraints. While instance dependent symmetry breaks have limited applicability since they grow enormously for graphs with more than 10 vertices, instance independent symmetry breaks have been successfully applied to compute new values in highly irregular graphs OEIS sequence for graphs with up to 20 vertices. For matrix search problems our focus is on instance dependent constraints.

Although, our approach is applicable only to graphs with small numbers of vertices, there are many open small graph search problems. For example the set of all Ramsey R(4, 5; 24) graphs has not been determined yet. We are currently trying to extend our techniques to apply to compute symmetry breaks for this problem which involves only 24 vertices.

We note that our approach can also apply to improve dynamic symmetry breaking techniques. Given a partially instantiated graph, to determine if it is extendable to a canonical graph, one need not consider all of the permutations related to the already instantiated part. This is because some of those permutations are redundant.

Finally, we note the distinction made in [19] between complete symmetry breaking and complete pruning for a set of symmetry breaking constraints. Symmetry breaks remove all symmetric solutions but not all symmetric branches of the search tree. An interesting future direction is to find a SAT encoding that enforces generalized arc consistency (GAC) on the set of symmetry breaking constraints. Perhaps an encoding that achieves this is not too big given the other constraints.