Breaking Symmetries in Graphs: The Nauty Way

Abstract

Symmetry breaking is an essential component when solving graph search problems as it restricts the search space to that of canonical representations. There are an abundance of powerful tools, such as nauty, which apply to find the canonical representation of a given graph and to test for isomorphisms given a set of graphs. In contrast, for graph search problems, current symmetry breaking techniques are partial and solvers unnecessarily explore an abundance of isomorphic parts of the search space. This paper is novel in that it introduces complete symmetry breaking for graph search problems by modeling, in terms of constraints, the same ideas underlying the algorithm applied in tools like nauty. Whereas nauty tests given graphs, symmetry breaks restrict the search space and apply during generation.

1 Introduction

Many problems, particularly in combinatorics, reduce to asking whether some graph with a given property exists. Such “graph search” or “graph existence” problems are notoriously difficult, in no small part due to the extremely large number of symmetries in graphs. General approaches to graph search problems involve either explicitly enumerating all (non-isomorphic) graphs and checking each for the given property, or encoding the problem for some general-purpose discrete satisfiability solver (i.e. SAT, integer programming, constraint programming), which does the enumeration implicitly. In this paper, we are largely concerned with this second approach.

To avoid symmetries in explicit enumeration approaches, ideally one designs a procedure which generates exactly one graph in each equivalence class. The classic “orderly generation” approach, due to Read [1], imposes a lexicographic order over matrix elements and systematically constructs canonical adjacency matrices of size $n+1$ from the canonical matrices of size n. For an example, in [2], the authors address the problem: does there exist a graph with 11 vertices which has a total magic labeling (TML)? To provide the negative answer the authors test each one of the 1,018,997,864 canonical graphs with 11 vertices and report that this task requires 13,595 days of CPU computation. Given that there are 165,091,172,592 canonical graphs with 12 vertices it clear that canonical graph enumeration based approaches cannot scale.

In contrast, symmetry breaking in SAT or CP [3–6] is done by adding additional constraints to eliminate non-canonical graphs.¹ Existing symmetry-breaking predicates are typically based on variants of the lexicographic ordering [4]. Incomplete symmetry breaks under this ordering are straightforward and compact, but leave many non-canonical graphs in each equivalence class. Complete symmetry breaks, on the other hand, are extremely large. Indeed, as deciding lexicographic canonicity of an adjacency matrix is NP-hard, the existence of a compact complete symmetry break seems unlikely.

By looking at vertex degrees and related properties, it is often possible to very quickly conclude that two graphs are not isomorphic. In fact, most non-isomorphic graphs may be distinguished in this way. It turns out that exploiting structural properties of graphs is critical in testing equivalence or finding canonical representations, and gave rise to a family of astonishingly effective isomorphism and canonical labeling tools. Many graph search problems instead generate candidate solutions, which are then reduced to canonical form using canonical label-ling tools such as nauty [9], bliss [10], or saucy [11]. This approach can be highly effective since these tools are amazingly efficient, but it can be overwhelmed by generating enormous numbers of copies of isomorphic graphs. For example there are 36,028,797,018,963,968 adjacency matrices on 11 vertices which is considerably more than the number of canonical graphs.

Ideally we would like to impose constraints defining the properties of the graph we are searching for together with a compact constraint on the structural properties of the graph to eliminate all non-canonical solutions. Then we could exploit state of the art declarative solvers, to solve graphs problems with arbitrary constraints and objective functions without being overwhelmed by symmetry in the search.

This paper makes two contributions. First, we introduce a polynomial sized SAT encoding of a partial symmetry-breaking predicate which exploits structural information in the style of nauty which eliminates many more non-canonical graphs than standard lex-based approaches. When combined with lexicographic symmetry breaking this predicate remains polynomial and breaks even more symmetries. Second, we illustrate how a technique, first presented in [12], can be generalized to compute complete symmetry-breaking predicates which enhance the nauty style structural break. While these predicates could be exponential in size, we show that they are very small in practice. We present experimental results to demonstrate the impact of both types of nauty style symmetry breaks: partial and complete.

The computations throughout the paper are performed using the finite-domain constraint compiler BEE [13] which compiles constraints to CNF, and solves it applying an underlying SAT solver. We use Glucose 4.0 [14] and Clasp 3.1.3 [15] as the underlying SAT solvers and specify for each computation which solver was used. All computations were performed on a cluster of Intel E8400 cores, each clocked at 2 GHz, able to run a total of 790 parallel threads. Each of the cores in the cluster has computational power comparable to a core on a standard desktop computer. Each SAT instance is run on a single thread.

In Sect. 2 we present preliminaries on graphs, graph isomorphism, on the nauty approach to graph isomorphism, and on symmetry breaking in graph search problems. Section 3 describes a symmetry breaking predicate which exploits structural information, emulating the nauty algorithm. This section also presents an experimental evaluation comparing the new symmetry breaks with other existing techniques. Finally, Sect. 4 concludes.

2 Preliminaries

2.1 Graphs, Permutations, Graph Isomorphism, Canonical Graphs

Throughout this paper we consider finite and simple graphs (undirected with no self loops). The set of simple graphs on n nodes is denoted $\mathcal{G}_n$. We assume that the vertex set of a graph, $G = (V,E)$, is $V=\{1,\ldots ,n\}$ and represent G by its $n\times n$ adjacency matrix A defined by $A_{i,j} = (1 \text{ if } (i,j) \in E \text{ else } 0)$. We write $A_i$ to denote the $i^{th}$ row of A.

The set of permutations $\pi :\{1,\ldots ,n\}\rightarrow \{1,\ldots ,n\}$ is denoted $S_n$. For convenience, we shall use $\pi _{i, j}$ to denote the permutation swapping i with j that maps every other element to itself.

For $G = (V,E) \in \mathcal {G}_n$ and $\pi \in S_n$, we define $\pi (G)=\{V, \{(\pi (u),\pi (v))| (u,v)\in E)\}$. Permutations act on adjacency matrices in the natural way: If A is the adjacency matrix of a graph G, then $\pi (A)$ is the adjacency matrix of $\pi (G)$ obtained by simultaneously permuting with $\pi$ the rows and columns of A.

Two graphs $G_1,G_2\in \mathcal{G}_n$ are isomorphic, denoted $G_1\approx G_2$, if there exists a permutation $\pi \in S_n$ such that $G_1 = \pi (G_2)$. Sometimes we write $G_1\approx _\pi G_2$ to emphasize that $\pi$ is the permutation such that $G_1=\pi (G_2)$. For sets of graphs $H_1, H_2$, we say that $H_1\approx H_2$ if for every $G_1\in H_1$ (likewise in $H_2$) there exists $G_2\in H_2$ (likewise in $H_1$) such that $G_1\approx G_2$. The equivalence classes of $\mathcal{G}$ modulo $\approx$ is denoted $\mathcal{G}_n^\approx$.

It is usual to define the canonical representation of (an equivalence class of) a graph in terms of some total ordering. A classic choice is the lexicographic ordering on graphs.

Definition 1

(lex ordering graphs). Let $G_1,G_2 \in \mathcal {G}_n$ and let $s_1, s_2$ be the strings obtained by concatenating the rows of the upper triangular parts of their corresponding adjacency matrices $A_1, A_2$ respectively. Then, $G_1 \preceq _{lex} G_2$ if and only if $s_1\preceq _{lex} s_2$. We also write $A_1 \preceq _{lex} A_2$.

The canonical representation of a graph, with respect to a given total order, is then the minimal element of its equivalence class.

Definition 2

(canonicity). The canonical representation of a graph $G\in \mathcal {G}_n$ with respect to a total ordering $\preceq$ is $can_\preceq (G) = \min _{\preceq }\left\{ ~\pi (G) \left| \begin{array}{l}\pi \in S_n\end{array} \right. \right\}$.

The combination of Definitions 1 and 2 provides a simple notion of canonicity defined in terms of lexical ordering of graphs which is often attributed to Read [1]. However, this definition completely ignores all of the structural information present in the graphs. A simple example of structural information is to focus on the degrees of vertices. Definitions that take advantage of structural properties of graphs simplify the processes of testing for graph isomorphism and testing for canonicity.

A structural property of a graph G is one which is invariant under permutation. In particular, if the property holds for a vertex v of G, then for a permutation $\pi$, it will hold also for $\pi (v)$ of $\pi (G)$. For simplicity, we will view a structural property of G as a mapping $\mu _G$ of graph vertices to integers such that for any permutation $\pi$ and vertex v, $\mu _G(v)=\mu _{\pi (G)}(\pi (v))$. We often omit the subscript and write $\mu$. For intuition, consider the structural property of vertex degree $\mu =\mathsf {deg}$ where $\mathsf {deg}_G(v)$ is the degree of v in G. For a structural property, $\mu _G$, on a graph G with vertices $V=\{1,\ldots ,n\}$, we denote $\bar{\mu }_G = \langle \mu _G(1),\ldots ,\mu _G(n) \rangle$. Given $\mu$, we introduce a total ordering $\preceq _{\mu }$ on graphs defined as follows.

Definition 3

( $\mu$ ordering graphs). Let $\mu$ be a structural property and $G_1,G_2 \in \mathcal {G}_n$. Then, $G_1\preceq _\mu G_2 \iff (\bar{\mu }_{G_1}\succ _{lex}\bar{\mu }_{G_2}) \vee ((\bar{\mu }_{G_1} = \bar{\mu }_{G_2}) \wedge {(G_1\preceq _{lex} G_2))}$.

It follows, from Definitions 2 and 3 that the canonical graph $G' = can_{\preceq _{\mu }}(G)$ has the property that $\mu _{G'}$ is sorted in decreasing order. Hence, throughout the paper, when given a structural property $\mu$, we will focus on graphs G such that $\mu _G$ is sorted in decreasing order. The reason that we take the reverse lexicographic order on the integer vectors in Definition 3 is to be consistent with the notion of a degree sequence [16]. When $\mu =\mathsf {deg}$ and G is canonical, then $\mu _G$ is the degree sequence of G.

Definition 4

(graph partitioning). A partitioning $\mathcal{P}$ of (vertex set) $V=\left\{ \begin{array}{l}1,\ldots ,n\end{array} \right\}$ is a sequence of k disjoint sets $\langle P_1,\ldots ,P_k \rangle$ such that $V=P_1\cup \cdots \cup P_k$. We refer to these sets as parts (rather than partitions) to avoid possible confusion. We also represent $\mathcal{P}$ as a sequence of integer values, $\mathcal{P}=\langle p_1,\ldots ,p_n \rangle$ such that $1\le p_i\le k$ for $1\le i\le n$. Here, $p_i=j$ means that vertex i is in part j. So, for $1\le j\le k$ we have $\mathcal{P}_j=\left\{ ~i\in V \left| \begin{array}{l}p_i=j\end{array} \right. \right\}$. To remove ambiguity from this representation, we assume that $\mathcal{P}$ is the smallest sequence (in the reverse lexicographic order) defining the given partitioning. We shall use $\mathcal{P}(i)$ to denote the part containing vertex i (that is, $p_i$). When referring to a sequence of partitionings, $\mathcal{P}^k$ shall be used to denote the $k^{th}$ element of the sequence.

The following example illustrates how structural information can be applied to partition the nodes of a graph. In the example, one can view the degree sequence of the graph as inducing a partitioning.

Example 1

Consider the graph G shown in Fig. 1(a). Discriminating vertices by degree establishes the partitioning $\langle \{v_5\}, \{v_1, v_2, v_3\},\{v_4\} \rangle$. The canonical graph $can_{\mathsf {deg}}(G)$ will contain these parts in order. Finding the canonical representation of G requires finding the permutation of $\{v_1, v_2, v_3\}$ which minimises the adjacency matrix. The resulting canonical matrix is shown in Fig. 1(b) together with the corresponding degree sequence. On the right is a binary representation of the partitioning. A one at row $i<n$ indicates that vertex $i+1$ starts a new part, and a zero, that it is in the same part.    $\square$

Fig. 1.

(a) A graph with partitions induced by degree, and (b) its canonical adjacency matrix under $\preceq _{\mathsf {deg}}$ with its degree sequence and binary partitioning to the right.

2.2 The Nauty Approach

The dominant approach for constructing canonical representations of graphs is the nauty algorithm, due to McKay [9, 17]. Our approach draws on the design of this algorithm. The algorithm consists of three phases applied in alternation to find a canonical representation of a given graph. Taking a very simplified view of the algorithm, we describe it in terms of two phases. The third phase, called automorphism detection [9, 17], is not detailed in our presentation. First, nauty partitions the vertices of the graph based on structural information. Then, it searches for a canonical representation given the partitioning of the first phase.

Phase One. Structural information in nauty : For a given graph, $G=(V,E)$, The algorithm extracts structural information derived from vertex degrees to incrementally refine a partitioning of the vertices starting from a single part, $\mathcal{P}=\langle V \rangle$. We first introduce the notion of degree by partition.

Definition 5

(degree by partition). Let $G=(V,E)$, $V=\{1,\ldots ,n\}$, $\mathcal{P}=\langle P_1,\ldots ,P_k \rangle$ be a partitioning of V, and $v\in V$. Then, $\mathsf {deg}(v,\mathcal{P}) = \langle d_1,\ldots ,d_k \rangle$ where $d_i = \left| \left\{ ~u\in P_i \left| \begin{array}{l}(u,v)\in E \end{array} \right. \right\} \right|$ counts the degrees of v into the parts of $\mathcal{P}$.

Algorithm 1 is what happens in the first phase of nauty. In the terminology of [9, 17], the partitioning computed by Algorithm 1 is said to be equitable; and a partitioning is said to be discrete if every equivalence class is a singleton.

Example 2

Recall the graph described in Example 1. The nauty algorithm, starting with $\mathcal{P}^0=\langle \{v_1,\ldots , v_5\} \rangle$, first distinguishes vertices by degree, obtaining the partitioning $\mathcal{P}^1=\langle \{v_1, v_2, v_3\}, \{v_4\}, \{v_5\} \rangle$ as in Example 1. Observe that $\mathsf {deg}(v_1,\mathcal{P}^1) = \langle 2,0,0 \rangle$ and $\mathsf {deg}(v_2,\mathcal{P}^1) = \mathsf {deg}(v_3,\mathcal{P}^1) = \langle 1,1,0 \rangle$. Hence, in $\mathcal{P}^2 = \langle \{v_1\}, \{v_2, v_3\}, \{v_4\}, \{v_5\} \rangle$, the vertex $v_1$ is separated from $v_2$ and $v_3$. The partitioning $\mathcal{P}^2$ is equitable – $\mathsf {deg}(v_2,\mathcal{P}^2) = \mathsf {deg}(v_3,\mathcal{P}^2) = \langle 1,0,1,0 \rangle$.    $\square$

Fig. 2.

The graph from Fig. 1 with (a) its partitioning $\mathcal{P}^1$ of vertices by degree, and (b) its refined partitioning $\mathcal{P}^2$. The partitioning in (b) is equitable.

Note that the order in which possible refinements are applied will not affect the composition of the resulting partitioning, but may change the order of parts. Any such order is acceptable, but it must be uniquely determined. In the following, we shall assume that at each step $i>0$, listing the variables in $\mathcal{P}^i$ from left to right as $\langle v_{j_1}, \ldots , v_{j_n} \rangle$ then the sequence of vectors, $\mathsf {deg}(v_{j_1},\mathcal{P}^{i-1}), \ldots , \mathsf {deg}(v_{j_n},\mathcal{P}^{i-1})$ is sorted in decreasing lexicographic order.

If the partition $\mathcal{P}^{i-1}$ is derived from a structural property, then the composition and order of its parts must be invariant under permutation. So then is each vector $\mathsf {deg}(v_{j}, \mathcal{P}^{i-1})$, as permuting vertices within a part has no effect on the degrees – thus $\mathcal{P}^i$ is also structural.

Phase Two. Searching for a canonical representation: In the following we denote by $\mathcal{P}$ the equitable partitioning resulting from phase one. If $\mathcal{P}$ is discrete, then a canonical labeling of vertices has been established. However, this is rarely the case. Indeed, for regular graphs all vertices have the same degree, and are thus indistinguishable. In search for a canonical representation, nauty artificially selects some vertex in a non-singleton set $P\in \mathcal{P}$ to be made distinct from the other vertices of P. However, as these vertices are thus far indistinguishable, this cannot be done in a label-invariant fashion. So, each vertex in P is tentatively selected in turn, and a candidate discrete partitioning recursively constructed for each. The canonical labeling is then the candidate partitioning which yields the smallest graph under some total ordering.

We do not elaborate on the details of how this search is made as efficient as possible in nauty as the encodings introduced in this paper will take an alternative approach to search for a canonical representation given a partitioning $\mathcal{P}$.

2.3 Graph Search Problems and Breaking Symmetry

Graph search problems are about the search for a graph that satisfies certain properties. We will focus on properties that relate to the structure of the graph that ignore the particular names of the vertices. So if G is a solution to a graph search problem, then so is any $G'$ that is isomorphic to G. More formally, an n-vertex graph search problem is a predicate, $\varphi (A)$, on an $n \times n$ matrix A of Boolean variables which is closed under isomorphism. A solution to $\varphi (A)$ is a satisfying assignment of the conjunction $\varphi (A) \wedge adj^n(A)$ where $adj^n(A)$ constrains A to be an $n\times n$ adjacency matrix. In Constraint (1), the left conjuct states that there are no self loops, and the right conjunct, that the edges are undirected.

$$\begin{aligned} adj^n(A) = \bigwedge \left\{ ~\lnot A_{i,i} \left| \begin{array}{l}1\le i\le n\end{array} \right. \right\} ~\wedge ~ \bigwedge \left\{ ~A_{i,j}\leftrightarrow A_{j,i} \left| \begin{array}{l}1\le i<j\le n\end{array} \right. \right\} \end{aligned}$$

(1)

The set of solutions of graph search problem $\varphi$ is denoted $sol(\varphi )$ and to make the variables explicit we write $sol(\varphi (A))$. Viewing $sol(\varphi )$ as a set of graphs, note that $sol( true )=\mathcal{G}_n$. The set $sol(\varphi )$ may include many isomorphic graphs; we write $sol_{\approx }(\varphi )$ to denote the set of solutions modulo graph isomorphism.

Example 3

The n vertex graph search problem $\varphi _{tm(n)}(G)$ is about the search for a Total Magic (TM) graph with n vertices. A graph $G=(V,E)$, with $|V|=n$ and $|E|=m$, is TM if there exist a one-to-one labeling $\lambda :V\cup E\rightarrow \left\{ \begin{array}{l}1,\ldots ,n+m\end{array} \right\}$ and two integer values h, k which satisfy the constraints below. The graph is modeled as an $n\times n$ adjacency matrix A of Boolean variables. The edges are the unknown, hence m is unknown. The labeling is modeled as a length n vector $\lambda ^V$ of integer variables for the vertices, and an $n \times n$ matrix $\lambda ^E$ of integer variables for the edges. Note that both A and $\lambda ^E$ are symmetric. Let $M = n(n-1)/2$ be the maximum number of edges. Values in $\lambda ^V$ are between 1 and $n+M$. Values in $\lambda ^E$ are between 0 and $n+M$ where 0 is the value for “non-edges”: $\lambda ^E_{i,j}$ is zero if and only if $A_{i,j}$ is false.

Constraint (2) enforces that A is an adjacency matrix, and that m is the number of edges in the graph. Constraint (3) enforces that node labels are between 1 and $n+M$, that edge labels are between 0 and $n+M$ and are non-zero if the edge exists, and $\lambda ^E$ is symmetric. Constraint (4) enforces that nodes and edges are labeled differently (the $\lambda ^E_{ij}$ with label 0 are non-existing edges), and that the maximum label used is $n+m$, hence there is a bijection from vertices and edges to $\left\{ \begin{array}{l}1,\ldots ,n+m\end{array} \right\}$. We use $+\!\!+$ to denote vector concatenation. Constraint (5) ensures the sum of the labels of each edge and its endpoints is k and the sum of the labels of each node and its incident edges is h.

$$\begin{aligned} \small adj^n(A) \wedge m = \sum _{i<j} A_{ij} \end{aligned}$$

(2)

$$\begin{aligned} \small \bigwedge _{1\le i<j\le n} \left( \begin{array}{l} (1 < \lambda ^V_{i}\le n{+}M) \wedge (0\le \lambda ^E_{ij}\le n{+}M) \\ \wedge ~ (\lambda ^E_{ij}>0\leftrightarrow A_{ij})\wedge (\lambda ^E_{ij}=\lambda ^E_{ji}) \end{array}\right) \end{aligned}$$

(3)

$$\begin{aligned} \small \mathsf {alldifferent\_except\_0}(\lambda ^V \!\!\!+\!\!+\left[ \lambda _{ij}^E | i < j \right] ) \quad \wedge \quad \max (\lambda ^V \!\!\!+\!\!+\lambda ^E)=n+m \end{aligned}$$

(4)

$$\begin{aligned} \small \bigwedge _{i<j} A_{ij} \rightarrow (\lambda ^V_i+\lambda ^V_j+\lambda ^E_{ij} = k) \quad \bigwedge \quad \bigwedge _{i \in V} (\lambda ^V_i + \sum _{j \in V} \lambda ^E_{ij}) = h \end{aligned}$$

(5)

There are only 6 TM graphs with up to 9 vertices and there exist no 10–11 vertex TM graphs [2]. The only known TM graphs, with ${>}11$ vertices, are composed of an odd number of triangles, or of an even number of triangles with a path of length 2. It is unknown if there exist other TM graphs with ${>}11$ vertices.    $\square$

Example 4

Several interesting relaxations of Total Magic graphs weaken the TM conditions. A graph is TM modulo p [2] if we replace the magic conditions with equality modulo p, that is replace Eq. (5) by

We are often interested in finding graphs which are TM modulo several radices: $p_1,p_2,\ldots ,p_k$.    $\square$

Solutions of a graph search problem are closed under permutations of the vertices. When solving graph search problems, it is essential to restrict the search space to break the symmetry between isomorphic solutions. Ideally, we would like to restrict the space to canonical representations.

Note however that we face a different problem to the methods described in Sect. 2.2. Canonicalization methods such as nauty take a fixed graph G, and compute some canonical representation $\mathsf {can}(G)$. Here, we must find some unknown graph satisfying $\varphi$, but wish to restrict our search to canonical representatives – that is, we wish to only accept graphs satisfying $G = \mathsf {can}(G)$.

A symmetry break is a predicate $\sigma (A)$ which is satisfied by at least one graph in each isomorphism class; a complete symmetry break is satisfied by exactly one graph in each equivalence class. A canonizing predicate, with respect to a total order $\preceq$ on graphs, is satisfied by exactly the set of minimal representations under $\preceq$. We shall use $sol_{\varphi }^{\sigma }(A)$ to denote the set of solutions to $\varphi (A)$ which satisfy the symmetry breaking predicate $\sigma (A)$.

Example 5

The following is a complete symmetry break, and a canonizing predicate with respect to $\preceq _{lex}$. It constrains A to be minimal with respect to all permutations of A.

$$\begin{aligned} \small \sigma _{\mathsf {clex}}(A) = \bigwedge _{\pi \in S_n} A \preceq _{lex} \pi (A) \end{aligned}$$

(6)

Unfortunately the set $S_n$ is prohibitively large, so this predicate is not at all practical.    $\square$

Example 6

The following is a partial symmetry break, introduced in [18]. It is a relaxation of $\sigma _{\mathsf {clex}}$. It constrains A to be minimal with respect to all those permutations of A which swap a pair of elements.

$$\begin{aligned}\small \sigma _{plex}(A) = \bigwedge _{1 \le i < j \le n} A \preceq _{lex} \pi _{i,j}(A) \end{aligned}$$

In practice this breaks many symmetries, and is of manageable size, and hence is often practically useful.    $\square$

In the following let $\mathcal{P}=\langle p_1,\ldots ,p_n \rangle$ be an unknown partitioning of the vertices $V=\{1,\ldots ,n\}$ of a graph expressed in terms of integer variables (so, when $p_i=p_j$ then vertices i and j are in the same part). We will make use of the following predicates:

The predicate $\mathsf {mono}(\mathcal{P})$ specifies that $\mathcal{P}$, represents a non-increasing sequence of values.

$$\small \mathsf {mono}(\mathcal{P}) = \bigwedge _{i=1}^{n-1} \mathcal{P}(i)\ge \mathcal{P}({i+1}) $$

The predicate $\mathsf {plex}(A,\mathcal{P})$ specifies that an adjacency matrix A is minimal with respect to permutations that swap pairs of vertices in the same part of $\mathcal{P}$.

$$\small \mathsf {plex}(A, \mathcal{P}) = \bigwedge _{1 \le i < j \le n} \mathcal{P}(i)=\mathcal{P}(j)\rightarrow A \preceq _{lex} \pi _{i,j}(A) $$

The predicate $\mathsf {clex}(A,\mathcal{P})$ specifies that an adjacency matrix A is minimal with respect to permutations that preserve the partitioning $\mathcal{P}$.

$$\begin{aligned} \small \mathsf {clex}(A, \mathcal{P}) = \bigwedge _{\pi \in S_n} \pi (\mathcal{P})=\mathcal{P}\rightarrow A \preceq _{lex} \pi (A) \end{aligned}$$

(7)

Note that $\mathsf {plex}(A, \mathcal{P})$ and $\mathsf {clex}(A, \mathcal{P})$ are not symmetry breaks unless we also constrain A to have a structural property with the corresponding partitioning $\mathcal{P}$. We illustrate this in the following example.

Example 7

Consider a structural property $\mu$ and a predicate $\mu (A,\mathcal{P})$ which encodes that A is an $n\times n$ adjacency matrix (of Boolean variables) and $\mathcal{P}=\langle p_1,\ldots ,p_n \rangle$ is a vector of integer variables such that $p_i=\mu _A(i)$. For instance, when $\mu =\mathsf {deg}$ we have

$$\begin{aligned} \mathsf {deg}(A,\mathcal{P}) = \bigwedge _{1\le i \le n} \mathcal{P}(i) = \varSigma A_i \end{aligned}$$

The following are respectively partial and complete symmetry breaks:

$$\begin{aligned} \sigma ^{plex}_{\mu }(A) = \exists \mathcal{P}.~ \mu (A,\mathcal{P}) \wedge \mathsf {mono}(\mathcal{P}) \wedge \mathsf {plex}(A, \mathcal{P}) \end{aligned}$$

$$\begin{aligned} \sigma ^{clex}_{\mu }(A) = \exists \mathcal{P}.~ \mu (A,\mathcal{P}) \wedge \mathsf {mono}(\mathcal{P}) \wedge \mathsf {clex}(A, \mathcal{P}) \end{aligned}$$

   $\square$

3 The Nauty Encoding

In this section we describe a SAT encoding to break symmetries in graph search problems inspired by the way that nauty is applied to map a given graph to a canonical representation. We introduce a complete symmetry breaking predicate, $\sigma _{\textsf {nauty}(k)}$, which similar to the nauty algorithm consists of two “phases” and takes the form:

$$ \sigma _{\textsf {nauty}(k)}(A) = \exists \mathcal{P}.~\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}(A,\mathcal{P}) \wedge \sigma _{\textsf {nauty}(k)}^{\textsf {phase}_2}(A,\mathcal{P}) $$

The predicate $\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}(A,\mathcal{P})$ accepts pairs consisting of an adjacency matrix A and a partitioning $\mathcal{P}$ such that executing the first phase of the nauty algorithm with k iterations on A results in the partitioning represented by $\mathcal{P}$, and the vertex order of A respects that partitioning. It further restricts A applying $\mathsf {plex}(A,\mathcal{P})$. The predicate $\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_2}(A,\mathcal{P})$ accepts a pair $(A,\mathcal{P})$ if A is minimal in the class of graphs isomorphic to A which preserve the structural information in $\mathcal{P}$. The predicate $\sigma _{\textsf {nauty}(k)}(A)$ accepts canonical adjacency matrices with respect to the structural information derived in the first phase of the nauty algorithm (k iterations). It is a complete symmetry break.

The essential difference between the encoding, $\sigma _{\textsf {nauty}(k)}(A)$, and the nauty algorithm presented in Sect. 2.2 is that the nauty algorithm performs on a given graph where as the encoding, $\sigma _{\textsf {nauty}(k)}(A)$, specifies constraints on an unknown graph A, restricting solutions for A to be canonical.

A partitioning $\mathcal{P}$ is represented as a vector $\langle p_1,\ldots ,p_n \rangle$ of integer variables such that vertices $v_i$ and $v_j$ are in the same part if and only if $p_i=p_j$. When $\mathcal{P}$ is constrained to be monotone ($i < j \rightarrow \mathcal{P}(i) \le \mathcal{P}(j)$) it may alternately be represented as a vector $\varDelta$ of $n-1$ of Boolean variables, such that $\varDelta _i \leftrightarrow \mathcal{P}(i) < \mathcal{P}(i+1)$. Then $v_i$ and $v_j$ are in the same part if and only if $\varDelta _i = \varDelta _{i+1} = \ldots = \varDelta _{j-1}$. The Boolean representation is more compact and performs better in our applications. Therefore, the nauty encoding is presented using the Boolean representation. Under the Boolean encoding, the predicate $\mathsf {plex}$ becomes:

$$ \mathsf {plex}(A, \varDelta ) = \displaystyle \bigwedge _{1 \le i< j \le n} (\displaystyle \bigwedge _{i \le k < j} \varDelta _k) \rightarrow A \preceq _{\mathsf {lex}} \pi _{i,j}(A) $$

3.1 Encoding the First Phase of Nauty

To encode $\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}$, we emulate the iterative refinement of partitionings. Let A be an $n\times n$ adjacency matrix and let $\varDelta ^{i}$ be the Boolean representation of the partitioning at step i of the nauty algorithm. We define a predicate $refine (\varDelta ^i, A, \varDelta ^{i+1})$ that specifies the partitioning, $\varDelta ^{i+1}$ at the next step of the algorithm. We then specify the predicate $\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}$ as an iteration of this refinement, starting from the initial partition $\varDelta ^0=\langle 0,\ldots ,0 \rangle$.

$$\begin{aligned} \begin{array}{lll} \sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}(A, \varDelta ) &{}=&{} iterate _k(\varDelta ^0, A, \varDelta ) ~\wedge ~ \mathsf {plex}(A,\varDelta )\\ iterate_k (\varDelta , A, \varDelta ') &{}=&{} \left\{ \begin{array}{lll} \exists \varDelta ''.&{} ~ refine (\varDelta , A, \varDelta '') \wedge iterate _{k-1}(\varDelta '',A,\varDelta ') &{} \text{ if } k > 0 \\ &{} ~\varDelta = \varDelta ' &{} \text{ if } k \le 0 \end{array} \right. \\ \end{array} \end{aligned}$$

As the graph is a “variable” (not given), we do not know in advance how many iterations are required to reach a fixpoint with respect to the structural information. However, as each non-trivial refinement must split some equivalence class, this process must reach a fixpoint after, at most, n iterations.

To facilitate the formal specification of the predicate $refine (\varDelta , A, \varDelta ')$ we first introduce several “helper” predicates.

The predicate $P_{\le }(\varDelta , L)$ : To compute structural information, it will be useful to identify those vertices appearing in parts up to the part containing some vertex v. The Boolean matrix L encodes this information.

$$ \begin{array}{rl} P_{\le }(\varDelta , L) &{} = \displaystyle \bigwedge _{1 \le i, j \le n} \left\{ \begin{array}{ll} L_{i, j} &{}~\mathbf{if }~j \le i \\ L_{i, j} \leftrightarrow L_{i,j-1} \wedge \lnot \varDelta _j &{}~\mathbf{otherwise } \end{array}\right. \end{array} $$

The predicate $\mathsf {lex}(\varDelta ,M)$ : This predicate specifies that the n rows of matrix M are non-increasing in the lexicographic order following the length $n-1$ vector $\varDelta$. The intention is that $\varDelta$ specifies a partitioning.

$$ \mathsf {lex}(\varDelta ,M) = \bigwedge _{1\le i < n} \left( \lnot \varDelta _i \rightarrow M_i \succeq _{lex} M_{i+1}\right) $$

The predicate $\mathsf {deg}(A,\varDelta ,M)$ : This predicate defines a relationship between: an $n\times n$ matrix, A, of Boolean variables (representing an unknown graph), a length $n-1$ vector, $\varDelta$, of Boolean variables (representing a partitioning of the vertices in A), and an $n\times n$ matrix, M, of integer variables such that $M_{i,j}$ represents the number of edges from vertex i to vertices in or before the part number containing vertex j. The rows of M are ordered lexicographically within each component of $\mathcal{P}$. The predicate is specified as:

$$ \mathsf {deg}(A,\varDelta ,M) = \bigwedge _{1\le i,j\le n} \left( M_{i,j} = \sum _{k=1}^n A_{i,k} \wedge L_{j, k} \right) ~\wedge ~ \mathsf {lex}(\varDelta ,M) $$

The predicate $refine (\varDelta ,A,\varDelta ')$ : This predicate states that $\varDelta '$ is a refinement of the partitioning $\varDelta$ of graph A obtained from a single iteration of partition refinement. The matrix M represents structural information of the vertices with respect to the partitioning $\varDelta$. Vertices are distinguished in the refinement $\varDelta '$: either because they were already distinguished in $\varDelta$, or else because they are distinguished by the corresponding structural information in M.

$$\begin{aligned} \begin{array}{rl} refine (\varDelta , A, \varDelta ')&= \left( \begin{array}{l} \exists M.~ \mathsf {deg}(A,\varDelta ,M) \wedge \displaystyle \bigwedge _{1 \le i < n} (\varDelta '_i \leftrightarrow \varDelta _i \vee M_i \succ _{lex} M_{i+1}) \end{array}\right) \end{array} \end{aligned}$$

The encoding of predicate $\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}$ is polynomial in the number of both clauses and variables. The dominating component of $refine$ is $\mathsf {deg}$, which introduces $O{(|V|^2)}$ order-encoded integer variables whose definitions are sums of Booleans, which have standard polynomial-size encodings (e.g. [13]).

Table 1. Enumerating graphs using $\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}$. Column “sat” is Clasp solving time (sec).

Table 1 illustrates the impact of structural information when breaking symmetries and enumerating the graphs obtained with n vertices. The column headed by $|\mathcal {G}_n^\approx |$ indicates the number of non-isomorphic graphs with n vertices. These numbers correspond to sequence A000088 of the OEIS [19]. The next columns, in groups of 4, are headed by $\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}$ for $0\le k\le 2$. Each such foursome details the size of the SAT encoding (number of clauses and variables), sat solving time (for all solutions in seconds), and the number of solutions found. When $k=0$ there is no structural information and the encoding corresponds to the one introduced in [18]. When $k=1$, the nodes of the graph are partitioned according to degree information. When $k>0$, the symmetry breaks are more refined than the one introduced in [18]. Notice that as we add structural information in the encoding (as k increases), the number of graphs decreases. For example, when $n=10$, using $k=0$ there are circa 184 million solutions, when $k=1$, circa 16 million, and $k=2$, circa 12 million (close to the true number $|\mathcal {G}_{10}^\approx |$). Note that as we add structural information, the cost of the solving time increases considerably. In the following we will show how to counter this increase.

Table 2 summarizes an application of symmetry breaking with the first phase of nauty to search for all TM graphs (modulo 2,3) (see Example 4). The columns, in groups of 4, are headed by $\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}$ for $0\le k\le 3$. Each such foursome details the size of the SAT encoding (number of clauses and variables), sat solving time in seconds unless indicated otherwise, and the number of solutions generated. The table illustrates the high cost of the nauty encoding: we can solve up to $n=9$, and then only for $k=1$. We will come back to resolve this problem below by decomposing the instances to consider given nauty partitionings.

Table 2. TM (modulo 2,3) graphs using $\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}$ (48 h timeout using Clasp).

3.2 Encoding the Second Phase of Nauty

We present a symmetry break predicate, $\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_2}$, which eliminates isomorphic graphs that have not been ruled out by the first phase predicate, $\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}$. In the second phase of nauty, the graph G is given, and so is the partitioning $\mathcal{P}$, from its first phase computation. In our case, we seek a predicate that states that an unknown graph, G, is canonical. The search strategy applied in nauty is not easily modeled as a propositional formula when G is unknown and so we introduce an alternative approach, assuming that the partitioning $\mathcal{P}$, from the first phase, is given. As a starting point, consider $\mathsf {clex}(A,\mathcal{P})$ given as Eq. (7). This predicate provides a complete symmetry break when combined with $\sigma _{\textsf {nauty}}^{\textsf {phase}_1}$. However, its implementation is inefficient as the encoding must consider each of the permutations in $S_n$ which preserve $\mathcal{P}$, and their number may be huge.

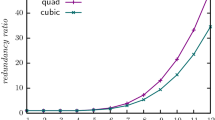
In [12] the authors show that complete symmetry breaks for graph isomorphism with n vertices can be obtained using only a small fraction of the required n! permutations. For example, [12] reports that a complete symmetry break for $n=10$ vertices involves only 7853 permutations whereas the complete symmetry break $\sigma _{\mathsf {clex}}(A)$ introduced as Eq. (6) in Example 5 involves $10!=3{,}628{,}800$ permutations. In this paper we enhance the approach of [12] to consider partitionings expressed by encodings of the first stage of the nauty algorithm.

A common approach for improving performance of combinatorial existence checking is decomposition: splitting the problem into a manageable set of disjoint subproblems, each of which can (ideally) be solved more easily. We can decompose a graph search problem with respect to the partitioning inferred by $\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}$. This results in a decomposition to $2^{n-1}$ subproblems, one for each partitioning.

To compute a concise and complete symmetry break for a partitioning $\mathcal{P}$ corresponding to the first phase $\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}$ we apply the same approach as advocated in [12], but restricted to break symmetries on graphs which have the structural information $\mathcal{P}$ after k iterations of the nauty first phase algorithm. This computation is performed by application of Algorithm 2 where we denote: (a) $S_n^\mathcal{P}$ the set of permutations that preserve a partitioning $\mathcal{P}$, and (b) for $\varPi \subseteq S_n$, $\min _\varPi (G) = \bigwedge \left\{ ~G \preceq \pi (G) \left| \begin{array}{l}\pi \in \varPi \end{array} \right. \right\}$.

For a given partitioning $\mathcal{P}$ and value k, Algorithm 2 starts with an empty set of permutations $\varPi$ and iterates adding permutations as long as the condition in Line 3 holds. The condition seeks a pair $(G,\pi )$ such that $\pi (G)\preceq G$, where $G\in sol(\sigma _{\textsf {nauty}(k)}^{\textsf {phase}_1}(A,\mathcal{P}))$ and $\pi$ preserves $\mathcal{P}$. Such a graph violates $\mathsf {clex}(\mathcal{P},G)$ and hence $\pi$ is added to $\varPi$. The implementation performs this check by invoking a SAT solver, the same as in [12].

We say that $\varPi$ is redundant if there exists $\pi$ such that for all G, $\min _\varPi (G) \leftrightarrow \min _{\varPi \setminus \{\pi \}}(G)$. The set computed by the while-loop at Line 3 may be non-minimal, as an existing permutation may become redundant in view of permutations added later. Thus the algorithm then iterates to remove redundant permutations applying the for-loop at Line 5.

Table 3 is about computing the permutations to make the nauty partitionings complete (phase2). For each n (number of vertices), we indicate (“parts”) the number of partitions. We detail separately the cost of computing the permutations for the regular partitioning (“regular part”) where degree-based structural information has no impact. These have the most permutations and are the most costly to compute. Then for $\sigma _{\textsf {nauty}(1)}$, $\sigma _{\textsf {nauty}(2)}$ and $\sigma _{\textsf {nauty}(3)}$ we detail the number of permutations and the time to compute them using Algorithm 2. For the number of permutations we detail x / y where x is the largest number of permutations computed for a single partitioning, and y is the total number. For the time we detail x / y where x is the longest time to compute for a single partitioning and y is the total time.

Notice how the required number of permutations decreases as structural information is added (k increases). For $n=10$ we have 8608 permutations with $k=1$, 3703 with $k=2$, and 1497 when $k=3$. Recall that without structural information 7853 permutations were required [12], and computation beyond 10 vertices was not possible. Moreover note that because of the decomposition to partitionings we require no more than 37 permutations to break all symmetries on 10 vertices given a partitioning derived from $\sigma _{\textsf {nauty}(3)}^{\textsf {phase}_1}$. The permutations computed here provide complete symmetry breaks for any graph search problem with up to 12 vertices.

Table 3. Canonizing sets per partitioning. Time in seconds except under the line (for $n=11,12$) where in hours. Timeout is 48 h using Glucose.

A first attempt to enumerate all TM graphs modulo 2,3 using the complete symmetry breaks $\sigma _{\textsf {nauty}(k)}$ per partitioning failed. The instances are simply too hard. To this end, we took a second approach where the encoding for each partitioning was enhanced with additional information on the degree sequences of solutions. Namely, the implementation considers for each partition all possible relevant degree sequences and solve each instance separately.

Table 4 summarizes the results. For each n we detail the results obtained using the complete symmetry breaks of [12] denoted by $\sigma _{clex}^*$ (these symmetry breaks are equivalent to $\sigma _{clex}(A)$ but are much compact), and then the results for $\sigma _{\textsf {nauty}(k)}$ with $k=1,2$. Here we detail the total number of instances (on all partitionings). For time we detail x / y where x is the time for the hardest instance and y is the total time. The number of solutions is the same as this is, in all three cases, the number of canonical solutions.

Table 4. Enumerating TM (modulo 2,3) graphs using $\sigma _{\textsf {nauty}(k)}$ complete symmetry breaks. Time in seconds except under the line (for $n=9,10$) where in hours. Column 1 computed with Clasp, column 2,3 computed with Glucose. (120 h timeout).

4 Conclusion

This paper presents polynomial-size static symmetry breaking predicates which encode structural properties in the same way that nauty exploits information when it maps graphs to their canonical representations. These structural breaks apply to strengthen existing incomplete symmetry-breaking predicates, and can be extended into complete symmetry breaks. These structural properties also yield a natural strategy for problem decomposition. We have described a SAT encoding for the structural symmetry-breaking predicates, and applied these to compute compact, complete symmetry breaks for graphs of up to 12 vertices. We also demonstrated the effectiveness of these structural techniques in accelerating the enumeration of TM graphs modulo 2, 3. Ongoing work focuses on an encoding that exploits on richer structural properties than the current focus on vertex degree. As described in [17], this is expected to improve the situation when breaking symmetries on regular graphs. We also plan to apply the same technique to compute sets of permutations with which to break symmetries for a given graph search problem. We expect to then be able to apply the technique for larger instances than those we can do now.