1 Introduction

In this paper we describe a limited memory quasi Newton (QN) algorithm for solving large nonlinear optimization problems. We write this problem as

$$\begin{aligned} \mathrm{min}\, f(x), \end{aligned}$$

where \(f:\mathbb {R}^n\rightarrow \mathbb {R}\) is a nonlinear and twice continuously differentiable function and the number of variables n is assumed to be large.

Problems with the size of thousands can be solved efficiently, only if the storage and computational cost of the optimization algorithm can be kept at a tolerable level. Among the methods for solving these problems are inexact Newton methods, sparse elimination techniques, limited memory QN methods and conjugate gradient methods [5]. In this paper the focus is directed toward the limited memory quasi-Newton methods.

The limited memory QN methods continuously refresh the correction set of small m positive integer vector pairs by removing and adding information at each iteration. The resulting vector pairs contain curvature information from only the \(m\) most recent iterations to construct Hessian approximation, so that the main properties of QN updates are maintained. These methods are robust, inexpensive and easy to implement and due to the low storage demand, they are suitable for large problems, see [5].

To improve the efficiency properties of the limited memory algorithm, one needs to achieve more accurate Hessian approximation at lower cost in computation and storage. As regards, the main contribution of this paper is to use a fourth order tensor model to derive a QN equation which enables us to modify the limited memory BFGS method.

In the following section, we describe derivation of the modified secant equation. The global and local convergence result of the modified limited memory BFGS method is presented in Sect. 3. In Sect. 4, we will describe the detailed algorithm of modified limited memory BFGS, Algorithm 2, based upon two loop recursive procedure. In Sect. 5, we compare the Dolan and Moré [2] performance profile of the new algorithm with LBFGS by Liu and Nocedal [4]. The conclusion is finally outlined in Sect. 6.

2 Derivation of modified secant equation

In this section we derive a more efficient QN equation by taking the forth order tensor model into account. The general idea can be delineated as follows: Recall that the ordinary QN method generates a sequence \(\{x_k\},\) at iterate \(k\), by

$$\begin{aligned} x_k=x_{k-1}-\alpha _{k-1}H_{k-1}g_{k-1}, \end{aligned}$$

where \(\alpha _{k-1}\) is the stepsize, \(g_{k-1}\) denotes the gradient of \(f\) at \(x_{k-1}\), and \(H_{k-1}\) is updated at every iteration to obtain \(H_k\) that satisfies the secant equation

$$\begin{aligned} H_k y_{k-1} = s_{k-1}, \end{aligned}$$
(1)

in which \(s_{k-1}=x_k-x_{k-1}\) and \(y_{k-1}=g_k-g_{k-1}\). Based on the fourth order tensor model, provided that \(s^{T}_{k-1}y_{k-1}\ne 0\), the secant equation can be modified in the following form

$$\begin{aligned} {H_k{\widetilde{y}}_{k-1}} = s_{k-1}, {{\widetilde{y}}_{k-1}}=\left( 1+\frac{\phi _{k-1}}{s^{T}_{k-1}y_{k-1}}\right) y_{k-1}, \end{aligned}$$
(2)

where \(\phi _{k-1}=4(f_{k-1}-f_{k}) + 2{(g_k+g_{k-1})}^T s_{k-1}.\) Furthermore, it is proved that if \(f\) is smooth enough, and \(\Vert s_{k-1}\Vert \) is sufficiently small, then

$$\begin{aligned} s^{T}_{k-1}G_ks_{k-1}-s^{T}_{k-1}{\widetilde{y}}_{k-1}=\frac{1}{6}s^{T}_{k-1}(T_k s_{k-1})s_{k-1}+O({\Vert s_{k-1}\Vert }^5), \end{aligned}$$
(3)

where \({T}_{k}\) is three-dimensional tensor of \(f\) at \(x_k\).

We produce the steps, that lead to a new modified secant equation as below: consider the fourth-order tensor model of the objective function about the iterate \(x_k\):

$$\begin{aligned} f(x_k+s)=f_k+g_k. s+\frac{1}{2}G_k. s^2+\frac{1}{6}T_k. s^3+\frac{1}{24}V_k. s^4+O({\Vert s\Vert }^5), \end{aligned}$$
(4)

where \({V}_{k}\) is a four-dimensional tensor of \(f\) at \(x_k\), see [6]. Substituting \(s = -s_{k-1}\) into (4), it follows that

$$\begin{aligned} f_{k-1} = f_k-g_k. s_{k-1}+\frac{1}{2}G_k. s^{2}_{k-1}-\frac{1}{6}T_k. s^{3}_{k-1}+\frac{1}{24}V_k. s^{4}_{k-1}+O({\Vert s_{k-1}\Vert }^5). \end{aligned}$$
(5)

Differentiate (4) at \(s = s_{k-1}\), and multiply both sides of the outcome by \(-s_{k-1}\), yields

$$\begin{aligned} g_{k-1}. s_{k-1}=g_k. s_{k-1}-G_k. s^{2}_{k-1}+ \frac{1}{2} T_k. s^{3}_{k-1}-\frac{1}{6}V_k. s^{4}_{k-1}+O({\Vert s_{k-1}\Vert }^5). \end{aligned}$$
(6)

After multiplying (5) by 4, and adding (6), the terms involving the tensor \(V_k\) is eliminated, and we get

$$\begin{aligned} s^{T}_{k-1}G_k s_{k-1}=y^{T}_{k-1}s_{k-1}+\phi _{k-1} +\frac{1}{6}s^{T}_{k-1}(T_k s_{k-1})s_{k-1}+O({\Vert s_{k-1}\Vert }^5). \end{aligned}$$
(7)

This ensures that with respect to the expression (2), the last relation is equivalent to (3). On the other direction, it can be readily seen that

$$\begin{aligned} s^{T}_{k-1}G_k s_{k-1}=s^{T}_{k-1}y_{k-1}+\phi _{k-1} +O({\Vert s_{k-1}\Vert }^3). \end{aligned}$$

This result suggests that the curvature \(s^{T}_{k-1}\widetilde{y}_{k-1}\) captures the second order curvature \(s^{T}_{k-1}G_k s_{k-1}\) with a higher precision (lower error). This high precision can be achieved with essentially no additional computational effort.

The modified \(QN\) Eq. (2) leads us to modify the inverse BFGS update formula, namely MBFGS update, as follows

$$\begin{aligned} H_k&= \left( I-\frac{s_{k-1}\widetilde{y}^{T}_{k-1}}{\widetilde{y}^{T}_{k-1}s_{k-1}}\right) H_{k-1} \left( I-\frac{\widetilde{y}_{k-1}s^{T}_{k-1}}{\widetilde{y}^{T}_{k-1}s_{k-1}}\right) +\frac{s_{k-1}s^{T}_{k-1}}{\widetilde{y}^{T}_{k-1}s_{k-1}} \nonumber \\&= V^{T}_{k-1}H_{k-1}V_{k-1}+\frac{\rho _{k-1}}{\beta _{k-1}}s_{k-1}s^{T}_{k-1}, \end{aligned}$$
(8)

where \(\rho _{k-1}=1/y^{T}_{k-1}s_{k-1}\), \(\beta _{k-1}=1+{\phi _{k-1}}\rho _{k-1}\) and \(V_{k-1}=I-\rho _{k-1}y_{k-1}s^{T}_{k-1}.\)

Formula (8) maintains the positive definiteness of \(H_k\) if

$$\begin{aligned} s^T_{k-1} y_{k-1}>0 \qquad \mathrm{and} \qquad s^T_{k-1} \widetilde{ y}_{k-1}>0. \end{aligned}$$

The left hand side inequality is guaranteed, since the steplength \(\alpha _{k-1}\) is computed such that the following Wolfe conditions hold:

$$\begin{aligned} f(x_{k-1}+\alpha _{k-1}p_{k-1})&\le f(x_{k-1})+c_1\alpha _{k-1}g^{T}_{k-1}p_{k-1},\end{aligned}$$
(9)
$$\begin{aligned} g^T(x_{k-1}+\alpha _{k-1}p_{k-1}) p_{k-1}&\ge c_2 g^{T}_{k-1}p_{k-1}, \end{aligned}$$
(10)

where \(p_{k-1}= - H_{k-1}g_{k-1}\) is the QN search direction, and \(c_1 \in (0, 1)\,\, \mathrm{and} \,\, c_2 \in (c_1, 1)\) are some constants. Hence to assure \(s^T_{k-1} \widetilde{ y}_{k-1}>0\), it is enough in the expression of \(\widetilde{y}_{k-1}\) defined by (2), \(\phi _{k-1}\) is replaced by

$$\begin{aligned} \phi _{k-1}=(\eta -1)s^{T}_{k-1}y_{k-1} \quad \mathrm{if}\quad \phi _{k-1}< (\eta -1)s^{T}_{k-1}y_{k-1}, \end{aligned}$$
(11)

where \(\eta \in (0,1)\), as suggested by Zhang and Xu [7]. This replacement yields the following inequalities

$$\begin{aligned} \phi _{k-1}&\ge (\eta -1)s^{T}_{k-1}y_{k-1};\\ \beta _{k-1}&\ge \eta ;\\ s^{T}_{k-1}\widetilde{y}_{k-1}&\ge \eta s^{T}_{k-1}y_{k-1}. \end{aligned}$$

These relations are needed in the next section.

3 Convergence property

In this section, the global and local convergence properties of the modified limited memory BFGS algorithm are studied. Technically, the modified LBFGS matrix \({H}_k\) is obtained by updating a bounded matrix, \(m\) times, using the MBFGS formula. For the purposes of our analysis, we shall use the direct update \({B}_k = H_k^{-1}\), which is the modified Hessian approximation to the objective function, associated with the modified Eq. (8).

figure a

For the purposes of this section, we make the following assumptions on the objective function.

Assumption 1

  1. (a)

    \(\varOmega = \{x\in \mathbb {R}^n : f(x) \le f(x_0) \}\) is a convex set.

  2. (b)

    \(f\) is twice continuously differentiable.

  3. (c)

    \(f\) is uniformly convex function, i.e. there exist positive constants \(M_1\) and \(M_2\) such that

    $$\begin{aligned} M_1 \Vert z\Vert ^2 \le z^T G(x) z \le M_2 \Vert z\Vert ^2, \end{aligned}$$
    (13)

    for all \(z \in \mathbb {R}^n\) and all \(x \in \varOmega .\)

In the sequal we show that the new algorithm is globally convergent, and its convergence rate is \(R\)-linear. The proof of Theorem 1 is an extension to that of [4].

Theorem 1

Let \(x_0\) be a starting point, for which \(f\) satisfies Assumptions 1, and suppose matrices \(B^{(0)}_k\) are symmetric positive definite initial matrices, for which \(\{\Vert B^{(0)}_k\Vert \}\) and \(\{\Vert {B^{(0)}_k}^{-1}\Vert \}\) are bounded. Then, the sequence \(\{x_k\}\) generated by Algorithm 1 converges to the unique \(x^*\) on \(\varOmega \), and the convergence rate is \(R\)-linear, that is, there is a constant \(0\le r <1\), such that

$$\begin{aligned} f(x_k)-f(x^*)\le r^k(f(x_0)-f(x^*)). \end{aligned}$$
(14)

Proof

Using the definition of \({\bar{G}}_{k-1} = \int ^1_0 G(x_{k-1} + \tau s_{k-1}) d\tau \), we have

$$\begin{aligned} y_{k-1} = {\bar{G}}_{k-1}s_{k-1}. \end{aligned}$$
(15)

Then Eqs. (13) and (15) give

$$\begin{aligned} M_1 \Vert s_{k-1}\Vert ^2 \le y^T_{k-1} s_{k-1} \le M_2 \Vert s_{k-1}\Vert ^2, \end{aligned}$$
(16)

and

$$\begin{aligned} \frac{\Vert y_{k-1}\Vert ^2}{y^T_{k-1}s_{k-1}} = \frac{s^T_{k-1} {\bar{G}}^2_{k-1} s_{k-1}}{s^T_{k-1} {\bar{G}}_{k-1} s_{k-1}} \le M_2. \end{aligned}$$
(17)

Moreover, because of the second order Taylor expansion, we have

$$\begin{aligned} |\phi _{k-1}|&= |4(f(x_{k-1}) - f(x_k)) + 2(g_{k-1}+g_k)^{T} s_{k-1}| \nonumber \\&\le 2| s^{T}_{k-1} G(x_{k-1}+ts_{k-1})s_{k-1} + (g_{k}-g_{k-1})^{T} s_{k-1}|. \end{aligned}$$
(18)

Now, from (18), (16) and (13), we obtain

$$\begin{aligned} |\phi _{k-1}| \le 4M_2\Vert s_{k-1}\Vert ^2. \end{aligned}$$
(19)

Since the strategy (11) implies \(\phi _{k-1}\ge (\eta -1)s^{T}_{k-1}y_{k-1} \), from (16) and inequality (19), we have

$$\begin{aligned} \eta \le |\beta _{k-1}| = \left| 1+\frac{\phi _{k-1}}{s^{T}_{k-1}y_{k-1}}\right| \le 1+\frac{4M_2}{M_1}. \end{aligned}$$
(20)

Subsequently, let \({B}^{(0)}_{k} = ({H}^{(0)}_{k})^{-1}\), and using the arguments in [5], the following inequality holds.

$$\begin{aligned} trace\left( {B}^{(j)}_{k-1}\right) \le trace\left( {B}^{(j-1)}_{k-1}\right) + \left( 1 + \frac{4M_2}{M_1}\right) M_2, \qquad j=1,2,\cdots ,m. \end{aligned}$$

Since \({B}^{(0)}_{k-1} \) is bounded, we obtain

$$\begin{aligned} trace({B}_{k}) = trace\left( {B}^{(m)}_{k-1}\right) \le {trace\left( {B}^{(0)}_{k-1}\right) } + m\left( 1+\frac{4M_2}{M_1}\right) M_2 \le M_3, \end{aligned}$$
(21)

for some positive constant \(M_3\). Analogically, we can also have a simple expression for the determinant as well, see [4].

$$\begin{aligned} det({B}_{k})&= det({B}^{(m)}_{k-1}) = det({B}^{(0)}_{k-1}) \displaystyle \prod ^{m}_{l=1}\frac{\widetilde{y}^{T}_{l}s_l}{s^{T}_{l}{B}^{(l)}_{k-1}s_l}\\&= det({B}^{(0)}_{k-1})\displaystyle \prod ^{m}_{l=1}\frac{\widetilde{y}^{T}_{l}s_l}{s^{T}_{l}s_{l}} \frac{s^{T}_{l}s_{l}}{s^{T}_{l}{B}^{(l)}_{k-1}s_l}\\&= det({B}^{(0)}_{k-1}) \displaystyle \prod ^{m}_{l=1}\beta _l\frac{y^{T}_{l}s_l}{s^{T}_{l}s_{l}}\frac{s^{T}_{l}s_{l}}{s^{T}_{l}{B}^{(l)}_{k-1}s_l}. \end{aligned}$$

Since by (21), the largest eigenvalue of \({B}^{(l)}_{k-1}\) is also less than \(M_3\), using the left hand side of (16), the boundedness of \(\Vert ({B}^{(0)}_{k-1})^{-1}\Vert \), and inequality (20), we have

$$\begin{aligned} det({B}_{k}) \ge det\left( {B}^{(0)}_{k-1}\right) \left| \prod ^{m}_{l=1}\beta _l\right| \left( \frac{M_1}{M_3}\right) ^m \ge M_4, \end{aligned}$$
(22)

for some positive constant \(M_4\).

Hence, by (21) and (22), there is a constant \(\delta > 0\) such that

$$\begin{aligned} \cos \theta _{k-1} = \frac{s^{T}_{k-1}{B}_{k-1}s_{k-1}}{\Vert s_{k-1}\Vert \Vert {B}_{k-1}s_{k-1}\Vert } \ge \delta . \end{aligned}$$
(23)

Moreover, the Wolfe conditions (9, 10) and Zoutendijk [6] theorem imply that

$$\begin{aligned} \sum _{k=1}^\infty \cos ^2 \theta _{k-1}\Vert g_{k-1}\Vert ^2 < \infty . \end{aligned}$$
(24)

Since \(\cos \theta _{k-1}\) is bounded away from zero for all \(k \ge 1\), then the sequence \(\{x_k\}\) converges to \(x^*\) in the sense that

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert g_{k-1}\Vert = 0. \end{aligned}$$
(25)

Now, because of the Wolfe conditions (9) and (10), and Assumptions 1, it can be shown (see [4] for details) that there is a constant \(c>0\), in which

$$\begin{aligned} f(x_k)-f(x^*)\le (1-c \cos ^2 \theta _{k-1})(f(x_{k-1})-f(x^*)). \end{aligned}$$
(26)

Applying (23) to the last inequality, gives rise to the conclusion (14).

Moreover, using (13) and Taylor expansion we have

$$\begin{aligned} \frac{1}{2} M_1 \Vert x_k - x_*\Vert ^2 \le f(x_k)-f(x^*), \end{aligned}$$
(27)

which together with (14) gives \(\Vert x_k - x_*\Vert \le r^{k/2}[2(f(x_0)-f(x^*)/M_1]^{1/2}\), implying that the convergence rate is \(R\)-linear.

4 The algorithm

In this section, we give a description of our ”Modified Limited memory BFGS ”, (MLBFGS) method. It is well known that the ordinary limited memory BFGS, (LBFGS) method, proposed by Liu and Nocedal [4], is adopted from the BFGS method to solve large scale problems. Very often, the QN methods can employ a scaled identity as an initial approximation to speed up the convergence. For this purpose, Liu and Nocedal [4] suggested the use of \(H^{(0)}_{k-1}=\gamma _{k-1} I\), where \(\gamma _{k-1} =y^T_{k-1}s_{k-1}/\Vert y_{k-1}\Vert ^2\). To explain the strategy of the limited memory BFGS method, we first assume that \(m\) is a given small positive integer. The LBFGS method keeps the \(m\) most recent correction pairs, \(\{s_i,y_i\}^{k-2}_{i=k-m-1}\), to update \(m\) times, the matrix \(H^{(0)}_{k-1}\), and computes the product \(H_{k-1} g_{k-1}\) efficiently via performing two-loop recursion procedure, see [4, 5]. To modify ordinary limited memory BFGS method, we require to redefine \(y_i\) via multiplying it by \(\beta _i\) for \(i = k-m-1, \, \ldots , \,{k-2}\). Therefore, our two loop recursion procedure of the MLBFGS method, for computing the product \(H_{k-1} g_{k-1}\), is given as follows:

figure b

5 Numerical experiments

This section evaluates the performance of the MLBFGS algorithm in comparison with the standard LBFGS algorithm of Liu and Nocedal [4]. Both codes are written in Fortran 77 in double precision. A line search routine is used based on the quadratic and cubic interpolations that satisfies the strong Wolfe conditions (9) and

$$\begin{aligned} |g^T(x_{k-1}+\alpha _{k-1}p_{k-1}) p_{k-1}|&\le c_2|g^{T}_{k-1}p_{k-1}|, \end{aligned}$$
(28)

with \(c_1=.01\) and \(c_2=.9\), see for example Fletcher [3].

we considered fifty large-scale unconstrained optimization test problems with the standard starting points selected from [1]. For each test problem, ten numerical experiments with dimension ranging from 1000 to 50,000 were performed. Extensive numerical testing of the methods are carried out by selecting three values for \(m\), i.e. 3, 5 and 7. As compared with the results of these values of m in the two limited memory BFGS algorithms, it is observed that the choice of the parameter m=5 gives the best result. To maintain positive definiteness of the curvature approximation, strategy (11) is employed whitin MLBFGS algorithm with \(\eta =10^{-4}\). All runs were terminated when

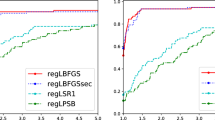
$$\begin{aligned} \Vert g_k\Vert \le 10^{-5} \mathrm{max}\{1,\Vert x_k\Vert \}. \end{aligned}$$

In the numerical comparisons we selected to use the performance profiles of Dolan and Moré [2] to present the results of the numerical experiments. The performance profiles correspond to the number of function–gradient evaluations metric. It is observed from Fig. 1 that the MLBFGS is always the top performer for all values of \(\tau \).

Fig. 1
figure 1

performance profiles based on function and gradient evaluations

Full size image

We observe that the amount of additional storage and arithmetics of MLBFGS algorithm are insignificant in comparison with those of the LBFGS method. The numerical result obtained reveals that a higher order accuracy in approximating the inverse Hessian matrix of the objective function takes place for the modified LBFGS method which enables it to outperforms the ordonary LBFGS method.

6 Conclusion

In this paper, we have explored a fourth order tensor model of the objective function to modify QN equation with the aim of attaining more accurate Hessian estimate. This enables us to design a more effective limited memory BFGS method to solve large-scale function minimization.

The major advantages of proposed algorithm are that it preserves the convergence properties of the LBFGS method, while allowing to obtain an overall computational saving, and it can be built very inexpensively.

Our experiments in the frame of LBFGS algorithm, showed that the MLBFGS is superior to the LBFGS algorithm.