A regularized limited memory BFGS method for large-scale unconstrained optimization and its efficient implementations

Abstract

The limited memory BFGS (L-BFGS) method is one of the popular methods for solving large-scale unconstrained optimization. Since the standard L-BFGS method uses a line search to guarantee its global convergence, it sometimes requires a large number of function evaluations. To overcome the difficulty, we propose a new L-BFGS with a certain regularization technique. We show its global convergence under the usual assumptions. In order to make the method more robust and efficient, we also extend it with several techniques such as the nonmonotone technique and simultaneous use of the Wolfe line search. Finally, we present some numerical results for test problems in CUTEst, which show that the proposed method is robust in terms of solving more problems.

1 Introduction

In this paper we consider the large-scale unconstrained optimization problem:

$$ \mathop {{\text{minimize}}}\limits_{{x \in \mathbb{R}^{n} }} f(x),{\text{ }} $$

(1.1)

where $f: \mathbb {R}^n \rightarrow \mathbb {R}$ is a smooth function. For solving it, we focus on the quasi-Newton type method as

$$\begin{aligned} x_{k+1}=x_k + d_k, \end{aligned}$$

where $x_k \in \mathbb {R}^n$ is the $k^{th}$ iteration and $d_k \in \mathbb {R}^n$ denotes a search direction obtained by a certain quasi-Newton method.

The standard solution methods to solve (1.1) such as the steepest descent method, the Newton’s method and the BFGS method [6, 13] are not suitable for the large-scale problems. This is because the steepest descent method generally converges slowly, while Newton’s method needs to compute the Hessian matrix and solve linear equations at each iteration. Moreover, the BFGS method requires $O(n^2)$ memory to store and calculate the approximate Hessian of f, which causes some difficulty for large-scale problems.

One of the popular quasi-Newton methods for solving large-scale problem is the limited memory BFGS(L-BFGS) [10, 12], which uses small memory to store an approximate Hessian of f. The L-BFGS method stores the last m vector pairs of $(s_{k-i},y_{k-i}),$ $i=0,1, \ldots ,m-1,$ to compute a search direction $d_k$, where

$$\begin{aligned} s_k =&\ x_{k+1}-x_{k}, \text {\ and \ } y_k = \nabla f(x_{k+1})-\nabla f(x_{k}), \end{aligned}$$

and computes $d_k$ in O(mn) time.

The usual L-BFGS adopts the Wolfe line search to guarantee its global convergence. The line search sometimes needs a large number of function evaluations. Thus, it is preferable to reduce the number of function evaluations as much as possible.

The trust region method (TR-method) can guarantee global convergence. It is known that the TR-method needs fewer function evaluations than the line search [3, 4, 11]. The L-BFGS method combined with the TR-method [3, 4] produces good performance for many benchmark problems in terms of the number of function evaluations. However, the TR-method must solve the constrained subproblem

$$\begin{aligned}&\text {minimize} \quad f(x_k) + \nabla f(x_k)^T d + \frac{1}{2} d^T B_k d \\&\text {subject to} \quad \Vert d\Vert \le \varDelta _k, \nonumber \end{aligned}$$

(1.2)

in each step, where $\varDelta _k$ is the trust-region radius and $B_k$ is an approximate Hessian obtained by L-BFGS. It takes a considerable amount of time to solve (1.2).

We note that Burakov et al. [2] proposed to combine limited-memory and trust region techniques. Their methods uses the eigenvalue decomposition of $B_k$ to solve the TR-subproblem, and produces competetive performance with the line search versions of the L-BFGS in terms of function evaluations.

To overcome the difficulty we consider adopting a regularization technique instead of the TR-method. This is motivated by the regularized Newton method proposed by Ueda and Yamashita [23,24,25]. The method computes a search direction $d_k$ as a solution of the following linear equations:

$$\begin{aligned} (\nabla ^2f(x_k)+ \mu _k I) d= -\nabla f(x_k), \end{aligned}$$

(1.3)

where $\mu _k>0$ is called a regularized parameter. If $B_k=\nabla ^2 f(x_k)$ and $\mu _k$ coincides with the value of the optimal Lagrange multiplier at a solution of problem (1.2), then $d_k$ is a solution of (1.2). Note that the linear equations (1.3) are simpler than subproblem (1.2) of the TR-method. The regularized Newton method [23] controls the parameter $\mu _k$ instead of computing the step length to guarantee global convergence. However, since the regularized Newton method in [23] is based on the Newton’s method, it must compute the Hessian matrix of f.

In this paper, we propose a novel approach that combines the L-BFGS method with the regularization technique instead of regularized Newton technique (1.3). We call the proposed method regularized L-BFGS method. One of the natural ways to implement the idea is to use a solution of the following equations as a search direction,

$$\begin{aligned} (B_k + \mu I) d = -\nabla f(x_k), \end{aligned}$$

(1.4)

where $B_k$ is an approximate Hessian given by a certain quasi-Newton method. However when $B_k$ is calculated by the L-BFGS method, it is difficult to compute¹$(B_k+\mu I)^{-1}$. Therefore, we try to directly construct $(B_k+\mu I)^{-1}$ by the L-BFGS method for $f(x)+\mu \Vert x\Vert ^2$, that is we use $(s_k,\hat{y}_k(\mu ))$, where $\hat{y}_k(\mu ) = y_k + \mu s_k$, instead of $(s_k,y_k)$. Note that the term $\mu s_k$ in $\hat{y}_k(\mu )$ plays the role of regularization. Then, the search direction $d_k$ can be computed in O(mn) time like the conventional L-BFGS method. For global convergence, we also control the regularized parameter $\mu _k$ in a way similar to the regularized Newton method [23]. We then show that the proposed algorithm ensures global convergence.

A drawback of the proposed method is that a step $d_k$ sometimes becomes small, and it causes a large number of iterations. To get a longer step, we propose two techniques: a nonmonotone technique and simultaneous use of the Wolfe line search. Recall that the step length given by the Wolfe condition is allowed to be larger than 1, and hence the step can explore a larger area. Thus, if $f(x_k+\alpha d_k)<f(x_k+d_k)$ for $\alpha >1$, it would be reasonable to find $\alpha$ via the Wolfe line search. We note that the current paper is an enhancement of the unpublished paper [20] that does not exploit the line search. Due to simultaneous use of line search the proposed method becomes more robust than that of [20], which we report in Sect. 5.

The paper is organized as follows. The regularized L-BFGS is presented in Sect. 2, and its global convergence is shown in Sect. 3. In Sect. 4 we discuss some implementation issues, such as simultaneous use of RL-BFGS and a nonmonotone technique. In Sect. 5, we present numerical results by comparing four algorithms: the standard L-BFGS, the existing regularized L-BFGS-type method [22], the regularized L-BFGS, and the regularized L-BFGS with simultaneous use of line search. Section 6 concludes the paper.

Throughout the paper, we use the following notations. For a vector $x \in \mathbb {R}^n$, $\Vert x\Vert$ denotes the Euclidean norm defined by $\Vert x\Vert := \sqrt{x^Tx}$. For a symmetric matrix $M \in \mathbb {R}^{n\times n}$, we denote the maximum and minimum eigenvalues of M as $\lambda _{\max }(M)$ and $\lambda _{\min }(M)$. Moreover, $\Vert M\Vert$ denotes the $l_2$ norm of M defined by $\Vert M\Vert := \sqrt{\lambda _{\max }(M^TM)}$. If M is a symmetric positive-semidefinite matrix, then $\Vert M\Vert = \lambda _{\max }(M)$.

Next, we give a definition of Lipschitz continuity.

Definition 1

(Lipschitz continuity) Let S be a subset of $\mathbb {R}^n$ and $f: S \rightarrow \mathbb {R}$.

• (i) The function f is said to be Lipschitz continuous on S if there exists a positive constant $L_f$ such that

  $$\begin{aligned} |f(x) - f(y)| \le L_f \Vert x- y \Vert \ \forall x,y \in S. \end{aligned}$$

• (ii) Suppose that the function f is differentiable. $\nabla f$ is said to be Lipschitz continuous on S if there exists a positive constant $L_g$ such that

  $$\begin{aligned} \Vert \nabla f(x) - \nabla f(y)\Vert \le L_g \Vert x-y\Vert \ \forall x,y \in S. \end{aligned}$$

2 The regularized L-BFGS method

In this section, we propose a regularized L-BFGS method that controls the regularized parameter at each iteration. In the following, $x_k$ denotes the k-th iterative point, $B_k$ denotes the approximate Hessian of $f(x_k)$, and $H_k^{-1} = B_k$.

We consider combining the L-BFGS method with the regularized Newton method (1.3). For this purpose, we may replace the Hessian $\nabla ^2 f(x_k)$ in Eq. (1.3) with the approximate Hessian $B_k$, that is, we define a search direction $d_k$ as a solution of

$$\begin{aligned} (B_k+ \mu I)^{-1}d_k = -\nabla f(x_k) . \end{aligned}$$

(2.1)

However, since the L-BFGS method updates $H_k$, it is not easy to construct $B_k$ explicitly. Furthermore, even if we obtain $B_k$, it takes a considerable amount of time to solve the linear Eq. (2.1) in large-scale cases.

Now, we may regard $B_k+\mu I$ as an approximation of $\nabla ^2 f(x) + \mu I$. Since $B_k$ is the approximate Hessian of $f(x_k)$, the matrix $B_k+\mu I$ is an approximate Hessian of $f(x)+\frac{\mu }{2}\Vert x\Vert ^2$. The L-BFGS method uses the vector pair $(s_k, y_k)$ to construct the approximate Hessian, where $s_k = x_{k+1} - x_{k}$ and $y_k = \nabla f(x_{k+1}) - \nabla f(x_k)$. Note that $y_k$ consists of the gradients of f. Therefore, when we compute the approximate Hessian of $f(x) + \frac{\mu }{2}\Vert x\Vert ^2$, we use the gradients of $f(x)+\frac{\mu }{2}\Vert x\Vert ^2$. That is, we adopt the following $\hat{y}_k(\mu )$ instead of $y_k$:

$$\begin{aligned} \hat{y}_k(\mu )&= (\nabla f(x_{k+1})+\mu x_{k+1} )-(\nabla f(x_k)+\mu x_{k}) = y_k + \mu s_k. \end{aligned}$$

Let $\hat{H}_k(\mu )$ be a matrix constructed by the L-BFGS method with m vector pairs $(s_i,\hat{y}_i(\mu ))$, $i=1,\ldots ,m$ and an appropriate initial matrix $\hat{H}_k^{(0)}(\mu )$. Then, the search direction $d_k =$ $-\hat{H}_k(\mu )\nabla f(x_k)$ is calculated in O(mn) time, which is the same as the original L-BFGS.

Note that if $s_k^T\hat{y}_k(\mu ) > 0$ and $\hat{H}_k^{(0)}$ is positive-definite, then $\hat{H}_k(\mu )$ is positive definite. When $s_k^T \hat{y}_k(\mu ) > 0$ is not satisfied, we may replace $\hat{y}_k(\mu )$ by $\tilde{y}_k(\mu )$:

$$\begin{aligned} \tilde{y}_k(\mu ) = y_k + \left( \max \left\{ 0,\frac{-s_k^Ty_k}{||s_k||^2}\right\} +\mu \right) s_k. \end{aligned}$$

Then, the inequality $s_k^T \tilde{y}_k(\mu ) > 0$ always holds because

$$\begin{aligned} s_k^T \tilde{y}_k(\mu ) = \max \{ 0,s_k^T y_k \}+\mu \Vert s_k\Vert ^2 >0 . \end{aligned}$$

In the following, $\hat{H}_{k}(\mu )$ is the matrix constructed by the L-BFGS method using the initial matrix $\hat{H}_k^{(0)}(\mu )$ and the vector pairs $(s_{k-i},\hat{y}_{k-i}(\mu )),~i=1,\cdots ,m$, and the search direction is given as $d_k(\mu ) = -\hat{H}_{k}(\mu )\nabla f(x_k)$.

The usual L-BFGS method uses $\gamma _k I$ as the initial matrix $H_k^{(0)}$, where $\gamma _k$ is a certain positive constant. Since $(B_k^{(0)})^{-1} = H_k^{(0)}$ and $\hat{H}_k^{(0)}$ is an approximation of $(B_k^{(0)} + \mu I)^{-1}$, we may set the initial matrix $\hat{H}_k^{(0)}(\mu )$ as

$$\begin{aligned} \hat{H}_k^{(0)}(\mu ) = (B_k^{(0)} + \mu I)^{-1} = \left( \frac{1}{\gamma _k} + \mu \right) ^{-1} I = \frac{\gamma _k}{1+\gamma _k\mu }I. \end{aligned}$$

(2.2)

The proposed method generates the next iterate as $x_{k+1} = x_k + d_k(\mu )$ without a step length. We control the parameter $\mu$ to guarantee the global convergence as in [23]. We exploit the idea of updating the trust-region radius in the TR-method to control $\mu$ to find an appropriate search direction, that is, we use the ratio of the reduction in the objective function value to that of the model function value. We define a ratio function $r_k(d_k(\mu ),\mu )$ by

$$\begin{aligned} r_k(d_k(\mu ), \mu ) = \frac{f(x_k) - f(x_k + d_k(\mu ))}{f(x_k) - q_k(d_k(\mu ),\mu )}, \end{aligned}$$

(2.3)

where $q_k : \mathbb {R}^n\times \mathbb {R} \rightarrow \mathbb {R}$ is given by

$$\begin{aligned} q_k(d_k(\mu ),\mu ) = f(x_k) + \nabla f(x_k)^Td_k(\mu ) + \frac{1}{2}d_k(\mu )^T\hat{H}_k(\mu )^{-1}d_k(\mu ). \end{aligned}$$

Note that we do not have to compute the matrix $\hat{H}_k(\mu )^{-1}$ explicitly in $q_k(d_k, \mu )$. Since $d_k(\mu ) = -\hat{H}_k(\mu )\nabla f(x_k)$, we have $d_k(\mu )^T\hat{H}_k(\mu )^{-1} d_k(\mu ) = -d_k(\mu )^T\nabla f(x_k)$. If the ratio $r_k(d_k(\mu ), \mu )$ is large, i.e., the reduction in the objective function f is sufficiently large compared to that of the model function, we adopt $d_k(\mu )$ and decrease the parameter $\mu$. On the other hand, if $r_k(d_k,\mu )$ is small, i.e., $f(x_k) - f(x_k+d_k)$ is small, we increase $\mu$ and compute $d_k(\mu )$ again.

Based on the above ideas, we propose the following regularized L-BFGS method.

In Step 2-1 we compute $d_k(\mu )$ from $(s_k, \hat{y}_{k}(\mu ))$ by the L-BFGS updating scheme in [12]. The details of step 2-1 are given as follows.

It is important to note that when $\mu$ varies, the regularized L-BFGS does not have to store $\hat{y}_{k}(\mu )$ because the L-BFGS stores $s_k$ and $y_k$ explicitly, and thus we can get $\hat{y}_{k}(\mu )$ immediately.

Remark 21

Tarzangh and Peyghami [22] proposed the L-BFGS with,

$$\begin{aligned} \bar{y}_k = y_k + \beta _k \frac{\omega _k}{s_k^Tu}u, \end{aligned}$$

(2.4)

where $u \in \mathbb {R}^n$ is a vector such that $s_k^Tu\ne 0$, $\omega _k=(2(f(x_k)-f(x_{k+1}))+(g_k+g_{k+1}))$ and $\beta _k \in \{0,1,2,3\}$. The additional term $\beta \frac{\omega _k}{s_k^Tu}u$ is considered as a regularization. Note that [22] does not control u for global convergence. Instead it adopts the usual line search.

3 Global convergence

In this section, we show the global convergence of the proposed algorithm. To this end, we need the following assumptions.

Assumption 31

• (i) The objective function f is twice continuously differentiable.

• (ii) The level set of f at the initial point $x_0$ is compact, i.e., $\varOmega =\{x\in \mathbb {R}^n| f(x)\le f(x_0)\}$ is compact.

• (iii) There exist positive constants $M_1$ and $M_2$ such that

  $$\begin{aligned} M_1\Vert z\Vert ^2 \le z^T \nabla ^2f(x) z \le M_2\Vert z\Vert ^2 ~\forall x \in \varOmega \text {~ and ~} z \in \mathbb {R}^n. \end{aligned}$$

• (iv) There exists a minimum $f_{\min }$ of f.

• (v) There exists a constant $\underline{\gamma }$ such that $\gamma _k \ge \underline{\gamma } > 0$ for all k, where $\gamma _k$ is a parameter in (2.2).

The above assumptions are the same as those for the global convergence of the original L-BFGS method [10].

Under these assumptions, we have the following several properties. First, let

$$\begin{aligned} G(x) = \nabla ^2 f(x),~~ G_k = G(x_k),~~ \bar{G}_k = \int _0^1 G(x_{k}+\tau d_k) d\tau . \end{aligned}$$

It then follows from mean value theorem that

$$\begin{aligned} y_k=\bar{G}_ks_k, \end{aligned}$$

(3.1)

as $s_k=x_{k+1}-x_k=(x_k+d_k)-x_k$ and $y_k = \nabla f(x_{k+1})-\nabla f(x_k)$ and hence we have

$$\begin{aligned} \hat{y}_k(\mu )= y_k + \mu s_k = (\bar{G}_k+\mu I)s_k. \end{aligned}$$

(3.2)

It follows from Assumption 31 (iii) that $\lambda _{\min }(\bar{G}_k) \ge M_1$ and $\lambda _{\max }(\bar{G}_k)\le M_2$. Therefore, we have that

$$\begin{aligned} M_1\Vert s_k\Vert ^2\le & {} s_k^Ty_k \le M_2\Vert s_k\Vert ^2, \nonumber \\ \frac{1}{M_2}\Vert y_k\Vert ^2\le & {} s_k^Ty_k \le \frac{1}{M_1}\Vert y_k\Vert ^2, \\ (M_1 + \mu )\Vert s_k\Vert ^2\le & {} s_k^T\hat{y}_k(\mu ) \le (M_2+\mu )\Vert s_k\Vert ^2. \nonumber \end{aligned}$$

(3.3)

Since the sequence $\{ x_k\}$ is included in the compact set $\varOmega$ and f is twice continuously differentiable under Assumption 31 (i) and (ii), there exists a positive constant $L_f$ such that

$$\begin{aligned} \Vert \nabla f(x_k)\Vert \le L_f~~~\mathrm{for~all}~k. \end{aligned}$$

(3.4)

Now, we investigate the behavior of the eigenvalues of $\hat{B}_k(\mu )$, which is the inverse of $\hat{H}_k(\mu )$. Note that the matrix $\hat{B}_k(\mu )$ is constructed by the BFGS formula with vector pairs ($s_k,\hat{y}_k(\mu )$) and initial matrix $\hat{B}_k^{(0)}(\mu ) = \hat{H}_k^{(0)}(\mu )^{-1}$. Thus, we have

$$\begin{aligned} \begin{aligned} \hat{B}_k(\mu )&= \hat{B}_k^{(\tilde{m}_k)}(\mu ) \\ \hat{B}_k^{(l+1)}(\mu )&= \hat{B}_k^{(l)}(\mu ) - \frac{\hat{B}_k^{(l)}(\mu ) s_{j_l} s_{j_l}^T \hat{B}_k^{(l)}(\mu )}{s_{j_l}^T \hat{B}_k^{(l)}(\mu ) s_{j_l}} + \frac{y_{j_l} \hat{y}_{j_l}^T}{\hat{y}_{j_l}^T s_{j_l}},~~l=0,\cdots ,\tilde{m}_k-1 \end{aligned} \end{aligned}$$

(3.5)

where $\tilde{m}_k=\min \{k+1,m\}$ and $j_l = k-\tilde{m}+l$. Note that these expressions are used in [5, 10].

We now focus on the trace and determinant of $\hat{B}_k(\mu )$. First, we show that the trace of $\hat{B}_k^{(l)}(\mu )$ is $O(\mu )$.

Lemma 31

Suppose that Assumption 31 holds. Then,

$$\begin{aligned} \mathrm{tr}(\hat{B}_{k}^{(l)}(\mu )) \le M_3 + (2m+n)\mu ,~~l=0,\cdots ,~\tilde{m}_k \end{aligned}$$

where $M_3 = \frac{n}{\underline{\gamma }}+m M_2.$

Proof

We have from Assumption 31, (3.1), and (3.3) that

$$\begin{aligned} \frac{\Vert \hat{y}_k(\mu )\Vert ^2}{s_k^T\hat{y}_k(\mu )}= &\,\, \frac{ \Vert y_k\Vert ^2 + 2\mu s_k^Ty_k + \mu ^2\Vert s_k\Vert }{s_k^Ty_k + \mu \Vert s_k\Vert ^2 } \nonumber \\= &\,\, \frac{\Vert y_k\Vert ^2 + \mu s_k^Ty_k }{s_k^Ty_k + \mu \Vert s_k\Vert ^2 } + \frac{\mu (s_k^Ty_k + \mu \Vert s_k\Vert ^2)}{ s_k^Ty_k + \mu \Vert s_k\Vert ^2} \nonumber \\\le &\,\, \frac{\Vert y_k\Vert ^2 + \mu s_k^Ty_k}{s_k^Ty_k} + \mu \nonumber \\\le &\,\, \frac{\Vert y_k\Vert ^2}{\frac{1}{M_2} \Vert y_k\Vert ^2} + 2\mu \nonumber \\= & \,\,M_2 + 2\mu . \end{aligned}$$

(3.6)

From the updating formula (3.5) of matrix $\hat{B}_k(\mu )$,

$$\begin{aligned} \mathrm{tr}(\hat{B}_{k}^{(l)}(\mu )) =\mathrm{tr}(\hat{B}_{k}^{(0)}(\mu )) + \sum _{t=0}^{l-1} \left( - \frac{\Vert \hat{B}_k^{(t)}(\mu ) s_{j_t} \Vert ^2}{s_{j_t}^T \hat{B}_k^{(t)}(\mu ) s_{j_t}} +\frac{\Vert \hat{y_{j_t}}(\mu )\Vert ^2}{s_{j_t}^T\hat{y}_{j_t}(\mu )} \right) . \end{aligned}$$

It then follows from (3.6) that

$$\begin{aligned} \mathrm{tr}(\hat{B}_{k}^{(l)}(\mu ))\le & {} \mathrm{tr}(\hat{B}_{k}^{(0)}(\mu )) + \sum _{t=0}^{l-1} \frac{\Vert \hat{y_{j_t}}(\mu )\Vert ^2}{s_{j_t}^T\hat{y}_{j_t}(\mu )} \\\le & {} \mathrm{tr}(\hat{B}_{k}^{(0)}(\mu )) + l ( M_2+ 2\mu ) \\= & {} n\left( \frac{1}{\gamma _{k}}+\mu \right) + l (M_2 + 2\mu ) \\\le & {} n\left( \frac{1}{\underline{\gamma }}+\mu \right) + m (M_2 + 2\mu ) \\\le & {} M_3 +(2m+n)\mu . \end{aligned}$$

This completes the proof. $\square$

The next lemma gives a lower bound for the determinant of $\hat{B}_k(\mu )$.

Lemma 32

Suppose that Assumption 31 holds. Then,

$$\begin{aligned} \mathrm{det}(\hat{B}_{k}(\mu ) ) \ge M_4\mu ^n, \end{aligned}$$

where

$$\begin{aligned} M_4 = \mathrm{\min }\left\{ \left( \frac{M_1}{M_3 + (2m+n)} \right) ^{\tilde{m}} , \left( \frac{1}{M_3 + (2m+n)} \right) ^{\tilde{m}} \right\} . \end{aligned}$$

Proof

Note that the determinant of the approximate matrix updated by the BFGS updating scheme has the following property [15, 16]:

$$\begin{aligned} \mathrm{det}(\hat{B}_k^{(l+1)}(\mu )) = \mathrm{det}(\hat{B}_k^{(l)}(\mu ))\frac{s_{j_l}^T \hat{y}_{j_l}(\mu )}{s_{j_l}^T \hat{B}_{k}^{(l)}(\mu ) s_{j_l} }. \end{aligned}$$

Then, we have

$$\begin{aligned} \mathrm{det}(\hat{B}_{k}(\mu ))= & {} \mathrm{det}(\hat{B}_{k}^{(0)}(\mu )) \prod _{l=0}^{\tilde{m}-1}\frac{ s_{j_l}^T\hat{y}_{j_l}(\mu ) }{ s_{j_l}^T\hat{B}_{k}^{(l)}(\mu ) s_{j_l} } \\= & {} \mathrm{det}( \hat{B}_{k}^{(l)}(\mu ) ) \prod _{l=0}^{\tilde{m}-1}\frac{ s_{j_l}^T\hat{y}_{j_l}(\mu ) }{ s_{j_l}^Ts_{j_l} }\frac{ s_{j_l}^Ts_{j_l} }{ s_{j_l}^T\hat{B}_{k}^{(l)}(\mu )s_{j_l} } \\\ge & {} \mathrm{det}( \hat{B}_{k}^{(0)}(\mu )) \prod _{l=0}^{\tilde{m}-1}\frac{ s_{j_l}^T\hat{y}_{j_l}(\mu ) }{ s_{j_l}^Ts_{j_l} }\frac{ s_{j_l}^Ts_{j_l} }{ \lambda _{\max }(\hat{B}_{k}^{(l)}(\mu )) s_{j_l}^Ts_{j_l} } \\= & {} \mathrm{det}(\hat{B}_k^{(0)}(\mu )) \prod _{l=0}^{\tilde{m}-1}\frac{s_{j_l}^T\hat{y}_{j_l}(\mu )}{\Vert s_{j_l}\Vert ^2}\frac{1}{\lambda _{\max }(\hat{B}_k^{(l)}(\mu ))}. \end{aligned}$$

Since $\hat{B}_k^{(0)}(\mu )$ is symmetric positive-definite, Lemma 31 implies that $\lambda _{\max }(\hat{B}_{k}^{(l)}(\mu )) \le M_3+(2m+n)\mu$. Furthermore, we have $\frac{s_{j_l}^T\hat{y}_{j_l}(\mu )}{\Vert s_{j_l}\Vert ^2} \ge M_1+\mu$ from (3.3). Therefore, it follows that

$$\begin{aligned} \mathrm{det}(\hat{B}_k(\mu ))\ge & {} \mathrm{det}( \hat{B}_{k}(\mu )^{(0)} ) \left( \frac{M_1+\mu }{M_3+(2m+n)\mu } \right) ^{\tilde{m}} \\= & {} \mathrm{det}\left( \frac{1+\gamma _{k}\mu }{\gamma _{k}}I\right) \left( \frac{M_1+\mu }{M_3+(2m+n)\mu }\right) ^{\tilde{m}}. \\ \end{aligned}$$

We have

$$\begin{aligned} \frac{M_1 + \mu }{M_3 + (2m+n)\mu } = \frac{ M_1}{M_3 + (2m+n)\mu } + \frac{\mu }{M_3 + (2m+n)\mu }. \end{aligned}$$

(3.7)

If $\mu \le 1$, then we have

$$\begin{aligned} \frac{M_1}{M_3 + (2m+n)\mu } \ge \frac{M_1}{M_3 + (2m+n)}, \end{aligned}$$

and if $\mu >1$, then we get

$$\begin{aligned} \frac{\mu }{M_3 + (2m+n)\mu } = \frac{1}{M_3/\mu + (2m+n)} \ge \frac{1}{M_3 + (2m+n)}. \end{aligned}$$

It then follows from (3.7) that

$$\begin{aligned} \left( \frac{M_1+\mu }{M_3+(2m+n)\mu } \right) ^{\tilde{m}} \ge M_4, \end{aligned}$$

where

$$\begin{aligned} M_4 = \mathrm \min \left\{ \left( \frac{M_1}{M_3 + (2m+n)} \right) ^{\tilde{m}} , \left( \frac{1}{M_3 + (2m+n)} \right) ^{\tilde{m}} \right\} . \end{aligned}$$

Consequently, we set

$$\begin{aligned} \mathrm{det}(\hat{B}_k(\mu ))\ge & {} \left( \frac{1}{\gamma _{k}}+\mu \right) ^n M_4\\\ge & {} M_4 \mu ^n. \end{aligned}$$

This completes the proof. $\square$

From the above two lemmas, we have $\lambda _{\max }(\hat{H}_{k}(\mu ) ) \rightarrow 0$ as $\mu \rightarrow \infty$.

Lemma 33

Suppose that Assumption 31 holds. Then, for all $k\ge 0$,

$$\begin{aligned} \lambda _{\max }(\hat{H}_k(\mu )) \le M_5 \frac{1}{\mu },~\forall \mu \in [ \mu _{\min },\infty ), \end{aligned}$$

where

$$\begin{aligned} M_5 =\frac{1}{M_4}\left( \frac{M_3}{\mu _{\min }} + (2m+n) \right) ^{n-1}. \end{aligned}$$

Furthermore, $\lim _{\mu \rightarrow \infty } \lambda _{\max }(\hat{H}_k(\mu )) = 0.$

Proof

We have from Lemmas 31 and 32 that

$$\begin{aligned} \mathrm{tr}(\hat{B}_k(\mu ))\le & {} M_3 + (2m+n)\mu , \\ \mathrm{det}(\hat{B}_{k}(\mu ) )\ge & {} M_4\mu ^n. \end{aligned}$$

Since $\hat{B}_k(\mu )$ is symmetric positive-definite, we have

$$\begin{aligned} \mathrm{tr}(\hat{B}_{k}(\mu ))\ge & {} \lambda _{\min }(\hat{B}_k(\mu )) \\ \det (\hat{B}_{k}(\mu ))\le & {} \lambda _{\min }(\hat{B}_k(\mu ) )\{\lambda _{\max }(\hat{B}_k(\mu ))\}^{n-1}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \lambda _{\min }(\hat{B}_k(\mu ))\ge & {} \frac{ \det (\hat{B}_{k}(\mu )) }{ \{\lambda _{\max } (\hat{B}_k(\mu ))\}^{n-1} } \\\ge & {} \frac{ M_4 \mu ^n }{ \{ (M_3 +(2m+n)\mu )\}^{n-1} }. \end{aligned}$$

It then follows from Assumption 31 (v) that

$$\begin{aligned} \lambda _{\max }(\hat{H}_k(\mu ))= & {} \frac{1}{\lambda _{\min }(\hat{H}_k^{-1}(\mu ))} \nonumber \\= & {} \frac{1}{\lambda _{\min }(\hat{B}_k(\mu ))} \nonumber \\\le & {} \frac{ \{(M_3 +(2m+n)\mu ) \}^{n-1} }{ M_4\mu ^n } \nonumber \\= & {} \frac{1}{M_4 }\left( \frac{M_3 + (2m+n)\mu }{\mu }\right) ^{n-1}\frac{1}{\mu }. \end{aligned}$$

(3.8)

Since $\mu \ge \mu _{\min }$, we have

$$\begin{aligned} \frac{M_3 + (2m+n)\mu }{\mu } = \frac{M_3}{\mu }+(2m+n) \le \frac{M_3}{\mu _{\min }}+(2m+n). \end{aligned}$$

It then follows from (3.8) that

$$\begin{aligned} \lambda _{\max }(\hat{H}_k(\mu ))\le & {} \frac{1}{M_4}\left( \frac{M_3}{\mu _{\min }} + (2m+n) \right) ^{n-1} \frac{1}{\mu } \\= & {} M_5 \frac{1}{\mu }. \end{aligned}$$

Hence, we have

$$\begin{aligned} \lim _{\mu \rightarrow \infty } \lambda _{\max }(\hat{H}_k(\mu )) = 0. \end{aligned}$$

This completes the proof. $\square$

Now, we give an upper bound for $\Vert d_k(\mu )\Vert$.

Lemma 34

Suppose that Assumption 31 holds. Then,

$$\begin{aligned} \Vert d_k(\mu )\Vert \le U_d, \end{aligned}$$

where

$$\begin{aligned} U_d = \frac{L_f M_5}{\mu _{\min }}. \end{aligned}$$

Proof

From the definition of $d_k(\mu )$, (3.4), and Lemma 33, we have that

$$\begin{aligned} \Vert d_k(\mu )\Vert= & {} \Vert \hat{H}_k(\mu )\nabla f(x_k)\Vert \\\le & {} \Vert \hat{H}_k(\mu )\Vert \Vert \nabla f(x_k)\Vert \\= & {} \lambda _{\max }(\hat{H}_k(\mu )) \Vert \nabla f(x_k)\Vert \\\le & {} \lambda _{\max }(\hat{H}_k(\mu )) L_f \\\le & {} \frac{L_f M_5}{\mu } \\\le & {} \frac{L_f M_5}{\mu _{\min }} = U_d. \end{aligned}$$

This completes the proof. $\square$

Lemma 34 implies that

$$\begin{aligned} x_k + \nu d_k(\mu ) \in \varOmega + \mathrm{B}(0,U_d),~~~\forall \nu \in [0,1],~~~\forall \mu \in [\mu _{\min },\infty ),~~~\forall k \ge 0. \end{aligned}$$

Moreover, since $\varOmega +\mathrm{B}(0,U_d)$ is compact and f is twice continuously differentiable, $\nabla f(x_k)$ is Lipschitz continuous on $\varOmega + \mathrm{B}(0,U_d)$. That is, there exists a positive constant $L_g$ such that

$$\begin{aligned} \Vert \nabla ^2 f(x_k)\Vert \le L_g~~~\forall x_k \in \varOmega +\mathrm{B}(0,U_d). \end{aligned}$$

(3.9)

Next, we investigate the values of $\mu$ that satisfy the termination condition $r_k(d_k(\mu ),$ $\mu )\ge \eta _1$ in the inner iterations of Step 2-2 in Algorithm 21.

Lemma 35

Suppose that Assumption 31 holds. Then, we have

$$\begin{aligned} f(x_k) - f(x_k+d_k(\mu )) - \eta _1 (f(x_k) - q_k(d_k(\mu ),\mu )) \\ \ge \frac{1}{2}((2-\eta _1) \lambda _{\min }(\hat{H}_k(\mu )^{-1}) - L_g)\Vert d_k(\mu )\Vert ^2. \end{aligned}$$

Proof

We have from Taylor’s theorem that

$$\begin{aligned} \begin{aligned} f(x_k+d_k(\mu ))&= f(x_k) + \int _0^1 \nabla f(x_k+\tau d_k(\mu ))^Td_k(\mu )d\tau \\&= f(x_k) + \nabla f(x_k)^Td_k(\mu ) + \int _0^1(\nabla f(x_k+\tau d_k(\mu )) \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad -\nabla f(x_k))^Td_k(\mu ) d \tau . \end{aligned} \end{aligned}$$

From the Lipschitz continuity of $\nabla f(x_k)$ in (3.9), we get

$$\begin{aligned} f(x_k) - f(x_k+d_k(\mu )) - \eta _1 (f(x_k) - q_k(d_k(\mu ),\mu )) \\ =-\nabla f(x_k)^Td_k(\mu ) - \int _0^1(\nabla f(x_k+\tau d_k(\mu ))- \nabla f(x_k))^Td_k(\mu ) d\tau \\ - \frac{\eta _1}{2}d_k(\mu )^T(\hat{H}_k(\mu )^{-1})d_k(\mu ) \\ \begin{aligned}&=\frac{(2-\eta _1)}{2}d_k(\mu )^T(\hat{H}_k(\mu )^{-1})d_k(\mu ) - \int _0^1(\nabla f(x_k+ \tau d_k(\mu )) \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad -\nabla f(x_k))^Td_k(\mu ) d\tau \\&\ge \frac{(2-\eta _1)}{2}\lambda _{\min }(\hat{H}_k(\mu )^{-1})\Vert d_k(\mu )\Vert ^2-\int _0^1L_g\tau \Vert d_k(\mu )\Vert ^2d\tau \\&=\frac{1}{2}((2-\eta _1)\lambda _{\min }(\hat{H}_k(\mu )^{-1}) - L_g)\Vert d_k(\mu )\Vert ^2. \end{aligned} \end{aligned}$$

This completes the proof. $\square$

From Lemma 35, if $\mu$ satisfies

$$\begin{aligned} \lambda _{\min }( \hat{H}_k^{-1}(\mu ) )\ge \frac{L_g}{2-\eta _1}, \end{aligned}$$

(3.10)

then we have

$$\begin{aligned} r_k(d_k(\mu ),\mu )\ge \eta _1, \end{aligned}$$

(3.11)

that is, the inner loops of Algorithm 21 must terminate.

Next, we give an upper bound for the parameter $\mu _k$.

Lemma 36

Suppose that Assumption 31 holds. Then, for any $k \ge 0$,

$$\begin{aligned} \mu _k^{*}\le U_{\mu }, \end{aligned}$$

where

$$\begin{aligned} U_{\mu } =\sigma _2 M_5 \frac{L_g}{2-\eta _1}. \end{aligned}$$

Proof

If $\bar{\mu }_{l_k}$ satisfies (3.10), then $r_k(d_k(\bar{\mu }_{l_k}),\bar{\mu }_{l_k})\ge \eta _1$ from Lemma 35. Therefore, the inner loops must terminate, and we set $\mu _k^{*} =\bar{\mu }_{l_k}$.

Now, we give the termination condition on $\mu$ for the inner loop. We have from Lemma 33 that

$$\begin{aligned} \lambda _{\min }(\hat{H}_k^{-1}(\mu ))= & {} \frac{1}{\lambda _{\max }(\hat{H}_k(\mu ))} \nonumber \\\ge & {} \frac{\mu }{M_5}. \end{aligned}$$

(3.12)

It then follows from (3.10) that the termination condition of the inner loop holds when

$$\begin{aligned} \mu \ge M_5\frac{L_g}{2-\eta _1}. \end{aligned}$$

(3.13)

Note that if the inner loop terminates at ${l_k}$, then (3.13) does not hold with $\mu = \mu _{l_k-1}$, that is,

$$\begin{aligned} \bar{\mu }_{l_k-1} < M_5 \frac{L_g}{2-\eta _1}. \end{aligned}$$

Since $\mu _k^{*} = \bar{\mu }_{l_k} = \sigma _2 \bar{\mu }_{l_k-1}$, we have

$$\begin{aligned} \mu _k^{*} = \sigma _2 \bar{\mu }_{l_k-1} < \sigma _2 M_5 \frac{L_g}{2-\eta _1} = U_{\mu }. \end{aligned}$$

(3.14)

This completes the proof. $\square$

Next, we give a lower bound for the reduction in the model function $q_k$.

Lemma 37

Suppose that Assumption 31 holds. Then, we have

$$\begin{aligned} f(x_k)-q_k(d_k(\mu ),\mu )\ge & {} M_6 \Vert \nabla f(x_k)\Vert ^2, \end{aligned}$$

where

$$\begin{aligned} M_6 = \frac{1}{2(M_3+(2m+n)\mu _{\min })}. \end{aligned}$$

Proof

It follows from the definition of the model function $q_k(d_k(\mu ),\mu )$ and Lemmas 31, 36 that

$$\begin{aligned} f(x_k)-q_k(d_k(\mu ),\mu )= & -\frac{1}{2} d_k(\mu )^T ( \hat{H}_k^{-1}(\mu ) )d_k(\mu ) - \nabla f(x_k)^Td_k(\mu )\\= & -\frac{1}{2}\nabla f(x_k)^T\hat{H}_k(\mu ) \nabla f(x_k) + \nabla f(x_k)^T \hat{H}_k(\mu )\nabla f(x_k)\\= & \frac{1}{2} \nabla f(x_k)^T\hat{H}_k(\mu ) \nabla f(x_k) \\\ge & \frac{1}{2} \lambda _{\min }( \hat{H}_k(\mu ) )\Vert \nabla f(x_k)\Vert ^2\\= & \frac{\Vert \nabla f(x_k)\Vert ^2}{2\lambda _{\max }( \hat{H}_k^{-1}(\mu ) )} \\= & \frac{\Vert \nabla f(x_k)\Vert ^2}{2\lambda _{\max }( \hat{B}_k(\mu ) )} \\\ge & \frac{\Vert \nabla f(x_k)\Vert ^2}{2\mathrm{tr}( \hat{B}_k(\mu ) )} \\\ge & \frac{\Vert \nabla f(x_k)\Vert ^2}{2(M_3+(2m+n)\mu )} \\= & \frac{1}{2(M_3+(2m+n)U_{\mu })} \Vert \nabla f(x_k)\Vert ^2 \\= & M_6 \Vert \nabla f(x_k)\Vert ^2. \end{aligned}$$

This completes the proof. $\square$

From this lemma, we can give a lower bound for the reduction in the objective function value when $x_k$ is not a stationary point.

Lemma 38

Suppose that Assumption 31 holds. If there exists a positive constant $\epsilon _g$ such that $\Vert \nabla f(x_k)\Vert \ge \epsilon _g$, then we have $f(x_k)-f(x_{k+1}) \ge \rho \epsilon _g^2$, where $\rho = \eta _1 M_6$.

Proof

It follows from Lemmas 36 and 37 that

$$\begin{aligned} f(x_k)-f(x_{k+1})\ge & \eta _1(f(x_k)-q_k(d_k(\mu _k^{*}),\mu _k^{*})) \\\ge & \eta _1 M_6 \Vert \nabla f(x_k)\Vert ^2 \\\ge & \rho \epsilon _g^2. \end{aligned}$$

This completes the proof. $\square$

We are now in a position to prove the main theorem of this section.

Theorem 31

Suppose that Assumption 31 holds. Then, $\liminf _{k\rightarrow \infty }\Vert \nabla f(x_k) \Vert =0$ or there exists $K\ge 0$ such that $\Vert \nabla f(x_K)\Vert =0$.

Proof

Suppose the contrary, that is, there exists a $\epsilon _g > 0$ such that $\Vert \nabla f(x_k)\Vert \ge \epsilon _g$ for all $k \ge 0$. It follows from Lemma 38 that

$$\begin{aligned} f(x_0)-f(x_k)= & {} \sum _{j=0}^{k-1} (f(x_j)-f(x_{j+1})) \\\ge & {} \sum _{j=0}^{k-1} \rho \epsilon _g^2 \\= & {} \rho \epsilon _g^2 k. \end{aligned}$$

Taking $k \rightarrow \infty$, the right-hand side of the final inequality goes to infinity, and hence

$$\begin{aligned} \lim _{k\rightarrow \infty } f(x_k) = -\infty . \end{aligned}$$

This contradicts the existence of $f_{\min }$ in Assumption 31 (iv). This completes the proof. $\square$

4 Implementation issues

The regularized L-BFGS method does not use a line search, and hence it can not take a longer step. Moreover, in our experience, the trust-region ratio of the regularized L-BFGS does not improve well and the regularized parameter $\mu$ becomes very large for some large-scale test problems. Both cases result in a short step, and hence the method conducts a large number of iterations to reach a solution. To overcome this difficulty we propose two techniques in this section. We also discuss how to set $\gamma _k$ in the initial matrix $\hat{H}_{k}(\mu )$.

4.1 Simultaneous use with Wolfe line search

The next iterate with line search is given as

$$\begin{aligned} x_{k+1} = x_k + \alpha _k d_k, \end{aligned}$$

(4.1)

where $\alpha _k$ is a step length. The usual L-BFGS [10, 12] uses a step length $\alpha _k$ that satisfies the Wolfe conditions,

$$\begin{aligned}&f(x_k+\alpha _k d_k) \le f(x_k) + c_1 \alpha _k d_k^T\nabla f(x_k); \end{aligned}$$

(4.2)

$$\begin{aligned}&d_k^T\nabla f(x_k+ \alpha _k d_k) \ge c_2 d_k^T \nabla f(x_k); \end{aligned}$$

(4.3)

$$\begin{aligned} ,&|d_k^T \nabla f(x_k + \alpha _k d_k) | \le c_2 |d_k^T \nabla f(x_k)| \end{aligned}$$

(4.4)

where $0<c_1<c_2<1$. Note that $\alpha _k$ can be larger than 1. Thus, $\alpha _k d_k$ might be larger, and make a large reduction of f. Thus, it might be reasonable to use a line search as well as the regularization technique. However, finding $\alpha _k$ takes much time, and hence we must avoid it if $\alpha _k d_k$ does not enough improvement.

For the efficient use of the line search, we exploit curvature condition (4.3). It is known that the curvature condition ensures that the step is not too short. Therefore, after step 3 of Algorithm 21, we first check whether $x_{k}+d_k(\mu )$ satisfies curvature condition ($\alpha _k=1$ in (4.3)) or not. The dissatisfaction of the curvature condition implies that $x_k +d_k(\mu )$ is a short step. Thus, we compute $\alpha _k$ by the strong Wolfe condition so that we can take a longer step. More precisely, we search $\alpha _k$ from $x_k +d_k(\mu )$ with the direction $d_k(\mu )$ so that (4.2)-(4.4) hold with $x_k:=x_k+d_k(\mu )$, $d_k:=d_k(\mu ),$ and then set $x_{k+1}=x_k+(1+\alpha _k) d_k(\mu )$.

We now discuss the conditions under which we conduct the Wolfe line search. As mentioned above, we exploit the strong Wolfe condition (4.3) when the following conditions hold,

$$\begin{aligned} d_k(\mu )^T\nabla f(x_k+ d_k(\mu )) < c_2 d_k(\mu )^T \nabla f(x_k)\quad \text { and }\quad \mu =\mu _{min}. \end{aligned}$$

(4.5)

Note that $\Vert d_k(\mu _{min})\Vert \ge \Vert d_k(\mu )\Vert$ if $\mu > \mu _{min}$. Thus, $d_k(\mu _{min})$ is the largest step when we apply RL-BFGS only. Condition (4.5) implies whenever $x_k+ d_k(\mu _{min})$ to make better progress, we take a longer step via a strong Wolfe line search. We call this method regularized L-BFGS with strong Wolfe line search method (RL-BFGS-SW) as an extended version of the proposed method. Now, we propose the RL-BFGS-SW as follows.

Under this procedure, we must replace $s_k$ and $\hat{y}_{k}(\mu )$ whenever we use the strong Wolfe line search. We summarize $y_k, \hat{y}_{k}(\mu )$ and $s_k$ in Table 1.

Table 1 Comparison of $y_k, \hat{y}_k$ and $s_k$

Note that we do not need to evaluate a new function and gradient values for conditions (4.5) since we have the gradient and function values to calculate the ratio $r_k(d_k(\mu ), \mu _k)$. Note also that Algorithm 41 still has the global convergence property since $f(x_k+d_k(\mu )) > f(x_k + (1+\alpha _k)d_k(\mu ))$ from (4.2) and (4.5).

4.2 Nonmonotone decreasing technique

In Algorithm 21, we control the regularized parameter $\mu$ to satisfy the descent condition $f(x_{k+1})$ $< f(x_k)$. However, $\mu$ sometimes becomes quite large for some ill-posed problems. In this situation, we require a large number of function evaluations. Therefore, we use the concept of a nonmonotone line search technique [9, 21] to overcome the difficulty. We replace the ratio function $r_k(d_k(\mu ),\mu )$ with the following new ratio function $\bar{r}_k(d_k(\mu ),\mu )$:

$$\begin{aligned} \bar{r}_k(d_k(\mu ),\mu ) = \frac{ \max _{0\le j\le m(k)}f(x_{k-j}) - f(x_k+d_k(\mu )) }{ f(x_k) - q_k(d_k(\mu ),\mu ) }, \end{aligned}$$

where

$$\begin{aligned} m(0) = 0,~~0 \le m(k) \le \min \{m(k-1)+1,M\}, \end{aligned}$$

and M is a nonnegative integer constant. This modification retains the global convergence of the regularized L-BFGS method.

In the numerical experiments reported in the next section, when $k<M$, we use the original ratio function $r_k(d_k(\mu ),\mu )$, and if $k\ge M$ then we use the new ratio function $\bar{r}_k(d_k(\mu ),\mu )$.

4.3 Scaling initial matrix

The regularized L-BFGS method uses the following initial matrix in each iteration:

$$\begin{aligned} \hat{H}_k^{(0)}(\mu ) = \frac{\gamma _k}{1+\gamma _k\mu } I. \end{aligned}$$

The parameter $\gamma _k$ represents the scale of $\nabla ^2f(x)$. Thus, we exploit the scaling parameter $\gamma _k$ used in [1, 4, 12, 17, 18], that is, we set

$$\begin{aligned} \gamma _k = \frac{s_{k-1}^Ty_{k-1}}{\Vert y_{k-1}\Vert ^2}. \end{aligned}$$

It is known that the L-BFGS method with this scaling in the initial matrix has an efficient performance [4, 12]. Note that we require $\gamma _k>0$ to ensure the positive-definiteness of $\hat{H}_k^{(0)}(\mu )$. If $s_{k-1}^Ty_{k-1} < \alpha \Vert s_{k-1}\Vert ^2$, then we set $\gamma _k = \alpha \frac{\Vert s_{k-1} \Vert ^2}{\Vert y_{k-1}\Vert ^2}$, where $\alpha$ is a small positive constant.

5 Numerical results

In this section, we compare the L-BFGS, the regularized L-BFGS (RL-BFGS), and the regularized L-BFGS with line search (RL-BFGS-SW). We also compare out method with the existing regularized L-BFGS [22]. For the regularized ones, we adopt the nonmonotone techniques and the initial matrix discussed in Section 4. We have used MCSRCH (Line search routine) and parameters of the original L-BFGS [14] to find a step length in the RL-BFGS-SW.

We have solved 297 problems chosen from CUTEst [8]. All algorithms were coded in MATLAB 2018a. We have used Intel Core i5 1.8GHz CPU with 8 GB RAM on Mac OS. We have chosen an initial point $x_0$ given in CUTEst.

We set the termination criteria as,

$$\begin{aligned} \frac{\Vert \nabla f(x_k)\Vert }{\text {max}(1,\Vert x_k\Vert )} < 10^{-5}\ \text {or}\ n_f> 50000\ \text {or}\ {k}>50000\ \text {or}\ \mu _k>10^{15}, \end{aligned}$$

(5.1)

where $n_f$ is the number of function evaluations. We regard the trails as fail when $n_f > 50000$ or number of iteration exceed 50000 or $\mu _k >10^{15}$.

We compare the algorithms from the distribution function proposed in [7]. Let $\mathcal {S}$ be a set of solvers and let ${\mathcal{P}}_{{\mathcal{S}}}$ be a set of problems that can be solved by all algorithms in $\mathcal {S}$. We measure required evaluations to solve problem p by solver $s\in \mathcal {S}$ as $t_{p,s}$, and the best $t_{p,s}$ for each p as $t^*_p,$ which means $t^*_p = \text {min}\{t_{p,s}| s \in \mathcal {S} \}$. The distribution function $F_s^{\mathcal {S}}(\tau )$, for a method s is defined by,

$$\begin{aligned} F_s^{\mathcal {S}}(\tau ) = \frac{|\{p \in \mathcal {P}_{\mathcal {S}}| t_{p,s} \le \tau t^*_p \}|}{|\mathcal {P}_{\mathcal {S}}|}, \ \tau \ge 1. \end{aligned}$$

(5.2)

The algorithm whose $F_s^{\mathcal {S}}(\tau )$ is close to 1 is considered to be superior compare to other algorithm in $\mathcal {S}$.

5.1 Numerical behavior for some parameters in RL-BFGS

Since the RL-BFGS uses several parameters, we need to investigate the effect of these parameters so that we choose optimal ones.

First we consider $\sigma _1$ and $\sigma _2$ that control regularized parameters. We perform numerical experiments with 9 different sets of $(\sigma _1,\sigma _2)$ in Table 2. The remaining parameters are set to

$$\begin{aligned} \eta _1=0.01, \eta _2=0.9, \mu _{min}=1.0\times 10^{-3},m=7, M=10. \end{aligned}$$

Table 2 shows the number of success and rate of success for all 297 problems. Figure 1 shows the distribution function of these parameter sets in terms of the CPU time.

Table 2 The number of success and rate of success at each $(\sigma _1,\sigma _2)$

Fig. 1

Comparison of $(\sigma _1,\sigma _2)$

From Table 2 and Fig. 1 it is clear that $(\sigma _1,\sigma _2)=(0.1,10.0)$ is the best. Therefore, we set $\sigma _1=0.1$ and $\sigma _2=10.0$ for all further experiments.

Next, we compare the number m of vector pairs in the L-BFGS procedure. Note that the original L-BFGS usually choose it in $3\le m \le 7$ [12]. Thus, we compare $m=3,5, 7$. The remaining parameters are set to

$$\begin{aligned} \sigma _1=0.1,\sigma _2=10, \eta _1=0.01,\eta _2=0.9,\mu _{min}=1.0\times 10^{-3},M=10. \end{aligned}$$

From Table 3 we see that $m=7$ is the best, also Fig. 2 shows that $m=7$ is better in terms of CPU time. Therefore, we set $m=7$ for further experiments.

Table 3 The number of success and rate of success at each m

Fig. 2

Comparison of $m=3,5,7$

Finally, we compare the behavior of nonmonotone parameters M. We compare $M=0,4,6,8,$ 10, 12. Note that $M=0$ implies the usual monotone decreasing case. The remaining parameters are set to

$$\begin{aligned} \sigma _1=0.1,\sigma _2=10, \eta _1=0.01,\eta _2=0.9,\mu _{min}=1.0\times 10^{-3},m=7. \end{aligned}$$

Figure 3 shows the distribution function of the nonmonotone parameter in terms of the CPU time.

Fig. 3

Comparison of M

From Table 4 and Fig. 3 it is clear that $M=10$ is better. Therefore, we use $M=10$ in the next section.

Table 4 The number of success and rate of success at each M

5.2 Comparisons of RL-BFGS-SW, RL-BFGS and L-BFGS method

We compare the RL-BFGS-SW, the RL-BFGS, and the L-BFGS methods in terms of the number of function evaluations and CPU time. For all numerical experiments, the parameters in RL-BFGS and RL-BFGS-SW are as follows:

$$\begin{aligned} \eta _1=0.01, \eta _2=0.9, \mu _{min} = 1.0 \times 10^{-3}, M=10, m=7, \sigma _1=0.1, \sigma _2=10. \end{aligned}$$

Figures 4 and 5 shows the results of the number of successes and rate of successes for $\mathcal {P}_{\mathcal {S}}$ in terms of function evaluations and CPU time, respectively. Here $\mathcal {S}$ is the set of problems that are solved by all three algorithms.

Fig. 4

Comparison of $n_f$

Fig. 5

Comparison of CPU time

Figure 4 shows that L-BFGS can solve 83.5% of test problems while RL-BFGS and RL-BFGS-SW can solve 89.22% and 87.87% of problems, respectively. On the other hand, Fig. 4 shows that L-BFGS is faster than the regularized ones for the solved problems in terms of the number of function evaluations for 75% of problems. However, RL-BFGS and RL-BFGS-SW can capture the attention with the ability to solve 89.22% and 87.87% respectively, as the height of the profile performance shows for $\tau > 4$. Moreover, Fig. 5 shows that all solvers takes almost equal time to solve 83.5% of the problems.

The above numerical results indicate that the numerical behaviors of the RL-BFGS and the RL-BFGS-SW are almost the same. To see the differences we present the numerical results which compare the performance of each algorithm.

We first observed that the RL-BFGS-SW performs the line search for 65 problems, and does not use it for the remaining problems. Then, we check the results for those 65 problems and compare in terms of function evaluations. We found that RL-BFGS-SW requires fewer number of function evaluations than that of RL-BFGS for 39 test problems while RL-BFGS requires fewer number of function evaluations than that of RL-BFGS-SW for 26 test problems among 65 test problems.

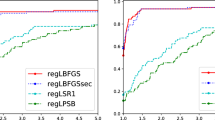
Now we compare our methods with the existing regularized L-BFGS methods [22], (see Remark 21). Note that the paper proposed several update rules of $\beta _k$ in (2.4). We choose two methods, RLQNWB and RLQNWB-L among them since they are superior to the other update rules. To compare the proposed methods with the RLQNWB and RLQNWB-L, we used the numerical results provided by Peyghami and Tarzanagh [22]². We solved 59 test problems in Table 5, and provide performance profiles in terms of function evaluations. We set the termination criteria as,

$$\begin{aligned} \Vert \nabla f(x_k)\Vert \le 10^{-5} \ \text {or}\ \mu _k>10^{15}, \end{aligned}$$

or the number of iterations and function evaluations exceed 10,000 and 50,000, respectively.

Table 5 Test functions [8]

We first note that RL-BFGS and RL-BFGS-SW were unable to solve a problem CHAINWOO. Figure 6 shows that both RL-BFGS and RL-BFGS-SW take the fewer number of function evaluations and slightly outperform the RLQNWB and RLQNWB-L, respectively.

Fig. 6

Comparison of $n_f$

Remark 51

Quite recently, Steck and Kanzow [19] proposed a similar regularized L-BFGS method that computes $(B_k + \mu I)^{-1}$ explicitly. They reported that their method outperforms the proposed RL-BFGS without line search because of $(B_k + \mu I)^{-1}$.

6 Conclusion

In this paper, we have proposed a combination of the L-BFGS and the regularization technique. We showed the global convergence under appropriate assumptions. We have also presented some efficient implementations. In numerical results, the overall comparison shows that the proposed method can solve more problems than the original L-BFGS. This result indicates that the proposed method is robust in terms of solving the number of problems.

For future work, we may consider the idea of Steck and Kanzow [19] with simultaneous use of line search for large-scale unconstrained optimization problems.