1 Introduction

A non-uniformly sampled-data (NUSD) system is one kind of general multi-rate sampled-data systems, in which the sampling intervals of the inputs and/or outputs are irregular. As the hardware limitation, environmental requirement and economic constraint, those systems are extensively used in industrial process [1,2,3,4]. Due to reflect the sampling characters and impact performance of control systems, NUSD systems have attracted much attention in recent years. For example, Jiang and Xie proposed iterative least squares/stochastic gradient methods [5,6,7] for NUSD CAR models. As single-innovation algorithms, the parameters estimation precision was low. To overcome influences of bad data and improve estimation precision, Ding presented a multi-innovation stochastic gradient algorithm, and also gave the convergence analysis [8]. However, the computational burden is large. Based on hierarchical identification principle, Liu reported a least squares algorithm to save computational cost [9]. Furthermore, the AM-MI-GESG and recursive least squares parameter estimation algorithm were developed for CARIMA and Box-Jenkins NUSD systems with colored noise, respectively [10, 11].

The nonlinear models are used to describe nonlinear systems, which exist extensively in industrial process. Commonly used nonlinear models are Hammerstein models, Wiener models and their combinations. Recently, the identification of these systems has attracted much research attention and many algorithms have introduced in the literature. For the nonlinear systems with polynomial nonlinearity, Bai proposed the iterative /recursive least square algorithm for Hammerstein systems [12]. An over-parameterization technique is introduced to deal with the identification of Hammerstein ARMAX, OE, OEMA systems, and some algorithms e.g. gradient-based, least square-based, auxiliary model based algorithm [13,14,15,16,17]. Moreover, the over-parameterization technique is extended to identify MISO Wiener system [18]. To reduce the computation, Ding studied the identification of these nonlinearity models, and presented several methods, e.g. projection methods, stochastic gradient algorithm, Newton strategy [19], hierarchical identification [20, 21], etc. Through the key term separation principle, Vörös studied the identification problems for the Hammerstein–Wiener models [22], Li et al. reported the maximum likelihood algorithm for Hammerstein and Wiener systems, respectively [23, 24]. Yu studied the identification of hard nonlinear systems with two-segment and dead-zone input nonlinearities [25, 26]. Voros studied modeling and parameter identification of systems with multi-segment piecewise-linear characteristics [27]. Based on the finite impulse response model and negative gradient search, Chen proposed stochastic gradient algorithm for identification of systems with preload nonlinearities [28]. Moreover, the estimation algorithm for Hammerstein systems with saturation and dead-zone nonlinearities was studied [29]. Ding studied the adaptive digital control of Hammerstein nonlinear systems with limited output sampling [30]. For the nonlinear dynamical adjustment models, Xiao proposed a parameter estimation algorithm [31]. And based on the Markov Chains, nonlinear stochastic systems with uncertainties and random delays modeled were studied [32]. However, most of the mentioned methods estimate the parameters of transformed models but the system models directly, which bring the burden computation meanwhile. What’s more, assumption of the polynomials with known orders restricts its application.

However, the above mentioned algorithms cannot be used directly to NUSDN systems. To solve this issue, Li proposed a least-squares-based iterative algorithm and the over-parameterization technique to estimate the parameters of Hammerstein systems with non-uniform sampling internal [33]. Furthermore, an auxiliary model-based recursive least-squares algorithm is derived under the constraints of causality to alleviate the computational burden [34]. However, achievements on the identification of NUSDN systems have so far been reported assumed that the nonlinear structure was known. To the best of our knowledge, few studies have addressed modeling and estimation issues for NUSDN systems with unknown nonlinear characters [35, 36].

Multi-model approach has its own advantages in model industrial processes, especially those with inherent nonlinearity, wide operating range or load disturbances [37]. Based on divide-and-conquer strategy, multi-model methods develop local linear models corresponding to typical operating regimes, and the global output is obtained by integration of local ones. As a major benefit of multi-model strategy, linear system theories can be used. It has been applied successfully in aviation industries [38], chemical industries [39, 40] and so on.

In this study, the multi-model method is extended to estimate the parameters of NUSDN systems. First, a discrete model of a NUSDN system is obtained by using the lifting technique. Second, on the basis of the multi-model method, a switching model is constructed. Then, a recursive least squares algorithm based on fuzzy c-mean (FCM) cluster is proposed to estimate the system structure and parameters simultaneously. The proposed algorithm is validated on a pH neutralization process.

The remainder of this paper is organized as follows. Sect. 2 depicts the NUSDN system and a model switching system is constructed to formulate it. Sect. 3 presents the derivation of the proposed algorithm. Sect. 4 provides the simulation of the pH neutralization and conclusions are summarized in Sect. 5.

2 Problem formulation

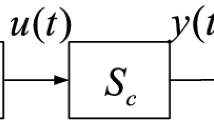
Consider a NUSDN system, as shown in Fig. 1.

Fig. 1
figure 1

Structure of NUSDN system

Full size image

where \(u(kT+t_{j-1} )\) and \(y(kT+T)\) are respectively the input and output of the system, u(t) and y(t) are respectively the input and output of the nonlinear part. \(H_\tau \) is a non-uniformly zero-order holder with irregularly sampled intervals \(\left\{ {\tau _1 ,\tau _2 ,\ldots ,\tau _m } \right\} \); The input updating frequency is set as \(kT+t_{j-1}, j=1,2,...,m\) (\(t_0 =0\), \(t_j :=\tau _1 +\tau _2 +...+\tau _j )\). \(S_c \) is a nonlinear dynamic block and \(S_T \) is a sampler with frame period \(T:=\tau _1 +\tau _2 +...+\tau _m =t_m \). By using the lifting technique, \(H_\tau \)is formulated as follows:

$$\begin{aligned} u(t)=\left\{ \begin{array}{l} u(kT),\,\,\,\,kT\le t<kT+t_1 \\ u(kT+t_1 ),\,\,\;kT+t_1 \le t<kT+t_2 \\ \,\,\vdots \,\,\qquad \qquad \qquad \qquad \,\,\vdots \\ u(kT+t_{m-1} ),\,\,kT+t_{m-1} \le t<kT+T \\ \end{array} \right. \end{aligned}$$
(1)

\(S_c \) is assumed as the state-space model of the nonlinear character

$$\begin{aligned} S_c :=\left\{ \begin{array}{l} {\dot{\mathbf{x }}}(t)=\Gamma (\mathbf{x}(t),u(t)) \\ y(t)=h(t) \\ \end{array} \right. \end{aligned}$$
(2)

where \(\mathbf{x}(t)\in R^{n}\) is the state vector, and \(y(t)\in R\) and \(u(t)\in R\) are the output and input of \(S_c \) respectively.

Fig. 2
figure 2

Schematic of model switching system

Full size image

2.1 Model switching systems

As a common form of multi-model, the local model networks (LMN) can be described as:

$$\begin{aligned} y(kT)=\sum _{q=1}^c {f_q (\phi (kT))} g_q (\varphi (kT)) \end{aligned}$$
(3)

where \(y(kT)\in R\) is the model output at time kT, and \(f_q (\cdot ),q=1,2,\ldots ,c\) are basis functions depend on the scheduling vector \(\phi (kT)\in R^{n_\phi }\); \(g_q (\cdot ),q=1,2,\ldots ,c\) are local models which rely on the information vector \(\varphi (kT)\in R^{n_\varphi }\). The number of local models is set as c. \(\phi (kT)\) and \(\varphi (kT)\) are defined as:

$$\begin{aligned} \begin{array}{ll} &{}\varphi (kT):=[-y(kT-T),-y(kT-2T),\ldots ,\\ &{}-y(kT-n_a T),\\ &{} u(kT),u(kT-T),\ldots , \\ &{}u(kT-n_b T),\,\,u(kT-T+t_1 ),\ldots ,u(kT-n_b T+t_1),\\ &{} \ldots ,u(kT-T+t_{m-1} ), \\ &{}\ldots ,u(kT-n_b T+t_{m-1} )]^{T}\in R^{n_\varphi },n_\varphi =n_a +mn_b +1 \\ \end{array}\nonumber \\ \end{aligned}$$
(4)
$$\begin{aligned} \begin{array}{ll} &{}\phi (kT):=[-y(kT-T),-y(kT-2T),\ldots ,\\ &{}-y(kT-n_{a_\phi } T),\\ &{}u(kT),u(kT-T),\ldots ,u(kT-n_{b_\phi } T), \\ &{}u(kT-T+t_1 ),\ldots ,u(kT-n_{b_\phi } T+t_1 ),\ldots ,\\ &{}u(kT-T+t_{m-1} ),\ldots ,u(kT-n_{b_\phi } T+t_{m-1} )]^{T}\\ &{}\in R^{n_\phi },n_\phi =n_{a_\phi } +mn_{b_\phi } +1 \\ \end{array} \end{aligned}$$
(5)

where \(n_a ,n_b \) are respectively the orders of output and input, satisfy \(0\le n_{a_\phi } \le n_a, 0\le n_{b_\phi } \le n_b\).

In theory, \(\phi (kT)\) can be taken as any functions effective in a local area. Here, the Gaussion bell is chosen:

$$\begin{aligned} \tilde{f}_q (\phi (kT))=\left( \exp \left( -\frac{(\phi (kT)-\hbar _q )^{T}(\phi (kT)-\hbar _q )}{s^{T}s}\right) \right) ^{\alpha }\nonumber \\ \end{aligned}$$
(6)

where \(\hbar _q \) and s are the center vector and width of the bell, \(\alpha \) satisfies\(1\le \alpha <\infty \). Upon normalizing Eq. (3), the LMN can be rewritten as

$$\begin{aligned} y(kT)=\sum _{q=1}^c {\left( \frac{\left( \exp (-\frac{(\phi (kT)-\hbar _q )^{T}(\phi (kT)-\hbar _q )}{s^{T}s})\right) ^{\alpha }}{\sum _{d=1}^c {\left( \exp \left( -\frac{(\phi (kT)-\hbar _d )^{T}(\phi (kT)-\hbar _d )}{s^{T}s}\right) \right) ^{\alpha }} } \cdot g_q [\varphi (kT)]\right) }\nonumber \\ \end{aligned}$$
(7)

Particularly, when \(\alpha =\infty \), Eq. (7) is described as

$$\begin{aligned} y(kT)=g_q (\varphi (kT)) \end{aligned}$$
(8)

where \(q=\arg \mathop {\min }\limits _{t=1,2,\ldots ,c} (\phi (kT)-\hbar _t )^{T}(\phi (kT)-\hbar _t )\).

It can be seen that LMN multi-model is depicted as the \(q^{th}\) local model whose center vector \(\hbar _t \) is nearest to \(\phi (kT)\). And q will switch with time changing. Therefore, Eq. (8) can also be called model switching system shown in Fig. 2. It can be expressed as another form as:

$$\begin{aligned}&R^{q}: \,\,if\,\,\phi (kT)\,\,is\,\,F_q \,\,then \,\,y(kT)=g_q [\varphi (kT)], \nonumber \\&k=1,2,\ldots ,N;\,\,q=1,2,\ldots ,c \end{aligned}$$
(9)

where \(F_q \) is scope of the \(q^{th}\) local model.

2.2 Local models

A nonlinear system can be seen as the combination of local models under a given condition. \(P^{q}\) is assumed as the state-space model of the \(q^{th}\) local model

$$\begin{aligned} P^{q}:=\left\{ {\begin{array}{l} {\dot{\mathbf{x }}}(t)=\mathbf{A }^{q}\mathbf{x }(t)+\mathbf{B }^{q}u(t) \\ y(t)=\mathbf{C }^{q}x(t)+D^{q}u(t) \\ \end{array}} \right. \end{aligned}$$
(10)

where \(\mathbf{A}^{q}\in R^{n\times n},\mathbf{B}^{q}\in R^{n},\mathbf{C}^{q}\in R^{1\times n},D^{q}\in R\) are parameter matrices. Upon Discretizing Eq. (10) with the frame period T [41], the \(q^{th}\) local model can be written as

$$\begin{aligned}&y(kT){=}\frac{\sum \limits _{j=1}^m {B_j^q (z^{-1})}}{A^{q}(z^{-1})}u(kT{+}t_{j-1}) {=}[1-A^{q}(z^{-1})]y(kT)\nonumber \\&+\sum _{j=1}^m {B_j^q (z^{-1})} u(kT+t_{j-1} )=g_q (\phi (kT)) \end{aligned}$$
(11)

with

$$\begin{aligned} A^{q}(z^{-1})=1+a_{q1} z^{-1}+a_{q2} z^{-2}+...+a_{qn_a } z^{-n_a } \end{aligned}$$
$$\begin{aligned} B_1^q (z^{-1})=b_{q10} +b_{q11} z^{-1}+...+b_{q1n_b } z^{-n_b } \end{aligned}$$
$$\begin{aligned}&B_j^q (z^{-1})=b_{qj1} z^{-1}+b_{qj2} z^{-2}+...+b_{qjn_b } z^{-n_b },\\&\quad j=2,3,\cdots ,m \end{aligned}$$

where \(z^{-1}\) is the backward shift operator: i.e. \(z^{-1}x(kT)=x(kT-T)\). Define the \(q^{th}\) local model parameter \(\varvec{\theta }_q \) as

$$\begin{aligned}&\varvec{\theta }_q :=[a_{q1} ,a_{q2} ,\ldots ,a_{qn_a } ,b_{q10} ,b_{q11} ,\ldots b_{q1n_b } ,b_{q21} ,\ldots ,\\&b_{q2n_b } ,\ldots ,b_{qm1} ,\ldots ,b_{qmn_b } ]^{T}\in R^{n_\varphi } \end{aligned}$$

The write noise is introduced, then Eq. (11) is rewritten as

$$\begin{aligned} y(kT)=g_q (\varphi (kT))+v(kT)=\varphi (kT)\varvec{\theta }_q +v(kT) \end{aligned}$$
(12)

where \(q=\arg {\min }_{t=1,2,\ldots ,c} (\phi (kT)- \hbar _t)^{T}(\phi (kT)-\hbar _t)\). Then, the system parameter vector \(\varvec{\theta }\) is formed

$$\begin{aligned} \varvec{\theta }:=[\varvec{\theta }_1^T ,\varvec{\theta }_2^T ,\ldots ,\varvec{\theta }_c^T ]^{T}\in R^{cn_\phi } \end{aligned}$$

3 Muti-model recursive least squares algorithm based on fuzzy c-mean cluster (FCM-MRLS)

The task of the identification is to determine \(c,\hbar _q ,s_q \) and \(\varvec{\theta }_q \) in Eq. (12). To alleviate the computational cost, the estimation is divided into two simple sub-tasks. First, for a given number of c, \(\hbar _q ,s_q \) can be determined by using FCM clustering algorithm, and \(\varvec{\varphi }(kT)\) is classified into c sets simultaneously. Then \(\varvec{\theta }_q \) can be estimated by using multi-mode recursive least squares algorithm.

3.1 Structure identification based on FCM

Set \(\mathbf{U}=[\mu _{i,k} ]_{c\times N} \) and \(\mathrm{\mathbf{{H}}}=[\hbar _1 ,\hbar _2 ,\ldots ,\hbar _c ]\) are separately the membership matrix and cluster centers matrix. Given the information vector \(\varvec{\Phi }=\{\phi (1),\phi (2),\ldots ,\phi (N)\}\), and a fuzziness parameter \(w\in (1,\infty )\) (usually \(w=2)\), FCM clustering algorithm aims to minimize the cost function

$$\begin{aligned} J(\mathbf{U},\mathrm{\mathbf{{H}}},\varvec{\Phi })=\sum _{q=1}^c {\sum _{k=1}^N {\mu _{q,k}^w ||\phi (kT)-\hbar _q ||^{2}} } \end{aligned}$$
(13)

where \(||\cdot ||\) is the vector norm. When c is known, FCM can be optimized by an alternating optimization (AO) algorithm [42] with the cluster centers which are randomly initialized as \(\mathbf{\mathrm{H}}^{(0)}\). After clustering, \(\mathbf{U}\) and \(\mathbf{\mathrm{H}}\) are obtained. Then, \(s_q \) is determined using a nearest neighbor heuristic method:

$$\begin{aligned} s_q =\left[ \frac{1}{p}\sum _{l=1}^p {(c_q -c_l )^{T}(c_q -c_l )} \right] ^{1/2},\,\, q=1,2,\ldots ,c \end{aligned}$$

where \(c_l (l=1,2,\ldots ,p)\) are the \(l^{th}\) nearest neighbors of \(c_q \), p is the number of the \(q^{th}\) nearest neighbors.

3.2 Parameters identification based on multi-model recursive least squares algorithm

By using the FCM Clustering algorithm, \(c,\hbar _q ,\mu _{q,k} \) are determined. Then, based on \(\phi (kT)\), the global model is obtained with local models switching, formulated as:

$$\begin{aligned} \begin{array}{l} y(kT)=g_q [\varphi (kT)]\,\,\,\,if \,\,q\\ =\arg \min \limits _{t=1,2,\ldots ,c} (\phi (kT)-\hbar _t )^{T}(\phi (kT)-\hbar _t )\\ k=1,2,\ldots ,N \,\, q=1,2,\ldots ,c \\ \end{array} \end{aligned}$$

and

$$\begin{aligned} \varphi (kT)\in F_q \,\,if\,\,\mu _{q,k} =\mathop {\max }\limits _{1\le t\le c} \{\mu _{t,k} \} \end{aligned}$$

The \(q^{th}\) local model is identified based on \(\phi (kT)\) which belongs to the \(q^{th}\) cluster. Then, a FCM-MRLS algorithm is proposed to identify \(\varvec{\theta }_q \)

$$\begin{aligned}&{\varvec{\hat{\theta }}}_q (kT)={\varvec{\hat{\theta }}}_q (kT-T)+\mathbf{L}_q (kT)[y(kT)\nonumber \\&\quad -\varvec{\varphi }^{T}(kT){\varvec{ \hat{\theta }}}_q (kT-T)]\end{aligned}$$
(14)
$$\begin{aligned}&\mathbf{L}_q (kT)=\mathbf{P}_q(kT-T)\varvec{\varphi }(kT)\nonumber \\&\quad [1+\varvec{\varphi }^{T}(kT)\mathbf{P}_q(kT-T)\varvec{\varphi }(kT)]^{-1} \end{aligned}$$
(15)
$$\begin{aligned}&\mathbf{P}_q (kT)=[\mathbf{I}-\mathbf{L}_q (kT)\varvec{\varphi }^{T}(kT)]\mathbf{P}_q (kT-T) \end{aligned}$$
(16)

where \({\varvec{\hat{\theta }}}_q (kT)\) is the estimate of \(\varvec{\theta }_q \) at time kT, \(\mathbf{I}\) is an identity matrix, and \(\mathbf{P}_q (kT)\) is covariance matrix.

The proposed FCM-MRLS algorithm is summarized as follows:

Step 1: Let c,\(\mathbf{\mathrm{H}}^{(0)}\) and \(k=1\), and set \({\varvec{\hat{\theta }}}(0)\) and \(\mathbf{P}(0)\) as

$$\begin{aligned} {\varvec{\hat{\theta }}}(0)=\mathbf{1}/p_0 ,\mathbf{P}(0)=p_0 \mathbf{1}, \end{aligned}$$

where \(\mathbf{1}\) is a column vector with appropriate dimension, whose entries are all 1, and \(p_0 =10^{6}\).

Step 2: Collect \(\{u(kT+t_{j-1} ),y(kT):j=1,2,\ldots ,m;k=1,2,\ldots ,N\}\), construct \(\varphi (kT)\) and \(\phi (kT)\) using Eqs.(4) and (5), separately. After FCM clustering, \(\hbar _q ,\mu _{q,k} ,q=1,2,\ldots ,ck=1,2,\ldots ,N\) are obtained, and \(\varphi (kT)\) is separated into c clusters, the data length \(num_q \) of each cluster is determined as well.

Step 3: Based on the data sets of c clusters, \(\hat{{\theta }}_q (kT),q=1,2,\ldots ,ck=1,2,\ldots ,num_q \) is identified using Eqs.(14),(15), (16).

Once \({\varvec{\hat{\theta }}}_q (kT),q=1,2,\ldots ,c\) is identified, \(\varvec{\theta }(kT)\) is obtained.

The flow chart of FCM-MRLS algorithm is shown in Fig. 3.

Fig. 3
figure 3

Flow chart of FCM-MRLS algorithm

Full size image

4 Case study

4.1 System description

Consider a pH neutralization process as shown in Fig. 4. Taken HNO\(_{3}\), NaOH, NaHCO\(_{3}\) as the reaction streams and pH-measurement as the output variable. Let \(F_a ,F_b ,F_c \) be flow rates of the three streams, respectively.

Fig. 4
figure 4

pH neutralization process

Full size image
Table 1 System operating parameters
Full size table
Table 2 Parameters estimates of six local models
Full size table
Fig. 5
figure 5

Comparison between true value and estimates of pH neutralization process

Full size image
Fig. 6
figure 6

Errors of FCM-MRLS algorithm

Full size image

A dynamical model of pH neutralization process is depicted as follows:

$$\begin{aligned} V\frac{dw_a }{dt}=F_a C_a -(F_a +F_b )w_a \end{aligned}$$
(17)
$$\begin{aligned} V\frac{dw_b }{dt}=F_b C_b -(F_a +F_b )w_b \end{aligned}$$
(18)

where \(C_a ,C_b \) respectively are the concentration of HNO\(_{3}\) and NaOH. V is the volume of the reactor. \(w_a ,w_b \) are respectively charge invariant and material invariant, defined as:

$$\begin{aligned} w_a =\text {[}H^{+}\text {]}-\text {[}OH^{-}\text {]}-\text {[}HCO_3^- \text {]}-2\text {[}CO_3^{2-} \text {]} \end{aligned}$$
$$\begin{aligned} w_b =\text {[}H_2 CO_3 \text {]}+\text {[}HCO_3^- \text {]}+\text {[}CO_3^{2-} \text {]} \end{aligned}$$

Let \(pK_a =-\log _{10} K_a \), where \(K_a =1.76\times 10^{-5}\) is the ionized constant of HNO\(_{3}\). Then, the static titration curve function is derived as:

$$\begin{aligned} w_b +10^{-pH}-10^{pH-14}-\frac{w_a }{1+10^{pK_a -pH}}=0 \end{aligned}$$
(19)

Equation (19) reflects the severe nonlinear of pH neutralization process.

4.2 Multi-model formulation

Considered a neutralization process of strong base-weak acid expressed as Eqs.(17), (18) ,(19). For a given \(F_a \), \(F_b \) and pH-measurement are respectively taken as the input \(u(kT+t_{j-1} )\) and output \(y_{pH} \). System operating parameters are shown in Table 1.

The sample sets \(\{F_b ,y_{pH} \}\) were gained from the mechanism model Eqs.(17), (18), (19). Then, 180 samples were obtained with a variation from −51.5 to 51.5 into \(F_b \). Set \(m=2,\tau _1 =0.5s,\tau _2 =1s\), then, \(t_0 =0s,t_1 =\tau _1 =0.5s\), \(t_2 =\tau _1 +\tau _2 =1.5s=T\), \(n_a =2,n_b =2\). In this case, u(kT) and \(u(kT+t_1 )\) were taken from the data sequence of \(F_b \), and y(kT) was got from \(y_{pH} \). After non-uniformly sampled, the data sets \(\{u(kT),u(kT+t_1 ),y(kT)\},k=1,2,\ldots 60\) were determined. \(\phi (kT)\) was chosen as

$$\begin{aligned} \begin{array}{ll} \phi (kT)=[-y(kT-T),-y(kT-2T),u(kT)&{},u(kT-T),\\ &{}u(kT-2T), \\ u(kT-T+t_1 ),u(kT-2T+t_1 )]^{T}&{} \\ \end{array} \end{aligned}$$

Set \(c=6\). Then, \(\varvec{\theta }_q ,q=1,2,\ldots ,c\)were identified using FCM-MRLS algorithm. The estimates were shown in Table 2, and the comparison between true value and estimates was presented in Fig. 4.

Fig. 7
figure 7

Local model of each sample

Full size image

In Fig. 5, the sampled data (black solid line) and estimates (blue dot-solid line) were shown in Fig. 5. The root mean square error (RMSE) was introduced to evaluate the performance of proposed algorithm, defined as [43]

RMSE of the pH identification is 0.0085, and the errors were depicted in Fig. 6. After FCM clustering, the local model of each sample was shown in Fig. 7.

It could be seen that the FCM-MRLS algorithm gave a good fit for pH-measurement and had captured the nonlinearity presented in the neutralization process.

5 Conclusions

Combining with the lifting technique and FCM clustering method, a Multi-model based RLS identification algorithm is derived for NUSDN systems. Simulation results demonstrate the effectiveness of the proposed algorithm. The identification of the local models does not limit to RLS only. With proper modification, other algorithm to estimate linear systems can also be applied to NUSDN systems. The method can also be extended to other signal-rate nonlinear systems, multi-rate nonlinear systems and MIMONUSDN systems and so on. However, the performance analysis of the FCM-MRLS algorithm needs further investigation.